Photon-Added Deformed Peremolov Coherent States and Quantum Entanglement
Abstract
1. Introduction
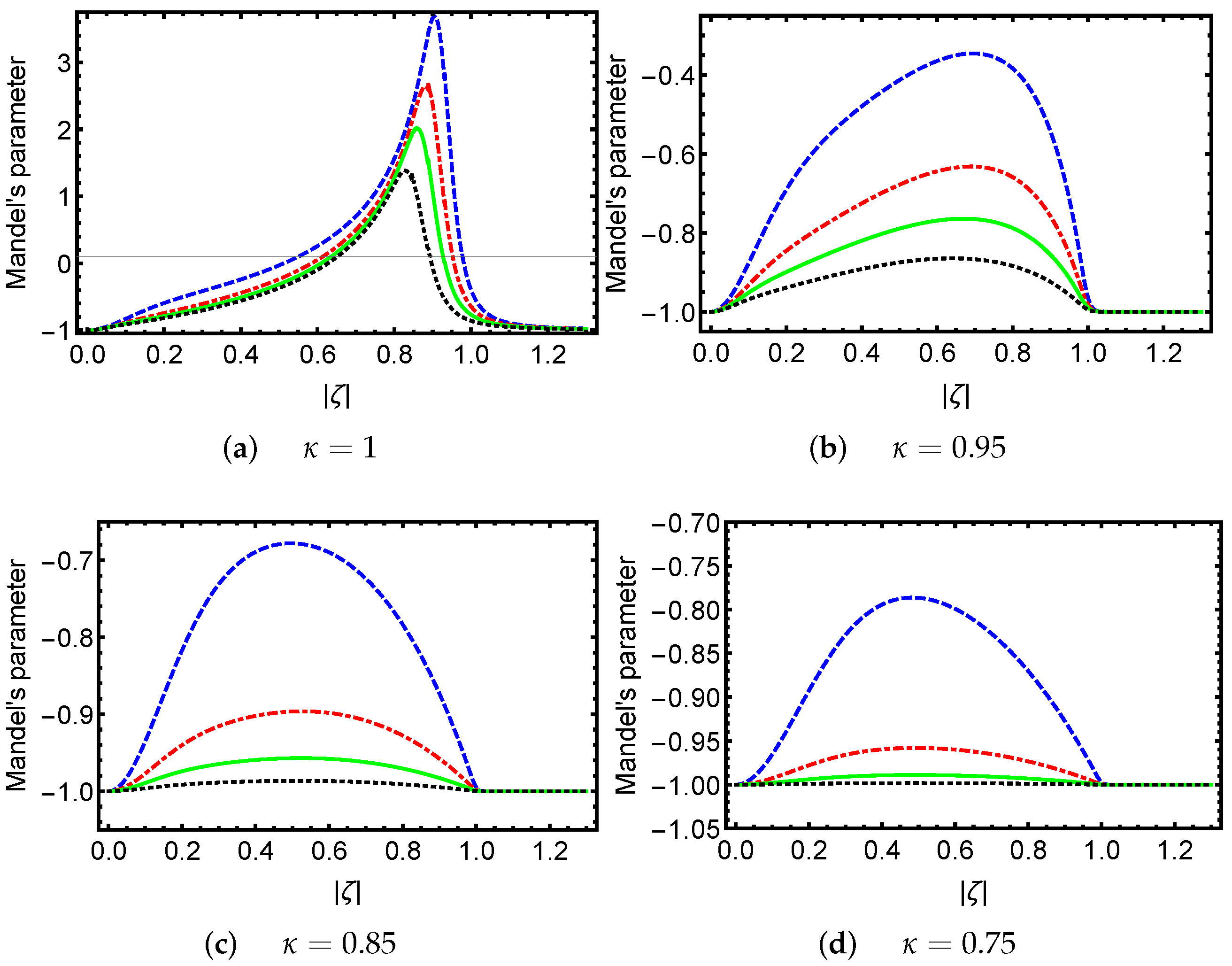
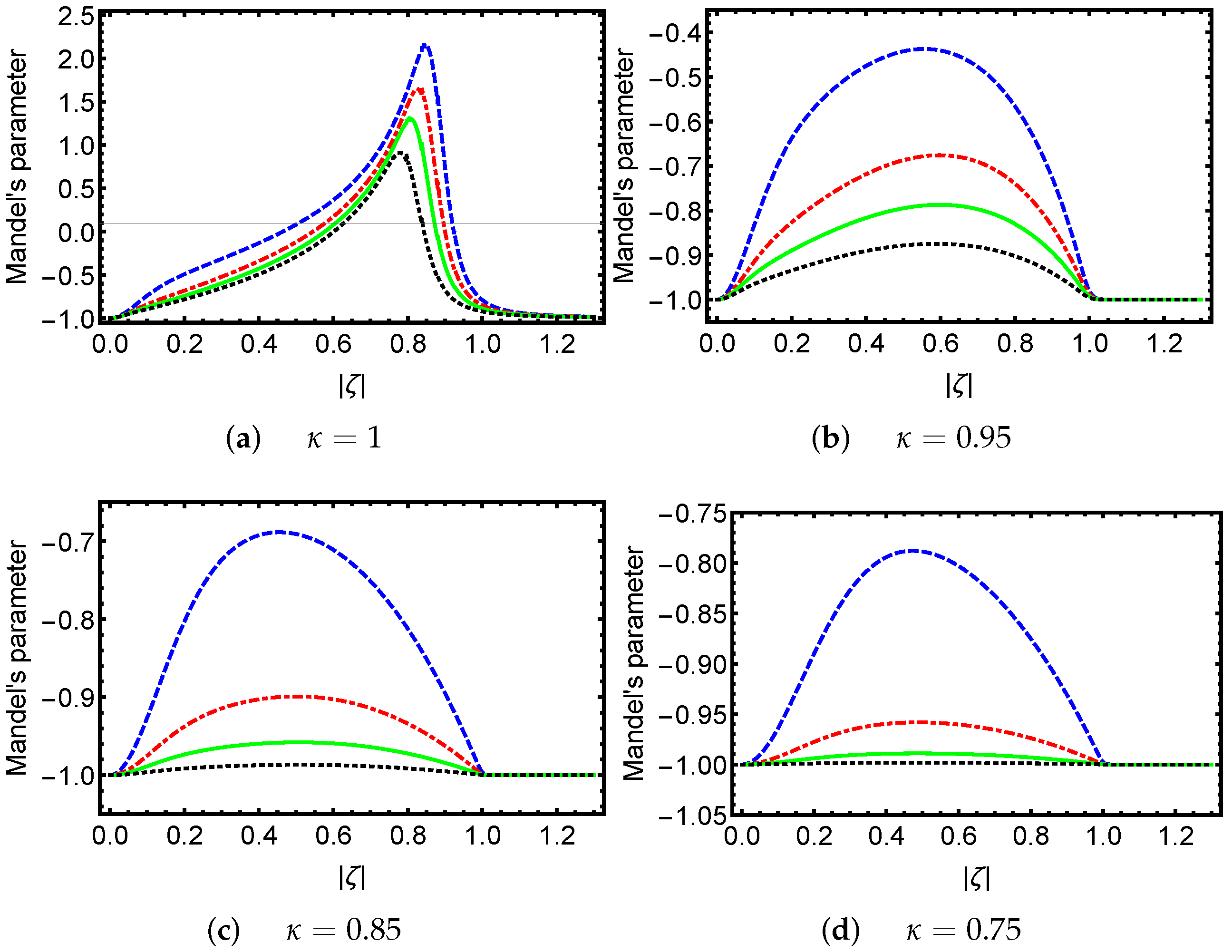
2. PA-DPCSs and Statistical Properties
- (a)
- Normalization conditionwhere represents the amplitude of the coherent state.
- (b)
- Continuity property
- (c)
- Resolution of the unity operatorwhere represents the measure in the label space.
3. Generation of the PA-DPCS
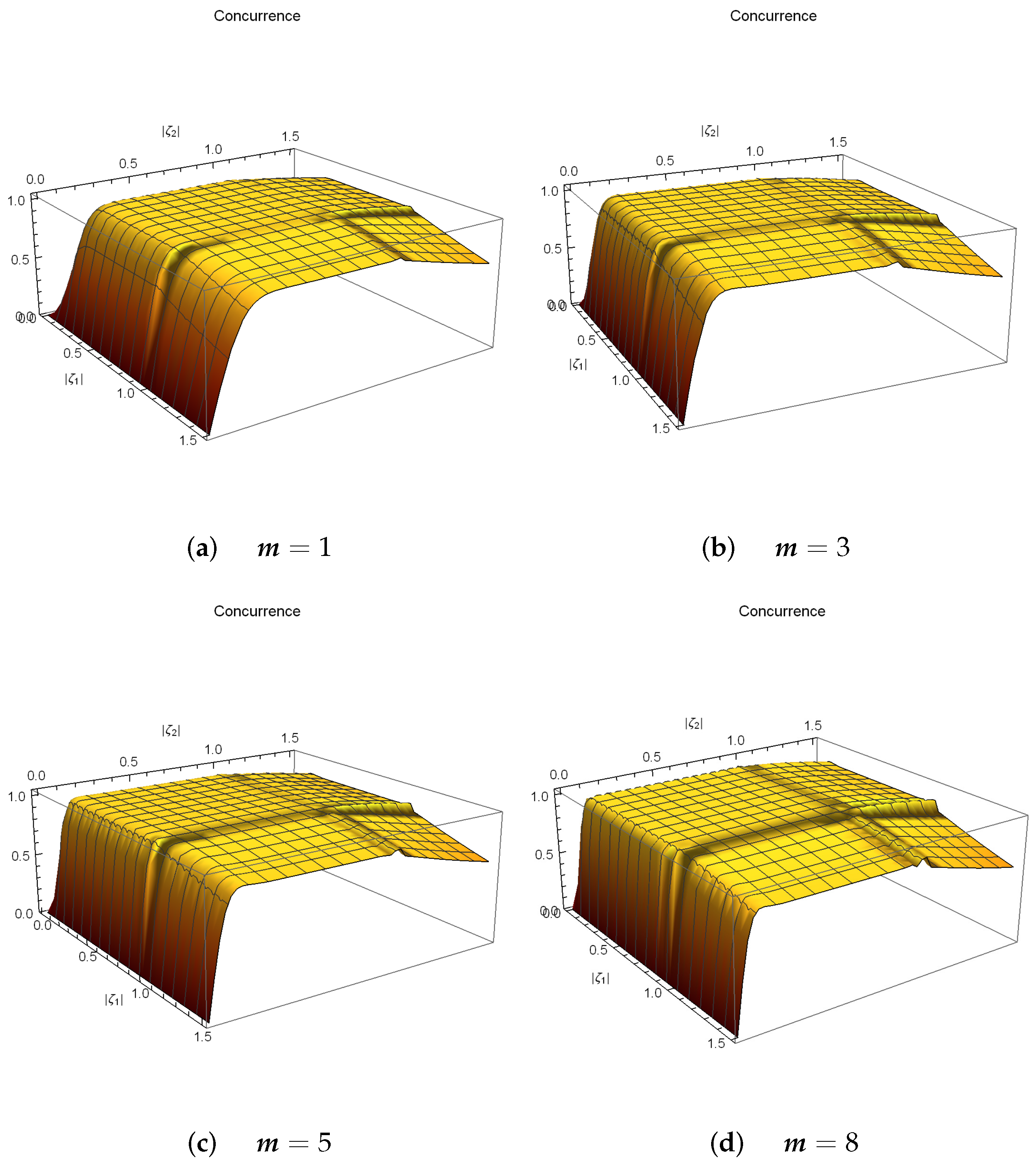
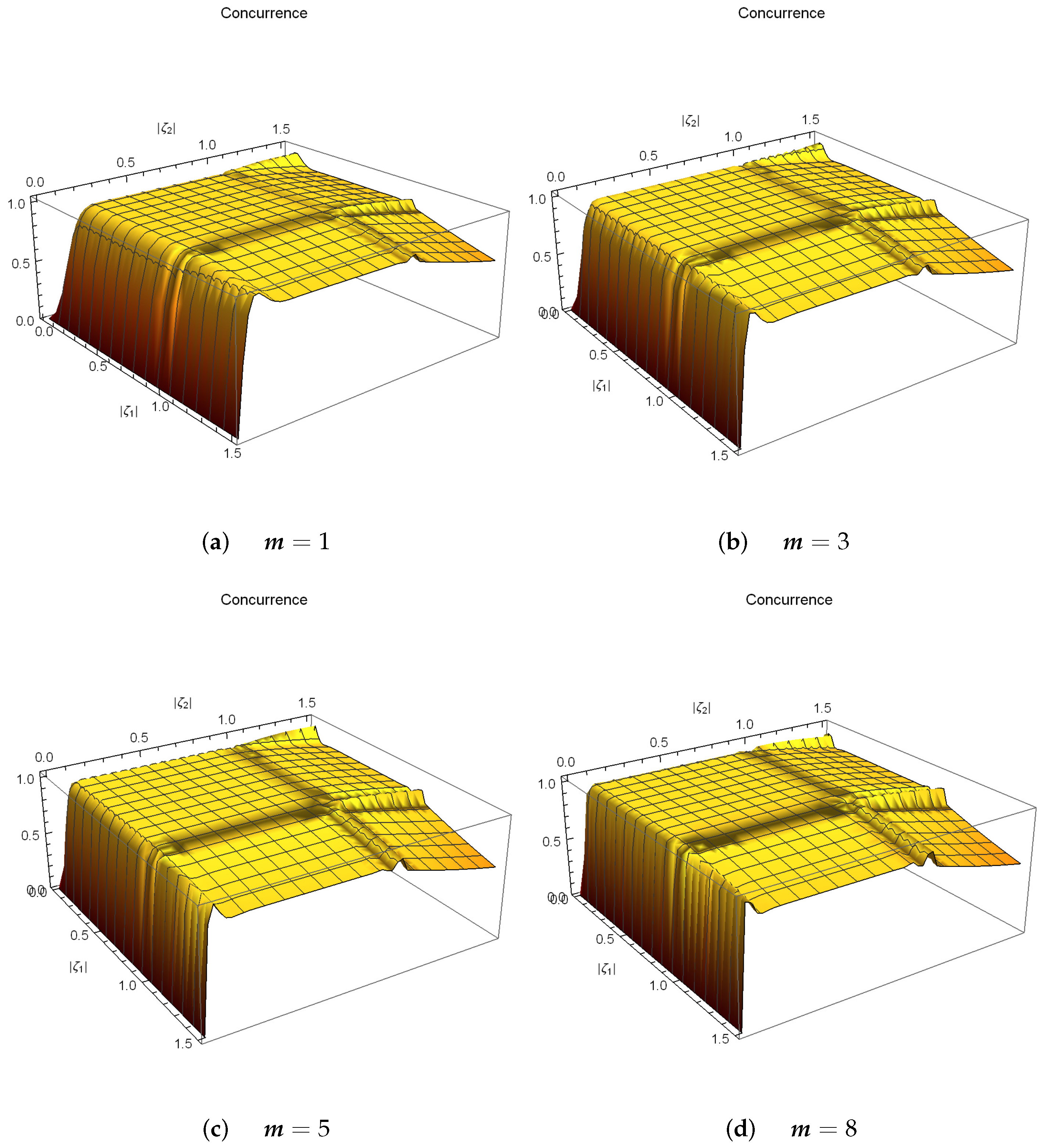
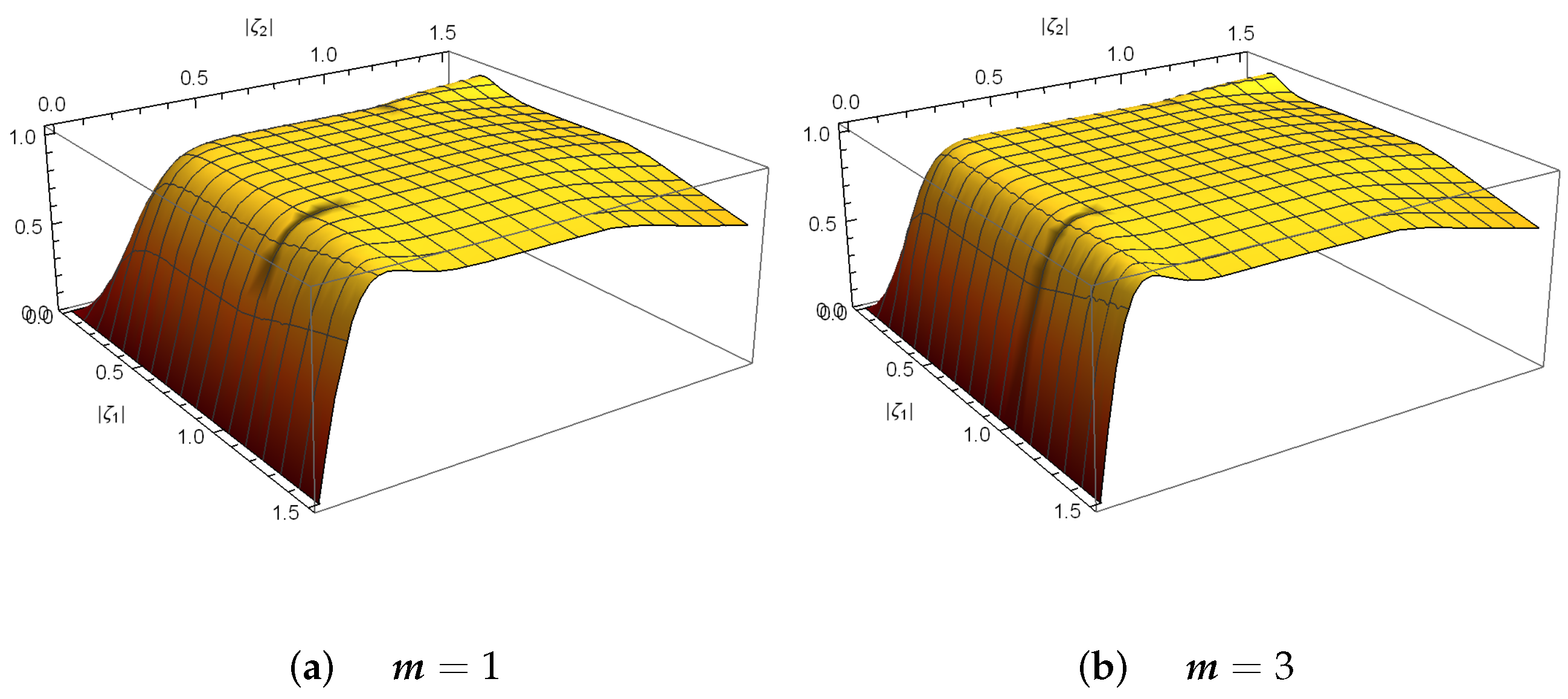
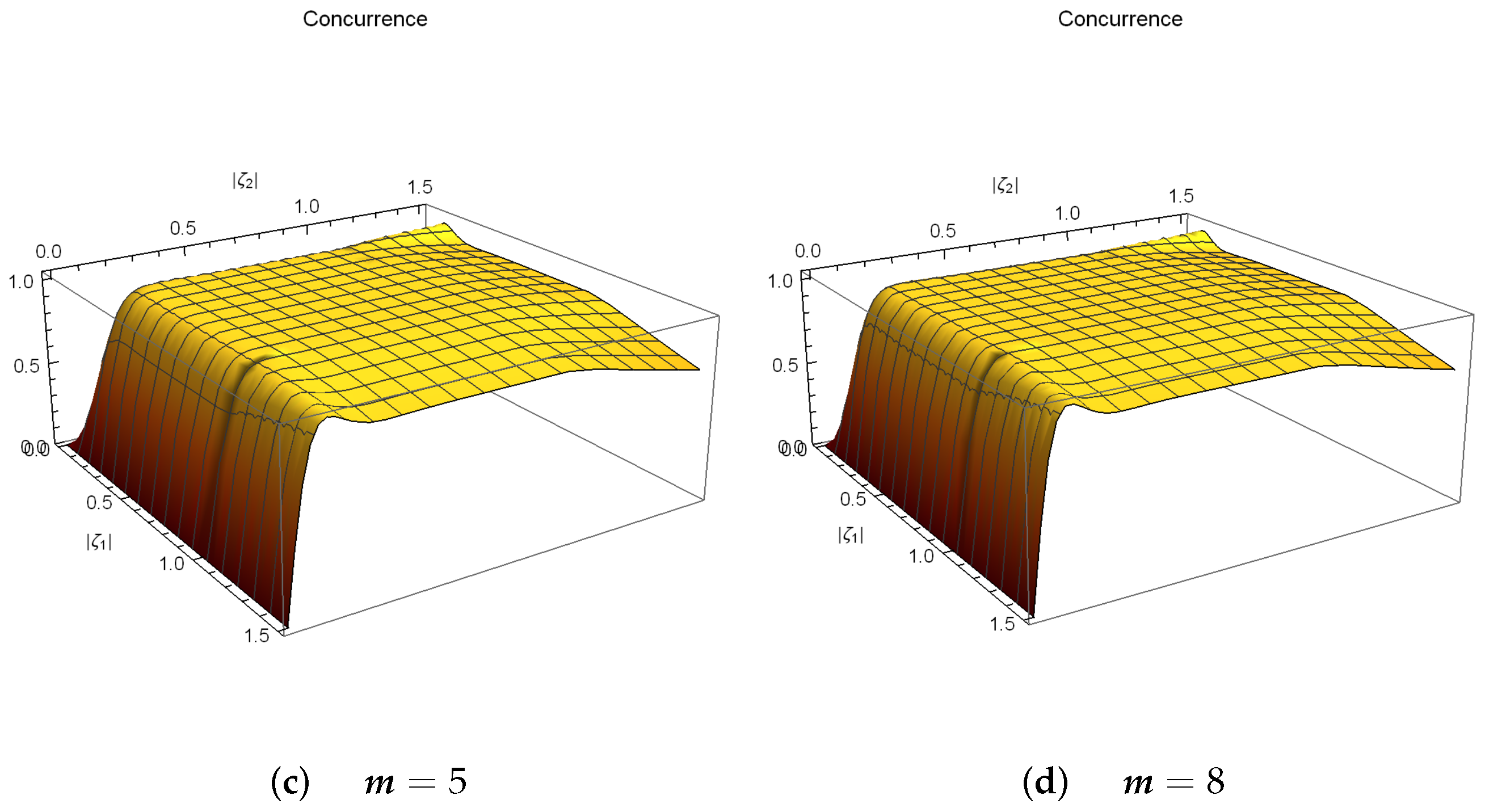
4. Entangled PA-DPCSs
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Klauder, J.R.; Skagerstam, B. Coherent States: Applications in Physics and Mathematical Physics; World Scientific: Singapore, 1985. [Google Scholar]
- Inomata, A.; Kuratsuji, H.; Gerry, C. Path Integrals and Coherent States of SU(2) and SU(1,1); World Scientific: Singapore, 1992. [Google Scholar]
- Flouris, K.; Jimenez, M.M.; Herrmann, H.J. Curvature-induced quantum spin-Hall effect on a Möbius strip. Phys. Rev. B 2022, 105, 235122. [Google Scholar] [CrossRef]
- Schrödinger, E. Der stetige Übergang von der Mikro-zur Makromechanik. Sci. Nat. 1926, 14, 664. [Google Scholar] [CrossRef]
- Glauber, R. The quantum theory of optical coherence. Phys. Rev. 1963, 130, 2529. [Google Scholar] [CrossRef]
- Glauber, R. Coherent and incoherent states of radiation field. J. Phys. Rev. 1963, 131, 2766. [Google Scholar] [CrossRef]
- Klauder, J.R. Continuous representation theory.I. Postulates of continuous representation theory. J. Math. Phys. 1963, 4, 1055. [Google Scholar] [CrossRef]
- Klauder, J.R. Generalized relation between quantum and classical dynamics. J. Math. Phys. 1963, 4, 1058. [Google Scholar] [CrossRef]
- Klauder, J.R.; Skagertan, B.-S. Coherent States; World Scientifique: Singapore, 1985. [Google Scholar]
- Perelomov, A.M. Generalized Coherent States and Their Applications; Springer: Berlin, Germany, 1986. [Google Scholar]
- Ali, S.T.; Antoine, J.-P.; Gazeau, J.-P. Coherent States, Wavelets and Their Generalizations; Springer: New York, NY, USA, 2000. [Google Scholar]
- Perelomov, A.M. Coherent states for arbitrary Lie group. Commun. Math. Phys. 1972, 26, 222. [Google Scholar] [CrossRef]
- Gilmore, R. Geometry of symmetrized states. Ann. Phys. 1972, 74, 391. [Google Scholar] [CrossRef]
- Drinfeld, V.G. Quantum Groups. In Proceedings of the 1986 International Congress of Mathematicians, Berkeley, CA, USA, 3–11 August 1986; American Mathematical Society: Providence, RI, USA, 1987; p. 798. [Google Scholar]
- Jimbo, M. A q-difference analogue of U(g) and the Yang-Baxter equation. Lett. Math. Phys. 1985, 10, 63. [Google Scholar] [CrossRef]
- Jurčo, B. On coherent states for the simplest quantum groups. Lett. Math. Phys. 1991, 21, 51. [Google Scholar] [CrossRef]
- Ellinas, D. Path integrals for quantum algebras and the classical limit. J. Phys. 1993, A26, L543. [Google Scholar] [CrossRef][Green Version]
- Schrödinger, E. Discussion of probability relations between separated systems. Proc. Cambridge Philos. Soc. 1935, 31, 555. [Google Scholar] [CrossRef]
- Einstein, A.; Podolsky, B.; Rosen, N. Can quantummechanical description of physical reality be considered complete? Phys. Rev. 1935, 47, 777. [Google Scholar] [CrossRef]
- Bell, J.S. On the Einstein–Podolsky-Rosen paradox. Physics 1964, 1, 195. [Google Scholar] [CrossRef]
- Aspect, A.; Grangier, P.; Roger, G. Experimental Tests of Realistic Local Theories via Bell’s Theorem. Phys. Rev. Lett. 1981, 47, 460. [Google Scholar] [CrossRef]
- Hensen, B.; Bernien, H.; Dréau, A.E.; Reiserer, A.; Kalb, N.; Blok, M.S.; Ruitenberg, J.; Vermeulen, R.F.L.; Schouten, R.N.; Abellán, C.; et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 2015, 526, 682. [Google Scholar] [CrossRef] [PubMed]
- Giustina, M.; Versteegh, M.; Wengerowsky, S.; Handsteiner, J.; Hochrainer, A.; Phelan, K.; Steinlechner, F.; Kofler, J.; Larsson, J.; Abellán, C.; et al. Significant-Loophole-Free Test of Bell’s Theorem with Entangled Photons. Phys. Rev. Lett. 2015, 115, 250401. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Wiesner, S.J. Communication via One and Two-Particle Operators on Einstein–Podolsky-Rosen States. Phys. Rev. Lett. 1992, 69, 2881. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an Unknown Quantum State via Dual Classical and Einstein–Podolsky-Rosen Channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G. Quantum cryptography: Public key distribution and coin tossing. In Proceedings of the IEEE International Conference on Computers Systems and Signal Processing, Bangalore, India, 10–12 December 1984; IEEE: New York, NY, USA, 1984; pp. 175–179. [Google Scholar]
- Qi, X.-L. Does gravity come from quantum information? Nat. Phys. 2018, 14, 984. [Google Scholar] [CrossRef]
- Amico, L.; Fazio, R.; Osterloh, A.; Vedral, V. Entanglement in many-body systems. Rev. Mod. Phys. 2008, 80, 517. [Google Scholar] [CrossRef]
- Agarwal, G.S.; Tara, K. Nonclassical properties of states generated by the excitations on a coherent state. Phys. Rev. A 1991, 43, 492. [Google Scholar] [CrossRef]
- Dodonov, V.V.; Marchiolli, M.A.; Korennoy, Y.A.; Man’ko, V.I.; Mouchin, Y.A. Dynamical squeezing of photon-added coherent states. Phys. Rev. A 1998, 58, 4087. [Google Scholar] [CrossRef]
- Popov, D. Photon-added Barut—Girardello coherent states of the pseudoharmonic oscillator. J. Phys. A Math. Gen. 2002, 35, 7205. [Google Scholar] [CrossRef]
- Bellini, M.; Coelho, A.S.; Filippov, S.N.; Man’ko, V.I.; Zavatta, A. Towards higher precision and operational use of optical homodyne tomograms. Phys. Rev. A 2012, 85, 052129. [Google Scholar] [CrossRef]
- Berrada, K. Construction of photon-added spin coherent states and their statistical properties. J. Math. Phys. 2015, 56, 072104. [Google Scholar] [CrossRef]
- Sixdeniers, J.-M.; Penson, K.A. On the completeness of photon-added coherent states. J. Phys. A Math. Gen. 2001, 34, 2859. [Google Scholar] [CrossRef]
- Safaeian, O.; Tavassoly, M.K. Deformed photon-added nonlinear coherent states and their non-classical properties. J. Phys. A Math. Theor. 2011, 44, 225301. [Google Scholar] [CrossRef]
- Dehghani, A.; Mojaveri, B.; Amiri Faseghandis, S. Photon added coherent states of the parity deformed oscillator. Mod. Phys. Lett. 2019, 34, 1950104. [Google Scholar] [CrossRef]
- Mojaveri, B.; Dehghani, A. Generation of photon-added coherent states via photon-subtracted generalised coherent states. Eur. Phys. J. 2014, 68, 315. [Google Scholar] [CrossRef]
- Usha Devi, A.R.; Prabhu, R.; Uma, M.S. Non-classicality of photon added coherent and thermal radiations. Eur. Phys. J.-At. Mol. Opt. Plasma Phys. 2006, 40, 133. [Google Scholar] [CrossRef]
- Dehghani, A.; Mojaveri, B.; Jafarzadeh Bahrbeig, R.; Vaez, M. Photon-added entangled Barut–Girardello coherent states: Non-classicality and generation. Eur. Phys. J. Plus 2020, 135, 258. [Google Scholar] [CrossRef]
- Arik, M.; Coon, D.D. Hilbert spaces of analytic functions and generalized coherent states. J. Math. Phys. 1976, 17, 524. [Google Scholar] [CrossRef]
- Perelomov, A.M. On the completeness of some subsystems of q-deformed coherent states. Helv. Phys. Acta 1996, 68, 554. [Google Scholar]
- Chakrabarti, R.; Jagannathan, R. A (p,q)-oscillator realization of two-parameter quantum algebras. J. Phys. 1991, A24, L711. [Google Scholar] [CrossRef]
- Chakrabarti, R.; Vasan, S. On completeness of Barut-Girardello coherent states of suq(1, 1) algebra. J. Phys. A Math. Gen. 2004, 37, 10561. [Google Scholar] [CrossRef]
- Gasper, G.; Rahman, M. Basic Hypergeometric Series. In Encyclopedia of Mathematics and Its applications, 35; Cambridge University Press: New York, NY, USA, 2011. [Google Scholar]
- El Baz, M.; Hassouni, Y.; Madouri, F. New construction of coherent states for generalized harmonic oscillators. Rep. Math. Phys. 2002, 50, 263. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Hillery, M.; Zubairy, M.S. Entanglement Conditions for Two-Mode States. Phys. Rev. Lett. 2006, 96, 050503. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of Formation and Concurrence. Quantum Inf. Comput. 2001, 1, 27. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berrada, K. Photon-Added Deformed Peremolov Coherent States and Quantum Entanglement. Axioms 2024, 13, 289. https://doi.org/10.3390/axioms13050289
Berrada K. Photon-Added Deformed Peremolov Coherent States and Quantum Entanglement. Axioms. 2024; 13(5):289. https://doi.org/10.3390/axioms13050289
Chicago/Turabian StyleBerrada, Kamal. 2024. "Photon-Added Deformed Peremolov Coherent States and Quantum Entanglement" Axioms 13, no. 5: 289. https://doi.org/10.3390/axioms13050289
APA StyleBerrada, K. (2024). Photon-Added Deformed Peremolov Coherent States and Quantum Entanglement. Axioms, 13(5), 289. https://doi.org/10.3390/axioms13050289




