In this section, we would like to show how our suggested method can be used to the real life situations. To this aim, we focus on two real-world count data sets.
6.1. The Asymptomatic COVID-19 Cases in China
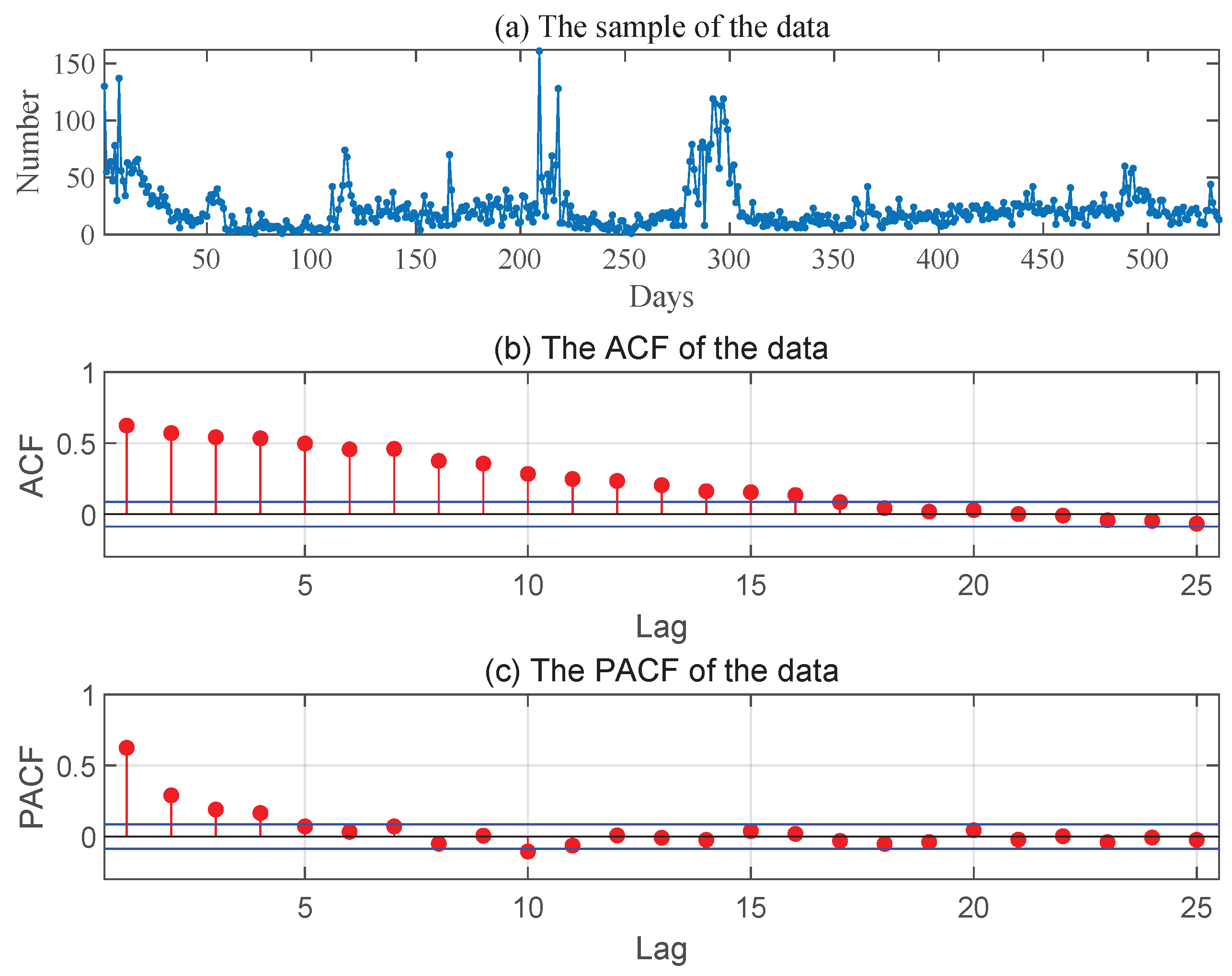
This data consist of the daily numbers of new asymptomatic COVID-19 cases in China, totally 534 observations (from 31 March to 15 September 2021) reported by the National Health Commission of the PRC.
Figure 2 gives the sample path, the ACF and PACF of the series, from which it is reasonable for us to assume that these data come from an INAR(1) process.
We mainly apply the following four models to fit and analyze the data, among which the latter two models are considered here in order to show the superiority of the models constructed by the negative binomial thinning operator.
(1) NBRCINAR(1) process: the first-order random coefficient integer-valued autoregressive process constructed by the negative binomial thinning operator, i.e.,
in which
.
(2) NBINAR(1) process: the first-order integer-valued autoregressive process with constant coefficient constructed by the negative binomial thinning operator, i.e.,
(3) BRCINAR(1) process: the first-order random coefficient integer-valued autoregressive process based on the binomial thinning operator, i.e.,
in which
.
(4) BINAR(1) process: the first-order integer-valued autoregressive process with constant coefficient based on the binomial thinning operator, i.e.,
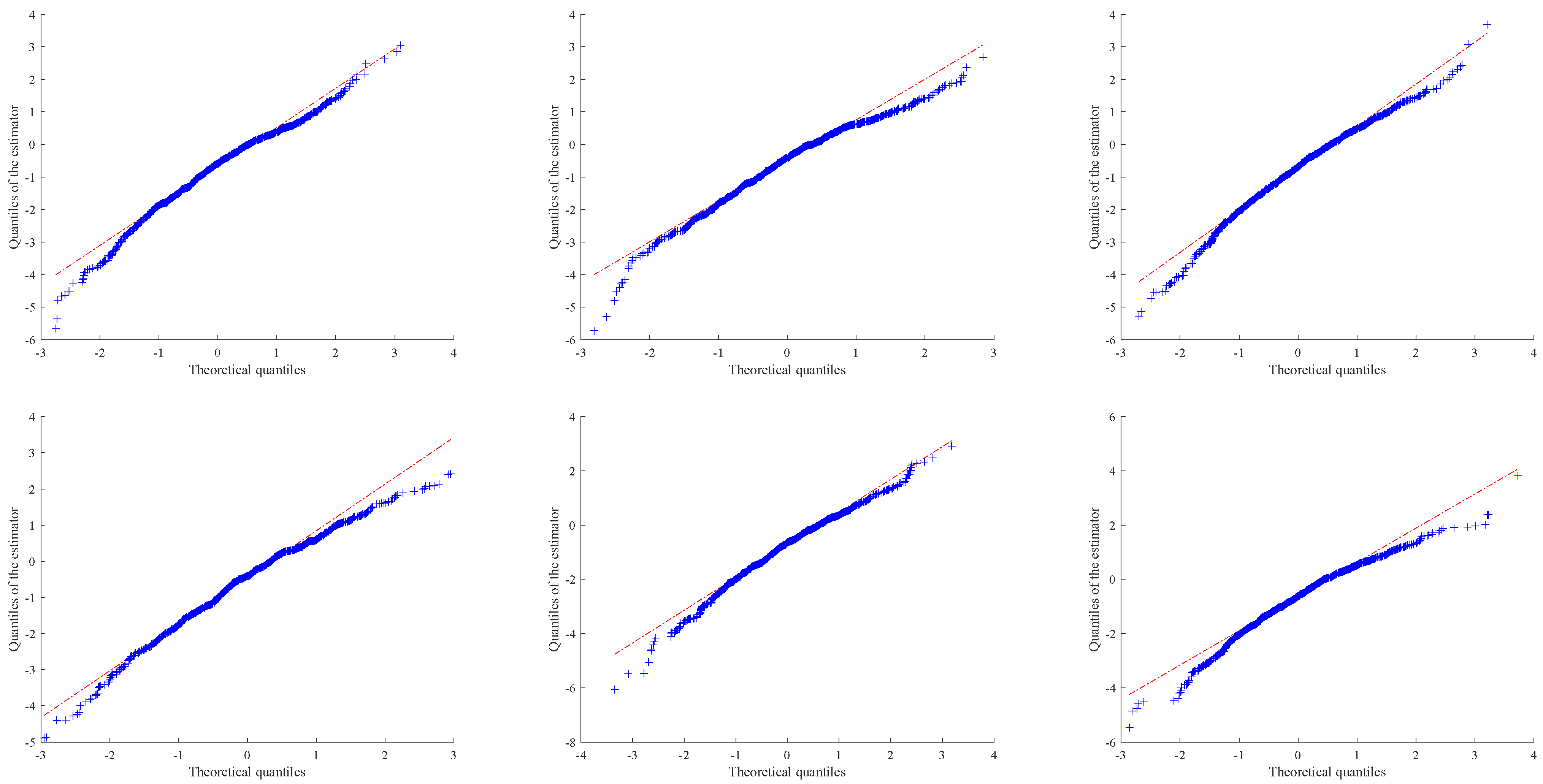
By using the method described in
Section 4 to test the randomness of the thinning parameter, we obtain that the
p-value is 0.0887, which suggests that we would reject the null hypothesis
in favor of the alternative hypothesis
at the significance level of
, and thus, we should apply the NBRCINAR(1) process to fit the data.
To make further comparisons between the aforementioned four models, we split the data set into two parts: the first 529 observations from 31 March to 10 September are considered as a training sample to estimate the parameters, retaining the last 5 observations from 11 September to 15 September as a forecasting evaluation sample to perform an out-of-sample experiment. When estimating the parameters, the two-step CLS method makes it not necessary to specify the distribution of the innovation
. Meanwhile, to improve the estimation performance, we use the block bootstrap method for the dependent time series proposed by Künsch [
36] to derive the model parameters (1000 replications) and then obtain the CLS estimates by averaging the sample bootstrap estimates. Moreover, the forecasting performance of the estimated INAR models is assessed by the forecast mean absolute error (FMAE) statistics of
h-step-ahead forecasts, which are defined by
where
,
, and
is the coherent prediction of
.
As for time series analysis, conditional expectation (CE for short) is the most common technique to construct forecasts, since it can lead to minimum mean squared error. However, for all the four models mentioned above, we have
which implies that we can not distinguish them because of the same CLS estimates of
and
. On the other hand, conditional expectation usually fails to preserve the integer-valued nature in making forecasts for count data time series. To cater these problems, Bisaglia and Gerolimetto [
37] proposes a new approach based on the autoregressive structure of the INAR model by means of bootstrap techniques. We will also employ this method for further analysis. Taking the NBRCINAR(1) process as an example, the corresponding algorithm steps of this method are given as follows:
Step 1. Estimate the unknown model parameters of interest and by two-step CLS method to obtain and .
Step 2. Compute the residuals as
in which
is a sequence of i.i.d. random variables drawn from Beta(
,
).
Step 3. Define the modified residuals
as
and then fit the empirical distribution
of
.
Step 4. Obtain the bootstrapped series
for
by
where
and
are i.i.d. random samples from Beta(
,
) and
, respectively.
Step 5. Based on the bootstrapped series , derive the estimators and of and as those in Step 1, respectively.
Step 6. Calculate the forecasts as
where
H denotes the largest prediction horizon,
, while
and
are i.i.d. random samples drawn from Beta(
,
) and
, respectively.
Step 7. Obtain , the point forecast of by taking the median of the replicates for .
Table 6 presents the results of parameter estimation for the four different models we consider in this paper, i.e., the NBRCINAR(1) process (
26), the NBINAR(1) process (
27), the BRCINAR(1) process (
28) and the BINAR(1) process (
29). After applying the two-step CLS method, it can be seen that
and
in all the four models have the same estimates. In addition, the estimates of
and
in NBRCINAR(1) process and BRCINAR(1) process are also equal, respectively, which makes us dedicate ourselves to developing other estimation methods for these models. Furthermore, when using the model-based INAR bootstrap (MBB for short) technique to construct the forecasts, we set
to achieve our goal for model selection, i.e., predict
by MBB 501 times, choose the median of the obtained results as the value of
, and then calculate the FMAE. According to the report in
Table 7, it can be observed that the models with random coefficients outperform the models with a constant coefficient, which is consistent with the hypothesis testing result we have obtained. Additionally, under the same assumption for the thinning parameters, the models based on the negative binomial thinning operator work better than the models based on the binomial thinning operator, and the NBRCINAR(1) process has the best predictive performance. Therefore, we can conclude that our suggested model and method can be very helpful in some practical applications.
6.2. Poliomyelitis Data in USA
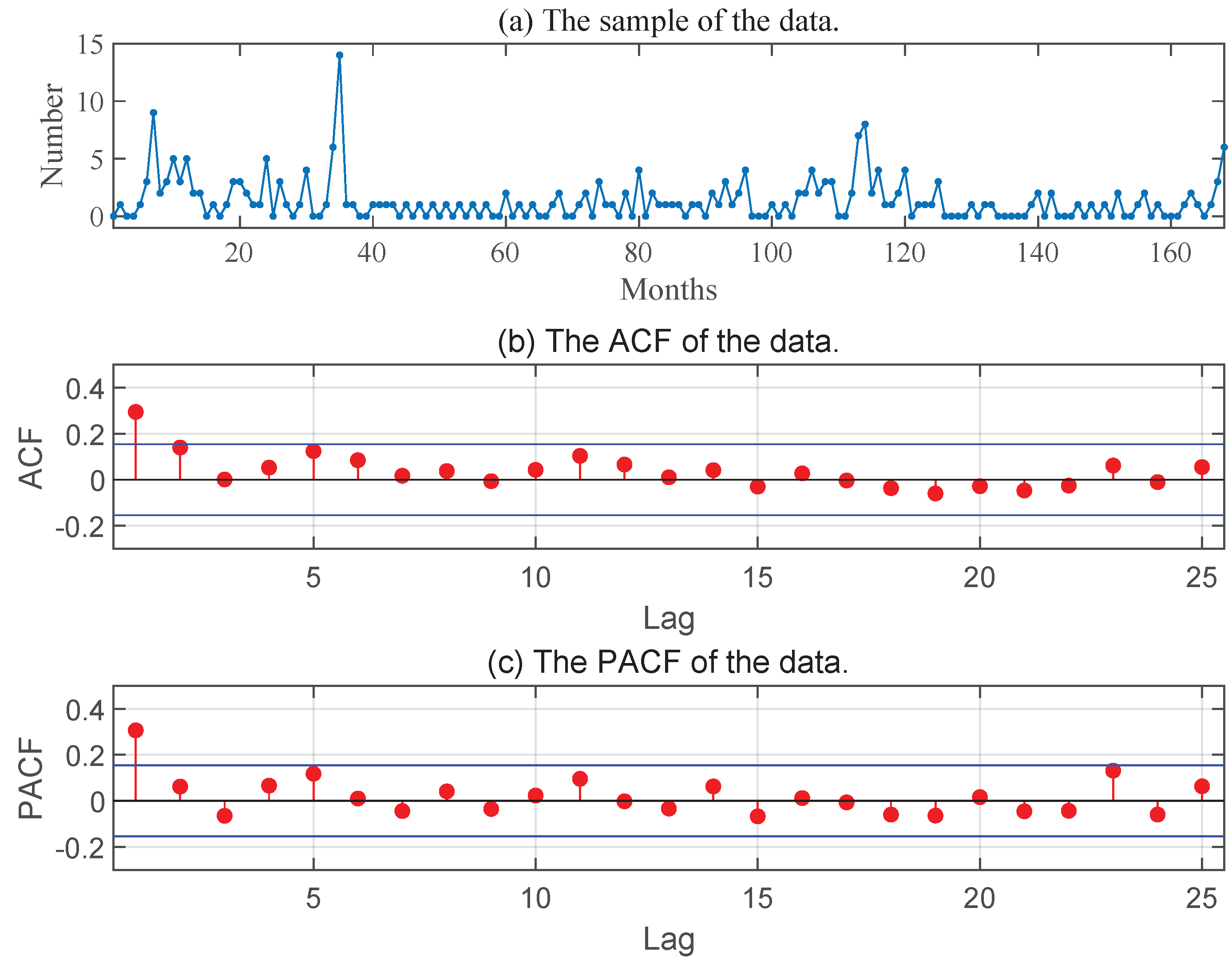
In this subsection, we turn to the data set that is comprised of the monthly number of poliomyelitis cases reported by the U.S. Centers for Disease Control. There are totally 168 observations, collected from January 1970 to December 1983.
Figure 3 presents the sample path, the ACF and PACF of the time series. This data set has been used by Awale et al. [
25] previously to test the constancy of the thinning parameter in a geometric INAR(1) models in which the distribution of the innovation
is given. Now, we relax this condition and apply the NBRCINAR(1) process (
26), the NBINAR(1) process (
27), the BRCINAR(1) process (
28) and the BINAR(1) process (
29) without specifying
to fit the Poliomyelitis data. With the method discussed in
Section 4, we carried out the test for
, and the
p-value turns out to be 0.4960. Hence, the same conclusion as Awale et al. [
25] can be reached, i.e, we can not reject the null hypothesis of the constant thinning parameter at the significance levels of
and
. In order to verify this assertion, we estimate the parameters of interest and list the results in
Table 8. Moreover, the predicted values are shown in
Table 9, from which it can be seen that the models with the constant coefficient are more appropriate than the models with random coefficients for this poliomyelitis data set.