Analysis of Thermal Mixing and Entropy Generation during Natural Convection Flows in Arbitrary Eccentric Annulus
Abstract
1. Introduction
2. Mathematical Formulation
2.1. Problem Setup
2.2. Governing Equations
2.3. Heat Transfer Parameters
2.3.1. Streamfunction
2.3.2. Nusselt Numbers
2.3.3. Entropy Generation
3. Numerical Implementation, Mesh Independence, and Validation Studies
3.1. Numerical Implementation
3.2. Mesh Independence Study
3.3. Validation Study
4. Numerical Results and Discussion
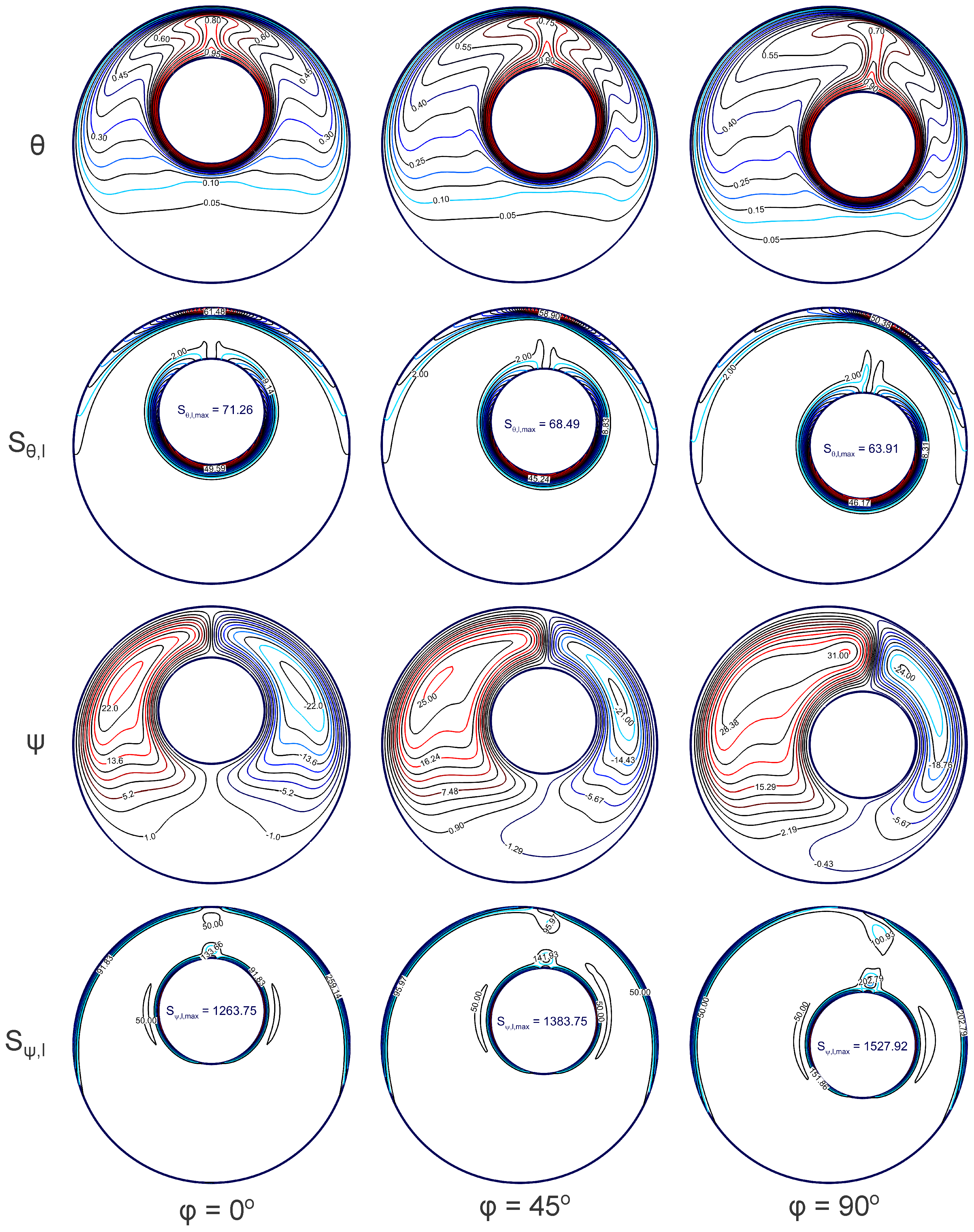
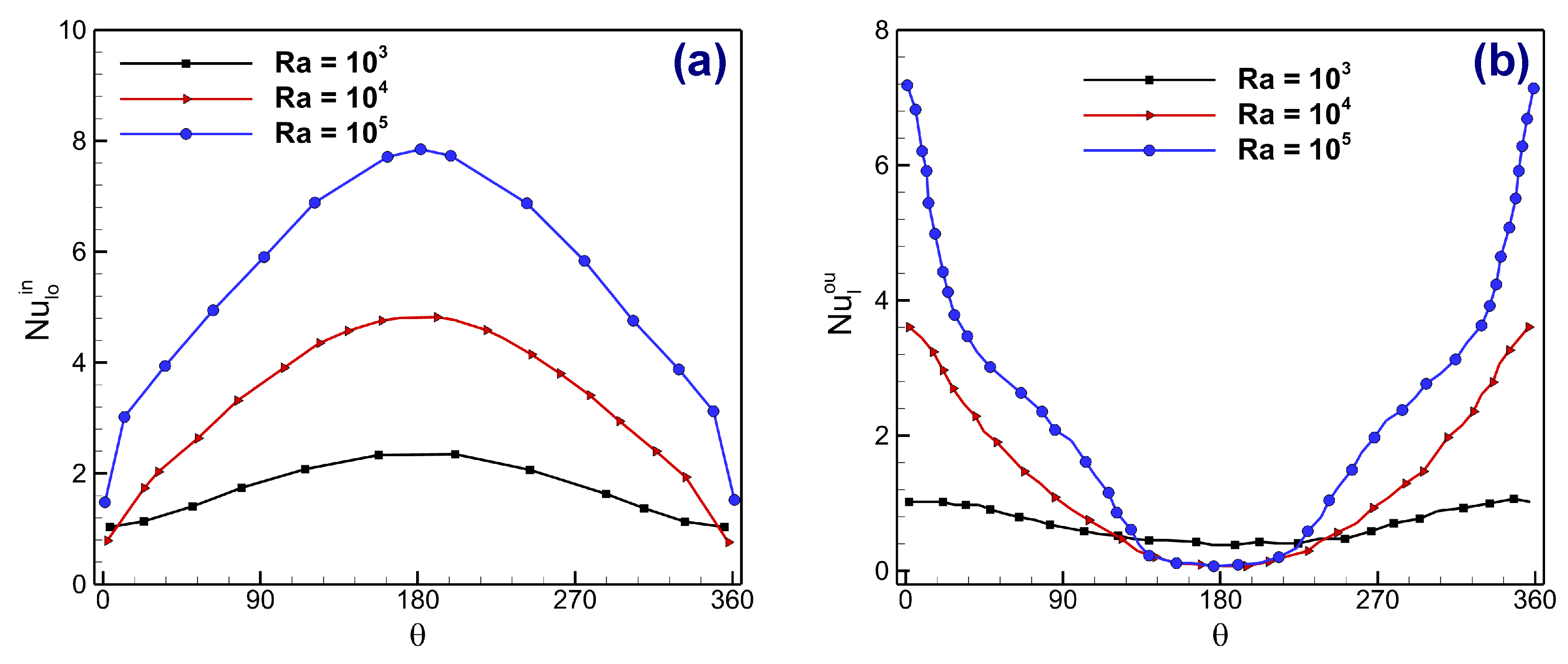
4.1. Case 1: Concentric Annulus with and
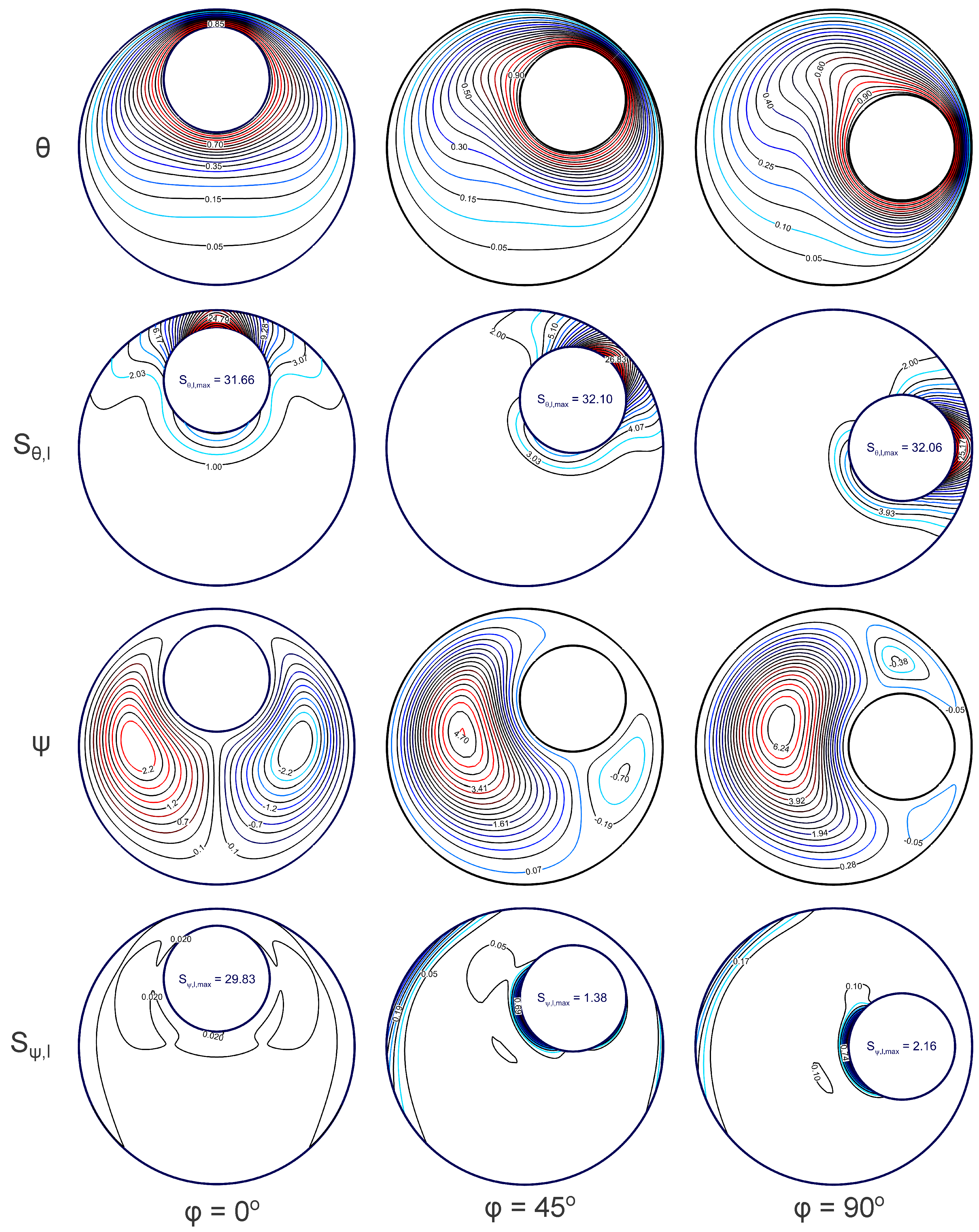
4.2. Case 2: Eccentric Annulus with and
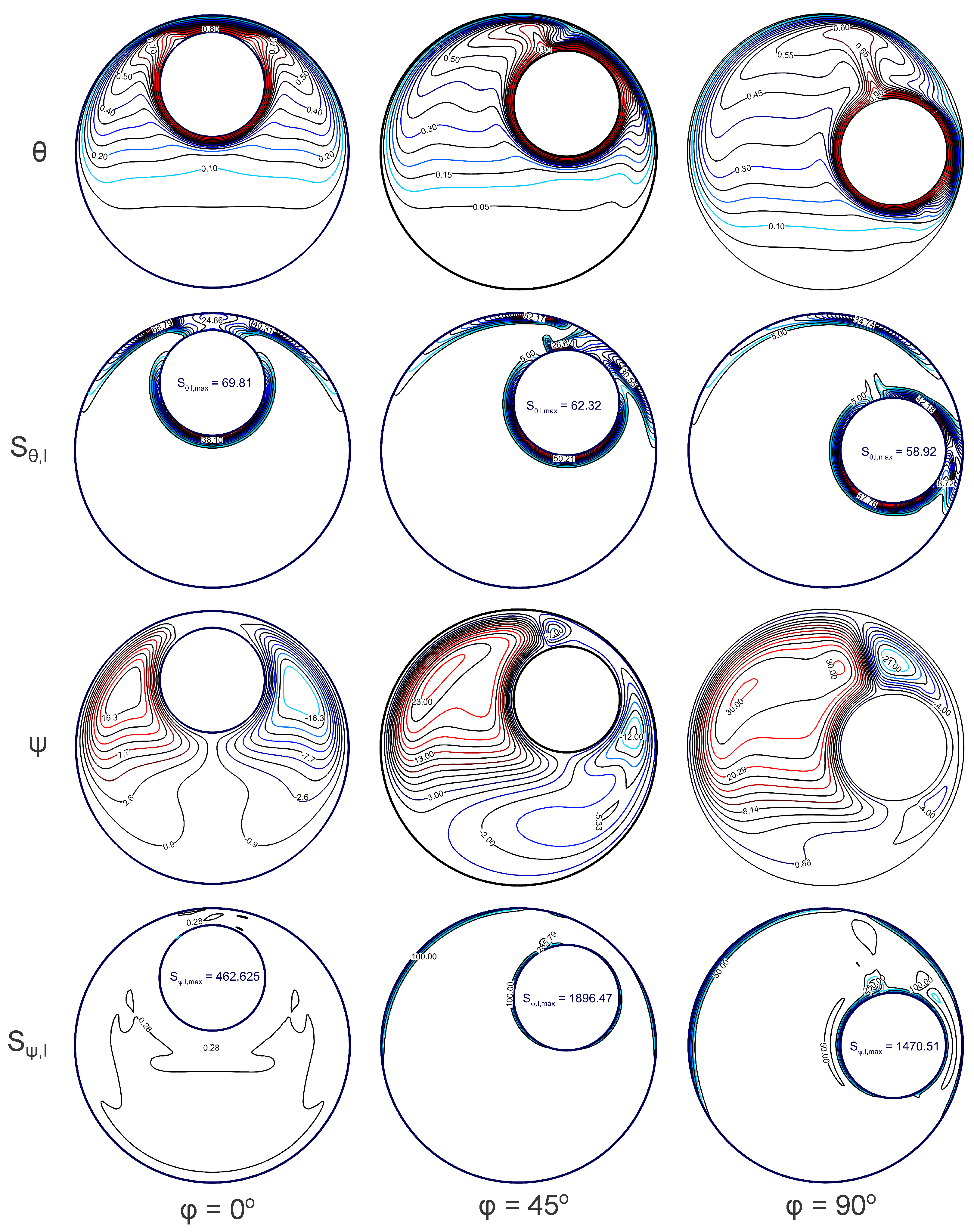
4.3. Case 3: Eccentric Annulus with and
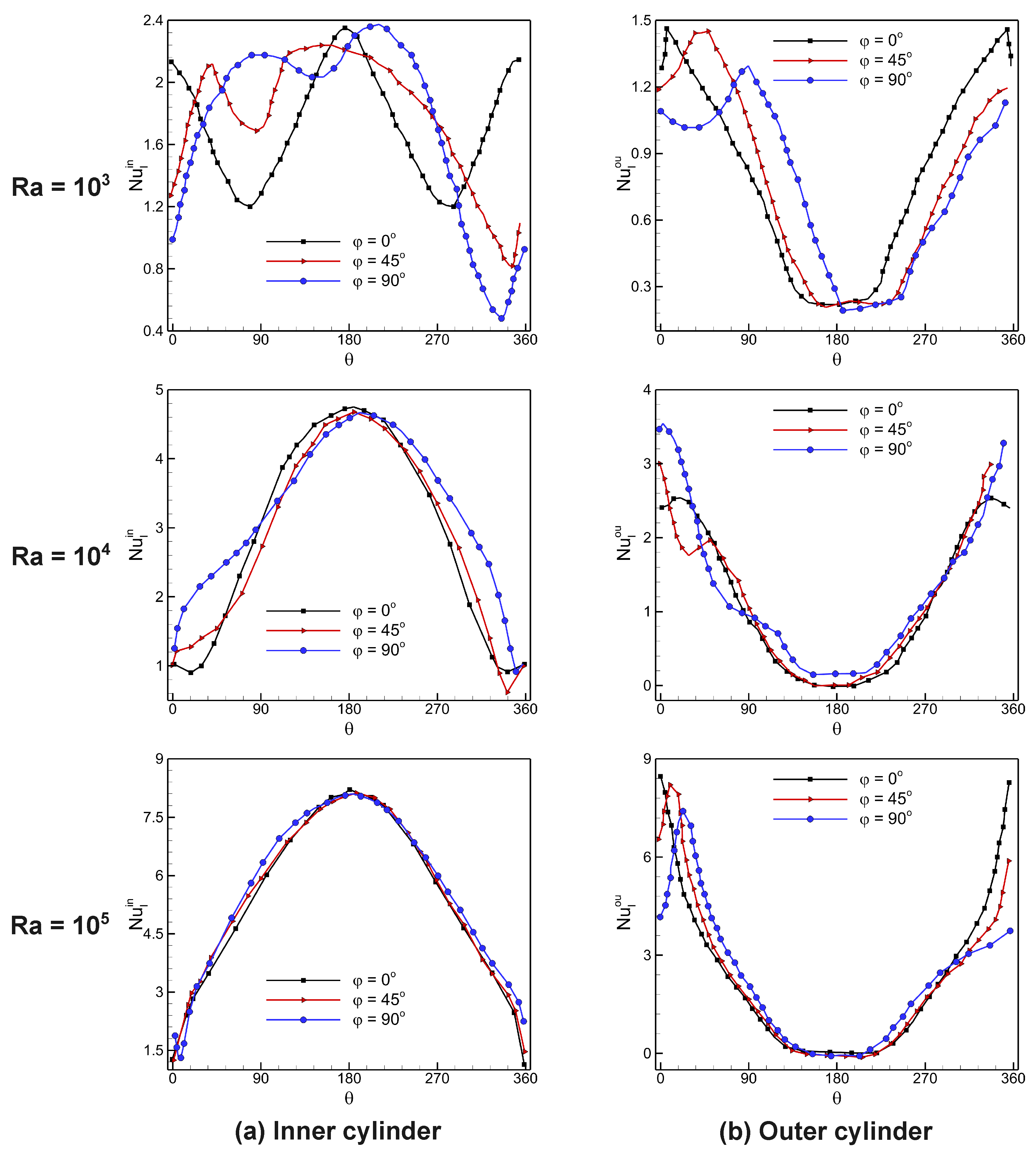
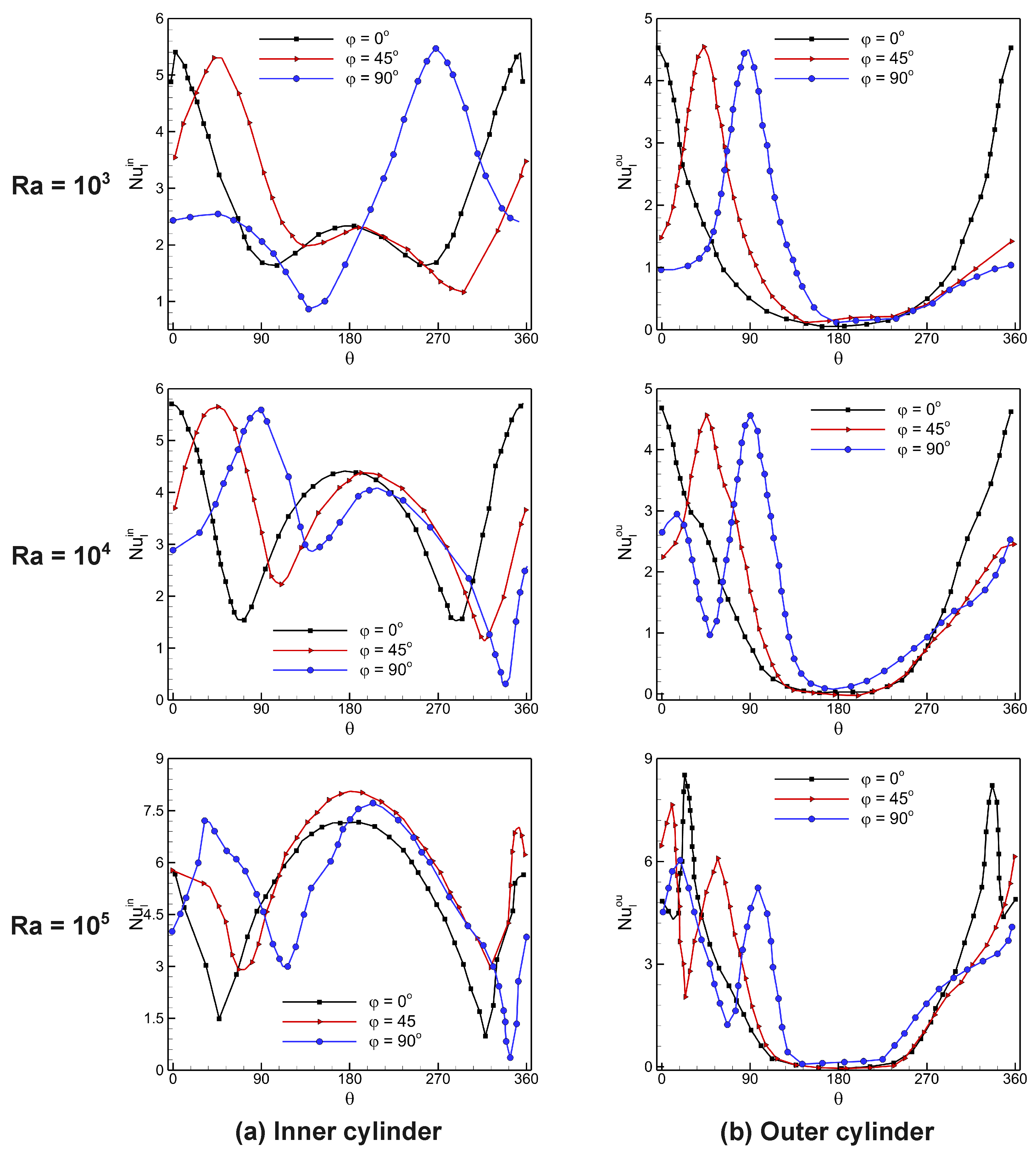
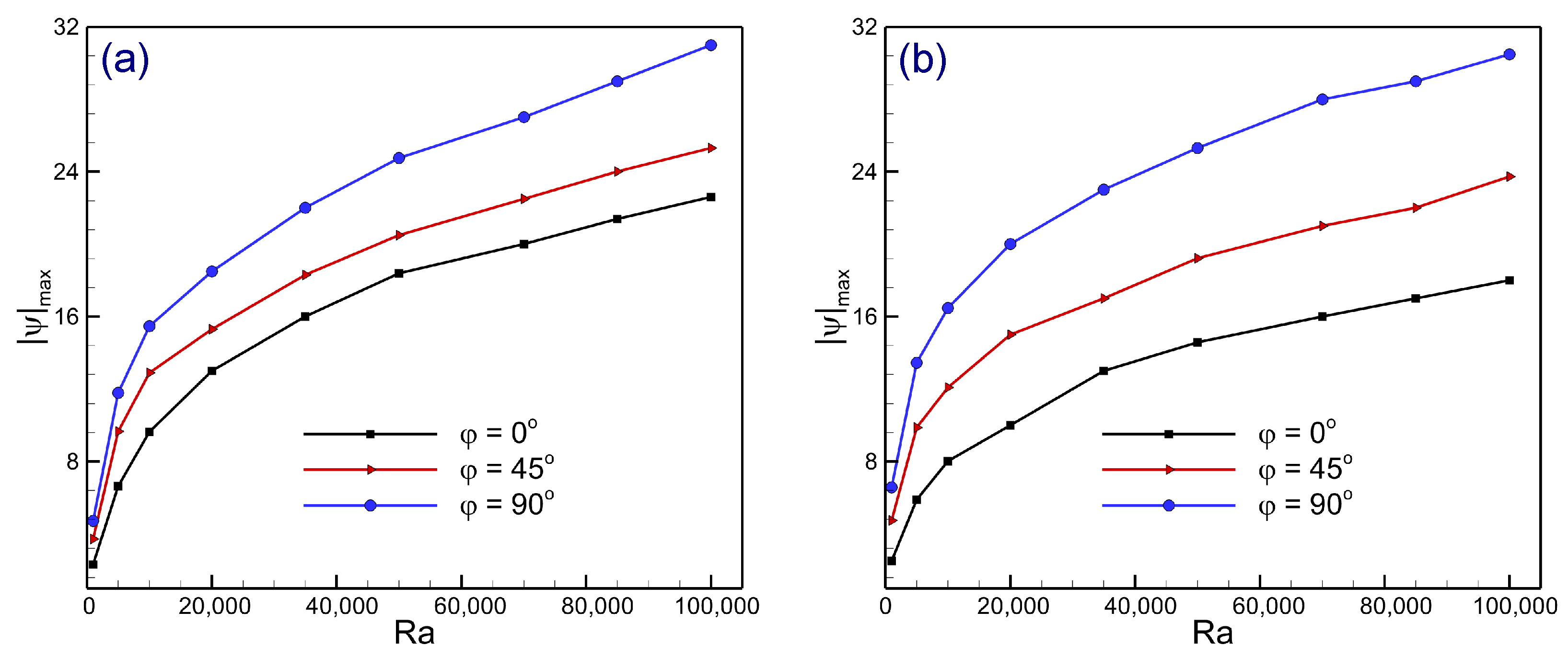
4.4. Quantitative Analysis of Heat Transfer Parameters
5. Concluding Remarks and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dawood, H.K.; Mohammed, H.A.; Sidik, N.A.C.; Munisamy, K.M.; Wahid, M.A. Forced, natural and mixed-convection heat transfer and fluid flow in annulus: A review. Int. Commun. Heat Mass Transf. 2015, 62, 45–57. [Google Scholar] [CrossRef]
- Rahimi, A.; Saee, A.D.; Kasaeipoor, A.; Malekshah, E.H. A comprehensive review on natural convection flow and heat transfer: The most practical geometries for engineering applications. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 834–877. [Google Scholar] [CrossRef]
- Geridonmez, B.P.; Oztop, H.F. The effect of inclined periodic magnetic field on natural convection flow of Al2O3-Cu/water nanofluid inside right isosceles triangular closed spaces. Eng. Anal. Bound. Elem. 2022, 141, 222–234. [Google Scholar] [CrossRef]
- Barnoon, P. Electroosmotic flow and heat transfer of a hybrid nanofluid in a microchannel: A structural optimization. Int. J. Thermofluids 2023, 20, 100499. [Google Scholar] [CrossRef]
- Geridonmez, B.P.; Oztop, H.F. Conjugate natural convection flow of a nanofluid with oxytactic bacteria under the effect of a periodic magnetic field. J. Magn. Magn. Mater. 2022, 564, 170135. [Google Scholar] [CrossRef]
- Barnoon, P.; Toghraie, D.; Dehkordi, R.B.; Afrand, M. Two phase natural convection and thermal radiation of Non-Newtonian nanofluid in a porous cavity considering inclined cavity and size of inside cylinders. Int. Commun. Heat Mass Transf. 2019, 108, 104285. [Google Scholar] [CrossRef]
- Geridonmez, B.P.; Oztop, H.F. MHD natural convection in a cavity in the presence of cross partial magnetic fields and Al2O3-water nanofluid. Comput. Math. Appl. 2020, 80, 2796–2810. [Google Scholar] [CrossRef]
- Beckmann, W. Die Wärmeübertragung in zylindrischen Gasschichten bei natürlicher Konvektion. Forsch. Geb. Ing. A 1931, 2, 165–178. [Google Scholar] [CrossRef]
- Crawford, L.; Lemlich, R. Natural convection in horizontal concentric cylindrical annuli. Ind. Eng. Chem. Res. 1962, 1, 260–264. [Google Scholar] [CrossRef]
- Abbott, M.R. A numerical method for solving the equations of natural convection in a narrow concentric cylindrical annulus with a horizontal axis. Q. J. Mech. Appl. Math. 1964, 17, 471–481. [Google Scholar] [CrossRef]
- Mack, L.R.; Bishop, E.H. Natural convection between horizontal concentric cylinders for low Rayleigh numbers. Q. J. Mech. Appl. Math. 1968, 21, 223–241. [Google Scholar] [CrossRef]
- Moukalled, F.; Acharya, S. Natural convection in the annulus between concentric horizontal circular and square cylinders. J. Thermophys. Heat Transf. 1996, 10, 524–531. [Google Scholar] [CrossRef]
- Powe, R.E.; Carley, C.T.; Carruth, S.L. A Numerical Solution for Natural Convection in Cylindrical Annuli. J. Heat Transf. 1971, 93, 210–220. [Google Scholar] [CrossRef]
- Kuehn, T.H.; Goldstein, R.J. An experimental and theoretical study of natural convection in the annulus between horizontal concentric cylinders. J. Fluid Mech. 1976, 74, 695–719. [Google Scholar] [CrossRef]
- Kumar, R. Study of natural convection in horizontal annuli. Int. J. Heat Mass Transf. 1988, 31, 1137–1148. [Google Scholar] [CrossRef]
- Labonia, G.; Guj, G. Natural convection in a horizontal concentric cylindrical annulus: Oscillatory flow and transition to chaos. J. Fluid Mech. 1998, 375, 179–202. [Google Scholar] [CrossRef]
- Dyko, M.P.; Vafai, K.; Mojtabi, A.K. A numerical and experimental investigation of stability of natural convective flows within a horizontal annulus. J. Fluid Mech. 1999, 381, 27–61. [Google Scholar] [CrossRef]
- Lshahrani, D.; Zeitoun, O. Natural convection in horizontal cylindrical annuli with fins. Alex. Eng. J. 2005, 44, 825–837. [Google Scholar]
- Teertstra, P.; Yovanovich, M.M.; Culham, J.R. Analytical modeling of natural convection in concentric spherical enclosures. J. Thermophys. Heat Transf. 2006, 20, 297–304. [Google Scholar] [CrossRef][Green Version]
- Sankar, M.; Venkatachalappa, M.; Shivakumara, I.S. Effect of magnetic field on natural convection in a vertical cylindrical annulus. Int. J. Eng. Sci. 2006, 44, 1556–1570. [Google Scholar] [CrossRef]
- Alsabery, A.I.; Naganthran, K.; Azizul, F.M.; Hashim, I.; Nazar, R. Numerical study of conjugate natural convection heat transfer of a blood filled horizontal concentric annulu. Int. Commun. Heat Mass Transf. 2020, 114, 104568. [Google Scholar] [CrossRef]
- Rana, S.; Sengupta, B.; Singh, S. Natural convection study in cylindrical annulus through OpenFOAM. In Computational Fluid Flow and Heat Transfer Advances, Design, Control, and Applications; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Trombetta, M.L. Laminar forced convection in eccentric annuli. Int. J. Heat Mass Transf. 1971, 14, 1161–1173. [Google Scholar] [CrossRef]
- Kuehn, T.H.; Goldstein, R.J. An experimental study of natural convection heat transfer in concentric and eccentric horizontal cylindrical annuli. J. Heat Transf. 1978, 100, 635–640. [Google Scholar] [CrossRef]
- Chakrabarti, S.; Probert, S.D.; Shilston, M.J. Optimal eccentric annuli (containing atmospheric-pressure air) for thermally insulating, horizontal, relatively cold pipes. Appl. Energy 1983, 14, 257–293. [Google Scholar] [CrossRef]
- Badr, H.M. Study of laminar free convection between two eccentric horizontal tubes. Trans. Can. Soc. Mech. Eng. 1983, 7, 190–197. [Google Scholar] [CrossRef]
- Prusa, J.; Yao, L.S. Natural convection heat transfer between eccentric horizontal cylinders. J. Heat Transf. 1983, 105, 108–116. [Google Scholar] [CrossRef]
- Guj, G.; Iannetta, S.; Moretti, G. Experimental analysis of thermal fields in horizontally eccentric cylindrical annuli. Exp. Fluids 1992, 12, 385–393. [Google Scholar] [CrossRef]
- Guj, G.; Stella, F. Natural convection in horizontal eccentric annuli: Numerical study. Numer. Heat Transf. A 1995, 27, 89–105. [Google Scholar] [CrossRef]
- Shu, C.; Yao, Y.; Yeo, K.S.; Zhu, Y.D. Numerical analysis of flow and thermal fields in arbitrary eccentric annulus by differential quadrature method. Heat Mass Transf. 2002, 38, 597–608. [Google Scholar] [CrossRef]
- Mahfouz, F.M. Natural convection within an eccentric annulus at different orientations. J. Thermophys. Heat Trans. 2012, 26, 665–672. [Google Scholar] [CrossRef]
- Yuan, X.; Tavakkoli, F.; Vafai, K. Analysis of natural convection in horizontal concentric annuli of varying inner shape. Numer. Heat Transf. Part A Appl. 2015, 68, 1155–1174. [Google Scholar] [CrossRef]
- Talukdar, D.; Tsubokura, M. Numerical study of natural-convection from horizontal cylinder at eccentric positions with change in aspect ratio of a cooled square enclosure. Heat Mass Transf. 2022, 58, 849–871. [Google Scholar] [CrossRef]
- Shahsavar, A.; Noori, S.; Toghraie, D.; Barnoon, P. Free convection of non-Newtonian nanofluid flow inside an eccentric annulus from the point of view of first-law and second-law of thermodynamics. ZAMM 2021, 101, e202000266. [Google Scholar] [CrossRef]
- Al-Sumaily, G.F.; Hussen, H.M.; Chaichan, M.T.; Dhahad, H.A.; Thompson, M.C. Numerical analysis of the effect of porous structure on free convection heat transfer inside an eccentric annular space. Therm. Sci. Eng. Prog. 2023, 37, 101579. [Google Scholar] [CrossRef]
- Bejan, A. Entropy Generation Minimization; CRC Press: Boca Raton, FL, USA, 1982. [Google Scholar]
- Mahmud, S.; Fraser, R.A. Analysis of entropy generation inside concentric cylindrical annuli with relative rotation. Int. J. Therm. Sci. 2003, 42, 513–521. [Google Scholar] [CrossRef]
- Haddad, O.M.; Alkam, M.K.; Khasawneh, M.T. Entropy generation due to laminar forced convection in the entrance region of a concentric annulus. Energy 2004, 29, 35–55. [Google Scholar] [CrossRef]
- Yari, M. Second-law analysis of flow and heat transfer inside a microannulus. Int. Commun. Heat Mass Transf. 2009, 36, 78–87. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Z.; Bao, S.; Zheng, C. Natural convection and entropy generation in a vertically concentric annular space. Int. J. Therm. Sci. 2010, 49, 2439–2452. [Google Scholar] [CrossRef]
- OpenFOAM. OpenFOAM Project Web Page of the OpenCFD LTD. 2022. Available online: https://www.openfoam.com (accessed on 31 December 2023).
- Singh, A.K.; Roy, S.; Basak, T. Analysis of Bejan’s heatlines on visualization of heat flow and thermal mixing in tilted square cavities. Int. J. Heat Mass Transf. 2012, 55, 2965–2983. [Google Scholar] [CrossRef]
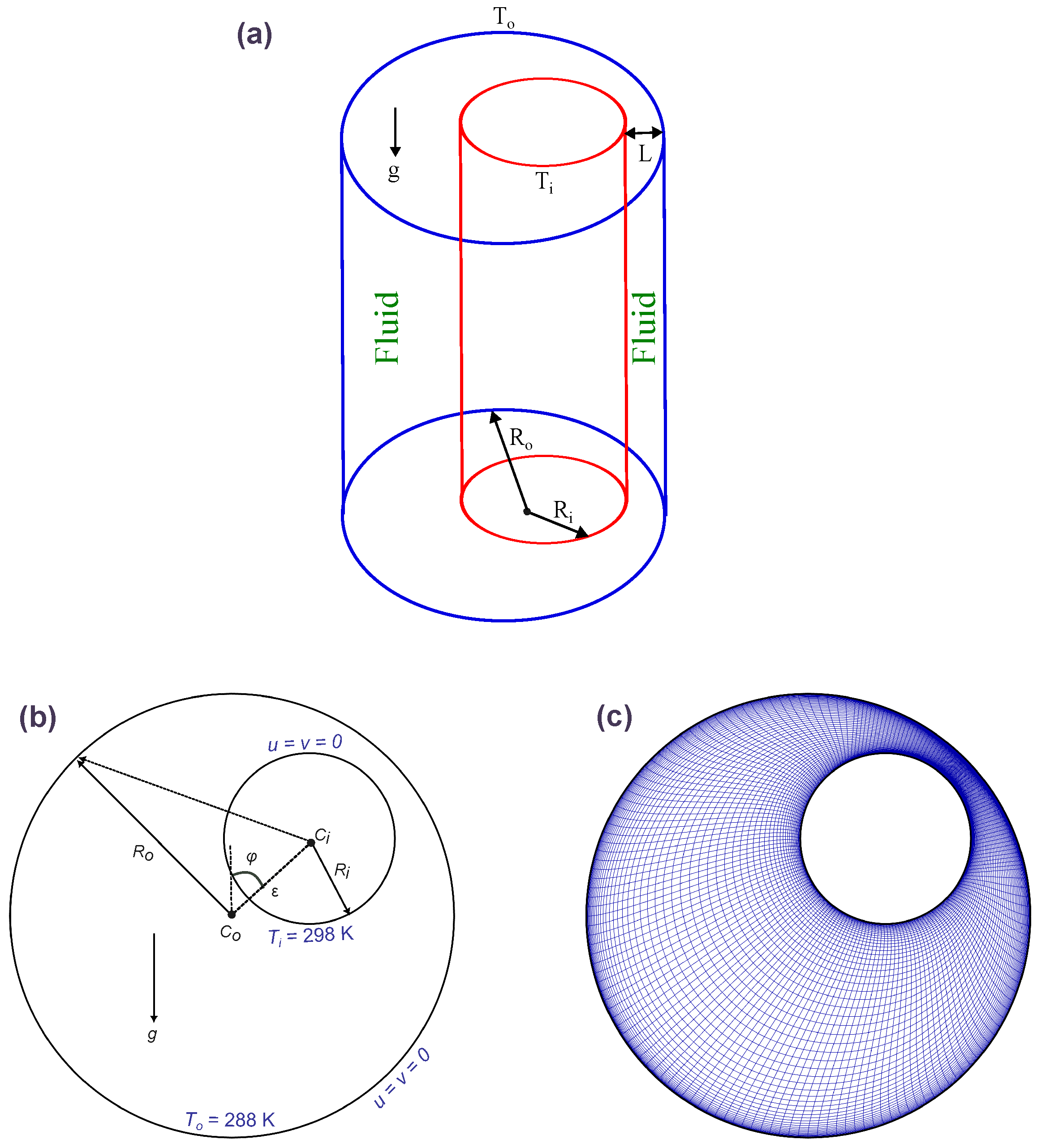
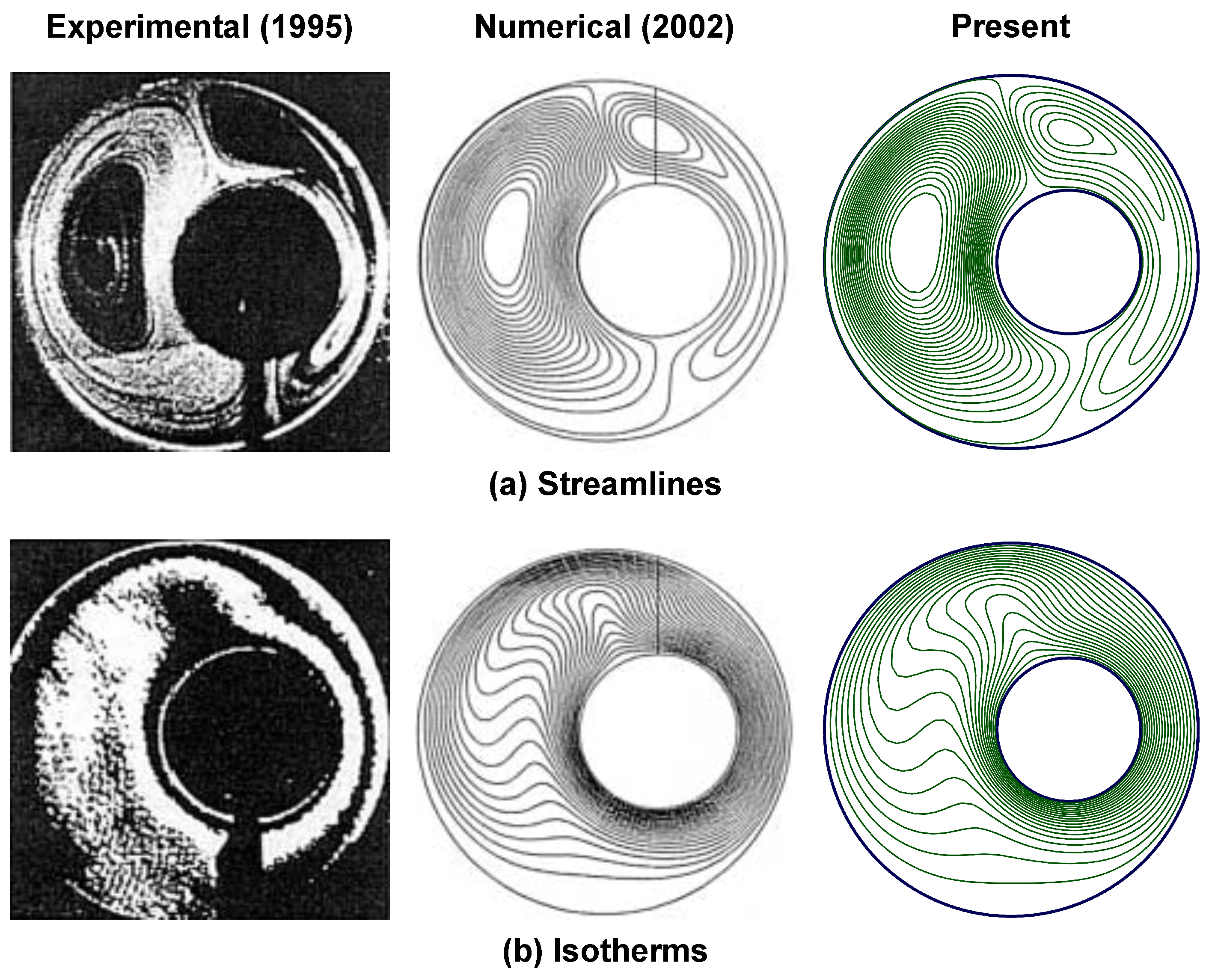
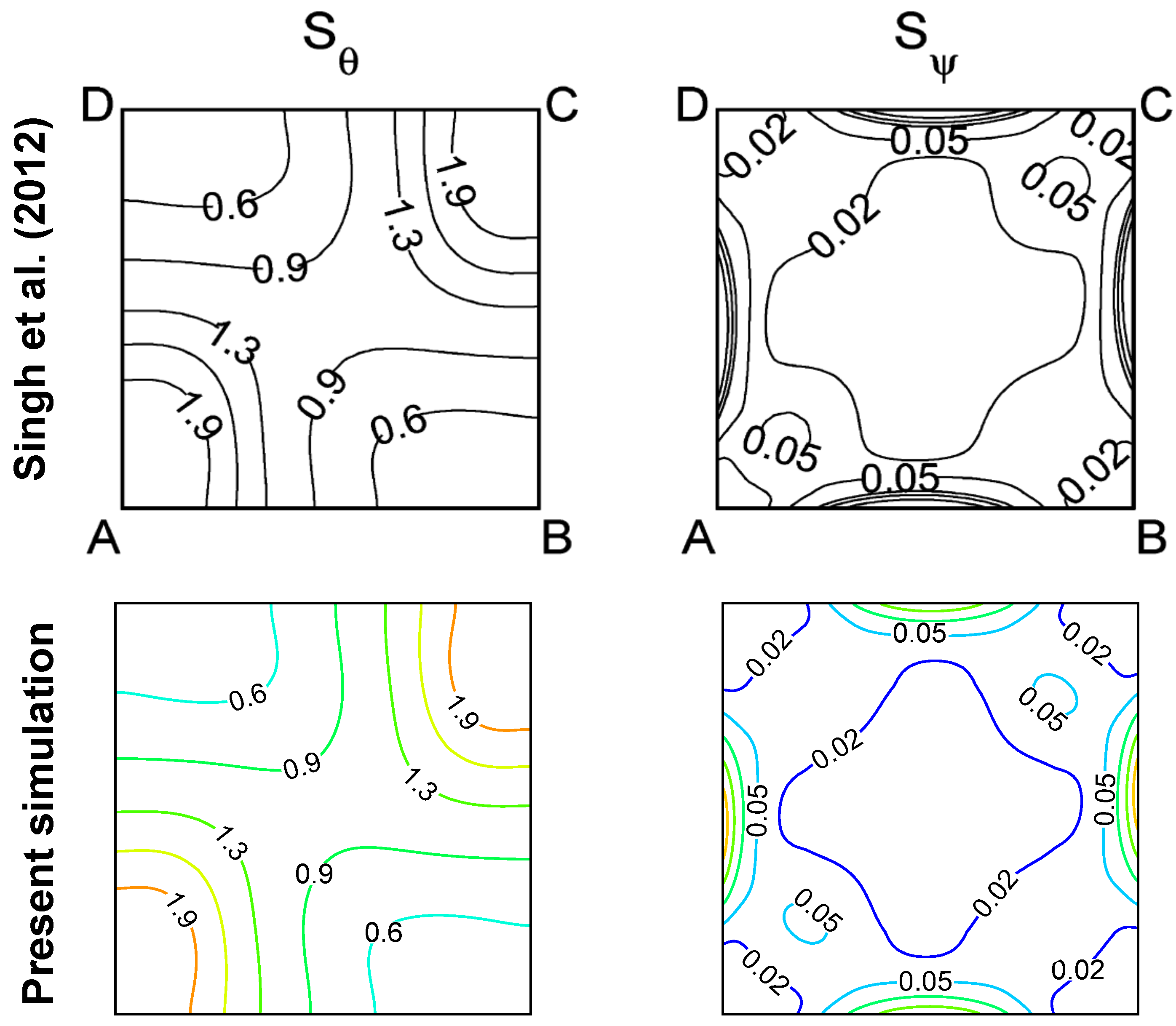



| Mesh Type | Total Elements | Total Nodes | Max Skewness | |||
|---|---|---|---|---|---|---|
| Mesh 1 | 2352 | 2400 | 0.16447 | 3.3555 | 1.30274 | 13.21 |
| Mesh 2 | 4802 | 4900 | 0.08069 | 3.3635 | 1.30115 | 12.89 |
| Mesh 3 | 9702 | 9900 | 0.03990 | 3.3659 | 1.30972 | 12.26 |
| Mesh 4 | 12,152 | 24,552 | 0.03181 | 3.3659 | 1.30972 | 12.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.; Sengupta, B.; Rana, S. Analysis of Thermal Mixing and Entropy Generation during Natural Convection Flows in Arbitrary Eccentric Annulus. Axioms 2024, 13, 233. https://doi.org/10.3390/axioms13040233
Singh S, Sengupta B, Rana S. Analysis of Thermal Mixing and Entropy Generation during Natural Convection Flows in Arbitrary Eccentric Annulus. Axioms. 2024; 13(4):233. https://doi.org/10.3390/axioms13040233
Chicago/Turabian StyleSingh, Satyvir, Bidesh Sengupta, and Seetu Rana. 2024. "Analysis of Thermal Mixing and Entropy Generation during Natural Convection Flows in Arbitrary Eccentric Annulus" Axioms 13, no. 4: 233. https://doi.org/10.3390/axioms13040233
APA StyleSingh, S., Sengupta, B., & Rana, S. (2024). Analysis of Thermal Mixing and Entropy Generation during Natural Convection Flows in Arbitrary Eccentric Annulus. Axioms, 13(4), 233. https://doi.org/10.3390/axioms13040233






