On Population Models with Delays and Dependence on Past Values
Abstract
1. Introduction
2. Materials and Methods
2.1. Population Growth Models
2.2. SIRS Models
2.3. Plant Virus with Vector Transmission Models
2.4. Within-Host Virus Infection Models
3. Results
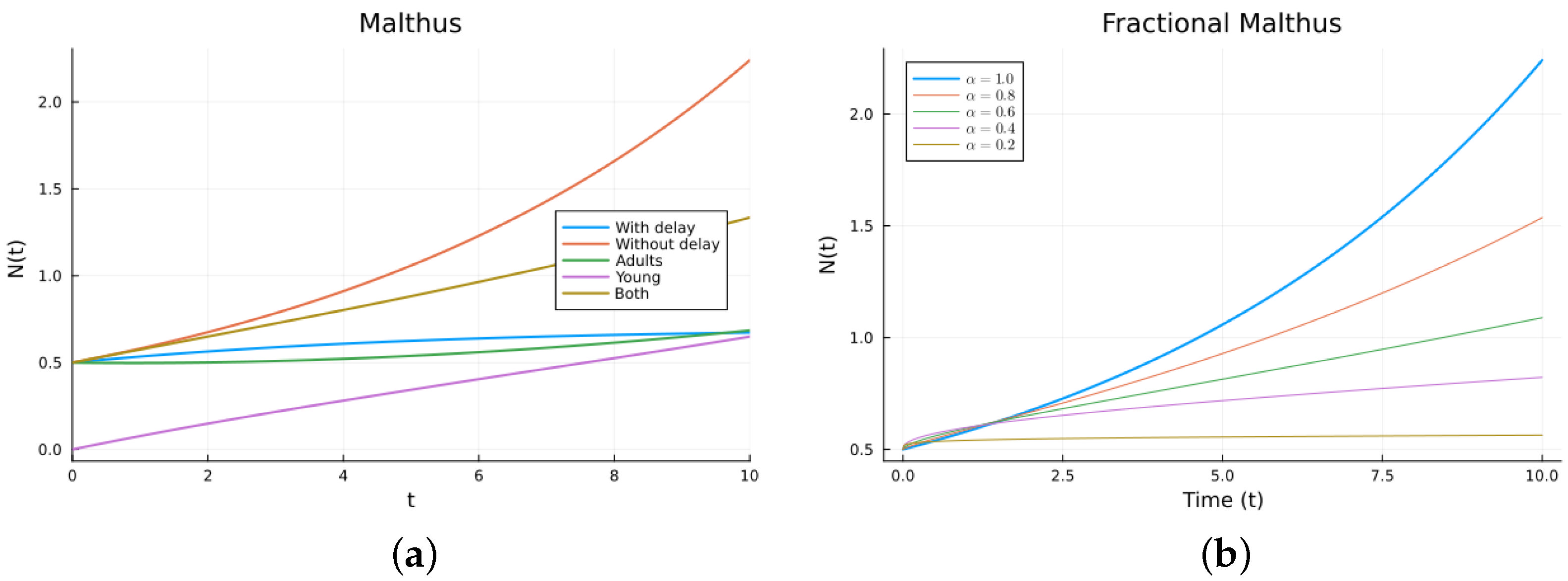
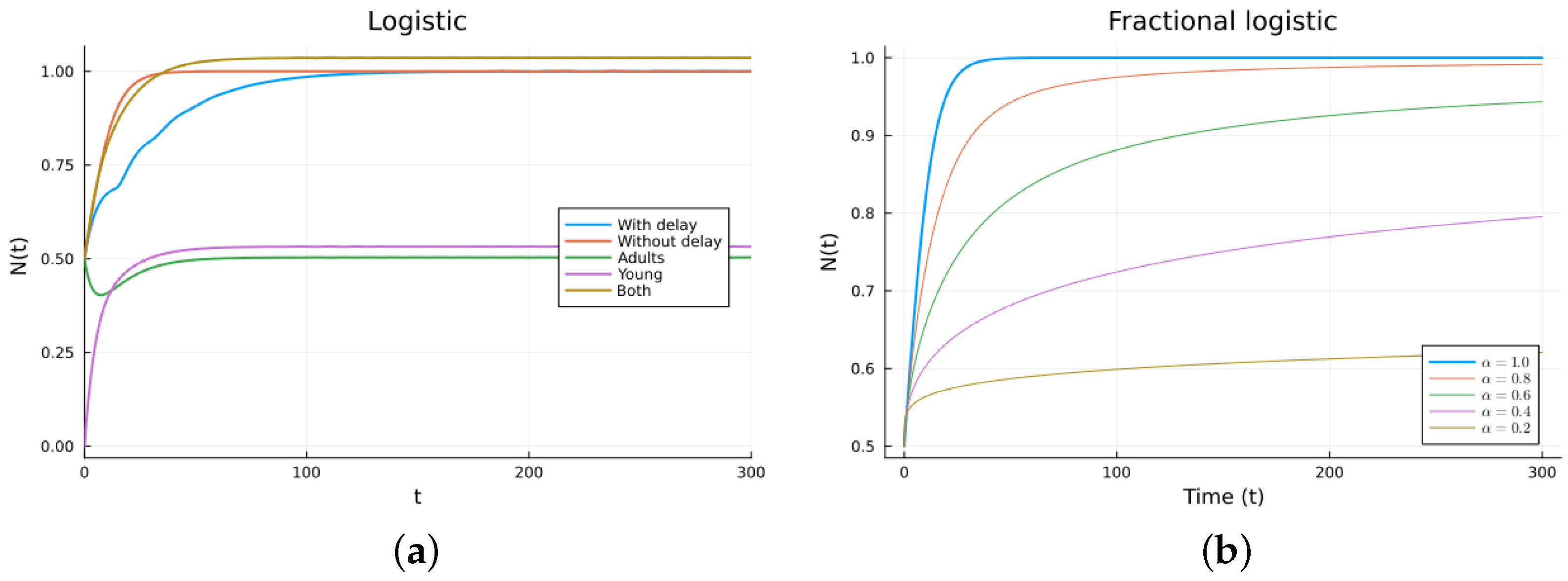
3.1. Population Growth Models
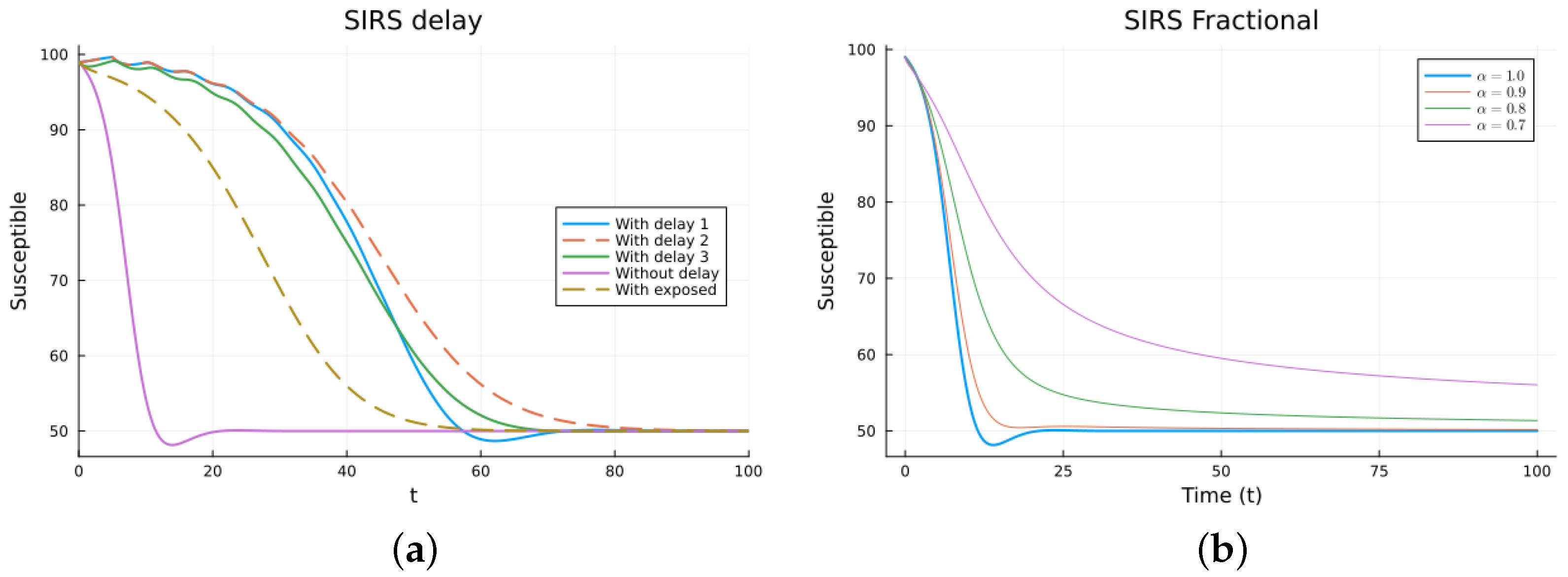
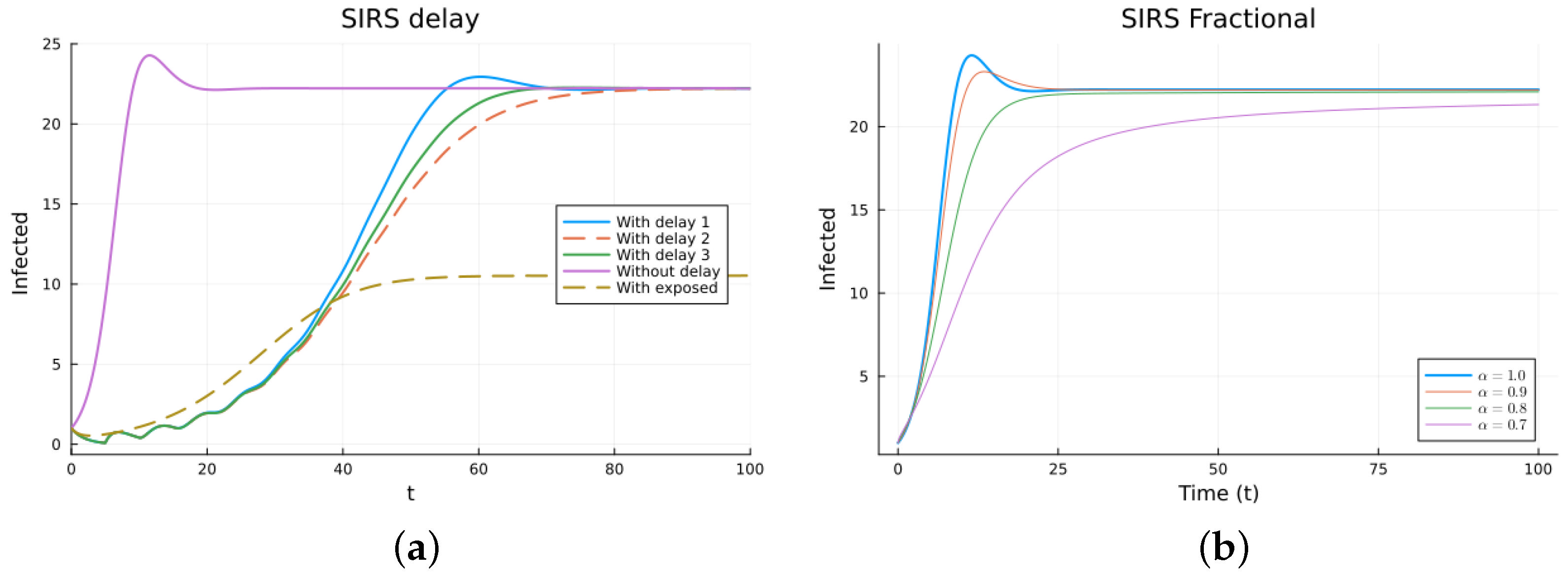
3.2. SIRS Models
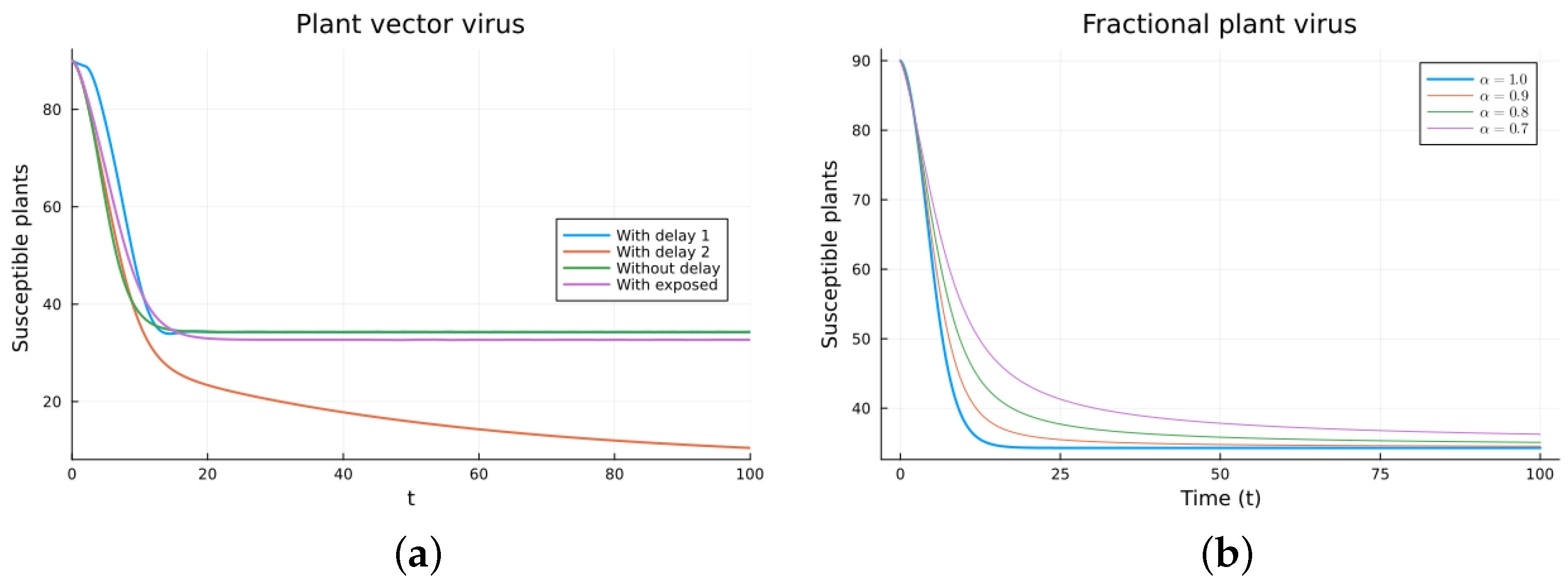
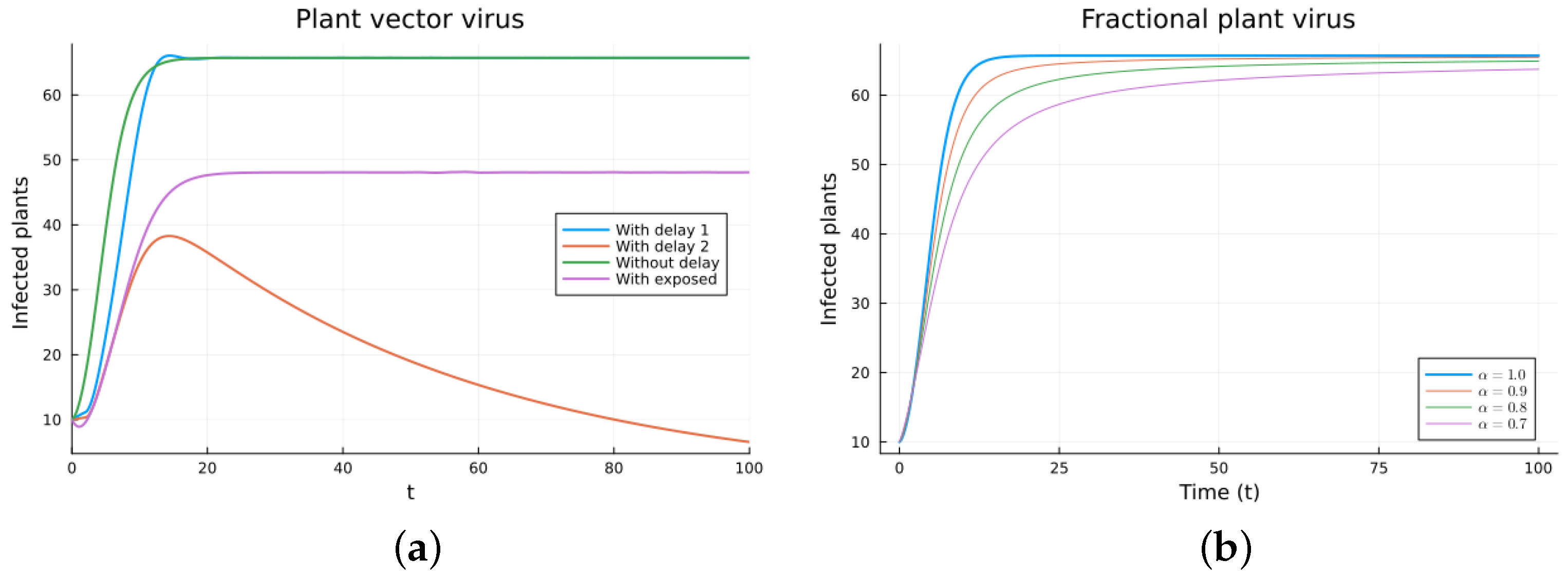
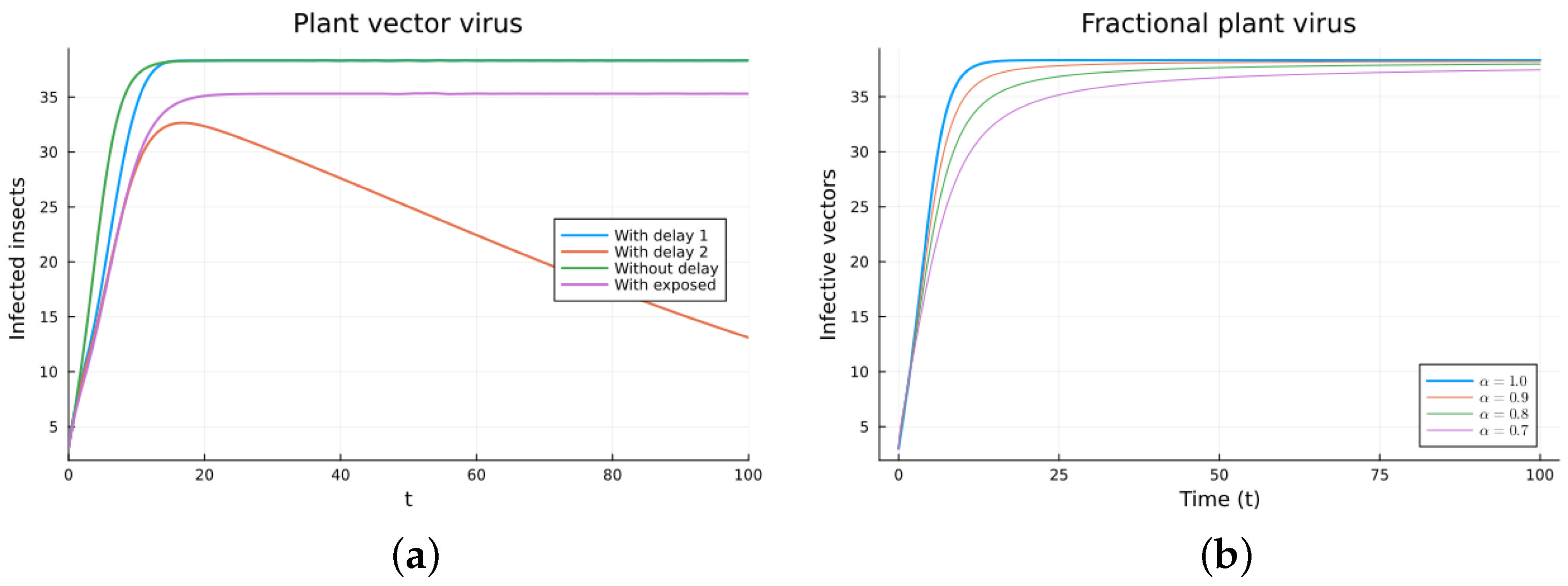
3.3. Plant Virus with Vector Transmission Models
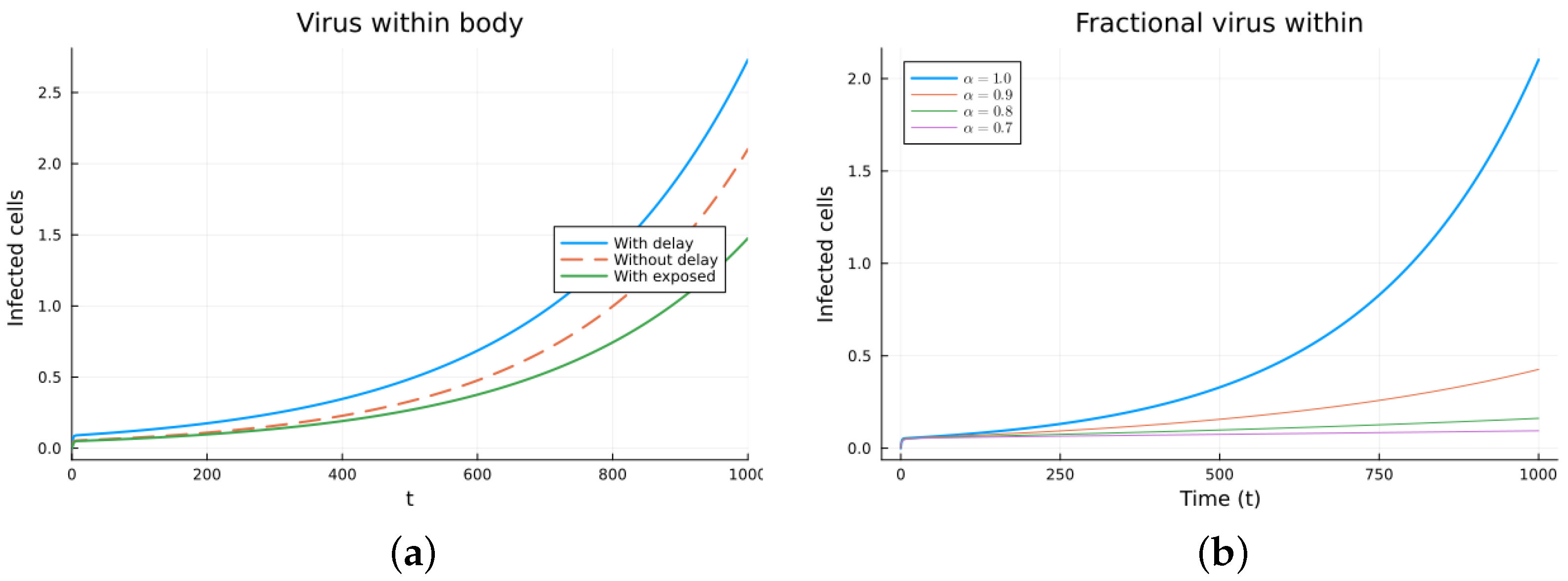
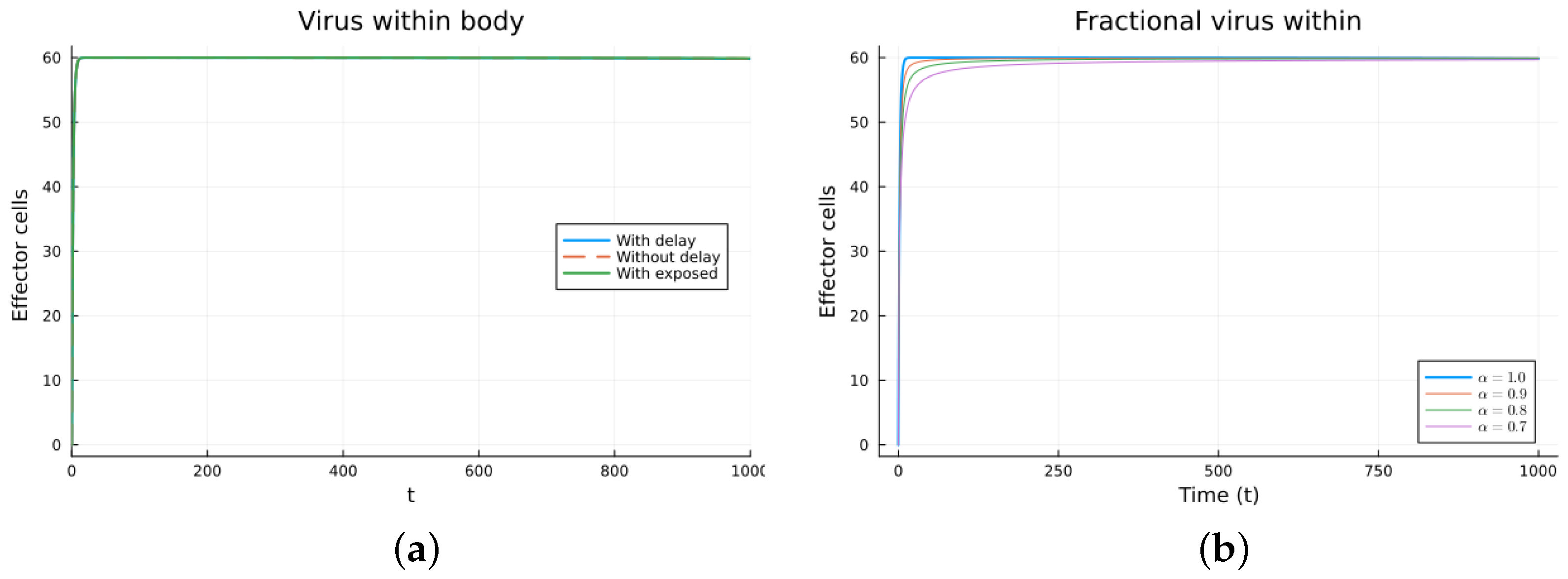
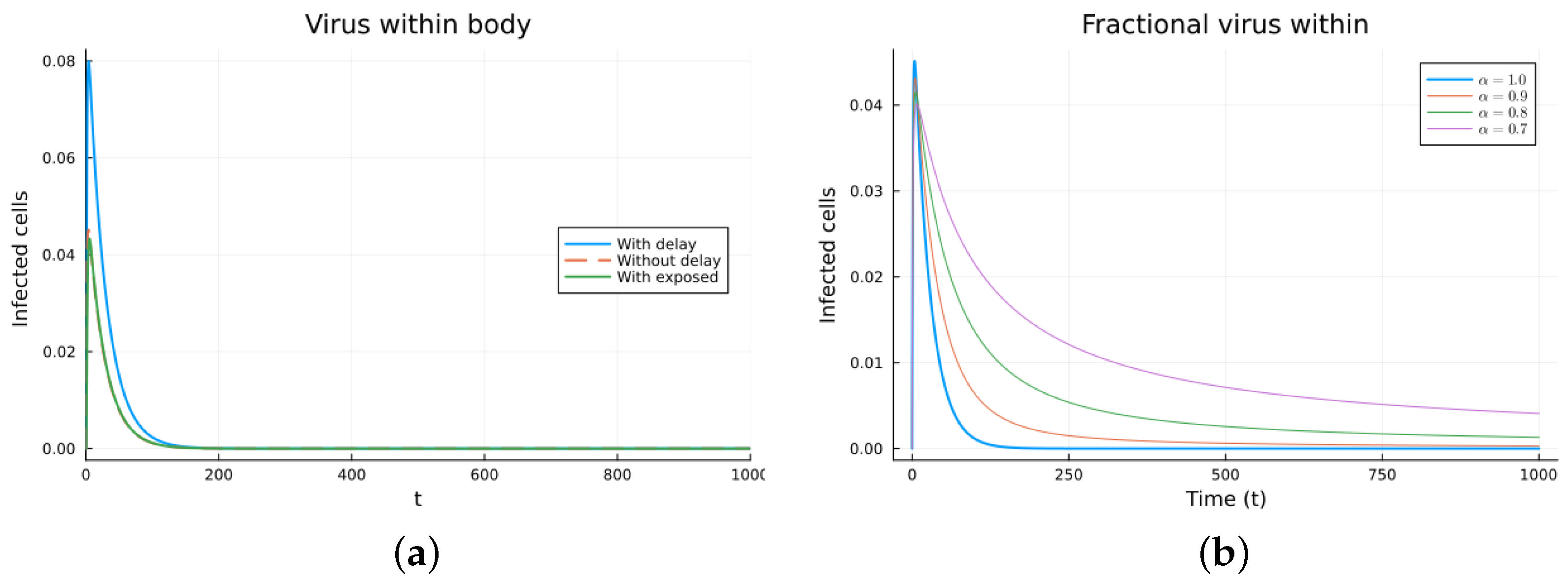
3.4. Within-Host Virus Propagation Models
4. Discussion
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ODE | ordinary differential equation |
| DDE | delay differential equation |
| FDE | fractional differential equation |
| DFE | disease-free equilibrium |
References
- Kuang, Y. Delay Differential Equations: With Applications in Population Dynamics; Academic Press: Cambridge, MA, USA, 1993. [Google Scholar]
- Bellen, A.; Zennaro, M. Numerical Methods for Delay Differential Equations; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Wang, W. Modeling of Epidemics with Delays and Spatial Heterogeneity. In Dynamical Modeling and Analysis of Epidemics; World Scientific: Singapore, 2009; pp. 201–272. [Google Scholar]
- Cooke, K.L. Stability analysis for a vector disease model. Rocky Mt. J. Math. 1979, 9, 31–42. [Google Scholar] [CrossRef]
- Ruan, S. Delay differential equations in single species dynamics. In Delay Differential Equations and Applications; Springer: Dordrecht, The Netherlands, 2006; pp. 477–517. [Google Scholar]
- McCluskey, C.C. Complete global stability for an SIR epidemic model with delay—Distributed or discrete. Nonlinear Anal. Real World Appl. 2010, 11, 55–59. [Google Scholar] [CrossRef]
- Avila-Vales, E.; Pérez, Á.G. Dynamics of a time-delayed SIR epidemic model with logistic growth and saturated treatment. Chaos Solitons Fractals 2019, 127, 55–69. [Google Scholar] [CrossRef]
- Kumar, A.; Goel, K.; Nilam. A deterministic time-delayed SIR epidemic model: Mathematical modeling and analysis. Theory Biosci. 2020, 139, 67–76. [Google Scholar] [CrossRef] [PubMed]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006; Volume 204. [Google Scholar]
- Li, C.; Zhang, F. A survey on the stability of fractional differential equations: Dedicated to Prof. YS Chen on the Occasion of his 80th Birthday. Eur. Phys. J. Spec. Top. 2011, 193, 27–47. [Google Scholar] [CrossRef]
- Jin, B. Fractional Differential Equations; Springer: Cham, Switzerland, 2021. [Google Scholar]
- González-Parra, G.; Arenas, A.J.; Chen-Charpentier, B.M. A fractional order epidemic model for the simulation of outbreaks of influenza A (H1N1). Math. Methods Appl. Sci. 2014, 37, 2218–2226. [Google Scholar] [CrossRef]
- Area, I.; Batarfi, H.; Losada, J.; Nieto, J.J.; Shammakh, W.; Torres, Á. On a fractional order Ebola epidemic model. Adv. Differ. Equ. 2015, 2015, 278. [Google Scholar] [CrossRef]
- Hamdan, N.; Kilicman, A. A fractional order SIR epidemic model for dengue transmission. Chaos Solitons Fractals 2018, 114, 55–62. [Google Scholar] [CrossRef]
- Chatterjee, A.N.; Ahmad, B. A fractional-order differential equation model of COVID-19 infection of epithelial cells. Chaos Solitons Fractals 2021, 147, 110952. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, F.; Yu, Q.; Li, T. Review of fractional epidemic models. Appl. Math. Model. 2021, 97, 281–307. [Google Scholar] [CrossRef]
- Petrás, I. Fractional Derivatives, Fractional Integrals, and Fractional Differential Equations in Matlab; IntechOpen: London, UK, 2011. [Google Scholar]
- Scherer, R.; Kalla, S.L.; Tang, Y.; Huang, J. The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 2011, 62, 902–917. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L.; Dehghan, S.; Chen, Y.; Xue, D. A review and evaluation of numerical tools for fractional calculus and fractional order controls. Int. J. Control 2017, 90, 1165–1181. [Google Scholar] [CrossRef]
- Garrappa, R. Numerical solution of fractional differential equations: A survey and a software tutorial. Mathematics 2018, 6, 16. [Google Scholar] [CrossRef]
- Li, T.; Wang, Y.; Liu, F.; Turner, I. Novel parameter estimation techniques for a multi-term fractional dynamical epidemic model of dengue fever. Numer. Algorithms 2019, 82, 1467–1495. [Google Scholar] [CrossRef]
- Das, M.; Samanta, G.; De la Sen, M. A Fractional Ordered COVID-19 Model Incorporating Comorbidity and Vaccination. Mathematics 2021, 9, 2806. [Google Scholar] [CrossRef]
- Atici, F.; Eloe, P. Initial value problems in discrete fractional calculus. Proc. Am. Math. Soc. 2009, 137, 981–989. [Google Scholar] [CrossRef]
- Cheng, J.F.; Chu, Y.M. Fractional difference equations with real variable. Abstr. Appl. Anal. 2012, 2012, 918529. [Google Scholar] [CrossRef]
- Ferreira, R.A. Discrete Fractional Calculus and Fractional Difference Equations; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Esteva, L.; Yang, H.M. Mathematical model to assess the control of Aedes aegypti mosquitoes by the sterile insect technique. Math. Biosci. 2005, 198, 132–147. [Google Scholar] [CrossRef]
- Anguelov, R.; Dumont, Y.; Lubuma, J. Mathematical modeling of sterile insect technology for control of anopheles mosquito. Comput. Math. Appl. 2012, 64, 374–389. [Google Scholar] [CrossRef]
- Li, M.Y.; Muldowney, J.S. Global stability for the SEIR model in epidemiology. Math. Biosci. 1995, 125, 155–164. [Google Scholar] [CrossRef]
- Jeger, M.; Madden, L.; Van Den Bosch, F. Plant virus epidemiology: Applications and prospects for mathematical modeling and analysis to improve understanding and disease control. Plant Dis. 2018, 102, 837–854. [Google Scholar] [CrossRef]
- He, S.; Peng, Y.; Sun, K. SEIR modeling of the COVID-19 and its dynamics. Nonlinear Dyn. 2020, 101, 1667–1680. [Google Scholar] [CrossRef]
- Agaba, G.O.; Soomiyol, M.C. Analysing the spread of COVID-19 using delay epidemic model with awareness. IOSR J. Math. 2020, 16, 52–59. [Google Scholar]
- Babasola, O.; Kayode, O.; Peter, O.J.; Onwuegbuche, F.C.; Oguntolu, F.A. Time-delayed modelling of the COVID-19 dynamics with a convex incidence rate. Inform. Med. Unlocked 2022, 35, 101124. [Google Scholar] [CrossRef]
- Sepulveda, G.; Arenas, A.J.; González-Parra, G. Mathematical Modeling of COVID-19 dynamics under two vaccination doses and delay effects. Mathematics 2023, 11, 369. [Google Scholar] [CrossRef]
- Zhang, J. Pandemic Mathematical Models, Epidemiology, and Virus Origins. In Optimization-Based Molecular Dynamics Studies of SARS-CoV-2 Molecular Structures: Research on COVID-19; Springer: Cham, Switzerland, 2023; pp. 897–908. [Google Scholar]
- Dickson, S.; Padmasekaran, S.; Kumar, P. Fractional order mathematical model for B. 1.1. 529 SARS-Cov-2 Omicron variant with quarantine and vaccination. Int. J. Dyn. Control 2023, 11, 2215–2231. [Google Scholar] [CrossRef]
- Allen, L. An Introduction to Mathematical Biology; Pearson-Prentice Hall: Hoboken, NJ, USA, 2007. [Google Scholar]
- Edelstein-Keshet, L. Mathematical Models in Biology; SIAM: Philadelphia, PA, USA, 2005. [Google Scholar]
- Castillo-Chavez, C.; Yakubu, A.A. Discrete-time SIS models with simple and complex population dynamics. IMA Vol. Math. Its Appl. 2002, 125, 153–164. [Google Scholar]
- Brauer, F.; Feng, Z.; Castillo-Chavez, C. Discrete epidemic models. Math. Biosci. Eng. 2009, 7, 1–15. [Google Scholar]
- Cooke, K.L.; Yorke, J.A. Some equations modelling growth processes and gonorrhea epidemics. Math. Biosci. 1973, 16, 75–101. [Google Scholar] [CrossRef]
- Khan, Q.J.A.; Krishnan, E.V. An Epidemic Model with a Time Delay in Transmission. Appl. Math. 2003, 48, 193–203. [Google Scholar] [CrossRef]
- Jackson, M.; Chen-Charpentier, B.M. Modeling plant virus propagation with delays. J. Comput. Appl. Math. 2017, 309, 611–621. [Google Scholar] [CrossRef]
- Liu, L. A delayed SIR model with general nonlinear incidence rate. Adv. Differ. Equ. 2015, 2015, 329. [Google Scholar] [CrossRef]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Al-Sulami, H.; El-Shahed, M.; Nieto, J.J.; Shammakh, W. On fractional order dengue epidemic model. Math. Probl. Eng. 2014, 2014, 456537. [Google Scholar] [CrossRef]
- Sardar, T.; Rana, S.; Bhattacharya, S.; Al-Khaled, K.; Chattopadhyay, J. A generic model for a single strain mosquito-transmitted disease with memory on the host and the vector. Math. Biosci. 2015, 263, 18–36. [Google Scholar] [CrossRef]
- Legg, J.P.; Kumar, P.L.; Makeshkumar, T.; Tripathi, L.; Ferguson, M.; Kanju, E.; Ntawuruhunga, P.; Cuellar, W. Cassava virus diseases: Biology, epidemiology, and management. In Advances in Virus Research; Elsevier: Amsterdam, The Netherlands, 2015; Volume 91, pp. 85–142. [Google Scholar]
- Gyamera, E.A.; Domfeh, O.; Ameyaw, G.A. Cacao Swollen Shoot Viruses in Ghana. Plant Dis. 2023, 107, 1261–1278. [Google Scholar] [CrossRef] [PubMed]
- Shi, R.; Zhao, H.; Tang, S. Global dynamic analysis of a vector-borne plant disease model. Adv. Differ. Equ. 2014, 2014, 59. [Google Scholar] [CrossRef]
- Erneux, T. Applied Delay Differential Equations; Springer Science & Business Media: New York, NY, USA, 2009; Volume 3. [Google Scholar]
- Anwar, N.; Naz, S.; Shoaib, M. Reliable numerical treatment with Adams and BDF methods for plant virus propagation model by vector with impact of time lag and density. Front. Appl. Math. Stat. 2022, 8, 1001392. [Google Scholar] [CrossRef]
- Diekmann, O.; Heesterbeek, J.; Roberts, M.G. The construction of next-generation matrices for compartmental epidemic models. J. R. Soc. Interface 2010, 7, 873–885. [Google Scholar] [CrossRef] [PubMed]
- Van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef] [PubMed]
- Ciupe, S.M.; Ribeiro, R.M.; Nelson, P.W.; Dusheiko, G.; Perelson, A.S. The role of cells refractory to productive infection in acute hepatitis B viral dynamics. Proc. Natl. Acad. Sci. USA 2007, 104, 5050–5055. [Google Scholar] [CrossRef]
- Kim, H.Y.; Kwon, H.D.; Jang, T.S.; Lim, J.; Lee, H.S. Mathematical modeling of triphasic viral dynamics in patients with HBeAg-positive chronic hepatitis B showing response to 24-week clevudine therapy. PLoS ONE 2012, 7, e50377. [Google Scholar] [CrossRef]
- Pourbashash, H.; Pilyugin, S.S.; De Leenheer, P.; McCluskey, C. Global analysis of within host virus models with cell-to-cell viral transmission. Discret. Contin. Dyn. Syst. Ser. B 2014, 19, 3341–3357. [Google Scholar] [CrossRef]
- Zhang, S.; Li, F.; Xu, X. Dynamics and control strategy for a delayed viral infection model. J. Biol. Dyn. 2022, 16, 44–63. [Google Scholar] [CrossRef]
- Rihan, F.A. Delay Differential Equations and Applications to Biology; Springer: Singapore, 2021. [Google Scholar]
- Wolfram Research, Inc. Mathematica, version 13.2; Wolfram: Champaign, IL, USA, 2022. [Google Scholar]
- Rackauckas, C.; Nie, Q. DifferentialEquations.jl—A Performant and Feature-Rich Ecosystem for Solving Differential Equations in Julia. J. Open Res. Softw. 2017, 5, 15. Available online: https://app.dimensions.aion2019/05/05 (accessed on 3 March 2024). [CrossRef]
- Widmann, D.; Rackauckas, C. DelayDiffEq: Generating Delay Differential Equation Solvers via Recursive Embedding of Ordinary Differential Equation Solvers. arXiv 2022, arXiv:2208.12879. [Google Scholar]
- Khalighi, M.; Benedetti, G.; Lahti, L. Fdesolver: A julia package for solving fractional differential equations. arXiv 2022, arXiv:2212.12550. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics–I. 1927. Bull. Math. Biol. 1991, 53, 33–55. [Google Scholar] [PubMed]
- Hattaf, K. On the Stability and Numerical Scheme of Fractional Differential Equations with Application to Biology. Computation 2022, 10, 97. [Google Scholar] [CrossRef]
- Chen-Charpentier, B. A Model of Hepatitis B Viral Dynamics with Delays. AppliedMath 2024, 4, 182–196. [Google Scholar] [CrossRef]
- Wu, C.; Wong, P.J. Dengue transmission: Mathematical model with discrete time delays and estimation of the reproduction number. J. Biol. Dyn. 2019, 13, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Dell’Anna, L. Solvable delay model for epidemic spreading: The case of Covid-19 in Italy. Sci. Rep. 2020, 10, 15763. [Google Scholar] [CrossRef] [PubMed]
- Shayak, B.; Sharma, M.M.; Rand, R.H.; Singh, A.; Misra, A. A Delay differential equation model for the spread of COVID-19. Int. J. Eng. Res. Appl. 2020, 10, 1–13. [Google Scholar]
- Saade, M.; Ghosh, S.; Banerjee, M.; Volpert, V. An epidemic model with time delays determined by the infectivity and disease durations. Math. Biosci. Eng. 2023, 20, 12864–12888. [Google Scholar] [CrossRef] [PubMed]
- Rihan, F.; Al-Mdallal, Q.; AlSakaji, H.; Hashish, A. A fractional-order epidemic model with time-delay and nonlinear incidence rate. Chaos Solitons Fractals 2019, 126, 97–105. [Google Scholar] [CrossRef]
- Singh, H. Numerical simulation for fractional delay differential equations. Int. J. Dyn. Control 2021, 9, 463–474. [Google Scholar] [CrossRef]
- Sun, D.; Liu, J.; Su, X.; Pei, G. Fractional differential equation modeling of the HBV infection with time delay and logistic proliferation. Front. Public Health 2022, 10, 1036901. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen-Charpentier, B. On Population Models with Delays and Dependence on Past Values. Axioms 2024, 13, 206. https://doi.org/10.3390/axioms13030206
Chen-Charpentier B. On Population Models with Delays and Dependence on Past Values. Axioms. 2024; 13(3):206. https://doi.org/10.3390/axioms13030206
Chicago/Turabian StyleChen-Charpentier, Benito. 2024. "On Population Models with Delays and Dependence on Past Values" Axioms 13, no. 3: 206. https://doi.org/10.3390/axioms13030206
APA StyleChen-Charpentier, B. (2024). On Population Models with Delays and Dependence on Past Values. Axioms, 13(3), 206. https://doi.org/10.3390/axioms13030206







