Limit Cycles of Discontinuous Piecewise Differential Hamiltonian Systems Separated by a Straight Line
Abstract
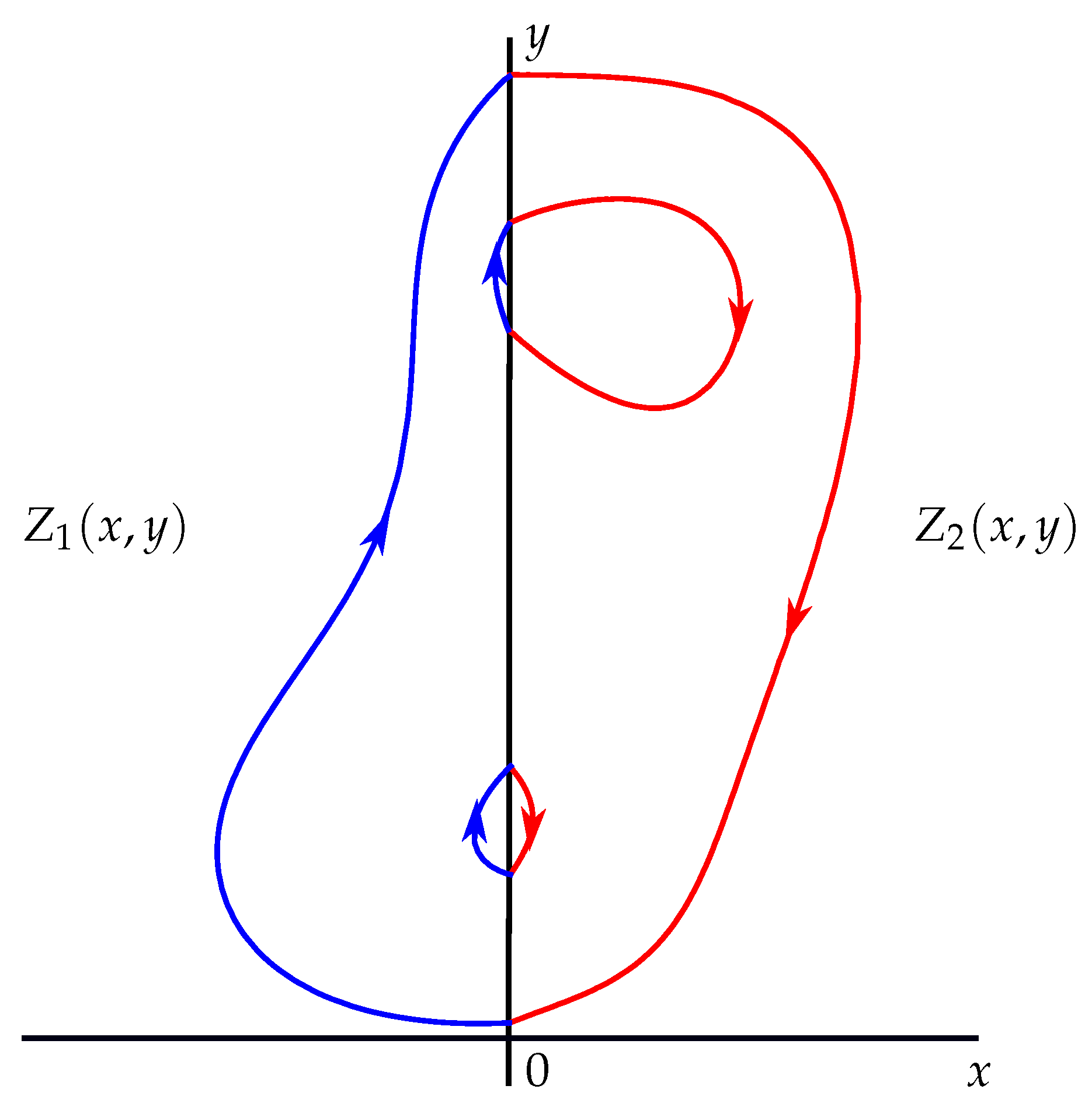
1. Introduction and Statement of the Main Results
2. Proof of Theorem 1
3. Examples
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Appell, J.; Hien, N.T.; Petrova, L.; Pryadko, I. Systems with Non-Smooth Inputs: Mathematical Models of Hysteresis Phenomena, Biological Systems, and Electric Circuits; Walter de Gruyter GmbH & Co KG: Berlin, Germany, 2021. [Google Scholar]
- Brhane, K.W.; Gebru, M.G.; Ahmad, A.G. Mathematical model for the dynamics of savanna ecosystem considering fire disturbances. J. Theor. Biol. 2021, 509, 110515. [Google Scholar] [CrossRef] [PubMed]
- Hening, A.; Li, Y. Stationary distributions of persistent ecological systems. J. Math. Biol. 2021, 82, 64. [Google Scholar] [CrossRef] [PubMed]
- Simpson, D.J.W. Bifurcations in Piecewise-Smooth Continuous Systems; World Scientific: Singapore, 2010; Volume 70. [Google Scholar]
- Bernardo, M.; Budd, C.; Champneys, A.R.; Kowalczyk, P. Piecewise-Smooth Dynamical Systems: Theory and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 163. [Google Scholar]
- Makarenkov, O.; Lamb, J.S. Dynamics and bifurcations of nonsmooth systems: A survey. Phys. D Nonlinear Phenom. 2012, 241, 826–1844. [Google Scholar] [CrossRef]
- Benabdallah, I.; Benterki, R.; Llibre, J. Limit cycles of discontinuous piecewise differential systems separated by a straight line and formed by cubic reversible isochronous centers having rational first integrals. Dyn. Contin. Discrete Impuls. Syst. Ser. B Appl. Algorithms 2024, 31, 1–23. [Google Scholar]
- Carmona, V.; Fernández-García, S.; Teruel, A. Saddle–node canard cycles in slow–fast planar piecewise linear differential systems. Nonlinear Anal. Hybrid Syst. 2024, 52, 101472. [Google Scholar] [CrossRef]
- Li, K.; Li, S. On the poincaré–bendixson index theorem for a class of piecewise linear differential systems. Qual. Theory Dyn. Syst. 2024, 23, 9. [Google Scholar] [CrossRef]
- Villanueva, Y.; Euzébio, R. Global dynamics of planar piecewise linear inelastic systems having straight lines as switching manifolds. Nonlinear Anal. Real World Appl. 2024, 76, 103994. [Google Scholar] [CrossRef]
- Zou, C.; Dong, G.; Liu, C.; Yang, J. The center problem on piecewise smooth differential systems with two zones. Discret. Contin. Dyn. Syst. 2024, 44, 523. [Google Scholar] [CrossRef]
- Chen, Z.; Zhu, J.; Liu, X. Non-differentiability of quasi-potential and non-smooth dynamics of optimal paths in the stochastic morris–lecar model: Type i and ii excitability. Nonlinear Dyn. 2019, 96, 2293–2305. [Google Scholar] [CrossRef]
- Artés, J.C.; Llibre, J.; Medrado, J.C.; Teixeira, M.A. Piecewise linear differential systems with two real saddles. Math. Comput. Simul. 2014, 95, 13–22. [Google Scholar] [CrossRef]
- Euzébio, R.D.; Llibre, J. On the number of limit cycles in discontinuous piecewise linear differential systems with two pieces separated by a straight line. J. Math. Anal. Appl. 2015, 424, 475–486. [Google Scholar] [CrossRef]
- Chen, H.; Li, D.; Xie, J.; Yue, Y. Limit cycles in planar continuous piecewise linear systems. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 438–454. [Google Scholar] [CrossRef]
- Freire, E.; Ponce, E.; Torres, F. A general mechanism to generate three limit cycles in planar filippov systems with two zones. Nonlinear Dyn. 2014, 78, 251–263. [Google Scholar] [CrossRef]
- Giannakopoulos, F.; Pliete, K. Planar systems of piecewise linear differential equations with a line of discontinuity. Nonlinearity 2001, 14, 1611. [Google Scholar] [CrossRef]
- Gouveia, M.R.; Llibre, J.; Novaes, D.D. On limit cycles bifurcating from the infinity in discontinuous piecewise linear differential systems. Appl. Math. Comput. 2015, 271, 365–374. [Google Scholar] [CrossRef]
- Huan, S.-M.; Yang, X.-S. Existence of limit cycles in general planar piecewise linear systems of saddle–saddle dynamics. Nonlinear Anal. Theory Methods Appl. 2013, 92, 82–95. [Google Scholar] [CrossRef]
- Huan, S.-M.; Yang, X.-S. On the number of limit cycles in general planar piecewise linear systems of node–node types. J. Math. Anal. Appl. 2014, 411, 340–353. [Google Scholar] [CrossRef]
- Li, L. Three crossing limit cycles in planar piecewise linear systems with saddle-focus type. Electron. J. Qual. Theory Differ. 2014, 2014, 1–14. [Google Scholar] [CrossRef]
- Filippov, A.F. Differential Equations with Discontinuous Righthand Sides: Control Systems; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 18. [Google Scholar]
- Fulton, W. Algebraic Curves: An Introduction to Algebaric Geometry; Addison-Wesley: Boston, MA, USA, 2008. [Google Scholar]
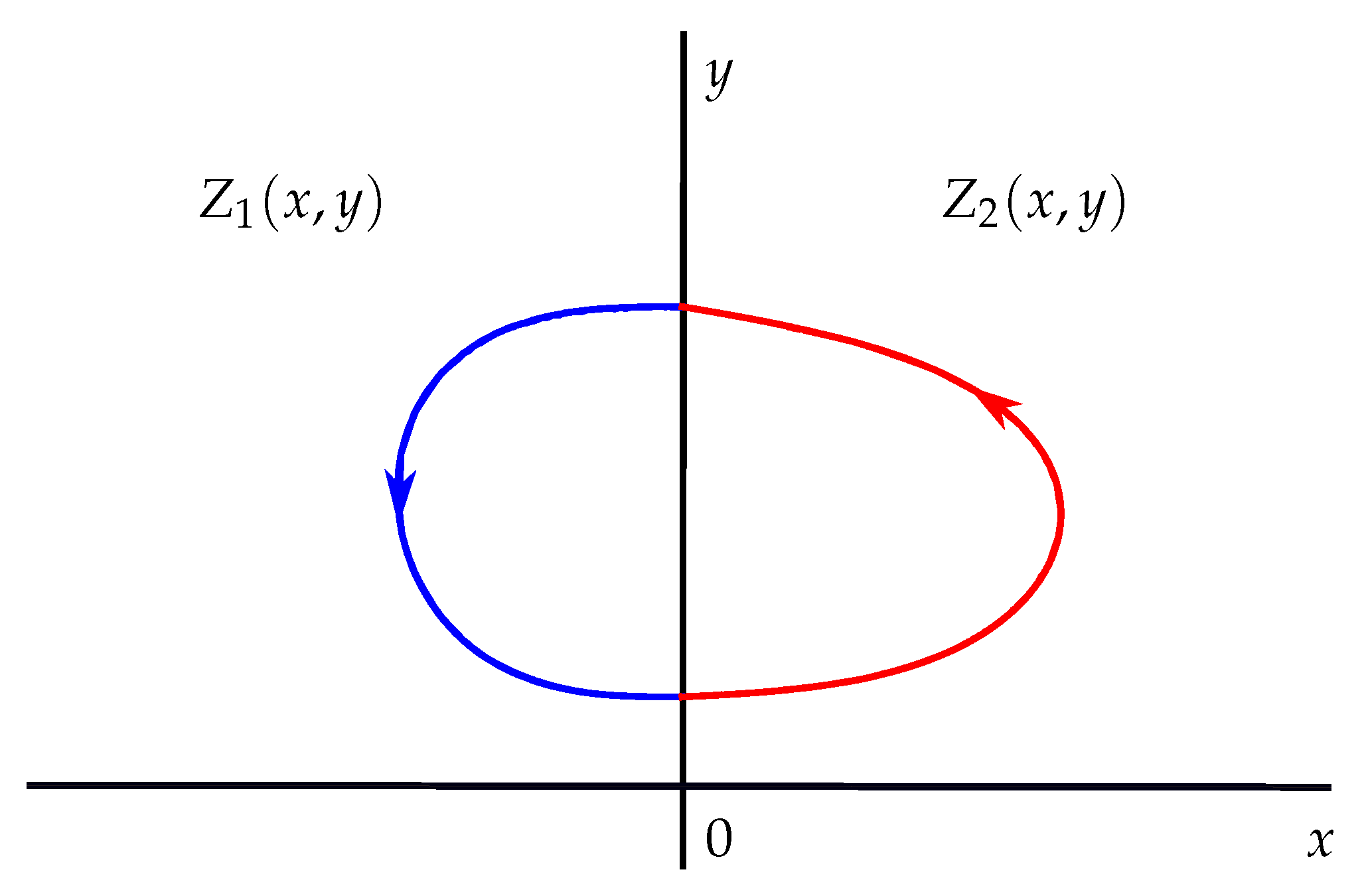
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Casimiro, J.A.; Llibre, J. Limit Cycles of Discontinuous Piecewise Differential Hamiltonian Systems Separated by a Straight Line. Axioms 2024, 13, 161. https://doi.org/10.3390/axioms13030161
Casimiro JA, Llibre J. Limit Cycles of Discontinuous Piecewise Differential Hamiltonian Systems Separated by a Straight Line. Axioms. 2024; 13(3):161. https://doi.org/10.3390/axioms13030161
Chicago/Turabian StyleCasimiro, Joyce A., and Jaume Llibre. 2024. "Limit Cycles of Discontinuous Piecewise Differential Hamiltonian Systems Separated by a Straight Line" Axioms 13, no. 3: 161. https://doi.org/10.3390/axioms13030161
APA StyleCasimiro, J. A., & Llibre, J. (2024). Limit Cycles of Discontinuous Piecewise Differential Hamiltonian Systems Separated by a Straight Line. Axioms, 13(3), 161. https://doi.org/10.3390/axioms13030161