Fuzzy-Set-Based Multi-Attribute Decision-Making, Its Computing Implementation, and Applications
Abstract
1. Introduction
2. Multi-Criteria Approach: Multi-Attribute Problems
2.1. Fuzzy Preference Modeling
- Reciprocal fuzzy preference relation is a fuzzy preference relation that satisfies the property of additive reciprocity (see expression in [59]).
- Nonreciprocal fuzzy preference relations are related to the notion of non-strict fuzzy preference relations associated with fuzzy preference structures [60].
2.2. Models and Their Construction
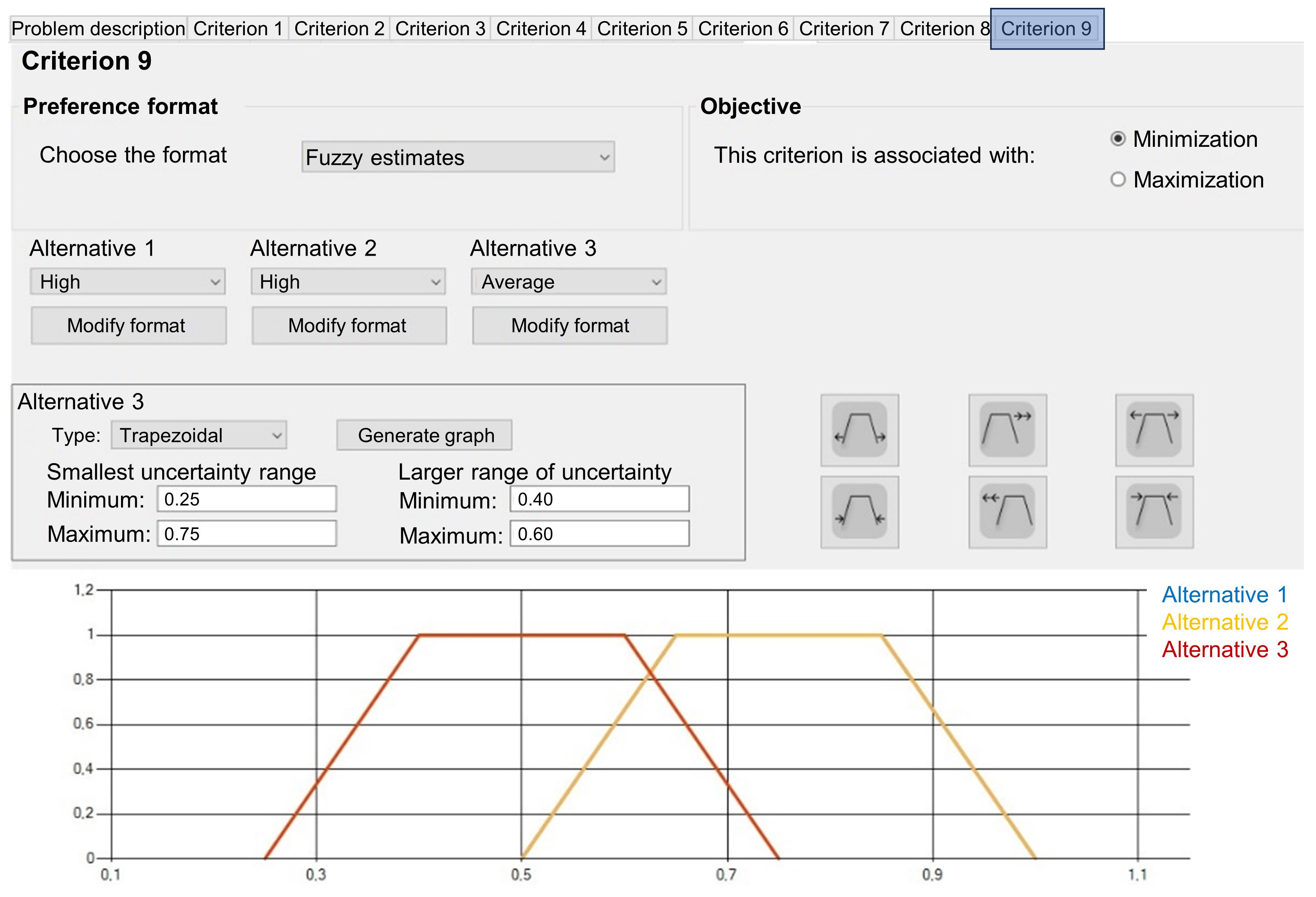
2.3. Preference Formats
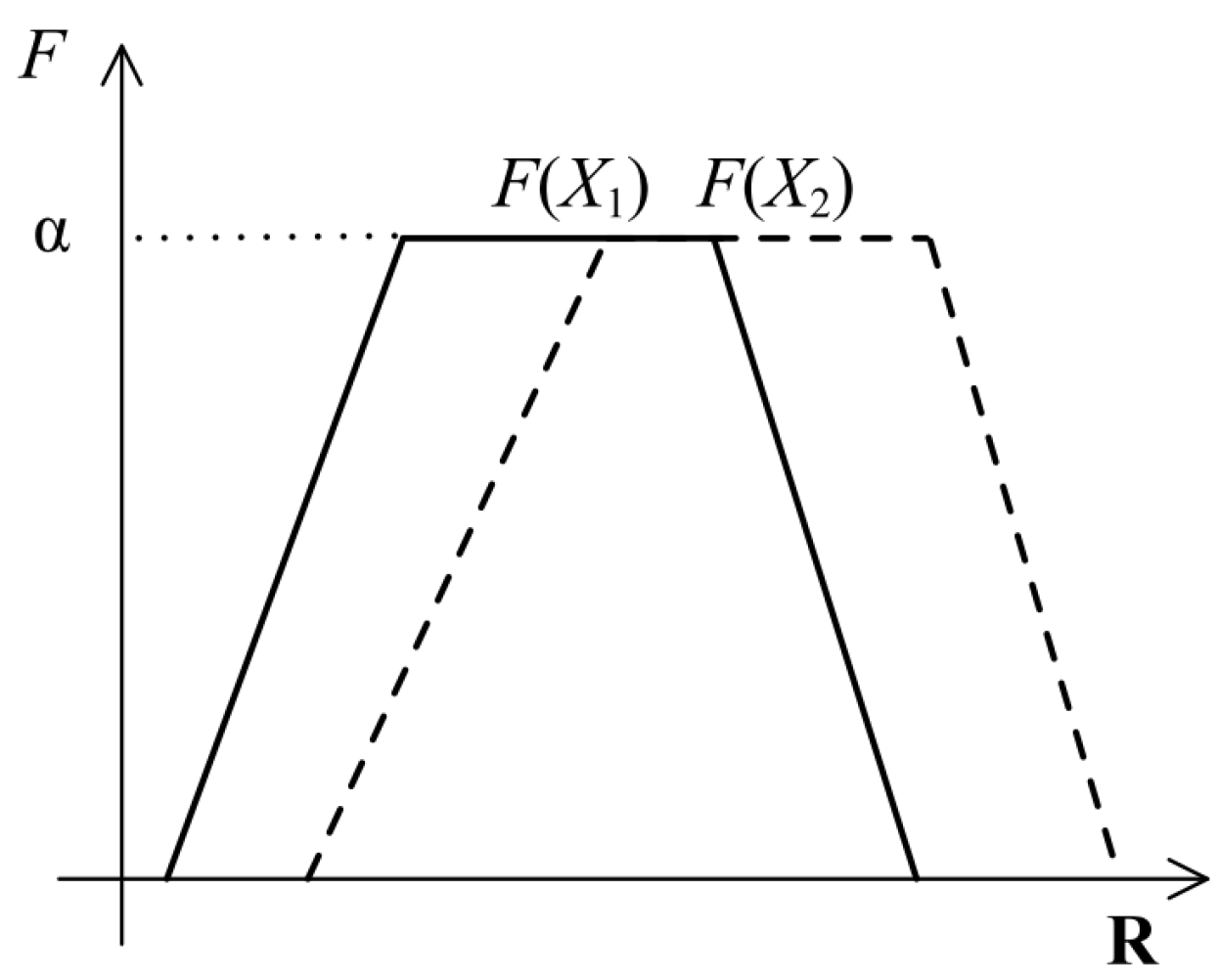
2.4. Transformation Functions
- Different formats are converted into a unique, single, and comparable format;
- Decision-makers choose the preferred format that they feel most comfortable with, offering psychological comfort in the evaluation process;
- Quantitative and qualitative information can be used concomitantly in the decision process through homogenization in the nonreciprocal fuzzy preference relations format.
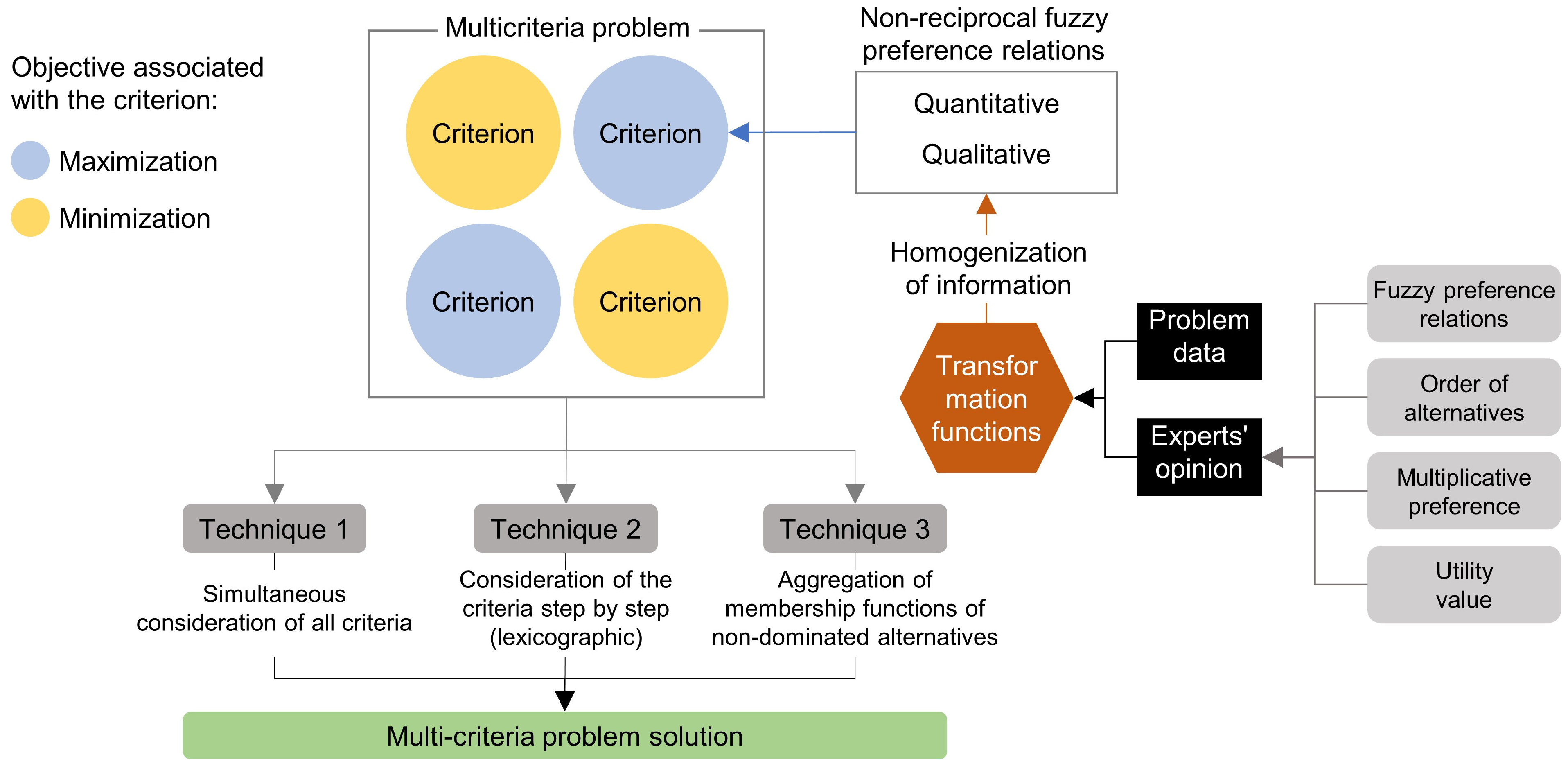
3. Multi-Criteria Decision-Making Techniques and Their Applications
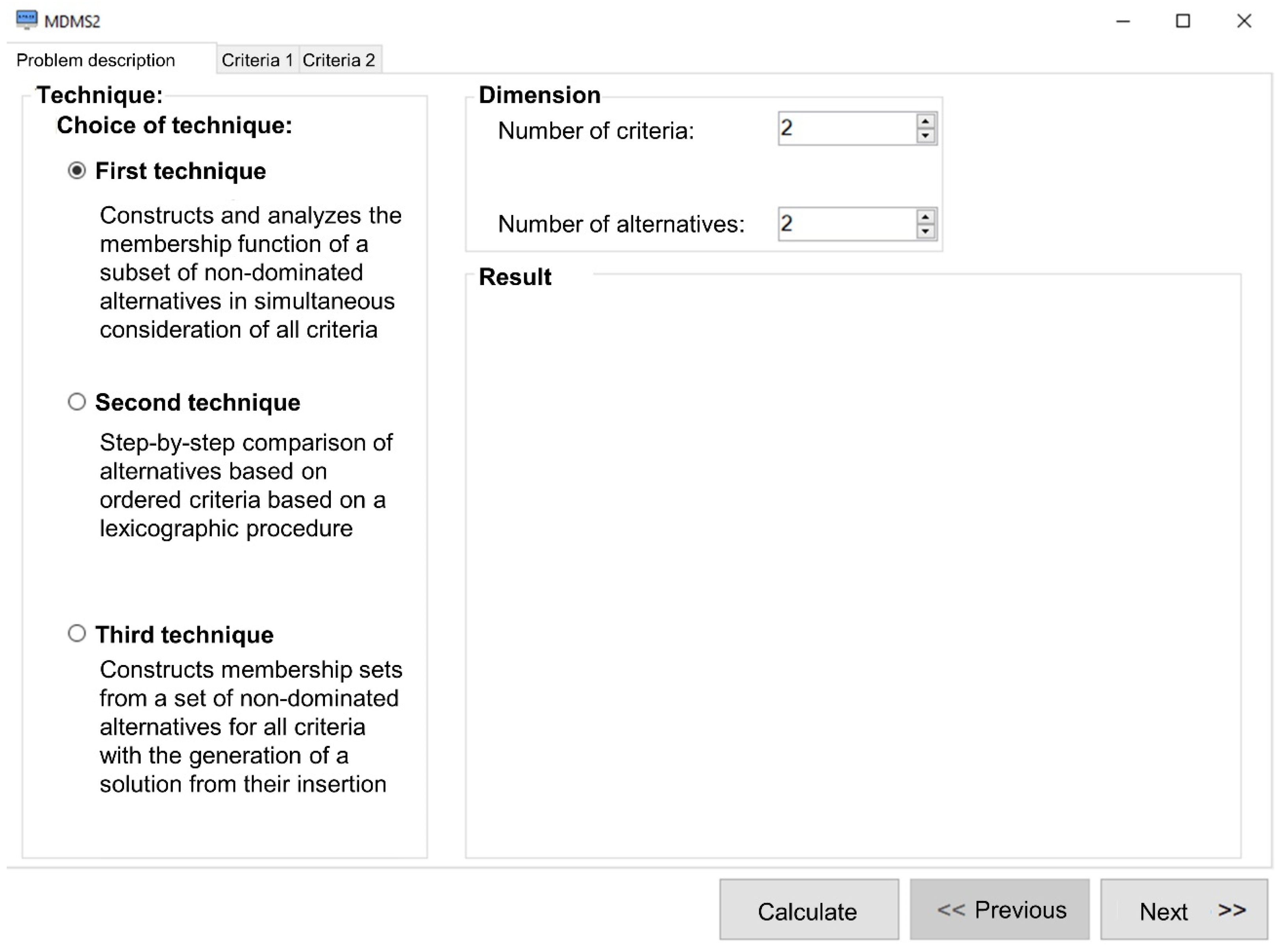
3.1. First Technique
3.2. Second Technique
3.3. Third Technique
4. Multi-Criteria Decision-Making System (MDMS2) Implementation
| Algorithm 1: Calculates and generates the result of the multi-attribute problem according to the first technique. |
| 1: public List<int> First-Technique() 2: double[][] intersection = Util.Copy-Matrix(Preference-Relations[0].Relations); 1st Step: 3: Perform the Intersection between all preference relations 4: for (int i = 1; i < Quantity-of-Criteria; i++) 5: for (int j = 0; j < intersection.Length; j++) 6: for (int k = 0; k < intersection[j].Length; k++) 7: if (Preference-Relations[i].Relacao[j][k] < intersection[j]k]) 8: intersection[j][k] = Preference-Relations[i]. Relation[j]k];; 9: Console.WriteLine("\nIntersection:\n"); 10: Console.WriteLine(Util.Print-Matrix(intersection)); 2nd Step: 11: Transform to the strict preference relation double[][] strict = To-Strict(intersection); 12: Console.WriteLine("\nStrict:\n"); 13: Console.WriteLine(Util.Print-Matrix(strict)); 3rd Step: 14: Generate the Non-Dominated Set of Alternatives double[] non-Dominated = Non-Dominated-Set(strict); 15: Console.WriteLine("\nSet of Non-Dominated:\n"); 16: Console.WriteLine(Util.Print-Vector(Non-Dominated)); 4th Step: 17: Generate the list of results with the indices of the alternatives return Result-ND(not-Dominated); |
| Algorithm 2: Method that transforms an ordered array into the additive reciprocal fuzzy preference relation. |
| 1: public static double[][] Ordered-To-Not-Reciprocal(int[] order-Alternatives) 2: int num-Alternatives = order- Alternatives.Length; double[][] 3: non-Reciprocal=new double[num-Alternatives][]; 4: for (int i = 0; i < num- Alternatives; i++) 5: no-Reciprocal[i]=new double[num-Alternatives]; 6: for (int j = 0; j < num Alternatives; j++) 7: if (order- Alternatives [i] > order- Alternatives [j]) 8: non-Reciprocal[i][j] = 0.5 + ((double)(order-Alternatives[j] - order-Alternatives[i]) / (2.0 * (double)(num-Alternatives - 1))); 9: else 10: non-Reciprocal[i][j] = 1; 11: return non-Reciprocal; |
5. Application Example: Choice of an Alternative Energy Source
5.1. Statement of the Decision Problem
- Alternative 1: Diesel generation source with an installed capacity of 23.0 MW;
- Alternative 2: Wind energy source with an installed capacity of 42.6 MW;
- Alternative 3: Solar energy source with an installed capacity of 69.0 MW.
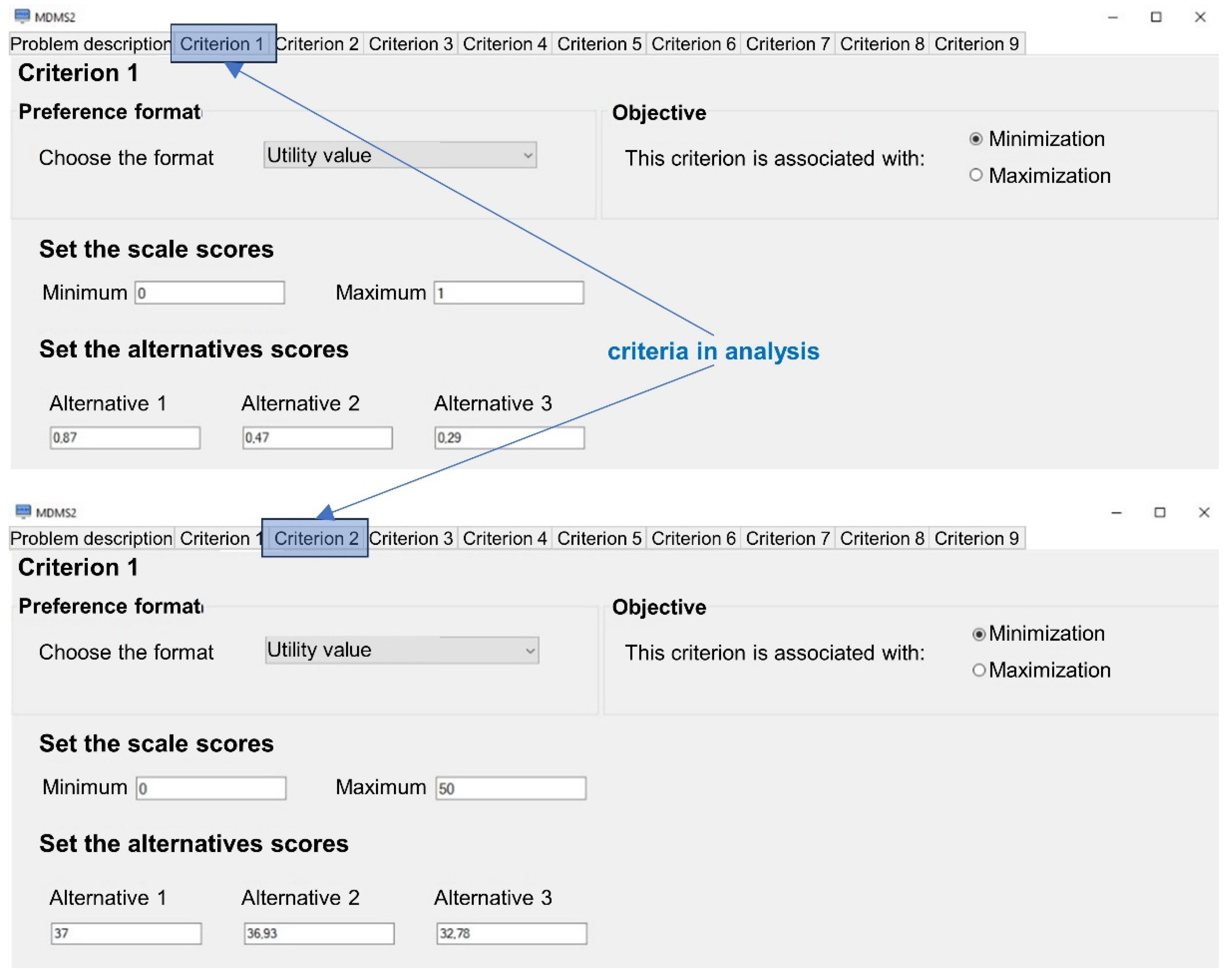
5.2. Steps to Solve the Problem
5.3. Processing and Solving the Decision Problem
5.4. Concluding Remarks
- Applying the second technique may lead to solutions different from the results obtained from the first technique.
- The first technique and the third share the same generic basis but may sometimes generate different solutions.
- The third technique is preferred from a substantial point of view.
- The first technique can lead to the choice of alternatives with a degree of non-dominance equal to one, which does not represent the best solution from the point of view of all preference relations.
- The third technique can generate alternatives with a degree of non-dominance equal to one only for alternatives that are the best solutions from the point of view of all fuzzy preference relations.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ibrahim, A.; Kadir, T.A.A.; Daniyal, H.; Kamaludin, A. Overviews of Uncertainty: Concepts, Categories and Coping Strategies in Decision-making. In Proceedings of International Conference on Emerging Technologies and Intelligent Systems: ICETIS 2021; Springer International Publishing: Cham, Switzerland, 2022; Volume 2, pp. 783–794. [Google Scholar]
- Bevan, L.D. The ambiguities of uncertainty: A review of uncertainty frameworks relevant to the assessment of environmental change. Futures 2022, 137, 102919. [Google Scholar] [CrossRef]
- Fallah Lajimi, H.; Jafari Soruni, Z. Suppliers Evaluation in Uncertain Conditions by Combining Dempster Shafer and Multi-Criteria Decision-making Techniques. J. Exec. Manag. 2020, 11, 115–150. [Google Scholar]
- Brodetskiy, G.L.; Gusev, D.A.; Shidlovskii, I.G. Multi-criteria optimisation under the conditions of uncertainty in logistics and supply chain management. Int. J. Logist. Syst. Manag. 2021, 39, 207–227. [Google Scholar] [CrossRef]
- Domnikov, A.; Khodorovsky, M.; Domnikova, L. Methodological approach to choosing alternatives for the development of energy systems in conditions of uncertainty and multi-criteria. Int. J. Energy Prod. Manag. 2022, 7, 276–286. [Google Scholar] [CrossRef]
- Wang, J.Q.; Peng, J.J.; Zhang, H.Y.; Liu, T.; Chen, X.H. An uncertain linguistic multi-criteria group decision-making method based on a cloud model. Group Decis. Negot. 2015, 24, 171–192. [Google Scholar] [CrossRef]
- Liu, P.; Diao, H.; Zou, L.; Deng, A. Uncertain multi-attribute group decision-making based on linguistic-valued intuitionistic fuzzy preference relations. Inf. Sci. 2020, 508, 293–308. [Google Scholar] [CrossRef]
- Yi, Z. Decision-making based on probabilistic linguistic term sets without loss of information. Complex Intell. Syst. 2022, 8, 2435–2449. [Google Scholar] [CrossRef]
- Maghrabie, H.F.; Beauregard, Y.; Schiffauerova, A. Grey-based Multi-Criteria Decision Analysis approach: Addressing uncertainty at complex decision problems. Technol. Forecast. Soc. Chang. 2019, 146, 366–379. [Google Scholar] [CrossRef]
- Pelissari, R.; Oliveira, M.C.; Abackerli, A.J.; Ben-Amor, S.; Assumpção, M.R.P. Techniques to model uncertain input data of multi-criteria decision-making problems: A literature review. Int. Trans. Oper. Res. 2021, 28, 523–559. [Google Scholar] [CrossRef]
- Garg, H.; Mahmood, T.; ur Rehman, U.; Nguyen, G.N. Multi-attribute decision-making approach based on Aczel-Alsina power aggregation operators under bipolar fuzzy information & its application to quantum computing. Alex. Eng. J. 2023, 82, 248–259. [Google Scholar]
- Whittemore, B.J.; Yovits, M.C. A generalized conceptual development for the analysis and flow of information. J. Am. Soc. Inf. Sci. 1973, 24, 221–231. [Google Scholar] [CrossRef]
- Rasconi, R.; Cesta, A.; Policella, N. Validating scheduling approaches against executional uncertainty. J. Intell. Manuf. 2010, 21, 49–64. [Google Scholar] [CrossRef]
- Broekhuizen, H.; Groothuis-Oudshoorn, C.G.; van Til, J.A.; Hummel, J.M.; IJzerman, M.J. A review and classification of approaches for dealing with uncertainty in multi-criteria decision analysis for healthcare decisions. Pharmacoeconomics 2015, 33, 445–455. [Google Scholar] [CrossRef] [PubMed]
- Kleyle, R.; De Korvin, A. A two-phase approach to making decisions involving goal uncertainty. J. Inf. Sci. 1985, 11, 161–171. [Google Scholar] [CrossRef]
- Alò, R.A.; de Korvin, A.; Kleyle, R. Emergence of a dominant course of action in a general feedback loop when goal uncertainty is present. J. Am. Soc. Inf. Sci. 1987, 38, 111–117. [Google Scholar] [CrossRef]
- Korvin, A.D.; Kleyle, R.M. Goal uncertainty and the supermartingale property in an information feedback loop. Stoch. Anal. Appl. 1989, 7, 291–307. [Google Scholar] [CrossRef]
- Brouwer, R.; De Blois, C. Integrated modelling of risk and uncertainty underlying the cost and effectiveness of water quality measures. Environ. Model. Softw. 2008, 23, 922–937. [Google Scholar] [CrossRef]
- Guillaume, J.H.; Arshad, M.; Jakeman, A.J.; Jalava, M.; Kummu, M. Robust discrimination between uncertain management alternatives by iterative reflection on crossover point scenarios: Principles, design and implementations. Environ. Model. Softw. 2016, 83, 326–343. [Google Scholar] [CrossRef]
- Ekel, P.; Pedrycz, W.; Pereira, J., Jr. Multi-Criteria Decision-Making under Conditions of Uncertainty: A Fuzzy Set Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Cámara, J.; Troya, J.; Vallecillo, A.; Bencomo, N.; Calinescu, R.; Cheng, B.H.; Garlan, D.; Schmerl, B. The uncertainty interaction problem in self-adaptive systems. Softw. Syst. Model. 2022, 21, 1277–1294. [Google Scholar] [CrossRef]
- Masoumi, R. A comprehensive multi-criteria decision-making system using analytical hierarchy process and decision tree tools to choose the best alternative for a refinery master plan. Int. J. Multicriteria Decis. Mak. 2015, 5, 182–210. [Google Scholar]
- Chatterjee, S.; Das, A. An ensemble algorithm using quantum evolutionary optimization of weighted type-II fuzzy system and staged Pegasos Quantum Support Vector Classifier with multi-criteria decision making system for diagnosis and grading of breast cancer. Soft Comput. 2023, 27, 7147–7178. [Google Scholar] [CrossRef]
- Medineckiene, M.; Zavadskas, E.K.; Björk, F.; Turskis, Z. Multi-criteria decision-making system for sustainable building assessment/certification. Arch. Civ. Mech. Eng. 2015, 15, 11–18. [Google Scholar] [CrossRef]
- Sun, W.; Zhang, Y.; Luo, M.; Zhang, Z.; Zhang, D. A multi-criteria decision-making system for selecting cutting parameters in milling process. J. Manuf. Syst. 2022, 65, 498–509. [Google Scholar] [CrossRef]
- Salem, O.M.; Miller, R.A.; Deshpande, A.S.; Arurkar, T.P. Multi-criteria decision-making system for selecting an effective plan for bridge rehabilitation. Struct. Infrastruct. Eng. 2013, 9, 806–816. [Google Scholar] [CrossRef]
- Yousefi, H.; Motlagh, S.G.; Montazeri, M. Multi-Criteria Decision-Making System for Wind Farm Site-Selection Using Geographic Information System (GIS): Case Study of Semnan Province, Iran. Sustainability 2022, 14, 7640. [Google Scholar] [CrossRef]
- Yigit, T.; Isik, A.H.; Ince, M. Multi criteria decision making system for learning object repository. Procedia-Soc. Behav. Sci. 2014, 141, 813–816. [Google Scholar] [CrossRef][Green Version]
- Haghighi Fard, S.M.; Doratli, N. Evaluation of Resilience in Historic Urban Areas by Combining Multi-Criteria Decision-Making System and GIS, with Sustainability and Regeneration Approach: The Case Study of Tehran (IRAN). Sustainability 2022, 14, 2495. [Google Scholar] [CrossRef]
- Ekel, P.; Pedrycz, W.; Schinzinger, R. A general approach to solving a wide class of fuzzy optimization problems. Fuzzy Sets Syst. 1998, 97, 49–66. [Google Scholar] [CrossRef]
- Pereira, J.G., Jr.; Ekel, P.Y.; Palhares, R.M.; Parreiras, R.O. On multi-criteria decision-making under conditions of uncertainty. Inf. Sci. 2015, 324, 44–59. [Google Scholar] [CrossRef]
- Stanojević, B.; Stanojević, M.; Nădăban, S. Reinstatement of the extension principle in approaching mathematical programming with fuzzy numbers. Mathematics 2021, 9, 1272. [Google Scholar] [CrossRef]
- Wu, H.C. Solving Fuzzy Optimization Problems Using Shapley Values and Evolutionary Algorithms. Mathematics 2023, 11, 4871. [Google Scholar] [CrossRef]
- Comes, T.; Hiete, M.; Schultmann, F. An approach to multi-criteria decision problems under severe uncertainty. J. Multi-Criteria Decis. Anal. 2013, 20, 29–48. [Google Scholar] [CrossRef]
- Ma, J.; Harstvedt, J.D.; Jaradat, R.; Smith, B. Sustainability driven multi-criteria project portfolio selection under uncertain decision-making environment. Comput. Ind. Eng. 2020, 140, 106236. [Google Scholar] [CrossRef]
- Sun, C.; Li, S.; Deng, Y. Determining weights in multi-criteria decision making based on negation of probability distribution under uncertain environment. Mathematics 2020, 8, 191. [Google Scholar] [CrossRef]
- Zhang, Z.; Liao, H.; Tang, A. Renewable energy portfolio optimization with public participation under uncertainty: A hybrid multi-attribute multi-objective decision-making method. Appl. Energy 2022, 307, 118267. [Google Scholar] [CrossRef]
- Li, Y.; Kou, G.; Li, G.; Hefni, M.A. Fuzzy multi-attribute information fusion approach for finance investment selection with the expert reliability. Appl. Soft Comput. 2022, 126, 109270. [Google Scholar] [CrossRef]
- Wu, X.; Liao, H. Geometric linguistic scale and its application in multi-attribute decision-making for green agricultural product supplier selection. Fuzzy Sets Syst. 2023, 458, 182–200. [Google Scholar] [CrossRef]
- Garcia-Garcia, G. Using Multi-Criteria Decision Making to optimise solid waste management. Curr. Opin. Green Sustain. Chem. 2022, 37, 100650. [Google Scholar] [CrossRef]
- Sarwar, A.; Imran, M. Prioritizing infection prevention and control activities for SARS-CoV-2 (COVID-19): A multi-criteria decision-analysis method. J. Healthc. Leadersh. 2021, 13, 77–84. [Google Scholar] [CrossRef]
- Sun, R.; Gong, Z.; Gao, G.; Shah, A.A. Comparative analysis of Multi-Criteria Decision-Making methods for flood disaster risk in the Yangtze River Delta. Int. J. Disaster Risk Reduct. 2020, 51, 101768. [Google Scholar] [CrossRef]
- Sharma, M.; Sehrawat, R. A hybrid multi-criteria decision-making method for cloud adoption: Evidence from the healthcare sector. Technol. Soc. 2020, 61, 101258. [Google Scholar] [CrossRef]
- Jing, D.; Imeni, M.; Edalatpanah, S.A.; Alburaikan, A.; Khalifa, H.A.E.W. Optimal selection of stock portfolios using multi-criteria decision-making methods. Mathematics 2023, 11, 415. [Google Scholar] [CrossRef]
- Kahraman, C.; Onar, S.C.; Oztaysi, B. Fuzzy multi-criteria decision-making: A literature review. Int. J. Comput. Intell. Syst. 2015, 8, 637–666. [Google Scholar] [CrossRef]
- Ekel, P.Y. Fuzzy sets and models of decision-making. Comput. Math. Appl. 2002, 44, 863–875. [Google Scholar] [CrossRef]
- Demirtas, E.A.; Üstün, Ö. An integrated multi-objective decision-making process for supplier selection and order allocation. Omega 2008, 36, 76–90. [Google Scholar] [CrossRef]
- Roijers, D.M.; Whiteson, S.; Brachman, R.; Stone, P. Multi-Objective Decision-Making; Morgan & Claypool: San Rafael, CA, USA, 2017. [Google Scholar]
- Maity, G.; Kumar Roy, S. Solving a multi-objective transportation problem with nonlinear cost and multi-choice demand. Int. J. Manag. Sci. Eng. Manag. 2016, 11, 62–70. [Google Scholar] [CrossRef]
- Alvarez, P.A.; Ishizaka, A.; Martínez, L. Multiple-criteria decision-making sorting methods: A survey. Expert Syst. Appl. 2021, 183, 115368. [Google Scholar] [CrossRef]
- Belyaev, L.S. A Practical Approach to Choosing Alternate Solutions to Complex Optimization Problems under Uncertainty; IASA: Laxenburg, Austria, 1977. [Google Scholar]
- Wang, G.; Wu, L.; Liu, Y.; Ye, X. A review on fuzzy preference modeling methods for group decision-making. J. Intell. Fuzzy Syst. 2021, 40, 10645–10660. [Google Scholar] [CrossRef]
- Perny, P.; Roubens, M. Fuzzy preference modeling. In Fuzzy Sets in Decision Analysis, Operations Research and Statistics; Springer: Boston, MA, USA, 1998; pp. 3–30. [Google Scholar]
- Büyüközkan, G.; Feyzioğlu, O. Group decision making to better respond customer needs in software development. Comput. Ind. Eng. 2005, 48, 427–441. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Feyzioğlu, O.; Ruan, D. Fuzzy group decision-making to multiple preference formats in quality function deployment. Comput. Ind. 2007, 58, 392–402. [Google Scholar] [CrossRef]
- Zhou, W.; Xu, Z. Asymmetric hesitant fuzzy sigmoid preference relations in the analytic hierarchy process. Inf. Sci. 2016, 358, 191–207. [Google Scholar] [CrossRef]
- Chiclana, F.; Herrera, F.; Herrera-Viedma, E. Reciprocity and consistency of fuzzy preference relations. Princ. Fuzzy Prefer. Model. Decis. Mak. 2003, 123–142. Available online: https://sci2s.ugr.es/sites/default/files/ficherosPublicaciones/0352_ReciprocityConsistency-2003.pdf (accessed on 9 February 2024).
- Dopazo, E.; Martínez-Céspedes, M.L. Rank aggregation methods dealing with ordinal uncertain preferences. Expert Syst. Appl. 2017, 78, 103–109. [Google Scholar] [CrossRef]
- Parreiras, R.; Ekel, P. Construction of nonreciprocal fuzzy preference relations with the use of preference functions. Pesqui. Oper. 2013, 33, 305–323. [Google Scholar] [CrossRef]
- Ramalho, F.D.; Ekel, P.Y.; Pedrycz, W.; Pereira, J.G., Jr.; Soares, G.L. Multi-criteria decision-making under conditions of uncertainty in application to multi-objective allocation of resources. Inf. Fusion 2019, 49, 249–261. [Google Scholar] [CrossRef]
- Fodor, J.C.; Roubens, M.R. Fuzzy Preference Modelling and Multi-Criteria Decision Support; Springer: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Orlovsky, S. Problems of Decision-Making with Fuzzy Information; IASA: Laxenburg, Austria, 1983. [Google Scholar]
- Ekel, P.; Kokshenev, I.; Parreiras, R.; Pedrycz, W.; Pereira Jr, J. Multiobjective and multiattribute decision making in a fuzzy environment and their power engineering applications. Inf. Sci. 2016, 361, 100–119. [Google Scholar] [CrossRef]
- Pedrycz, W.; Ekel, P.; Parreiras, R. Fuzzy Multi-Criteria Decision-Making: Models, Methods, and Applications; John Wiley & Sons: Chichester, UK, 2011. [Google Scholar]
- Ekel, P.Y.; Neto, F.H.S. Algorithms of discrete optimization and their application to problems with fuzzy coefficients. Inf. Sci. 2006, 176, 2846–2868. [Google Scholar] [CrossRef]
- Kokshenev, I.; Parreiras, R.O.; Ekel, P.Y.; Alves, G.B.; Menicucci, S.V. A Web-based Decision Support Center for Electrical Energy Companies. IEEE Trans. Fuzzy Syst. 2014, 23, 16–28. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, J.C.; Chong, P.P. Decision consolidation: Criteria weight determination using multiple preference formats. Decis. Support Syst. 2004, 38, 247–258. [Google Scholar] [CrossRef]
- Chao, X.; Kou, G.; Peng, Y.; Viedma, E.H. Large-scale group decision-making with non-cooperative behaviors and heterogeneous preferences: An application in financial inclusion. Eur. J. Oper. Res. 2021, 288, 271–293. [Google Scholar] [CrossRef]
- Wang, Y.M.; Chin, K.S. A linear goal programming approach to determining the relative importance weights of customer requirements in quality function deployment. Inf. Sci. 2011, 181, 5523–5533. [Google Scholar] [CrossRef]
- Wu, Z.; Liao, H. A consensus reaching process for large-scale group decision making with heterogeneous preference information. Int. J. Intell. Syst. 2021, 36, 4560–4591. [Google Scholar] [CrossRef]
- Libório, M.P.; Ekel, P.I.; Bernardes, P.; Gomes LF, A.M.; Vieira, D.A.G. Specialists’ knowledge and cognitive stress in making pairwise comparisons. OPSEARCH 2023, 1–20. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Herrera, F.; Chiclana, F. A consensus model for multiperson decision-making with different preference structures. IEEE Trans. Syst. Man Cybern. Part A Syst. Hum. 2002, 32, 394–402. [Google Scholar] [CrossRef]
- Herrera-Viedma, E.; Herrera, F.; Chiclana, F.; Luque, M. Some issues on consistency of fuzzy preference relations. Eur. J. Oper. Res. 2004, 154, 98–109. [Google Scholar] [CrossRef]
- Chiclana, F.; Herrera, F.; Herrera-Viedma, E. Integrating three representation models in fuzzy multipurpose decision-making based on fuzzy preference relations. Fuzzy Sets Syst. 1998, 97, 33–48. [Google Scholar] [CrossRef]
- Chiclana, F.; Herrera, F.; Herrera-Viedma, E. Integrating multiplicative preference relations in a multipurpose decision-making model based on fuzzy preference relations. Fuzzy Sets Syst. 2001, 122, 277–291. [Google Scholar] [CrossRef]
- Saaty, T.L. Decision making—The analytic hierarchy and network processes (AHP/ANP). J. Syst. Sci. Syst. Eng. 2004, 13, 1–35. [Google Scholar] [CrossRef]
- Banerjee, A. Rational choice under fuzzy preferences: The Orlovsky choice function. Fuzzy Sets Syst. 1993, 32, 295–299. [Google Scholar] [CrossRef]
- Bellman, R.E.; Zadeh, L.A. Decision-making in a fuzzy environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Saraswat, S.K.; Digalwar, A.K. Evaluation of energy alternatives for sustainable development of energy sector in India: An integrated Shannon’s entropy fuzzy multi-criteria decision approach. Renew. Energy 2021, 171, 58–74. [Google Scholar] [CrossRef]
- Shatnawi, N.; Abu-Qdais, H.; Abu Qdais, F. Selecting renewable energy options: An application of multi-criteria decision making for Jordan. Sustain. Sci. Pract. Policy 2021, 17, 209–219. [Google Scholar] [CrossRef]
- Xue, X.; Zhang, Q.; Cai, X.; Ponkratov, V.V. Multi-Criteria Decision Analysis for Evaluating the Effectiveness of Alternative Energy Sources in China. Sustainability 2023, 15, 8142. [Google Scholar] [CrossRef]
- Husain, A.M.; Hasan, M.M.; Khan, Z.A.; Asjad, M. A robust decision-making approach for the selection of an optimal renewable energy source in India. Energy Convers. Manag. 2024, 301, 117989. [Google Scholar] [CrossRef]
- Silva, L.M.L.; Ekel, P.; Vieira, D.A.G.; Libório, M.P.; D’angelo, M.F.S.V. Spatial Decision-Making under Uncertainties for Supporting the Prospection of Sites for Hybrid Renewable Energy Generation Systems. Energies 2023, 16, 4880. [Google Scholar]
- Libório, M.P.; Martinuci, O.D.; Bernardes, P.; Krohling, N.C.; Castro, G.; Guerra, H.L.; Ribeiro, E.A.; Fonzar, U.J.; Francisco, Í.D. Social vulnerability and COVID-19 in Maringá, Brazil. Spat. Inf. Res. 2023, 31, 51–59. [Google Scholar] [CrossRef]
- Fusco, E.; Libório, M.P.; Rabiei-Dastjerdi, H.; Vidoli, F.; Brunsdon, C.; Ekel, P.I. Harnessing Spatial Heterogeneity in Composite Indicators through the Ordered Geographically Weighted Averaging (OGWA) Operator. Geogr. Anal. 2023. [Google Scholar] [CrossRef]
- Xenodoxidou, E.; Theodorou, P.; Karagianni, R.; Intas, G.; Platis, C. Factors that determine parents’ satisfaction with the care given to their children in two Greek public hospitals. Health Res. J. 2022, 8, 97–110. [Google Scholar] [CrossRef]
- Ribeiro, L.; Diniz, A.M.; Lages, L.B. Decision-making in an inquisitorial system: Lessons from Brazil. Law Soc. Rev. 2022, 56, 101–121. [Google Scholar] [CrossRef]
- Pinto, M.R.; Salume, P.K.; Barbosa, M.W.; de Sousa, P.R. The path to digital maturity: A cluster analysis of the retail industry in an emerging economy. Technol. Soc. 2023, 72, 102191. [Google Scholar] [CrossRef]
- Rabiei-Dastjerdi, H.; Mohammadi, S.; Samouei, R.; Kazemi, M.; Matthews, S.; McArdle, G.; Homayouni, S.; Kiani, B.; Sadeghi, R. Measuring Spatial Accessibility to Healthcare Facilities in Isfahan Metropolitan Area in Iran. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, 10, 623–630. [Google Scholar] [CrossRef]
- Morais, D.C.; de Almeida, A.T.; Figueira, J.R. A sorting model for group decision making: A case study of water losses in Brazil. Group Decis. Negot. 2014, 23, 937–960. [Google Scholar] [CrossRef]
- Figueiredo, L.R.; Frej, E.A.; Soares, G.L.; Ekel, P.Y. Group Decision-Based Construction of Scenarios for Multicriteria Analysis in Conditions of Uncertainty on the Basis of Quantitative and Qualitative Information. Group Decis. Negot. 2021, 30, 665–696. [Google Scholar] [CrossRef]
| Criteria | Scale | Diesel Generation | Wind Generation | Solar Generation | |
|---|---|---|---|---|---|
| 1 | Capacity factor | % | 87 | 47 | 29 |
| 2 | Levelized cost of energy | USD/kW | 37.00 | 36.93 | 0.08 |
| 3 | Deployment time | Months | 24 | 30 | 22 |
| 4 | Space requirement | m2/kW | 4 | 43 | 23 |
| 5 | Power-plant lifetime | Years | 15 | 30 | 25 |
| 6 | Greenhouse gas emissions | tCO2/MWh | 0.76 | 0.00 | 0.00 |
| 7 | Environment risk | High | Low | High | |
| 8 | Corporate image risk | High | Low | Low | |
| 9 | Technological maturity | High | High | Medium |
| Criterion 1 | Criterion 4 | Criterion 7 |
| Criterion 2 | Criterion 5 | Criterion 8 |
| Criterion 3 | Criterion 6 | Criterion 9 |
| Intersection between Fuzzy Preference Matrices | Strict Fuzzy Preference Relation of the Intersection | Set of Non-Dominated Alternatives |
|---|---|---|
Energy source chosen: Alternative 3 (solar) |
| Criterion 6 | Criterion 7 | Criterion 8 | |
|---|---|---|---|
| Strict fuzzy preference relation | |||
| Set of non-dominated alternatives | |||
| Energy source | Alternative 2 (wind) | ||
| Criterion 1 | Criterion 4 | Criterion 7 | |
| Fuzzy strict preference relation | |||
| Non-dominated set of alternatives | |||
| Criterion 2 | Criterion 5 | Criterion 8 | |
| Fuzzy strict preference relation | |||
| Non-dominated set of alternatives | |||
| Criterion 3 | Criterion 6 | Criterion 9 | |
| Fuzzy strict preference relation | |||
| Non-dominated set of alternatives | |||
| Insertion of the non-dominated set of alternatives | Energy source chosen: | Alternative 3 (solar) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, M.A.D.d.O.; Ribeiro, L.C.; Schuffner, H.S.; Libório, M.P.; Ekel, P.I. Fuzzy-Set-Based Multi-Attribute Decision-Making, Its Computing Implementation, and Applications. Axioms 2024, 13, 142. https://doi.org/10.3390/axioms13030142
Ferreira MADdO, Ribeiro LC, Schuffner HS, Libório MP, Ekel PI. Fuzzy-Set-Based Multi-Attribute Decision-Making, Its Computing Implementation, and Applications. Axioms. 2024; 13(3):142. https://doi.org/10.3390/axioms13030142
Chicago/Turabian StyleFerreira, Mateus Alberto Dorna de Oliveira, Laura Cozzi Ribeiro, Henrique Silva Schuffner, Matheus Pereira Libório, and Petr Iakovlevitch Ekel. 2024. "Fuzzy-Set-Based Multi-Attribute Decision-Making, Its Computing Implementation, and Applications" Axioms 13, no. 3: 142. https://doi.org/10.3390/axioms13030142
APA StyleFerreira, M. A. D. d. O., Ribeiro, L. C., Schuffner, H. S., Libório, M. P., & Ekel, P. I. (2024). Fuzzy-Set-Based Multi-Attribute Decision-Making, Its Computing Implementation, and Applications. Axioms, 13(3), 142. https://doi.org/10.3390/axioms13030142





