Integrating the Coupled Markov Chain and Fuzzy Analytic Hierarchy Process Model for Dynamic Decision Making

Abstract

This paper introduces a pioneering model that merges coupled Markov chains (CMC) with the fuzzy analytic hierarchy process (FAHP) to enhance multi-criteria decision making (MCDM) amidst the dynamic interplay of criteria. Traditional MCDM frameworks often lack the granularity to manage the intricate and changing relationships among criteria. Our model addresses this gap by integrating fuzzy numbers into AHP, providing a nuanced means to handle the inherent uncertainty of decision criteria. The application of the Kronecker product in CMC enriches our approach, offering a data-driven analysis while mitigating excessive dependence on subjective expert opinion. A comprehensive numerical example underlines the model’s improved decision-making accuracy and efficiency, marking a substantial advancement in MCDM methodologies. This research contributes to the field by presenting a sophisticated yet practical framework for dynamic decision analysis in complex uncertain environments.

1. Introduction

The endeavor of multi-criteria decision making (MCDM) has consistently sought to mirror the intricacy and dynamism inherent in decision making across various domains. Despite the significant strides made with methodologies like the best worst method (BWM) [1] and the full consistency method (FUCOM) [2], these approaches often presuppose static relationships among decision criteria. Such an assumption falls short in the face of the fluid and interdependent nature of criteria that characterize contemporary decision landscapes [3,4]. Acknowledging the limitations of traditional MCDM techniques, this paper ventures into the domain of dynamic decision making. It leverages the strengths of the analytic hierarchy process (AHP), a paradigm widely adopted for its structured pairwise comparisons to gauge the relative importance of criteria [5]. However, the conventional form of AHP is not without criticisms, as it inadequately captures the objective uncertainty and temporal evolution of criteria interdependencies, which are pivotal in dynamic contexts [6].

The inception of fuzzy numbers in MCDM, introduced by [7], revolutionized handling uncertainties and imprecisions that are endemic to human judgments [8], pioneering work on embedding fuzzy numbers into AHP, thus forming the fuzzy analytic hierarchy process (FAHP), marking a departure from rigid numerical assessments to a flexible methodology capable of incorporating the subtleties and subjectivity of expert opinions. Innovative MCDM methodologies now embed interdependencies and uncertainties, marking a significant shift towards more adaptable decision-making models. In [9], they made significant contributions with their integrated fuzzy MCDM approach, which amalgamates the FAHP and fuzzy technique for order of preference by similarity to ideal solution (TOPSIS), underscoring the imperative of managing uncertainties. Similarly, [10] has innovated within this space, introducing a hybrid MCDM framework that synergizes the spherical fuzzy analytic hierarchy process (SF-AHP) and weighted aggregated sum product assessment (WASPAS) for complex site selection processes.

On the other hand, coupled Markov chains (CMC) have further broadened the MCDM horizon, offering nuanced insights into the interdependencies of criteria. The approaches of [11] in credit risk modeling and [12] in loan portfolios exhibited superior performance over conventional methods. [13] reinforced the versatility of CMC in complex decision-making systems through their work on distributed algorithms for Markov chain redesign. In contrast to most MCDM methods, which do not inherently consider dynamic properties, CMC addresses dynamic interdependencies. This is a crucial differentiation from methods like the analytic network process (ANP) [14] and others, only addressing static interdependencies rather than conducting dynamic interrelationships between the criteria we focus on here.

This paper aims to amalgamate the finesse of FAHP and the dynamic modeling capabilities of CMC to devise a more versatile and precise MCDM framework capable of capturing the ever-evolving interdependencies among criteria. This novel integration addresses the limitations inherent in traditional methods and exploits the strengths of both FAHP and CMC to deliver a sophisticated data-driven perspective essential for modeling the intricacies of real-world decision-making scenarios. The numerical example indicates that the derived results from the proposed method are significantly different from the AHP, which justifies the consideration of the dynamic interdependency between criteria.

The ensuing sections of this paper are organized as follows: Section 2 reviews the literature, underpinning the development of our integrated model. Section 3 delineates the proposed method, elaborating on the step-by-step integration of FAHP and CMC. Section 4 presents a numerical example that showcases the application and advantages of our model over traditional methods. Section 5 discusses the implications of our findings and Section 6 concludes with a reflection on the future direction of MCDM research.

2. Literature Review

Recent MCDM research has increasingly focused on decision criteria’s dynamic interplay and interconnectivity. Traditional MCDM approaches, while foundational, are often limited by their static assumptions. This section critically reviews the evolution of MCDM methodologies from classical approaches to incorporating dynamic elements and interdependencies, highlighting the need for advanced models such as FAHP and CMC.

2.1. Methods for Interdependency between Criteria

The intricate nature of decision making has catalyzed the evolution of MCDM methodologies, particularly those that acknowledge the interconnectedness of criteria. [15] offered a comprehensive overview of MCDM techniques, emphasizing the critical role of interactions among preferences, criteria, and utilities. This growing recognition of interdependencies is epitomized in the ANP, developed by [14], which extends the AHP to include feedback and interactions, thereby providing a robust framework for complex decision scenarios by incorporating feedback loops between clusters of elements (criteria, sub-criteria, alternatives, etc.), enabling a network rather than a hierarchical structure.

In ANP, the interdependencies are characterized by a network where elements within and between clusters are compared pairwise, forming a supermatrix. This supermatrix is then raised to limiting powers to capture the influence of all elements over one another, leading to a limit supermatrix where each column converges to the priority vector of the corresponding element. Mathematically, if C represents a set of criteria and A is the supermatrix, the limit supermatrix W can be calculated as

$$li{m}_{k\to \infty }{\mathit{A}}^k=\mathit{W}$$

(1)

Each column of W provides the evaluations of pairwise comparisons of alternatives based on preference, considering the entire network of interdependencies. However, the hardest problem of the ANP is to derive the supermatrix, which needs much time to form the pairwise comparison matrices (PCMs).

Besides the ANP, hybrid models have been developed to conduct the interdependency between criteria. For example, the DEMATEL-ANP integration has been applied in urban planning, demonstrating its efficacy in managing complex decision criteria [16]. Similarly, the model proposed by [17] integrated a modified TOPSIS with a PGP model, demonstrating the versatility of hybrid approaches in accommodating interdependencies in supplier selection contexts. In addition, [18] combined DEMATEL and fuzzy cognitive maps to provide more information to help decision making by considering the interdependency between criteria.

Despite these advancements, challenges persist, particularly in integrating different methodologies. The lack of a unified approach in combining methods like DEMATEL within the ANP framework, as highlighted by [19], can lead to inconsistencies and confusion for decision-makers. Introducing hybrid models, such as the FCM-AHP method suggested by [20], adds further complexity, relying heavily on expert opinions and potentially increasing subjectivity. This complexity underscores the necessity for continued research into MCDM methods that account for criterion dependencies, as emphasized by [21]. Exploring these methods’ advantages and limitations in varied decision-making contexts remains a fertile area for academic inquiry.

As we move towards addressing the uncertainties and subjective elements in decision making, the integration of fuzzy numbers with AHP, known as FAHP, emerges as a pivotal development. FAHP, which will be discussed in the subsequent section, represents an evolution in MCDM methodologies, blending the systematic approach of AHP with the flexibility of fuzzy numbers to better capture the vagueness and imprecision inherent in human judgments.

2.2. FAHP

AHP is an MCDM technique devised by Saaty in the early 1980s [5]. AHP has gained widespread popularity as a tool assisting decision-makers in evaluating and prioritizing multiple competing factors across various application fields. The technique is anchored in pairwise comparisons, wherein a decision-maker juxtaposes various criteria and alternatives to ascertain their relative significance in a hierarchical structure [6]. The process is initiated by deconstructing the decision-making problem into a hierarchical structure comprising a goal, criteria, sub-criteria, and alternatives. Each component within the hierarchy is then juxtaposed with other components at the same level via a pairwise comparison, leading to a set of evaluations of pairwise comparisons of alternatives based on preference [22].

The problem of the AHP can be represented as solving the following eigenvalue problem:

$$\mathit{A}\mathit{w}={\lambda }_{\max }\mathit{w}$$

(2)

where $\mathit{A}$ is the PCM, $\mathit{w}$ denotes the evaluation vector of pairwise comparisons of alternatives based on preference, and ${\lambda }_{\max }$ denotes the maximum eigenvalue. AHP’s methodology also accounts for the consistency of the decision-maker’s judgments. [5] proposed the consistency ratio (CR), which compares the consistency index (CI) to the random index (RI)—an average index derived from randomly generated matrices. A CR less than or equal to 0.10 is generally considered acceptable [5], indicating that the decision-maker’s judgments exhibit a reasonable level of consistency. CR and CI can be formulated as follows:

$$CR=\frac{CI}{RI}=\frac{{\lambda }_{\max }-n}{n-1}/RI$$

(3)

where n denotes the number of criteria and RI is used to estimate the average consistency of a randomly generated PCM and can refer to

Table 1. RI table.

Number of Criteria	Random Index
3	0.58
4	0.90
5	1.12
6	1.24
7	1.32

.

AHP has been applied to various decision-making problems across various domains. For example, [23] utilized AHP to select the best supplier in an automotive parts manufacturer context. Despite the widespread adoption of AHP, researchers continue to explore its potential and limitations and integrate it with other decision-making methods, such as the TOPSIS and the elimination and choice expressing reality (ELECTRE) [24]. Even recently, the AHP has addressed more complicated problems. For example, [25] discussed the use of improvements to the m-polar fuzzy set (mFS) elimination and choice translating reality-I (ELECTRE-I) approach for calculating criteria weights for the selection of non-traditional machining (NTM) processes.

In advancing the AHP, FAHP combines the systematic approach of AHP with the nuanced handling of uncertainty inherent in fuzzy numbers. A critical aspect of FAHP is the fuzzy eigenvalue method, which begins by constructing a fuzzy pairwise comparison matrix (FPCM). Each element of this matrix is a triangular fuzzy number (TFN), ${\tilde{a}}_{ij}=\left(l_{ij},m_{ij},u_{ij}\right)$, representing the relative importance of criteria i and j, where $l_{ij}\le m_{ij}\le u_{ij}$, which captures the range of possible evaluations that are called the fuzzy numbers’ left, center, and right values. This matrix is then normalized to form R, where each element $R_{ij}={\tilde{a}}_{ij}/{\sum }_k{\tilde{a}}_{ik}$ is also a TFN. The fuzzy geometric mean of each row of R is calculated as

$$w_i={\left({\prod }_k{R}_{ik}\right)}^{1/n}$$

(4)

representing the fuzzy evaluations of pairwise comparisons of alternatives based on preference, which is subsequently defuzzified to obtain crisp criterion weights [8].

On the other hand, the extent analysis method involves constructing a fuzzy preference matrix (FPM), where each element $p_j\left(i\right)$ is a TFN indicating the degree to which criterion j is preferred over criterion i. The fuzzy preference scores for each criterion are calculated as

$$F_j={\sum }_i{p}_j\left(i\right)$$

(5)

and these scores are normalized to form

$${\tilde{w}}_j={\tilde{F}}_j/{\sum }_k{\tilde{F}}_k$$

(6)

The process concludes with a defuzzification step to determine crisp weights for each criterion [26]. Another nuanced FAHP method is the fuzzy logarithmic least-squares method, which starts similarly with the construction of an FPCM. A logarithmic transformation is applied to each element of this matrix:

$$l_{ij}=ln\left({\tilde{a}}_{ij}\right)$$

(7)

The method then minimizes the sum of squared deviations between the transformed FPCM and a calculated fuzzy weight matrix such that

$$\mathrm{Minimize} {\sum }_{ij}{\left(l_{ij}-ln\left({\tilde{w}}_{ij}\right)\right)}^2$$

(8)

An inverse logarithm transformation ${\tilde{w}}_{ij}=exp\left(l_{ij}\right)$ and subsequent defuzzification are applied to obtain crisp weights [27].

Lastly, the hesitant fuzzy AHP method incorporates a hesitant fuzzy pairwise comparison matrix (HFPCM), where each element $a_{ij}$ is a set of TFNs representing varied opinions about the relative importance of criteria i and j. This method involves aggregating these TFNs using average, median, or ordered weighted averaging (OWA) techniques, followed by defuzzification to obtain crisp weights. Consistency checks and sensitivity analysis are crucial in this method to ensure the reliability of the decision-making process [28].

Having explored the intricacies and methodologies of FAHP, it is evident that this approach significantly enhances the traditional AHP by accommodating the uncertainties and subjective nature of decision making. The incorporation of fuzzy numbers allows for a more flexible and realistic evaluation of criteria, aligning with the dynamic and complex environments encountered in practical scenarios. However, this evolution in AHP methodology brings forth a need for an even more sophisticated approach to handle the temporal dynamics of criteria, which are often overlooked. CMC offers a robust framework for capturing the time-variant behavior and interdependencies of criteria, a feature critical to dynamic decision-making processes. In the following section, we delve into the concept of CMC, exploring its foundational principles and the potential it holds in combination with FAHP for developing a comprehensive decision-making model that is both adaptive and reflective of real-world complexities.

2.3. TFNs and Fuzzy Operations

In fuzzy set theory, a TFN is defined as an ordered triplet $\left(l,m,u\right)$, where $l\le m\le u$. These parameters represent the lower limit, the mode (most probable value), and the upper limit of the fuzzy number, respectively. The function of a TFN is typically a piecewise linear function, defined as

$$f\left(x;l,m,u\right)=\left\{\begin{array}{c}\begin{array}{c}0 for x<l \\ \frac{x-l}{m-l} for l\le x\le m\\ \frac{u-x}{u-m} for m\le x\le u\end{array}\\ 0 for x>u \end{array}\right.$$

(9)

For two positive TFNs $\tilde{A}=\left(l_A,m_A,u_A\right)$ and $\tilde{B}=\left(l_B,m_B,u_B\right)$, the operations are defined as

• Addition: $\tilde{A}+\tilde{B}=\left(l_A+l_B,m_A+m_B,u_A+u_B\right)$;
• Subtraction: $\tilde{A}-\tilde{B}=\left(l_A-u_B,m_A-m_B,u_A-l_B\right)$;
• Multiplication: For multiplication, each end of the resulting TFN is obtained by multiplying the respective ends of the original TFNs. The formula is: $\tilde{A}\times \tilde{B}=\left(l_A\times l_B,m_A\times m_B,u_A\times u_B\right)$;
• Division: Assuming $\tilde{B}$ does not contain zero (to avoid division by zero), the division formula is: $\tilde{A}/\tilde{B}=\left(\frac{l_A}{u_B},\frac{m_A}{m_B},\frac{u_A}{l_B}\right)$.

Among these operations, multicalication and division operations can result in non-triangular shapes. In addition, Zadeh’s extension principle [7] is another way of extending operations on crisp numbers to fuzzy numbers. The principle states that any function defined on a crisp set can be extended to a function on fuzzy sets. This extension is achieved by applying the function to the fuzzy sets’ membership functions, thus producing a fuzzy set result.

Taking the multiplication and division for example, for two positive TFNs $\tilde{A}=\left(l_A,m_A,u_A\right)$ and $\tilde{B}=\left(l_B,m_B,u_B\right)$, the product, according to Zadeh’s extension principle, is a fuzzy number $\tilde{C}=\tilde{A}\times \tilde{B}$ with the following membership function:

$$\tilde{C}\left(x\right)=ma{x}_{xy=z}min\left(\tilde{A}\left(y\right),\tilde{B}\left(z/y\right)\right)$$

(10)

where x represents an element in the resulting fuzzy set after performing the operation, y represents an element in the first fuzzy number, and z is the product value under consideration, which is the outcome of multiplying specific elements from $\tilde{A}$ and $\tilde{B}$. This operation results in a fuzzy number that is generally not triangular. The resulting set $\tilde{C}$ is derived by considering all possible products of elements from $\tilde{A}$ and $\tilde{B}$ that contribute to a particular element in $\tilde{C}$. Similarly, for division, if $\tilde{B}$ does not contain zero, the quotient $\tilde{D}=\tilde{A}/\tilde{B}$ is determined by

$$\tilde{D}\left(x\right)=ma{x}_{y/z=x}min\left(\tilde{A}\left(y\right),\tilde{B}\left(z\right)\right)$$

(11)

Like multiplication, the division of TFNs using Zadeh’s extension principle results in a fuzzy number that may not retain the triangular form. The direct application of Zadeh’s extension principle to the multiplication and division of TFNs is computationally intensive due to the involvement of the maximization of the minima of the membership functions.

In practice, approximate methods or numerical techniques are often employed to handle these operations, especially in complex decision-making models where computational efficiency is crucial. The use of simplified arithmetic, while an approximation, significantly reduces computational complexity, which is vital in large MCDM models. The selection of TFNs in this paper over other fuzzy numbers, like trapezoidal fuzzy numbers, is because of its simplicity and ease of interpretation to indicate the most likely believable value, while the base width indicates the range of uncertainty. In addition, the proposed method can easily shift to trapezoidal fuzzy numbers without modifying our algorithm.

Last, defuzzification is the process of converting fuzzy numbers into crisp scores for actionable decision making. We employ the centroid method here due to its effectiveness in balancing precision and computational feasibility. The method calculates the center of gravity of the TFN, resulting in a crisp value that represents the fuzzy evaluation. For a positive TFN $\tilde{A}=\left(l_A,m_A,u_A\right)$, the defuzzified value D of a TFN is calculated by finding the centroid of the triangular area representing the fuzzy number. Mathematically, it is given by

$$D=\frac{l_A+m_A+u_A}{3}$$

(12)

The centroid formula calculates the average of the three points, effectively finding the center of gravity of the triangle formed by the TFN. The value D is a crisp number that best represents the average value of the fuzzy number, taking into account its entire range and the highest point of membership.

2.4. CMC

A Markov chain is a stochastic process that models the behavior of a system transitioning between a finite number of states over time. The fundamental assumption of a Markov chain is the Markov property, which asserts that future states depend only on the current state and not on any previous states [29]. Mathematically, this property can be expressed as

$$P\left(x_{n+1}=x_{n+1}|X_n=x_n,X_{n-1}=x_{n-1},\dots ,X_0=x_{n=0}\right)=P\left(x_{n+1}=x_{n+1}|X_n=x_n\right)$$

(13)

where $X_n$ represents the state of the system at nth step.

In many real-world scenarios, especially in dynamic decision-making environments, the assumption of independent criteria often fails. CMC extends the concept of Markov chains to interconnected systems where multiple chains interact, influencing each other’s state transitions. Suppose we have M Markov chains, where each chain has N_i states, and we want to model the joint behavior of the chains. We can represent the state of the joint system at time t using a probability vector x(t) of length N, where N = N₁ $\times$ N₂ $\times$ … $\times$ N_M is the total number of possible joint states. We can also represent the joint system using a set of transition matrices {P₁, P₂, …, P_M}, where each matrix P_i has dimensions N_i $\times$ N_i and represents the transition probabilities for chain i. Notably, transition matrices can usually be estimated by the maximum likelihood estimation (MLE), hidden Markov model (HMM) [30], and Kalman filters. However, these methods require historical data and may be unavailable in practice or the usual situation in MCDM.

To model the behavior of the CMC, we need to define the joint transition probabilities between the possible joint states. One way to do this is by using the Kronecker product, which allows us to combine the transition matrices for the individual chains to obtain a joint transition matrix for the entire system. If we define the joint transition matrix P_c for the coupled system as the Kronecker product of the individual transition matrices, we can model the CMC behavior as follows:

$${\mathit{P}}_c={\mathit{P}}_1\otimes {\mathit{P}}_2\otimes \cdots \otimes {\mathit{P}}_m\in {\mathfrak{R}}^{n{k}^2\times n{k}^2}$$

(14)

where n denotes the number of the Markov chains, k denotes the number of statuses, and $\otimes$ denotes the Kronecker product. Then, the (i, j) entry of P_c represents the probability of transitioning from joint state i to joint state j in a single time step. By analyzing the composite transition matrix, we can understand the original chains’ joint behavior, compute the composite chain’s steady-state probabilities, or investigate the interdependent behavior of the chains. Finally, the results of the composite chain can be mapped back to the original chains by considering the marginal probabilities or other relevant measures.

Notably, the ordering of criteria when taking the Kronecker product of the transition matrices depends on how the state space of the joint system is defined. In a multivariate Markov chain, the joint state at a given time is represented as a combination of the states of each individual chain. The way in which we combine the states to define the joint state will determine the order in which we should take the Kronecker product of the transition matrices. For example, if we represent a joint state as the order of the state of A and state of B, then we should compute the Kronecker product as $P_A\otimes P_B$, where $P_A$ and $P_B$ are the transition matrices for chains A and B, respectively. Conversely, if we represent a joint state as the order of the state of B and state of A, then we should compute the Kronecker product as $P_B\otimes P_A$. The ordering of the criteria should be consistent with how the joint states are represented so that the resulting joint transition matrix correctly reflects the transition probabilities between joint states.

Once we obtain P_c, we can derive its steady-state status by using the iterative multiplication method as follows:

$$\mathit{\pi }\left(t\right)={\mathit{P}}_c\times \mathit{\pi }\left(t-1\right)\in {\mathfrak{R}}^{n{k}^2}$$

(15)

where $\mathit{\pi }\left(0\right)$ denotes the initial weight vector and is the uniform distribution here since it plays no influence in the CMC because of the memoryless property of the Markov chain. The process continues until the difference between $\mathit{\pi }\left(t\right)$ and $\mathit{\pi }\left(t-1\right)$ is less than the given threshold.

However, implementing CMC poses significant challenges, particularly in estimating transition probabilities in the absence of comprehensive historical data. The next sections will delve deeper into the theoretical underpinnings and practical applications of these methodologies, illustrating their transformative impact on the field of MCDM.

3. Methodology

The methodology presented in this paper seeks to amalgamate CMC with the FAHP for managing time-varying dependent criteria in decision making, as shown in Figure 1. We should highlight that the past MCDM methods, like ANP and DEMATEL, account for the static interdependency between criteria rather than dynamic interdependency. This property distinguishes our method from others. The proposed approach unfolds in five systematic steps:

• Define the FAHP hierarchy: The proposed methodology begins with constructing the FAHP hierarchy, which comprises three critical elements: the goal, the criteria, and the alternatives. The goal embodies the overarching objective of the decision-making problem, the criteria denote various influential factors within the decision, and the alternatives signify potential options to be evaluated against the criteria. The FAHP hierarchy is created by quantifying the FPCMs to generate initial weights for the criteria and alternatives via the FAHP. These weights articulate the relative significance of each criterion and alternative, laying the groundwork for additional analysis;
• Quantify FPCM and Obtain Initial Weights: Utilize the FPCM to determine initial weights for criteria and alternatives. Weights are synthesized from FPCMs using fuzzy consensus methods to represent expert judgment comprehensively;
• Derive Transition Probability Matrices: The following stage establishes transition probability matrices utilizing the Genetic Algorithm (GA). These matrices display the evolution of weights for criteria and alternatives over time, showcasing their interdependencies. In the fourth stage, interdependent weights for different periods are computed by applying the transition probability matrices obtained previously to the initial weights. This stage illuminates the dynamic nature of weights for criteria and alternatives and their interconnections;
• Obtain Fuzzy Interdependent Weights: Upon determining interdependent weights, the next stage involves their aggregation. This process compiles the interdependent weights for each criterion and alternative, considering their values over several periods. The concluding stage integrates the aggregated interdependent weights with the FAHP, culminating in a comprehensive decision-making framework that accommodates the interdependencies of criteria and alternatives. Fusing these steps results in an innovative method designed to mitigate the limitations of the conventional static FAHP, offering a more robust solution for complex decision-making problems involving interdependent criteria;
• Aggregate Fuzzy Interdependent Weights and Rank Alternative: We can use any weighted operations to aggregate the scores of alternatives and rank them for consideration in decision making.

Given that the first two steps are the standard FAHP process, we will concentrate on Step 3. A CMC model is formulated for each criterion, considering the dependencies among the criteria. Each criterion’s model comprises transition probability matrices, signifying the likelihood of transitioning from one state (weight) to another over time. These matrices are determined using historical data, expert judgments, or a combination thereof. In this context, we propose using an entropy-based function to ascertain transition probability matrices.

We can derive the transition matrices for each Markov chain as follows in the first place. For a specific criterion, we start by setting up the Lagrangian function based on the entropy function and constraints as

$$L(P,\lambda ,\mu )=-{\displaystyle \sum (P_{ij}\times \ln P_{ij})+{\displaystyle \sum {\lambda }_i({\displaystyle \sum P_{ij}-1}})+{\displaystyle \sum {\mu }_i({\displaystyle \sum P_{ij}\times {\pi }_j})-{\pi }_i)}}$$

(16)

where P is the matrix of transition probabilities, ${\lambda }_i$ and ${\mu }_j$ are Lagrange multipliers, and ${\pi }_j$ is the expected long-term distribution. The entropy function is given by $-{\displaystyle \sum (P_{ij}\times \ln P_{ij})}$ and the two conditions are the row sum and steady-state constraints, respectively.

Next, we calculate the partial derivatives of the Lagrangian function with respect to each $P_{ij}$ and set them equal to zero as follows:

$$\partial L/\partial P_{ij}=-\ln (P_{ij})-1+{\lambda }_i+{\mu }_i\times {\pi }_j=0,\forall i,j=1,2,3.$$

(17)

We rearrange each partial derivative Equation to solve for the values of $P_{ij}$ in terms of the Lagrange multipliers and the corresponding row sum and steady-state constraints as

$$P_{ij}=\exp (-1+{\lambda }_i+{\mu }_i\times {\pi }_j),\forall i,j=1,2,3$$

(18)

$${\displaystyle \sum P_{ij}=1,\forall i=1,2,3}$$

(19)

$${\displaystyle \sum (P_{ij}\times {\pi }_j)={\pi }_i,\forall i=1,2,3}$$

(20)

The common way to derive the solution of constrained optimization is to consider the Lagragine function as the objective function and use the Gridient Decient method to iteratively derive the unconstrained optimization problem. However, in practical consideration, we can directly use sequential least squares programming (SLSQP) that combines Lagrange multipliers and quadratic approximation to formulate Equation (13) as the objectives and Equations (14)–(16) as the constraints. However, since the system above is nonlinear, it is hard to derive the solution above, even with numerical iterative methods.

Hence, we employed a GA [31] to optimize the transition matrix for the Markov chain problem here. The basic idea behind GAs is to iteratively evolve a population of candidate solutions to find an optimal or near-optimal solution eventually. Each individual in the population represents a potential solution encoded as a chromosome consisting of genes representing the solution’s variables or components. The algorithm employs genetic operators such as selection, crossover, and mutation to create new generations of solutions, gradually improving the population’s overall performance. GAs explore the solution space and exploit the most promising areas to find optimal or near-optimal solutions by iterating through these steps. In the context of our proposed methodology, we employed a GA to optimize the transition matrices for the Markov chains, allowing for the consideration of time-varying interdependencies between criteria.

The main steps of the GA are as follows:

• Initialization: Create an initial population of individuals, each representing a potential solution (i.e., a transition matrix). For example, if the steady-state distribution has three values, it means that each individual has nine chromosomes. Notably, all chromosomes range between [0, 1];
• Evaluation: Calculate the fitness of each individual using the objective function. The objective function computes the difference between the steady-state distribution of the current transition matrix and the desired distribution:

$$\frac{1}{n}{‖Q-e/n\times \underset{n\to \infty }{\lim }{\left(P\right)}^n‖}_2+ \mathrm{penalty} \mathrm{function}$$

(21)

where the penalty function means we added a large number to the solution against the probability matrix property;

3.

Selection: Select a subset of the population for mating and reproduction based on their fitness values. In this paper, we used the tournament selection method as described as follows. In the tournament selection process, a fixed number of individuals are randomly selected from the current population. The individuals in the tournament compete based on their fitness values, i.e., the objective function here. The individual with the best among the tournament participants is selected as the winner. The selection process is repeated until the desired number of individuals for the next generation is chosen;

4.

Crossover: Generate offspring by combining the genes of selected individuals. We used the blend crossover method in this paper. The concrete step of the crossover can be described as follows. Let two parent individuals be as follows:

Parent 1: [0.2, 0.4, 0.6, 0.8]

Parent 2: [0.6, 0.8, 1.0, 1.2]

For each corresponding position in the parent individuals, interpolate the values to create the offspring as follows:

$$\alpha \times Parent1\left[i\right]+\left(1-\alpha \right)\times Parent2\left[i\right], \forall i$$

(22)

where i denotes the position of the chromosome, $\alpha$ denotes the crossover parameter, and is 0.5 in the paper. Notably, the crossover rate is a balance between maintaining the reasonable solutions found so far (exploitation) and generating new solutions for exploration; a crossover rate of 0.5 means that, on average, half of the population will be produced by crossover [32]. Hence, the parent individuals above can generate the new offspring as:

$$\left[0.5\times 0.2+\left(1-0.5\right)\times \mathrm{0.6,0.5}\times 0.4+\dots +\left(1-0.5\right)\times 1.2\right]=\left[\mathrm{0.4,0.6,0.8,1.0}\right];$$

5.

Mutation: Introduce random variations in the offspring by altering their genes. In this case, we used Gaussian mutation. We use the new offspring above $\left[\mathrm{0.4,0.6,0.8,1.0}\right]$ and set the standard deviation ($\sigma$) as 0.2 and independent probability as 0.1 in this paper as the example and assume that the first and third genes are selected for mutation. Notably, Gaussian mutation is often used in evolutionary algorithms because it introduces diversity into the population and balances exploration and exploitation. The standard deviation σ in Gaussian mutation controls the step size of the mutation and a smaller σ (like 0.2) means that the mutations are local and fine-grained, which can help fine-tune the solutions. The independent probability parameter controls the likelihood of a mutation occurring. A value of 0.1 means that each gene has a 10% chance of undergoing mutation. This relatively low probability helps maintain stability in the population while allowing for the possibility of exploration. Readers can refer to [33] for more details on the parameter selection of GA. For the selected genes, we generate random values from the Gaussian distribution and multiply them by $\sigma =0.2$. Assume the following random values are generated as follows:

  Random value for Gene 1: −0.15
Random value for Gene 3: 0.08

Then, the mutation for Gene 1 and Gene 3 are

$$\begin{array}{c}\mathrm{Mutation} \mathrm{for} \mathrm{Gene} 1:-0.15\times 0.2=-0.03\hfill \\ \mathrm{Mutation} \mathrm{for} \mathrm{Gene} 3: 0.08\times 0.2=0.016\hfill \end{array}$$

Finally, we adjust the selected genes’ values by adding the following computed mutations:

Mutated Individual: [0.4 − 0.03, 0.6, 0.8 + 0.016, 1.0] = [0.37, 0.6, 0.816, 1.0];

6.

Replacement: Replace the old population with the offspring and repeat the process from step 2 for a specified number of generations.

In each generation, the elite strategy is used to keep track of the best individuals to monitor the progress of the optimization process.

Once we derive the steady-state status, i.e., $\mathit{\pi }\left(t\right)$ of the CMC process, we can use it to adjust the weights of the AHP to account for the time-varying behavior of the weights as follows. First, $\mathit{\pi }\left(t\right)$ is reshaped as

$${\mathsf{\Pi }}_{\mathit{c}\mathit{r}\mathit{i}\mathit{t}\mathit{e}\mathit{r}\mathit{i}\mathit{a}}\left(t\right)=\mathit{r}\mathit{e}\mathit{s}\mathit{h}\mathit{a}\mathit{p}\mathit{e}\left(\mathit{\pi }\left(t\right)\right)\in {\mathfrak{R}}^{n\times k\times k}$$

(23)

Here, ${\mathsf{\Pi }}_{\mathit{c}\mathit{r}\mathit{i}\mathit{t}\mathit{e}\mathit{r}\mathit{i}\mathit{a}}\left(t\right)$ represents the reshaped matrix of steady-state probabilities for each criterion at time t. The reshaping allows for the representation of the interdependencies between criteria and the evolution of weights over time. Then, we can use the summarization method to calculate the weight-adjusted matrix as

$$\mathsf{\Pi }\left(t\right)\left[i,:\right]=\mathit{S}\mathit{u}\mathit{m}\left({\mathsf{\Pi }}_{\mathit{c}\mathit{r}\mathit{i}\mathit{t}\mathit{e}\mathit{r}\mathit{i}\mathit{a}}\left(t\right)\right)\in {\mathfrak{R}}^{n\times n}$$

(24)

where $Sum\left(·\right)$ is the row vector of the summed values across the states of other criteria for each state of ith criterion. Equation (14) is used to calculate the adjusted weights for each criterion based on the time-varying weights obtained from the CMC process. Finally, the time-varying weights of the FAHP can be calculated as

$$AH{P}_{\tilde{\mathit{w}}}^{\prime }=N\left(\mathsf{\Pi }\left(t\right)⨁{AHP}_{\tilde{\mathit{w}}}\right) \in {\mathfrak{R}}^n$$

(25)

where $N\left(·\right)$ indicates the normalized function such that the center value sum of the fuzzy weights is equal to one and $⨁$ is a special operation and indicates the summation of the outer sum operator. Let $\mathit{A}\in {\mathfrak{R}}^{3\times 3}$ and $\mathit{B}\in {\mathfrak{R}}^{3\times 1}$ be two matrices, such that the $⨁$ operator between two matrices can be calculated as:

$$\mathit{A}⨁\mathit{B}=\left[\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right]⨁\left[\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right]=\left[\begin{array}{c}{b}_1\left(a_{11}+a_{12}+a_{13}\right)\\ b_2\left(a_{21}+a_{22}+a_{23}\right)\\ b_3\left(a_{31}+a_{32}+a_{33}\right)\end{array}\right]$$

In conclusion, this innovative methodology integrates CMC with FAHP, representing a significant advancement in addressing the dynamic nature of decision-making criteria. The robust genetic algorithm is employed to optimize transition matrices, detailing each step of the process to enhance the accuracy of criteria weighting and account for their time-varying interdependencies. The subsequent section will delve into practical applications, demonstrating this methodology’s efficacy through real-world examples and case studies, validating our theoretical constructs, and showcasing our integrated approach’s practical relevance and applicability in diverse decision-making scenarios.

4. Numerical Example

Suppose we have a decision-making problem that involves three criteria, quality, price, and delivery, and each criterion has its own Markov chain. We assume these chains are not independent and, therefore, give the reason to use the CMC to explore the interdependent behavior. The decision hierarchy of the example is presented as shown in Figure 2.

First, we can calculate the weights of the criteria by using the eigenvalue method on the FPCM as follows:

PCM	Quality	Price	Delivery	Fuzzy Weights
Quality	1	(1,2,3)	(2,3,4)	(0.3873, 0.5390, 0.6328)
Price	(1/3,1/2,1)	1	(1,2,3)	(0.1924, 0.2973, 0.4429)
Delivery	(1/4,1/3,1/2)	(3/1,1/2,1)	1	(0.1199, 0.1638, 0.2611)
Notably, fuzzy weights were derived using Buckley’s method, which utilizes triangular fuzzy numbers to represent the relative importance and uncertainty in the pairwise comparison matrix.

Then, we will use the proposed method to adjust the derived weights above by considering its time-varying relationship of criteria as follows. Assume the state space for each chain contains three possible states, low (L), medium (M), and high (H), and the transition matrix for each Markov chain is used to describe the probabilities of transitioning from one state to another. For example, a low status of quality has a 0.3 probability of resulting in a low status of quality. While detailed historical data or specific expert knowledge about transition probabilities may not be available, it is often possible for experts to provide reliable estimates of the steady-state distributions, which represent the long-term behavior of the system. These estimates can be drawn from observing the relative frequency of each state over a long period. Hence, let us assume experts know the steady-state distribution for quality, price, and delivery for each state as follows: quality: [0.40, 0.30, 0.30], price: [0.50, 0.30, 0.20], and delivery: [0.25, 0.50, 0.25], since these results might be easily observed from the phenomena. Once we obtain the information above, we can use the GA optimization procedure to find the optimal transition matrices for quality, price, and delivery.

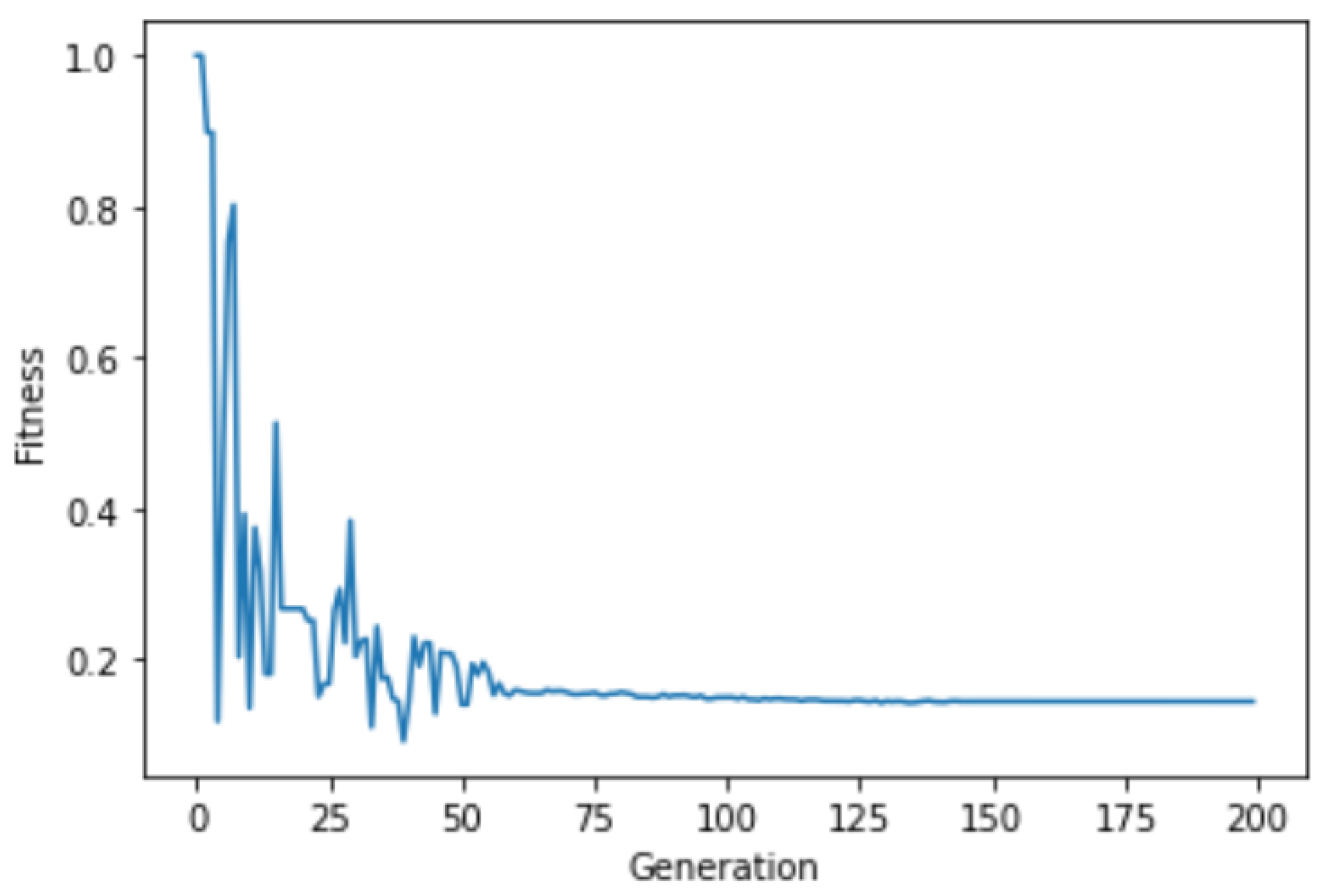
Take criterion quality, for example, we use GA to derive the transition matrix. The objective function used here is the mean square error (MSE) between the steady-state weight distribution and the estimated steady-state weight distribution. We add the penalty function to avoid the irrational results of negative values in the transition matrix. The genetic algorithm was configured with a population size of 100 and 200 generations, based on preliminary tests indicating an optimal balance between solution quality and computational effort. Finally, we set the population as 100, the number of generations as 200, the blend crossover rate as 0.5, and the standard deviation σ = 0.2 and independent probability = 0.1 in Gaussian mutation. The fitness of the best individual in each generation can be depicted in Figure 3, ensuring the convergent result after 100 generations.

The transition matrix between period t to t + 1 for the quality chain can be derived as

$$P_Q=\begin{array}{c}\begin{array}{ccc}{}_{t\to t+1}{}^{ }\mathit{Low}_{ }^{ }& Medium& High\end{array}\\ \begin{array}{c}Low\\ Medium\\ High\end{array}\left[\begin{array}{ccc}0.462 & 0.344 & 0.193\\ 0.411 & 0.295 & 0.292\\ 0.275 & 0.278 & 0.445\end{array}\right]\in {\Re }^{3\times 3}\end{array}$$

where the estimated steady-state distribution for quality is [0.390, 0.310, 0.300], which is similar to the values that the expert provided previously. The next two transition matrices for the price and deliver can be derived, respectively, as:

$$P_P=\left[\begin{array}{ccc}0.465 & 0.292& 0.241\\ 0.532& 0.241& 0.226\\ 0.507& 0.364& 0.127\end{array}\right]\in {\Re }^{3\times 3}$$

where the estimated steady-state distribution for price is [0.494, 0.293, 0.213].

$$P_D=\left[\begin{array}{ccc}0.252& 0.469& 0.279\\ 0.209& 0.499& 0.292\\ 0.362& 0.495& 0.143\end{array}\right]\in {\Re }^{3\times 3}$$

where the estimated steady-state distribution for delivery is [0.258, 0.491, 0.251].

Then, based on the information on the three transition matrices above, we need to create the composite transition matrix by using the Kronecker product as follows:

$${\mathit{P}}_c=\left[\begin{array}{cccc}0.0542& 0.1010& \cdots & 0.0130\\ 0.0451& 0.1073& \cdots & 0.0136\\ ⋮& ⋮& \ddots & ⋮\\ 0.0506& 0.0694& \cdots & 0.0081\end{array}\right]\in {\Re }^{27\times 27}$$

and we use the initial uniform weights $\mathit{w}\left(0\right)$ as

$$\mathit{w}\left(0\right)=\frac{1}{3}{\times \mathit{e}}_{27}\in {\mathfrak{N}}^{27}$$

where e is the one vector in which every entry is equal to one. The Kronecker product combines individual chain matrices into a comprehensive matrix, providing a holistic view of the system’s state transitions. Notably, the choice of initial weights in a Markov chain does not affect its long-term behavior due to the memoryless property, which ensures convergence to a steady-state distribution.

Next, we can calculate the steady-state vector of the CMC, which is used to adjust the AHP’s weights, as follows:

$$\mathit{\pi }\left(t\right)={\mathit{P}}_c\times \mathit{\pi }\left(t-1\right)=\left[\mathrm{0.4397,0.8338},\dots ,\mathrm{0.3029,0.1552}\right]\in {\mathfrak{N}}^{27},$$

where t = 8 research the convergence threshold, i.e., 0.00001 here. To calculate the steady-state vector, we iteratively multiply the composite transition matrix with the vector from the previous iteration until convergence. Then, we can reshape the steady-state vector into a $3\times 3\times 3$ steady-state matrix for quality, price, and delivery, respectively, as follows:

$${\mathsf{\Pi }}_{\mathrm{Q}\mathrm{u}\mathrm{a}\mathrm{l}\mathrm{i}\mathrm{t}\mathrm{y}}\left(t\right)=\left[\begin{array}{ccc}0.4397& 0.8338& 0.4272\\ 0.2605& 0.4940& 0.2513\\ 0.2062& 0.3911& 0.2004\end{array}\right]$$

$${\mathsf{\Pi }}_{\mathrm{P}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{e}}\left(t\right)=\left[\begin{array}{ccc}0.3483& 0.6605& 0.3384\\ 0.2063& 0.3913& 0.2005\\ 0.1633& 0.3098& 0.1587\end{array}\right]$$

$${\mathsf{\Pi }}_{\mathit{D}\mathit{e}\mathit{l}\mathit{i}\mathit{v}\mathit{e}\mathit{r}\mathit{y}}\left(t\right)=\left[\begin{array}{ccc}0.3406& 0.6459& 0.3309\\ 0.2018& 0.3826& 0.1960\\ 0.1597& 0.3029& 0.1552\end{array}\right]$$

Notably, the reshape operation transforms the steady-state vector into a matrix format, facilitating a clearer understanding of criteria interdependencies. Furthermore, we can calculate the marginal steady-state vector for each criterion as the adjusted matrix for the AHP’s weights. For example, to calculate the quality vector, we can sum the values of the second and third axes, which represent price and delivery states. Then, we can obtain the weight-adjusted matrix as follows:

$$\mathsf{\Pi }\left(t\right)=\begin{array}{c}Quality\\ Price\\ Delivery\end{array}\left[\begin{array}{ccc}3.5064& 2.7775& 2.7161\\ 4.3658& 2.5864& 2.0478\\ 2.3270& 4.4121& 2.2609\end{array}\right]\in {\mathfrak{N}}^{3\times 3}$$

For each criterion, the marginal steady-state vector is computed by summing across the respective rows of the reshaped matrix, representing combined influences from all states. For example, we can calculate the element values of $\mathsf{\Pi }\left(t\right)\left[\mathrm{1,1}\right]$ and $\mathsf{\Pi }\left(t\right)\left[\mathrm{2,1}\right]$ as follows:

$$\mathsf{\Pi }\left(\mathrm{t}\right)\left[\mathrm{1,1}\right]=0.4397+0.8338+\dots +0.2062+0.3911+0.2004=3.5064$$

$$\mathsf{\Pi }\left(t\right)\left[\mathrm{2,1}\right]=0.4397+0.8338+\dots +0.3406+0.6459+0.3309=4.3658$$

The weights derived from FAHP are adjusted using the time-variant weights from the CMC model to reflect dynamic changes in criteria importance. Finally, the adjusted matrix $\mathsf{\Pi }\left(t\right)$ is then used to adjust the weights derived from the AHP as follows:

$$AH{P}_{\mathit{w}}^{\prime }=N\left(\left[\begin{array}{ccc}3.5064& 2.7775& 2.7161\\ 4.3658& 2.5864& 2.0478\\ 2.3270& 4.4121& 2.2609\end{array}\right]\left[\begin{array}{c}\left(\mathrm{0.3873,0.5390,0.6328}\right)\\ \left(0.1924,0.2973,0.4429\right)\\ \left(0.1199,0.1638,0.2611\right)\end{array}\right]\right)=\left[\begin{array}{c}\left(\mathrm{0.3546,0.5053,0.6648}\right)\\ \left(\mathrm{0.2328,0.3307,0.4249}\right)\\ \left(\mathrm{0.1129,0.1640,0.2244}\right)\end{array}\right]$$

To evaluate the performance and validate the effectiveness of the proposed approach, we compare it with conventional AHP, as shown in

Table 2. The fuzzy weight comparisons between the conventional and the proposed methods.

Method	Quality	Price	Delivery
FAHP	(0.3873, 0.5390, 0.6328)	(0.1924, 0.2973, 0.4429)	(0.1199, 0.1638, 0.2611)
FAHP (CMC)	(0.3546, 0.5053, 0.6648)	(0.2328, 0.3307, 0.4249)	(0.1129, 0.1640, 0.2244)

.

Then, we can use a procedure similar to the FAHP above to obtain the fuzzy scores of the alternatives and then calculate the defuzzified scores of the alternatives by using the centroid method. Finally, we can determine the rank of the alternatives accordingly, as shown in

Table 3. The defuzzied scores and rank of the alternatives.

Alternatives	Quality	Price	Delivery	Defuzzified Scores	Rank
Alternative 1	(0.3, 0.36, 0.5)	(0.2, 0.3, 0.4)	(0.2, 0.3, 0.4)	0.3697	1
Alternative 2	(0.2, 0.34, 0.4)	(0.3, 0.45, 0.5)	(0.2, 0.3, 0.4)	0.3681	2
Alternative 3	(0.2, 0.3, 0.4)	(0.2, 0.25, 0.4)	(0.3, 0.4, 0.5)	0.3381	3
FAHP	(0.3873, 0.5390, 0.6328)	(0.1924, 0.2973, 0.4429)	(0.1199, 0.1638, 0.2611)
Alternative 1	(0.3, 0.36, 0.5)	(0.2, 0.3, 0.4)	(0.2, 0.3, 0.4)	0.3660	2
Alternative 2	(0.2, 0.34, 0.4)	(0.3, 0.45, 0.5)	(0.2, 0.3, 0.4)	0.3671	1
Alternative 3	(0.2, 0.3, 0.4)	(0.2, 0.25, 0.4)	(0.3, 0.4, 0.5)	0.3331	3
FAHP (CMC)	(0.3546, 0.5053, 0.6648)	(0.2328, 0.3307, 0.4249)	(0.1129, 0.1640, 0.2244)

. Since the purpose here is to illustrate the proposed method, we can assume the fuzzy scores of the alternatives are presented as shown in Table 3 for simplicity.

In Table 3, we observe a fascinating rank reversal situation when applying the conventional FAHP and the proposed method, i.e., FAHP (CMC), to evaluate and rank three alternatives based on quality, price, and delivery criteria. For FAHP, the defuzzified scores resulted in Alternative 1 leading with a score of 0.3697, followed by Alternative 2 at 0.3681, and Alternative 3 trailing with 0.3381. These results are based on the conventional FAHP model, where the weights are (0.3873, 0.5390, and 0.6328) for quality, (0.1924, 0.2973, and 0.4429) for price, and (0.1199, 0.1638, and 0.2611) for delivery. However, a notable rank reversal is observed when applying the FAHP (CMC) method. In this scenario, Alternative 2 ascends to the top position with a defuzzified score of 0.3671, surpassing Alternative 1, which now takes the second spot with a score of 0.3660. Alternative 3 remains in the third position with a score of 0.3331. The FAHP (CMC) model uses the adjusted weights of (0.3546, 0.5053, and 0.6648) for quality, (0.2328, 0.3307, and 0.4249) for price, and (0.1129, 0.1640, and 0.2244) for delivery. This rank reversal phenomenon highlights the sensitivity of multi-criteria decision-making models to the methodological nuances and underlines the importance of choosing an appropriate model based on the specific context and nature of the decision problem. It showcases how incorporating dynamic criteria weights in the FAHP (CMC) can lead to different prioritization of alternatives compared to the standard FAHP method.

5. Discussion

The suggested methodology that integrates interdependencies between criteria through the mechanism of CMC introduces numerous benefits. Firstly, it promotes the utilization of data from individual criterion Markov chains for estimating evolving weights, empowering decision-makers to make more knowledgeable and accurate choices. Secondly, the adoption of GA presents a flexible way to derive the transition matrix for each criterion. Thirdly, the strategy remains effective even without the presence of historical data or expert insight concerning the transition probabilities of Markov chains. Finally, the proposed method can be additional information to adjust the conventional methods.

The utilization of the Kronecker product to amalgamate individual criterion matrices into a comprehensive matrix is a methodological highlight. This step ensures a holistic representation of the system’s state transitions and intricately maps the interdependencies among criteria. The iterative calculation of the steady-state vector and its subsequent reshaping into a matrix format is a testament to the model’s ability to unravel and quantify the complex interactions between criteria, a feature often oversimplified or overlooked in conventional decision-making models.

The observed shift in weights—specifically, the decrease in Quality’s weight and the increase in Price’s weight—reflects more than just numerical adjustments. These changes encapsulate a variety of external and internal factors, such as market trends, consumer preferences, and operational alterations, demonstrating the model’s sensitivity to the nuances of the decision-making environment. This adjustment validates the model’s theoretical robustness and enhances its practical applicability by aligning the decision-making process with real-world dynamics.

The comparison of the conventional FAHP weights with the CMC-adjusted weights, as presented in Table 2, clearly illustrates the proposed model’s dynamic adaptability. This comparative analysis demonstrates not merely computational capability but a robust validation of the model’s practical utility. The differences between the conventional and adjusted weights highlight the model’s nuanced approach to decision making, offering a more realistic representation of evolving criteria interdependencies. The FAHP-CMC integration’s ability to dynamically adjust criteria weights in response to changing conditions positions it as an invaluable tool in various decision-making scenarios, such as business strategy development, policy formulation, and resource allocation. Its applicability in diverse fields underlines its versatility and adaptability, making it a significant contribution to the landscape of decision-making models.

The managerial implications of the paper can be described as follows. For managers, the primary benefit lies in the model’s ability to incorporate uncertainty and temporal evolution in decision-making processes. This feature is crucial in today’s fast-paced business world, where decisions must account for both current circumstances and future uncertainties. The model’s data-driven nature, supported by the Kronecker product in CMC, reduces the reliance on subjective expert opinions, leading to more objective and reliable decision making. The integration of FAHP and CMC thus equips managers with a sophisticated practical framework for making informed decisions in complex uncertain environments, enhancing their ability to respond effectively to dynamic market conditions.

While the model demonstrates significant advances, it also opens avenues for future research. Investigations into the impact of varying sample sizes, estimation methods, and optimization algorithms on the model’s performance could yield further enhancements. Empirical studies across different sectors would provide deeper insights into the model’s efficacy in real-world scenarios. In summary, the discussion of the numerical example underlines the proposed methodology’s capability to enhance decision-making accuracy in dynamic environments. By integrating CMC with FAHP, the model addresses the limitations of static decision-making approaches and paves the way for a more evolved, data-driven, and realistic approach to multi-criteria decision making.

6. Conclusions

This study presents a novel methodology integrating CMC with FAHP, marking a significant improvement over traditional static interdependent methods. It enables the incorporation of dynamic criteria weights and their interdependencies, enhancing the decision-making process’s sophistication and relevance. Key contributions of this research include the successful application of genetic algorithms for optimizing transition matrices and the resilience of the method in scenarios with limited data. Future research should explore the impact of various factors, such as sample size and estimation methods, on the methodology’s performance. Empirical studies in diverse contexts will further validate the effectiveness of this approach. The FAHP-CMC methodology offers a groundbreaking approach to dynamic time-variant decision making, showcasing potential for wide-ranging applications in complex decision environments.

However, the study has limitations and areas for future exploration. First, the reliance on the Kronecker product for integrating individual Markov chains may introduce complexities in interpreting and applying the model, especially in scenarios with a large number of criteria. Future research could explore simplifying these mathematical processes or developing more intuitive tools for implementation. Second, while the paper discusses the application of genetic algorithms for optimizing transition matrices, the robustness of these algorithms in diverse scenarios, especially those with limited or noisy data, remains to be explored in depth. Future studies could test the model’s performance with varied data quality and in different decision-making contexts.