Analysis of Epidemic Models in Complex Networks and Node Isolation Strategie Proposal for Reducing Virus Propagation
Abstract
1. Introduction
2. Epidemiology Mathematical Models
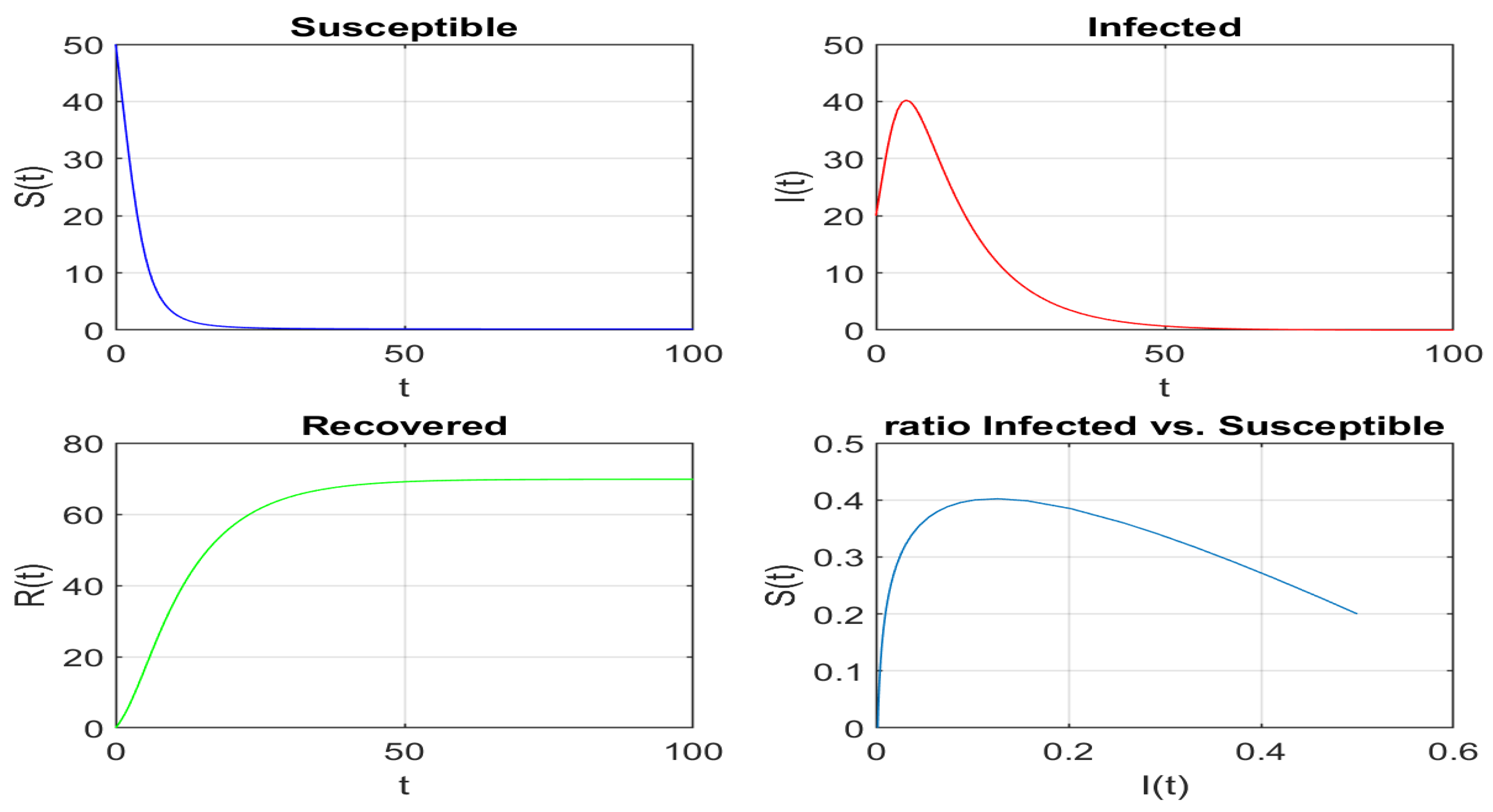
Formulation of the Fisrt Two Basic Epidemiology Models
3. Discrete Epidemic Models in Networks
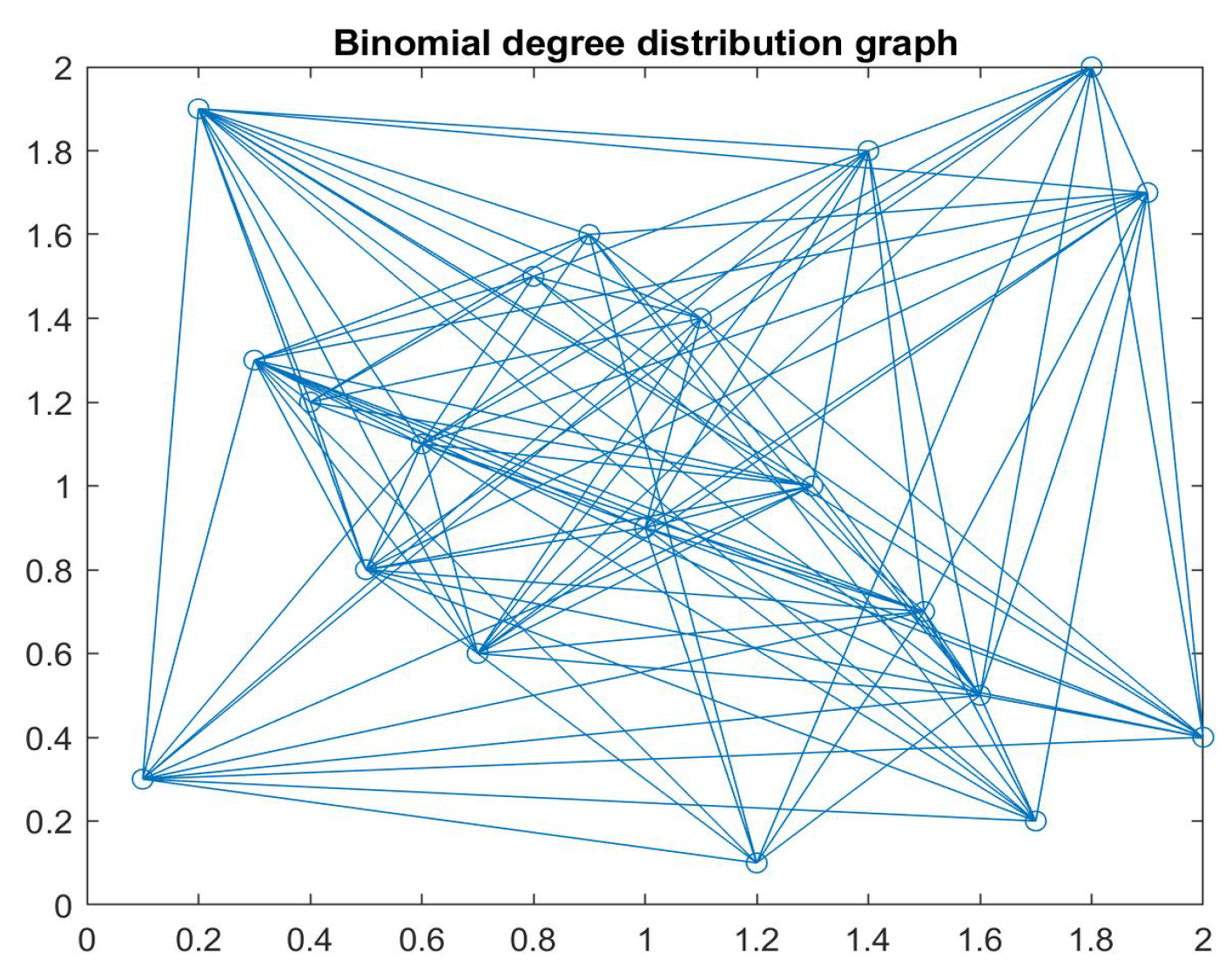
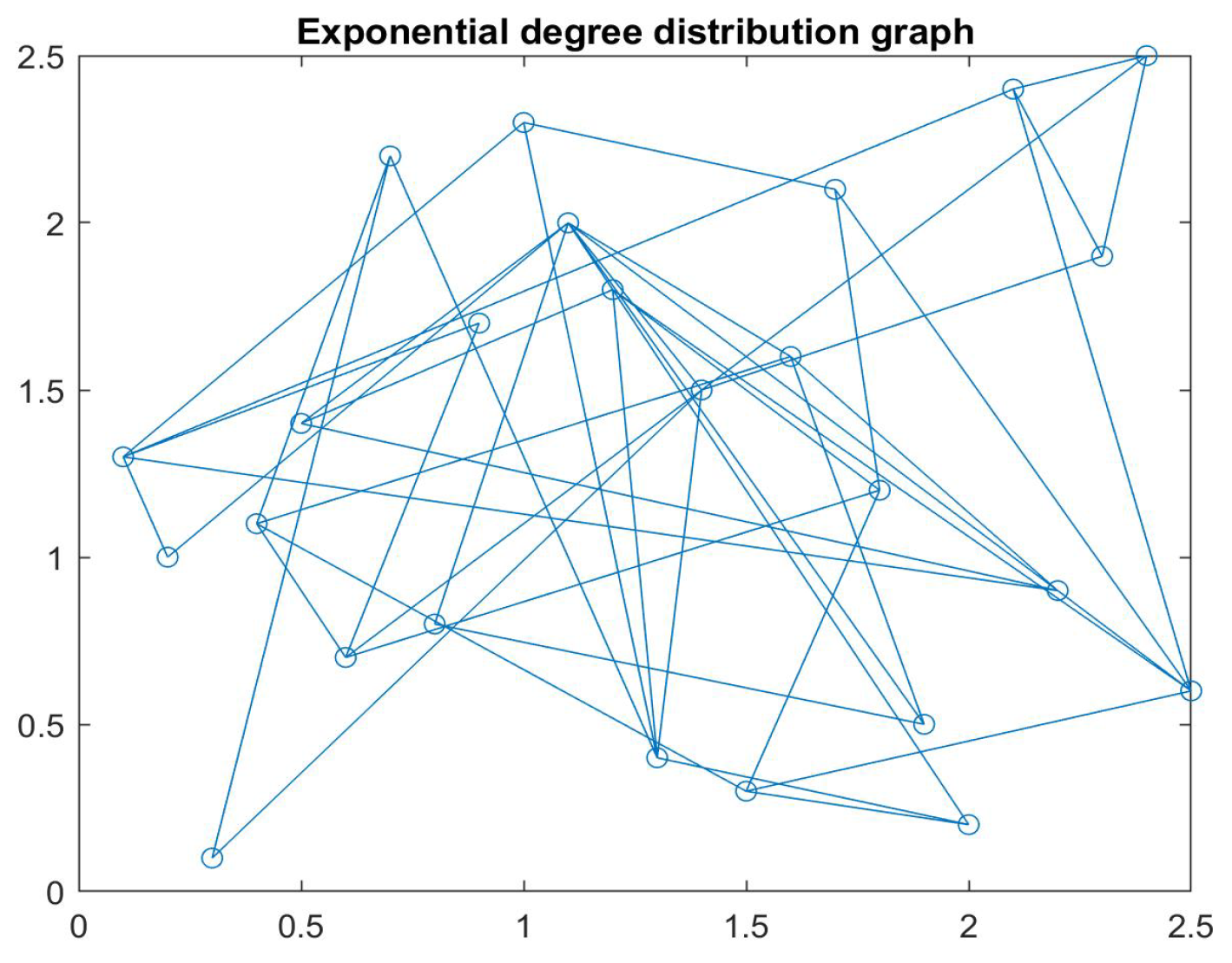
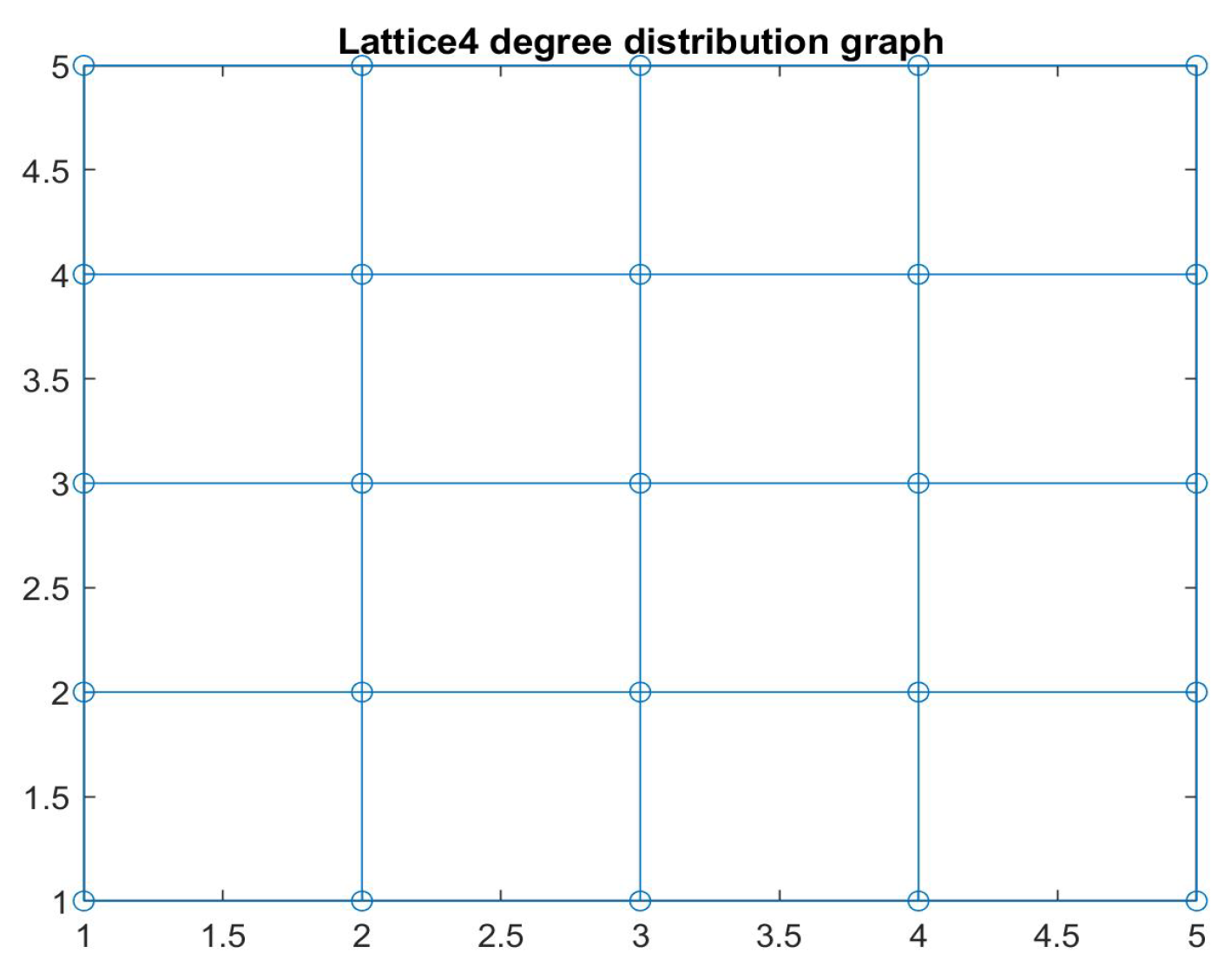
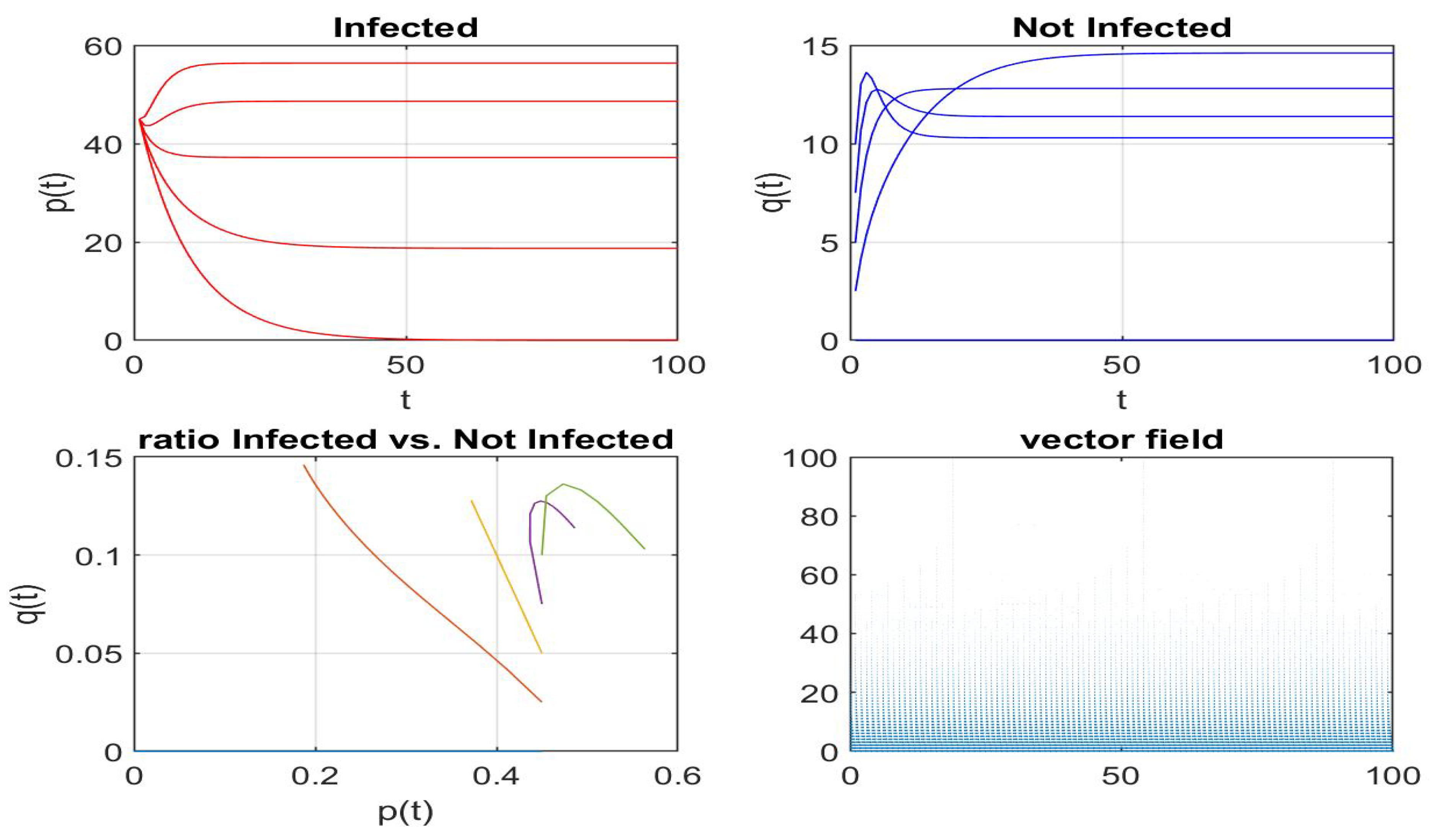
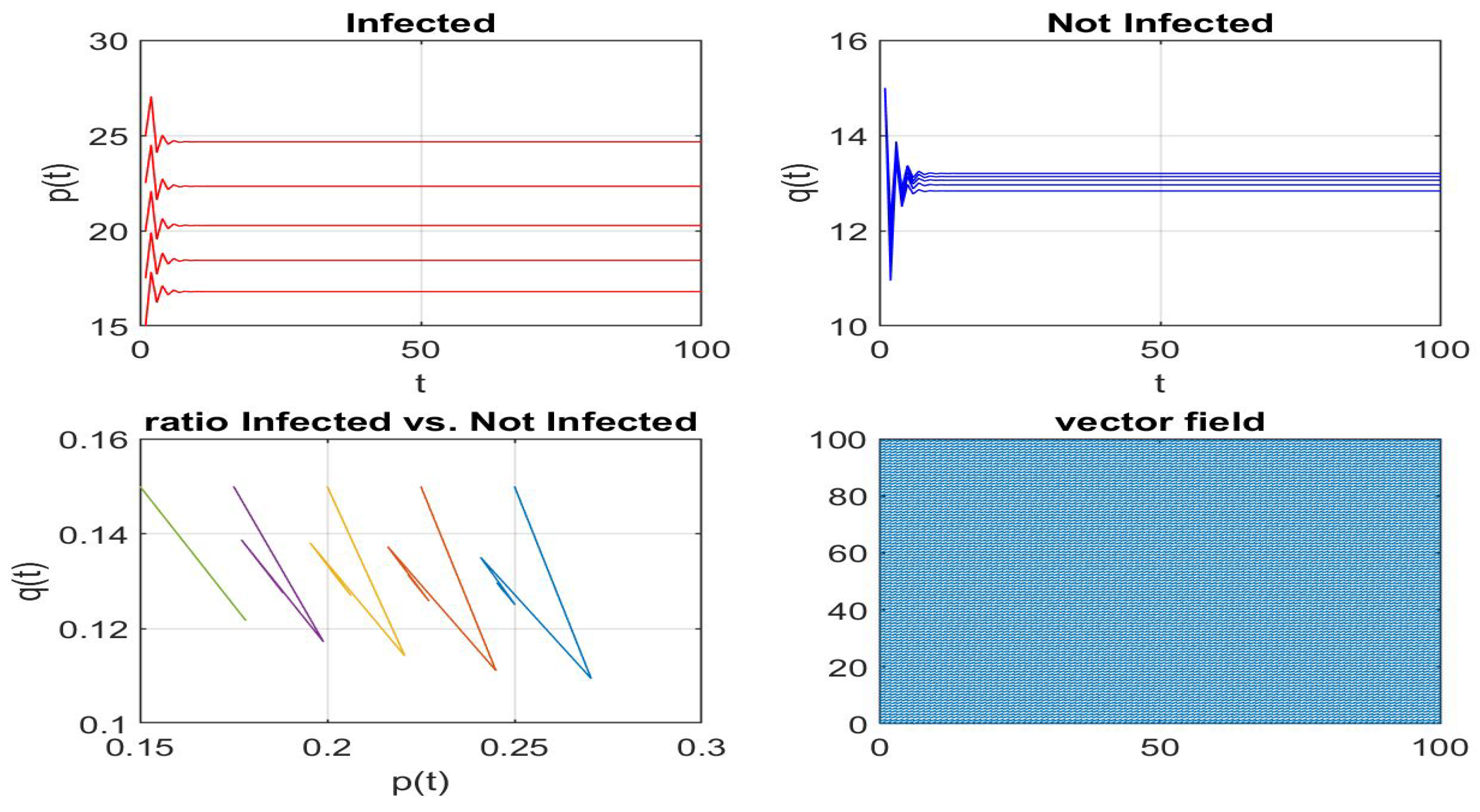
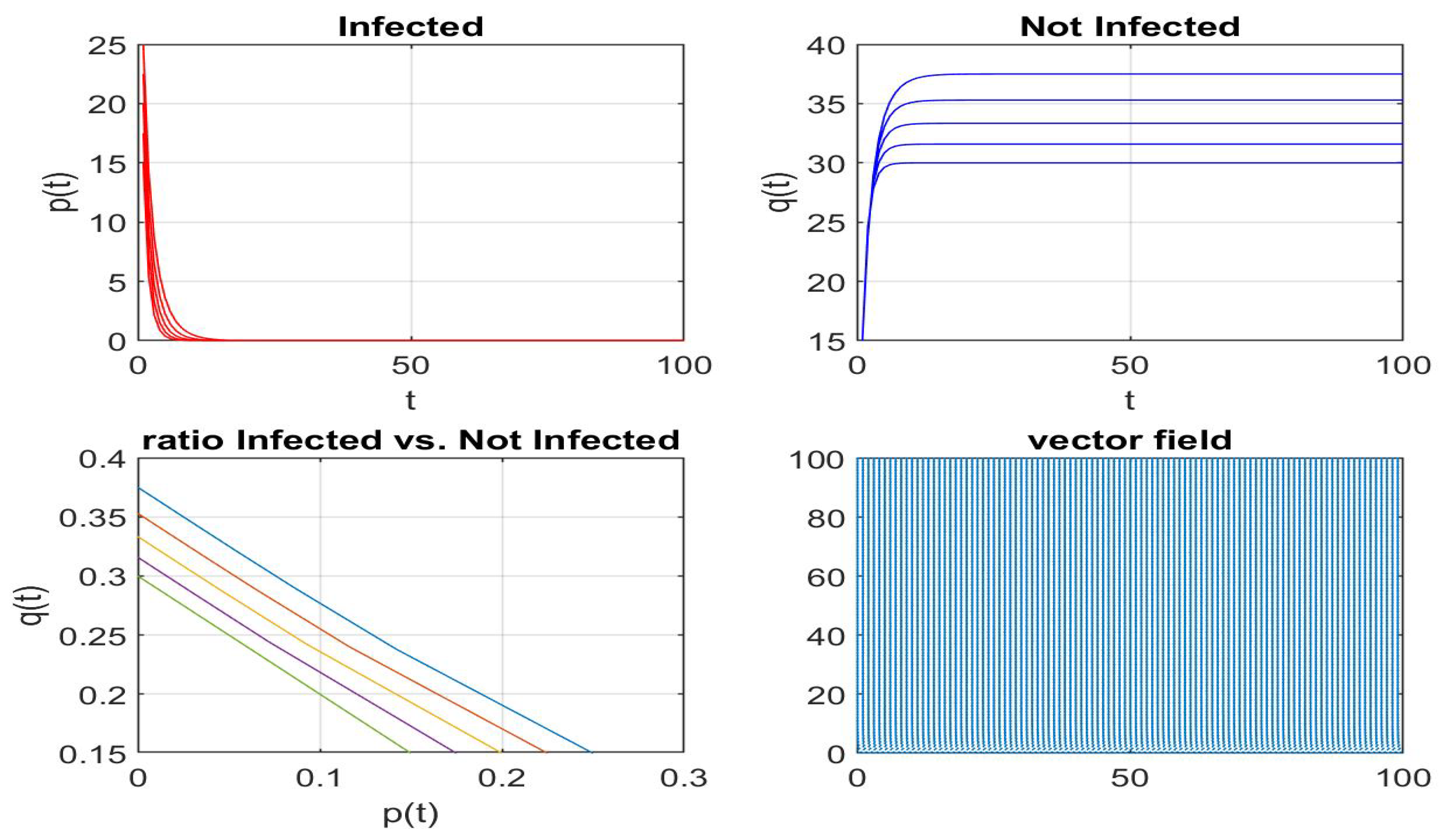
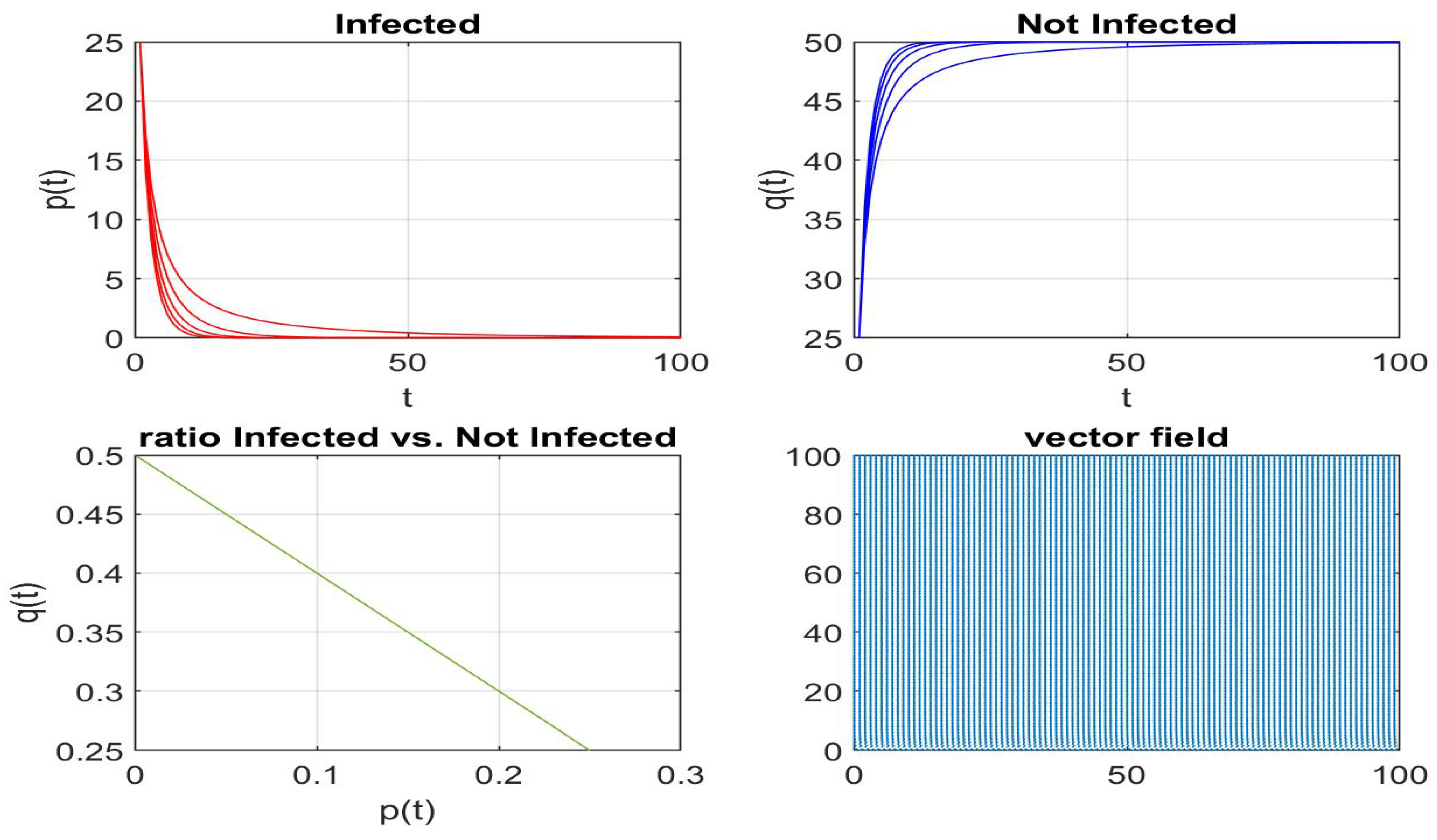
3.1. Discrete SIS and SIRS Epidemic Models
3.2. Time Complexity of the Simulations
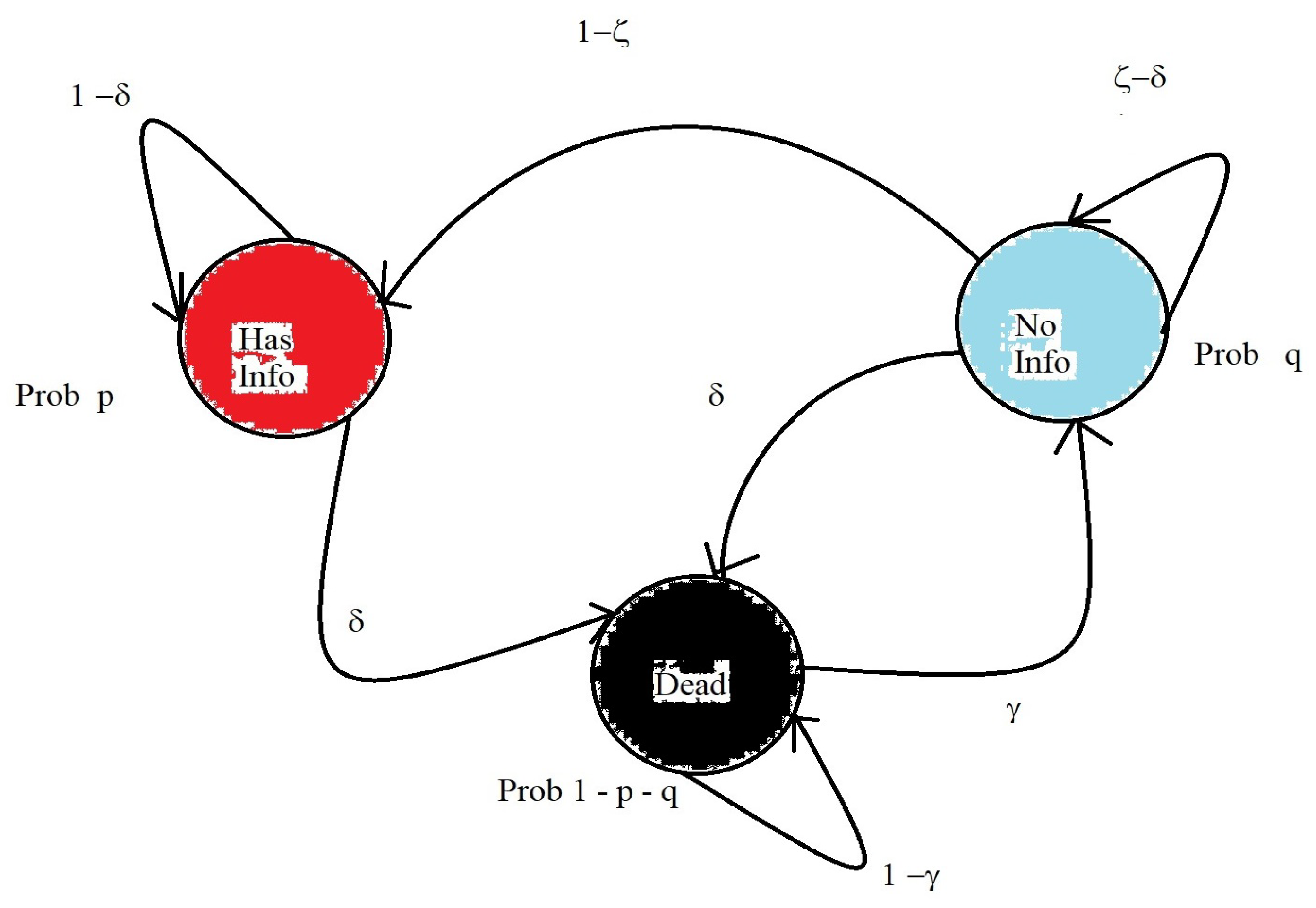
4. Isolation Strategies
- Infected nodes are healing
- Susceptible nodes are becoming infected
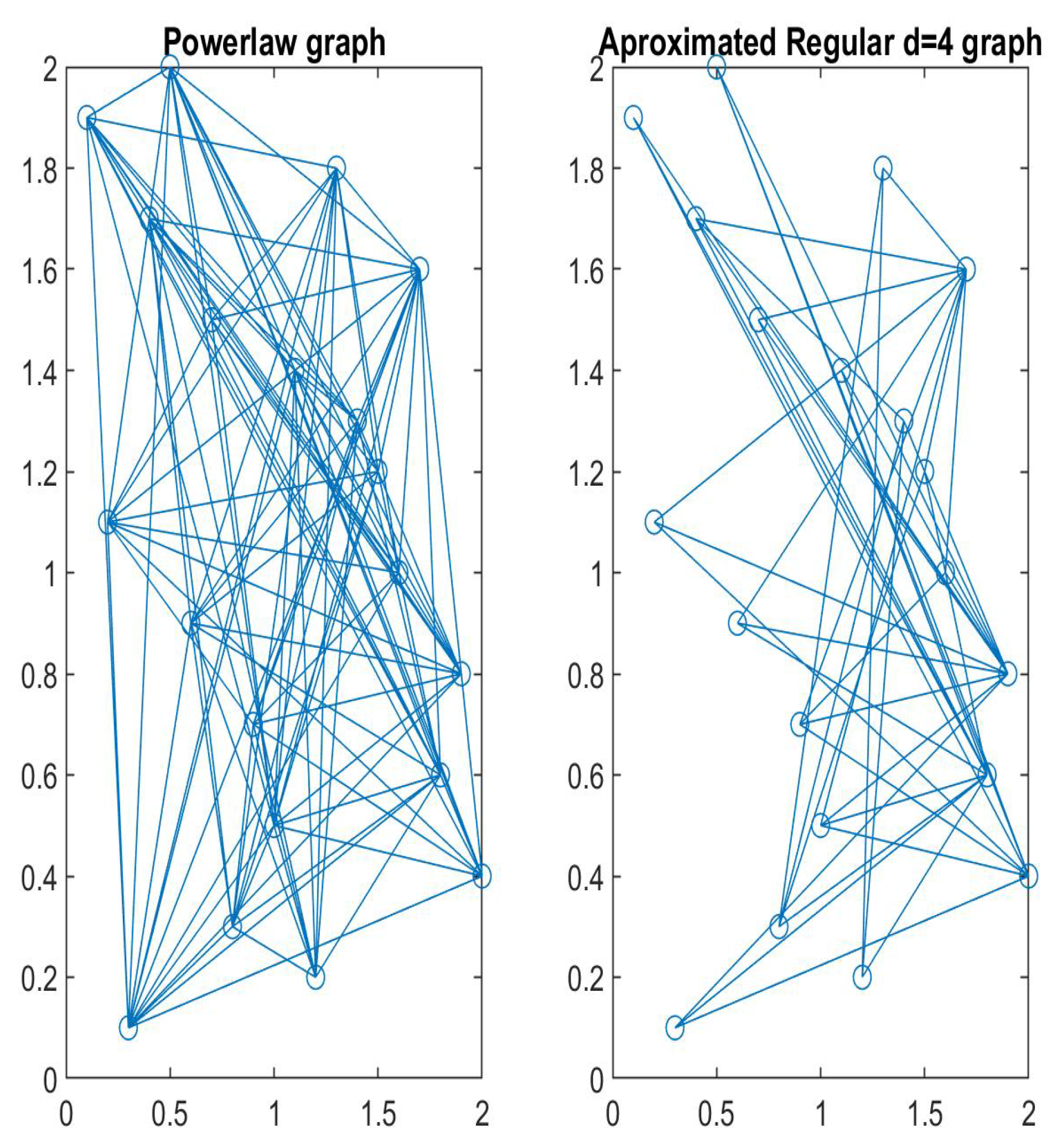
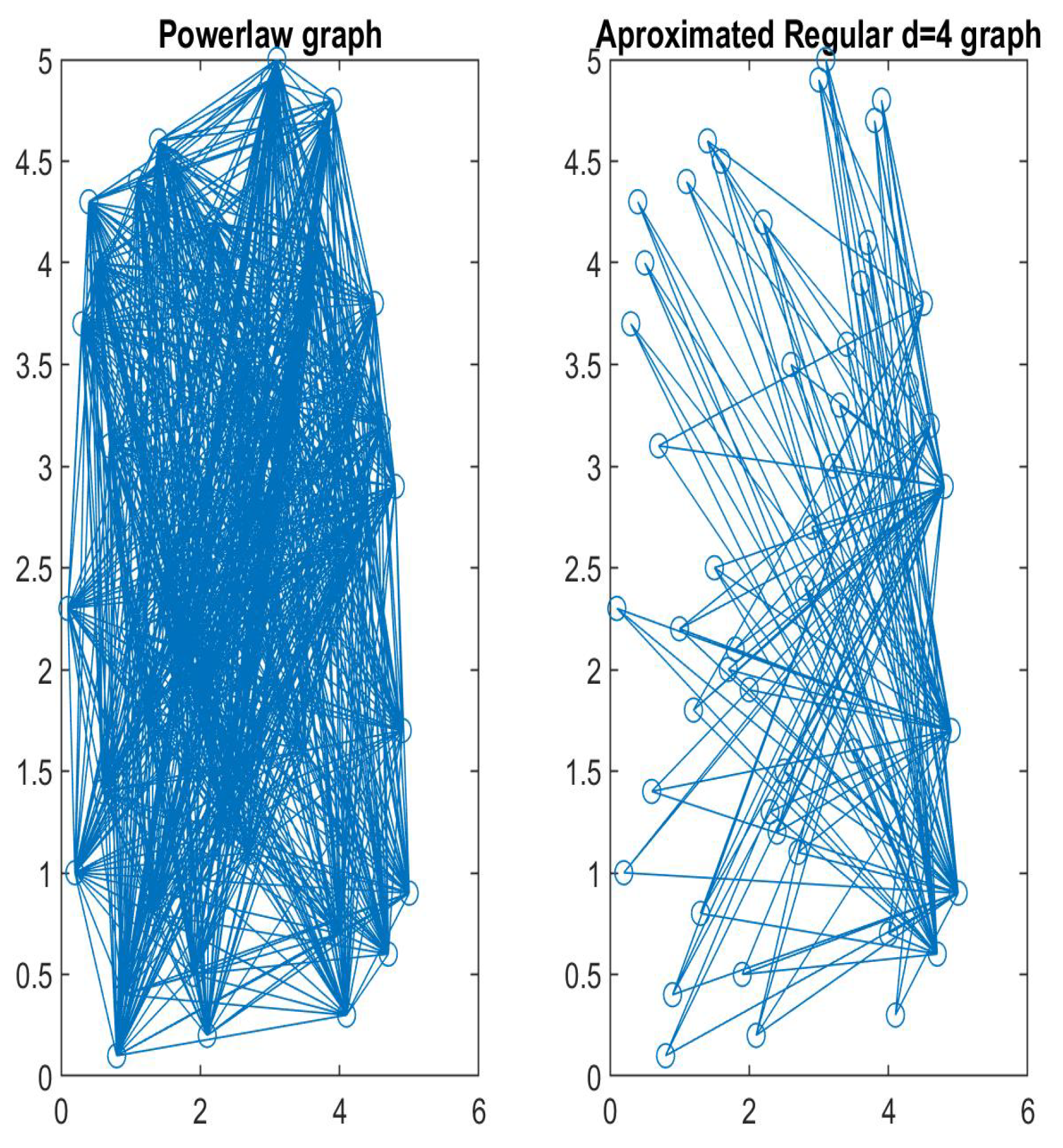
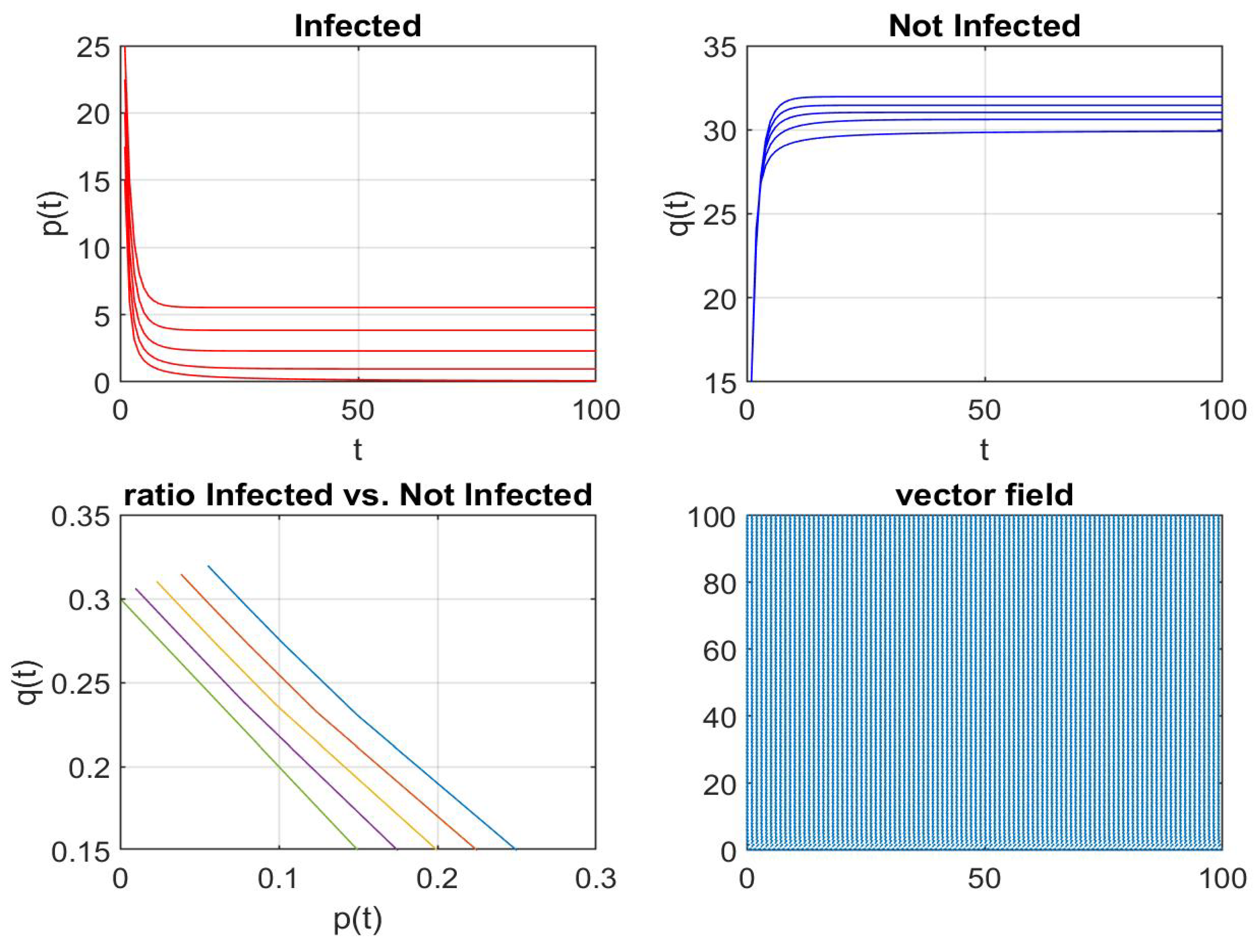
4.1. Previous Results in Isolation Strategies
4.2. My Node Isolation Strategy Proposal
5. Conclusions and Future Work
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SIR model | Susceptible, Infected and Recovered model |
| SIS model | Susceptible, Infected and Susceptible model |
| SIRS model | Susceptible, Infected, Recovered and Susceptible model |
| LSRM | Link Spectral Radius Minimization |
References
- Prakash, B.A.; Chakrabarti, D.; Faloutsos, M.; Valler, N.; Faloutsos, C. Got the Flu (or Mumps)? Check the Eigenvalue! arXiv 2010, arXiv:1004.0060. [Google Scholar]
- Chakrabarti, D.; Wang, Y.; Wang, C.; Leskovec, J.; Faloutsos, C. Epidemic Thresholds in Real Networks. Acm Trans. Inf. Syst. Secur. 2008, 10, 13. [Google Scholar] [CrossRef]
- Hethcote, H.W. The Mathematics of Infectious Diseases. Siam Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Durrett, R. Random Graph Dynamics; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Bernoulli, D. Esai d’une nouvelle analyse de la mortalité causeé par la petite vérole et des avantages de l’inoculation pour la prévenir. In Memoires de Mathématiques et de Physique; Académie Royale des Sciences: Paris, France, 1760; pp. 1–45. [Google Scholar]
- Hamer, W.H. Epidemic disease in England. Lancet 1906, 1, 733–739. [Google Scholar]
- Ross, R. The Prevention of Malaria, 2nd ed.; Murray: London, UK, 1911. [Google Scholar]
- Bailey, N.T.J. The Mathematical Theory of Infectious Diseases, 2nd ed.; Hafner: New York, NY, USA, 1975. [Google Scholar]
- Dietz, K. Epidemics and rumours: A survey. J. R. Stat. Soc. Ser. A 1967, 130, 505–528. [Google Scholar] [CrossRef]
- Dietz, K. The first epidemic model: A historical note on P. D. En’ko. Austral. J. Stat. 1988, 30, 56–65. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics part 1. Proc. R. Soc. Lond. Ser. A 1927, 115, 700–721. [Google Scholar]
- McKendrick, A.G. Applications of mathematics to medical problems. Proc. Edinb. Math. Soc. 1926, 44, 98–130. [Google Scholar] [CrossRef]
- Durrett, R.; Liu, X.-F. The contact process on a finite set. Ann. Probab. 1988, 16, 1158–1173. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.L.; Jeong, H. Error and attack tolerance of complex networks. Nature 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.L.; Albert, R. Emergence of scaling in random graphs. Science 1999, 286, 509–512. [Google Scholar] [CrossRef]
- Ben-Avraham, D.; Barabási, A.L.; Schwartz, N.; Cohen, R.; Havlin, S. Percolation in directed scale-free networks. Phys. Rev. E 2002, 66, 0151041–0151044. [Google Scholar]
- Pastor-Satorras, R.; Vespignani, A. Epidemic dynamics and endemic states in complex networks. Phys. Rev. E 2001, 63, 0661171–0661178. [Google Scholar] [CrossRef] [PubMed]
- Pastor-Satorras, R.; Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001, 86, 3200–3203. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic dynamics in finite size scale-free networks. Phys. Rev. E 2002, 65, 0351081–0351084. [Google Scholar] [CrossRef] [PubMed]
- Kempe, D.; Kleinberg, J. Protocols and impossibility results for gossip-based communication mechanisms. In Proceedings of the Symposium on Foundations of Computer Science (FOCS 2002), Vancouver, BC, Canada, 19 November 2002. [Google Scholar]
- Borgs, C.; Chayes, J.; Ganesh, A.; Saberi, A. How to distribute antidote to control epidemics. Random Struct. Algorithms 2010, 37, 204–222. [Google Scholar] [CrossRef]
- Faloutsos, C.; Madden, S.; Guestrin, C.; Leskovec, J.; Chakrabarti, D.; Faloutsos, M. Information survival threshold in sensor and p2p networks. In Proceedings of the IEEE INFOCOM 2007, Anchorage, AK, USA, 6–12 May 2007. [Google Scholar]
- Krivelevich, M.; Sudakov, B. The largest eigenvalue of sparse random graphs. arXiv 2001, arXiv:math/0106066v1. [Google Scholar] [CrossRef]
- Rodríguez Lucatero, C.; Bernal Jaquez, R. Virus and Warning Spread in Dynamical Networks. Adv. Complex Syst. 2011, 14, 341–358. [Google Scholar] [CrossRef]
- Van Mieghem, P.; Omic, J.; Kooij, R. Virus Spread in Networks. IEEE/Acm Trans. Netw. 2009, 7, 1–14. [Google Scholar] [CrossRef]
- Van Mieghem, P.; Stevanovi’c, D.; Kuipers, F.; Li, C.; van de Bovenkamp, R.; Liu, D.; Wang, H. Decreasing the spectral radius of a graph by link removals. Phys. Rev. 2011, 84, 016101. [Google Scholar] [CrossRef] [PubMed]
- Van Mieghem, P. Graph Spectra for Complex Networks; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]





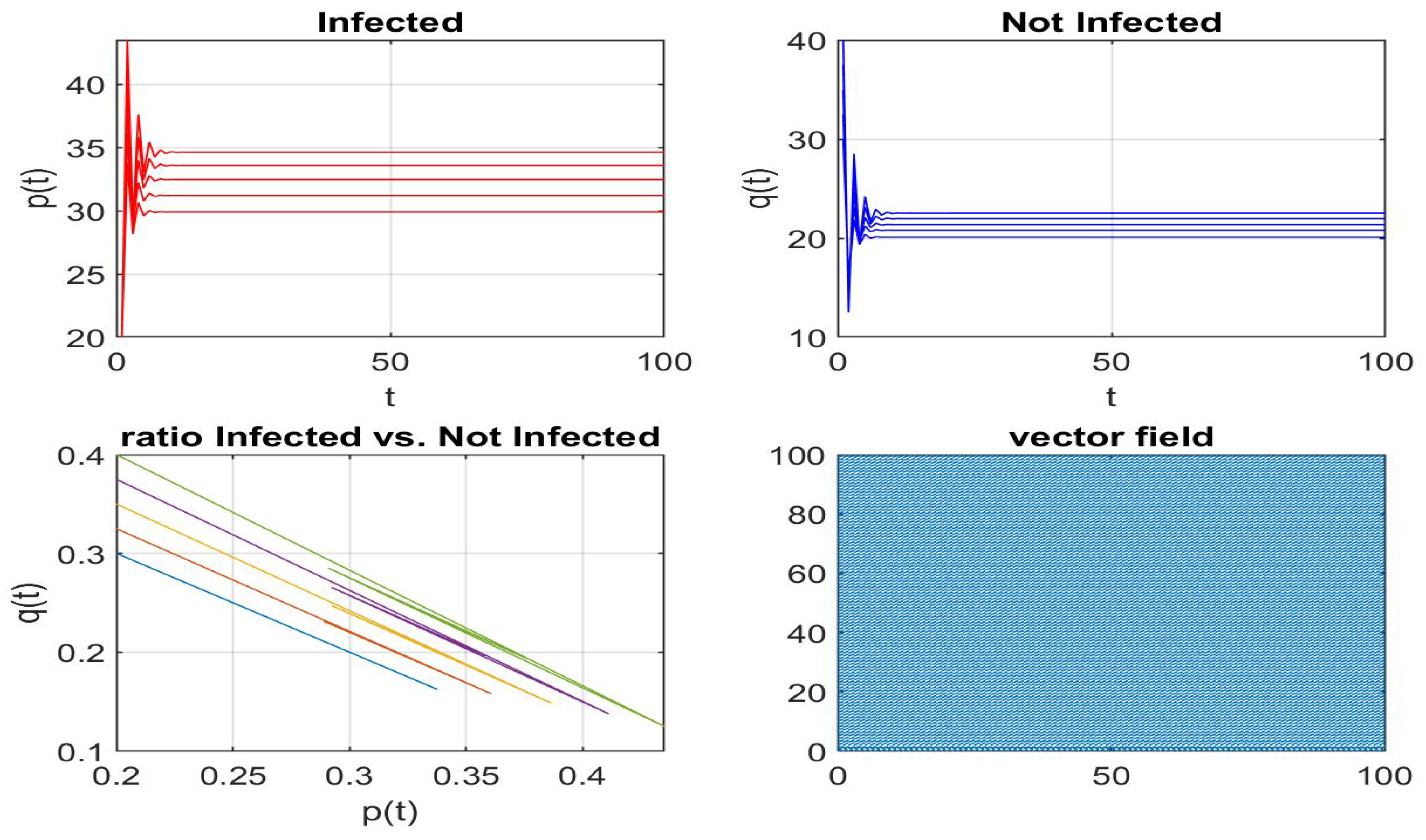
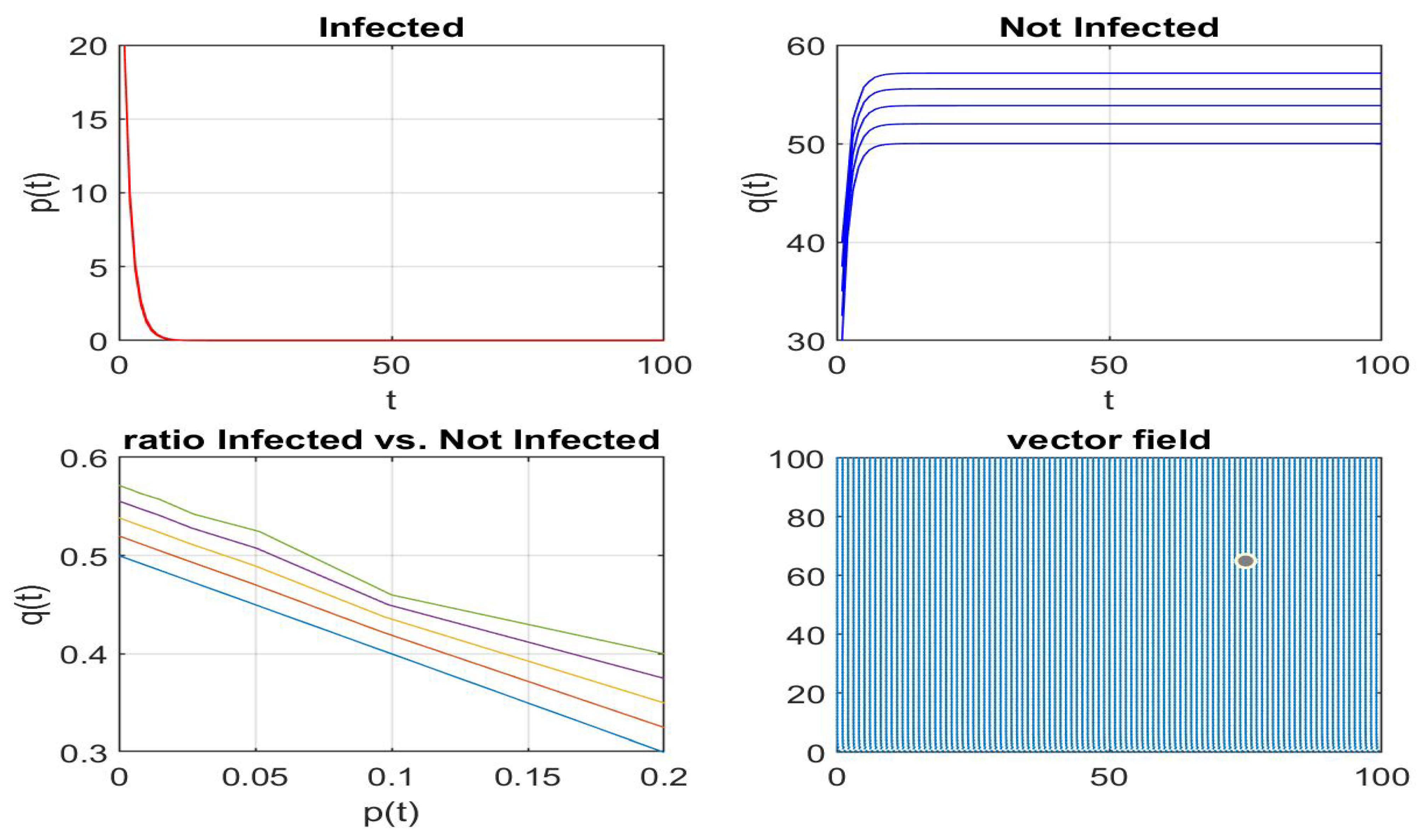
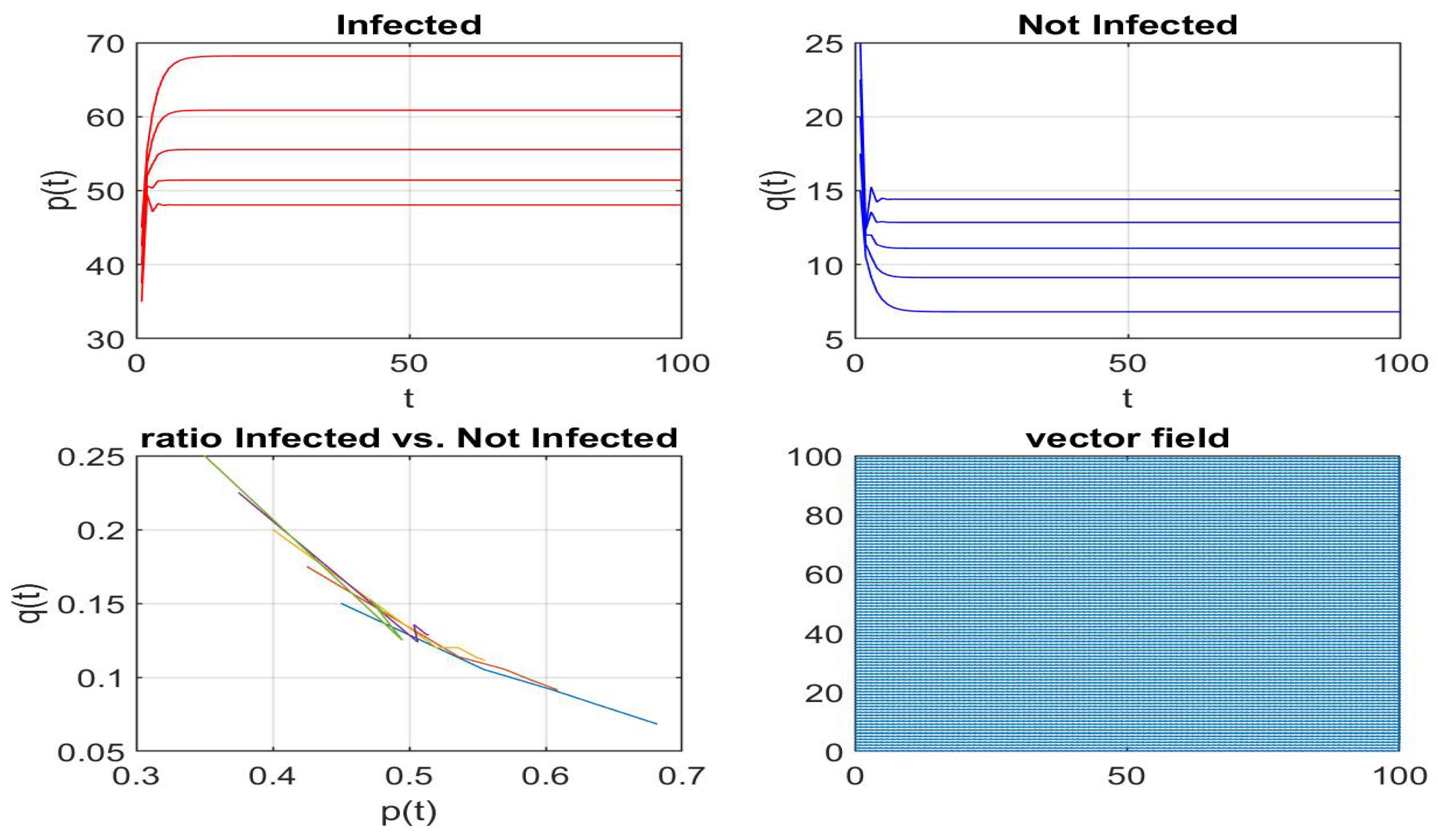
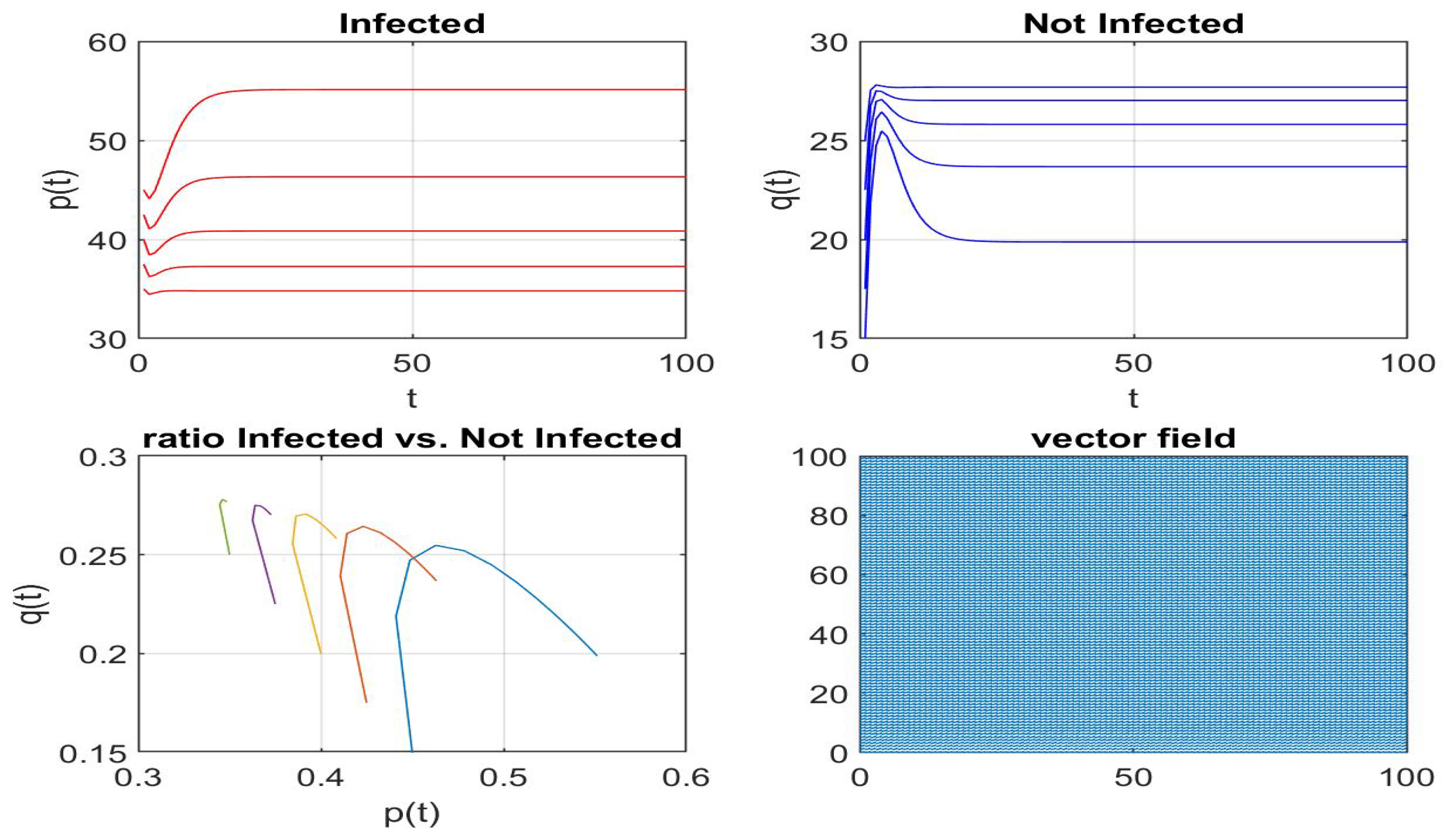


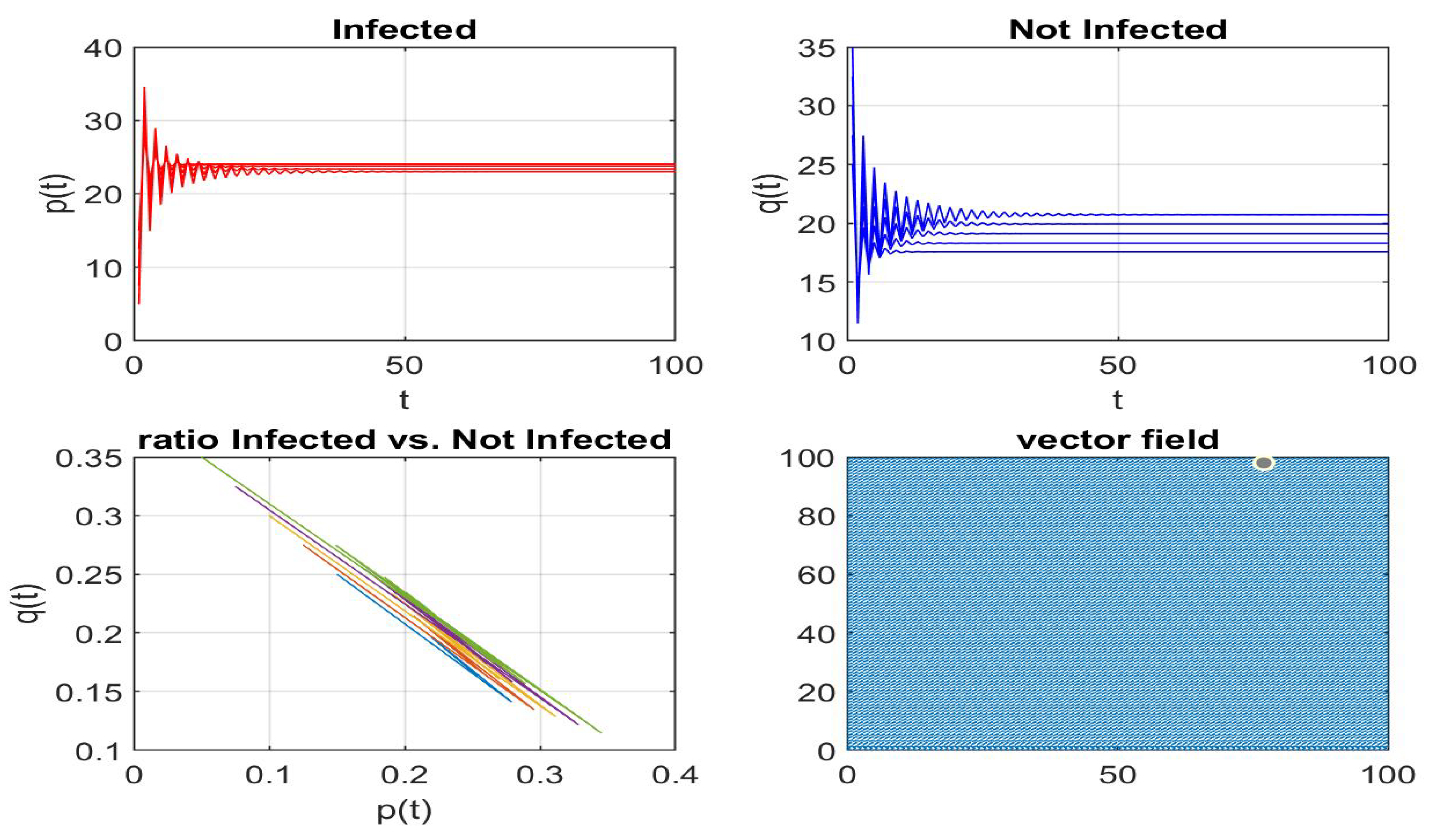
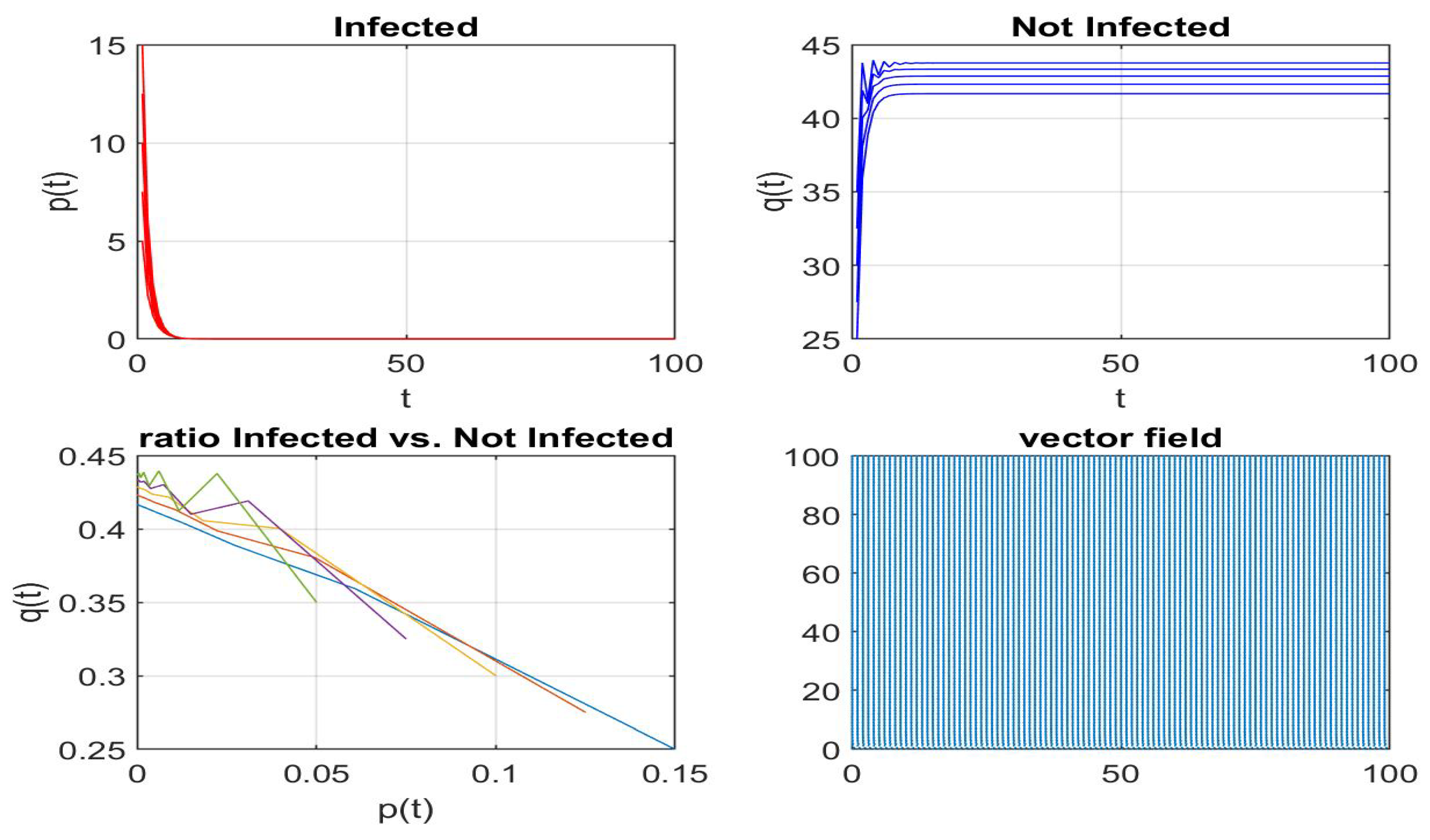
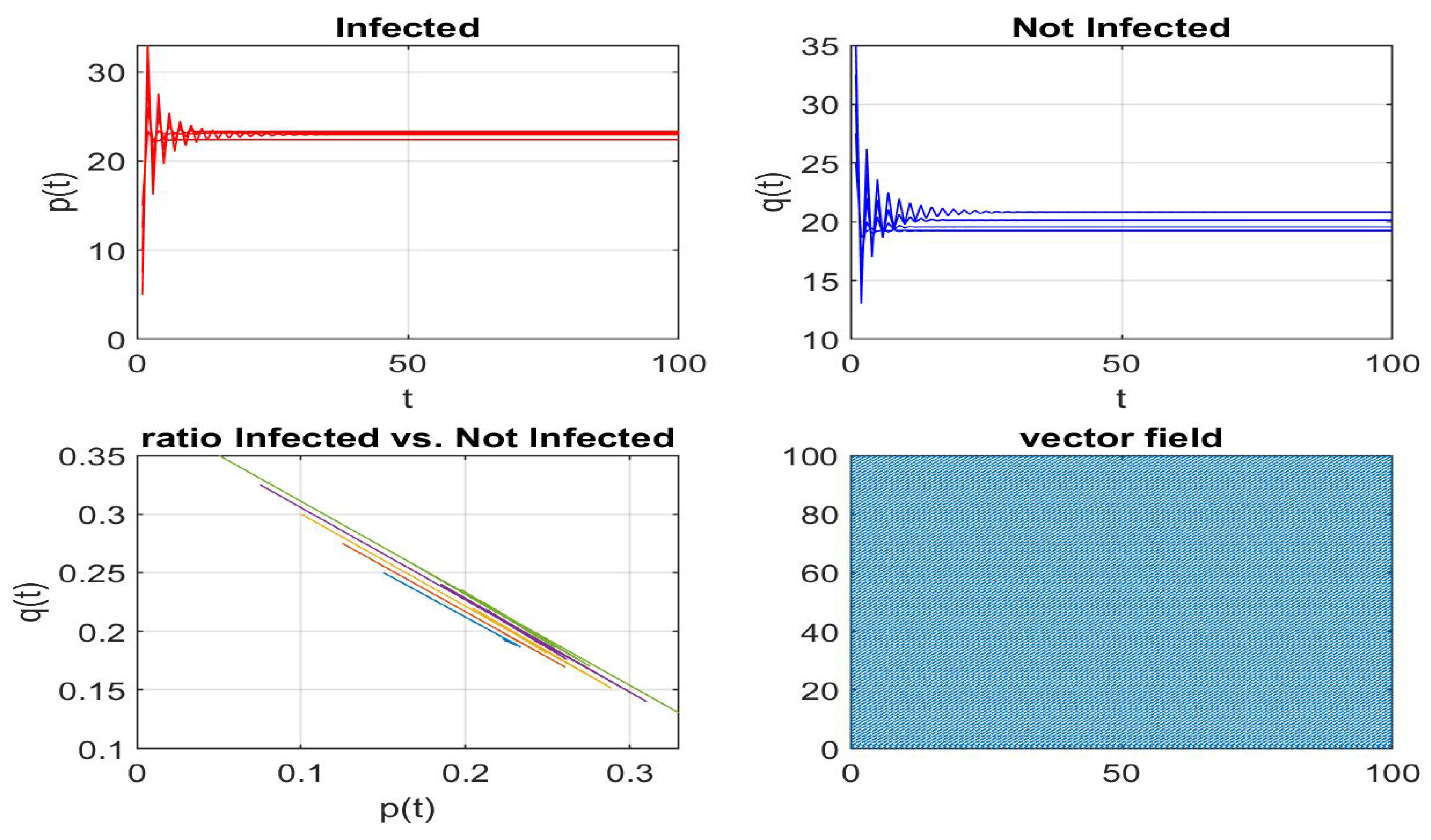
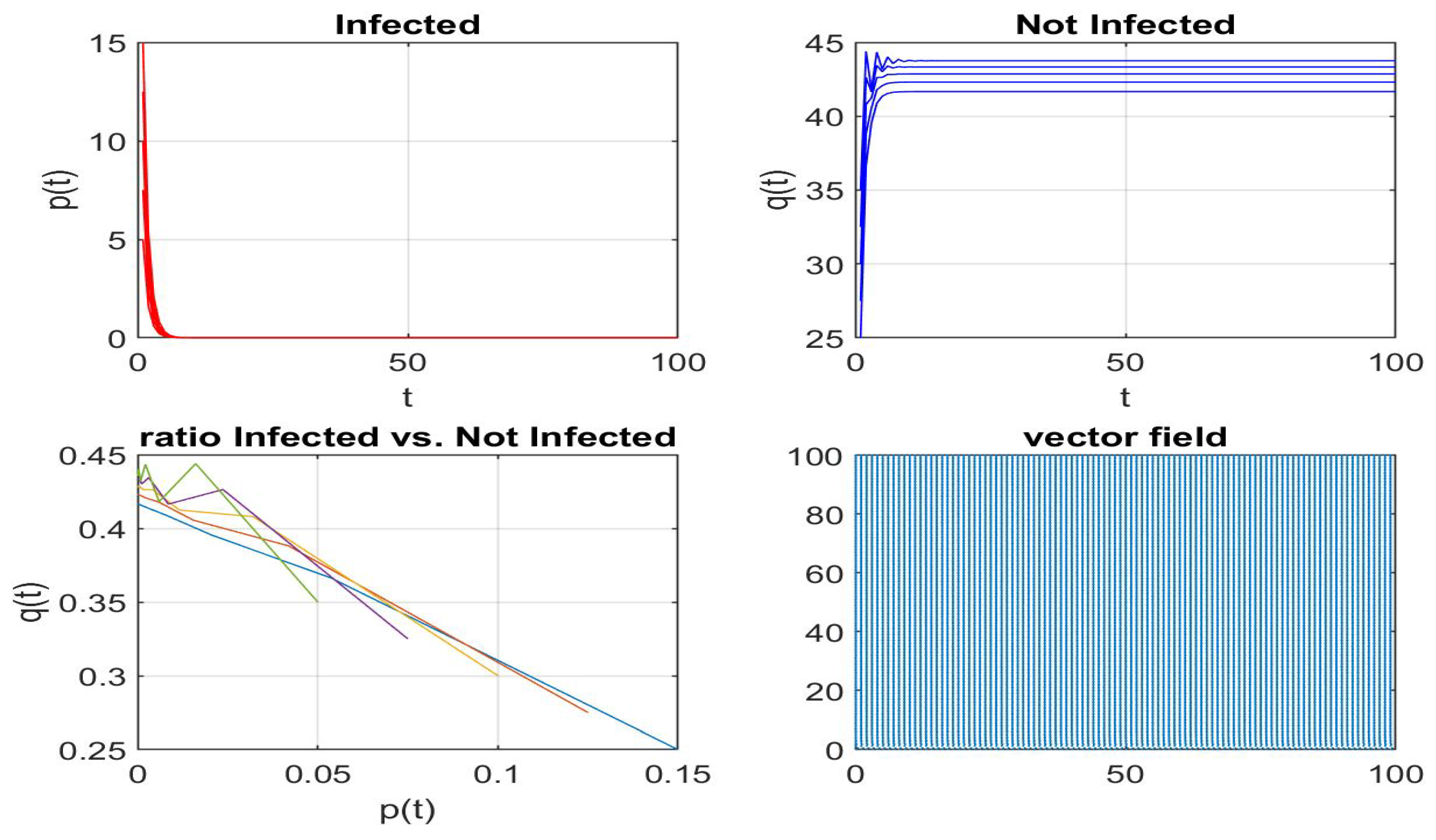
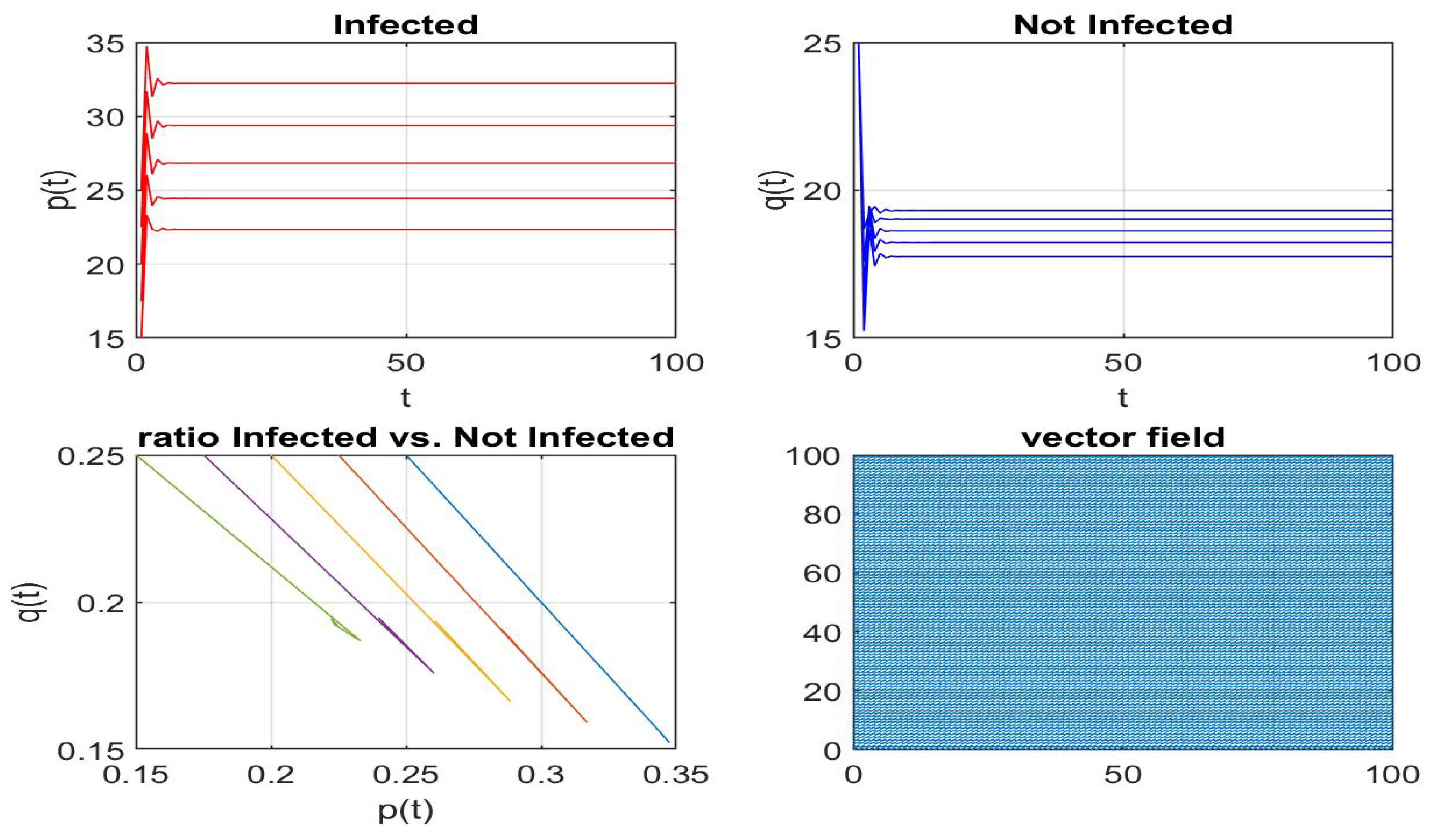
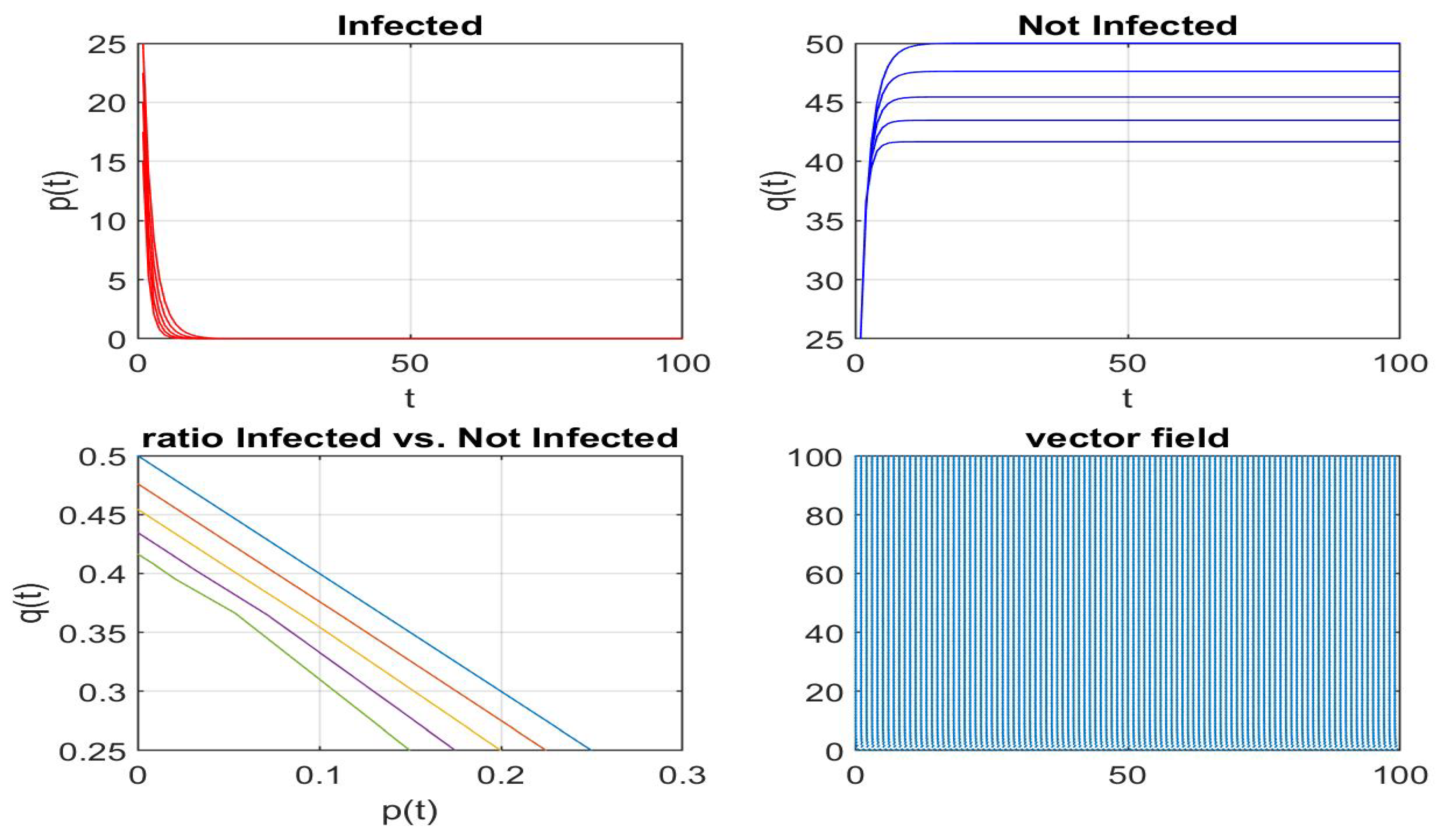
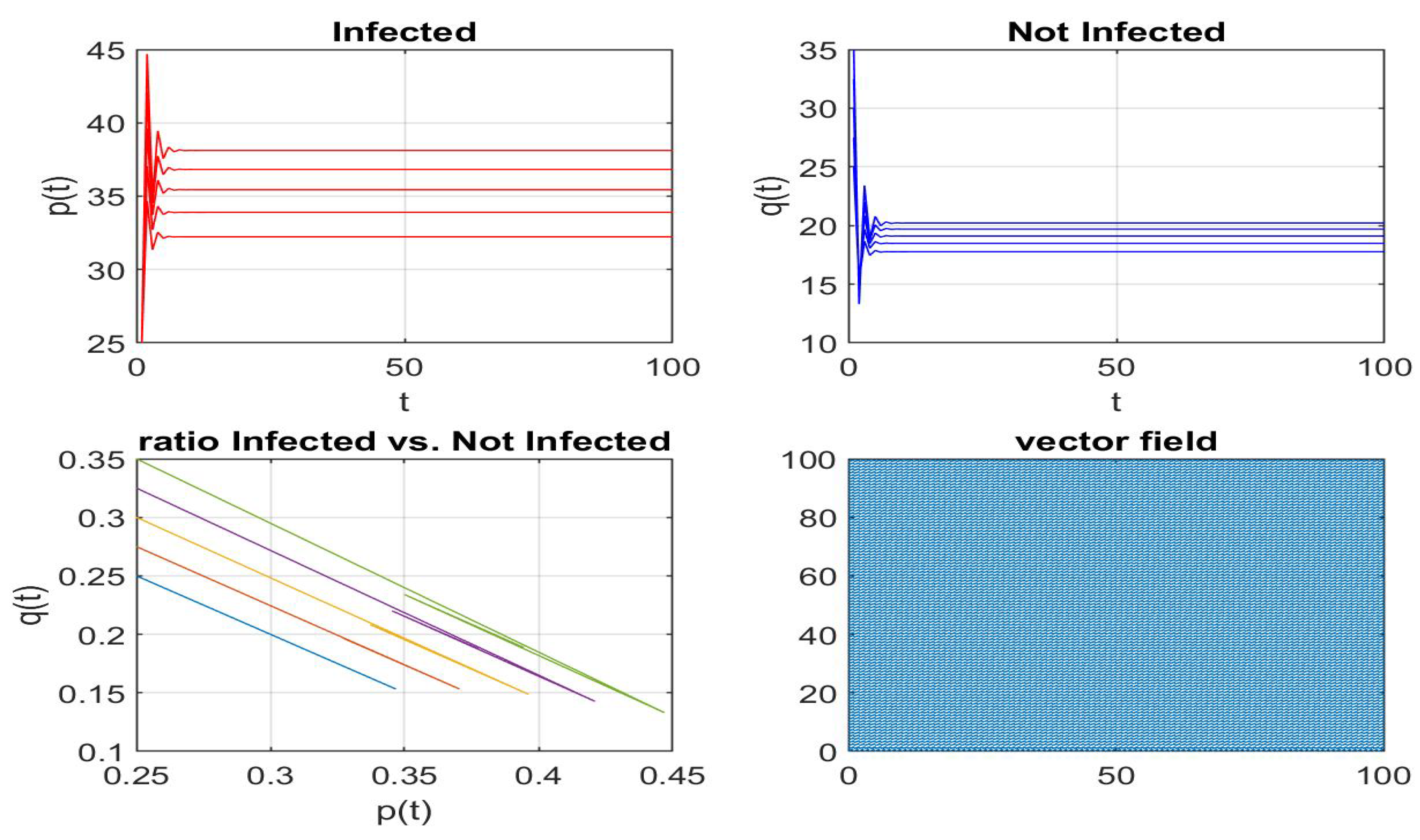
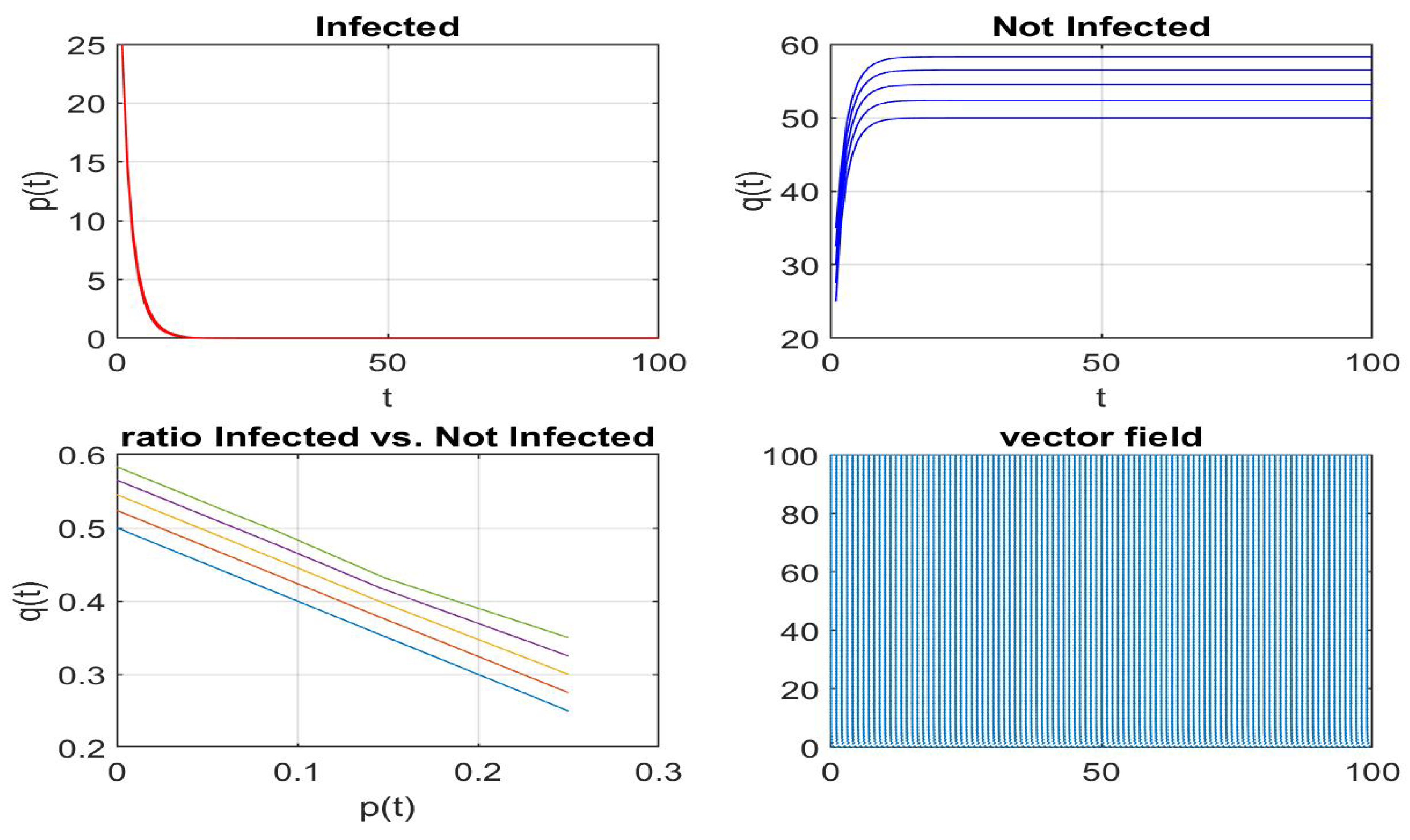

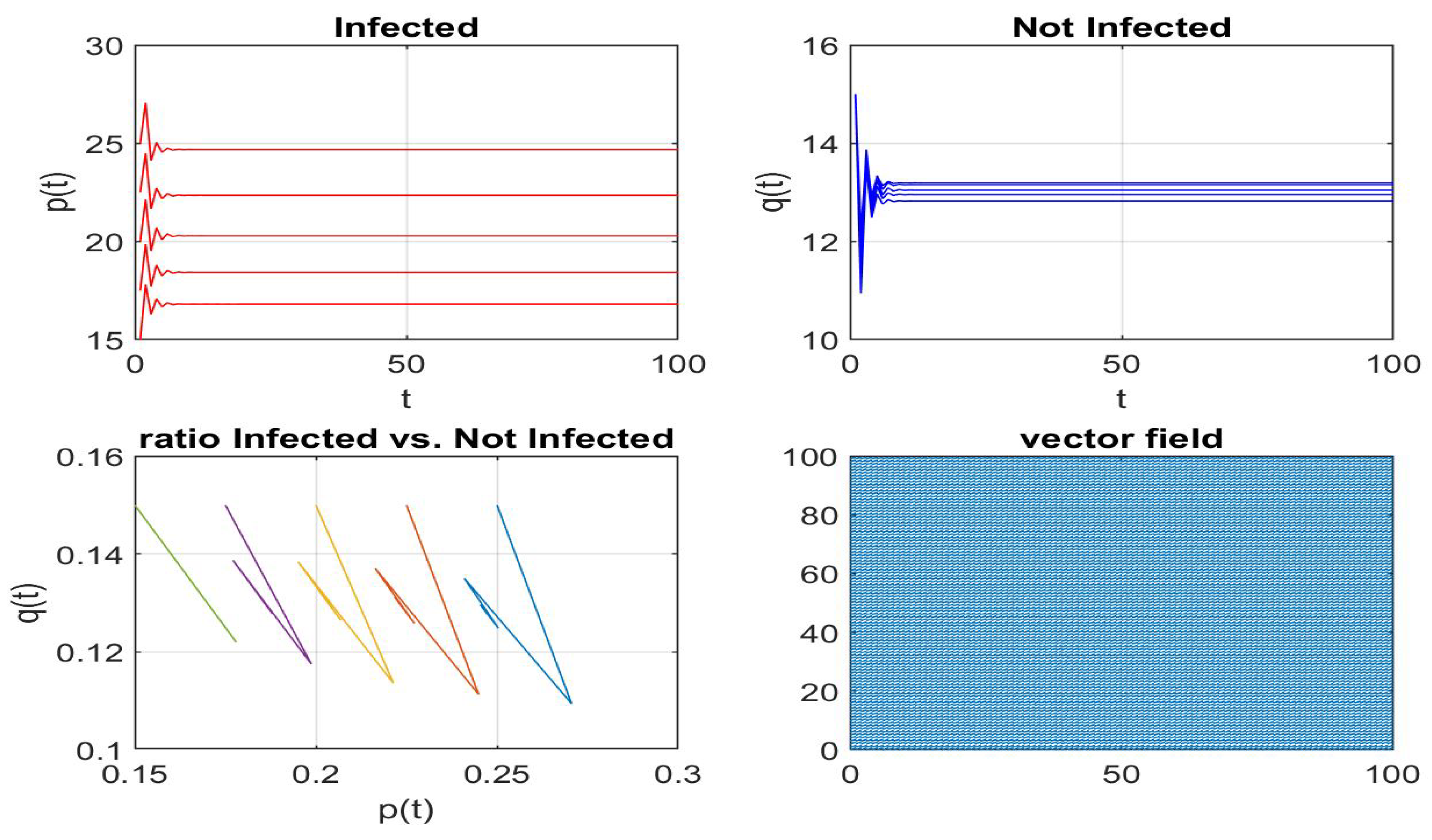
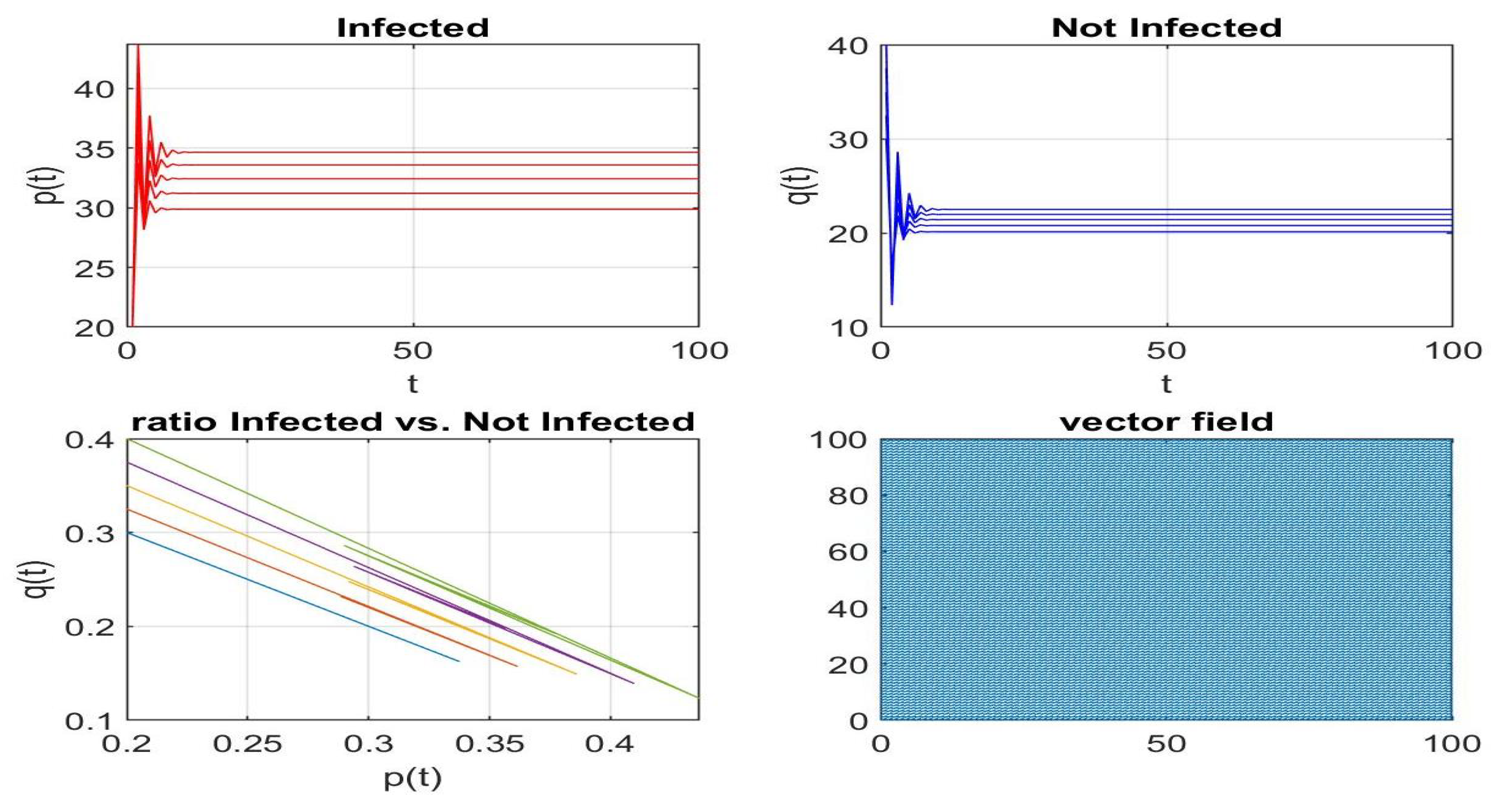
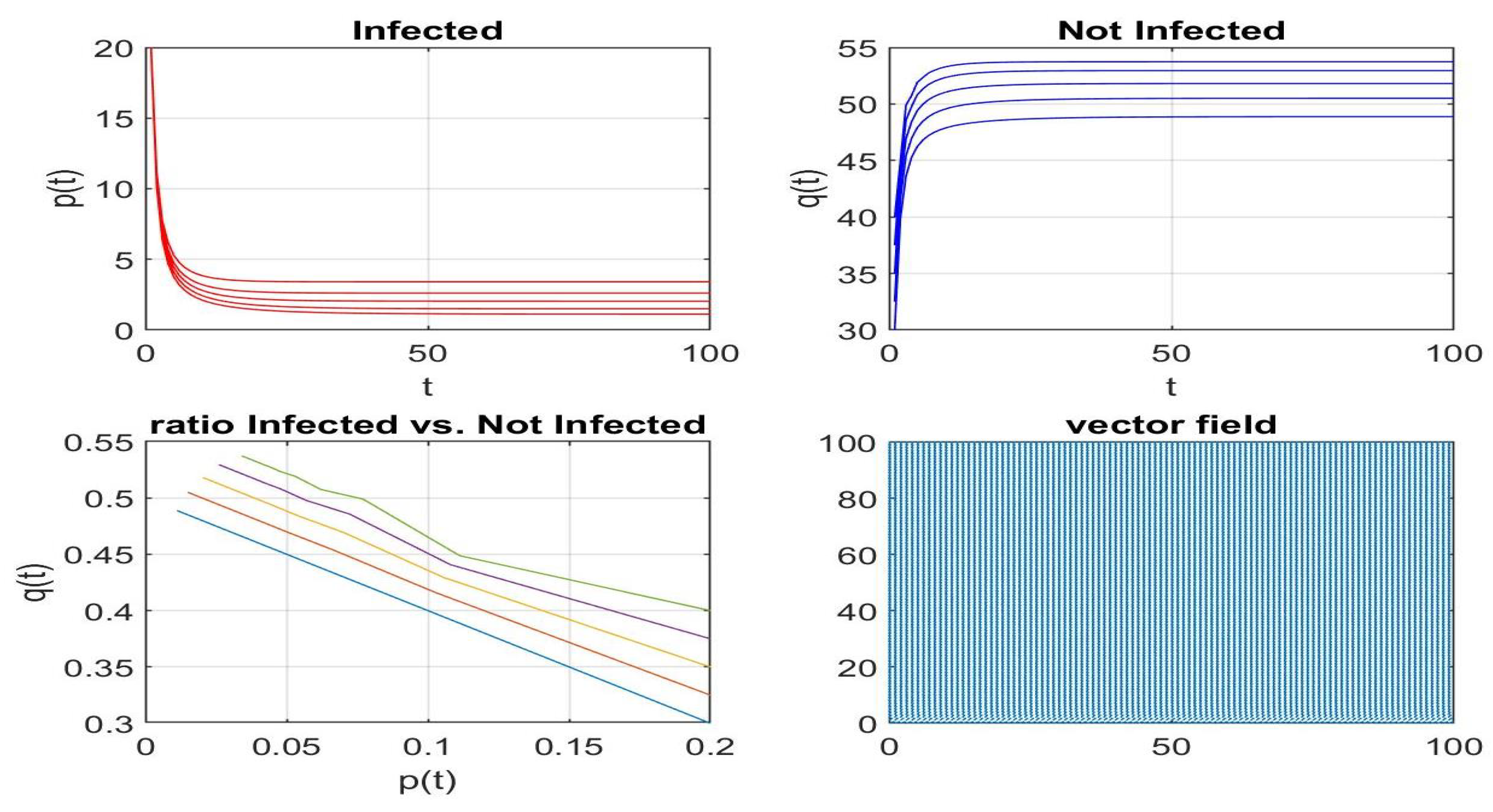
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodríguez Lucatero, C. Analysis of Epidemic Models in Complex Networks and Node Isolation Strategie Proposal for Reducing Virus Propagation. Axioms 2024, 13, 79. https://doi.org/10.3390/axioms13020079
Rodríguez Lucatero C. Analysis of Epidemic Models in Complex Networks and Node Isolation Strategie Proposal for Reducing Virus Propagation. Axioms. 2024; 13(2):79. https://doi.org/10.3390/axioms13020079
Chicago/Turabian StyleRodríguez Lucatero, Carlos. 2024. "Analysis of Epidemic Models in Complex Networks and Node Isolation Strategie Proposal for Reducing Virus Propagation" Axioms 13, no. 2: 79. https://doi.org/10.3390/axioms13020079
APA StyleRodríguez Lucatero, C. (2024). Analysis of Epidemic Models in Complex Networks and Node Isolation Strategie Proposal for Reducing Virus Propagation. Axioms, 13(2), 79. https://doi.org/10.3390/axioms13020079





