Abstract
As digital technologies continue to reshape economic landscapes, the comprehensive evaluation of digital economy (DE) development in provincial regions becomes a critical endeavor. This article proposes a novel approach, integrating the linear programming method, fuzzy logic, and the alternative ranking order method accounting for two-step normalization (AROMAN), to assess the multifaceted facets of DE growth. The primary contribution of the AROMAN is the coupling of vector and linear normalization techniques in order to produce accurate data structures that are subsequently utilized in calculations. The proposed methodology accommodates the inherent uncertainties and complexities associated with the evaluation process, offering a robust framework for decision-makers. The linear programming aspect optimizes the weightings assigned to different evaluation criteria, ensuring a dynamic and context-specific assessment. By incorporating fuzzy logic, the model captures the vagueness and imprecision inherent in qualitative assessments, providing a more realistic representation of the DE’s multifaceted nature. The AROMAN further refines the ranking process, considering the interdependencies among the criteria and enhancing the accuracy of the evaluation. In order to ascertain the efficacy of the suggested methodology, a case study is undertaken pertaining to provincial areas, showcasing its implementation in the evaluation and a comparison of DE progress in various geographical settings. The outcomes illustrate the capacity of the model to produce perceptive and implementable insights for policymakers, thereby enabling them to make well-informed decisions and implement focused interventions that promote the expansion of the DE. Moreover, managerial implications, theoretical limitations, and a comparative analysis are also given of the proposed method.
MSC:
03E72; 94D05; 90B50
1. Introduction
A critical juncture in economic development has been reached with the evolution and pervasive adoption of cutting-edge digital innovations, including but not limited to artificial intelligence, cloud computing, blockchain, and virtual reality. The emergence of this paradigm shift in the economy is widely acknowledged as the DE [1]. The DE sets itself apart from traditional industrial models by virtue of its cleanliness, efficiency, environmental tolerance, and recyclability. The fundamental nature of the DE represents a radical shift away from the conventional industrial paradigm, encapsulating a progressive strategy for worldwide economic progress. Its ability to effectively navigate and prosper in the aftermath of unanticipated obstacles, such as the prolonged COVID-19 pandemic, is especially remarkable [2]. Amidst the persistent disruptions of our time, the DE stands out as a symbol of adaptability and resilience, guiding economic advancement toward a sustainable and dynamic future [3].
The DE has successfully eliminated obstacles that previously impeded in-person interactions, thereby guaranteeing smooth economic transactions both within countries and across borders. Its contributions have been crucial in guiding society through significant public health emergencies and influencing the course of the era following the epidemic [4]. The DE is driven by emergent technologies and governed by innovative development paradigms; its operation is contingent on the integration of information networks and platforms [5]. This methodology promotes the ongoing transformation of elements and assets, shifting its attention toward sustainable and high-quality progress, a fundamental pillar in the establishment of a modern economic structure. This profound expedition exposes participants to unprecedented perils and prospects [6]. Under the guidance of innovative development concepts, the DE continues to expand its reach and integrate more closely with economic and social sectors. The aforementioned synergy serves as a catalyst for a sequence of digital transformations, which introduce novel models, fresh technologies, and innovative industry attributes into society, industry, and business [7]. As a result, this dynamic process promotes a model of sustainable economic development that is propelled by innovation. Moreover, in addition to reshaping industrial and economic structures, the DE ushers in a new era of technological transformation, which generates favorable responses from the technology sector. The wide-ranging consequences of this profound impact extend to businesses, the general public, and governments in numerous countries, instigating a paradigm shift among numerous stakeholders [8]. The continuous process of restructuring and innovation transcends economic domains and permeates societal and industrial sectors as well. This creates an environment in which technological innovations serve as catalysts for sustainable progress [9].
The foundation of the DE is an ongoing cycle of information and communication technology (ICT) advancements and innovations. The inventive digital environment not only impacts conventional economic elements like the demographic dividend, market dynamics, wages, and foreign investments but also functions as a valuable repository of information and data that are vital for industrial progress and economic growth. The productivity recovery that has been propelled by the development and implementation of information and communication technologies is exemplified by the United States [10]. Oliner and Dale W, among other scholars, have quantified the undeniable contribution of ICT to economic expansion in the United States. In the same way, Abdul’s research underscores the substantial influence that information and communication technology has had on India’s economic expansion. This highlights the critical significance of ICT in facilitating the economic advancement of both developed and developing countries. One aspect to consider is that the continuous advancements and innovations in digital technology give rise to a multitude of nascent industries [11]. This suggests that heightened efficiency in innovation processes expedites the formation of fresh sectors. Conversely, the rapid cross-border integration of digital technology across various industries is facilitated by its integration and iteration with conventional counterparts. This exemplifies the remarkable permeability of digital technology. These two aspects operate in tandem to offer countries and societies innovative technologies, markets, and labor forces, thus instigating significant social transformations and technological advancements. This process of transformation yields economic and social development of superior quality [12].
Concurrently, the digital age emerges as a formidable new factor of production, upheaving conventional production patterns due to the exponential growth of digital information. Significant changes in the position of elements occur as a result of this shift in production factors; new factors are integrated, the diffusion of knowledge and technology is accelerated, resource allocation is optimized, and the development of green, clean, and intelligent industrial chains is expedited. This irreversible reshaping of the global industry value chain is a result of the DE’s spurious economic expansion [13]. The progressive integration of information elements, technological innovation, and the overall expansion of the DE all contribute to the increasing share of output value associated with the DE in the economies of all countries. The increasing impact of this phenomenon serves to further sustain economic expansion, solidifying the position of the DE as an irreversible catalyst in influencing the course of worldwide economic progress [14].
Amidst the present global environment, countries across the globe are actively involved in investigating a variety of frameworks to facilitate the growth of the DE. The objective is to capitalize on the prospects offered by the DE-driven new economic revolution in order to establish a dominant position in the trajectory of global economic progress. The introduction of the DE has brought about a significant shift in the competitive environment between countries, serving as a crucial catalyst for economic advancement. A comprehensive and empirical evaluation of the current stage of development of the DE is therefore essential. This evaluation achieves the goal of precisely comprehending the intricacies of the dynamic competition environment among nations [15]. Furthermore, it establishes a fundamental basis for discerning the merits and demerits linked to the promotion of the DE. Consequently, this enables the creation of pragmatic and focused suggestions designed to guarantee the ongoing and expeditious growth of the DE. This meticulous evaluation is of the utmost significance for China. It functions as a strategic instrument for precisely assessing the country’s position within the worldwide DE domain. Furthermore, it establishes the foundation for developing precise and efficacious approaches that have the potential to elevate China to a status of formidable global competitiveness [16]. The consequences of conducting such a thorough assessment go beyond theoretical deliberations; they directly guide China in determining the practical actions and strategies required to establish a new trajectory of development. In its endeavor to establish itself as a highly competitive nation on the global stage, China can greatly advantage from the knowledge gained from a comprehensive assessment of its DE progress. This procedure not only facilitates the identification and exploitation of current benefits but also sheds light on specific domains that necessitate concentrated effort and enhancement. In essence, this strategic approach is of immeasurable value as it directs China toward the establishment of a novel development paradigm—one that nurtures sustainable and high-quality economic progress in the age of digitalization [17].
In this paper, the level of development of China’s DE will be estimated utilizing the fuzzy decision-making theory. The structure of the subsequent sections of this manuscript is as follows: The Literature Review Section presents a compilation of the latest research findings from relevant scholars regarding the DE. Section 3 describes the imprecise AROMAN based on linear programming. Section 4 comprises a number of evaluation criteria for DE. The results of a case study are discussed in Section 5. In addition to a succinct summary of the research findings, the concluding section of this paper provides pertinent recommendations.
2. Literature Review
In this section, the definition of DE and some work related to the DE is given.
2.1. Definition of Digital Economy
The DE, which serves as a crucial strategy for driving global economic progress, has a significant impact on numerous spheres, including the transformation of industrial structures, the improvement in international competitiveness, and the restructuring of the manufacturing sector. Introduced in the 1990s as a technical term, the DE evolved conceptually over time. Tapscott [18] introduced the term “era of networked intelligence” in 1996, delineating it as a technologically crafted network system by humans. The complex network that links knowledge, expertise, and innovation facilitates groundbreaking concepts that drive economic growth and contribute to the betterment of society. According to Moulton [19], information technology and electronic commerce are fundamental elements of the DE. Further elaborating on this, Brynjolfsson and Kahin [20] contend that the digital infrastructure is the foundation of the DE. With the progression of the scientific and technological revolution, the fundamental nature of the DE experiences a significant expansion. It is worth noting that commodity trading and services that are built upon information and communication technology are regarded as essential elements that merit inclusion.
The significance of the DE in influencing global economic dynamics is underscored by its multifaceted nature. The dynamic perspectives offered by numerous academicians and experts enhance the overall comprehension of its complex elements, underscoring the imperative nature of incorporating digital infrastructure, information technology, and e-commerce into its comprehensive definition [21]. The ability to adjust to the ongoing technological revolution exemplifies the inclusive and dynamic characteristics of the DE, which establishes it as a significant catalyst in determining the features of modern economic environments. In addition to digital products and services, the government of the United Kingdom suggests that the DE should also encompass digital enterprises that implement digital technologies for modernization and transformation [22]. Despite the absence of a universally accepted definition of the DE, the definition put forth by the G20 is generally acknowledged within the academic community. It is of the opinion that the DE comprises a sequence of economic activities that leverage information and communication technology to facilitate the optimization of the economic structure and to enhance efficiency, with digital knowledge and information serving as critical production factors.
2.2. Evaluation of the Digital Economy
The white paper published by the Chinese Academy of Information and Communications in 2017 outlines the assessment index system for China’s DE index, which consists of three components. The initial component is the leading index, an assemblage of eight factors. The consistency index, the second component, comprises ten indications. The latency index constitutes the third component and is made up of four measures. In contrast to its predecessor, this index system incorporates lagging indicators and takes into account the expansion of the DE facilitated by emerging digital technologies [23]. A DE research institution published a paper that assembles sixteen indicators into a DE development indicator system. In addition to assessing the level of development of the DE, this index system also evaluates its industrial structure and development trajectory [24]. Zhang et al. examine the comprehensive progress of China’s DE by analyzing the infrastructure, fundamental and sophisticated uses of information and communication technology, enterprise digital development, and growth of the information and communication technology industry [25]. Chen [26] demonstrates exhaustively that, in terms of propelling factors, the level of scientific and technological advancement, the framework, of industry, human resources, and scientific and technological progress could significantly promote the development of the DE, whereas government interference would impede its progress. The development of the DE is significantly impacted by scientific and technological progress and trademark assurance, among other factors. Li and Han [27] develop a quantitative indication system to measure the extent of DE development. This method takes into account technological infrastructure, digital industrialization, and industrial digitization, as well as the underlying meaning and expansion of the DE. Subsequently, the growth trajectory of the DE in China was assessed over the period of 2010 to 2018 in order to predict its future development from 2019 to 2028. From the vantage points of fundamental resources, integrative improvement, innovation capability, societal advantages, and network protection, Li [28] develops an all-encompassing, scientific, and exhaustive index system for assessing the level of development of the DE.
Chen et al. [29] estimate the DE using nocturnal light remote sensing data and assess the DE growth at the city level using Zipf’s law. The Composite I-distance Indicator (CIDI) is utilized by Dobrota et al. [30] to rank and assess the digital achievement of twenty-eight European Union member states. A fuzzy hierarchical statistical model-based regional economic development coordination management system is introduced by Xu and Li [31]. A dynamic multi-attribute evaluation of the development of the DE in China is presented by Xiao et al. [32], with an emphasis on the importance of interaction effects. This research illuminates the intricacies that are intrinsic in evaluating the DE, considering various characteristics. By analyzing the development of the DE in Guangdong province using an enhanced entropy method and multivariate statistical analysis, Deng et al. [33] make a scholarly contribution. The utilization of a fuzzy information evaluation and analysis technique in the advancement of rural e-commerce at the regional level is investigated by Wang [34]. This research contributes to the body of knowledge by examining the unique circumstances of rural regions, thereby showcasing the versatility of fuzzy logic in various economic environments. Li and Xue [35] make a scholarly contribution to the field by employing a fuzzy hierarchical algorithm to examine the ramifications of the regional total factor production on the DE. Their research contributes to the body of knowledge regarding the determinants of DE growth by highlighting the significance of factor production as a whole. In their study, Su et al. [36] apply the multi-attribute decision theory to assess the level of development in the DE. The research they conducted provides valuable insights into the utilization of decision theory in this particular domain. It establishes a systematic framework for thoroughly evaluating various factors that impact the advancement of the DE.
Upon reviewing the existing literature, it becomes apparent that foreign studies on the DE commenced earlier, featuring well-established index systems tested over an extended period, garnering significant credibility and authority. In contrast, domestic exploration into the DE was initiated later; however, the evaluation indicator system for DE development exhibits a more comprehensive nature. A notable observation is the scarcity of literature addressing the comprehensive evaluation of DE development utilizing MCDM models. Traditional research in this domain predominantly relied on statistical data for measuring DE development. However, challenges arise due to the infrequency and difficulty in obtaining coherent and comparable objective data. The collection process is labor-intensive, and not all gathered objective data are universally applicable across diverse areas [37]. Consequently, the analysis of DE development encounters hurdles due to data limitations. Moreover, prior investigations predominantly operated at the national level, overlooking regional disparities. By recognizing that each provincial-level region in China has distinct DE development strategies and plans, evaluating the DE development level on a provincial scale offers more nuanced insights. This approach provides valuable policy support tailored to the specific developmental needs of each provincial-level region. In light of these considerations, this study undertakes an evaluation and analysis of the provincial-level DE development in China. The objective is to present targeted suggestions aligned with the distinctive developmental characteristics of the provincial DE. This endeavor aims to expedite the high-level and high-quality development of the DE in China [38].
2.3. Uncertain Data Modeling
For a long period of time, the task of managing uncertain and insufficient information has consistently been a significant concern. The consolidation of knowledge is a crucial factor in decision-making across diverse fields, like business, engineering, management, social sciences, psychology, and artificial intelligence. Historically, options have typically been seen as simple numerical values when it comes to information. Nevertheless, in the modern era, information seldom takes on such a rudimentary structure, necessitating careful consideration to resolve discrepancies in facts. Recognizing the intricate nature of the problem, Zadeh [39] proposes the notion of the fuzzy set, utilizing the membership function as a tool to depict and unify things with indistinct borders. The fuzzy set is a valuable mathematical concept that allows for the definition and organization of things with unclear boundaries, using membership grades. This creative method is crucial for understanding the complexities of modern information, where simplicity often yields to the subtle and intricate structure of data.
Awodi et al. [40] present a fuzzy TOPSIS-based risk assessment model for nuclear decommissioning, contributing to effective risk management in the intricate field of nuclear energy. Meanwhile, Chisale and Lee [41] address renewable energy challenges in Malawi, utilizing the AHP and fuzzy TOPSIS to evaluate barriers and propose solutions. Their study provides insights into sustainable energy development in the African context. Ghose et al. [42] present an integrated fuzzy COPRAS model designed to determine the most suitable materials for applications in solar electric vehicles. Their contribution to the field is the provision of a comprehensive framework for decision-making in the electric vehicle sector that is specifically designed to promote sustainable development. Olabanji and Mpofu [43] extend the applicability of the fuzzy COPRAS methodology to the optimization of product design in a related context. The research highlights the adaptability of the fuzzy COPRAS model by illustrating its effectiveness in improving decision-making processes that extend beyond particular domains. Recent studies employing the fuzzy DEMATEL methodology have advanced the understanding and application of decision-making processes in various industries. Çelik and Arslankaya [44] conduct an analysis of quality control criteria in a business context, using the fuzzy DEMATEL method and offering insights into effective quality management, illustrated through a glass business example. In maritime transportation, Kuzu [45] applies the fuzzy DEMATEL approach to conduct a risk analysis of anchor loss, demonstrating its utility in assessing complex factors and enhancing decision-making in the maritime industry. Furthermore, Mohapatra et al. [46] present a sustainable solution for addressing lean barriers in the Indian manufacturing industry, employing a fuzzy DEMATEL methodology. Opreana et al. [47] propose a fuzzy analytic network process (ANP) integrated with principal component analysis to establish a comprehensive bank performance model, particularly considering country risk as a significant factor. This study contributes to the field of financial decision-making by offering an advanced approach for assessing and predicting bank performance under uncertain conditions. In a different context, Allahviranloo et al. [48] explore the application of the analytical hierarchy process (AHP) in a fuzzy environment, providing a theoretical foundation. Additionally, Hii et al. [49] focus on e-learning postadoption success, introducing a model based on the fuzzy ANP to evaluate information system success. Oubahman and Duleba [50] employ a fuzzy PROMETHEE model to analyze public transport mode choice, offering an innovative approach to addressing the complexity of decision-making in transportation planning. This study contributes to the field by demonstrating the adaptability of fuzzy PROMETHEE models in capturing the nuances of individuals’ preferences and uncertainties associated with mode choice. In a separate application, Liang et al. [51] introduce a novel robustness PROMETHEE method for blockchain technology-enhanced supplier selection. Their approach integrates learning interactive criteria and historical information, showcasing the versatility of the fuzzy PROMETHEE in supplier selection processes enhanced by emerging technologies. In the realm of multi-criteria decision-making, the authors propose q-rung orthopair fuzzy Aczel–Alsina AOs [52], offering flexibility in handling complex decision scenarios. Additionally, a prior study by Farid and Riaz [53] introduces generalized q-rung orthopair fuzzy Einstein interactive geometric AOs. Tolga et al. [54] introduce finite-interval-valued Type-2 Gaussian fuzzy numbers to enhance the fuzzy TODIM method. This innovative approach is applied to a healthcare problem, showcasing the versatility of fuzzy logic in addressing uncertainties in decision-making. Similarly, Deveci et al. [55] evaluate the metaverse integration of freight fluidity measurement alternatives using the fuzzy Dombi EDAS model, emphasizing the applicability of fuzzy logic in the evolving landscape of metaverse technologies. In the realm of agriculture, Tolga and Basar [56] assess a smart system in hydroponic vertical farming through fuzzy MCDM methods. This study exemplifies the utilization of fuzzy logic in optimizing decision processes within the agricultural sector. Moving to logistics, Tütüncü et al. [57] employ an integer linear programming approach to address the personnel shuttle routing problem at the Yıldız Campus, Istanbul, underscoring the effectiveness of mathematical models augmented with fuzzy concepts in solving real-world logistical challenges. In the healthcare sector, Ghoushchi and Sarvi [58] extend the use of fuzzy logic by prioritizing and evaluating the risks associated with ordering and prescribing in the chemotherapy process. Their study utilizes an extended SWARA and MOORA approach under fuzzy Z-numbers, showcasing the adaptability of fuzzy logic to handle uncertainties in risk assessment.
We employ a novel strategy to address methodological challenges and the research gap in the evaluation of the DE. Specifically, we apply the recently proposed fuzzy AROMAN, which is based on linear programming, and use criteria that are closely connected to the DE. The way the data are normalized and the final ranking is determined distinguish the AROMAN from other MCDM methodologies. The technique of data normalization involves transforming the input data of a decision-making matrix within a range of 0 to 1. This process frequently assists decision-makers in obtaining identical data structures, which facilitates and improves the relevance of subsequent calculations. It is very important to utilize normalization to make alternative comparisons easier when criteria are assigned different kinds of numerical values. The relative location of the criteria value within the value range determines the normalized value. As a result, choosing the appropriate normalization method is crucial since it influences subsequent calculations made during the decision-making process. One kind of normalization serves as the foundation for numerous MCDM techniques. However, while one normalization process is straightforward and subjective, relying solely on it may result in inaccurate information. Two different forms of normalization are used in the recently introduced AROMAN, and the normalized values that are acquired are then combined to create the averaged normalized decision-making matrix. In order to acquire more accurate normalized data, we link two normalization strategies (the linear and vector) in this study using arithmetic means. This is due to the expectation that combining the two approaches will result in a description of empirical data that is more accurate. In order to identify the variations among the methodologies taken into consideration, the final ranking results are also compared to the other MCDM techniques.
3. Linear Programming-Based Fuzzy AROMAN
In contrast to a single-criterion method, a decision-making problem considers numerous criteria in order to determine which alternative among a given set is the best. Numerous MCDM techniques are employed now to address a range of issues. The majority of these techniques are predicated on comparable decision-making concepts. A preliminary decision-making matrix is included, with several options juxtaposed against various competing standards. Any MCDM method’s output is a final ranking of options that aids in decision-makers’ selection of the best option. This research proposes a linear programming-based fuzzy alternative ranking order method accounting for two-step normalization (AROMAN). Using this technique, normalized data from the two-step normalization are combined to generate an average matrix.
Assume that there are n alternatives given as and that comprise the finite set of m criteria. The subsequent stages delineate the fuzzy AROMAN, which is founded upon linear programming.
Stage 1:
Obtain the fuzzy decision matrix from the decision-makers (DMs) as .
Stage 2:
Using this fuzzy decision matrix as a basis  , a weighted sum of the scores of each alternate is determined by
where, be the WV of the given criterion.
, a weighted sum of the scores of each alternate is determined by
where, be the WV of the given criterion.
 , a weighted sum of the scores of each alternate is determined by
, a weighted sum of the scores of each alternate is determined by
Let us consider a scenario in which the weights are considered to be indeterminate. In this context, we will denote a subset of these weights as ¥. In order to assess the indeterminate weights, we employ the aforementioned mathematical formulation.
Subject to the above conditions, the equation holds true. Through the utilization of this specific information, the WV undergoes a process of normalization. By employing a linear programming framework, the weights of criteria are computed while adhering to specific constraints.
Linear programming is a method of mathematical optimization that is employed to get the optimal solution in a mathematical model that is defined by linear connections. The process entails optimizing a linear objective function while adhering to a collection of linear equality and inequality constraints. Linear programming is frequently used in operations research, economics, and management science to systematically allocate limited resources and make optimum judgments in many disciplines.
Stage 3:
After find the criteria weights, the third step is to normalize the input data. There are two types of normalization, Equations (1) and (2) are employed to normalize the decision matrix. Equation (1) gave the linear form normalization and Equation (2) gave the vector form normalization. The normalization techniques in the step 3 are used for both criterion types (benefit and cost).
Stage 4:
The process of aggregated averaged normalization is achieved by implementing the following Equation (3).
For our specific situation, we assigned a value of is 0.50. is a weighting factor varying from 0 to 1. Within the discipline of MCDM, various methodologies exist for approaching the aggregation process. These include the utilization of the geometric mean or the centroid mean. Nevertheless, we choose to utilize the arithmetic mean as it is widely recognized as the most commonly employed measure of central tendency.
Stage 5:
Compute the product of the aggregated averaged normalized decision-making matrix using Equation (4) and the criteria weights to derive the weighted decision matrix.
Stage 6:
Evaluate the normalized weighted values of the cost type criteria and the benefit type criteria . This can be calculated by applying Equation (5) and Equation (6), respectively.
Stage 7:
Find the final ranking values by using the following Equation (7).
denotes the coefficient degree of the criterion type. By including both sorts of criteria, we determined that parameter had a value of 0.5.
Nevertheless, it is feasible to generate different iterations of the parameter when taking into account the type of criterion. For instance, if the decision-making problem has two criteria that are of the cost type and one criterion that is of the benefit type, then the coefficient should be equal to . This reasoning can be applied to determine the preference among the options that are being investigated.
A pictorial view of Algorithm is given in Figure 1.
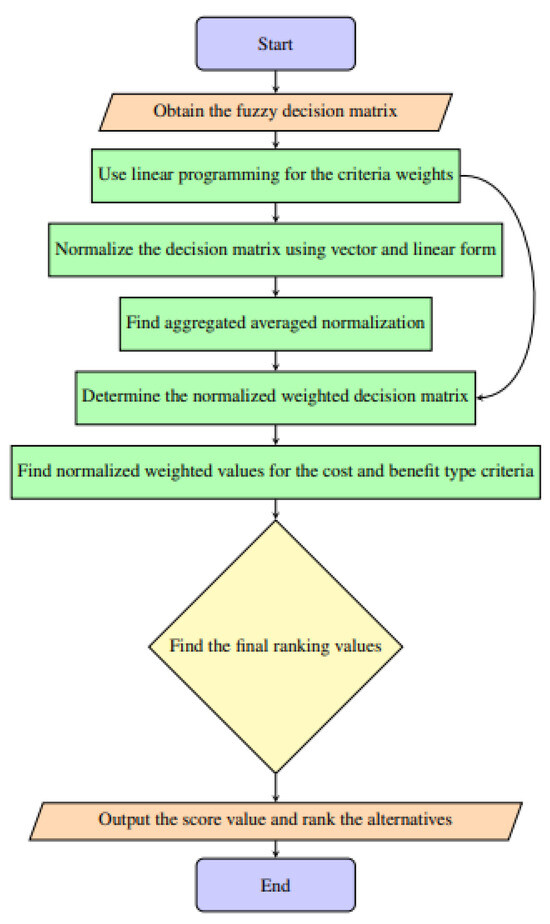
Figure 1.
Pictorial view of Algorithm.
4. Indicator for Comprehensive Evaluation on DE Development
To make a full set of indicators that can be used to measure the progress of different areas in the DE, many technological, infrastructure, connectivity, and socio-economic factors must be taken into account. We consider six criteria based on some previous studies. Several indicators are provided here.
- Digital infrastructure: In gauging the DE development of diverse regions, a multifaceted evaluation must delve into critical aspects of digital infrastructure. Internet penetration, a cornerstone metric, illuminates the extent of connectivity within a population. The assessment expands to encompass broadband availability, scrutinizing not just its ubiquity but also the quality of high-speed services, crucial for fostering a thriving digital ecosystem. Mobile network coverage emerges as another linchpin, exploring the reach and reliability of wireless communication networks that underpin mobile connectivity. This triad of metrics illuminates the accessibility and resilience of a region’s digital fabric. However, an astute evaluation goes beyond quantitative measures, considering the socio-economic implications of this infrastructure. It assesses how digital accessibility empowers communities economically and socially, fostering inclusivity. Moreover, a comprehensive review extends to the regulatory frameworks shaping these digital landscapes. It examines policies governing internet access, data privacy, and technology innovation, offering insights into a region’s commitment to fostering a secure and conducive digital environment. In essence, this holistic evaluation embraces both the tangible infrastructure metrics and the intangible socio-economic dynamics, painting a nuanced picture of a region’s DE evolution.
- Digitalization cost per capita (DCpC): The DCpC is a pivotal metric for evaluating the DE development across regions. This metric encapsulates the average expenditure per capita in implementing and sustaining digital infrastructure, services, and technology. A lower value in this indicator signifies an efficient allocation of resources in the region’s digitalization endeavors. It implies that the region is adept at optimizing costs while achieving a robust digital infrastructure. Conversely, higher values in the DCpC warrant scrutiny, suggesting potential challenges or barriers hindering widespread digital adoption. This could stem from inefficient resource utilization, inadequate infrastructure planning, or regulatory impediments. As a result, regions with elevated digitalization costs may need to reassess their strategies to enhance efficiency and overcome obstacles inhibiting broader technological integration. A nuanced interpretation of this indicator considers not only the absolute cost but also the effectiveness and impact of the digitalization efforts. It prompts a qualitative examination of how well the allocated resources translate into tangible benefits, fostering a holistic understanding of a region’s DE. By incorporating the DCpC into the evaluation framework, stakeholders can gain insights into the economic efficiency and sustainability of a region’s digital transformation initiatives.
- Education and skills: Assessing the DE development across diverse regions necessitates a meticulous examination of educational and skills-related indicators. Digital literacy rates, a pivotal metric, gauge the percentage of the population equipped with fundamental digital skills. This parameter serves as a foundational element, signifying the region’s capacity for technological assimilation at a grassroots level. Furthermore, the evaluation extends to STEM Education, scrutinizing the availability and enrollment in science, technology, engineering, and mathematics programs. The prominence of these disciplines is indicative of a region’s commitment to nurturing a workforce proficient in fields crucial to digital innovation and advancement. Online learning emerges as another vital facet, elucidating the region’s accessibility and utilization of digital educational resources. A high prevalence of online learning suggests a dynamic educational landscape embracing digital tools for knowledge dissemination.This trio of indicators collectively paints a comprehensive picture of a region’s educational infrastructure and preparedness for the digital age. Beyond mere enrollment figures, the focus lies on the practical application of digital skills and the adaptability of educational systems to online platforms. A nuanced evaluation of education and skills metrics enriches the understanding of how well a region is cultivating a digitally literate and technologically adept populace, essential for sustained DE development.
- Social inclusion: In evaluating the DE development of various regions, a crucial aspect lies in the examination of social inclusion metrics. Digital inclusion programs, a cornerstone indicator, shed light on initiatives undertaken to guarantee universal access to digital resources. This not only reflects a region’s commitment to bridging digital disparities but also underscores the inclusivity of its digital development strategies. The assessment extends to online social services, elucidating the availability of digital platforms for crucial domains, such as healthcare, education, and social welfare. A region’s investment in these online services speaks to its dedication to leveraging technology for the betterment of societal well-being. The digital divide index, a quantitative measure, becomes instrumental in understanding the extent of inequality in digital access across demographic groups. A lower index suggests a more equitable distribution of digital resources, indicating a region’s success in minimizing disparities in technological access and utilization.This triad of social inclusion indicators provides a nuanced understanding of how technology is harnessed to ensure that the benefits of the DE are accessible to all segments of society. The evaluation not only considers the presence of initiatives but also their effectiveness in fostering an inclusive digital ecosystem, thereby contributing to a more comprehensive appraisal of a region’s digital economic development.
- Regulatory environment: Analyzing the DE development of diverse regions necessitates a thorough exploration of the regulatory landscape governing technology and innovation. The first crucial aspect is the existence and effectiveness of policies supporting digital innovation. This gauges a region’s commitment to fostering a conducive environment for technological advancement, showcasing its proactive stance in propelling digital economic growth. Equally significant is the scrutiny of the strength and enforcement of regulations safeguarding digital privacy. This dimension highlights the region’s dedication to ensuring the protection of individuals’ digital information, a fundamental element for fostering trust in digital interactions. Further, the evaluation extends to the regulatory environment for tech companies and startups. A supportive regulatory framework can stimulate entrepreneurship, innovation, and economic dynamism. Assessing the ease of doing business and the adaptability of regulations to the rapidly evolving tech landscape provides insights into a region’s capability to nurture a thriving digital ecosystem.
- Environmental sustainability: Evaluating the DE development across diverse regions necessitates a conscientious examination of environmental sustainability indicators. One pivotal facet is the extent of green tech adoption, assessing the integration of environmentally friendly technologies. This metric underscores a region’s commitment to leveraging digital innovations that not only drive economic growth but also align with ecological sustainability goals, contributing to a greener and more sustainable future. Complementing this, the focus extends to energy efficiency, gauging the adoption of practices within the digital sector that minimize energy consumption and the environmental impact. A region’s emphasis on energy-efficient technologies and operations not only reflects environmental responsibility but also contributes to long-term economic resilience by reducing operational costs. This dual-pronged evaluation in environmental sustainability offers a holistic view, considering both the nature of technologies embraced and the efficiency of their energy utilization. Regions that successfully integrate green tech and prioritize energy efficiency are positioned not only as digital leaders but also as environmentally conscious entities, acknowledging the intrinsic link between digital progress and ecological well-being [59].In the era of rapid technological advancement, an astute evaluation of environmental sustainability indicators becomes imperative, recognizing the importance of responsible digital development that harmonizes with broader ecological imperatives. Such an assessment unveils the regions at the forefront of a balanced and sustainable DE.
5. Case Analysis
Provinces assume a crucial role in influencing the trajectory of the DE amidst the ever-changing digital transformation landscape. A comprehensive assessment of the development of the DE in 20 provincial regions is conducted in this case study, utilizing six essential criteria. The aim is to acquire a deeper understanding of the advancements, obstacles, and prospects that these areas confront as they undergo a digital transformation. The primary goals of this evaluation are to assess the state of the DE development in provincial regions and identify areas for improvement. The criteria chosen for evaluation encompass a holistic view of the digital ecosystem. The details of the six criteria are given in Section 4. In this case study, digitalization cost per capita, digital infrastructure, education and skills, social inclusion, regulatory environment, and environmental sustainability. is the cost-type criteria and the remaining are all of the benefit type. Here, we take 20 provinces of China as alternatives. In these 20 provinces of China, we evaluate the performance of the DE.
Stage 1:
Obtain the fuzzy decision matrix from the decision-makers (DMs) as , given in Table 1.

Table 1.
Fuzzy decision matrix.
Stage 2:
Consider that the DMs provide the following partial weight details about the attribute weights:
, , , , , .
Relying on these data, the following optimization framework can be developed:
such that
, , , ,
, , , .
By solving this model, we obtain .
Stage 3:
Employ Equations (1) and (2) to normalize the fuzzy decision matrix. Equation (1) gives the linear form normalization and Equation (2) gives the vector form normalization, given in Table 2 and Table 3, respectively.

Table 2.
Linear normalization of fuzzy decision matrix.

Table 3.
Vector normalization of fuzzy decision matrix.
Stage 4:
Find the aggregated averaged normalization values by using Equation (3), by taking the value of as 0.50, given in Table 4.

Table 4.
Aggregated averaged normalization values.
Stage 5:

Table 5.
Aggregated averaged normalization values.
Stage 6:
Evaluate the normalized weighted values of the cost-type criteria and the benefit-type criteria . This can be calculated by applying Equations (5) and (6), given in Table 6 and Table 7, respectively.

Table 6.
Sum of all benefit criteria values.

Table 7.
Sum of all cost criteria values.
Stage 7:

Table 8.
Final ranking values.
In accordance with the ultimate classification, twenty provinces are categorized into four categories. As shown in Table 9, the classification of the development level of the provincial DE is possible.

Table 9.
Final ranking values.
5.1. Managerial Implications
The proposed methodology equips decision-makers with a comprehensive tool to assess and understand the multifaceted dimensions of digital economy (DE) development. By employing linear programming and fuzzy logic, decision-makers can make more informed and nuanced decisions, considering the complexities and uncertainties associated with DE growth. The linear programming aspect of the methodology allows decision-makers to dynamically optimize the weightings assigned to different evaluation criteria. This ensures a context-specific assessment that aligns with the evolving nature of the DE landscape, enabling managers to prioritize areas crucial for sustainable development. Incorporating fuzzy logic into the evaluation model enables a more realistic representation of the vagueness and imprecision inherent in qualitative assessments of DE. Managers can gain insights into the nuanced aspects of DE progress, facilitating a deeper understanding of the challenges and opportunities unique to each provincial region. The AROMAN, with its two-step normalization process, enhances the accuracy of the ranking system by considering interdependencies among criteria. This refinement in the ranking process provides decision-makers with a more reliable basis for prioritizing interventions and allocating resources effectively. The outcomes of this case study highlight the model’s capacity to generate perceptive and implementable insights for policymakers. This empowers managers to not only understand the current state of DE development but also to implement targeted interventions that align with the unique challenges and opportunities in each region. The proposed methodology offers a powerful managerial tool that goes beyond traditional evaluation approaches. Decision-makers can leverage this methodology to navigate the complexities of DE development, fostering strategic and effective interventions for sustainable growth in provincial regions.
5.2. Theoretical Limitations
The linear programming aspect optimizes weightings dynamically, and it operates under the assumption that the identified weightings remain static over time. In reality, the dynamic nature of the digital economy may lead to shifts in the significance of criteria, potentially challenging the model’s adaptability to evolving economic landscapes. The AROMAN relies on the coupling of vector and linear normalization techniques for accurate data structures. The theoretical limitations lie in the sensitivity of the model to the choice of these normalization techniques, which may impact the robustness of the calculations and the subsequent evaluations. While the AROMAN aims to refine the ranking process by considering the interdependencies among the criteria, the theoretical challenge lies in modeling a truly comprehensive interdependency structure. The complexity of real-world interactions may surpass the model’s capacity to fully capture the intricate relationships among diverse factors influencing DE growth. Despite efforts to accommodate uncertainties, the inherent unpredictability of technological advancements, market dynamics, and policy changes in the digital economy introduces a theoretical limitation. The model may struggle to fully account for unforeseen events and disruptions that significantly influence DE development. Understanding these theoretical limitations is crucial for researchers and practitioners to interpret the results of the proposed methodology critically.
5.3. Comparative Analysis
An extensive comparative analysis was undertaken to evaluate the effectiveness of the AROMAN against various alternative methodologies. Although minor discrepancies were observed in the arrangement of options, as detailed in Table 10, a consistent pattern emerged with the alternatives securing the highest rankings. It is imperative to acknowledge that the AROMAN stands out for its noteworthy computational capability, particularly in determining the utility degree for each alternative. This intrinsic feature significantly enhances the precision and efficacy of the model, particularly in MCDM scenarios. The introduction of this methodology is poised to elevate the decision-making process, offering stakeholders a valuable tool to make well-informed choices aligned with sustainability objectives.

Table 10.
The comparative analysis.
6. Conclusions
This research underscores the imperative need for a nuanced and comprehensive evaluation framework as digital technologies continue to reshape economic landscapes, particularly in provincial regions. The introduced methodology, namely, the AROMAN, contributes significantly to the existing literature by addressing the multifaceted facets of DE growth through its unique integration of linear programming, fuzzy logic, and a two-step normalization process. The primary innovation of the AROMAN lies in its adept coupling of vector and linear normalization techniques, ensuring the generation of accurate data structures for subsequent calculations. This feature not only enhances the precision of the evaluation but also establishes a robust foundation for decision-makers navigating the complexities and uncertainties inherent in the assessment process. The dynamic nature of the linear programming aspect, optimizing weightings in accordance with different evaluation criteria, further distinguishes the AROMAN. This dynamism enables a context-specific assessment that aligns with the evolving nature of the DE landscape. By incorporating fuzzy logic, the model successfully captures the vagueness and imprecision intrinsic to qualitative assessments, providing decision-makers with a more realistic portrayal of the multifaceted nature of DE development. The proposed methodology equips policymakers with a powerful tool to make well-informed decisions and implement targeted interventions that foster the expansion of the digital economy. By addressing the theoretical and practical complexities associated with DE development, the AROMAN emerges as a valuable asset in shaping sustainable and forward-thinking strategies for provincial regions in the digital era. In future studies, the application of the proposed methodology can be seen in the circular economy [60], transportation scheduling problems [61], location–allocation modeling [62], and financial risk prediction [63].
Author Contributions
Conceptualization, H.X. and M.R.; methodology, H.M.A.F. and M.R.; software, H.M.A.F. and M.R.; validation, M.R.; data curation, H.M.A.F. and M.R.; writing—original draft preparation, M.R. and H.X.; writing—review and editing, M.R.; visualization, M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used to support the findings of the study are included within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Mao, Y.; Zhu, Y.; Tang, Z.; Chen, Z. A Novel Airspace Planning Algorithm for Cooperative Target Localization. Electronics 2022, 11, 2950. [Google Scholar] [CrossRef]
- Hu, F.; Qiu, L.; Xi, X.; Zhou, H.; Hu, T.; Su, N.; Duan, Z. Has COVID-19 Changed China’s Digital Trade?—Implications for Health Economics. Front. Public Health 2022, 10, 831549. [Google Scholar] [CrossRef]
- Zhao, S.; Zhang, L.; An, H.; Peng, L.; Zhou, H.; Hu, F. Has China’s low-carbon strategy pushed forward the digital transformation of manufacturing enterprises? Evidence from the low-carbon city pilot policy. Environ. Impact Assess. Rev. 2023, 102, 107184. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, G.; Kong, M.; Yin, Z.; Li, X.; Yin, L.; Zheng, W. Developing Multi-Labelled Corpus of Twitter Short Texts: A Semi-Automatic Method. Systems 2023, 11, 390. [Google Scholar] [CrossRef]
- He, C.; Huang, K.; Lin, J.; Wang, T.; Zhang, Z. Explain systemic risk of commodity futures market by dynamic network. Int. Rev. Financ. Anal. 2023, 88, 102658. [Google Scholar] [CrossRef]
- Li, X.; Sun, Y. Stock intelligent investment strategy based on support vector machine parameter optimization algorithm. Neural Comput. Appl. 2020, 32, 1765–1775. [Google Scholar] [CrossRef]
- Li, X.; Sun, Y. Application of RBF neural network optimal segmentation algorithm in credit rating. Neural Comput. Appl. 2021, 33, 8227–8235. [Google Scholar] [CrossRef]
- Xu, A.; Qiu, K.; Zhu, Y. The measurements and decomposition of innovation inequality: Based on Industry—University—Research perspective. J. Bus. Res. 2023, 157, 113556. [Google Scholar] [CrossRef]
- Hu, F.; Qiu, L.; Wei, S.; Zhou, H.; Bathuure, I.A.; Hu, H. The spatiotemporal evolution of global innovation networks and the changing position of China: A social network analysis based on cooperative patents. R&D Manag. 2023. [Google Scholar] [CrossRef]
- Jiang, Z.; Xu, C. Disrupting the Technology Innovation Efficiency of Manufacturing Enterprises Through Digital Technology Promotion: An Evidence of 5G Technology Construction in China. IEEE Trans. Eng. Manag. 2023. [Google Scholar] [CrossRef]
- Jiang, B.; Zhao, Y.; Dong, J.; Hu, J. Analysis of the influence of trust in opposing opinions: An inclusiveness-degree based Signed Deffuant–Weisbush model. Inf. Fusion 2024, 104, 102173. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Zhao, C. From riches to digitalization: The role of AMC in overcoming challenges of digital transformation in resource-rich regions. Technol. Forecast. Soc. Chang. 2024, 200, 123153. [Google Scholar] [CrossRef]
- Xu, X.; Lin, Z.; Li, X.; Shang, C.; Shen, Q. Multi-objective robust optimisation model for MDVRPLS in refined oil distribution. Int. J. Prod. Res. 2022, 60, 6772–6792. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, Y.; Yang, Z.; Zhao, Y. Do adaptive policy adjustments deliver ecosystem-agriculture-economy co-benefits in land degradation neutrality efforts? Evidence from southeast coast of China. Environ. Monit. Assess. 2023, 195, 1215. [Google Scholar] [CrossRef]
- Xu, X.; Liu, W.; Yu, L. Trajectory prediction for heterogeneous traffic-agents using knowledge correction data-driven model. Inf. Sci. 2022, 608, 375–391. [Google Scholar] [CrossRef]
- Chen, D.; Wang, Q.; Li, Y.; Li, Y.; Zhou, H.; Fan, Y. A general linear free energy relationship for predicting partition coefficients of neutral organic compounds. Chemosphere 2020, 247, 125869. [Google Scholar] [CrossRef]
- Dong, J.; Hu, J.; Zhao, Y.; Peng, Y. Opinion formation analysis for Expressed and Private Opinions (EPOs) models: Reasoning private opinions from behaviors in group decision-making systems. Expert Syst. Appl. 2024, 236, 121292. [Google Scholar] [CrossRef]
- Tapscott, D. The Digital Economy. Promise and Peril in the Age of Networked Intelligence; McGraw-Hill: New York, NY, USA, 1996. [Google Scholar]
- Moulton Brent, R. GDP and the Digital Economy: Keeping up with the Changes. Underst. Digit. Econ. Data 1999, 4, 34–48. [Google Scholar]
- Brynjolfsson, E.; Kahin, B. Understanding the Digital Economy Data Tools, and Research; The MIT Press: Cambridge, MA, USA, 2002; pp. 27–30. [Google Scholar]
- Rob, K.; Roberta, L. IT and organizational change in digital economies. ACM SIGCAS Comput. Soc. 1999, 29, 17–25. [Google Scholar]
- UK Government. Digital Economy Act 2010 [EB/OL]. Available online: https://www.legislation.gov.uk/ukpga/2010/24/contents (accessed on 1 January 2020).
- China Academy of Information and Communications. White Paper on the Development of China’s Digital Economy; China Information Communication Research Institute: Beijing, China, 2017. [Google Scholar]
- Digital Economy Forum, KPMG, Ali Research Institute. 2018 Global Digital Economy Development Index Report; Digital Economy Forum: Beijing, China, 2018. [Google Scholar]
- Zhang, X.; Jiao, Y. China’s digital economy development index and its application. Zhejiang Soc. Sci. Dep. Sci. 2017, 4, 32–40. [Google Scholar]
- Chen, K. Evaluation, regional differences and driving factors of China’s Provincial Digital Economy Development. North China Financ. 2022, 14, 52–61. [Google Scholar]
- Li, Y.; Han, P. Comprehensive evaluation and prediction of China’s digital economy development. Stat. Decis. Mak. 2022, 38, 90–94. [Google Scholar]
- Li, P. Research on Comprehensive Evaluation of Digital Economy Development Level; Nanjing University: Nanjing, China, 2020. [Google Scholar]
- Chen, Z.; Wei, Y.; Shi, K.; Zhao, Z.; Wang, C.; Wu, B.; Qiu, B.; Yu, B. The potential of nighttime light remote sensing data to evaluate the development of digital economy: A case study of China at the city level. Comput. Environ. Urban Syst. 2022, 92, 101749. [Google Scholar] [CrossRef]
- Milosevic, N.; Dobrota, M.; Rakocevic, S.B. Digital economy in Europe: Evaluation of countries’ performances. Proc. Rij. Sch. Econ. 2018, 36, 861–880. [Google Scholar]
- Xu, Y.; Li, A. Regional economic development coordination management system based on fuzzy hierarchical statistical model. Neural Comput. Appl. 2019, 31, 8305–8315. [Google Scholar] [CrossRef]
- Xiao, Q.; Gao, M.; Chen, L.; Jiang, J. Dynamic multi-attribute evaluation of digital economy development in China: A perspective from interaction effect. Technol. Econ. Dev. Econ. 2023, 29, 1728–1752. [Google Scholar] [CrossRef]
- Deng, X.; Liu, Y.; Xiong, Y. Analysis on the development of digital economy in guangdong province based on improved entropy method and multivariate statistical analysis. Entropy 2020, 22, 1441. [Google Scholar] [CrossRef] [PubMed]
- Wang, L. Application of a Fuzzy Information Analysis and Evaluation Method in the Development of Regional Rural e-Commerce. Adv. Multimed. 2022, 2022. [Google Scholar] [CrossRef]
- Li, H.; Xue, W. A Study on the Impact of Regional Total Factor Production in Digital Economy Based on Fuzzy Hierarchical VISC Algorithm. Comput. Intell. Neurosci. 2022, 2022, 6903836. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Su, K.; Wang, S. Evaluation of digital economy development level based on multi-attribute decision theory. PLoS ONE 2022, 17, e0270859. [Google Scholar] [CrossRef] [PubMed]
- Mendes, M.V.I. The limitations of international relations regarding MNCs and the digital economy: Evidence from Brazil. Rev. Political Econ. 2021, 33, 67–87. [Google Scholar] [CrossRef]
- Kim, J. Infrastructure of the digital economy: Some empirical findings with the case of Korea. Technol. Forecast. Soc. Chang. 2006, 73, 377–389. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control. 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Awodi, N.J.; Liu, Y.K.; Ayo-Imoru, R.M.; Ayodeji, A. Fuzzy TOPSIS-based risk assessment model for effective nuclear decommissioning risk management. Prog. Nucl. Energy 2023, 155, 104524. [Google Scholar] [CrossRef]
- Chisale, S.W.; Lee, H.S. Evaluation of barriers and solutions to renewable energy acceleration in Malawi, Africa, using AHP and fuzzy TOPSIS approach. Energy Sustain. Dev. 2023, 76, 101272. [Google Scholar] [CrossRef]
- Ghose, D.; Pradhan, S.; Tamuli, P.; Shabbiruddin. Optimal material for solar electric vehicle application using an integrated Fuzzy-COPRAS model. Energy Sources Part A Recover. Util. Environ. Eff. 2023, 45, 3859–3878. [Google Scholar] [CrossRef]
- Olabanji, O.M.; Mpofu, K. Extending the application of fuzzy COPRAS to optimal product design. Procedia CIRP 2023, 119, 182–192. [Google Scholar] [CrossRef]
- Çelik, M.T.; Arslankaya, S. Analysis of quality control criteria in an business with the fuzzy DEMATEL method: Glass business example. J. Eng. Res. 2023, 11, 100039. [Google Scholar] [CrossRef]
- Kuzu, A.C. Application of fuzzy DEMATEL approach in maritime transportation: A risk analysis of anchor loss. Ocean. Eng. 2023, 273, 113786. [Google Scholar] [CrossRef]
- Mohapatra, B.; Tripathy, S.; Singhal, D. A sustainable solution for lean barriers through a fuzzy DEMATEL methodology with a case study from the Indian manufacturing industry. Int. J. Lean Six Sigma 2023, 14, 815–843. [Google Scholar] [CrossRef]
- Opreana, A.; Vinerean, S.; Mihaiu, D.M.; Barbu, L.; Șerban, R.A. Fuzzy Analytic Network Process with Principal Component Analysis to Establish a Bank Performance Model under the Assumption of Country Risk. Mathematics 2023, 11, 3257. [Google Scholar] [CrossRef]
- Allahviranloo, T.; Pedrycz, W.; Shahriari, M.; Sharafi, H.; Razipour GhalehJough, S. Analytical Hierarchy Process (AHP) in Fuzzy Environment. In Fuzzy Decision Analysis: Multi Attribute Decision Making Approach; Springer International Publishing: Cham, Switzerland, 2023; pp. 215–237. [Google Scholar]
- Hii, P.K.; Goh, C.F.; Tan, O.K.; Amran, R.; Ong, C.H. An information system success model for e-learning postadoption using the fuzzy analytic network process. Educ. Inf. Technol. 2023, 28, 10731–10752. [Google Scholar] [CrossRef]
- Oubahman, L.; Duleba, S. Fuzzy PROMETHEE model for public transport mode choice analysis. Evol. Syst. 2023, 1–18. [Google Scholar] [CrossRef]
- Liang, D.; Fu, Y.; Garg, H. A novel robustness PROMETHEE method by learning interactive criteria and historical information for blockchain technology-enhanced supplier selection. Expert Syst. Appl. 2024, 235, 121107. [Google Scholar] [CrossRef]
- Farid, H.M.A.; Riaz, M. q-rung orthopair fuzzy Aczel–Alsina aggregation operators with multi-criteria decision-making. Eng. Appl. Artif. Intell. 2023, 122, 106105. [Google Scholar] [CrossRef]
- Farid, H.M.A.; Riaz, M. Some generalized q-rung orthopair fuzzy Einstein interactive geometric aggregation operators with improved operational laws. Int. J. Intell. Syst. 2021, 36, 7239–7273. [Google Scholar] [CrossRef]
- Tolga, A.C.; Parlak, I.B.; Castillo, O. Finite-interval-valued Type-2 Gaussian fuzzy numbers applied to fuzzy TODIM in a healthcare problem. Eng. Appl. Artif. Intell. 2020, 87, 103352. [Google Scholar] [CrossRef]
- Deveci, M.; Gokasar, I.; Castillo, O.; Daim, T. Evaluation of Metaverse integration of freight fluidity measurement alternatives using fuzzy Dombi EDAS model. Comput. Ind. Eng. 2022, 174, 108773. [Google Scholar] [CrossRef]
- Cagri Tolga, A.; Basar, M. The assessment of a smart system in hydroponic vertical farming via fuzzy MCDM methods. J. Intell. Fuzzy Syst. 2022, 42, 1–12. [Google Scholar] [CrossRef]
- Tütüncü, K.A.; Gül, N.N.; Bölükbaş, U.; Güneri, A.F. Integer Linear Programming Approach for the Personnel Shuttles Routing Problem in Yıldız Campus in Istanbul. J. Soft Comput. Decis. Anal. 2023, 1, 303–316. [Google Scholar] [CrossRef]
- Ghoushchi, S.J.; Sarvi, S. Prioritizing and evaluating risks of ordering and prescribing in the chemotherapy process using an extended SWARA and MOORA under fuzzy Z-numbers. J. Oper. Intell. 2023, 1, 44–66. [Google Scholar] [CrossRef]
- Xu, X.; Wang, C.; Zhou, P. GVRP considered oil-gas recovery in refined oil distribution: From an environmental perspective. Int. J. Prod. Econ. 2021, 235, 108078. [Google Scholar] [CrossRef]
- Luo, J.; Zhuo, W.; Xu, B. The bigger, the better? Optimal NGO size of human resources and governance quality of entrepreneurship in circular economy. Manag. Decis. 2023. ahead-of-print. [Google Scholar] [CrossRef]
- Mou, J.; Gao, K.; Duan, P.; Li, J.; Garg, A.; Sharma, R. A Machine Learning Approach for Energy-Efficient Intelligent Transportation Scheduling Problem in a Real-World Dynamic Circumstances. IEEE Trans. Intell. Transp. Syst. 2023, 24, 15527–15539. [Google Scholar] [CrossRef]
- Pan, J.; Deng, Y.; Yang, Y.; Zhang, Y. Location-allocation modelling for rational health planning: Applying a two-step optimization approach to evaluate the spatial accessibility improvement of newly added tertiary hospitals in a metropolitan city of China. Soc. Sci. Med. 2023, 338, 116296. [Google Scholar] [CrossRef]
- Luo, J.; Zhuo, W.; Xu, B. A Deep Neural Network-based Assistive Decision Method for Financial Risk Prediction in Carbon Trading Market. J. Circuits Syst. Comput. 2023. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).