Efficient Newton-Type Solvers Based on for Finding the Solution of Nonlinear Algebraic Problems
Abstract
1. Background and Introductory Notes
- Section 2 provides a discussion of multi-step schemes comprising three substeps to reach fast convergence, while utilizing a minimal number of LU decompositions (also known as lower–upper (LU) decomposition).
- Section 3 includes an error analysis and assesses convergence rates.
- The dynamic characteristics of the proposed schemes in contrast to those of the available solvers are compared in Section 4.
- Additionally, Section 5 applies the proposed method to several test problems.
- Finally, Section 6 concludes with findings and outlines future research directions.
2. A New Procedure
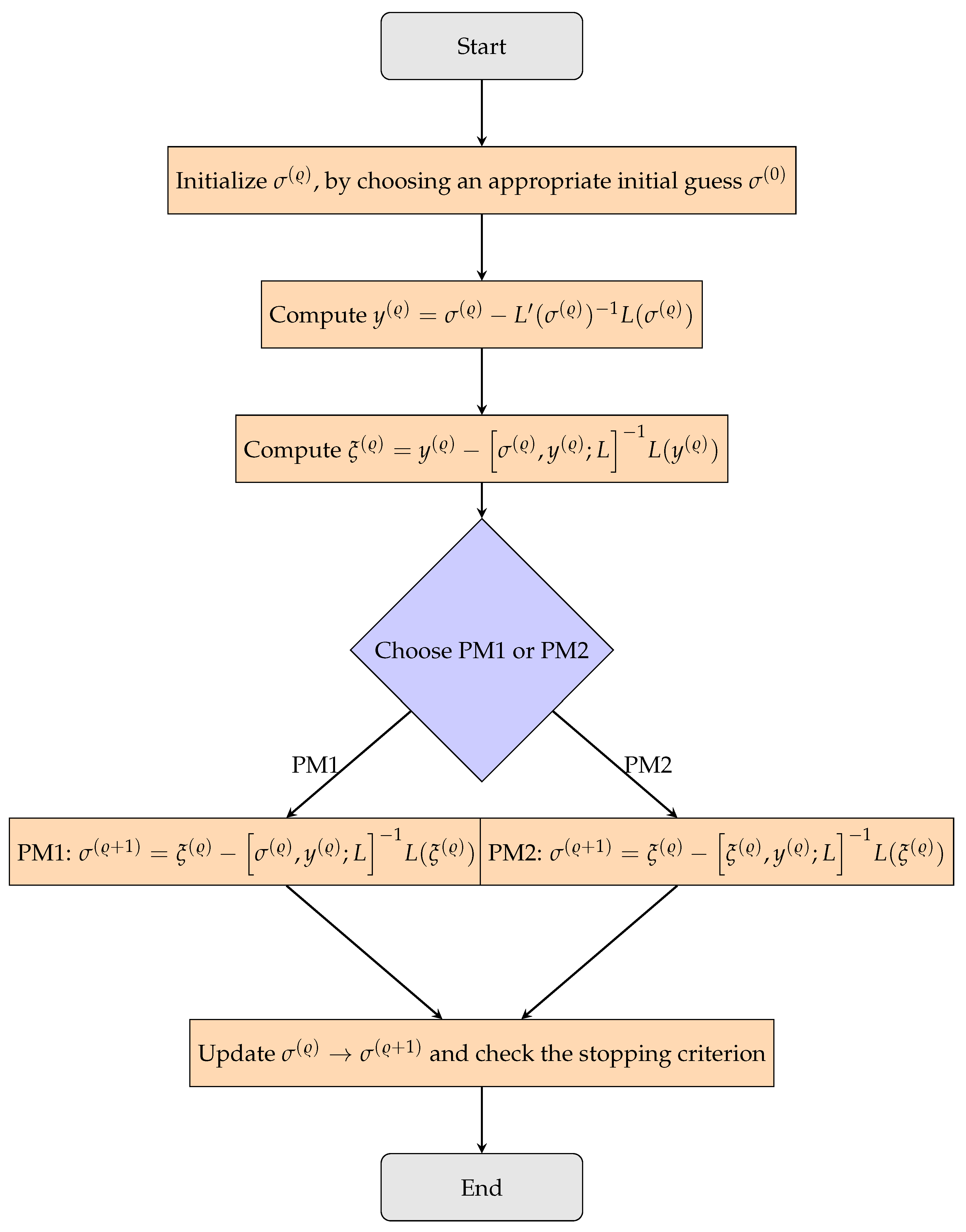
| Algorithm 1 The algorithmic format of the multi-step iterative schemes (PM1 and PM2). |
|
3. Rates for Convergence
4. Dynamical Behavior
5. Computational Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khandani, H. New algorithms to estimate the real roots of differentiable functions and polynomials on a closed finite interval. J. Math. Model. 2023, 11, 631–647. [Google Scholar]
- Singh, H.; Sharma, J.R. A two-point Newton-like method of optimal fourth order convergence for systems of nonlinear equations. Complexity 2025, 86, 101907. [Google Scholar] [CrossRef]
- Moscoso-Martínez, M.; Chicharro, F.I.; Cordero, A.; Torregrosa, J.R.; Ureña-Callay, G. Achieving optimal order in a novel family of numerical methods: Insights from convergence and dynamical analysis results. Axioms 2024, 13, 458. [Google Scholar] [CrossRef]
- McNamee, J.M.; Pan, V.Y. Numerical Methods for Roots of Polynomials–Part I; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- McNamee, J.M.; Pan, V.Y. Numerical Methods for Roots of Polynomials–Part II; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Khdhr, F.W.; Soleymani, F.; Saeed, R.K.; Akgül, A. An optimized Steffensen–type iterative method with memory associated with annuity calculation. Eur. Phys. J. Plus 2019, 134, 146. [Google Scholar] [CrossRef]
- Noda, T. The Steffensen iteration method for systems of nonlinear equations. Proc. Jpn. Acad. 1987, 63, 186–189. [Google Scholar] [CrossRef]
- Grau-Sánchez, M.; Grau, À.; Noguera, M. On the computational efficiency index and some iterative methods for solving systems of nonlinear equations. J. Comput. Appl. Math. 2011, 236, 1259–1266. [Google Scholar] [CrossRef]
- Rostami, M.; Lotfi, T.; Brahmand, A. A fast derivative-free iteration scheme for nonlinear systems and integral equations. Mathematics 2019, 7, 637. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice Hall: New York, NY, USA, 1964. [Google Scholar]
- Cordero, A.; Hueso, J.L.; Martínez, E.; Torregrosa, J.R. A modified Newton-Jarratt’s composition. Numer. Algorithms 2010, 55, 87–99. [Google Scholar] [CrossRef]
- Kansal, M.; Cordero, A.; Bhalla, S.; Torregrosa, J.R. New fourth-and sixth-order classes of iterative methods for solving systems of nonlinear equations and their stability analysis. Numer. Algorithms 2021, 87, 1017–1060. [Google Scholar] [CrossRef]
- Montazeri, H.; Soleymani, F.; Shateyi, S.; Motsa, S.S. On a new method for computing the numerical solution of systems of nonlinear equations. J. Appl. Math. 2012, 2012, 751975. [Google Scholar] [CrossRef]
- Chang, C.-W.; Qureshi, S.; Argyros, I.K.; Saraz, K.M.; Hincal, E. A modified fractional Newton’s solver. Axioms 2024, 13, 689. [Google Scholar] [CrossRef]
- Ogbereyivwe, O.; Atajeromavwo, E.J.; Umar, S.S. Jarratt and Jarratt-variant families of iterative schemes for scalar and system of nonlinear equations, Iran. J. Numer. Anal. Optim. 2024, 14, 391–416. [Google Scholar]
- Soheili, A.R.; Soleymani, F. Iterative methods for nonlinear systems associated with finite difference approach in stochastic differential equations. Numer. Algorithms 2016, 71, 89–102. [Google Scholar] [CrossRef]
- Cordero, A.; Leonardo-Sepúlveda, M.A.; Torregrosa, J.R.; Vassileva, M.P. Increasing in three units the order of convergence of iterative methods for solving nonlinear systems. Math. Comput. Simul. 2024, 223, 509–522. [Google Scholar] [CrossRef]
- Sharma, J.R.; Guha, R.K.; Sharma, R. An efficient fourth order weighted-Newton method for systems of nonlinear equations. Numer. Algorithms 2013, 62, 307–323. [Google Scholar] [CrossRef]
- Shi, L.; Ullah, M.Z.; Nashine, H.K.; Alansari, M.; Shateyi, S. An enhanced numerical iterative method for expanding the attraction basins when computing matrix signs of invertible matrices. Fractal Fract. 2023, 7, 684. [Google Scholar] [CrossRef]
- Dubin, D. Numerical and Analytical Methods for Scientists and Engineers Using Mathematica; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Clark, J.; Kapadia, D. Introduction to Calculus: A Computational Approach; Wolfram Media: Champaign, IL, USA, 2024. [Google Scholar]
- Lotfi, T.; Momenzadeh, M. Constructing an efficient multi-step iterative scheme for nonlinear system of equations. Comput. Methods Differ. Equ. 2021, 9, 710–721. [Google Scholar]
- Ma, X.; Nashine, H.K.; Shil, S.; Soleymani, F. Exploiting higher computational efficiency index for computing outer generalized inverses. Appl. Numer. Math. 2022, 175, 18–28. [Google Scholar] [CrossRef]
- Shil, S.; Nashine, H.K.; Soleymani, F. On an inversion-free algorithm for the nonlinear matrix problem . Int. J. Comput. Math. 2022, 99, 2555–2567. [Google Scholar] [CrossRef]
- Shahriari, M.; Saray, B.N.; Mohammadalipour, B.; Saeidian, S. Pseudospectral method for solving the fractional one-dimensional Dirac operator using Chebyshev cardinal functions. Phys. Scr. 2023, 98, 055205. [Google Scholar] [CrossRef]
- Saray, B.N. Abel’s integral operator: Sparse representation based on multiwavelets. BIT 2021, 61, 587–606. [Google Scholar] [CrossRef]
- Saray, B.N.; Lakestani, M.; Dehghan, M. On the sparse multiscale representation of 2-D Burgers equations by an efficient algorithm based on multiwavelets, Numer. Methods Partial. Differ. Equ. 2023, 39, 1938–1961. [Google Scholar] [CrossRef]
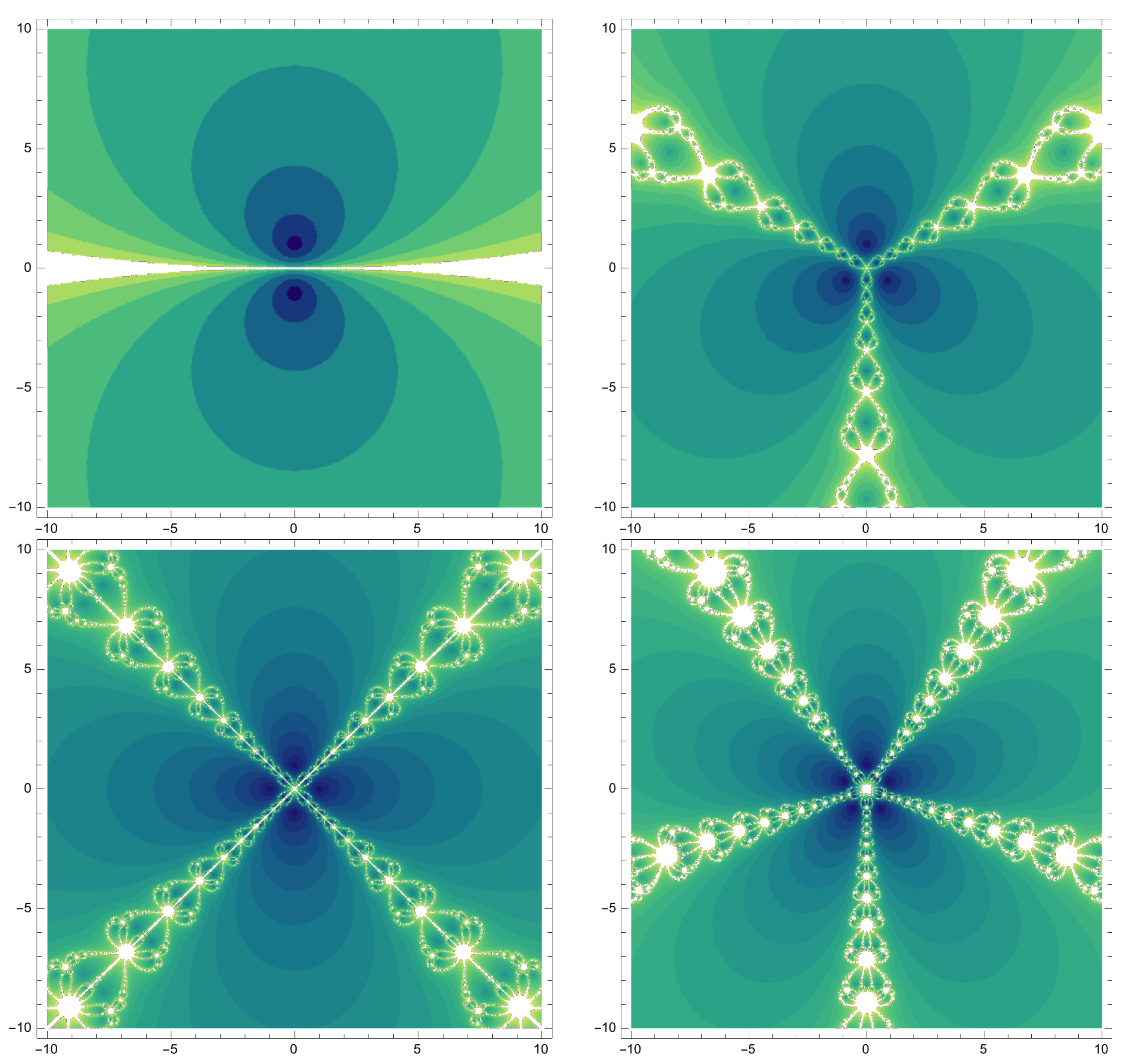
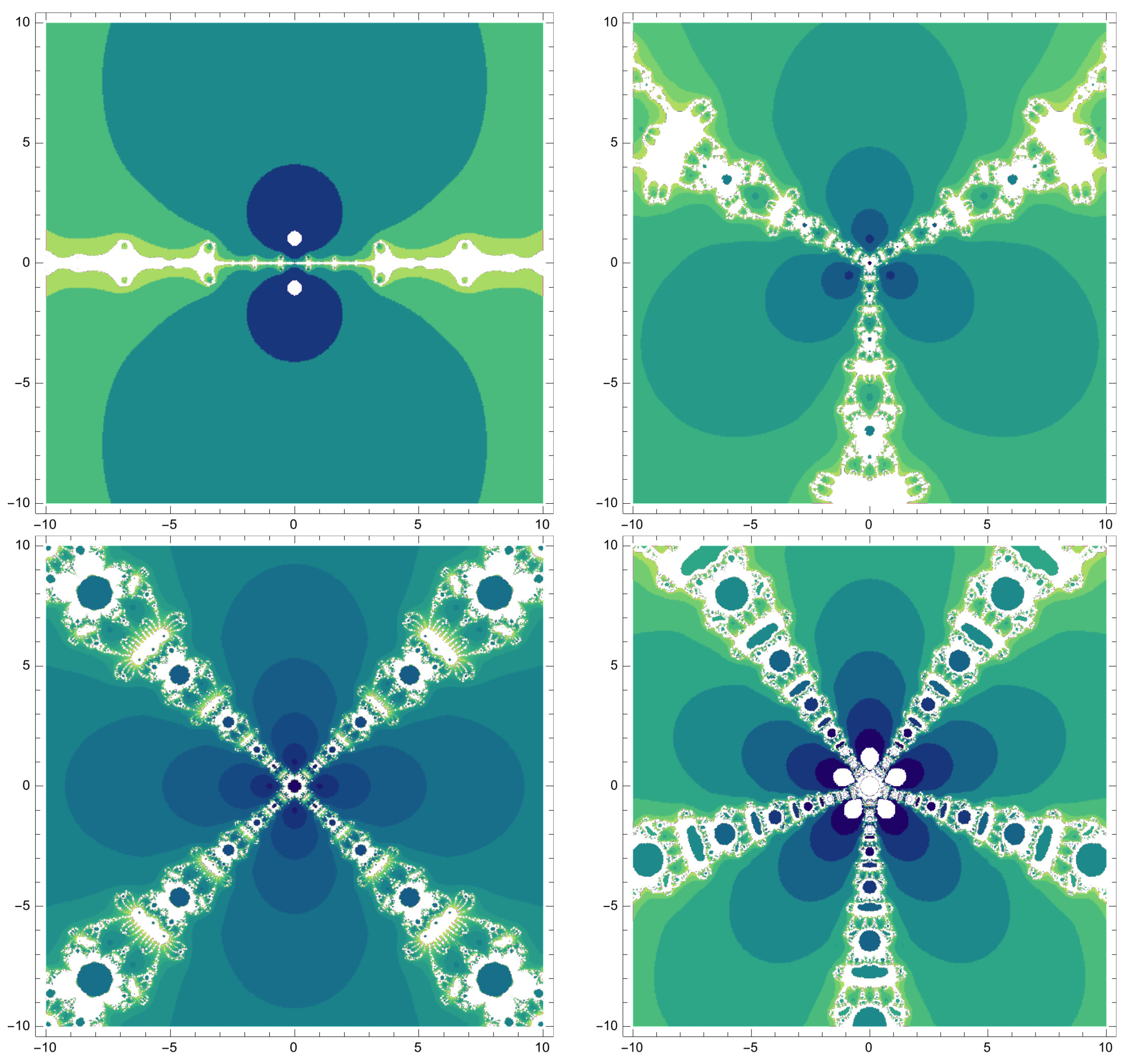
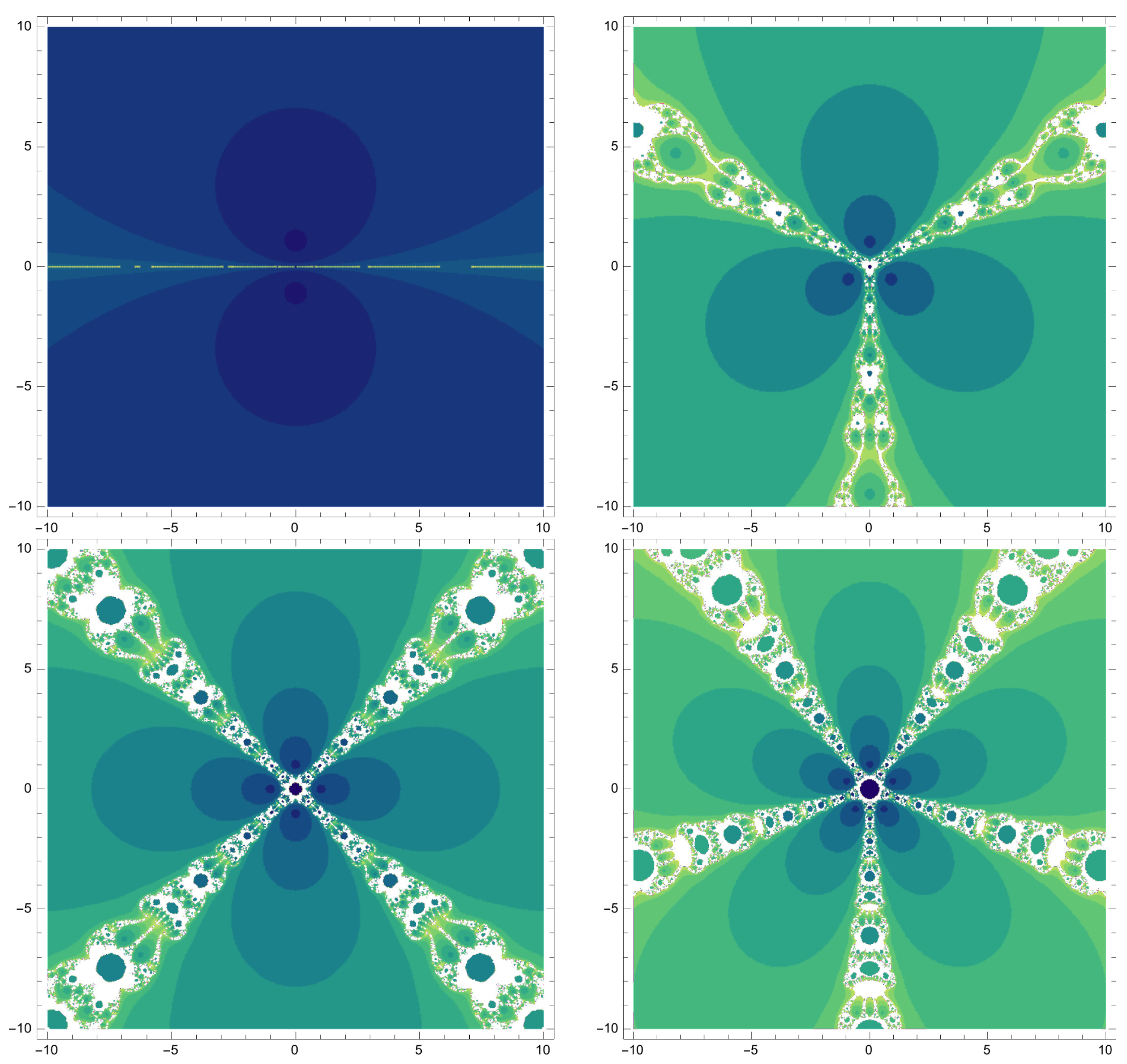

| Methods | ||||||
|---|---|---|---|---|---|---|
| NM2 | ||||||
| SM2 | ||||||
| PM1 | ||||||
| PM2 |
| Methods | ||||||
|---|---|---|---|---|---|---|
| NM2 | ||||||
| SM2 | ||||||
| PM1 | ||||||
| JM4 | ||||||
| PM2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jebreen, H.B.; Wang, H.; Chalco-Cano, Y. Efficient Newton-Type Solvers Based on for Finding the Solution of Nonlinear Algebraic Problems. Axioms 2024, 13, 880. https://doi.org/10.3390/axioms13120880
Jebreen HB, Wang H, Chalco-Cano Y. Efficient Newton-Type Solvers Based on for Finding the Solution of Nonlinear Algebraic Problems. Axioms. 2024; 13(12):880. https://doi.org/10.3390/axioms13120880
Chicago/Turabian StyleJebreen, Haifa Bin, Hongzhou Wang, and Yurilev Chalco-Cano. 2024. "Efficient Newton-Type Solvers Based on for Finding the Solution of Nonlinear Algebraic Problems" Axioms 13, no. 12: 880. https://doi.org/10.3390/axioms13120880
APA StyleJebreen, H. B., Wang, H., & Chalco-Cano, Y. (2024). Efficient Newton-Type Solvers Based on for Finding the Solution of Nonlinear Algebraic Problems. Axioms, 13(12), 880. https://doi.org/10.3390/axioms13120880









