Fractal Differential Equations of 2α-Order
Abstract
1. Introduction
2. Overview of Fractal Calculus on Fractal Sets
3. Preliminaries on the -Order Fractal Differential Equation
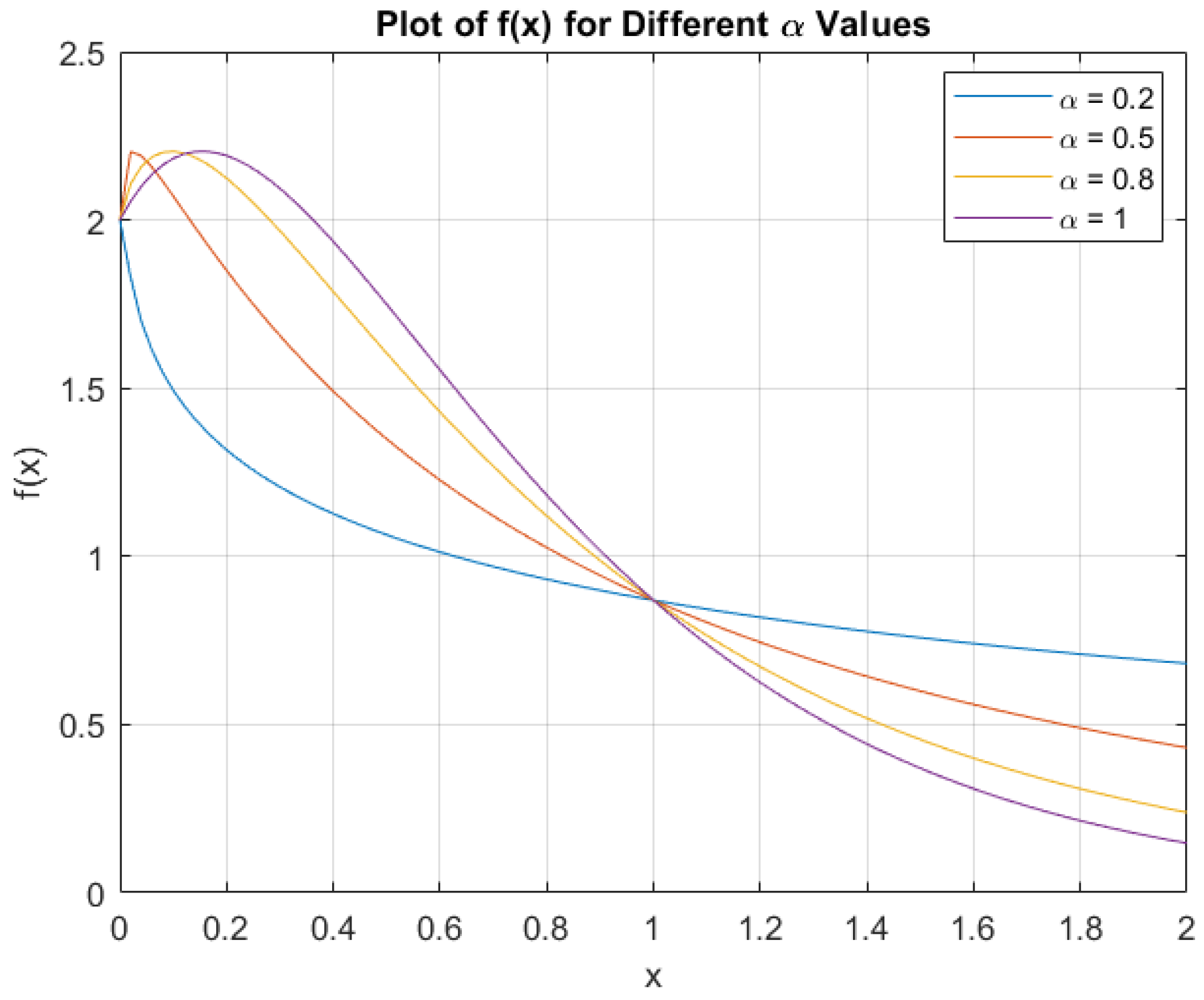
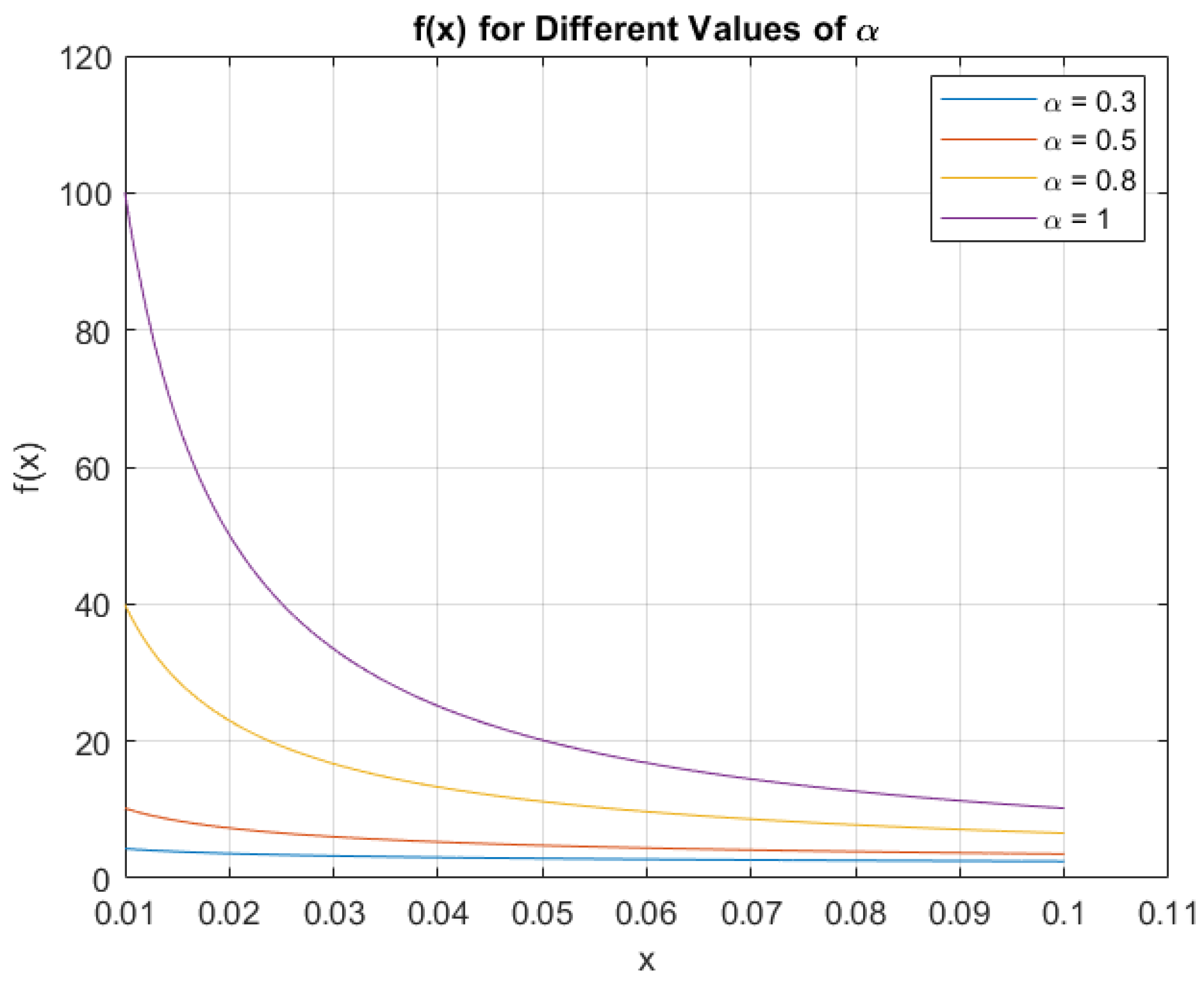
-Order Fractal Differential Equation with Constant Coefficient
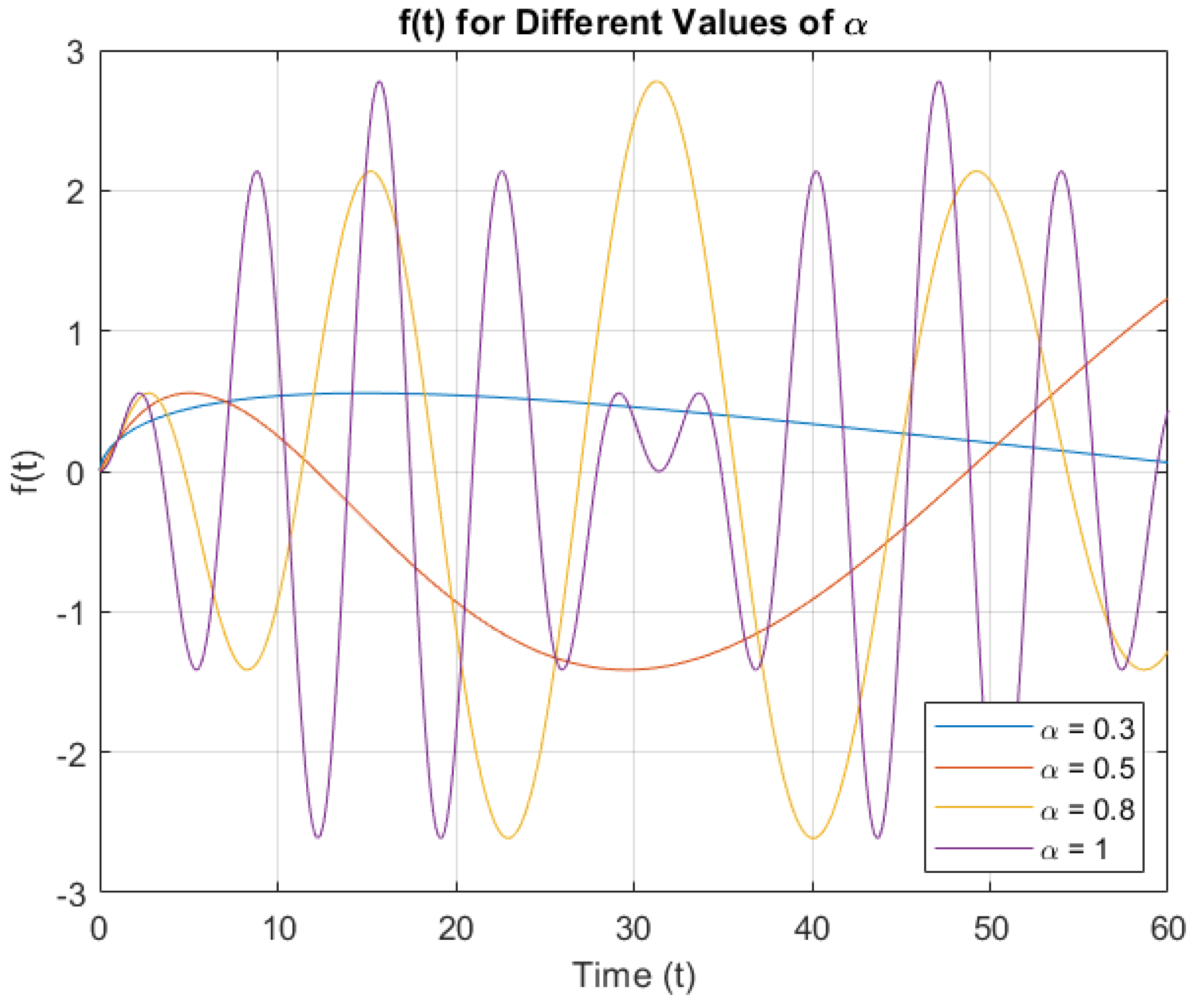
4. Uniqueness Theorem for -Order Fractal Linear Differential Equations
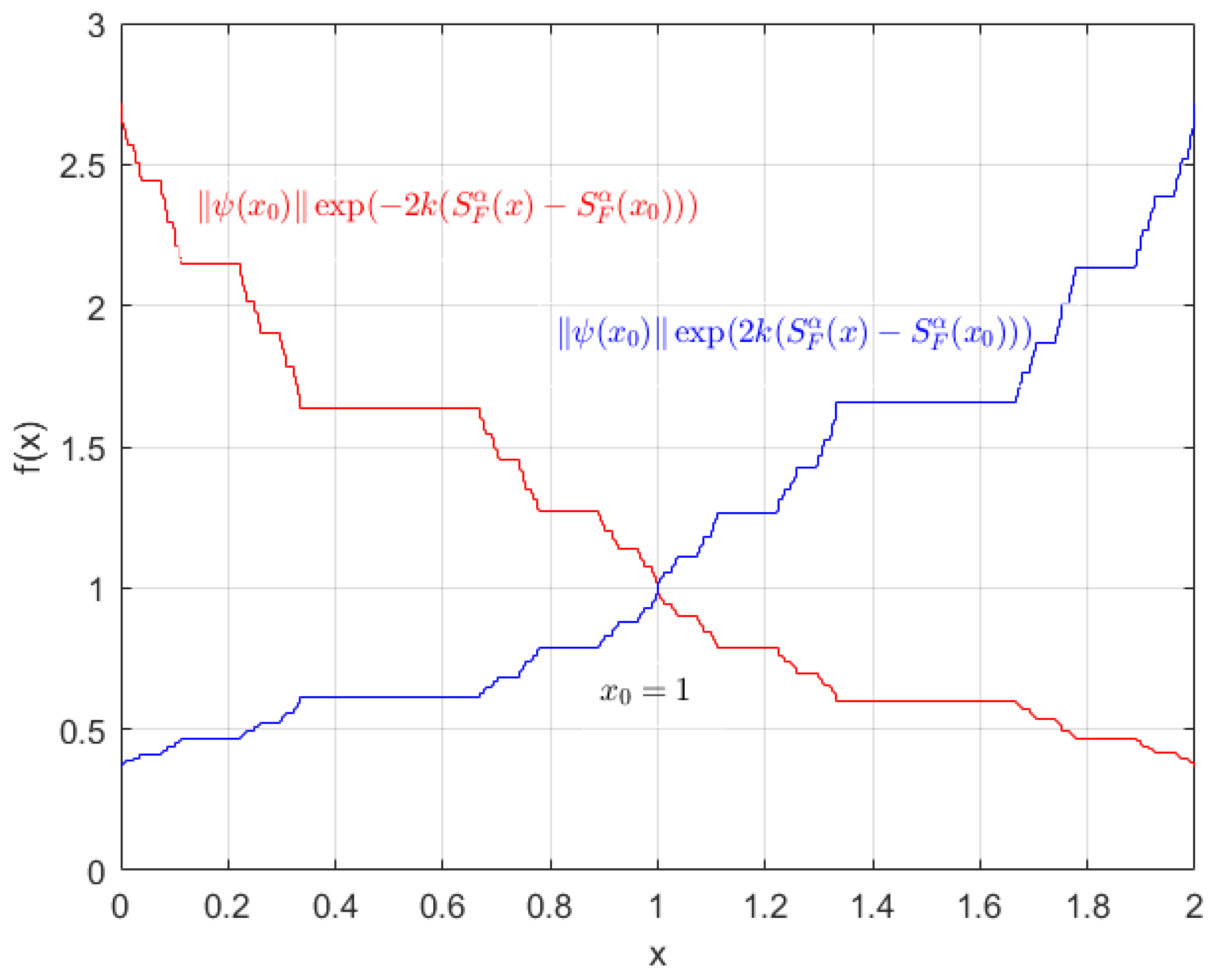
5. Exact -Order Fractal Differential Equation
6. Nonhomogeneous -Order Fractal Differential Equation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982. [Google Scholar]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons: New York, NY, USA, 2004. [Google Scholar]
- Jorgensen, P.E. Analysis and Probability: Wavelets, Signals, Fractals; Springer Science & Business Media: Cham, Switzerland, 2006; Volume 234. [Google Scholar]
- Massopust, P.R. Fractal Functions, Fractal Surfaces, and Wavelets; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Lapidus, M.L.; Radunović, G.; Žubrinić, D. Fractal Zeta Functions and Fractal Drums; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Husain, A.; Nanda, M.N.; Chowdary, M.S.; Sajid, M. Fractals: An eclectic survey, part I. Fractal Fract. 2022, 6, 89. [Google Scholar] [CrossRef]
- Husain, A.; Nanda, M.N.; Chowdary, M.S.; Sajid, M. Fractals: An eclectic survey, part II. Fractal Fract. 2022, 6, 379. [Google Scholar] [CrossRef]
- Patiño-Ortiz, M.; Patiño-Ortiz, J.; Martínez-Cruz, M.Á.; Esquivel-Patiño, F.R.; Balankin, A.S. Morphological Features of Mathematical and Real-World Fractals: A Survey. Fractal Fract. 2024, 8, 440. [Google Scholar] [CrossRef]
- Rogers, C.A. Hausdorff Measures; Cambridge University Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Lesmoir-Gordon, N.; Rood, B. Introducing Fractal Geometry; Icon Books: London, UK, 2000. [Google Scholar]
- Barnsley, M.F. Fractals Everywhere; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Dewey, T.G. Fractals in Molecular Biophysics; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Rosenberg, E. Fractal Dimensions of Networks; Springer: Berlin/Heidelberg, Germany, 2020; Volume 1. [Google Scholar]
- Pietronero, L.; Tosatti, E. (Eds.) Fractals in Physics; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Bishop, C.J.; Peres, Y. Fractals in Probability and Analysis; Cambridge University Press: Cambridge, MA, USA, 2017; Volume 162. [Google Scholar]
- Bunde, A.; Havlin, S. Fractals in Science; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kigami, J. Analysis on Fractals; Number 143; Cambridge University Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Strichartz, R.S. Differential Equations on Fractals; Princeton University Press: Princeton, NJ, USA, 2018. [Google Scholar]
- Giona, M. Fractal calculus on [0, 1]. Chaos Solit. Fractals 1995, 5, 987–1000. [Google Scholar] [CrossRef]
- Freiberg, U.; Zähle, M. Harmonic calculus on fractals-a measure geometric approach I. Potential Anal. 2002, 16, 265–277. [Google Scholar] [CrossRef]
- Jiang, H.; Su, W. Some fundamental results of calculus on fractal sets. Commun. Nonlinear Sci. Numer. Simul. 1998, 3, 22–26. [Google Scholar] [CrossRef]
- Bongiorno, D. Derivatives not first return integrable on a fractal set. Ric. Mat. 2018, 67, 597–604. [Google Scholar] [CrossRef]
- Bongiorno, D.; Corrao, G. On the fundamental theorem of calculus for fractal sets. Fractals 2015, 23, 1550008. [Google Scholar] [CrossRef]
- Bongiorno, D.; Corrao, G. An integral on a complete metric measure space. Real Anal. Exch. 2015, 40, 157–178. [Google Scholar] [CrossRef]
- Stillinger, F.H. Axiomatic basis for spaces with noninteger dimension. J. Math. Phys. 1977, 18, 1224–1234. [Google Scholar] [CrossRef]
- Barlow, M.T.; Perkins, E.A. Brownian motion on the Sierpinski gasket. Probab. Theory Relat. Fields 1988, 79, 543–623. [Google Scholar] [CrossRef]
- Deppman, A.; Megías, E.; Pasechnik, R. Fractal Derivatives, Fractional Derivatives and q-Deformed Calculus. Entropy 2023, 25, 1008. [Google Scholar] [CrossRef] [PubMed]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2. [Google Scholar]
- Damián Adame, L.; Gutiérrez-Torres, C.d.C.; Figueroa-Espinoza, B.; Barbosa-Saldaña, J.G.; Jiménez-Bernal, J.A. A Mechanical Picture of Fractal Darcy’s Law. Fractal Fract. 2023, 7, 639. [Google Scholar] [CrossRef]
- Samayoa Ochoa, D.; Damián Adame, L.; Kryvko, A. Map of a Bending Problem for Self-Similar Beams into the Fractal Continuum Using the Euler-Bernoulli Principle. Fractal Fract. 2022, 6, 230. [Google Scholar] [CrossRef]
- Sandev, T.; Tomovski, Ž. Fractional Equations and Models; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Nottale, L. Scale Relativity and Fractal Space-Time: A New Approach to Unifying Relativity and Quantum Mechanics; World Scientific: Singapore, 2011. [Google Scholar]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real line-I: Formulation. Fractals 2009, 17, 53–81. [Google Scholar] [CrossRef]
- Parvate, A.; Satin, S.; Gangal, A. Calculus on fractal curves in Rn. Fractals 2011, 19, 15–27. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K. Fractal Calculus and its Applications; World Scientific: Singapore, 2022. [Google Scholar]
- Banchuin, R. Nonlocal fractal calculus based analyses of electrical circuits on fractal set. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2022, 41, 528–549. [Google Scholar] [CrossRef]
- Banchuin, R. On the noise performances of fractal-fractional electrical circuits. Int. J. Circuit Theory Appl. 2023, 51, 80–96. [Google Scholar] [CrossRef]
- Banchuin, R. Noise analysis of electrical circuits on fractal set. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2022, 41, 1464–1490. [Google Scholar] [CrossRef]
- Balankin, A.S.; Mena, B. Vector differential operators in a fractional dimensional space, on fractals, and in fractal continua. Chaos Solit. Fractals 2023, 168, 113203. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Ontiveros, L.A.O. Fractal calculus approach to diffusion on fractal combs. Chaos Solit. Fractals 2023, 175, 114021. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Tejado, I.; Sevli, H.; Valdés, J.E.N. On initial value problems of fractal delay equations. Appl. Math. Comput. 2023, 449, 127980. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Welch, K.; Serpa, C.; Jørgensen, P.E. Non-standard analysis for fractal calculus. J. Anal. 2023, 31, 1895–1916. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Depollier, C.; Pham, D. Higher order fractal differential equations. Mod. Phys. Lett. A 2024, 39, 2450127. [Google Scholar] [CrossRef]
- Faghih, N. An Introduction to Time and Fractals: Perspectives in Economics, Entrepreneurship, and Management; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar]
- Welch, K. A Fractal Topology of Time: Deepening into Timelessness; Fox Finding Press: Austin, TX, USA, 2020. [Google Scholar]
- Vrobel, S. Fractal Time; World Scientific: Singapore, 2011. [Google Scholar]
- Shlesinger, M.F. Fractal Time in Condensed Matter. Annu. Rev. Phys. Chem. 1988, 39, 269–290. [Google Scholar] [CrossRef]
- Plonka, A. Fractal time rate processes in polymer systems. Radiat. Phys. Chem. 1995, 45, 67–70. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Bongiorno, D. Exact solutions of some fractal differential equations. Appl. Math. Comput. 2024, 472, 128633. [Google Scholar] [CrossRef]
- Peano, G. Sur le déterminant Wronskien. Mathesis 1889, 9, 75–76. [Google Scholar]
- Apostol, T. Mathematical Analysis; Addison-Wesley: Boston, MA, USA, 1974. [Google Scholar]
- Dovgoshey, O.; Martio, O.; Ryazanov, V.; Vuorinen, M. The cantor function. Expo. Math. 2006, 24, 1–37. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalili Golmankhaneh, A.; Bongiorno, D. Fractal Differential Equations of 2α-Order. Axioms 2024, 13, 786. https://doi.org/10.3390/axioms13110786
Khalili Golmankhaneh A, Bongiorno D. Fractal Differential Equations of 2α-Order. Axioms. 2024; 13(11):786. https://doi.org/10.3390/axioms13110786
Chicago/Turabian StyleKhalili Golmankhaneh, Alireza, and Donatella Bongiorno. 2024. "Fractal Differential Equations of 2α-Order" Axioms 13, no. 11: 786. https://doi.org/10.3390/axioms13110786
APA StyleKhalili Golmankhaneh, A., & Bongiorno, D. (2024). Fractal Differential Equations of 2α-Order. Axioms, 13(11), 786. https://doi.org/10.3390/axioms13110786







