Finite-Region State Feedback Control for 2-D Switched Systems with Actuator Saturation Under the Weighted Average Dwell Time Technique
Abstract
1. Introduction
2. Problem Statements and Preliminaries
3. Finite-Region Stability Analysis and Stabilization
3.1. Finite-Region Stability Analysis
3.2. Finite-Region Stabilization
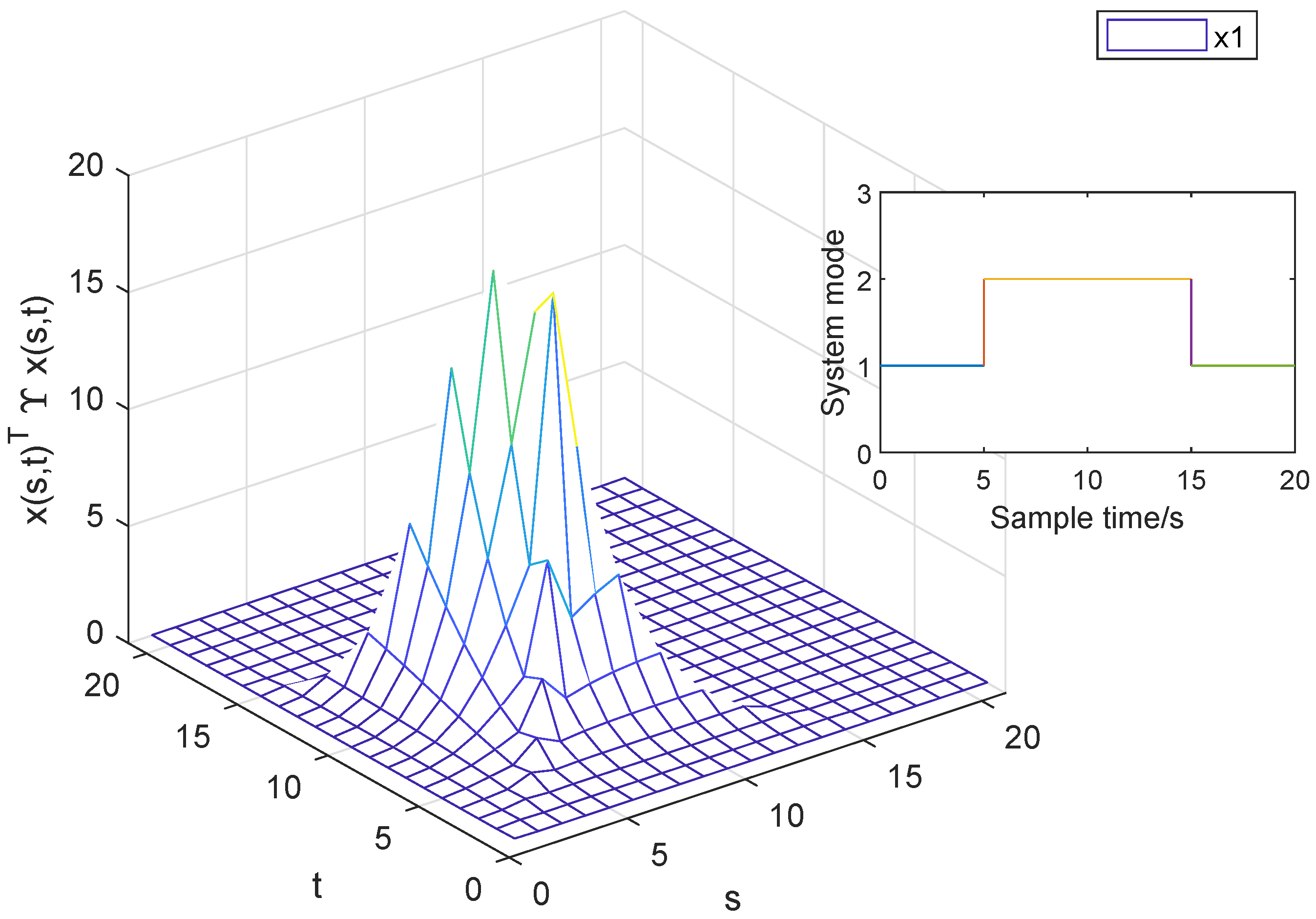
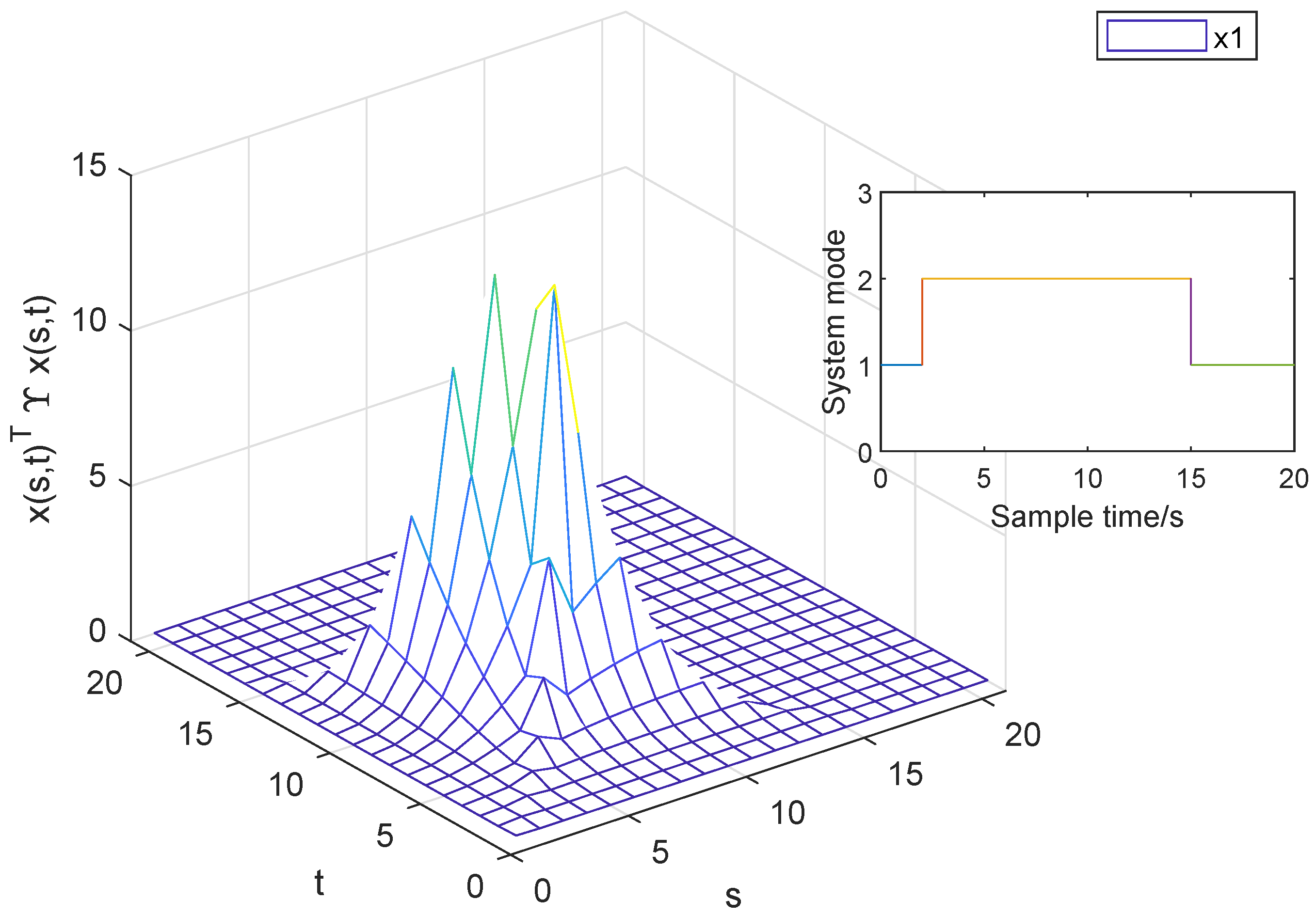
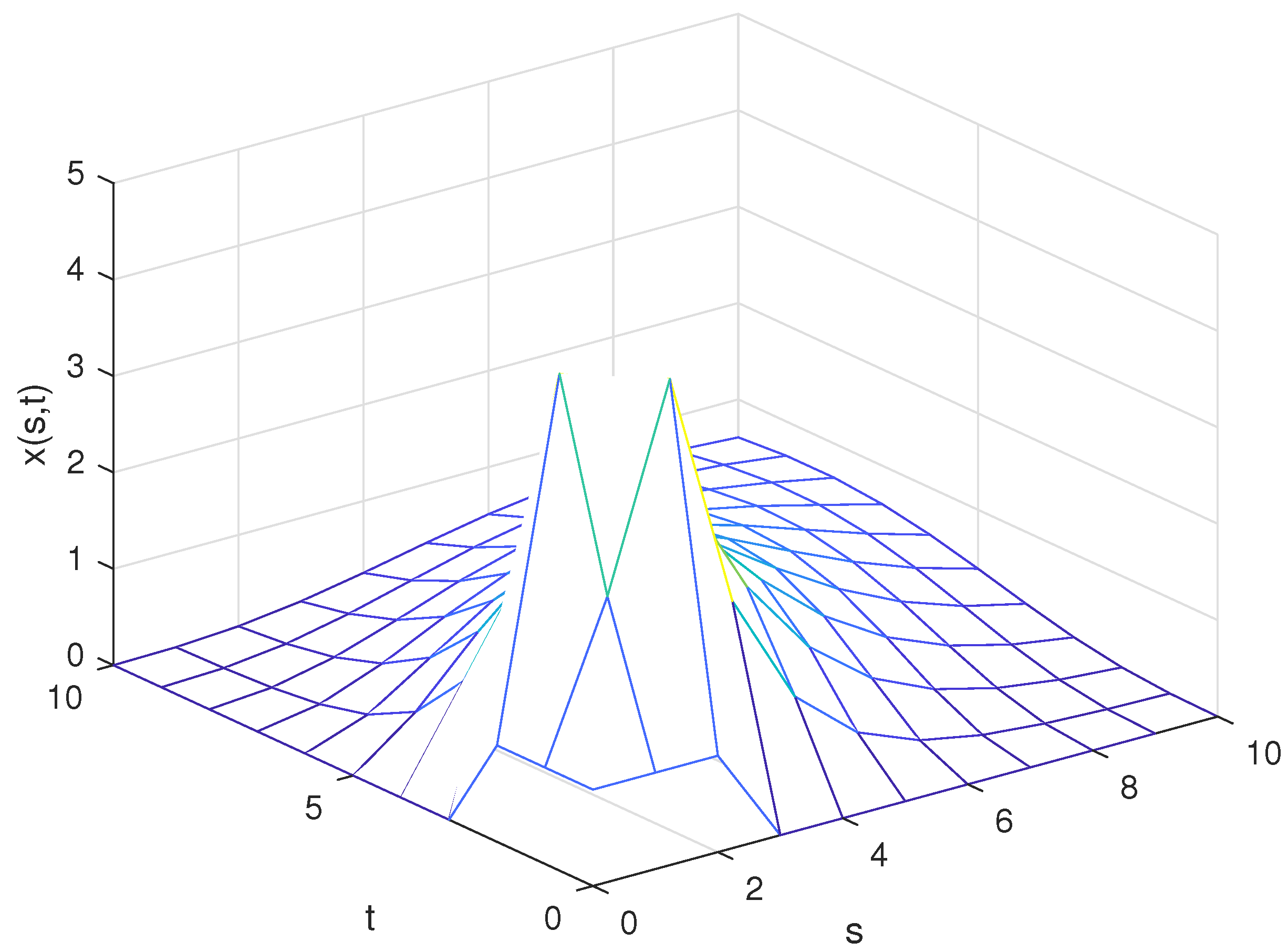
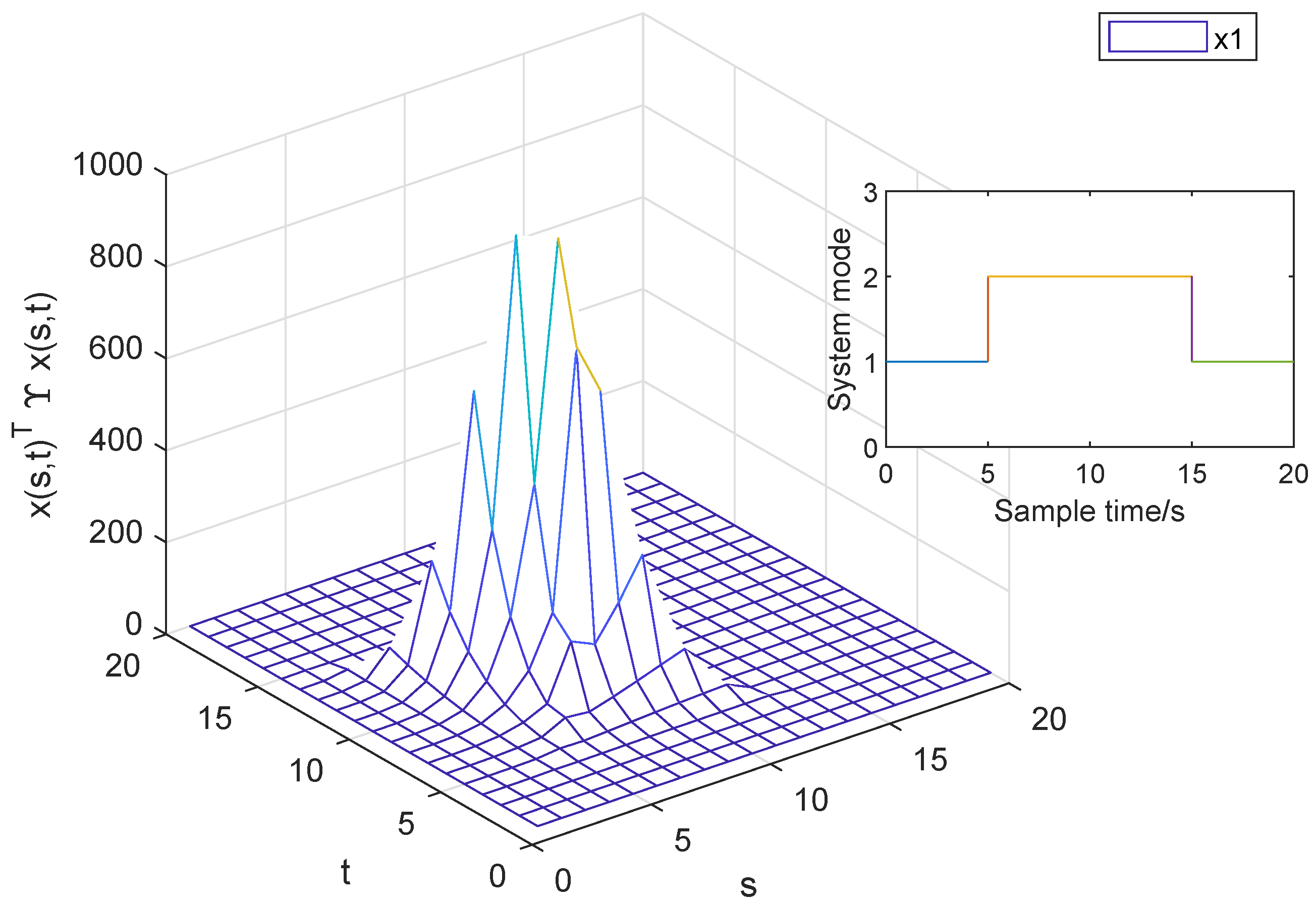
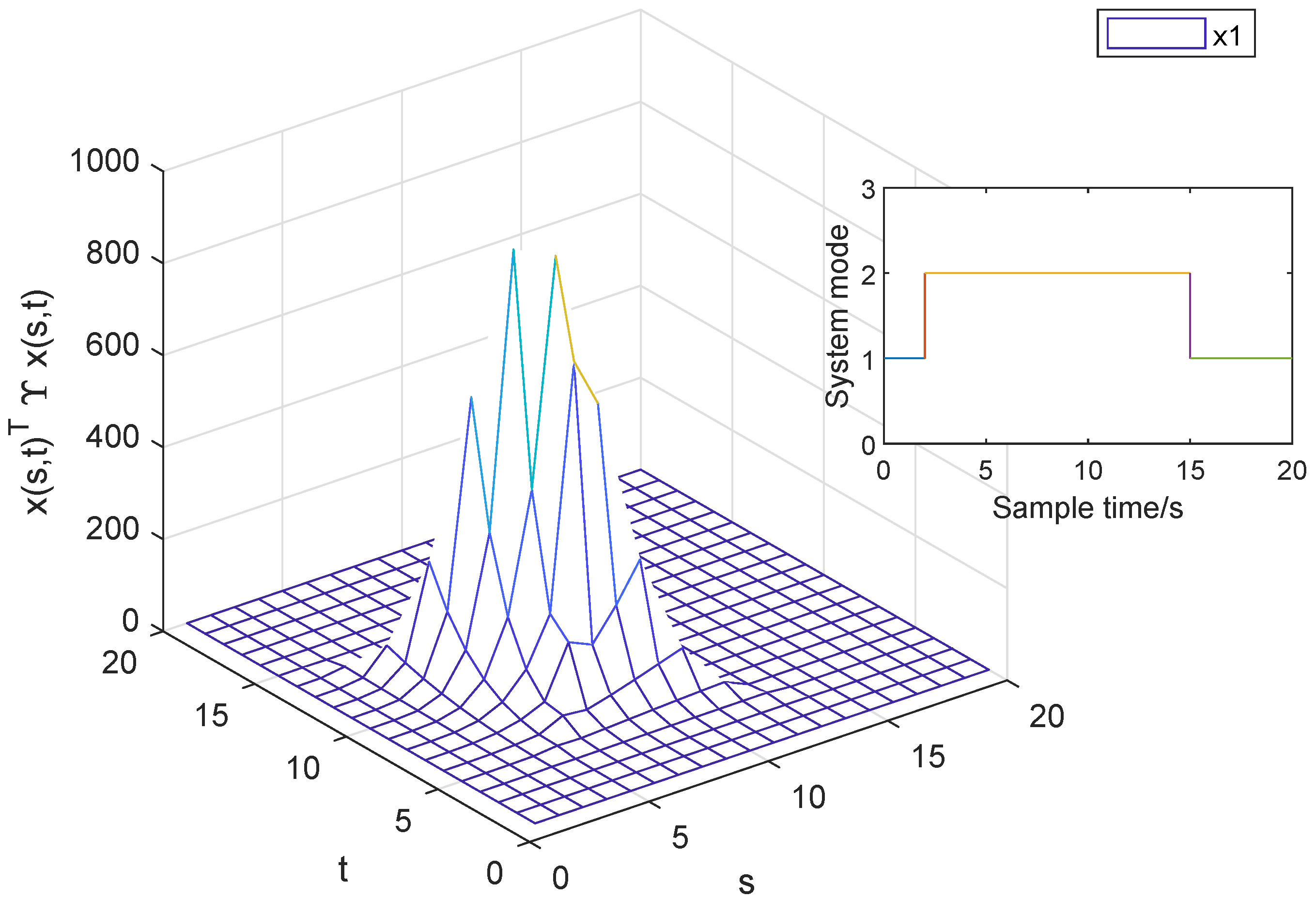
4. A Numerical Example
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| Abbreviations | |
| FMLSS | Fornasini–Marchesini local state-space |
| ADT | Average dwell time |
| MDADT | Mode-dependent average dwell time |
| WADT | Weighted average dwell time |
| FRS | Finite-region stability |
| LAS | Lyapunov asymptotic stability |
| Notation | Description |
| the Euclidean vector norm | |
| The n-dimensional Euclidean space | |
| The set of natural numbers | |
| The set of positive integers | |
| X is a positive definite and real symmetric matrix | |
| The transpose of matrix X | |
| I | Identity matrix |
| * | The omitted symbol of the term caused by symmetry |
| A diagonal matrix with diagonal elements | |
| The eigenvalues of a matrix X | |
| The minimum eigenvalue of a matrix X | |
| The maximum eigenvalue of a matrix X | |
| □ | The completion of the proof |
References
- Kaczorek, T. Two-Dimension Linear Systems; Spring: Berlin, Germany, 1985. [Google Scholar]
- Du, C.; Xie, L. H∞ Control and Filtering of Two-Dimensional Systems; Springer: Berlin, Germany, 2002. [Google Scholar]
- Cheng, P.; Wang, H.; Stojanovic, V.; He, S.; Shi, K.; Luan, X. Asynchronous fault detection observer for 2-D Markov jump systems. IEEE Trans. Cybern. 2021, 52, 13623–13634. [Google Scholar] [CrossRef] [PubMed]
- Yeganefar, N.; Ghamgui, M.; Moulay, E. Lyapunov theory for 2-D nonlinear Roesser models: Application to asymptotic and exponential stability. IEEE Trans. Autom. Control 2013, 58, 1299–1304. [Google Scholar] [CrossRef]
- Duan, Z.; Liang, J.; Xiang, Z. H∞ control for continuous-discret system in T-S fuzzy model with finite frequency specifications. Discrete Cont. Dyn.-S 2022, 15, 3155–3172. [Google Scholar]
- Bachelier, O.; Yeganefar, N.; Mehdi, D.; Paszke, W. On stabilization of 2D Roesser Models. IEEE Trans. Autom. Control 2017, 62, 2505–2511. [Google Scholar] [CrossRef]
- Shi, S.; Fei, Z.; Li, J. Finite-time H∞ control of switched systems with mode-dependent average dwell time. J. Franklin Inst. 2016, 353, 221–234. [Google Scholar] [CrossRef]
- Wang, J.; Liang, J.; Zhang, C.T. Dissipativity analysis and synthesis for positive Roesser systems under the switched mechanism and Takagi-Sugeno fuzzy rules. Inform. Sci. 2021, 546, 234–252. [Google Scholar] [CrossRef]
- Wang, L.; Chen, W.; Li, L. Dissipative stability analysis and control of two-dimensional Fornasinia-Marchesini local state-space model. Int. J. Syst. Sci. 2017, 48, 1744–1751. [Google Scholar] [CrossRef]
- Sakthivel, R.; Saravanakumar, T.; Kaviarasan, B.; Marshar, A.S. Dissipativity based repetitive control for switched stochastic dynamical systems. Appl. Math. Comput. 2016, 291, 340–353. [Google Scholar] [CrossRef]
- Yang, R.; Ding, S.; Zheng, W.X. Co-design of event-triggered mechanism and dissipativity-based output feedback controller for two-dimensional systems. Automatica 2021, 130, 109694. [Google Scholar] [CrossRef]
- Wang, J.; Liang, J.; Zhang, C.-T.; Fan, D. Robust dissipative filtering for impulsive switched positive systems described by the Fornasini-Marchesini second model. J. Franklin Inst. 2022, 359, 123–144. [Google Scholar] [CrossRef]
- Duan, Z.; Zhou, J.; Shen, J. Finite frequency filter design for nonlinear 2-D continuous systems in T-S form. J. Franklin Inst. 2017, 354, 8606–8625. [Google Scholar] [CrossRef]
- Duan, Z.; Ding, F.; Liang, J.; Xiang, Z. Observer-based fault detection for continuous-discrete systems in T-S fuzzy model. Nonlinear Anal. Hybrid Syst. 2023, 50, 101379. [Google Scholar] [CrossRef]
- Li, X.; Gao, H. Robust finite frequency H∞ filtering for uncertain 2-D Roesser systems. Automatica 2012, 48, 1163–1170. [Google Scholar] [CrossRef]
- Ahn, C.K.; Shi, P.; Basin, M.V. Two-dimensional dissipative control and filtering for Roesser model. IEEE Trans. Autom. Control 2015, 60, 1745–1759. [Google Scholar] [CrossRef]
- Wu, L.; Yang, R.; Shi, P.; Su, X. Stability analysis and stabilization of 2-D switched systems under arbitrary and restricted switchings. Automatica 2015, 59, 206–215. [Google Scholar] [CrossRef]
- Xiang, Z.; Huang, S. Stability analysis and stabilization of discrete-time 2D switched systems. Circ. Syst. Signal Process. 2013, 32, 401–414. [Google Scholar] [CrossRef]
- Duan, Z.; Xiang, Z.; Karimi, H.R. Delay-dependent exponential stabilization of positive 2D switched state-delayed systems in the Roesser model. Inform. Sci. 2014, 272, 173–184. [Google Scholar] [CrossRef]
- Wang, J.; Liang, J. Robust finite-horizon stability and stabilization for positive switched FM-II model with actuator saturation. Nonlinear Anal. Hybrid Syst. 2020, 35, 100829. [Google Scholar] [CrossRef]
- Fei, Z.; Shi, S.; Zhao, C.; Wu, L. Asynchronous control for 2-D switched systems with mode-dependent average dwell time. Automatica 2017, 79, 198–206. [Google Scholar] [CrossRef]
- Yu, Q.; Lv, H. Stability analysis for discret-time switched systems with stable and unstable modes based on a weighted average dwell time approach. Nonlinear Anal. Hybrid Syst. 2020, 38, 100949. [Google Scholar] [CrossRef]
- Zhang, T.; Cao, J.; Li, X. Lyapunov conditions for finite-time input-to-state stability of impulsive switched systems. IEEE/CAA J. Autom. Sin. 2024, 11, 1057–1059. [Google Scholar] [CrossRef]
- Wang, W.; Qi, X.; Zhong, S.; Liu, F. Finite-time boundedness and control design of uncertain switched systems with time-varying delay under new switching rules. Int. J. Robust Nonlinear Control 2024, 34, 456–480. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, W. Finite-region stability and finite-region boundedness for 2-D Roesser models. Math. Methods Appl. Sci. 2016, 39, 5757–5769. [Google Scholar] [CrossRef]
- Zhang, G.; Harry, H.L.; Wang, W.; Gao, J. Input-output finite-region stability and stabilization for discrete 2-D Fornasini-Marchesini models. Syst. Control Lett. 2017, 99, 9–16. [Google Scholar] [CrossRef]
- Li, L.; Yang, R.; Feng, Z.; Wu, L. Event-triggered dissipative control for 2-D switched systems. Inf. Sci. 2022, 589, 802–812. [Google Scholar] [CrossRef]
- Yang, R.; Li, L.; Su, X. Finite-region dissipative dynamic output feedback control for 2-D FM systems with missing measurements. Inf. Sci. 2020, 514, 1–14. [Google Scholar] [CrossRef]
- Hua, D.; Wang, W.; Yu, W.; Wang, Y. Finite-region stabilization via dynamic output feedback for 2-D Roesser models. Math. Methods Appl. Sci. 2018, 41, 2140–2151. [Google Scholar] [CrossRef]
- Hua, D.; Wang, W.; Ren, Y.; Yao, J. Finite-region stabilization and H∞ control for 2-D FMLSS asynchronously switched system. J. Frankl. Inst. 2020, 357, 9127–9153. [Google Scholar] [CrossRef]
- Yu, Q.; Zhai, G.S. New stability criteria of switched systems with unstable modes under a weighted ADT scheme. Int. J. Syst. Sci. 2021, 52, 2735–2751. [Google Scholar] [CrossRef]
- Yu, Q.; Yuan, X.Y. Stability analysis for positive switched systems having stable and unstable subsystems based on a weighted average dwell time scheme. ISA Trans. 2023, 136, 275–283. [Google Scholar] [CrossRef]
- Hu, T.; Lin, Z. Control Systems with Actuator Saturation; Springer: Boston, MA, USA, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Q.; Su, W. Finite-Region State Feedback Control for 2-D Switched Systems with Actuator Saturation Under the Weighted Average Dwell Time Technique. Axioms 2024, 13, 752. https://doi.org/10.3390/axioms13110752
Yu Q, Su W. Finite-Region State Feedback Control for 2-D Switched Systems with Actuator Saturation Under the Weighted Average Dwell Time Technique. Axioms. 2024; 13(11):752. https://doi.org/10.3390/axioms13110752
Chicago/Turabian StyleYu, Qiang, and Wangxian Su. 2024. "Finite-Region State Feedback Control for 2-D Switched Systems with Actuator Saturation Under the Weighted Average Dwell Time Technique" Axioms 13, no. 11: 752. https://doi.org/10.3390/axioms13110752
APA StyleYu, Q., & Su, W. (2024). Finite-Region State Feedback Control for 2-D Switched Systems with Actuator Saturation Under the Weighted Average Dwell Time Technique. Axioms, 13(11), 752. https://doi.org/10.3390/axioms13110752