Abstract
Logics of Formal Inconsistency ( for short) are a class of paraconsistent logics that validate the principle of gentle explosion, meaning that any formula can be derived from the set of formulas: , and . A unique feature of is the use of the symbol ‘∘’ to represent notions of consistency at the object-language level. These logics are simple in essence, built upon all the axiom schemas of positive classical logic, axioms for negation and the so-called ‘consistency operator’ ∘, with the only inference rule being detachment. In this paper, we propose an alternative foundation for , which is the positive fragment of intuitionistic propositional logic. We present bi-valuational ‘Loparić-like’ semantics for the resulting logics and discuss their potential extensions.
Keywords:
paraconsistent logic; da Costa’s logic; logics of formal inconsistency; consistency operator; intuitionistic implication MSC:
03B20; 03B53
1. Introduction
Let denote the denumerable set of all propositional variables: p, q, , , …. The set of formulas is standardly defined using propositional variables from and the symbols ∼, ∨, ∧ and → for negation, disjunction, conjunction and implication, respectively. The connective of equivalence, , is definable through implication and conjunction in the standard way. We expand the language with a unary connective ‘∘’. By placing the symbol ‘∘’ in front of a formula , we indicate that ‘ is consistent’. The fundamental idea behind this is not significantly different from that given to the law of non-contradiction in da Costa’s C-systems (see [1,2,3,4], for details). However, in contrast to da Costa’s systems, consistency is represented using a single connective (see [5,6] for a philosophical discussion on the topic).
We say that a calculus (identified with the triple and determined by its set of axioms which is included in ) is paraconsistent if (1) the principle of explosion, , does not hold in , and (2) is not trivial. We say that is trivial iff for any formula , is a thesis of . Logics of Formal Inconsistency satisfy these conditions. They also validate the principle of gentle explosion: . ‘A fundamental example of (…) where consistency is rendered expressible by means of a specific new primitive connective’ ([6], p. 3) is . The calculus contains all the axiom schemas of the positive fragment of classical propositional calculus (abbreviated as ), specifically all instances of the following schemas:
()
()
()
()
()
()
()
()
() ,
and, additionally:
() ;
.
The only inference rule is the detachment rule (MP) .
Remark 1.
() is independent in .
Proof.
It is easy to check that the matrix with 1 as the sole designated value, and the connectives given by the truth-tables:
| ∼ | ∘ | → | 1 | 2 | 0 | ∨ | 1 | 2 | 0 | ∧ | 1 | 2 | 0 | ||||
| 1 | 0 | 0 | 1 | 1 | 2 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | |||
| 2 | 1 | 0 | 2 | 1 | 1 | 0 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 0 | |||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 0 |
verifies the axioms ()–(), (), and (MP), but not () when is assigned the value 2 and takes the value 0. □
The intuitionistic variant of , which is obtained by removing the axiom () from , was examined in Section 5.1.4 of [7]. However, it would be more interesting to extend with one of the following formulas: or (cf. Remarks 3 and 7 below) and subsequently discuss the intuitionistic variants of some well-known (see Section 3 and Section 4 below).
2. Calculi and
The calculus as introduced in [6] (see Definition 102, p. 62) is defined by the postulates of , , () and (MP). Since , (), () and (MP) define the logic (see [8] for details), can be viewed as an extension of by two axioms involving the consistency connective: and .
Definition 1.
For any and any , we say that α is provable from within (in symbols: ) iff there is a finite sequence of formulas, , , ⋯, such that and for each , either , or ia an axiom of , or for some , we have . A formula α is a thesis of iff α is provable from ∅ within .
Before proceeding, let us review some results regarding . Some of these results are quite evident, while others are well-established; therefore, they will be presented without proofs.
Remark 2.
The following formulas are provable in :
.
Lemma 1.
For every and , we have:
(1) iff for some finite ,
(2) If , then
(3) If and , then
(4) If and, for every such that , then
(5) If and , then ,
in particular, if and α is a thesis of , then .
Lemma 2.
For any and , we have:
() if and , then
() iff .
() if , then
() if , then ,
where stands for ‘, and ’.
The results, with the exception of () and () from Lemma 2, apply to every calculus discussed in this paper
Remark 3.
The axiom () is dependent in .
Proof.
Note first that is a thesis of (this can shown by applying (), , , and (MP)). Then, we have: by (); by , , , (MP); by , , (MP); by , , (MP); by , (MP); by (), , (MP); by the thesis of , (MP); and finally, by (). Notice, in passing, that the same proof can be provided to show that () is derivable in (see Definition 75, [6], p. 52.) □
This suggests that may be regarded as a calculus ‘built upon’ of da Costa, defined by –, , and (MP) (see [2,9,10], for details), rather than .
Definition 2
([6], p. 63). A -valuation is a function that satisfies, for any , all the conditions of -valuation, i.e.,:
() = 1 iff = 1 and = 1
() = 1 iff = 1 or = 1
() = 1 iff = 0 or = 1
() if = 0, then = 1
() if = 1, then = 1,
and the following clauses:
() if = 1, then = 0 or = 0
() if = 1, then = = 1.
Definition 3.
A formula α is a -tautology iff for every -valuation v, = 1. For any and , α is a semantic consequence of Γ (in symbols: ) iff for any -valuation v: if = 1 for any , then = 1.
Theorem 1.
For all and : iff .
By adding to the postulates of , we obtain the calculus (see [6] Definition 105, p. 64). has some interesting properties:
Remark 4.
The axiom can be replaced by .
Proof.
: , by (); by , (MP); , by (), (), (MP); by , (MP); by ().
: by (); by , , (MP); by , , (MP); by , (MP); by (). □
Remark 5.
The axiom can be replaced by .
Proof.
follows from applying (), , and (MP).
: by (); by , , , (MP); by , and (MP); by , (MP); and finally by (). □
As noted in the remarks above, can be defined by the axioms of , , (MP) and one of the following pairs of formulas: and or and .
Definition 4.
A -valuation is a function that satisfies, for any , all the conditions of -valuation, and additionally:
() if = 1, then = 0 or = 0
() if = 1, then = 1
() if = 1, then = 0.
Definition 5.
A formula α is a -tautology iff for every -valuation v, = 1. For any and , α is a semantic consequence of Γ (in symbols: ) iff for any -valuation v: if = 1 for any , then = 1.
Remark 6.
Given that v is a -valuation. Then, v has the following properties: ()’ if = 0, then = 1; ()’ = 1 iff = 0 or = 0; ()’ = 1 iff = 0.
A slightly different bivaluation semantics for was proposed in [6], p. 67, where a -valuation is defined as a function that meets, for any , all the conditions of -valuation, along with the following additional clauses:
() if = 1, then = 0 or = 0
(): if = 1, then = 1 and = 1.
It is easy to see that the formula being an instance of the axiom is not valid for every -valuation . This indicates that the semantics proposed in [6] is an adequate semantics for , but not for .
Theorem 2.
For all and : if , then .
The proof of soundness proceeds in the standard way, by induction on the length of a derivation in . For the proof of completeness, we will employ a method based on the concept of maximal non-trivial sets of formulas (see, e.g., Section 2.2 of [7]). We begin by recalling the basic definitions and lemmas. The latter are generally well-known; therefore, they will be presented without proofs (see, e.g., [11,12], for further details).
Definition 6.
Let = be a calculus satisfying Tarskian properties and . We say that Δ is a closed theory of if, and only if for any : iff . We say that Δ is maximal non-trivial with respect to in , if, and only if (1) , and (2) for every , if then .
Lemma 3
(Lemma 2.2.5 of [7]). Every maximal non-trivial set with respect to some formula is a closed theory.
Notice that the lemma holds for . We also have:
Lemma 4.
For any maximal non-trivial set Δ with respect to α in the mapping defined, for any , as (): = 1 iff , is a -valuation.
Proof.
The proof is by cases. The cases () to () are those of and are thus omitted.
(): Assume, for a contradiction, that = 1, = 1 and = 1. Then, by (), we have , and , which entails, by Lemma 1(2), that , and , that is, . Since is transitive, is an axiom of and () of Lemma 2 holds true, then . Recall that is a closed theory, so . But, from the main assumption, we have . This leads to a contradiction.
(): Assume that = 1. Then, by (), we have , which entails, by Lemma 1(2), that . Since is transitive, is a thesis of and () holds in , then . Given that is a closed theory, we have , which implies, by (), that = 1.
(): Suppose, for a contradiction, that = 1 and = 1. Then, by (), we have and , which entails and , that is, . Since is transitive, is a thesis of and () holds true, then . Given that is a closed theory, we have . But, from our main assumption, we know that . This leads to a contradiction. □
Lemma 5
(Theorem 3.31 of [11]). For any and such that , there is a maximal non-trivial set Δ with respect to α in such that .
Notice that Lindenbaum–Łoś theorem holds for any finitary calculus . Hence, the completeness for follows:
Theorem 3.
For all and : if , then .
Proof.
The proof is by contraposition. Suppose that and is a maximal non-trivial set with respect to in such that . Then, we obtain that . By Lemma 4, there is a -valuation v such that = 0 and = 1, for any , which implies that and, in particular, . This completes the proof. □
As a final remark in this section, let us observe that () is redundant not only in (and in ), but also in an alternative weakening of .
Remark 7.
() is dependent in the calculus obtained by dropping from the set of axioms of .
Proof.
The proof follows a similar structure to that of Remark 3. The only significant difference is that after deriving by , and (MP), we obtain by , , (MP); by , (MP); and finally, we derive using (). □
3. Intuitionistic Implication and
Although is axiomatized over the positive fragment of intuitionistic propositional logic, the negation-free fragment of corresponds to positive classical logic. Here, we suggest, by the example of , how to ‘fix the asymmetry’. First, we will establish some auxiliary results.
Remark 8.
The axiom is equivalent to the triple of postulates: and and .
Proof.
: See of Remark 4; and follow from (), (), (), , and (MP).
: , , by (); by (), (MP); by , (MP); by (), (MP); by , (MP); by , (MP); and finally by (). □
Lemma 6.
The axioms of , , , , and (MP) axiomatize .
Remark 9.
The postulate is independent of the other axioms.
Proof.
The matrix with 1 and 2 as the designated values, and the connectives defined by the truth-tables:
| ∼ | ∘ | → | 1 | 2 | 0 | ∨ | 1 | 2 | 0 | ∧ | 1 | 2 | 0 | ||||
| 1 | 0 | 1 | 1 | 1 | 2 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 0 | |||
| 2 | 1 | 1 | 2 | 1 | 2 | 0 | 2 | 1 | 2 | 2 | 2 | 2 | 2 | 0 | |||
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 2 | 0 | 0 | 0 | 0 | 0 |
verifies the axioms of , , , and (MP), but not when is assigned the value 2. □
Let denote the calculus obtained by dropping from the set of axiom schemas of (see Lemma 6). Observe that a weaker version of , i.e., , is still provable in .
Remark 10.
Neither , nor , nor is provable in .
Proof.
The matrix with 1 as the sole designated value; negation, consistency connective, conjunction and disjunction interpreted as in , and implication defined by the truth-table:
| → | 1 | 2 | 0 |
| 1 | 1 | 2 | 0 |
| 2 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 |
validates the axioms of and (MP), but it falsifies , and when and are assigned the values 2 and 0, respectively. □
Remark 11.
and are provable in .
Proof.
: by (); by , , (MP); by , , (MP); by , (MP); by ().
: , , by (); by (), (MP); by , (MP); by , (MP); and finally, by (). □
Remark 12.
The axiom can be replaced by .
Proof.
: See the proof of Remark 11; follows from applying (), , , , and (MP). □
Clearly, can be defined by the axioms of , , , and (MP). Moreover, enjoys intuitionistic (not classical) implication. A semantics for is established by reproducing the axiom schemas of in ‘Loparić-like’ semantics. The idea behind it traces back to the 1986 paper by Loparić, in which the semantics for was first introduced.
Definition 7
(cf. [9], p. 74). An -semi-valuation is a function that satisfies, for any , all the conditions of -semi-valuation, that is,
() = 1 iff = 1 and = 1
() = 1 iff = 1 or = 1
() if = 1, then = 0 or = 1
() if = 0, then = 0
() if = 0, then = 1
() if = 1, then = 1,
and the following clauses:
() if = 1, then = 0 or = 0
() if = 1, then = 0
() if = 1, then = 1.
Definition 8
(cf. [9], p. 74). An -valuation is an -semi-valuation for which the following holds: if = 0, where and , then there is an -semi-valuation s such that, for , = 1 and = 0.
Definition 9.
A formula α is an -tautology iff for every -valuation v, = 1. For any and , α is a semantic consequence of Γ (in symbols: ) iff for any -valuation v: if = 1 for any , then = 1.
There are two key distinctions between a -valuation and an -valuation (excluding the clause () (resp. ()) where ‘’ is assigned the value 1). Firstly, when the implication connective is assigned the value 0, Definition 4 states that the antecedent is assigned the value 1, while the consequent is assigned the value 0. In contrast, for an -semi-valuation, if the implication is assigned the value 0, the consequent takes the value 0, but the antecedent is not assigned any logical value. Secondly, an -valuation is established through a two-step process. This approach is significant because it allows for saving many useful tautologies that would otherwise be ‘lost’ without Definition 8. This two-step method is not required for a -valuation.
Theorem 4.
For all and : if , then .
Proof.
We proceed in a manner similar to the proof of Theorem 4.4 in [9]. □
For completeness, we will apply the method based on the concept of saturated sets. To begin, we will review some auxiliary results.
Definition 10.
Let = be a calculus and . We say that Δ is saturated with respect to in , or simply Δ is an α-saturated set, if (1) , and (2) for every , if then .
Lemma 7
([9], Lemma 3.2). If , then there is an α-saturated set Δ such that .
Lemma 8
([9], Lemma 3.3). If Δ is an α-saturated set, then iff , for every .
It follows from the lemmas that:
Lemma 9
([9], Lemma 3.5). If Δ an α-saturated set and , where , then there is an -saturated set such that .
Now, we need to prove an auxiliary lemma:
Lemma 10.
If Δ is α-saturated, then for any , we have:
() if , then and
() if , then or
() if , then or
() if , then and
() if , then or
() if , then
(∼) if , then
() if , then
() if , then or
() if , then
() if , then .
Proof.
Cases ()–() are those of and hence omitted.
Case (): Assume, for a contradiction, that , and . This implies, by Lemma 8, that , and . By (), and the transitivity of , we obtain , which results in . But is an -saturated set, so and consequently, . This leads to a contradiction.
Case (): Suppose that . Then, by Lemma 8, we have . By applying (), and by the transitivity of , we obtain that . Since is an -saturated set, then .
Case (): The proof is analogous to the proof of ‘Case ()’. It requires to be used. □
By applying Lemma 10, we obtain the following:
Lemma 11.
The characteristic function of an α-saturated set is an -semi-valuation.
From Lemmas 9 and 11, along with the definition of -valuation, we obtain the following result:
Lemma 12.
The characteristic function of an α-saturated set is an -valuation.
Theorem 5.
For all and : if , then .
Proof.
Assume that . By Lemmas 7 and 8, there is an -saturated set such that and . Given that Lemma 12 holds for , there is an –valuation v such that = 0 and = 1, for any , which means that and in particular . This completes the proof. □
As shown, removing from the set of axiom schemas of yields a calculus with the positive intuitionistic basis. Now, consider an extension of by , for brevity.
Remark 13.
and are not provable in .
Proof.
: See the proof Remark 9; : Likewise, the matrix invalidates if and are assigned the values 2 and 0, respectively. □
Definition 11.
A -valuation is a function that satisfies, for any , all the conditions of -valuation, and additionally:
() if = 1, then = 0 or = 0
() if = 1, then = 1
() if = 1, then = 0.
Definition 12.
A formula α is a -tautology iff for every -valuation v, = 1. For any and , α is a semantic consequence of Γ (in symbols: ) iff for any -valuation v: if = 1 for any , then = 1.
Theorem 6.
For all and : iff .
Proof.
The proof is similar to the proofs of Theorem 1 and 2. □
4. , and More
Here, we consider some extensions of that differ from those presented in Section 3. The first extension, which refer to as from this point forward, is obtained by adding , where , to the postulates of . It is straightforward to demonstrate that the following two observations are true:
Remark 14
(cf. [6], p. 68). is equivalent to the triple of axiom schemas: , and .
Remark 15.
Neither () nor is provable in .
The negation-free part of is intuitionistic propositional logic. Therefore, a semantics for can be established quite easily by adding an additional clause to Definition 7.
Definition 13.
An -semi-valuation is a function that satisfies, for any , all the conditions of -semi-valuation, and the following clause: () if = = 1, then = 1, where .
An -valuation, -tautology and a semantic consequence in are defined similarly as in Definitions 8 and 9.
Theorem 7.
For all and : iff .
Proof.
The proof is carried out similarly as for (see the proofs of Theorems 4 and 5). The key point is to show that the following lemma holds:
Lemma 13.
If Δ is α-saturated, then we have, for any , that all the clauses of hold (see Lemma 10 above), and additionally: () if and , then , where .
This can be performed by means of the axioms of . □
The second extension, for short, is obtained by adding , where , to the postulates of .
Remark 16
(cf. [6], pp. 71–72; [13], Section 3). is equivalent to the triple of axiom schemas: , and .
From Remark 16 and the fact that and are provable in , we deduce and , where . This leads to counter-intuitive consequences; for example, a single consistent conjunct makes consistent the whole conjunction. Specifically, we have , for every such that and .
Definition 14.
An -semi-valuation is a function that satisfies, for any , all the conditions of -semi-valuation, and additionally: () if = 1 or = 1, then = 1, where .
An -valuation, -tautology and a semantic consequence in are defined similarly as in Definitions 8 and 9.
Theorem 8.
For all and : iff .
Remark 17.
is a proper subsystem of .
Proof.
By , and (MP), we obtain . Conversely, there are theses of (see, e.g., Remark 16) that are unprovable in . □
Remark 18.
Enriching the set of axiom schemas of (resp. ) with results in obtaining (resp. ).
The calculi and are known in the literature and have been studied by various authors (see, e.g., Section 5.2 of [6] and Chapter 8 of [14]). It is important to emphasize that extending (resp. ) with does not yield (resp. ). To clarify, let (resp. ) be defined by the postulates of , (MP) and (resp. ).
Remark 19.
and are provable in neither , nor .
Proof.
See the proof of Remark 13. □
A bivaluation semantics for (and ) can be obtained from that for .
Definition 15.
A -valuation (resp. -valuation) is a function that satisfies, for any , all the conditions of -valuation, and additionally:
() if = = 1, then = 1 (resp. () if = 1 or = 1, then = 1), where .
The notions of tautology and semantic consequence are defined in the standard manner.
Theorem 9.
For all and : iff , where X stands for or .
Proof.
The proof is similar to the proofs of Theorem 1 and 2. □
5. Conclusions
This paper presents theoretical results on (for a discussion on the practical implications of , particularly its potential applications in evolutionary databases, see [15]; for a discussion on paraconsistent reasoning in science, see, for example, [16]). It has been demonstrated that certain , typically regarded as axiomatic extensions of , can also be considered extensions of the positive fragment of intuitionistic propositional logic (see Appendix A). Although this concept has already been addressed in the literature (see, e.g., [7], pp. 187–191), neither the intuitionistic variant of , , nor has been discussed thus far. As shown, the intuitionistic version of is obtained simply by removing () from the axioms of . This approach is not applicable to or its extensions, as the postulate () is dependent on the other axioms (see Remark 3 above). Nevertheless, an alternative approach is available. First, it is essential to recognize that can be replaced by the triple of formulas: , and . This assertion holds true not only for but also for (as evidenced by the proof in Remark 8, which depends solely on the rules of ), indicating that the axioms of , , , and (MP) axiomatize . The postulate is particularly important in this context: it is independent of the other axioms, and its removal from the set of axioms results in the intuitionistic variant of and its extensions: , and . Additionally, as demonstrated in [17], a similar approach can be applied to da Costa’s hierarchy of -calculi ().
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Listed below are the logical calculi discussed in this paper.
- *
- = +…++++(MP)
- *
- = +
- *
- = ++
- *
- = +++
- *
- = +
- *
- = +++ = ++++
- *
- = +
- *
- = +
- *
- = ++ = +++
- *
- = +
- *
- = +
- *
- = ++ = +++,
where ‘’ (or, ‘’) means ‘the postulates: a, b and c axiomatize X’ (resp. ‘the postulates of Y and c axiomatize X’).
They all form together the structure shown in Figure A1.
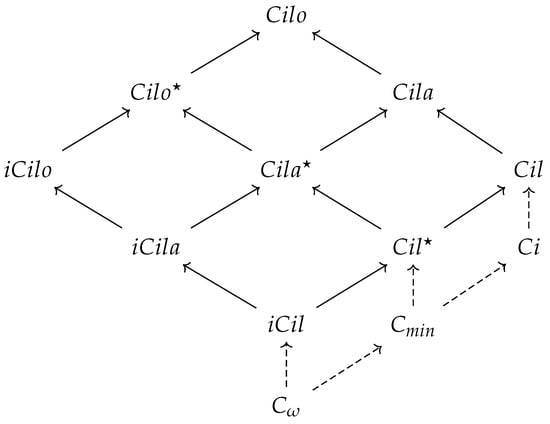
Figure A1.
Extensions of .
References
- Da Costa, N.C.A. Calculs propositionnels pour les systèmes formels inconsistants. C. R. Acad. Sci. Paris 1963, 257, 3790–3793. [Google Scholar]
- Da Costa, N.C.A. On the Theory of Inconsistent Formal systems. Notre Dame J. Form. Log. 1974, 15, 497–510. [Google Scholar] [CrossRef]
- Arruda, A.I. A Survey of Paraconsistent Logic. In Mathematical Logic in Latin America: Proceedings of the IV Latin American Symposium on Mathematical Logic Held in Santiago, December 1978; Arruda, A.I., Chuaqui, R., Da Costa, N.C.A., Eds.; Elsevier: Amsterdam, The Netherlands, 1980; pp. 1–41. [Google Scholar]
- D’Ottaviano, I.M.L. On the Development of Paraconsistent Logic and da Costa’s Work. J. -Non-Class. Log. 1990, 7, 9–72. [Google Scholar]
- Carnielli, W.A.; Marcos, J. A Taxonomy of C-Systems. In Paraconsistency. The Logical Way to the Inconsistent; Carnielli, W.A., Coniglio, M.E., D’Ottaviano, I.M.L., Eds.; CRC Press: Boca Raton, FL, USA, 2002; Chapter 1. [Google Scholar]
- Carnielli, W.A.; Coniglio, M.E.; Marcos, J. Logics of formal inconsistency. In Handbook of Philosophical Logic, 2nd ed.; Gabbay, D.M., Guenthner, F., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; Volume 14, pp. 1–93. [Google Scholar]
- Carnielli, W.; Coniglio, M.E. Paraconsistent Logic: Consistency, Contradiction and Negation, Logic, Epistemology, and the Unity of Science; Springer: Berlin/Heidelberg, Germany, 2016; Volume 40. [Google Scholar]
- Carnielli, W.; Marcos, J. Limits for paraconsistent calculi. Notre Dame J. Form. Log. 1999, 40, 375–390. [Google Scholar] [CrossRef]
- Loparić, A. A semantical study of some propositional calculi. J. -Non-Class. Log. 1986, 3, 73–95. [Google Scholar]
- Sylvan, R. Variations on da Costa C Systems and Dual-Intuitionistic Logics I. Analyses of Cω and CCω. Stud. Log. 1990, 49, 47–65. [Google Scholar] [CrossRef]
- Pogorzelski, W.A.; Wojtylak, P. Completeness Theory for Propositional Logics; Studies in Universal Logic; Birkhäuser: Basel, Switzerland, 2008. [Google Scholar]
- Wójcicki, R. Lectures on Propositional Calculi; Ossolineum, Pub. House of the Polish Academy of Sciences: Warszawa, Poland, 1984. [Google Scholar]
- Da Costa, N.C.A.; Béziau, J.-Y.; Bueno, O.A.S. Aspects of Paraconsistent Logic. Log. J. IGPL 1995, 3, 597–614. [Google Scholar] [CrossRef]
- Avron, A.; Arieli, O.; Zamansky, A. Theory of Effective Propositional Paraconsistent Logics; College Publications: London, UK, 2018. [Google Scholar]
- Carnielli, W.; Marcos, J.; de Amo, S. Formal inconsistency and evolutionary databases. Log. Log. Philos. 2000, 8, 115–152. [Google Scholar] [CrossRef]
- Verdée, P.; Andreas, H. (Eds.) Logical Studies of Paraconsistent Reasoning in Science and Mathematics; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Ciuciura, J. Da Costa’s logics: A look beneath the surface. Stud. Log. 2024; submitted. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).