A Heuristic Attribute-Reduction Algorithm Based on Conditional Entropy for Incomplete Information Systems
Abstract
1. Introduction
2. Preliminaries
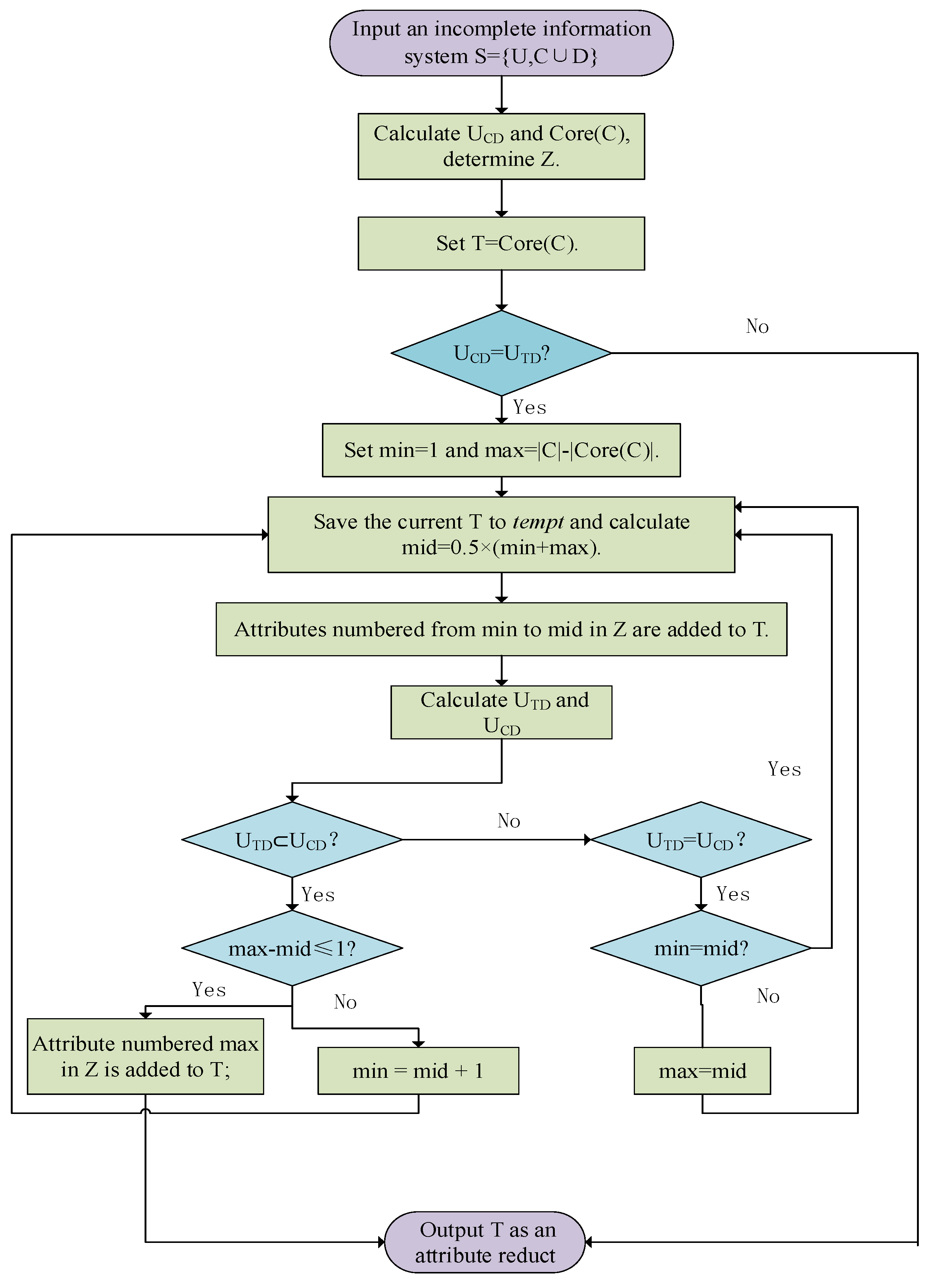
3. Binsearch Heuristic Reduction Algorithm Based on Conditional Entropy
| Algorithm 1 Process of the binsearch heuristic reduction algorithm based on conditional entropy |
|
4. Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Akram, M.; Ali, G.; Alcantud, J.C.R. Attributes reduction algorithms for m-polar fuzzy relation decision systems. Int. J. Approx. Reason. 2022, 140, 232–254. [Google Scholar] [CrossRef]
- Chu, X.L.; Sun, B.Z.; Chu, X.D.; Wu, J.Q.; Han, K.Y.; Zhang, Y.; Huang, Q.C. Multi-granularity dominance rough concept attribute reduction over hybrid information systems and its application in clinical decision-making. Inf. Sci. 2022, 597, 274–299. [Google Scholar] [CrossRef]
- He, J.L.; Qu, L.D.; Wang, Z.H.; Chen, Y.Y.; Luo, D.M. Attribute reduction in an incomplete categorical decision information system based on fuzzy rough sets. Artif. Intell. Rev. 2022, 55, 5313–5348. [Google Scholar] [CrossRef]
- Hu, M.; Tsang, E.C.C.; Guo, Y.T.; Chen, D.G.; Xu, W.H. Attribute reduction based on overlap degree and k-nearest-neighbor rough sets in decision information systems. Inf. Sci. 2022, 584, 301–324. [Google Scholar] [CrossRef]
- Hu, M.; Tsang, E.C.C.; Guo, Y.T.; Xu, W.H. Fast and robust attribute reduction based on the separability in fuzzy decision systems. IEEE Trans. Cybern. 2021, 52, 5559–5572. [Google Scholar] [CrossRef]
- Huang, C.; Huang, C.-C.; Chen, D.-N.; Wang, Y. Decision rules for renewable energy utilization using rough set theory. Axioms 2023, 12, 811. [Google Scholar] [CrossRef]
- Lang, G.M.; Cai, M.J.; Fujita, H.M.H.; Xiao, Q.M. Related families-based attribute reduction of dynamic covering decision information systems. Knowl. Based Syst. 2018, 162, 161–173. [Google Scholar] [CrossRef]
- Zhou, Y.; Bao, Y.L. A novel attribute reduction algorithm for incomplete information systems based on a binary similarity matrix. Symmetry 2023, 15, 674. [Google Scholar] [CrossRef]
- Liang, B.H.; Jin, E.L.; Wei, L.F.; Hu, R.Y. Knowledge granularity attribute reduction algorithm for incomplete systems in a clustering context. Mathematics 2024, 12, 333. [Google Scholar] [CrossRef]
- Liu, X.F.; Dai, J.H.; Chen, J.L.; Zhang, C.C. A fuzzy [formula omitted]-similarity relation-based attribute reduction approach in incomplete interval-valued information systems. Appl. Soft Comput. J. 2021, 109, 107593. [Google Scholar] [CrossRef]
- Zhang, C.L.; Li, J.J.; Lin, Y.D. Knowledge reduction of pessimistic multigranulation rough sets in incomplete information systems. Soft Comput. 2021, 25, 12825–12838. [Google Scholar] [CrossRef]
- Skowron, A.; Rauszer, C. The discernibility matrices and functions in information systems. Intell. Decis. Support 1992, 21, 331–362. [Google Scholar]
- Liu, G.L. Attribute reduction algorithms determined by invariants for decision tables. Cogn. Comput. 2022, 14, 1818–1825. [Google Scholar] [CrossRef]
- Liu, G.L. Using covering reduction to identify reducts for object-oriented concept lattices. Axioms 2022, 11, 381. [Google Scholar] [CrossRef]
- Liu, G.L.; Hua, Z.; Chen, Z.H. A general reduction algorithm for relation decision systems and its application. Knowl. Based Syst. 2017, 119, 87–93. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 623–656. [Google Scholar] [CrossRef]
- Zheng, K.F.; Wang, X.J. Feature selection method with joint maximal information entropy between features and class. Pattern Recognit. 2018, 77, 30–44. [Google Scholar] [CrossRef]
- Jiang, F.; Sui, Y.F.; Zhou, L. A relative decision entropy-based feature selection approach. Pattern Recognit. 2015, 48, 2151–2163. [Google Scholar] [CrossRef]
- Dai, J.H.; Wang, W.T.; Tian, H.W.; Liu, L. Attribute selection based on a new conditional entropy for incomplete decision systems. Knowl. Based Syst. 2013, 39, 207–213. [Google Scholar] [CrossRef]
- Thuy, N.; Wongthanavasu, S. On reduction of attributes in inconsistent decision tables based on information entropies and stripped quotient sets. Expert Syst. Appl. 2019, 137, 308–323. [Google Scholar] [CrossRef]
- Zou, L.; Ren, S.Y.; Sun YBYang, X.H. Attribute reduction algorithm of neighborhood rough set based on supervised granulation and its application. Soft Comput. 2023, 27, 1565–1582. [Google Scholar] [CrossRef]
- Chen, J.Y.; Zhu, P. A variable precision multigranulation rough set model and attribute reduction. Soft Comput. 2023, 27, 85–106. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, E.; Li, Y.H.; Wang, Z.; Liu, Z.X.; Bai, X.Y.; Huang, X.Y. A new attribute reduction algorithm dealing with the incomplete information system. In Proceedings of the International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, Zhangjiajie, China, 10–11 October 2009; pp. 12–19. [Google Scholar]
- Liu, G.L.; Li, L.; Yang, J.T.; Feng, Y.B.; Zhu, K. Attribute reduction approaches for general relation decision systems. Pattern Recognit. Lett. 2015, 65, 81–87. [Google Scholar] [CrossRef]
- Shannon, C.; Weaver, W. The Mathematical Theory of Communication; The University of Illinois Press: Urbana, IL, USA, 1949; p. 60. [Google Scholar]
- Zhao, X.Q. Basis and Application of Information Theory; Mechanical Industry Press: Beijing, China, 2015. (In Chinese) [Google Scholar]
| d | |||||
|---|---|---|---|---|---|
| 2 | 3 | 2 | 0 | 1 | |
| ∗ | 2 | ∗ | 1 | 2 | |
| ∗ | 2 | ∗ | 1 | 1 | |
| 2 | 3 | 2 | 1 | 1 | |
| 3 | ∗ | ∗ | 3 | 2 | |
| ∗ | 0 | 0 | ∗ | 1 | |
| 3 | 2 | 1 | 3 | 1 | |
| 1 | ∗ | ∗ | ∗ | 2 |
| d | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3 | 2 | 1 | 1 | 1 | 0 | ∗ | ∗ | 0 | |
| 2 | 3 | 2 | 0 | ∗ | 1 | 3 | 1 | 0 | |
| 2 | 3 | 2 | 0 | 1 | ∗ | 3 | 1 | 1 | |
| ∗ | 2 | ∗ | 1 | ∗ | 2 | 0 | 1 | 1 | |
| ∗ | 2 | ∗ | 1 | 1 | 2 | 0 | 1 | 1 | |
| 2 | 3 | 2 | 1 | 3 | 1 | ∗ | 1 | 1 | |
| 3 | ∗ | ∗ | 3 | 1 | 0 | 2 | ∗ | 0 | |
| ∗ | 0 | 0 | ∗ | ∗ | 0 | 2 | 0 | 1 | |
| 3 | 2 | 1 | 3 | 1 | 1 | 2 | 1 | 1 | |
| 1 | ∗ | ∗ | ∗ | 1 | 0 | ∗ | 0 | 0 | |
| ∗ | 2 | ∗ | ∗ | 1 | ∗ | 0 | 1 | 0 | |
| 3 | 2 | 1 | ∗ | ∗ | 0 | 2 | 3 | 0 |
| a | b | c | d | e |
| f | g | h | i | j |
| k | l | m | n | o |
| p | q | r | s | w |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bao, Y.; Cheng, S. A Heuristic Attribute-Reduction Algorithm Based on Conditional Entropy for Incomplete Information Systems. Axioms 2024, 13, 736. https://doi.org/10.3390/axioms13110736
Bao Y, Cheng S. A Heuristic Attribute-Reduction Algorithm Based on Conditional Entropy for Incomplete Information Systems. Axioms. 2024; 13(11):736. https://doi.org/10.3390/axioms13110736
Chicago/Turabian StyleBao, Yanling, and Shumin Cheng. 2024. "A Heuristic Attribute-Reduction Algorithm Based on Conditional Entropy for Incomplete Information Systems" Axioms 13, no. 11: 736. https://doi.org/10.3390/axioms13110736
APA StyleBao, Y., & Cheng, S. (2024). A Heuristic Attribute-Reduction Algorithm Based on Conditional Entropy for Incomplete Information Systems. Axioms, 13(11), 736. https://doi.org/10.3390/axioms13110736






