Starlikeness and Convexity of Generalized Bessel-Maitland Function

Abstract

The main objective of this research is to examine a specific sufficiency criteria for the starlikeness and convexity of order $\delta$, k-uniform starlikeness, k-uniform convexity, lemniscate starlikeness and convexity, exponential starlikeness and convexity, uniform convexity of the Generalized Bessel-Maitland function. Applications of these conclusions to the concept of corollaries are also provided. Additionally, an illustrated representation of these outcomes will be presented. So functional inequalities involving gamma function will be the main research tools of this exploration. The outcomes from this study generalize a number of conclusions from earlier studies.

1. Introduction

Generalized hypergeometric functions (series) and their contribution to geometric function theory has been recognized for decades, especially because of de Branges’ response to the Bieberbach problem. Function theory has encountered a renewed interest over the past few decades due to surprising applications of this family of functions. Geometric Characteristics of various hypergeometric functions have been extensively studied [1,2,3,4,5,6], particularly for Gaussian, Kummer, and generalized hypergeometric functions. Numerous researchers [7,8,9] have established sufficient criteria for hypergeometric functions such that these functions are convex, starlike, and close-to-convex functions. For the study of the convexity, starlikeness, and local univalence of particular hypergeometric functions, Miller and Mocanu [2] utilized the differential subordinations approach. Along with presenting various expansions of Miller and Mocanu’s results, Ponnusamy and Vuorinen [5,6] further described the conditions under which Kummer and Gaussian hypergeometric functions are close to convex. The same method has recently been used by other investigators to find further sufficient criteria for convexity and starlikeness for the Kummer and Gaussian hypergeometric functions [10,11].

Now, consider the Wright function, which is defined as

$${\mathcal{W}}_{v,s}\left(\zeta \right)=\sum _{u=0}^{\infty }{\displaystyle \frac{{\zeta }^u}{u!\Gamma (s+vu)}},v>-1,s\in \mathbb{C},$$

where $\Gamma$ is the symbol for the Gamma function. A representation of the Wright function ${\mathcal{W}}_{v,s}$ in terms of the more widely known generalized hypergeometric function may be found in ([12], Section 2.1) in case of v to be a positive rational number. To be more precise, the functions ${\mathcal{W}}_{1,𝓁+1}\left({\displaystyle \frac{-{\zeta }^2}{4}}\right)$ are defined in terms of the Bessel functions ([13], p. 40), ${\mathcal{J}}_{𝓁}$, for $v=1\mathrm{and}s=𝓁+1$ as

$${\mathcal{J}}_{𝓁}\left(\zeta \right)={\left({\displaystyle \frac{\zeta }{2}}\right)}^{𝓁}{\mathcal{W}}_{1,𝓁+1}\left({\displaystyle \frac{-{\zeta }^2}{4}}\right)=\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^u}{u!\Gamma (u+𝓁+1)}}{\left({\displaystyle \frac{\zeta }{2}}\right)}^{2u+𝓁}\forall \zeta \in \mathbb{C},$$

which satisfies the second-order differential equation ([13], p. 38) also known as Bessel’s equation given as

$$z^2{w}^{″}\left(z\right)+z{w}^{\prime }\left(z\right)+(z^2-{𝓁}^2)w\left(z\right)=0,$$

(1)

where ℓ is any real (or complex) number. Also, when we change the coefficient of w in (1), we get

$$z^2{w}^{″}\left(z\right)+z{w}^{\prime }\left(z\right)-(z^2+{𝓁}^2)w\left(z\right)=0.$$

It appears frequently in mathematical physics problems. The Bessel function of the first kind of order ℓ, which is its particular solution, is expressed as

$${\mathcal{I}}_{𝓁}\left(\zeta \right)=\sum _{u=0}^{\infty }{\displaystyle \frac{1}{u!\Gamma (u+𝓁+1)}}{\left({\displaystyle \frac{\zeta }{2}}\right)}^{2u+𝓁}\forall \zeta \in \mathbb{C}.$$

Moreover, when we change the coefficient of $w^{\prime }$ and w, we have

$$z^2{w}^{″}\left(z\right)+2z{w}^{\prime }\left(z\right)+[z^2-𝓁(𝓁+1))]w\left(z\right)=0.$$

It is known as the spherical Bessel equation. The spherical Bessel function of the first kind of order ℓ, which is its particular solution, is defined by

$${\mathcal{S}}_{𝓁}\left(\zeta \right)=\sum _{u=0}^{\infty }{\displaystyle \frac{{(-1)}^u}{u!\Gamma \left(u+𝓁+\frac{3}{2}\right)}}{\left({\displaystyle \frac{\zeta }{2}}\right)}^{2u+𝓁}\forall \zeta \in \mathbb{C}.$$

In many areas of applied mathematics and engineering sciences, Bessel functions of the first kind are fundamental. Bessel functions are the subject of an extensive array of literature and have been the subject of several scientific investigations into their properties. Furthermore, the function

$${\mathcal{W}}_{v,𝓁+1}(-\zeta )={\mathcal{J}}_{𝓁}^{v}v>0,𝓁>-1$$

is referred to as the Bessel-Maitland function, which is also known as the generalized Bessel function (see [14]). Its series representation is given by the relation

$${\mathcal{J}}_{𝓁}^v\left(\zeta \right)=\sum _{u=0}^{\infty }{\displaystyle \frac{{(-\zeta )}^u}{u!\Gamma (vu+1+𝓁)}}.$$

The generalized Bessel-Maitland function ${\mathcal{J}}_{𝓁,b}^v\left(\zeta \right)$ is defined as

$${\mathcal{J}}_{𝓁,b}^v\left(\zeta \right)=\sum _{u=0}^{\infty }{\displaystyle \frac{{(-b)}^u}{u!\Gamma (vu+𝓁+1)}}{\zeta }^{u}b\in \mathbb{C}-\left\{0\right\},v>0,𝓁>-1\mathrm{and}\zeta \in \mathcal{D}.$$

Certain properties of a newly proposed integral with a generalised Bessel-Maitland kernel are examined in [15]. In [16], an additional intriguing method for approaching the generalized Bessel-Maitland function is suggested. This new study establishes the integral representation of the function by the use of the residue theorem, the beta function representation, the Gauss multiplication theorem, and the Mellin-Barnes representation.

Let $\mathcal{D}=\{\zeta \in \mathbb{C}:|\zeta |<1\}$ be an open unit disk and $\mathcal{H}$ be the class of all analytic functions in $\mathcal{D}$. Likewise, let $\mathcal{A}$ be the class of normalized analytic functions f in $\mathcal{D}$ such that $f\left(0\right)=f^{\prime }\left(0\right)-1=0$. For any $f\in \mathcal{A}$, the Maclaurin’s series expansion has the form

$$f\left(\zeta \right)=\zeta +\sum _{u\ge 2}{a}_u{\zeta }^u,\zeta \in \mathcal{D}.$$

Additionally, the class of functions inside the open unit disc $\mathcal{D}$ which are both univalent and analytic is denoted by $\mathcal{S}$ class. Let us assume that there are two functions $p,q\in \mathcal{H}$. If a function $w\in \mathcal{H}$ with $\left|w\right(\zeta \left)\right|<\left|\zeta \right|,\zeta \in \mathcal{D}$ exists such that $p\left(\zeta \right)=q\left(w\right(\zeta \left)\right)$ in $\mathcal{D}$, then p is subordinated by q and written as $p\left(\zeta \right)\prec q\left(\zeta \right)$. Furthermore, $p\left(\zeta \right)\prec q\left(\zeta \right)$ if q is univalent in $\mathcal{D}$, provided that $p\left(0\right)=q\left(0\right)\mathrm{and}p\left(\mathcal{D}\right)\subset q\left(\mathcal{D}\right)$.

A domain $\Delta \mathrm{in}\mathbb{C}$ is said to be starlike with respect to the point ${\zeta }_0$ if the line segment joining ${\zeta }_0$ to any other point $\zeta$ in $\Delta$, remains in $\Delta$. If $f(\Delta )$ is starlike, then the function $f\in \mathcal{A}$ is considered as starlike. The following is its analytical representation

$${\mathcal{S}}^{*}=\left\{f:f\in \mathcal{A},\Re \left({\displaystyle \frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}}\right)>0,\zeta \in \mathcal{D}\right\}.$$

The class ${\mathcal{S}}^{*}$ is a subclass of $\mathcal{S}$, see ([17], Theorem 2.1.1). Similarly for $\delta \in [0,1)$, the class

$${\mathcal{S}}^{*}\left(\delta \right)=\left\{f:f\in \mathcal{A},\Re \left({\displaystyle \frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}}\right)>\delta ,\zeta \in \mathcal{D}\right\}$$

is known as the class of starlike functions of order $\delta$. A domain $\Delta \mathrm{in}\mathbb{C}$ is said to be convex if it is starlike with respect to each point in $\Delta$. If $f(\Delta )$ is convex, then a function $f\in \mathcal{A}$ is considered as convex. The following is its analytical representation

$$\mathcal{C}=\left\{f:f\in \mathcal{A},\Re \left(1+{\displaystyle \frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}}\right)>0,\zeta \in \mathcal{D}\right\}.$$

The class $\mathcal{C}$ is a subclass of $\mathcal{S}$, see ([17], Theorem 2.1.2). Similarly for $\delta \in [0,1)$, the class

$$\mathcal{C}\left(\delta \right)=\left\{f:f\in \mathcal{A},\Re \left(1+{\displaystyle \frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}}\right)>\delta ,\zeta \in \mathcal{D}\right\}$$

is known as a family of convex functions with order $\delta$. Geometrically $f\in {\mathcal{S}}^{*}\left(\delta \right)\left(\mathcal{C}\left(\delta \right)\right)$ if the function $\mathcal{SV}=\zeta {\displaystyle \frac{f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}}\left(\mathcal{CV}=1+\zeta {\displaystyle \frac{f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}}\right)$ maps $\mathcal{D}$ in the right half plane such that $\Re SV>\delta \left(\Re CV>\delta \right)$.

Wisniowska and Kanas [18] established the class $k-\mathcal{UCV}$ of k-uniformly convex functions, if the image of any circular arc of a function $f\in \mathcal{A}$ remains in $\mathcal{D}$, with center $\zeta$, where $\left|\zeta \right|\le k$, is convex. They also gave the single variable criteria for functions in the class $k-\mathcal{UCV}$. Assume that $k\in [0,\infty )$ and $f\in \mathcal{A}$ then it is k-uniformly convex if and only if

$$\Re \left(1+{\displaystyle \frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}}\right)>k\left|{\displaystyle \frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}}\right|\mathrm{for}\zeta \in \mathcal{D}.$$

We see that $0-\mathcal{UCV}=\mathcal{C}$ and $1-\mathcal{UCV}=\mathcal{UCV}$ is the class of uniformly convex functions, [19]. The class $k-\mathcal{ST}$ of k-uniformly starlike function was introduced by Kanas and Wisniowska in [20]. A function $f\in \mathcal{A}$ is in $k-\mathcal{ST}$ if and only if

$$\Re \left({\displaystyle \frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}}\right)>k\left|{\displaystyle \frac{\zeta f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}}-1\right|\mathrm{for}0\le k<\infty ,\zeta \in \mathcal{D}.$$

Here $0-\mathcal{ST}$= ${\mathcal{S}}^{*}$. The class ${\mathcal{S}}_p$ can be obtained by taking $k=1$, in $k-\mathcal{ST}$ which was studied by Rønning, see [21]. The class $k-\mathcal{ST}(k-\mathcal{UCV})$ can be defined geometrically as $f\in k-\mathcal{ST}(f\in k-\mathcal{UCV})$ if ${\mathcal{SQ}}_f\left(\mathcal{D}\right)\left({\mathcal{CQ}}_f\left(\mathcal{D}\right)\right)$ is contained in the conic domain ${\Omega }_k$, where ${\mathcal{SQ}}_f\left(\zeta \right)=\zeta {\displaystyle \frac{f^{\prime }\left(\zeta \right)}{f\left(\zeta \right)}}\left({\mathcal{CQ}}_f\left(\zeta \right)=1+\zeta {\displaystyle \frac{f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}}\right)$ with $1\in {\Omega }_k$ and ${\Omega }_k$ bounded by the curve which is given by

$$\partial {\Omega }_k=\left\{\omega =u+iv\in \mathbb{C}:u^2>k^2{(u-1)}^2+k^2{v}^2\right\},k\in [0,\infty ).$$

Therefore ${\Omega }_k$ gives the plane on right when $k=0$; a parabolic region for $k=1$; it gives hyperbolic regions (right branch) for $0<k<1$; and elliptic regions when $k>1$. Thus the functions ${\mathcal{SQ}}_f\left(\zeta \right)\left({\mathcal{CQ}}_f\left(\zeta \right)\right)$ map $\mathcal{D}$ onto the right half plane, hyperbolic regions (right branch, a parabolic region and elliptic regions when for particular values of k. The classes ${\mathcal{S}}_e^{*}$ and ${\mathcal{S}}_{\mathcal{L}}^{*}$ are related to exponential functions and lemniscate of Bernoulli respectively, see [22,23]. These subclasses are linked with a domain which is symmetric with respect to the real axis. By using ${\mathcal{SQ}}_f$ and ${\mathcal{CQ}}_f$ further define these classes. If $\left\{{\mathcal{SQ}}_f\left(\zeta \right):\left|\zeta \right|<1\right\}\left(\left\{{\mathcal{CQ}}_f\left(\zeta \right):\left|\zeta \right|<1\right\}\right)$ are situated inside the region that the right half of Bernoulli’s lemniscate given by

$$\mathcal{L}=\left\{\omega \in \mathbb{C}:\Re \left(\omega \right)>0,\left|{\omega }^2-1\right|=1\right\},$$

then a function $f\in \mathcal{A}$ belongs to ${\mathcal{S}}_{\mathcal{L}}^{*}\left({\mathcal{C}}_{\mathcal{L}}\right)$ and known as classes of starlike(convex) functions related with Bernoulli’s lemniscate. The convex and star-like functions related to exponential functions are represented by ${\mathcal{S}}_e^{*}$ and ${\mathcal{C}}_e^{*}$. These are given as follows:

$${\mathcal{S}}_e^{*}=\left\{f\in \mathcal{A}:{\mathcal{SQ}}_f\left(\mathcal{D}\right)\subset \Theta \right\}\mathrm{and}{\mathcal{C}}_e=\left\{f\in \mathcal{A}:{\mathcal{CQ}}_f\left(\mathcal{D}\right)\subset \Theta \right\},$$

where $\Theta =\left\{exp\left(\zeta \right):\zeta \in \mathcal{D}\right\}$. The symmetry of the domains $\mathcal{L}$ and $\Theta$ are readily apparent [24].

The function ${\mathcal{J}}_{𝓁,b}^v\left(\zeta \right)$ does not belongs to class $\mathcal{A}$. Thus, consider a normalized function ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)$ such that ${\mathbb{J}}_{𝓁,b}^v\left(0\right)={{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(0\right)-1=0$ and of the form

$${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)=\zeta +\sum _{u=1}^{\infty }{\displaystyle \frac{{(-b)}^u\Gamma (1+𝓁)}{u!\Gamma (vu+1+𝓁)}}{\zeta }^{u+1}.$$

Recently, Soni and Bansal [25] have studied starlikeness and convexity of ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)$ in $\mathcal{D}$ by restricting $𝓁,b\mathrm{and}v$ to be real numbers. For some geometric properties of ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)$ and its related functions, we refer [26,27,28]. In this paper, we study starlikeness and convexity with respect to some symmetrical domain in $\mathcal{D}$.

2. Relevant Lemmas

Now we include a few lemmas that are helpful in demonstrating the main results in this section.

Lemma 1 

([29]). If $f\in \mathcal{A}$ and satisfies $\left|{\displaystyle \frac{\zeta f^{″}\left(\zeta \right)}{f^{\prime }\left(\zeta \right)}}\right|<{\displaystyle \frac{1}{2}}$, then $f\in \mathcal{UCV}.$

Lemma 2 

([30]). Let $t\in \mathbb{R},t>1$, the function $\psi \left(t\right)={\displaystyle \frac{{\Gamma }^{\prime }\left(t\right)}{\Gamma \left(t\right)}}$ known as digamma function satisfies the relation:

$$\mathit{log}\left(t\right)-\gamma \le \psi \left(t\right)\le \mathit{log}\left(t\right),$$

where Γ and γ are gamma and Euler-Mascheroni constant.

Lemma 3 

([20]). Let $f\in \mathcal{A}$ with $f\left(z\right)=z+{\sum }_{u=2}^{\infty }{a}_u{z}^u$. If

$$\sum _{u=2}^{\infty }(u+k(u-1))\left|a_u\right|<1,\mathit{for}\mathit{some}0\le k<\infty ,$$

then $f\in k-\mathcal{ST}.$

Lemma 4 

([18]). Let $f\in \mathcal{A}$ with $f\left(z\right)=z+{\sum }_{u=2}^{\infty }{a}_u{z}^u$. If

$$\sum _{u=2}^{\infty }\left(u(u-1)\right)\left|a_u\right|<{\displaystyle \frac{1}{k+2}},\mathit{for}\mathit{some}0\le k<\infty ,$$

then $f\in k-\mathcal{UCV}.$

3. Main Results

Now we derive sufficient conditions on parameters such that the generalized Bessel Maitland function ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)$ is starlike, convex of order $\delta$ and uniformly convexity. Furthermore, we provide examples and their mappings under $\mathcal{D}$ which confirm the assertions of our results.

Theorem 1. 

Let $𝓁\ge 0$ and $v>0$ and $\left|b\right|<{\displaystyle \frac{(1+𝓁)(2+𝓁)}{9𝓁+17}}.$ Then ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in \mathcal{UCV}$.

Proof. 

Now,

$$\left|{{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)\right|=\left|\sum _{u=1}^{\infty }{\displaystyle \frac{{(-b)}^u\Gamma (1+𝓁)u(u+1)}{u!\Gamma (vu+1+𝓁)}}{\zeta }^{u-1}\right|\le \sum _{u=1}^{\infty }{\displaystyle \frac{{\left|b\right|}^u\Gamma (1+𝓁)(u^2+u)}{u!\Gamma (vu+1+𝓁)}}.$$

By using

$${\displaystyle \frac{\Gamma (1+𝓁)}{\Gamma (vu+1+𝓁)}}\le {\displaystyle \frac{1}{(1+𝓁)(2+𝓁)\cdots (u+𝓁)}}\forall u\in \mathbb{N},$$

we have

$$\left|{{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)\right|\le \sum _{u=1}^{\infty }{\displaystyle \frac{{\left|b\right|}^u(u^2+u)}{u!(1+𝓁)(2+𝓁)\cdots (u+𝓁)}}.$$

So, by using the inequality $3u!{(2+𝓁)}_u>(u^2+u){(2+𝓁)}^u,$ we can write

$$\begin{array}{ccc}\hfill \left|{{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)\right|& <& {\displaystyle \frac{3\left|b\right|}{1+𝓁}}\sum _{u=0}^{\infty }{\left({\displaystyle \frac{\left|b\right|}{2+𝓁}}\right)}^u\hfill \\ & =& {\displaystyle \frac{3\left|b\right|(2+𝓁)}{(1+𝓁)(2+𝓁-\left|b\right|)}}.\hfill \end{array}$$

Thus,

$$\left|{{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)\right|<{\displaystyle \frac{3\left|b\right|(2+𝓁)}{(1+𝓁)(2+𝓁-\left|b\right|)}}.$$

(2)

Also,

$$\left|{\displaystyle \frac{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}{\zeta }}\right|\ge 1-\left|\sum _{u=1}^{\infty }{\displaystyle \frac{{(-b)}^u\Gamma (1+𝓁)(u+1){\zeta }^{u-1}}{u!\Gamma (vu+1+𝓁)}}\right|\ge 1-\sum _{u=1}^{\infty }{\displaystyle \frac{{\left|b\right|}^u\Gamma (1+𝓁)(u+1)}{u!\Gamma (vu+1+𝓁)}}.$$

Again by using

$${\displaystyle \frac{\Gamma (1+𝓁)}{\Gamma (vu+1+𝓁)}}\le {\displaystyle \frac{1}{(1+𝓁)(2+𝓁)\cdots (u+𝓁)}}\forall u\in \mathbb{N},$$

we have

$$\left|{\displaystyle \frac{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}{\zeta }}\right|\ge 1-\sum _{u=1}^{\infty }{\displaystyle \frac{{\left|b\right|}^u(u+1)}{u!(1+𝓁)(2+𝓁)\cdots (u+𝓁)}}.$$

Also from the inequality $2u!{(2+𝓁)}_u>(u+1){(2+𝓁)}^u,$ we have

$$\begin{array}{ccc}\hfill \left|{\displaystyle \frac{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}{\zeta }}\right|& >& 1-{\displaystyle \frac{2\left|b\right|}{1+𝓁}}\sum _{u=0}^{\infty }{\left({\displaystyle \frac{\left|b\right|}{2+𝓁}}\right)}^u\hfill \\ & =& {\displaystyle \frac{(1+𝓁)(2+𝓁-\left|b\right|)-2\left|b\right|(2+𝓁)}{(1+𝓁)(2+𝓁-\left|b\right|)}}.\hfill \end{array}$$

Thus,

$$\left|{\displaystyle \frac{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}{\zeta }}\right|>{\displaystyle \frac{(1+𝓁)(2+𝓁-\left|b\right|)-2\left|b\right|(2+𝓁)}{(1+𝓁)(2+𝓁-\left|b\right|)}}.$$

(3)

Now, by using (2) and (3), we get

$$\begin{array}{ccc}\hfill \left|{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right|& <& {\displaystyle \frac{3\left|b\right|(2+𝓁)}{(1+𝓁)(2+𝓁-\left|b\right|)-2\left|b\right|(2+𝓁)}}\hfill \\ & =& {\displaystyle \frac{3\left|b\right|(2+𝓁)}{(1+𝓁)(2+𝓁)-\left|b\right|(3t+5)}}.\hfill \end{array}$$

So,

$$\left|{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right|<{\displaystyle \frac{3\left|b\right|(2+𝓁)}{(1+𝓁)(2+𝓁)-\left|b\right|(3t+5)}}.$$

By using Lemma 1, we have

$$\left|{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right|<{\displaystyle \frac{1}{2}},$$

if

$$\left|b\right|<{\displaystyle \frac{(1+𝓁)(2+𝓁)}{9𝓁+17}}.$$

□

Example 1. 

(i) The function ${\mathbb{J}}_{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{8}}}^{{\displaystyle \frac{1}{4}}}\left(\zeta \right)\in \mathcal{UCV}.$

(ii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{5}{2}},{\displaystyle \frac{-1}{7}}}^{{\displaystyle \frac{2}{3}}}\left(\zeta \right)\in \mathcal{UCV}.$

(iii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{2}{3}},{\displaystyle \frac{2}{15}}}^{{\displaystyle \frac{3}{4}}}\left(\zeta \right)\in \mathcal{UCV}.$

(iv) 

The function ${\mathbb{J}}_{{\displaystyle \frac{3}{4}},{\displaystyle \frac{-1}{18}}}^{{\displaystyle \frac{5}{6}}}\left(\zeta \right)\in \mathcal{UCV}.$

(v) 

The function ${\mathbb{J}}_{0,{\displaystyle \frac{2}{19}}}^{{\displaystyle \frac{2}{5}}}\left(\zeta \right)\in \mathcal{UCV}.$

Theorem 2. 

Assume that $𝓁\ge 0,v>0\mathit{and}b\in \mathbb{C}-\left\{0\right\}$, and let

(a) 

$e^{1+\gamma (1+v)}<2{(v+1+𝓁)}^v,$

(b) 

$\left|b\right|(2-\delta )\Gamma (1+𝓁)<(1-\left|b\right|)(1-\delta )\Gamma (v+1+𝓁),$

then ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in {\mathcal{S}}^{*}\left(\delta \right).$

Proof. 

To prove the necessary outcome, it needs to demonstrate that

$$\left|{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}}-1\right|=\left|{\displaystyle \frac{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)-\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}{\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}}\right|<1-\delta (\forall \zeta \in \mathcal{D}).$$

Now,

$$\left|{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)-{\displaystyle \frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}\right|=\left|\sum _{u=1}^{\infty }{\displaystyle \frac{u{(-b)}^u\Gamma (1+𝓁)}{u!\Gamma (vu+1+𝓁)}}{\zeta }^u\right|<\Gamma (1+𝓁)\sum _{u=1}^{\infty }{d}_u(𝓁,v){\left|b\right|}^u,$$

(4)

where

$$d_u=d_u(𝓁,v)={\displaystyle \frac{u}{u!\Gamma (vu+1+𝓁)}},u\in \mathbb{N}.$$

The function ${\mathcal{D}}_1:[1,\infty )\to \mathbb{R}$ now can be defined as

$${\mathcal{D}}_1\left(r\right)={\displaystyle \frac{r}{r!\Gamma (vr+1+𝓁)}},r\in [1,\infty ).$$

Therefore,

$${{\mathcal{D}}_1}^{\prime }\left(r\right)={\mathcal{D}}_1\left(r\right){\mathcal{D}}_2\left(r\right),$$

where ${\mathcal{D}}_2\left(r\right)$ is provided below

$${\mathcal{D}}_2\left(r\right)={\displaystyle \frac{1}{r}}-\psi (r+1)-v\psi (vr+1+𝓁),r\in [1,\infty ).$$

From Lemma 2, we obtain

$${\mathcal{D}}_2\left(r\right)\le {\displaystyle \frac{1}{r}}-\mathit{log}(r+1)-v\mathit{log}(vr+1+𝓁)+\gamma (1+v)={\mathcal{D}}_3\left(r\right),r\in [1,\infty ).$$

This leads to

$${{\mathcal{D}}_3}^{\prime }\left(r\right)=-{\displaystyle \frac{1}{r^2}}-{\displaystyle \frac{1}{r+1}}-{\displaystyle \frac{v^2}{vr+1+𝓁}}<0,r\in [1,\infty ).$$

It means that on $[1,\infty )$, ${\mathcal{D}}_3\left(r\right)$ is decreasing. Additionally, ${\mathcal{D}}_3\left(1\right)<0$ under the stated hypothesis (a) and therefore, ${{\mathcal{D}}_1}^{\prime }\left(r\right)<0$ for $r\in [1,\infty )$.

As a result, the above mentioned sequence ${\left\{d_u\right\}}_{u\ge 1}$ is decreasing. Therefore (4) gives us

$$\begin{array}{ccc}\hfill \left|{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)-{\displaystyle \frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}\right|& <& \Gamma (1+𝓁)\sum _{u=1}^{\infty }{d}_1(𝓁,v){\left|b\right|}^u\hfill \\ & =& \Gamma (1+𝓁)d_1(𝓁,v)\sum _{u=1}^{\infty }{\left|b\right|}^u\hfill \\ & =& {\displaystyle \frac{\Gamma (1+𝓁)\left|b\right|d_1(𝓁,v)}{1-\left|b\right|}},(\forall \zeta \in \mathcal{D}).\hfill \end{array}$$

(5)

Now,

$$\begin{array}{ccc}\hfill \left|{\displaystyle \frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}\right|& \ge & 1-\left|\sum _{u=1}^{\infty }{\displaystyle \frac{{(-a)}^u\Gamma (1+𝓁)}{u!\Gamma (vu+1+𝓁)}}{\zeta }^u\right|\hfill \\ & \ge & 1-\sum _{u=1}^{\infty }{s}_u(𝓁,v){\left|b\right|}^u,(\forall \zeta \in \mathcal{D}),\hfill \end{array}$$

(6)

where

$$s_u=s_u(𝓁,v)={\displaystyle \frac{\Gamma (1+𝓁)}{u!\Gamma (vu+1+𝓁)}}.$$

In the same way, ${\left\{s_u\right\}}_{u\ge 1}$ can be demonstrated to represent a decreasing sequence. Consequently, using (6), we have

$$\left|{\displaystyle \frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}\right|\ge 1-\sum _{u=1}^{\infty }{s}_1(𝓁,v){\left|b\right|}^u=1-{\displaystyle \frac{s_1(𝓁,v)\left|b\right|}{1-\left|b\right|}},(\forall \zeta \in \mathcal{D}).$$

(7)

Combining (5) and (7), we have

$$\left|{\displaystyle \frac{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)-\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}{\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}}\right|<{\displaystyle \frac{\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)-\Gamma (1+𝓁)\left|b\right|}}.$$

The following is true based on hypothesis (b):

$${\displaystyle \frac{\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)-\Gamma (1+𝓁)\left|b\right|}}<1-\delta .$$

Hence, the theorem is proved. □

Example 2. 

(i) The function ${\mathbb{J}}_{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}}}^2\left(\zeta \right)\in {\mathcal{S}}^{*}\left(\delta \right),0\le \delta <{\delta }_0,{\delta }_0={\displaystyle \frac{7}{11}}$.

(ii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{-1}{2}}}^3\left(\zeta \right)\in {\mathcal{S}}^{*}\left(\delta \right),0\le \delta <{\delta }_1,{\delta }_1={\displaystyle \frac{299}{307}}$.

(iii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{4}{3}},{\displaystyle \frac{1}{4}}}^{{\displaystyle \frac{3}{2}}}\left(\zeta \right)\in {\mathcal{S}}^{*}\left(\delta \right),0\le \delta <{\delta }_2,{\delta }_2\approx 0.9115946$.

(iv) 

The function ${\mathbb{J}}_{{\displaystyle \frac{5}{3}},{\displaystyle \frac{1}{5}}}^{{\displaystyle \frac{4}{3}}}\left(\zeta \right)\in {\mathcal{S}}^{*}\left(\delta \right),0\le \delta <{\delta }_3,{\delta }_3\approx 0.9331164$.

(v) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{4}},{\displaystyle \frac{1}{3}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)\in {\mathcal{S}}^{*}\left(\delta \right),0\le \delta <{\delta }_4,{\delta }_4\approx 0.8858371$.

Theorem 3. 

Assume that $𝓁\ge 0,v>0\mathit{and}b\in \mathbb{C}-\left\{0\right\}$, and let

(a) 

$e^{{\displaystyle \frac{3}{2}}+\gamma (1+u)}<2{(v+1+𝓁)}^v,$

(b) 

$\left|b\right|(2-\delta )\Gamma (1+𝓁)<(1-\left|b\right|)(1-\delta )\Gamma (v+1+𝓁),$

then ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in \mathcal{C}\left(\delta \right).$

Proof. 

Certainly, if we shall demonstrate the following we are done. That is

$$\left|{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right|<1-\delta (\forall \zeta \in \mathcal{D}).$$

Now,

$$\left|\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)\right|=\left|\sum _{u=1}^{\infty }{\displaystyle \frac{u(u+1){(-b)}^u\Gamma (1+𝓁)}{u!\Gamma (vu+1+𝓁)}}{\zeta }^u\right|<\Gamma (1+𝓁)\sum _{u=1}^{\infty }{h}_u(𝓁,v){\left|b\right|}^u,$$

(8)

where

$$h_u=h_u(𝓁,v)={\displaystyle \frac{u(u+1)}{u!\Gamma (vu+1+𝓁)}},u\in \mathbb{N}.$$

Now, the function ${\mathcal{H}}_1:[1,\infty )\to \mathbb{R}$ can be considered as

$${\mathcal{H}}_1\left(r\right)={\displaystyle \frac{r(r+1)}{r!\Gamma (vr+1+𝓁)}},r\in [1,\infty ).$$

Therefore,

$${{\mathcal{H}}_1}^{\prime }\left(r\right)={\mathcal{H}}_1\left(r\right){\mathcal{H}}_2\left(r\right),$$

where ${\mathcal{H}}_2\left(r\right)$ is given by

$${\mathcal{H}}_2\left(r\right)={\displaystyle \frac{2r+1}{r(r+1)}}-\psi (r+1)-v\psi (vr+1+𝓁),r\in [1,\infty ).$$

From Lemma 2, we obtain

$${\mathcal{H}}_2\left(r\right)\le {\displaystyle \frac{2r+1}{r(r+1)}}-\mathit{log}(r+1)-v\mathit{log}(vr+1+𝓁)+\gamma (1+v)={\mathcal{H}}_3\left(r\right),r\in [1,\infty ).$$

This leads to

$${{\mathcal{H}}_3}^{\prime }\left(r\right)=-{\displaystyle \frac{2r^2+2r+1}{r^2{(r+1)}^2}}-{\displaystyle \frac{1}{r+1}}-{\displaystyle \frac{v^2}{vr+1+𝓁}}<0,r\in [1,\infty ).$$

It means that on $[1,\infty )$, ${\mathcal{H}}_3\left(r\right)$ is decreasing. Additionally, ${\mathcal{H}}_3\left(1\right)<0$ under the stated hypothesis (a) and therefore, ${{\mathcal{H}}_1}^{\prime }\left(r\right)<0$ for $r\in [1,\infty )$. As a result, the above mentioned sequence ${\left\{h_u\right\}}_{u\ge 1}$ is decreasing. Therefore (8) gives us

$$\begin{array}{ccc}\hfill \left|\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)\right|& <& \Gamma (1+𝓁)\sum _{u=1}^{\infty }{h}_1(𝓁,v){\left|b\right|}^u\hfill \\ & =& \Gamma (1+𝓁)h_1(𝓁,v)\sum _{u=1}^{\infty }{\left|b\right|}^u\hfill \\ & =& {\displaystyle \frac{\Gamma (1+𝓁)\left|b\right|h_1(𝓁,v)}{1-\left|b\right|}},(\forall \zeta \in \mathcal{D}).\hfill \end{array}$$

(9)

Now,

$$\left|{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)\right|\ge 1-\sum _{u=1}^{\infty }{j}_u(𝓁,v){\left|b\right|}^u,(\forall \zeta \in \mathcal{D}),$$

(10)

where

$$j_u=j_u(𝓁,v)={\displaystyle \frac{(u+1)\Gamma (1+𝓁)}{u!\Gamma (vu+1+𝓁)}}.$$

In the same way, ${\left\{j_u\right\}}_{u\ge 1}$ can be demonstrated to represent a decreasing sequence. Consequently, using (10), we have

$$\left|{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)\right|\ge 1-\sum _{u=1}^{\infty }{j}_1(𝓁,v){\left|b\right|}^u=1-{\displaystyle \frac{j_1(𝓁,v)\left|b\right|}{1-\left|b\right|}},(\forall \zeta \in \mathcal{D}).$$

(11)

Combining (9) and (11), we have

$$\left|{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right|<{\displaystyle \frac{2\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)-2\Gamma (1+𝓁)\left|b\right|}}.$$

(12)

Thus hypothesis (b) completes the proof. □

Example 3. 

(i) The function ${\mathbb{J}}_{{\displaystyle \frac{4}{3}},{\displaystyle \frac{1}{3}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)\in \mathcal{C}\left(\delta \right),0\le \delta <{\delta }_0,{\delta }_0\approx 0.9671730$.

(ii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{1}{4}}}^2\left(\zeta \right)\in \mathcal{C}\left(\delta \right),0\le \delta <{\delta }_1,{\delta }_1={\displaystyle \frac{97}{101}}$.

(iii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{5}}}^3\left(\zeta \right)\in \mathcal{C}\left(\delta \right),0\le \delta <{\delta }_2,{\delta }_2={\displaystyle \frac{101}{103}}$.

(iv) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{4}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)\in \mathcal{C}\left(\delta \right),0\le \delta <{\delta }_3,{\delta }_3\approx 0.9351295$.

(v) 

The function ${\mathbb{J}}_{2,{\displaystyle \frac{1}{3}}}^{{\displaystyle \frac{3}{2}}}\left(\zeta \right)\in \mathcal{C}\left(\delta \right),0\le \delta <{\delta }_4,{\delta }_4\approx 0.9059420$.

Figure 1 illustrates the mappings of functions ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)$ in $\mathcal{D}$ provided in Examples 2 and 3. We have included the first two cases of each example. The figure shows the mappings of these functions under $\mathcal{D}$. The first two figures show that the mappings are starlike concerning origin and the second two show that these are convex. These figures validate our results.

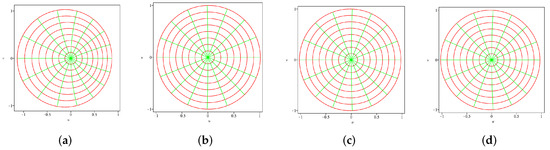
Figure 1. ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)$ mappings onto $\mathcal{D}$ given in Examples 2 (i,ii) and 3 (i,ii). (a) ${\mathbb{J}}_{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}}}^2\left(\zeta \right)$ mapping onto $\mathcal{D}$. (b) ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{-1}{2}}}^3\left(\zeta \right)$ mapping onto $\mathcal{D}$. (c) ${\mathbb{J}}_{{\displaystyle \frac{4}{3}},{\displaystyle \frac{1}{3}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)$ mapping onto $\mathcal{D}$. (d) ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{1}{4}}}^2\left(\zeta \right)$ mapping onto $\mathcal{D}$.

4. k-Uniformly Starlikeness and k-Uniform Convexity

Theorem 4. 

Assume that $𝓁\ge 0,v>0\mathit{and}b\in \mathbb{C}-\left\{0\right\}$, and let

(a) 

$e^{{\displaystyle \frac{k+1}{k+2}}+\gamma (1+v)}<2{(v+1+𝓁)}^v,$

(b) 

$\left|b\right|(2+k)\Gamma (1+𝓁)<(1-\left|b\right|)\Gamma (v+1+𝓁),$

then ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in k-\mathcal{ST}.$

Proof. 

By using Lemma 3, it is sufficient to demonstrate that the following inequality is true under the defined hypothesis:

$$\sum _{u=2}^{\infty }(u+k(u-1))\left|{\displaystyle \frac{{(-b)}^{u-1}\Gamma (1+𝓁)}{(u-1)!\Gamma (vu-v+1+𝓁)}}\right|<1,\mathrm{for}0\le k<\infty .$$

(13)

Let

$$y_u=y_u(𝓁,v)={\displaystyle \frac{u+k(u-1)}{(u-1)!\Gamma (vu-v+1+𝓁)}},2\le u<\infty ,$$

and consider the function ${\mathcal{Y}}_1:[2,\infty )\to \mathbb{R}$ can be defined as

$${\mathcal{Y}}_1\left(r\right)={\displaystyle \frac{r+k(r-1)}{(r-1)!\Gamma (vr-v+1+𝓁)}},r\in [2,\infty ).$$

Then

$${{\mathcal{Y}}_1}^{\prime }\left(r\right)={\mathcal{Y}}_1\left(r\right){\mathcal{Y}}_2\left(r\right),$$

(14)

where

$${\mathcal{Y}}_2\left(r\right)={\displaystyle \frac{k+1}{r+k(r-1)}}-\psi \left(r\right)-v\psi (vr-v+1+𝓁),r\in [2,\infty ).$$

Applying Lemma 2, we obtain

$${\mathcal{Y}}_2\left(r\right)\le {\displaystyle \frac{k+1}{r+k(r-1)}}-\mathit{log}\left(r\right)-v\mathit{log}(vr-v+1+𝓁)+\gamma (1+v)={\mathcal{Y}}_3\left(r\right),r\in [2,\infty ).$$

(15)

Thus, we have

$${{\mathcal{Y}}_3}^{\prime }\left(r\right)=-{\displaystyle \frac{{(k+1)}^2}{{(r+k(r-1))}^2}}-{\displaystyle \frac{1}{r}}-{\displaystyle \frac{v^2}{vr-v+1+𝓁}}<0,r\in [2,\infty ).$$

It follows that ${\mathcal{Y}}_3\left(r\right)$ is decreasing on $[2,\infty )$. Additionally, ${\mathcal{Y}}_3\left(2\right)<0$ under the stated hypothesis (a). So, ${\mathcal{Y}}_3\left(r\right)<0$ for $r\in [2,\infty )$. Therefore, the function ${\mathcal{Y}}_1\left(r\right)$ is decreasing with the help of (14) and (15). Hence, the above mentioned sequence ${\left\{y_u\right\}}_{u\ge 2}$ is decreasing. Therefore (13) gives us

$$\begin{array}{ccc}\hfill \sum _{u=2}^{\infty }(u+k(u-1))\left|{\displaystyle \frac{{(-b)}^{u-1}\Gamma (1+𝓁)}{(u-1)!\Gamma (vu-v+1+𝓁)}}\right|& =& \Gamma (1+𝓁)\sum _{u=2}^{\infty }{y}_u(𝓁,v){\left|b\right|}^{u-1}\hfill \\ & \le & {\displaystyle \frac{\Gamma (1+𝓁)y_2(𝓁,v)\left|b\right|}{1-\left|b\right|}}\hfill \\ & =& {\displaystyle \frac{\left|b\right|(2+k)\Gamma (1+𝓁)}{\Gamma (v+1+𝓁)(1-\left|b\right|)}},(\zeta \in \mathcal{D}).\hfill \end{array}$$

Finally, the desired result may be established by using the provided hypothesis (b). □

Example 4. 

(i) The function ${\mathbb{J}}_{1,{\displaystyle \frac{1}{4}}}^{{\displaystyle \frac{3}{2}}}\left(\zeta \right)\in k-\mathcal{ST}$ in $\mathcal{D}$.

(ii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{1}{2}}}^{{\displaystyle \frac{4}{3}}}\left(\zeta \right)\in k-\mathcal{ST}$ in $\mathcal{D}$.

(iii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{4}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)\in k-\mathcal{ST}$ in $\mathcal{D}$.

(iv) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{5}}}^3\left(\zeta \right)\in k-\mathcal{ST}$ in $\mathcal{D}$.

(v) 

The function ${\mathbb{J}}_{2,{\displaystyle \frac{2}{5}}}^1\left(\zeta \right)\in k-\mathcal{ST}$ in $\mathcal{D}$.

Theorem 5. 

Assume that $𝓁\ge 0,v>0\mathit{and}b\in \mathbb{C}-\left\{0\right\}$, and let

(a) 

$e^{3+\gamma (2+v)}<2{(v+1+𝓁)}^v,$

(b) 

$\left|b\right|(2+k)\Gamma (1+𝓁)<(1-\left|b\right|)\Gamma (v+1+𝓁),$

then ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in k-\mathcal{UCV}.$

Proof. 

By applying the Lemma 4, we demonstrate that

$$\sum _{u=2}^{\infty }u(u-1)\left|{\displaystyle \frac{{(-b)}^{u-1}\Gamma (1+𝓁)}{(u-1)!\Gamma (vu-v+1+𝓁)}}\right|<{\displaystyle \frac{1}{k+2}},\mathrm{for}0\le k<\infty .$$

(16)

Let

$$p_u=p_u(𝓁,v)={\displaystyle \frac{\Gamma (u+1)}{(u-1)!\Gamma (vu-v+1+𝓁)\Gamma (u-1)}},2\le u<\infty .$$

Now, the function ${\mathcal{P}}_1:[2,\infty )\to \mathbb{R}$ can be defined as

$${\mathcal{P}}_1\left(r\right)={\displaystyle \frac{\Gamma (r+1)}{(r-1)!\Gamma (vr-v+1+𝓁)\Gamma (r-1)}},r\in [2,\infty ).$$

By taking derivative, we have

$${{\mathcal{P}}_1}^{\prime }\left(r\right)={\mathcal{P}}_1\left(r\right){\mathcal{P}}_2\left(r\right),$$

(17)

where

$${\mathcal{P}}_2\left(r\right)=\psi (r+1)-\psi (r-1)-\psi \left(r\right)-v\psi (vr-v+1+𝓁),r\in [2,\infty ).$$

Again applying Lemma 2, we obtain

$${\mathcal{P}}_2\left(r\right)\le \mathit{log}(r+1)-\mathit{log}(r-1)-\mathit{log}\left(r\right)-v\mathit{log}(vr-v+1+𝓁)+\gamma (2+v)={\mathcal{Y}}_3\left(r\right),r\in [2,\infty ).$$

(18)

Thus, we have

$${{\mathcal{P}}_3}^{\prime }\left(r\right)=-{\displaystyle \frac{2}{{(r-1)}^2}}-{\displaystyle \frac{1}{r}}-{\displaystyle \frac{v^2}{vr-v+1+𝓁}}<0,r\in [2,\infty ).$$

It follows that ${\mathcal{P}}_3\left(r\right)$ is decreasing on $[2,\infty )$. Additionally, ${\mathcal{P}}_3\left(2\right)<0$ under the stated hypothesis (a). So, ${\mathcal{P}}_3\left(r\right)<0$ for $r\in [2,\infty )$. Together with (17) and (18), this implies that the function ${\mathcal{P}}_1\left(r\right)$ is decreasing. Therefore (16) gives

$$\begin{array}{ccc}\hfill \sum _{u=2}^{\infty }u(u-1)\left|{\displaystyle \frac{{(-b)}^{u-1}\Gamma (1+𝓁)}{(u-1)!\Gamma (vu-v+1+𝓁)}}\right|& =& \Gamma (1+𝓁)\sum _{u=2}^{\infty }{p}_u(𝓁,v){\left|b\right|}^{u-1}\hfill \\ & \le & {\displaystyle \frac{\Gamma (1+𝓁)p_2(𝓁,v)\left|b\right|}{1-\left|b\right|}}\hfill \\ & =& {\displaystyle \frac{2\left|b\right|(2+k)\Gamma (1+𝓁)}{\Gamma (v+1+𝓁)(1-\left|b\right|)}},(\forall \zeta \in \mathcal{D}).\hfill \end{array}$$

Finally, the desired result may be established by using the provided hypothesis (b). □

Example 5. 

(i) The function ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{1}{4}}}^2\left(\zeta \right)\in k-\mathcal{UCV}$ in $\mathcal{D}$.

(ii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{5}}}^3\left(\zeta \right)\in k-\mathcal{UCV}$ in $\mathcal{D}$.

(iii) 

The function ${\mathbb{J}}_{2,{\displaystyle \frac{1}{3}}}^{{\displaystyle \frac{3}{2}}}\left(\zeta \right)\in k-\mathcal{UCV}$ in $\mathcal{D}$.

(iv) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{3}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)\in k-\mathcal{UCV}$ in $\mathcal{D}$.

(v) 

The function ${\mathbb{J}}_{{\displaystyle \frac{4}{3}},{\displaystyle \frac{1}{6}}}^{{\displaystyle \frac{3}{2}}}\left(\zeta \right)\in k-\mathcal{UCV}$ in $\mathcal{D}$.

Figure 2 illustrates the mappings of ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)$ in $\mathcal{D}$ provided in Example 4 and 5.

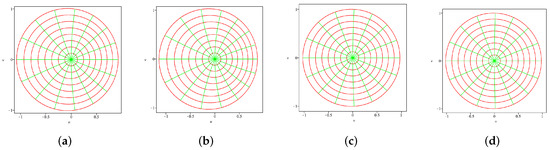
Figure 2. ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)$ mappings onto $\mathcal{D}$ given in Examples 4 (i,ii) and 5 (i,ii). (a) ${\mathbb{J}}_{1,{\displaystyle \frac{1}{4}}}^{{\displaystyle \frac{3}{2}}}\left(\zeta \right)$ mapping onto $\mathcal{D}$. (b) ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{1}{2}}}^{{\displaystyle \frac{4}{3}}}\left(\zeta \right)$ mapping onto $\mathcal{D}$. (c) ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{1}{4}}}^2\left(\zeta \right)$ mapping onto $\mathcal{D}$. (d) ${\mathbb{J}}_{{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{5}}}^3\left(\zeta \right)$ mapping onto $\mathcal{D}$.

5. Starlikeness and Convexity Associated with Exponential Function and Bernoulli Lemniscate

Theorem 6. 

Assume that $𝓁\ge 0,v>0\mathit{and}b\in \mathbb{C}-\left\{0\right\}$, and let

(a) 

$e^{1+(1+v)\gamma }<2{(v+1+𝓁)}^v,$

(b) 

$\left|b\right|(2e-1)\Gamma (1+𝓁)<(e-1)(1-\left|b\right|)\Gamma (v+1+𝓁),$

then ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in {\mathcal{S}}_e^{*}\mathit{in}\mathcal{D}.$

Proof. 

To establish that ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in {\mathcal{S}}_e^{*}$in$\mathcal{D}$, we have to show that by using a result due to [22]. That is

$$\left|{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}}-1\right|=\left|{\displaystyle \frac{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)-\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}{\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}}\right|<1-{\displaystyle \frac{1}{e}}.$$

Now using Theorem 2 for $\delta =0$, we obtain the required result. □

Example 6. 

(i) The function ${\mathbb{J}}_{{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{4}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)\in {\mathcal{S}}_e^{*}$in$\mathcal{D}$.

(ii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{5}{4}},{\displaystyle \frac{1}{3}}}^{{\displaystyle \frac{4}{3}}}\left(\zeta \right)\in {\mathcal{S}}_e^{*}$in$\mathcal{D}$.

(iii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{4}{3}},{\displaystyle \frac{1}{6}}}^{{\displaystyle \frac{3}{2}}}\left(\zeta \right)\in {\mathcal{S}}_e^{*}$in$\mathcal{D}$.

(iv) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{2}}}^2\left(\zeta \right)\in {\mathcal{S}}_e^{*}$in$\mathcal{D}$.

(v) 

The function ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{-1}{2}}}^3\left(\zeta \right)\in {\mathcal{S}}_e^{*}$in$\mathcal{D}$.

Theorem 7. 

Assume that $𝓁\ge 0,v>0\mathit{and}b\in \mathbb{C}-\left\{0\right\}$, and let

(a) 

$e^{{\displaystyle \frac{3}{2}}+(1+v)\gamma }<2{(v+1+𝓁)}^v,$

(b) 

$2\left|b\right|(2e-1)\Gamma (1+𝓁)<(e-1)(1-\left|b\right|)\Gamma (v+1+𝓁),$

then ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in {\mathcal{C}}_e\mathit{in}\mathcal{D}.$

Proof. 

To prove that ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in {\mathcal{C}}_e,$ we have to show that

$$\left|{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right|<1-{\displaystyle \frac{1}{e}}.$$

Now using Theorem 3 for $\delta =0$, we obtain the required result. □

Example 7. 

(i) The function ${\mathbb{J}}_{{\displaystyle \frac{4}{3}},{\displaystyle \frac{1}{3}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)\in {\mathcal{C}}_e$in$\mathcal{D}$.

(ii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{1}{4}}}^2\left(\zeta \right)\in {\mathcal{C}}_e$in$\mathcal{D}$.

(iii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{5}}}^3\left(\zeta \right)\in {\mathcal{C}}_e$in$\mathcal{D}$.

(iv) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{6}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)\in {\mathcal{C}}_e$in$\mathcal{D}$.

(v) 

The function ${\mathbb{J}}_{{\displaystyle \frac{5}{4}},{\displaystyle \frac{1}{2}}}^3\left(\zeta \right)\in {\mathcal{C}}_e$in$\mathcal{D}$.

Theorem 8. 

Assume that $𝓁\ge 0,v>0\mathit{and}b\in \mathbb{C}-\left\{0\right\}$, and let

(a) 

$e^{1+(1+v)\gamma }<2{(v+1+𝓁)}^v,$

(b) 

$${\displaystyle \frac{\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)}}\times \left({\displaystyle \frac{\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)}}+2\right)<{\displaystyle \frac{1}{2}},$$

then ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in {\mathcal{S}}_L^{*}\mathit{in}\mathcal{D}.$

Proof. 

It is sufficient to construct the following inequality to justify the outcome:

$$\left|{\left({\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right)}^2-1\right|={\displaystyle \frac{\left|{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)+\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }\right|\left|{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)-\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }\right|}{{\left|\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }\right|}^2}}<1.$$

(19)

After simple computation, we have

$$\left|{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)+{\displaystyle \frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}\right|<2+\sum _{u=1}^{\infty }\Gamma (1+𝓁)l_u(𝓁,v){\left|b\right|}^u,$$

(20)

where

$$l_u=l_u(𝓁,v)={\displaystyle \frac{u+2}{u!\Gamma (vu+1+𝓁)}},u\in \mathbb{N}.$$

Now, the function ${\mathcal{L}}_1:[1,\infty )\to \mathbb{R}$ can be defined as

$${\mathcal{L}}_1\left(r\right)={\displaystyle \frac{r+2}{r!\Gamma (vr+1+𝓁)}},r\in [1,\infty ).$$

Taking logarithmic differentiation

$${{\mathcal{L}}_1}^{\prime }\left(r\right)={\mathcal{L}}_1\left(r\right){\mathcal{L}}_2\left(r\right),$$

where ${\mathcal{L}}_2\left(r\right)$ is given by

$${\mathcal{L}}_2\left(r\right)={\displaystyle \frac{1}{r+2}}-\psi (r+1)-v\psi (vr+1+𝓁),r\in [1,\infty ).$$

By using Lemma 2, we obtain

$${\mathcal{L}}_2\left(r\right)\le {\displaystyle \frac{1}{r+2}}-\mathit{log}(r+1)-v\mathit{log}(vr+1+𝓁)+\gamma (1+v)={\mathcal{L}}_3\left(r\right),r\in [1,\infty ).$$

Since

$${{\mathcal{L}}_3}^{\prime }\left(r\right)=-{\displaystyle \frac{1}{{(r+2)}^2}}-{\displaystyle \frac{1}{r+1}}-{\displaystyle \frac{v^2}{vr+1+𝓁}}<0,r\in [1,\infty )$$

because of ${\mathcal{L}}_3\left(1\right)<0$ and ${\mathcal{L}}_1\left(r\right)$ being a decreasing function on $[1,\infty )$, we ultimately arrive at the conclusion that the sequence mentioned above ${\left\{l_u\right\}}_{u\ge 1}$ is decreasing. Hence, based on (20), the subsequent is true:

$$\begin{array}{ccc}\hfill \left|{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)+{\displaystyle \frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }}\right|& <& 2+\sum _{u=1}^{\infty }\Gamma (1+𝓁)l_1(𝓁,v){\left|b\right|}^u\hfill \\ & =& 2+{\displaystyle \frac{\Gamma (1+𝓁)\left|b\right|l_1(𝓁,v)}{1-\left|b\right|}},(\forall \zeta \in \mathcal{D}).\hfill \end{array}$$

(21)

Combining (5), (7) and (21)

$$\begin{array}{ccc}\hfill {\displaystyle \frac{\left|{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)+\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }\right|\left|{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)-\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }\right|}{{\left|\frac{{\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)}{\zeta }\right|}^2}}& <& {\displaystyle \frac{\left(2+\frac{\Gamma (1+𝓁)\left|b\right|l_1(𝓁,v)}{1-\left|b\right|}\right)\times \left(\frac{\Gamma (1+𝓁)\left|b\right|d_1(𝓁,v)}{1-\left|b\right|}\right)}{{\left(1-\frac{s_1(𝓁,v)\left|b\right|}{1-\left|b\right|}\right)}^2}}\hfill \\ & =& {\displaystyle \frac{\left(2+\frac{3\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)}\right)\times \left(\frac{\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)}\right)}{{\left(1-\frac{\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)}\right)}^2}}.\hfill \end{array}$$

(22)

The proof is concluded by inequality (19), which is the result of hypothesis (b) and (22). □

Example 8. 

(i) The function ${\mathbb{J}}_{{\displaystyle \frac{3}{5}},{\displaystyle \frac{1}{3}}}^2\left(\zeta \right)\in {\mathcal{S}}_L^{*}$in$\mathcal{D}$.

(ii) 

The function ${\mathbb{J}}_{1,{\displaystyle \frac{1}{4}}}^{{\displaystyle \frac{3}{2}}}\left(\zeta \right)\in {\mathcal{S}}_L^{*}$in$\mathcal{D}$.

(iii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{5}}}^3\left(\zeta \right)\in {\mathcal{S}}_L^{*}$in$\mathcal{D}$.

(iv) 

The function ${\mathbb{J}}_{2,{\displaystyle \frac{1}{6}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)\in {\mathcal{S}}_L^{*}$in$\mathcal{D}$.

(v) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{4}},{\displaystyle \frac{2}{3}}}^{{\displaystyle \frac{7}{2}}}\left(\zeta \right)\in {\mathcal{S}}_L^{*}$in$\mathcal{D}$.

Theorem 9. 

Assume that $𝓁\ge 0,v>0\mathit{and}b\in \mathbb{C}-\left\{0\right\}$, and let

(a) 

$e^{{\displaystyle \frac{3}{2}}+(1+v)\gamma }<2{(v+1+𝓁)}^v,$

(b) 

$${\displaystyle \frac{4\left|b\right|\Gamma (1+𝓁)}{\Gamma (v+1+𝓁)(1-\left|b\right|)-2\left|b\right|\Gamma (1+𝓁)}}\times \left({\displaystyle \frac{\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)-2\left|b\right|\Gamma (1+𝓁)}}+1\right)<1,$$

then ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)\in {\mathcal{C}}_L\mathit{in}\mathcal{D}.$

Proof. 

Using (12), we have

$$\begin{array}{ccc}\hfill \left|{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right|\left|2+{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right|& <& {\displaystyle \frac{2\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)-2\Gamma (1+𝓁)\left|b\right|}}\hfill \\ & & \times \left(2+{\displaystyle \frac{2\Gamma (1+𝓁)\left|b\right|}{\Gamma (v+1+𝓁)(1-\left|b\right|)-2\Gamma (1+𝓁)\left|b\right|}}\right).\hfill \end{array}$$

Finally, the following result may be established by using the provided hypothesis (b).

$$\left|{\left(1+{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right)}^2-1\right|=\left|{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right|\left|2+{\displaystyle \frac{\zeta {{\mathbb{J}}_{𝓁,b}^v}^{″}\left(\zeta \right)}{{{\mathbb{J}}_{𝓁,b}^v}^{\prime }\left(\zeta \right)}}\right|<1,(\forall \zeta \in \mathcal{D}).$$

It brings the proof to the end. □

Example 9. 

(i) The function ${\mathbb{J}}_{2,{\displaystyle \frac{1}{3}}}^{{\displaystyle \frac{3}{2}}}\left(\zeta \right)\in {\mathcal{C}}_L$in$\mathcal{D}$.

(ii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{3}{2}},{\displaystyle \frac{1}{2}}}^3\left(\zeta \right)\in {\mathcal{C}}_L$in$\mathcal{D}$.

(iii) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{2}},{\displaystyle \frac{1}{5}}}^{{\displaystyle \frac{5}{2}}}\left(\zeta \right)\in {\mathcal{C}}_L$in$\mathcal{D}$.

(iv) 

The function ${\mathbb{J}}_{{\displaystyle \frac{1}{3}},{\displaystyle \frac{1}{6}}}^4\left(\zeta \right)\in {\mathcal{C}}_L$in$\mathcal{D}$.

(v) 

The function ${\mathbb{J}}_{{\displaystyle \frac{3}{5}},{\displaystyle \frac{1}{4}}}^2\left(\zeta \right)\in {\mathcal{C}}_L$in$\mathcal{D}$.

6. Conclusions

In this article, we have studied the generalized Bessel-Maitland functions. We have investigated starlikeness and convexity of the function ${\mathbb{J}}_{𝓁,b}^v\left(\zeta \right)$. In particular, we have investigated k-uniformly starlike and convexity, starlikeness, and convexity related to the exponential functions and lemniscate of Bernoulli. The main tool in this investigation is an inequality related to the digamma function. By using this inequality more geometric properties of certain special functions can be studied such as the Struve function, Lommel function, Wright function, and many more. We can also investigate the convexity and starlikeness associated with certain subclasses of analytic functions such as classes related with lune, trigonometric functions, hyperbolic functions, sigmoid function and some other geometrically defined classes.