A Novel Methodology for Forecasting Business Cycles Using ARIMA and Neural Network with Weighted Fuzzy Membership Functions
Abstract
1. Introduction
- The proposed approach is efficient for handling large amounts of time series data.
- It overcomes the limitations of linear models and takes advantage of nonlinear models to improve prediction and classification performance.
- Through experiments, it is demonstrated that the proposed integrated model outperformed the single linear model ARIMA in both classification and prediction.
2. Methodology
3. Dataset
4. Autoregressive Integrated Moving Average (ARIMA) Model
4.1. Characteristics of the Model
4.2. Implementation Using Minitab Software
4.3. Selection and Assessment
4.4. Forecasting Time Series Using the ARIMA (1,1,3) Model
5. Neural Network with Weighted Fuzzy Membership Functions (NEWFM) Model
5.1. Characteristics of the Model
5.2. Classification Using the ARIMA–NEWFM Model
5.3. Defuzzification and Trend Line of the Business Cycle
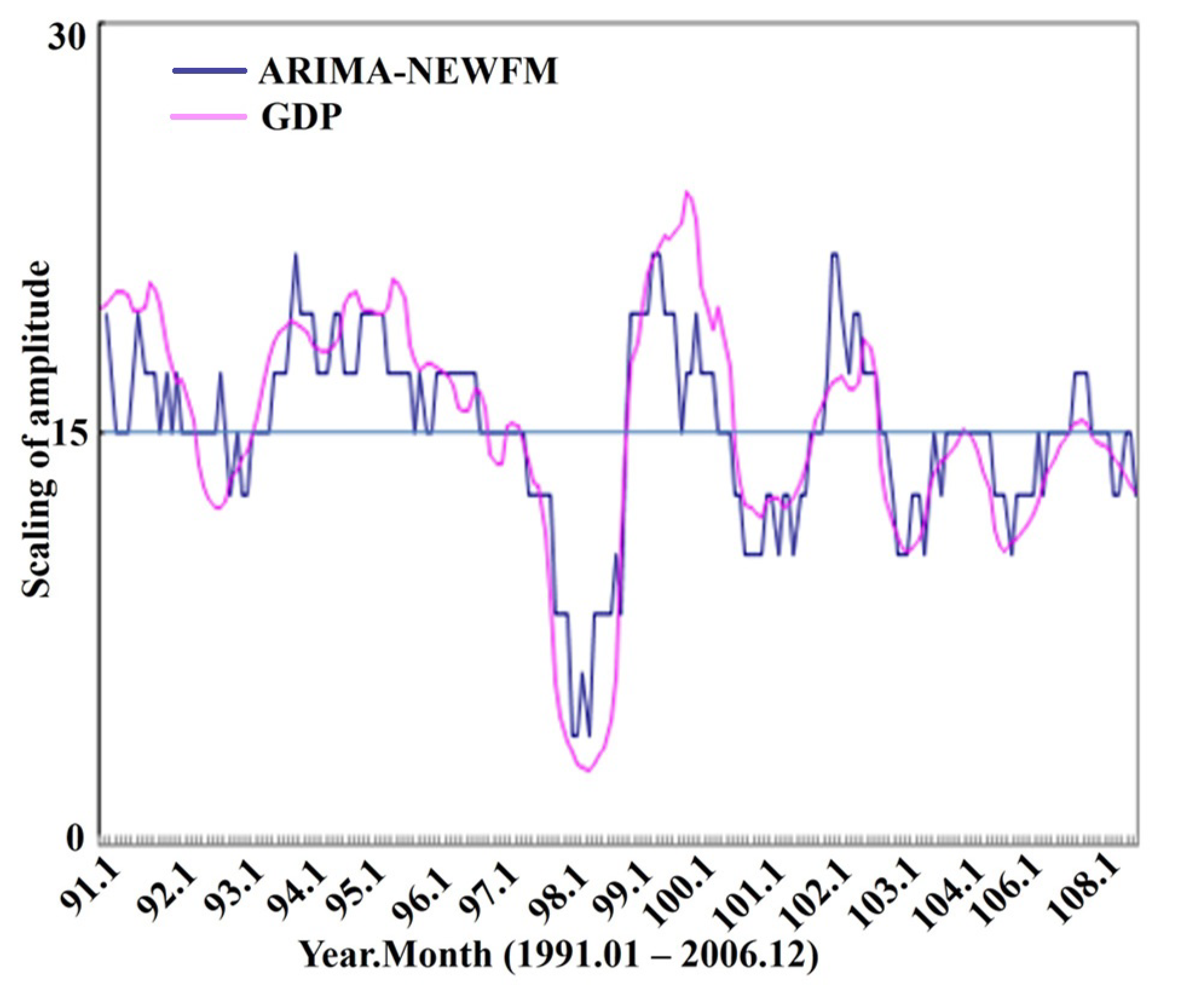
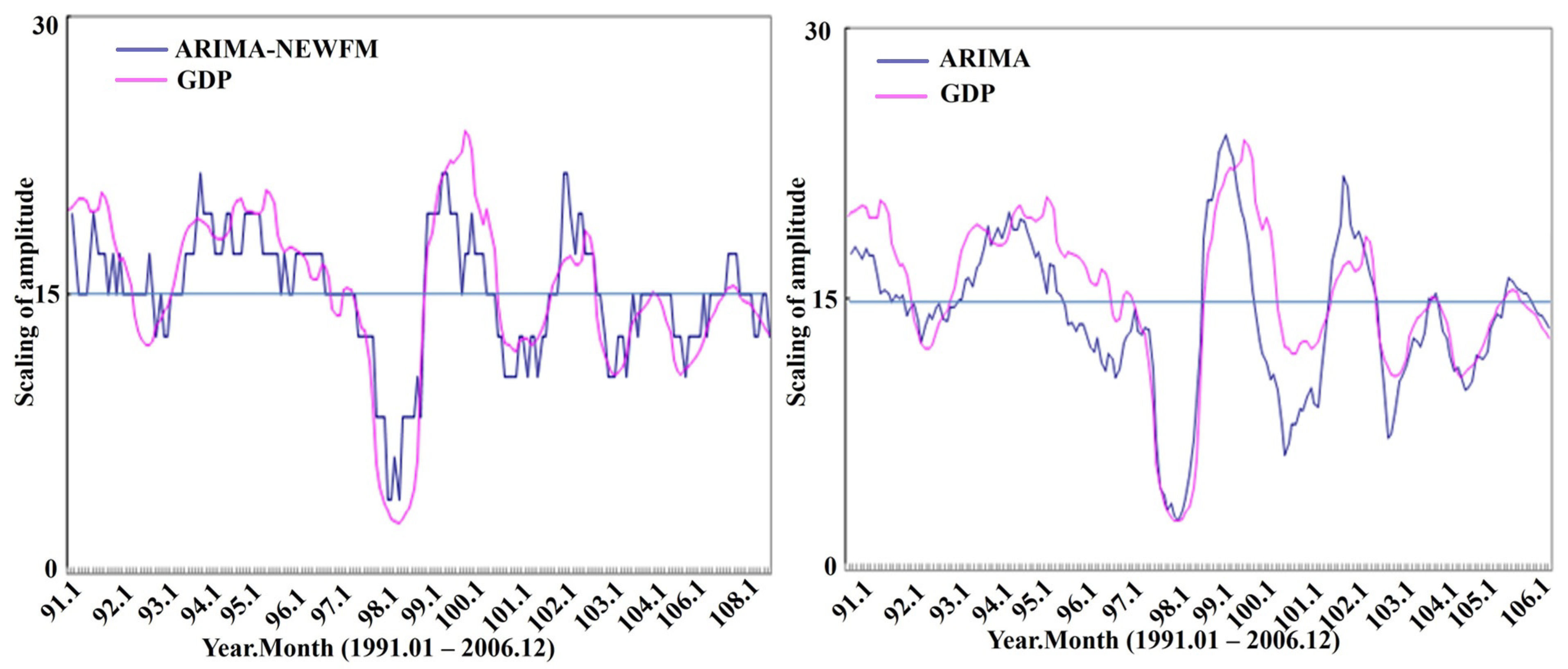
6. Results and Discussion
6.1. Forecasting Capability
6.2. Discussion
7. Conclusions
8. Limitations
- There is a limitation in the present model. In this study, NEWFM was implemented using JAVA programming language. So, program execution speed is somewhat slow. The speed of the program might be improved by implementing a tensorflow version of NEWFM. Further experiments using different datasets that are sufficiently long to cover the lost time series in adjusting and smoothening process of the time series by ARIMA are required.
- The presented ARIMA and ARIMA-NEWFM models, despite their high accuracy and reliability, face limitations due to the manual specification of model parameters, requiring multiple trials and modifications to find the optimal configuration.
- This study may face limitations due to the limited number of observations of the GDP series. The presented work is restricted to the use of monthly observation datasets from 1991 to 2005 for training and the following 12 months for testing the outlook.
- The model’s reliability and accuracy depend on the reliability and differencing of historical data, which must be collected accurately and over a long period for accurate results and forecasts.
- The model’s limitations include its reliance on data collection and the manual trial-and-error process needed to determine optimal parameter values.
9. Future Work
- The accuracy and robustness of forecasting could be improved by combining the advantages of the hybrid ARIMA and NEWFM models. The suggested methodology’s performance can be improved over extended periods. This could entail finding the best configurations by methodically changing the parameters in the ARIMA and NEWFM models. Various forecasting models, such as deep learning and machine learning techniques, can be examined and contrasted with the suggested ARIMA and NEWFM methodologies. To assess the methodology’s practical applicability, it can be tested in real-time forecasting scenarios, but it will have some limitations.
- The ARIMA-NEWFM and ARIMA models are suitable for current observations, but future research could benefit from comparing other forecasting techniques, such as exponential smoothing, vector autoregressive models, neural networks, etc.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Layton, A.P. Dating and predicting phase changes in the US business cycle. Int. J. Forecast. 1996, 12, 417–428. [Google Scholar] [CrossRef]
- Layton, A.P. A further test of the influence of leading indicators on the probability of US business cycle phase shifts. Int. J. Forecast. 1998, 14, 63–70. [Google Scholar] [CrossRef]
- McDonald, S.; Coleman, S.; McGinnity, T.M.; Li, Y. A hybrid forecasting approach using ARIMA models and self-organising fuzzy neural networks for capital markets. In Proceedings of the 2013 International Joint Conference on Neural Networks (IJCNN), Dallas, TX, USA, 4–9 August 2013; pp. 1–7. [Google Scholar] [CrossRef]
- Chai, S.H.; Lim, J.S. Business Cycle Forecasting using Fuzzy Interactive Naïve Bayesian Network. Indian J. Sci. Technol. 2015, 8, 1–6. [Google Scholar] [CrossRef]
- Hung, K.C.; Lin, K.P.A. Long-term business cycle forecasting through a potential intuitionistic fuzzy least-squares support vector regression approach. Inf. Sci. 2013, 224, 37–48. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.; Smola, A. Support vector machine for function approximation, regression estimation, and signal processing. Adv. Neural Inf. Process. Syst. 1996, 9, 281–287. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1968, 20, 87–96. [Google Scholar] [CrossRef]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Li, X.; Hu, B.; Du, R. Predicting the parts weight in plastic injection molding using least squares support vector regression. IEEE Trans. Syst. Man Cybernet. Part C Appl. Rev. 2008, 38, 827–833. [Google Scholar] [CrossRef]
- Chai, S.H.; Lim, J.S. Forecasting business cycle with chaotic time series based on neural network with weighted fuzzy membership functions. Chaos Solitons Fractal 2016, 90, 118–126. [Google Scholar] [CrossRef]
- Hong, D.H.; Hwang, C. Support vector fuzzy regression machines. Fuzzy Sets Syst. 2003, 138, 271–281. [Google Scholar] [CrossRef]
- Faruk, D.Ö. A hybrid neural network and ARIMA model for water quality time series prediction. Eng. Appl. Artif. Intell. 2010, 23, 586–594. [Google Scholar] [CrossRef]
- Lim, J.S. Finding Features for Real-Time Premature Ventricular Contraction Detection Using a Fuzzy Neural Network System. IEEE Trans. Neural Netw. 2009, 20, 522–527. [Google Scholar] [CrossRef]
- Lim, J.S. Finding Fuzzy Rules for IRIS by Neural Network with Weighted Membership Functions. Int. J. Fuzzy Log. Intell. Syst. 2004, 4, 211–216. [Google Scholar]
- The Bank of Korea. The Korean Business Cycle; Monthly Bulletin; The Bank of Korea: Seoul, Republic of Korea, 2004; pp. 31–53. [Google Scholar]
- Chai, S.H.; Lim, J.S. Economic Turning Point Forecasting Using Neural Network with Weighted Fuzzy Membership Functions. In New Trends in Applied Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2007; pp. 145–154, IEA/AIE 2007, LNAI 4570. [Google Scholar]
- Minitab Inc. Minitab Release 14; Minitab Inc.: Arizona AZ, USA, 2005. [Google Scholar]
- Tagaki, T.; Sugeno, M. Fuzzy Identification of systems and its Application to Modeling and Control. IEEE Trans. SMC 1985, 15, 116–132. [Google Scholar]
- Adhikari, R.; Agrawal, R.K. An Introductory Study on Time Series Modeling and Forecasting; LAP Lambert Academic Publishing: London, UK, 2013; ISBN 978-3-659-33508-2. [Google Scholar]
- Example of ARIMA. Available online: https://support.minitab.com/en-us/minitab/21/help-and-how-to/statistical-modeling/time-series/how-to/arima/before-you-start/example/ (accessed on 25 October 2023).
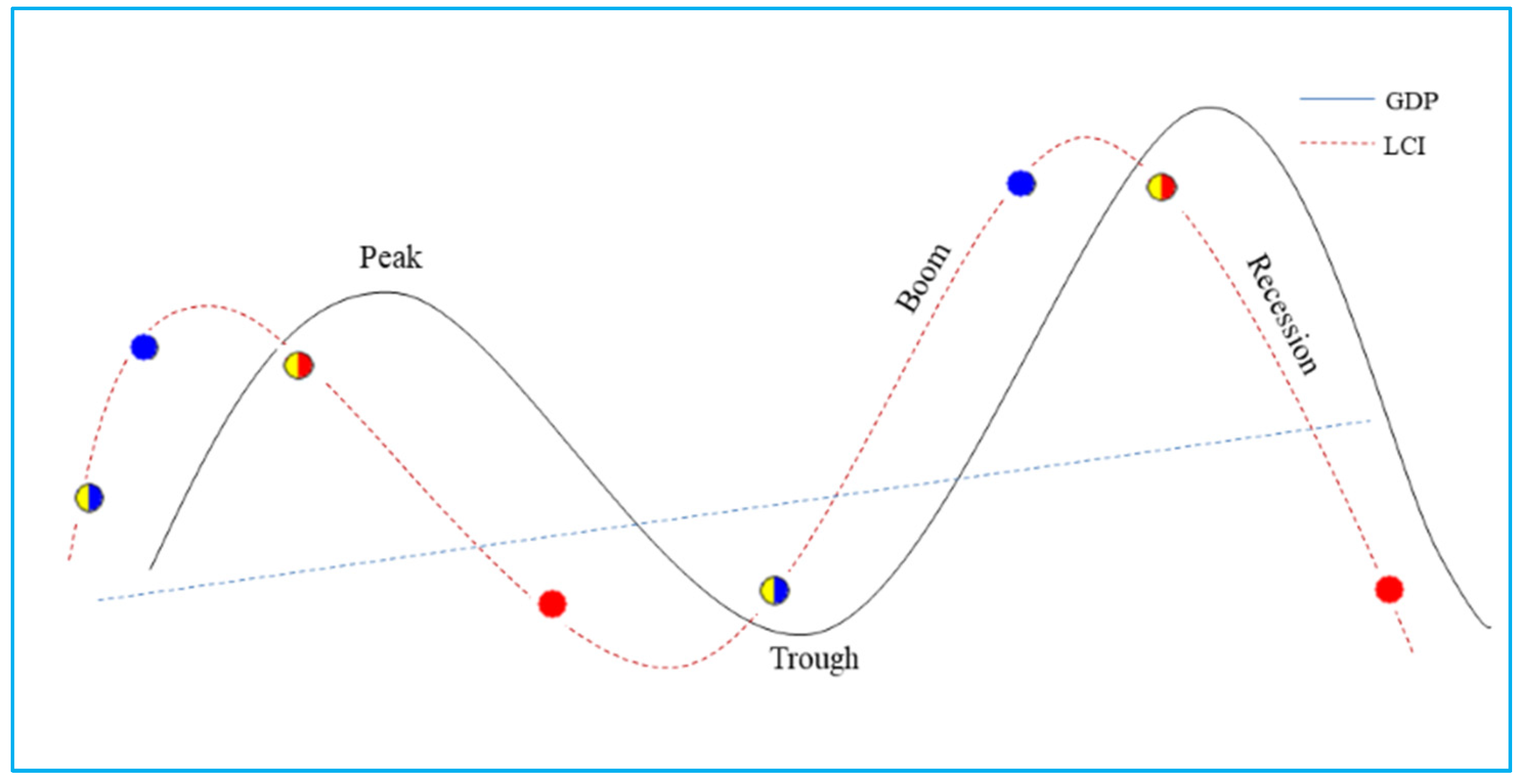
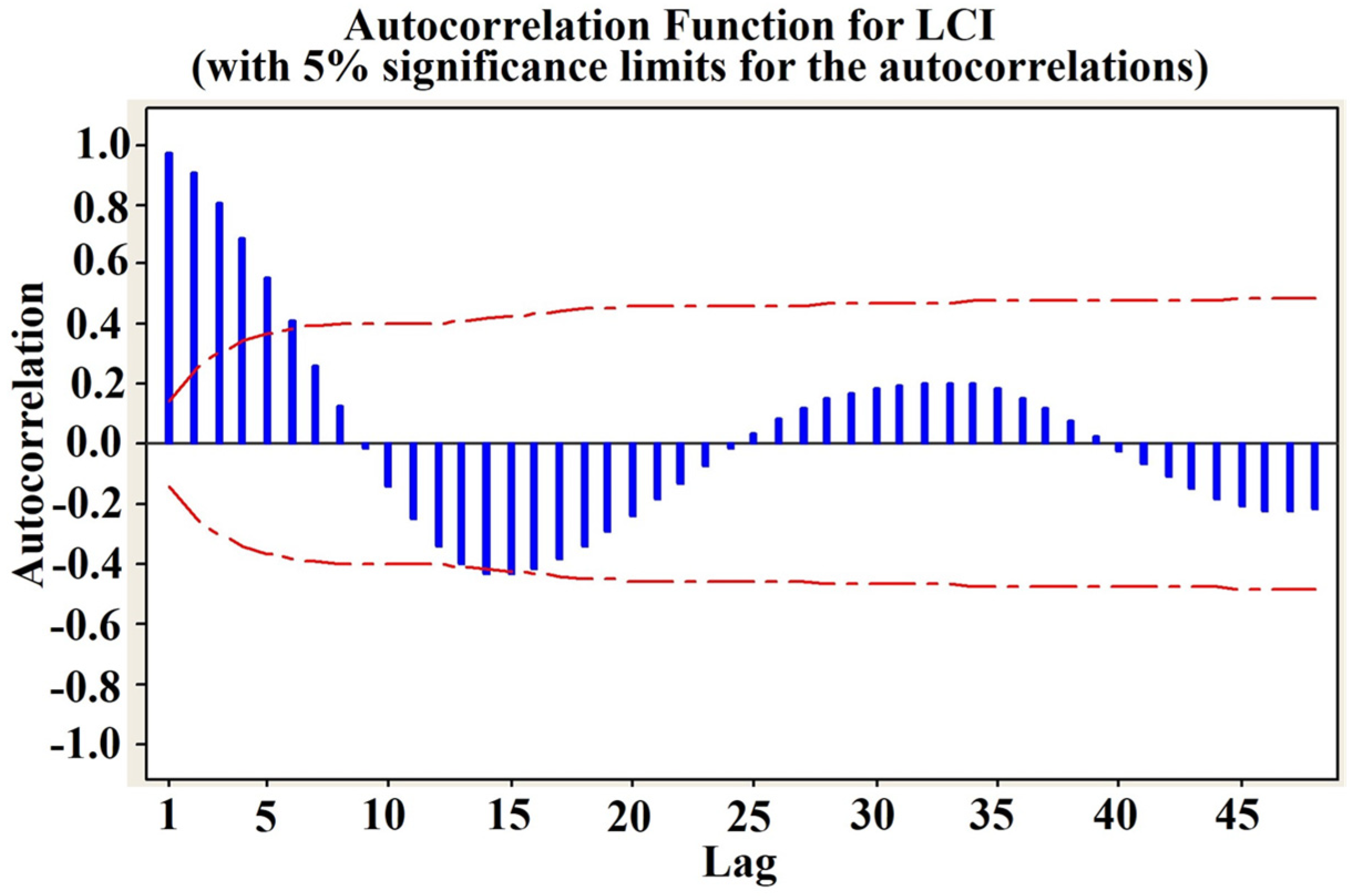

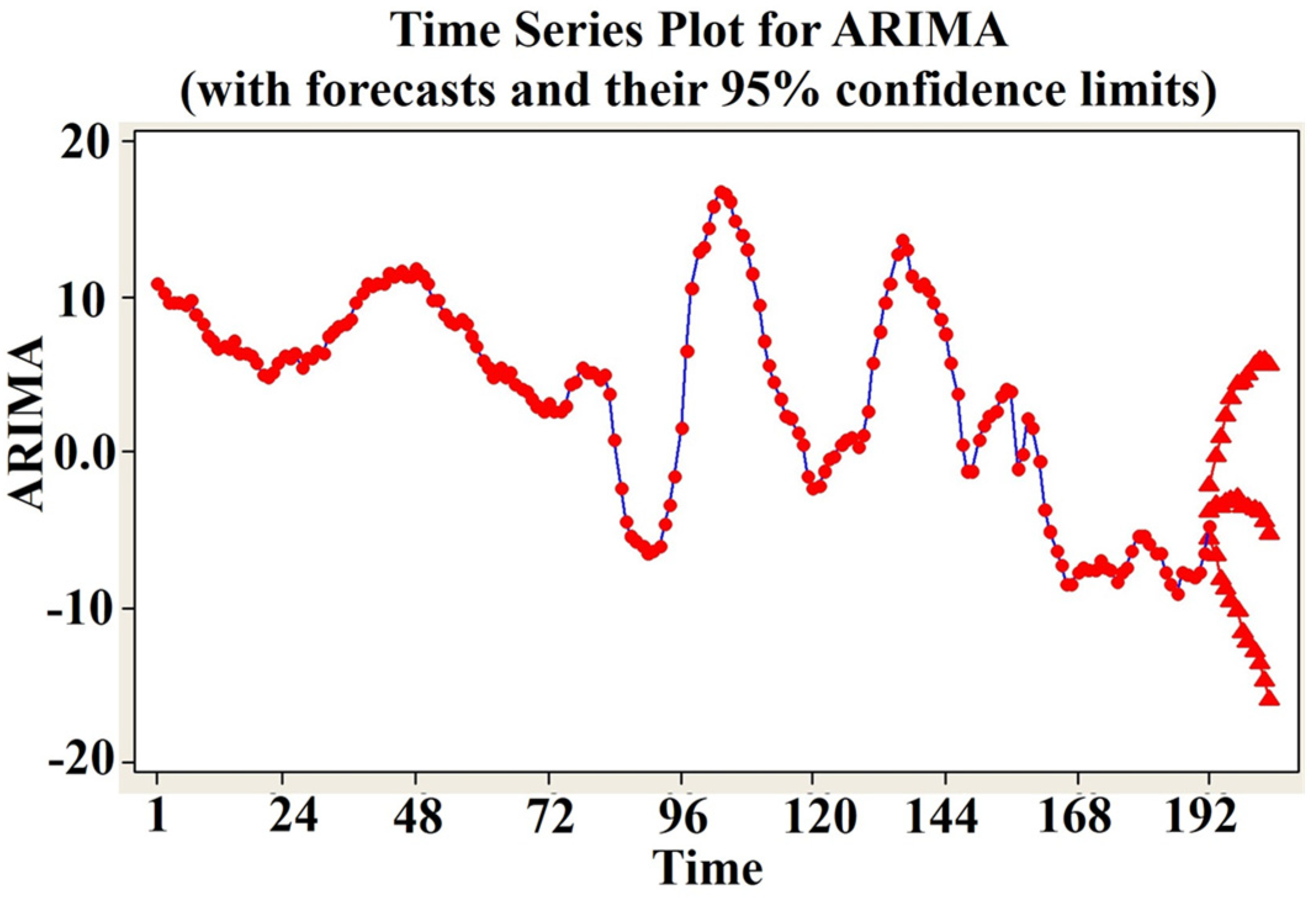

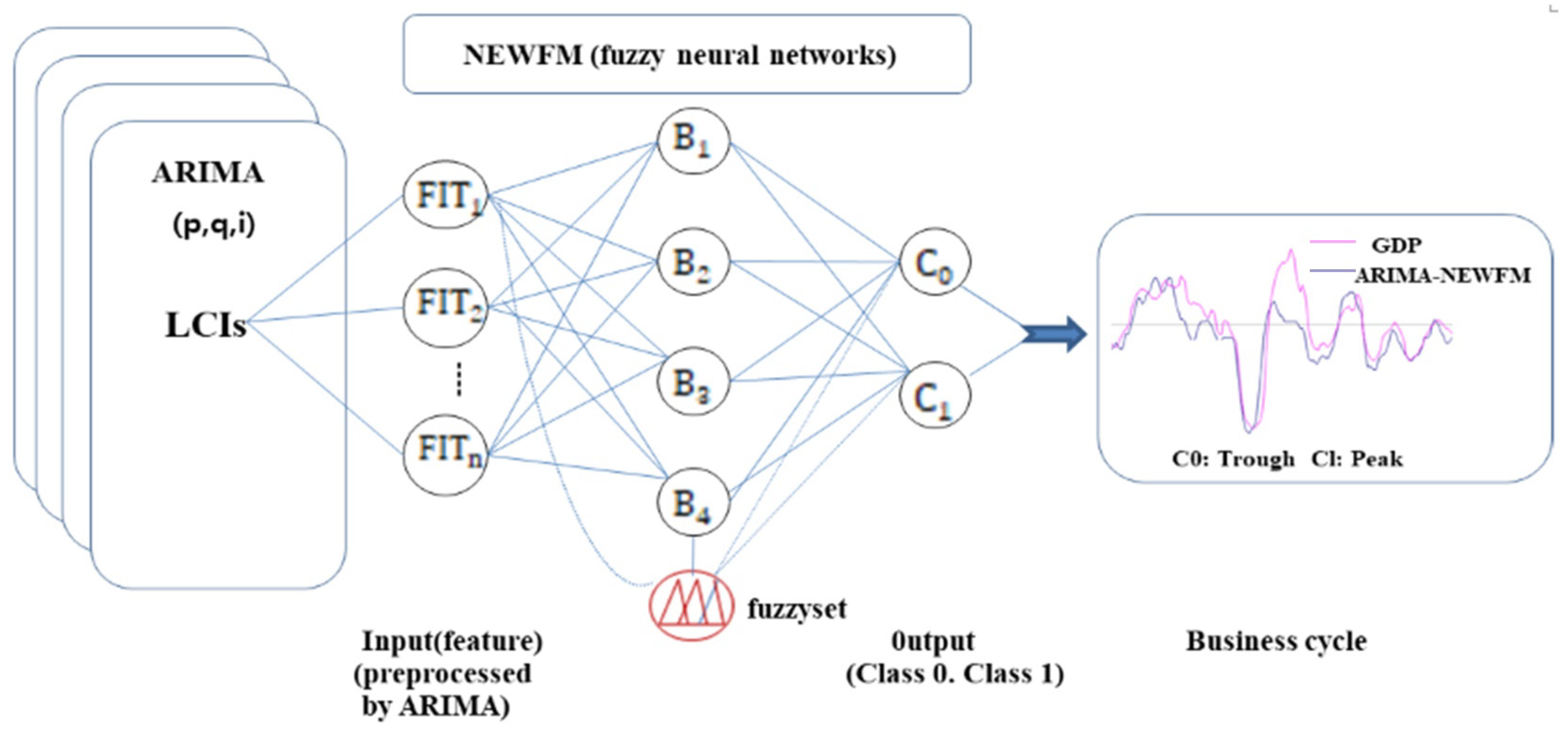

| Constituents of LCI (Input) | Number of Data Instances | Target | Trough (Class 0) | Peak (Class 1) | |
|---|---|---|---|---|---|
| Training (Fitting) | Testing (Forecast) | ||||
| Dataset related to jobs, consumption, trade, production, and finance | 180 (1991.1–2005.12) | 12 (2006.1–2006.12) | GDP | GDP < 5.5% (GDP average growth rate) | GDP > 5.5% (GDP average growth rate) |
| (a) Final Estimates of Parameters | ||||
| Type | Coef. | SE Coef. | T-Value | p-Value |
| AR 1 | 1.0245 | 0.0887 | 11.55 | 0.000 |
| AR 2 | 0.169 | 0.137 | 1.23 | 0.221 |
| AR 3 | −0.2837 | 0.0875 | −3.24 | 0.001 |
| MA 1 | 0.0888 | 0.0743 | 1.19 | 0.234 |
| MA 2 | 0.1303 | 0.0723 | 1.80 | 0.073 |
| MA 3 | 0.7640 | 0.0644 | 11.86 | 0.000 |
| Constant | −0.000106 | 0.000119 | −0.89 | 0.376 |
| Differencing: 1 regular difference | ||||
| Number of observations: original series 192, after differencing 191 | ||||
| (b) Residual Sums of Squares | ||||
| DF | SS | MS | ||
| 184 | 0.115198 | 0.0006261 | ||
| Back forecasts excluded | ||||
| (c) Modified Box–Pierce (Ljung–Box) Chi-Square Statistic | ||||
| Lag | 12 | 24 | 36 | 48 |
| Chi-Square | 52.71 | 81.40 | 96.38 | 102.08 |
| DF | 5 | 17 | 29 | 41 |
| p-Value | 0.000 | 0.000 | 0.000 | 0.000 |
| Data | Classification Rate (%) | Error Rate (%) |
|---|---|---|
| Training (year/month) 180 (91/1 to 05/12) | 83.79 | 16.21 |
| Forecasting (year/month) 12 (06/1 to 06/12) | 83.33 | 16.67 |
| Data | Classification Rate (%) | Error Rate (%) |
|---|---|---|
| Training (year/month) 180 (91/1 to 05/12) | 91.61 | 8.39 |
| Forecasting (year/month) 12 (06/1 to 06/12) | 91.61 | 8.39 |
| Data | Classification Rate (%) | |
|---|---|---|
| ARIMA–NEWFM | ARIMA | |
| Training (year/month) 180 (91/1 to 05/12) | 91.61 | 83.79 |
| Forecasting (year/month) 12 (06/1 to 06/12) | 91.61 | 83.33 |
| Models | GDP | |
|---|---|---|
| (%) | ||
| ARIMA–NEWFM | 71.0 | 2.0471 |
| ARIMA | 69.1 | 2.1696 |
| Regression Analysis | ||||||||||||||||||||
| GDP versus ARIMA–NEWFM | GDP versus ARIMA | |||||||||||||||||||
| regression equation | GDP = 0.122 + 0.864 ARIMA–NEWFM | GDP = 0.237 + 0.812 ARIMA 191 cases used, 1 case contains missing values | ||||||||||||||||||
| Predictor | Constant | ARIMA–NEWFM | Constant | ARIMA | ||||||||||||||||
| Coef. | 0.12236 | 0.86434 | 0.23706 | 0.81173 | ||||||||||||||||
| SE Coef. | 0.02634 | 0.04010 | 0.02224 | 0.03948 | ||||||||||||||||
| T | 4.65 | 21.55 | 10.66 | 20.56 | ||||||||||||||||
| p | 0.000 | 0.000 | 0.000 | 0.000 | ||||||||||||||||
| S = 0.103798, R-Sq = 71.0%, R-Sq(adj) = 70.8% | S = 0.107141, R-Sq = 69.1%, R-Sq(adj) = 68.9% | |||||||||||||||||||
| Analysis of Variance | ||||||||||||||||||||
| Source | DF | SS | MS | F | P | DF | SS | MS | F | P | ||||||||||
| Regression | 1 | 5.0048 | 5.0048 | 464.52 | 0.000 | 1 | 4.8518 | 4.8518 | 422.66 | 0.000 | ||||||||||
| Residual Error | 190 | 2.0471 | 0.0108 | 189 | 2.1696 | 0.0115 | ||||||||||||||
| Total | 191 | 7.0518 | 190 | 7.0214 | ||||||||||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chai, S.H.; Lim, J.S.; Yoon, H.; Wang, B. A Novel Methodology for Forecasting Business Cycles Using ARIMA and Neural Network with Weighted Fuzzy Membership Functions. Axioms 2024, 13, 56. https://doi.org/10.3390/axioms13010056
Chai SH, Lim JS, Yoon H, Wang B. A Novel Methodology for Forecasting Business Cycles Using ARIMA and Neural Network with Weighted Fuzzy Membership Functions. Axioms. 2024; 13(1):56. https://doi.org/10.3390/axioms13010056
Chicago/Turabian StyleChai, Soo H., Joon S. Lim, Heejin Yoon, and Bohyun Wang. 2024. "A Novel Methodology for Forecasting Business Cycles Using ARIMA and Neural Network with Weighted Fuzzy Membership Functions" Axioms 13, no. 1: 56. https://doi.org/10.3390/axioms13010056
APA StyleChai, S. H., Lim, J. S., Yoon, H., & Wang, B. (2024). A Novel Methodology for Forecasting Business Cycles Using ARIMA and Neural Network with Weighted Fuzzy Membership Functions. Axioms, 13(1), 56. https://doi.org/10.3390/axioms13010056









