Chaotic Characteristics in Devaney’s Framework for Set-Valued Discrete Dynamical Systems

Abstract

This paper focuses on the relationship between a non-autonomous discrete dynamical system (NDDS) $(H,f_{1,\infty })$ and its induced set-valued discrete dynamical systems $(\mathcal{K}\left(H\right),{\overline{f}}_{1,\infty })$. Specifically, it explores the chaotic properties of these systems. The main finding is that $f_{1,\infty }$ is Devaney chaotic if and only if ${\overline{f}}_{1,\infty }$ is Devaney chaotic in $w^e$-topology. The paper also provides similar conclusions for weak mixing, mixing, mild mixing, chain-transitivity, and chain-mixing in non-autonomous set-valued discrete dynamical systems (NSDDSs). Additionally, the paper proves that weak mixing implies sensitivity in NSDDSs.

1. Introduction

Dynamical systems are mathematical models that evolve over time. They provide insights into the rules and behaviors that govern a collection of entities, such as numbers or states. Discrete dynamical systems play a crucial role in modeling situations where changes occur at specific intervals rather than continuously [1]. Hence, the primary objective of studying discrete dynamical systems is to gain a comprehensive understanding of how situations progress step by step over time, starting from the initial state. However, merely comprehending the movement of points in the state space is insufficient, particularly in fields like ecology, biology, and social sciences [2,3,4]. The state variables often represent groups of entities rather than individual entities. Therefore, it is significant to capture the patterns of change exhibited by the smaller paths within the state space [5].

Currently, considerable advancements have been made in autonomous set-valued discrete dynamical systems (ASDDSs). In 2003, Roman-Flores successfully demonstrated that collective transitivity implies transitivity in ASDDSs [5]. Following this, Liu in [6] presented an example that illustrated how the sensitivity of the original system does not necessarily imply sensitivity in its induced set-valued system, unless the ASDDS equipped $w^e$-topology. Gu in [7] uncovered the connections between regularity, mixing, mild mixing, weak mixing, and totally transitivity in both systems. In [8] Liao proposed that the weak mixing of $(H,f)$ implies transitivity of $(\mathcal{K}\left(H\right),\overline{f})$. In [9], extending the concept of topological conjugacy to the set-valued context, Roman-Flores and Chalco-Cano discussed the Robinson chaos in $(H,f)$ and $(\mathcal{K}\left(H\right),\overline{f})$. Additionally, in [10], Gu established the equivalence between Kato’s (respectively, Ruelle-Takens) chaos of $(\mathcal{K}\left(H\right),\overline{f})$ in $w^e$-topology. In [11] Fedeli also investigated the correlation between continuous mappings on the invariant subsystems of $(\mathcal{K}\left(H\right),\overline{f})$ and the original system $(H,f)$. For some other research about ASDDSs, see [12,13,14,15,16,17,18].

In numerous real-world situations, such as medicine, biology, and physics, many intricate systems are challenging to represent using autonomous frameworks. Consequently, non-autonomous discrete dynamical systems assume paramount importance [19].

However, the investigation of non-autonomous set-valued discrete dynamical systems (NSDDSs) remains considerably limited. In [20,21,22], Shao established that properties such as the specification property, mixing, the property P, and topological conjugacy equivalence are held between $(H,f_{1,\infty })$ and $(\mathcal{K}\left(H\right),{\overline{f}}_{1,\infty })$. Furthermore, under some specific conditions, the equivalence of Robinson chaos and Kato chaos has been demonstrated between $(H,f_{1,\infty })$ and $(\mathcal{K}\left(H\right),{\overline{f}}_{1,\infty })$. Additionally, examinations of the interrelationship between Li–Yorke chaos, distributional chaos, topological equi-conjugacy, and topological entropy across these two systems have been discussed.

In the current paper, we delve into an in-depth exploration of the chaotic attributes exhibited by the orbit $\{x,x_1,\dots ,x_n,\dots \}$ within the SNDDS $(\mathcal{K}\left(H\right),{\overline{f}}_{1,\infty })$, yielding several significant findings. The existence of transitivity (or sensitivity) in $f_{1,\infty }$ is well-established and has been shown to be directly related to the transitivity (or sensitivity) observed in ${\overline{f}}_{1,\infty }$, specifically in $w^e$-topology. When considering the family of all nonempty compact convex subsets of H, it has been found that $(H,f_{1,\infty })$ exhibits periodic density with a periodicity of n if and only if ${\overline{f}}_{1,\infty }$ displays periodic density with the same periodicity of n in $w^e$-topology. Then, we achieve chaos in the sense of Devaney for NSDDSs. Additionally, we have established correlations between the mixing properties of an NDDS and the corresponding mixing properties of the associated NSDDS and revealed a link between weak mixing and sensitivity in NSDDS. Moreover, an example is given to demonstrate that the logistic map retains sensitivity to initial values in both point systems and set-valued systems. A simple numerical simulation is conducted to deepen the understanding of this concept. These series of findings not only enrich our theoretical understanding of the characteristics of dynamic systems but also provide new perspectives and profound insights for research in the field of set theory.

2. Preliminaries

Let an infinite compact metric space denoted as $(H,d)$, and a continuous mapping sequence $f_i:H\to H$ denoted as $f_{1,\infty }$, where $i\in \mathbb{N}=\{1,2,\dots \}$. The pair $(H,f_{1,\infty })$ is referred to as a non-autonomous discrete dynamical system. For any initial value $x_0$, the orbit of H under $f_{1,\infty }$ is represented as $Or{b}_{f_{1,\infty }}\left(x_0\right)=\{f_n\circ f_{n-1}\circ \cdots \circ f_1\left(x_0\right):n\in \mathbb{N}\}$.

It is mentioned that an ’$ϵ$ neighborhood’ of a set A in a space H is defined as the set of points that are at a distance less than $ϵ$ from A. This is denoted as $N(A,ϵ)$ and can be mathematically represented as

$$N(A,ϵ)=\{x\in H:d(x,A)<ϵ\}.$$

The definition of the Hausdorff separation $\rho (A,B)$ for $A,B\in \mathcal{K}\left(H\right)$ is

$$\rho (A,B)=inf\{ϵ>0:A\subseteq N(B,ϵ\left)\right\}.$$

Furthermore, the following introduces the concept of the Hausdorff metric on $\mathcal{K}\left(H\right)$, denoted as $\mathcal{H}(A,B)$. This metric is defined as the maximum of the two Hausdorff separations, $\rho (A,B)$ and $\rho (B,A)$. Mathematically, this can be represented as

$$\mathcal{H}(A,B)=max\left\{\rho \right(A,B),\rho (B,A\left)\right\}.$$

Reference [5] tell us that the metric space $\left(\mathcal{K}\right(H),\mathcal{H})$ is complete, separable, and compact if and only if the metric space $(H,d)$ is complete, separable, and compact.

In 2005, Ref. [12] discussed the topological properties of $\mathcal{K}\left(H\right)$ when it is equipped with the Vietoris topology. This topology is defined by a set of basic open sets, denoted as $\mathcal{V}(U_1,\dots ,U_k)$, where K is an element of $\mathcal{K}\left(H\right)$ satisfying the conditions that K is a subset of the union of $U_1,\dots ,U_k$ and K intersects with each $U_i$ for $i=1,\dots ,k$. It is important to note that each $U_i$ is a nonempty open subset of H.

The ball $B(K,ϵ)$ represents a set in which the center is the point A and the radius is $ϵ$ in the $\mathcal{H}$-metric. The maps ${\overline{f}}_i$, which are functions from $\mathcal{K}\left(H\right)$ to $\mathcal{K}\left(H\right)$ resulting from $f_i$ for i belonging to the natural numbers, are defined as follows: ${\overline{f}}_1^n\left(K\right)$ is equal to $f_1^n\left(K\right)$, which is the set of all points obtained by applying $f_1^n$ to each point in K. This definition holds for any K belonging to $\mathcal{K}\left(H\right)$.

Definition 1

([22]). A set K of $\mathcal{K}\left(H\right)$ is said to be a periodic point of $(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$ if for any natural number k, there exists a natural number n such that ${\overline{f}}_1^k\left(K\right)={\overline{f}}_1^{k+n}\left(K\right).$

Definition 2.

The mapping sequence ${\overline{f}}_{1,\infty }$ is considered periodic if there exists a natural number $p\in \mathbb{N}$ such that ${\overline{f}}_n={\overline{f}}_{n+p}$ for all $n\in \mathbb{N}$. The period of ${\overline{f}}_{1,\infty }$, denoted as p, is the smallest positive integer that satisfies this equation.

Definition 3

([23]). The mapping sequence ${\overline{f}}_{1,\infty }$ is said to be commutative in $\left(\mathcal{K}\right(H),\mathcal{H})$ if it satisfies the condition that for any $n\in \mathbb{N}$ and $K\in \mathcal{K}\left(H\right),f_1^n\circ f_1^m\left(x\right)=f_1^m\circ f_1^n\left(x\right).$

Inspired by references [24,25], we define Devaney chaos in NSDDSs as follows.

Definition 4.

The mapping sequence ${\overline{f}}_{1,\infty }$ is considered to be

(1) 

topologically transitive if for any nonempty open subsets $\mathcal{U}$ and $\mathcal{V}$ of $\mathcal{K}\left(H\right)$, there exists a natural number $n\in \mathbb{N}$ such that $f_1^n\left(\mathcal{U}\right)\cap \mathcal{V}\ne \varnothing$. In other words, the mapping sequence is transitive if there is a trajectory that can connect any two open subsets.

(2) 

periodically dense if the set of periodic points of ${\overline{f}}_{1,\infty }$ is dense in $\mathcal{K}\left(H\right)$. This means that for any point in $\mathcal{K}\left(H\right)$, there is a sequence of periodic points that can approximate it arbitrarily closely.

(3) 

sensitively dependent on initial conditions if there exists a positive number δ, called the sensitivity constant, such that for every point $K\in \mathcal{K}\left(H\right)$ and every neighborhood $\mathcal{N}$ of K, there exists a set $M\in \mathcal{N}$ and a non-negative integer n such that the difference between ${\overline{f}}_1^n\left(M\right)$ and ${\overline{f}}_1^n\left(K\right)$, denoted as $\mathcal{H}({\overline{f}}_1^n\left(M\right),{\overline{f}}_1^n\left(K\right)$), is greater than or equal to δ. In simpler terms, a small change in the initial condition can lead to a significantly different outcome after a number of iterations.

A system is referred to as transitive (respectively, other chaotic properties) system if its mapping (or mapping sequence) is transitive (respectively, other chaotic properties).

Definition 5.

The system $(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$ is considered Devaney chaotic if it is topologically transitive, periodically dense, and sensitively dependent on initial conditions. This definition requires the property of topological transitivity, which means that there is a point in the phase space that can be arbitrarily close to any other point after a certain number of iterations. Additionally, the system should exhibit periodic density. Finally, the system must also demonstrate sensitive dependence on initial conditions, implying that small perturbations in the initial conditions can lead to significantly different trajectories.

Here are some other chaotic properties associated with Devaney chaos.

Definition 6

([7]). Let $H_1,H_2$ be two infinite compact metric spaces. The system $(\mathcal{K}\left(H_1\right),{\mathcal{H}}_1,{\overline{f}}_{1,\infty })$ is called weakly disjoint with the system $(\mathcal{K}\left(H_2\right),{\mathcal{H}}_2,{\overline{g}}_{1,\infty })$ if $(\mathcal{K}\left(H_1\right)\times \mathcal{K}\left(H_2\right),{\mathcal{H}}^{*},{\overline{f}}_{1,\infty }\times {\overline{g}}_{1,\infty })$ is transitive, where ${\mathcal{H}}_1,{\mathcal{H}}_2$, and ${\mathcal{H}}^{*}$ are metrics on $\mathcal{K}\left(H_1\right),\mathcal{K}\left(H_2\right)$, and $\mathcal{K}\left(H_1\right)\times \mathcal{K}\left(H_2\right)$, respectively.

Definition 7.

The system $(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$, known as an n-periodically dense system, is characterized by the density of n periodic points in $\mathcal{K}\left(H\right)$ under the action of ${\overline{f}}_{1,\infty }$.

Definition 8.

The mapping sequence ${\overline{f}}_{1,\infty }$ is said to be

(1) 

topologically weakly mixing if, for every pair of nonempty open subsets ${\mathcal{U}}_i,{\mathcal{V}}_i\subseteq \mathcal{K}\left(H\right)$, there exists $k\ge 1$ such that the images of ${\mathcal{U}}_i$ under ${\overline{f}}_1^k$ intersect with ${\mathcal{V}}_i$, i.e., ${\overline{f}}_1^k\left({\mathcal{U}}_i\right)\cap {\mathcal{V}}_i\ne \varnothing$.

(2) 

topologically mixing if, for any nonempty subsets $\mathcal{U},\mathcal{V}\subseteq \mathcal{K}\left(H\right)$, there exists an integer $N>0$ such that for all $n\ge N$, the images of $\mathcal{U}$ under ${\overline{f}}^n$ intersect with $\mathcal{V}$.

(3) 

topologically mildly mixing if it exhibits weak disjointness with any transitive system.

Definition 9

([26]). Let M and N be two distinct sets in $\mathcal{K}\left(H\right)$. An ϵ-chain of length $n+1$ connecting M to N is represented by a sequence $\{K_0,K_1,\dots ,K_n\}$, which satisfies the condition that $K_0$ is equivalent to M, $K_n$ is equivalent to N, and $\mathcal{H}({\overline{f}}_i\left(K_i\right),K_{i+1})<ϵ$ for each i in the range 1 to $n-1$.

The notation $M\stackrel{ϵ}{\sim }N$ is used to represent the existence of both an $ϵ$-chain from M to N and an $ϵ$-chain from N to M.

Definition 10.

The system $(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$, is chain-transitive if there exist some $ϵ>0$ such that $M\stackrel{ϵ}{\sim }N$ for every pair of elements $M,N$ in $\mathcal{K}\left(H\right)$.

Definition 11.

The system $(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$ is chain-mixing if for every pair of elements $M,N$ in $\mathcal{K}\left(H\right)$ and any positive value $ϵ>0$, there must exist a natural number $N_0$ with the property that, for all integers $n\ge N_0$, it is possible to establish an ϵ-chain with a length of n connecting M and N.

Definition 12

([5]). The extension of a subset A in $\mathcal{K}\left(H\right)$, denoted as $e\left(A\right)$, is the aggregate of all elements K in $\mathcal{K}\left(H\right)$ for which K is encompassed by A.

Lemma 1.

Let A and B are two subsets of H. Then

(1) 

the non-emptiness of set A is equivalent to the non-emptiness of the image of set A under function e;

(2) 

$e\left(A\right)$ is an open subset of $\mathcal{K}\left(H\right)$ under the condition that A is an open subset of H;

(3) 

$e(A\cap B)=e\left(A\right)\cap e\left(B\right)$;

(4) 

the closure of $f_{1,\infty }\left(A\right)$ is included in $e\left({\overline{f}}_{1,\infty }\left(A\right)\right)$;

(5) 

$\overline{f_i^n}={\overline{f}}_i^n(i\in \mathbb{N})$ for any positive integer n.

Proof. 

The proof of (1), (2), (3), (5) can be found in [5]. Only the proof of (4) is given here.

In fact, if K is an element of ${\overline{f}}_1^n\left(e\left(A\right)\right)$, then there exists a $K_1$ in $e\left(A\right)$ such that K is equal to ${\overline{f}}_1^n\left(K_1\right)$, which can also be represented as $\left\{f_1^n\left(x\right)\right|x\in K_1\}$. By observing that $K_1$ is a subset of A, it can be inferred that K is also a subset of ${\overline{f}}_1^n\left(A\right)$. In other words, K belongs to $e\left({\overline{f}}_1^n\left(A\right)\right)$. Therefore, it can be concluded that ${\overline{f}}_{1,\infty }\left(e\left(A\right)\right)$ is a subset of $e\left({\overline{f}}_{1,\infty }\left(A\right)\right)$. □

3. Chaotic Properties Related to Devaney Chaos

This section presents several equivalence relations for topology transitivity, sensitivity, periodic density, and mixing between NDDSs and its induced set-valued discrete systems under certain predetermined conditions.

Lemma 2.

Let $(H,d_1)$ and $(Y,d_2)$ represent two compact metric spaces, and let $f_{1,\infty }:H\to Y$ be a sequence of mappings. Then, $f_{1,\infty }$ is uniformly continuous if and only if ${\overline{f}}_{1,\infty }:\mathcal{K}\left(H\right)\to \mathcal{K}\left(Y\right)$ is uniformly continuous in $\mathcal{H}$-metric.

Proof. 

(Necessity) Assume that $f_{1,\infty }$ is uniformly continuous. Then, by the compactness of H and Y, $f_1^n$ is uniformly continuous for any $n\in \mathbb{N}$. Thus, for every positive value of $ϵ$, there exists a positive value of $\delta$ such that $d_1(x,y)<\delta$ implies $d_2(f_1^n\left(x\right),f_1^n\left(y\right))<ϵ.$

For any $A,B\in \mathcal{K}\left(H\right)$ satisfying $\mathcal{H}(A,B)<\delta$, one can obtain that A is a subset of the neighborhood of B with a radius of $\delta$, denoted as $N(B,\delta )$. Similarly, B is a subset of the neighborhood of A with a radius of $\delta$, denoted as $N(A,\delta )$. Then, for any element a in the set A, the distance between a and B, denoted as $d_1(a,B)$, is less than $\delta$. Similarly, for any element b in the set B, the distance between b and A, denoted as $d_1(b,A)$, is less than $\delta$.

Therefore, for any given $a\in A$ there exists a $b\in B$ such that $d_1(a,b)<\delta$, and then, $d_2(f_1^n\left(a\right),f_1^n\left(b\right))<ϵ$. Consequently, $d_2(f_1^n\left(a\right),f_1^n\left(B\right))<ϵ(\forall a\in A)$. That is, $f_1^n\left(A\right)\subseteq N(f_1^n\left(B\right),ϵ).$

By employing a comparable rationale, it can be deduced that $f_1^n\left(B\right)$ is a subset of $N(f_1^n\left(A\right),ϵ)$. Additionally, taking into account the condition $\mathcal{H}(f_1^n\left(A\right),f_1^n\left(B\right))<ϵ$, it can be inferred that ${\overline{f}}_{1,\infty }$ exhibits uniform continuity on $\mathcal{K}\left(H\right)$.

(Sufficiency) Suppose that ${\overline{f}}_{1,\infty }$ displays uniform continuity. In light of the compact nature of $\mathcal{K}\left(H\right)$ and $\mathcal{K}\left(Y\right)$, it follows that ${\overline{f}}_1^n$ exhibits uniform continuity as well. Consequently, given any $ϵ>0$, there exists a corresponding $\delta >0$ such that the condition $\mathcal{H}(A,B)<\delta$ leads to the implication $\mathcal{H}({\overline{f}}_{1,\infty }\left(A\right),{\overline{f}}_{1,\infty }\left(B\right))<ϵ$.

In particular, if $d(x,y)<\delta$ for any $\left\{x\right\},\left\{y\right\}\in \mathcal{K}\left(H\right)$, then $\mathcal{H}\left(\right\{x\},\{y\left\}\right)<\delta$. This implies that $\mathcal{H}({\overline{f}}_1^n\left(\left\{x\right\}\right),{\overline{f}}_1^n\left(\left\{y\right\}\right))<ϵ$. Furthermore, it can be shown that

$$\mathcal{H}({\overline{f}}_1^n\left(\left\{x\right\}\right),{\overline{f}}_1^n\left(\left\{y\right\}\right))=\mathcal{H}(\left\{f_1^n\left(x\right)\right\},\left\{f_1^n\left(y\right)\right\})=d(f_1^n\left(x\right),f_1^n\left(y\right)).$$

Hence, we can conclude that $d(f_1^n\left(x\right),f_1^n\left(y\right))<ϵ$. As a result, it can be deduced that $f_{1,\infty }$ is uniformly continuous. □

Corollary 1.

In the context of mapping sequences, the continuity of $f_{1,\infty }$ aligns with the continuity of ${\overline{f}}_{1,\infty }$ in $\mathcal{H}$-metric.

Now let us examine the conditions of Devaney chaos.

Theorem 1.

If the mapping sequence $f_{1,\infty }$ exhibit topological transitivity, then the mapping sequence ${\overline{f}}_{1,\infty }$ demonstrates topological transitivity too.

Proof. 

Assume that U and V are two open subsets of H that are nonempty. We can select an element x from U, an element y from V, and a positive value $ϵ$ such that the ball $B(x,ϵ)$ is a subset of U and the ball $B(y,ϵ)$ is a subset of V. Now, let us consider the open sets $B\left(\right\{x\},ϵ)$ and $B\left(\right\{y\},ϵ)$, which are balls in the metric space $\mathcal{K}\left(H\right)$. By applying the transitivity property of ${\overline{f}}_{1,\infty }$, we can find an integer $n\in \mathbb{N}$ such that the intersection between ${\overline{f}}_1^n\left(B(\left\{x\right\},ϵ)\right)$ and $B\left(\right\{y\},ϵ)$ is not empty. Hence, there exists a set G in $B\left(\right\{x\},ϵ)$ such that ${\overline{f}}_1^n\left(G\right)=f_1^n\left(G\right)$ is an element of $B\left(\right\{y\},ϵ)$. This implies that G is also contained within $B(x,ϵ)$ for the reason that $\mathcal{H}(G,\{x\left\}\right)$ is less than $ϵ$. In other words, $\mathcal{H}(G,\{x\left\}\right)<ϵ$. According to the definition of $\mathcal{H}$, we have

$$\mathcal{H}(G,\{x\left\}\right)=max\left\{\rho \right(G,\left\{x\right\}),\rho (\left\{x\right\},G\left)\right\}.$$

Therefore, we can conclude that $\mathcal{H}(G,\{x\left\}\right)=\rho (G,\{x\left\}\right)<ϵ$. Thus, G is a subset of $B(x,ϵ)$ and, likewise, $f_1^n\left(G\right)$ is an element of $B(y,ϵ)$. This implies that the intersection between $f_1^n\left(B(x,ϵ)\right)$ and $B(y,ϵ)$ is not empty. Consequently, we can deduce that $f_1^n\left(U\right)\bigcap V\ne \varnothing$, which means that ${\overline{f}}_{1,\infty }$ is topologically transitive. □

Can the theorem be applied in reverse? To address this question, we equip $\mathcal{K}\left(H\right)$ with the $w^e$-topology and partly answer the theorem. The $w^e$-topology is a topology that can be defined in the following way. It includes the empty set ∅, the collection of compact subsets of the Hilbert space H denoted as $\mathcal{K}\left(H\right)$, every finite intersection of the sets $e\left(A\right)$, and all possible unions of these finite intersections.

Theorem 2.

The topological transitivity of the mapping sequence $f_{1,\infty }$ implies that the mapping sequence ${\overline{f}}_{1,\infty }$ is also topologically transitive in $w^e$-topology.

Proof. 

Assume that there are two nonempty open sets, $\mathcal{U}$ and $\mathcal{V}$, in $\mathcal{K}\left(H\right)$, both defined in $w^e$-topology. Without loss of generality, we can express these sets as follows:

$$\mathcal{U}=\bigcup _{i}e\left(A_i\right)\mathrm{and}\mathcal{V}=\bigcup _{j}e\left(B_j\right),i,j=1,2,\dots ,$$

where, $A_i$ and $B_j$ represent nonempty open sets in H. Let us fix $i_0$ and $j_0$ and consider an element x from $A_{i_0}$ and an element y from $B_{j_0}$. We can find an $ϵ>0$ such that $B(x,ϵ)\subseteq A_{i_0}$ and $B(y,ϵ)\subseteq B_{j_0}$. By utilizing the transitivity of $f_{1,\infty }$, one can find a z in $B(x,ϵ)$ and some k in $\mathbb{N}$ such that $f_1^k\left(z\right)\in B(y,ϵ)$. Therefore, $\left\{z\right\}\in e\left(A_{i_0}\right)$ and ${\overline{f}}_1^k\left(\left\{z\right\}\right)=\left\{f_1^k\left(z\right)\right\}\in e\left(B_{j_0}\right)$. Consequently, ${\overline{f}}_1^k\left(e\left(A_{i_0}\right)\right)\cap e\left(B_{j_0}\right)\ne \varnothing$, which implies that ${\overline{f}}_1^k\left(\mathcal{U}\right)\cap \mathcal{V}\ne \varnothing$. In conclusion, we can establish that ${\overline{f}}_{1,\infty }$ is topologically transitive in $w^e$-topology. □

By combining Theorems 1 and 2, one can deduce that the aforementioned conclusion holds true.

Theorem 3.

The mapping sequence $f_{1,\infty }$ being topologically transitive is equivalent to the mapping sequence ${\overline{f}}_{1,\infty }$ being topologically transitive in $w^e$-topology.

Let ${\mathcal{K}}_c\left(H\right)$ be all nonempty compact convex subsets of H. Then one can obtain the following result.

Theorem 4.

The mapping sequence $f_{1,\infty }$ having n periodically dense implies the mapping sequence ${\overline{f}}_{1,\infty }$ having n periodically dense on ${\mathcal{K}}_c\left(H\right).$

Proof. 

Let us consider $K\in \mathcal{K}\left(H\right)$ and assume that $\frac{ϵ}{2}>0$. As a result of this assumption, we can establish the existence of a $\frac{ϵ}{2}$-net that covers K. This implies the existence of m distinct points denoted as $x_1,x_2,\cdots ,x_m$ in K. These points satisfy the condition that the entirety of

$$K\subset B\left(x_1,\frac{ϵ}{2}\right)\cup \dots \cup B\left(x_m,\frac{ϵ}{2}\right).$$

Since $f_{1,\infty }:H\to H$ has n periodically dense, then there is an n periodic point in each $B\left(x_i,\frac{ϵ}{2}\right)(1\le i\le m)$. Thus, there exist $y_i\in B\left(x_i,\frac{ϵ}{2}\right)(\forall i\in \{1,\dots ,m\})$ such that

$$f_1^{n+k}\left(y_i\right)=f_1^k\left(y_i\right),\forall i=1,\dots ,m,\forall k\in \mathbb{N}.$$

Write $G=\{y_1,y_2,\cdots ,y_m\}$. By construction, it follows that $H(K,G)<ϵ$. Furthermore, $f_1^{n+k}\left(y_i\right)=f_1^k\left(y_i\right)$ for every $i\in \{1,\dots ,m\}$ and every $k\in \mathbb{N}$. Consequently,

$${\overline{f}}_1^{n+k}\left(G\right)={\overline{f}}_1^k\left(G\right),\forall k\in \mathbb{N},$$

which indicates that the mapping ${\overline{f}}_{1,\infty }:\mathcal{K}\left(H\right)\to \mathcal{K}\left(H\right)$ exhibits n periodic density. □

Is it feasible to apply this theorem in the reverse direction? For the theorem to be valid in reverse, additional conditions must be introduced.

Theorem 5.

Let H be a nonempty compact convex set with metric d and $f_{1,\infty }$ be a periodic mapping sequence with period n on $(H,d)$. If the sequence ${\overline{f}}_{1,\infty }$ exhibits n periodic points densely distributed on ${\mathcal{K}}_c\left(H\right)$, then the sequence $f_{1,\infty }$ similarly has densely distributed n periodic points in $(H,d)$.

Proof. 

Given that $\left\{x\right\}$ forms a convex subset in ${\mathcal{K}}_c\left(H\right)$ and ${\overline{f}}_{1,\infty }:{\mathcal{K}}_c\left(H\right)\to {\mathcal{K}}_c\left(H\right)$ exhibits periodic point density of n, it follows that for any $ϵ>0$ and any $k\in \mathbb{N}$, there exists a $K\in {\mathcal{K}}_c\left(H\right)$ satisfying

$$\mathcal{H}(\left\{x_0\right\},K)<ϵ\mathrm{and}{\overline{f}}_1^{n+k}\left(K\right)={\overline{f}}_1^k\left(K\right).$$

In particular, if $k=0$, one has $f_1^n\left(K\right)=K$. Then,

$${\overline{f}}_1^n\left(K\right)=\overline{f_1^n}\left(K\right)=f_1^n\left(K\right)=K.$$

Based on Schauder’s fixed-point theorem, it can be concluded that there exists a $y\in K$ ensuring the continuity of $f_1^n$ on K and satisfying $f_1^n\left(y\right)=y$. And because $f_{1,\infty }:(H,d)\to (H,d)$ is periodic with period n, one has

$$f_1^{n+k}\left(y\right)=f_1^k\left(y\right),\forall k\in \mathbb{N}.$$

Thus, y is an n periodic point of $f_{1,\infty }$ and $d(x,y)<ϵ$. Consequently, $f_{1,\infty }$ has n periodic density on H. □

The sensitivity aspect in Devaney’s chaos definition is taken into consideration in the following.

Theorem 6.

The sensitivity of the mapping sequence ${\overline{f}}_{1,\infty }$ in $w^e$-topology is equivalent to the sensitivity of the mapping sequence $f_{1,\infty }$.

Proof. 

(Necessity) Assume that $f_{1,\infty }$ is a sensitive function with $\delta >0$ being a sensitive constant. In this case, we consider a nonempty open subset $\mathcal{U}$ in $w^e$-topology of ${\mathcal{K}}_c\left(H\right)$. This implies that there exist nonempty open subsets $A_i$ of H, indexed by $i=1,2,\dots$, such that $\mathcal{U}$ is the union of these subsets. Additionally, we fix an index $i_0$ and utilize the sensitivity of $f_{1,\infty }$ to show that for any given $ϵ>0$, there exist two points x and y in $A_{i_0}$, as well as a positive integer n, such that the distance between $f_1^n\left(x\right)$ and $f_1^n\left(y\right)$ is greater than $ϵ$. If we define A to be the singleton set $\left\{x\right\}$ and B to be the singleton set $\left\{y\right\}$, then both A and B belong to $e\left(A_{i_0}\right)$, which is a subset of $\mathcal{U}$. Moreover, the Hausdorff distance between the closures of $f_1^n\left(A\right)$ and $f_1^n\left(B\right)$, denoted by $\mathcal{H}({\overline{f}}_1^n\left(A\right),{\overline{f}}_1^n\left(B\right))$, is equal to the distance $d(f_1^n\left(x\right),f_1^n\left(y\right))$, which is greater than the sensitive constant $\delta$.

Thus, ${\overline{f}}_{1,\infty }$ is sensitive in $w^e$-topology.

(Sufficiency) In light of the fact that ${\overline{f}}_{1,\infty }$ is sensitive, there is a positive constant $\delta$ such that for any $K\in {\mathcal{K}}_c\left(H\right)$ and any $ϵ>0$, there is a set G contained in the $ϵ$-neighborhood $B(K,ϵ)$ that also belongs to ${\mathcal{K}}_c\left(H\right)$, and there is an n in the set of natural numbers such that

$$\mathcal{H}\left({\overline{f}}_1^n\left(K\right),{\overline{f}}_1^n\left(G\right)\right)\ge \delta .$$

Now, take an arbitrary point $x\in H$ and let $ϵ>0$. By considering K as the set containing only x, i.e., $K=\left\{x\right\}\in {\mathcal{K}}_c\left(H\right)$, one can establish the existence of a set G contained in the $ϵ$-neighborhood $B\left(\right\{x\},ϵ)$ and an n in the set of natural numbers such that

$$\mathcal{H}\left({\overline{f}}_1^n\left(\left\{x\right\}\right),{\overline{f}}_1^n\left(G\right)\right)=\mathcal{H}\left(\left\{{\overline{f}}_1^n\left(x\right)\right\},{\overline{f}}_1^n\left(G\right)\right)\ge \delta .$$

As a result, one has

$$\mathcal{H}\left(\left\{{\overline{f}}_1^n\left(x\right)\right\},{\overline{f}}_1^n\left(G\right)\right)=\underset{y\in G}{sup}d\left(f_1^n\left(x\right),f_1^n\left(y\right)\right)\ge \delta .$$

Taking into account the compactness of G and the continuity of $f_{1,\infty }$, there exists a point $y_0$ in G such that

$$\mathcal{H}\left(\left\{f_1^n\left(x\right)\right\},{\overline{f}}_1^n\left(G\right)\right)=d\left(f_1^n\left(x\right),f_1^n\left(y_0\right)\right)\ge \delta .$$

The statement $G\in B\left(\right\{x\},ϵ)$ implies that the set G is a subset of $B(x,ϵ)$. This subsequently demonstrates that $y_0$ belongs to the set $B(x,ϵ)$. Therefore, it can be concluded that $f_{1,\infty }$ exhibits sensitivity. □

Theorem 7.

Let H be a convex infinitely compact metric space with metric d and let $f_{1,\infty }$ be periodic with period n on $(H,d)$. Then, (1), (2), and (3) are held. That is to say, $f_{1,\infty }$ is Devaney chaotic in the sense of n periodically dense if and only if ${\overline{f}}_{1,\infty }:{\mathcal{K}}_c\left(H\right)\to {\mathcal{K}}_c\left(H\right)$ is Devaney chaotic in the sense of n periodically dense in $w^e$-topology.

(1) 

The transitivity of $f_{1,\infty }$ is equivalent to the transitivity of ${\overline{f}}_{1,\infty }$ in $w^e$-topology.

(2) 

$f_{1,\infty }$ is considered to be n periodically dense if and only if ${\overline{f}}_{1,\infty }$ is n periodically dense in $w^e$-topology.

(3) 

The sensitivity of $f_{1,\infty }$ is consistent with the sensitivity in $w^e$-topology of ${\overline{f}}_{1,\infty }$.

Proof. 

Based on Theorems 3–6, the proof is valid. □

4. Other Chaotic Properties in Set-Valued Systems

Theorem 8.

The system $(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$ is chain-transitive if and only if this property holds true for the system $(H,d,f_{1,\infty })$ as well.

Proof. 

(Necessity) Assume that $f_{1,\infty }$ is chain-transitive. Let K and $K^{\prime }$ be two nonempty open subsets of H. For any x in K and y in $K^{\prime }$, as well as any positive number $ϵ$, one has $x\stackrel{ϵ}{\sim }y$. That is to say, there are $x_0,x_1,\dots ,x_n\subset H(x_0=x,x_n=y)$ with the property that $d(f_i\left(x_i\right),x_{i+1})<ϵ(i=1,2,\dots ,n-1)$. And there exists a $k_1\in H$ such that $d(k_1,f_1\left(x\right))<ϵ$ for any $x\in K$. Then, $\mathcal{H}(\left\{k_1\right\},{\overline{f}}_1\left(K\right))<ϵ.$

Similarly, there are $\left\{k_i\right\},\left\{k_{i+1}\right\}\in \mathcal{K}\left(H\right)$ such that

$$\mathcal{H}({\overline{f}}_i\left(\left\{k_i\right\}\right),\left\{k_{i+1}\right\})<ϵ(i=2,3,\dots ,n-2)\mathrm{and}\mathcal{H}({\overline{f}}_{n-1}\left(\left\{k_{n-1}\right\}\right),K^{\prime })<ϵ.$$

Thus, $\{K,\left\{k_1\right\},\dots ,\left\{k_{n-1}\right\},K^{\prime }\}$ is an $ϵ$-chain from K to $K^{\prime }$. In the same way, it can be proved that there is also an $ϵ$-chain from $K^{\prime }$ to K.

Therefore, $(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$ is chain-transitive.

(Sufficiency) By selecting any positive number $ϵ$ and considering two elements x and y in set H, we will now provide a proof that demonstrates the existence of an $ϵ$-chain from x to y as well as from y to x. Let $A=\left\{x\right\}$, $B=\left\{y\right\}$. Then $A,B\in \mathcal{K}\left(H\right)$. From the chain-transitivity of ${\overline{f}}_{1,\infty }$, one can conclude that there exists an $ϵ$-chain from A to B. That is, there exist $K_0,K_1,\dots ,K_n\in \mathcal{K}\left(H\right)$ with $K_0=A,K_n=B$ and $\mathcal{H}({\overline{f}}_i\left(K_i\right),K_{i+1})<ϵ$ holds for all $i=1,2,\dots ,n-1$. Then

$$\underset{a\in {\overline{f}}_i\left(K_i\right)}{sup}d(a,K_{i+1})<\epsilon (i=1,2,\dots ,n-1).$$

Take any $a\in {\overline{f}}_i\left(K_i\right)$; one has $d(a,K_{i+1})<ϵ$. There exist $x_{i+1}\in K_{i+1}$ such that $d(a,x_{i+1})<ϵ$. And by $a\in {\overline{f}}_i\left(K_i\right)$, one can find that there exist $x_i\in K_i$ such that $a=f_i\left(x_i\right)$. Therefore, for any $i=0,1,\dots ,n-1$, $d(f_i\left(x_i\right),x_{i+1})<ϵ$, where $x_i\in K_i$, $x_{i+1}\in K_{i+1}$. Thus, $\{x_0,x_1,\dots ,x_n\}$ is an $ϵ$-chain from x to y.

Similarly, it can be proved that there is also an $ϵ$-chain from y to x.

Thus, $f_{1,\infty }$ is chain-transitive. □

The subsequent conclusions pertain to the mixing properties of NSDDSs.

Theorem 9.

For the systems $(H,d,f_{1,\infty })$ and $(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$, the statements below highlight the equivalence of certain properties of them.

(1) 

$(H,d,f_{1,\infty })$ exhibits weak mixing;

(2) 

$(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$ displays weak mixing;

(3) 

$(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$ demonstrates transitivity.

Proof. 

$\left(1\right)\Rightarrow \left(2\right)$. If the weak mixing property holds for $f_{1,\infty }$, then the transitivity of the m-product map

$$\underset{m\text{-}\mathrm{times}}{\underbrace{f_{1,\infty }\times f_{1,\infty }\times \cdots \times f_{1,\infty }}}:H\times H\times \cdots \times H\to H\times H\times \cdots \times H$$

is guaranteed for all $m\in \mathbb{N}$. To demonstrate this, it suffices to establish that for any given pair of open sets $\mathcal{V}(U_1^i,\dots ,U_k^i),\mathcal{V}(V_1^i,\dots ,V_k^i)$ (where $i=1,2$), within the canonical base of the Vietoris topology on $\mathcal{K}\left(H\right)$, there exists an $n\in \mathbb{N}$ such that

$${\overline{f}}_1^n\left(\mathcal{V}(U_1^i,\dots ,U_k^i)\right)\cap \mathcal{V}(V_1^i,\dots ,V_k^i)\ne \varnothing ,i=1,2.$$

Indeed, if $m=2k$, there is an $n\in \mathbb{N}$ such that

$$f_1^n\left(U_j^i\right)\cap V_j^i\ne \varnothing ,i=1,2;j=1,\dots ,k.$$

By selecting $x_{i,j}\in U_j^i$ in such a way that $y_{i,j}=f_1^n\left(x_{i,j}\right)\in V_j^i$ (where $i=1,2$ and $j=1,\dots ,k$), we can define $K_1=\{x_{1,1},\dots ,x_{1,k}\}$ and $K_2=\{x_{2,1},\dots ,x_{2,k}\}$. Consequently, we have $K_i\in \mathcal{V}(U_1^i,\dots ,U_k^i)$ and ${\overline{f}}_1^n\left(K_i\right)\in \mathcal{V}(V_1^i,\dots ,V_k^i)$ for $i=1,2$. This implies that ${\overline{f}}_{1,\infty }$ exhibits weak mixing.

$\left(2\right)\Rightarrow \left(3\right)$. By the definitions of weak mixing and transitivity, it is obvious.

$\left(3\right)\Rightarrow \left(1\right)$. The objective is to demonstrate the existence of four distinct open sets $U_1,U_2,V_1,V_2\in H$ such that there exists an $n\in \mathbb{N}$ satisfying the conditions

$$f_1^n\left(U_1\right)\cap V_1\ne \varnothing \mathrm{and}{f}_1^n\left(U_2\right)\cap V_2\ne \varnothing .$$

By utilizing the transitivity of ${\overline{f}}_{1,\infty }$, one can establish the existence of $K\in \mathcal{V}(U_1,U_2)$ and $n\in \mathbb{N}$, which satisfying ${\overline{f}}_1^n\left(K\right)\in \mathcal{V}(V_1,V_2).$ Consequently, it follows that there exist $x\in U_1$ and $y\in U_2$ such that $f_1^n\left(x\right)\in V_1$ and $f_1^n\left(y\right)\in V_2.$ Hence, the conclusion can be drawn that $f_{1,\infty }$ possesses the property of weak mixing. □

Theorem 10.

The mapping sequence ${\overline{f}}_{1,\infty }$ exhibits mixing behavior if and only if the mapping sequence $f_{1,\infty }$ is also displaying mixing behavior.

Proof. 

(Necessity) Assume that ${\overline{f}}_{1,\infty }$ is mixing. Let U and V are two nonempty open subsets of H. Given that both $e\left(U\right)$ and $e\left(V\right)$ are nonempty open subsets of $\mathcal{K}\left(H\right)$, it follows that there exists a positive integer N such that for any $n\ge N$,

$${\overline{f}}_1^n\left(e\left(U\right)\right)\cap e\left(V\right)\ne \varnothing .$$

Moreover, we can observe that

$${\overline{f}}_1^n\left(e\left(U\right)\right)\cap e\left(V\right)\subset e\left(f_1^n\left(U\right)\right)\cap e\left(V\right)=e(f_1^n\left(U\right)\cap V).$$

Consequently, $f_1^n\left(U\right)\cap V\ne \varnothing$ for any $n\ge N$. Hence, we can infer that $f_{1,\infty }$ is a mixing function.

(Sufficiency) Assume that $f_{1,\infty }$ is mixing. Considering two nonempty open subsets ${\mathcal{U}}^{\prime }$ and ${\mathcal{V}}^{\prime }$ of $\mathcal{K}\left(H\right)$, there are subsets $U_1,U_2,\dots ,U_k$ and $V_1,V_2,\dots ,V_k$ of H such that

$$\mathcal{V}(U_1,U_2,\dots ,U_k)\subset {\mathcal{U}}^{\prime }\mathrm{and}\mathcal{V}(V_1,V_2,\dots ,V_k)\subset {\mathcal{V}}^{\prime }.$$

Given the mixing property of $f_{1,\infty }$, it follows that for every $j\in \{1,2,\dots ,k\}$, there exists a positive integer $N_j$ such that

$$f_1^n\left(U_j\right)\cap V_j\ne \varnothing$$

for any $n\ge N_j$.

Assume that N is the maximum value among all $N_j$ ($1\le j\le k$). For any integer n greater than or equal to N, if the intersection of $f_1^n\left(U_j\right)$ and $V_j$ is not empty, then there exists a point $x_j$ in $U_j$ such that $f_1^n\left(x_j\right)$ belongs to $V_j$ for j ranging from 1 to k. Let $A=\{x_1,x_2,\dots ,x_k\}$. It is evident that A belongs to the set $\mathcal{K}\left(H\right)$ and also lies in the set $\mathcal{V}(U_1,U_2,\dots ,U_k)$, which is a subset of ${\mathcal{U}}^{\prime }$. Additionally, ${\overline{f}}_1^n\left(A\right)$ belongs to $\mathcal{V}(V_1,V_2,\dots ,V_k)$, which is also a subset of ${\mathcal{V}}^{\prime }$.

Therefore, for every positive integer $n\ge N$, it can be observed that there exists a nonempty set ${\mathcal{V}}^{\prime }$ which intersects with ${\overline{f}}_1^n\left({\mathcal{U}}^{\prime }\right)$. This fact convincingly demonstrates the property of mixing for ${\overline{f}}_{1,\infty }$. □

To consider the mild mixing of both systems, the precondition that $f_{1,\infty }$ is commutative is required.

Lemma 3.

If the mapping sequence $f_{1,\infty }$ is commutative and mildly mixing, then for any transitive system $(\mathrm{\Omega },T)$,

$$(\underset{ktimes}{\underbrace{H\times H\times \cdots \times H}}\times \mathrm{\Omega },\underset{ktimes}{\underbrace{f_{1,\infty }\times f_{1,\infty }\times \cdots \times f_{1,\infty }}}\times T)$$

is transitive.

Proof. 

First, $f_{1,\infty }$ being mildly mixing implies that $f_{1,\infty }$ is weakly mixing. If $U_1,V_1,U_2,V_2$ are open subsets of H, then there exists a $k\ge 0$ such that $f_1^k(U_1\times U_2)\cap (V_1\times V_2)\ne \varnothing$. This means that $f_1^k\left(U_1\right)\cap V_1\ne \varnothing$ and $f_1^k\left(U_2\right)\cap V_2\ne \varnothing$. Let $f_1^k\left(U_1\right)\cap V_1=A_1$, $f_1^k\left(U_2\right)\cap V_2=B_1$. If $n\in N(A_1,B_1)=\{n\in \mathbb{N}:f_1^n\left(A_1\right)\cap B_1\ne \varnothing \}$, then

$$f_1^n(f_1^k\left(U_1\right)\cap V_1)\cap (f_1^k\left(U_2\right)\cap V_2)\ne \varnothing .$$

That is to say, $f_1^n\left(V_1\right)\cap V_2\ne \varnothing$ and $f_1^n\left(f_1^k\left(U_1\right)\right)\cap f_1^k\left(U_2\right)\ne \varnothing$. Since $f_{1,\infty }$ is commutative, then $f_1^n\circ f_1^k=f_1^k\circ f_1^n$, which implies $f_1^n\left(U_1\right)\cap U_2\ne \varnothing$. And so, $N(A_1,B_1)\subset N(U_1,U_2)\cap N(V_1,V_2)$.

By analogy, there are sets A, B in H such that

$$N(A,B)\subset \bigcap _{i=1}^{k}N(U_i,V_i).$$

And because $f_{1,\infty }$ is weakly mixing, then

$$N(A,B)\cap N({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2)\ne \varnothing$$

for any ${\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\subset \mathrm{\Omega }.$

That is to say,

$$[\bigcap _{i=1}^{k}N(U_i,V_i)]\cap N({\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2)\ne \varnothing$$

for any ${\mathrm{\Omega }}_1,{\mathrm{\Omega }}_2\subset \mathrm{\Omega }$.

Therefore,

$$(\underset{ktimes}{\underbrace{H\times H\times \cdots \times H}}\times \mathrm{\Omega },\underset{ktimes}{\underbrace{f_{1,\infty }\times f_{1,\infty }\times \cdots \times f_{1,\infty }}}\times T)$$

is transitive. □

Theorem 11.

Under the condition that $f_{1,\infty }$ exhibits commutativity, the mild mixing property is preserved by ${\overline{f}}_{1,\infty }$ if and only if it is preserved by $f_{1,\infty }$.

Proof. 

(Necessity) Assume that ${\overline{f}}_{1,\infty }$ is mildly mixing. For any transitive system $(\mathrm{\Omega },T)$, it can be shown that $(H\times \mathrm{\Omega },f_{1,\infty }\times T)$ is also a transitive system. Let $U_1\times V_1$ and $U_2\times V_2$ be two nonempty open subsets of $H\times \mathrm{\Omega }$. By considering the sets $e\left(U_1\right)\times V_1$ and $e\left(U_2\right)\times V_2$ in $\mathcal{K}\left(H\right)\times \mathrm{\Omega }$, which are open subsets, we can apply the fact that ${\overline{f}}_{1,\infty }\times T$ is transitive. This means that there exists a point $(A,y)\in e\left(U_1\right)\times V_1$ and a positive integer n such that

$$({\overline{f}}_1^n\times T^n)\left((A,y)\right)=({\overline{f}}_1^n\left(A\right),T^n\left(y\right))\in e\left(U_2\right)\times V_2.$$

Then, it follows that ${\overline{f}}_1^n\left(A\right)\in e\left(U_2\right)$ and $T^n\left(y\right)\in V_2$. For any point $x\in A\subset U_1$, we have $f_1^n\left(x\right)\in f_1^n\left(A\right)\subset U_2$. Therefore, if $(x,y)\in U_1\times V_1$, it can be shown that

$$(f_1^n\times T^n)\left((x,y)\right)=(f_1^n\left(x\right),T^n\left(y\right))\in U_2\times V_2.$$

As a result, it can be concluded that $(H\times \mathrm{\Omega },f_{1,\infty }\times T)$ is a transitive system, which further demonstrates that $f_{1,\infty }$ is mildly mixing.

(Sufficiency) Assume that ${\overline{f}}_{1,\infty }$ exhibits mild mixing properties. For any transitive system $(\mathrm{\Omega },T)$, the subsequent discussion will demonstrate that $(\mathcal{K}\left(H\right)\times \mathrm{\Omega },{\overline{f}}_{1,\infty }\times T)$ can be regarded as a transitive system. Consider two nonempty open subsets ${\mathcal{U}}_1\times V_1$ and ${\mathcal{U}}_2\times V_2$ of $\mathcal{K}\left(H\right)\times \mathrm{\Omega }$. One can find open subsets $U_1^i,U_2^i,\dots ,U_k^i$ of H such that

$$\mathcal{V}(U_1^i,U_2^i,\dots ,U_k^i)\subset {\mathcal{U}}_i,i=1,2.$$

Given the mildly mixing nature of $f_{1,\infty }$, it can be inferred that the system $(H\times \mathrm{\Omega },f_{1,\infty }\times T)$ is indeed transitive. This conclusion can be drawn by employing Lemma 3: one can find that

$$(\underset{ktimes}{\underbrace{H\times H\times \cdots \times H}}\times \mathrm{\Omega },\underset{ktimes}{\underbrace{f_{1,\infty }\times f_{1,\infty }\times \cdots \times f_{1,\infty }}}\times T)$$

is a transitive system.

Hence, for two open subsets $U_1^1\times U_2^1\times \cdots \times U_k^1\times V_1$ and $U_1^2\times U_2^2\times \cdots \times U_k^2\times V_2$ of $H\times H\times \cdots \times H\times \mathrm{\Omega },$ there exists a specific point $(x_1,x_2,\dots ,x_k,y)\in U_1^1\times U_2^1\times \cdots \times U_k^1\times V_1$ and a positive integer indicated as n such that

$$(f_1^n\times f_1^n\times \cdots \times f_1^n\times T^n)\left((x_1,x_2,\dots ,x_k,y)\right)=(f_1^n\left(x_1\right),f_1^n\left(x_2\right),\dots ,f_1^n\left(x_k\right),T^n\left(y\right))$$

is in $U_1^2\times U_2^2\times \cdots \times U_k^2\times V_2.$

Assuming B is a set consisting of elements $x_1,x_2,\dots ,x_k$, then $B\in ⟨U_1^1,U_2^1,\dots ,U_k^1⟩\subset {\mathcal{U}}_1$ and ${\overline{f}}^n\left(B\right)\in ⟨U_1^2,U_2^2,\dots ,U_k^2⟩\subset {\mathcal{U}}_2.$ Therefore $,(B,y)\in {\mathcal{U}}_1\times {\mathcal{V}}_1$ and

$${\overline{f}}_1^n\left(B\right)\times T^n\left(y\right)=({\overline{f}}_1^n\times T^n)\left((B,y)\right)\in {\mathcal{U}}_2\times {\mathcal{V}}_2.$$

Hence, $(\mathcal{K}\left(H\right)\times \mathrm{\Omega },{\overline{f}}_{1,\infty }\times T)$ constitutes a transitive system. This demonstrates that ${\overline{f}}_{1,\infty }$ possesses mild mixing properties. □

Theorem 12.

The chain-mixing property is present in the system $(H,d,f_{1,\infty })$ if and only if it is also present in the system $(\mathcal{K}\left(H\right),\mathcal{H},{\overline{f}}_{1,\infty })$.

Proof. 

The conclusion can be proved using a method similar to Theorem 6. □

Furthermore, the following theorem indicates that weak mixing is stronger than sensitivity.

Theorem 13.

If the mapping sequence ${\overline{f}}_{1,\infty }$ is weakly mixing, then it is also sensitive.

Proof. 

Assume that ${\overline{f}}_{1,\infty }$ exhibits a weak mixing property. For any ${ϵ}_0>0$, select two distinct sets $K_1$ and $K_2$ belonging to the set $\mathcal{K}\left(H\right)$ such that

$$\frac{1}{8}\mathcal{H}(K_1,K_2)={ϵ}_0.$$

For any set K in $\mathcal{K}\left(H\right)$, it is established that $\mathcal{H}(K,K_1)\ge 4{ϵ}_0$ or $\mathcal{H}(K,K_2)\ge 4{ϵ}_0$.

Assume that $\mathcal{H}(K,K_1)\ge 4{ϵ}_0$, since ${\overline{f}}_{1,\infty }$ is weakly mixing, for any $0\le ϵ\le {ϵ}_0$, there is a positive integer n such that

$${\overline{f}}_1^n\left(B_{ϵ}\left(K\right)\right)\cap B_{{ϵ}_0}\left(K_1\right)\ne \varnothing \mathrm{and}{\overline{f}}_1^n\left(B_{ϵ}\left(K\right)\right)\cap B_{{ϵ}_0}\left(K_2\right)\ne \varnothing .$$

Then there are two sets $K_3,K_4\in B_{ϵ}\left(K\right)$ such that ${\overline{f}}_1^n\left(K_3\right)\in B_{{ϵ}_0}\left(K_1\right)$, ${\overline{f}}_1^n\left(K_4\right)\in B_{{ϵ}_0}\left(K_2\right).$ So,

$$\begin{array}{cc}\hfill \mathcal{H}({\overline{f}}_1^n\left(K_3\right),{\overline{f}}_1^n\left(K\right))+\mathcal{H}({\overline{f}}_1^n\left(K_4\right),{\overline{f}}_1^n\left(K\right))& \ge \mathcal{H}({\overline{f}}_1^n\left(K_3\right),{\overline{f}}_1^n\left(K_4\right))\hfill \\ \hfill & \ge \mathcal{H}(K_1,K)-\mathcal{H}(K_1,{\overline{f}}_1^n\left(K_3\right))-\mathcal{H}(K,{\overline{f}}_1^n\left(K_4\right))\hfill \\ \hfill & \ge 4{ϵ}_0-{ϵ}_0-{ϵ}_0=2{ϵ}_0.\hfill \end{array}$$

Thus,

$$\mathcal{H}({\overline{f}}_1^n\left(K_3\right),{\overline{f}}_1^n\left(K\right))\ge {ϵ}_0\mathrm{or}\mathcal{H}({\overline{f}}_1^n\left(K_4\right),{\overline{f}}_1^n\left(K\right))\ge {ϵ}_0.$$

Hence, ${\overline{f}}_{1,\infty }$ possesses sensitivity. □

Some mappings retain certain chaotic properties when transitioning from point systems to set-valued systems. For instance, consider the hallmark characteristic ‘sensitive dependence on initial conditions’ of chaotic systems. The following example demonstrates how the logistic map maintains its sensitivity in both point and set-valued systems.

Example 1.

Consider the logistic map defined by $L\left(x\right)=4x(1-x)$ and the tent map given by

$$T\left(x\right)=\left\{\begin{array}{cc}2x\hfill & \mathrm{for}x\in [0,\frac{1}{2}];\hfill \\ 2(1-x)\hfill & \mathrm{for}x\in (\frac{1}{2},1].\hfill \end{array}\right.$$

There exists a mapping $h\left(x\right)={sin}^2\left(\frac{\pi }{2}x\right)$ for $x\in [0,1]$ such that the following diagram commutes.

$$\begin{array}{ccc}[0,1]& \stackrel{T}{\to }& [0,1]\\ \downarrow h& & \downarrow h\\ [0,1]& \underset{L}{\to }& [0,1]\end{array}$$

This indicates that T and L are topologically conjugate.

For the known fact of sensitive dependence on initial conditions of the tent map T and the fact that T and L are topologically conjugate, we can infer that L also exhibits sensitivity due to the preservation of sensitivity under topological conjugation. As established in Example 4.3 of [5], $\overline{T}$ shows sensitivity. Furthermore, Theorem 4 in [9] supports that $\overline{L}$ demonstrates this sensitivity as well, implying sensitivity of the logistic map in set-valued dynamical systems. Numerical simulations further corroborate these conclusions.

In chaotic dynamical systems, one of the key characteristics is the high sensitivity to minor variations in the initial state, leading to significantly different long-term evolutions even with slight differences in initial conditions. To explore the dynamic properties of the logistic map, this research utilizes it as a numerical tool, examining its behavior in both single-point and set-valued contexts. In the upcoming numerical simulations, we will focus on the evolution over time and through iterations of two initially proximate points within a single-point system. This observation will aid in our deep exploration and understanding of how minor initial state differences in a single-point system can impact long-term dynamic behavior.

Figure 1 shows that two initial values ($0.5$ and $0.5001$), which are very close to each other, exhibit significantly different states ($0.15205$ and $0.91534$) after 7632 iterations under the logistic map.

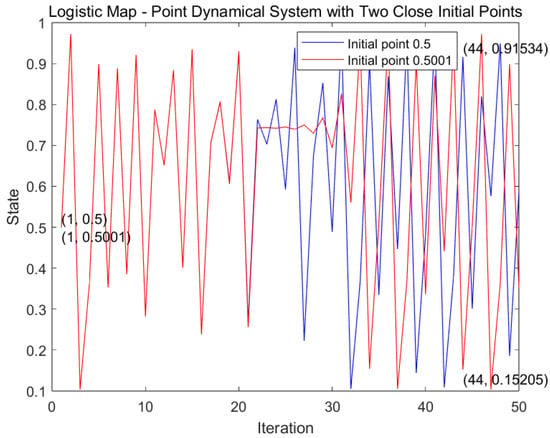
Figure 1. The sensitivity of Logistic map.

For the set-valued system, attention is directed towards a defined group of points, especially focusing on the effects of minor disturbances introduced at select locations.

From Figure 2 and Figure 3, one can observe that initially, the trajectories of the two sets of points are almost identical. However, as the number of iterations increases, the trajectories of the two point sets become completely different.

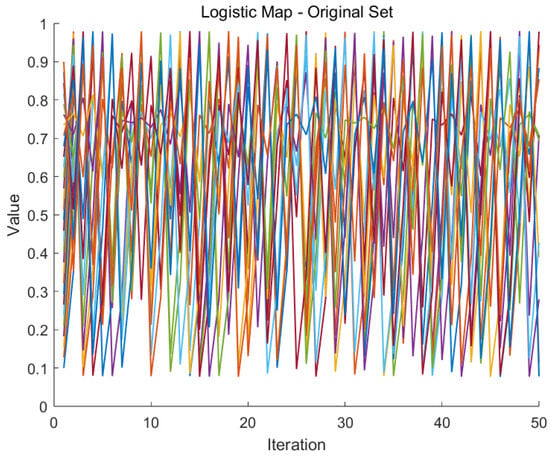
Figure 2. Trajectories of 30 equidistant points in [0.1,0.9] under the Logistic mapping (each point is randomly assigned a color).

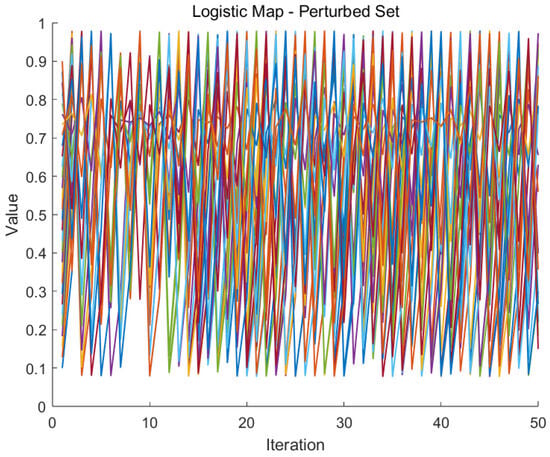
Figure 3. Trajectories of the new points obtained by adding small perturbations ${10}^{-5}$ to 30 points in Figure 2 under the Logistic mapping (each new point is assigned a corresponding color).

Based on numerical simulations of the logistic map in point systems and set-valued systems, the research finds that even minimal initial differences can significantly affect the system’s long-term behavior. In point systems, initially close points evolve into different trajectories over time. In set-valued systems, as iterations increase, the initial set and its perturbed counterpart transition from similar to entirely different trajectories, highlighting the sensitivity to initial values and unpredictability inherent in chaotic systems.

5. Conclusions

The study presented in this article elucidates the interconnectedness of chaotic characteristics between the dynamic systems $(\mathcal{K}\left(H\right),{\overline{f}}_{1,\infty })$ and $(H,f_{1,\infty })$. It establishes that $(\mathcal{K}\left(H\right),{\overline{f}}_{1,\infty })$ Devaney chaos aligns with that of $(H,f_{1,\infty })$ when additional specific conditions are applied. This research also substantiates that various mixing attributes of $(\mathcal{K}\left(H\right),{\overline{f}}_{1,\infty })$, such as weak mixing, mild mixing, chain-transitivity, and chain-mixing, correspond directly to those observed in $(H,f_{1,\infty })$. Moreover, this paper confirms that the presence of weak mixing in $(\mathcal{K}\left(H\right),{\overline{f}}_{1,\infty })$ inherently implies its sensitivity.

Finally, to illustrate the persistence of sensitivity in both original systems and set-valued systems within the logistic map, a simple numerical simulation is provided as an example. This demonstration highlights how the map maintains this fundamental characteristic across different system types.

This paper examines the connections between transitivity, sensitivity, mixing, and other properties of non-autonomous discrete dynamical systems and induced set-valued discrete dynamical systems. However, it does not delve into exploring stronger forms of m-transitivity and sensitivity, such as collective, ergodic, or syndetic cases. Additionally, the $\mathcal{F}$-chaotic and other properties of set-valued discrete dynamical systems (both autonomous and non-autonomous) remain unaddressed in this study. These topics, however, hold significant research value and will be further discussed in our upcoming research endeavors.