Abstract
This paper explores the cumulative entropy of the lifetime of an n-component coherent system, given the precondition that all system components have experienced failure at time t. This investigation utilizes the system signature to compute the cumulative entropy of the system’s lifetime, shedding light on a crucial facet of a system’s predictability. In the course of this research, we unearth a series of noteworthy discoveries. These include formulating expressions, defining bounds, and identifying orderings related to this measure. Further, we propose a technique to identify a preferred system on the basis of cumulative Kullback–Leibler discriminating information, which exhibits a strong relation with the parallel system. These findings contribute significantly to our understanding of the predictability of a coherent system’s lifetime, underscoring the importance of this field of study. The outcomes offer potential benefits for a wide range of applications where system predictability is paramount, and where the comparative evaluation of different systems on the basis of discriminating information is needed.
MSC:
60E05; 62B10; 62N05; 94A17
1. Introduction
The Shannon differential entropy has gained widespread adoption as a measure across various fields of research. It was introduced by Shannon in their article [1], and since then, it has become a cornerstone of probability theory. Suppose we have a non-negative random variable X, which is absolutely continuous with a probability density function . If the expected value of the logarithm exists, then the expression is referred to as the Shannon differential entropy. This is the situation being described in this scenario. This definition allows us to quantify the uncertainty associated with the random variable X by measuring the amount of information required to describe it. Owing to its adaptability and usefulness, this metric has gained widespread adoption in a multitude of research domains, making it an essential tool for any researcher looking to explore probability distributions.
While differential entropy has many advantages, a fascinating substitute for conventional entropy was suggested by Rao and colleagues in their paper [2], which they called cumulative residual entropy (CRE). Unlike differential entropy, which uses , CRE uses to obtain a measure of entropy. The definition of CRE is given by
.
With its ability to capture the residual uncertainty of a distribution, CRE is particularly useful in situations where the tails of the distribution are of interest. The CRE has emerged as the preferred measure for characterizing information dispersion in problems related to reliability theory, which is a robust metric that has been extensively employed in numerous studies, such as those carried out by [3,4,5,6,7,8], to name a few. A representation of the cumulative entropy (CE), which is an information measure similar to Equation (1), is provided by Di Crescenzo and Longobardi in their work [9] given by
where is the cumulative distribution function (cdf) of a random variable . Like CRE, CE is nonnegative and if, and only if, X is a constant.
Several measures of dynamic information have been proposed to characterize the uncertainty in suitable functionals of the random lifetime X of a system. We review two such measures, namely, the dynamic cumulative residual entropy (introduced by Asadi and Zohrevand [10]) and the cumulative past entropy (proposed by Di Crescenzo and Longobardi in [11]), which are defined as the dynamic cumulative entropy of and , respectively. In this case, the dynamic cumulative residual entropy is defined as
where is the survival function of . Di Crescenzo and Longobardi [11] pointed out that in many realistic scenarios, uncertainty is not necessarily related to the future. For example, if a system that starts operating at time 0 is only observed at predetermined inspection times and is found to be “down” at time t, then the uncertainty is dependent on the specific moment within at which it failed. When faced with such scenarios, the cumulative past entropy proves to be a valuable metric. It is defined as follows:
where is the cdf of . Uncertainty is a fundamental characteristic of numerous real-world systems, impacting not only future events but also past occurrences. As a result, the concept of entropy has been extended to encompass the uncertainty associated with past events, distinct from residual entropy, which quantifies uncertainty in future events. The exploration of past entropy and its statistical applications has garnered significant attention in the literature, as evidenced by notable works such as Di Crescenzo and Longobardi [9] and Nair and Sunoj [12]. Gupta et al. [13] have made substantial contributions to the field by delving into the properties and applications of past entropy within the framework of order statistics. Their research focuses on investigating the residual and past entropies of order statistics and establishing stochastic comparisons between them. Through their investigations, they have shed new light on the fundamental principles underpinning past entropy and its role in statistical analysis. The works of Gupta et al. [13], along with the aforementioned studies, collectively highlight the growing interest and significance of past entropy in various domains. These studies provide valuable insights into the statistical properties and practical applications of past entropy, contributing to a deeper understanding of the role of uncertainty in both past and future events. In the recent years, numerous researchers have demonstrated a strong inclination toward investigating the information characteristics of coherent systems, which can be seen in [8,14,15,16,17,18] and the references therein. Recently, Kayid [19] investigated the Tsallis entropy of coherent systems when all components are alive at time . Mesfioui et al. [20] have also delved into the Tsallis entropy such systems, adding to the current body of captivating research in this area. More recently, Kayid and Shrahili [21,22] investigated the Shannon differential and Renyi entropy of coherent systems when all components have failed at time . The aim of this study is to examine the uncertainty properties of the lifetimes of coherent systems, with a particular focus on the cumulative past entropy. In fact, when all components have failed at time , we focus on coherent systems consisting of n components by utilizing the system signature.
Therefore, the result of this paper is organized as follows: In Section 2, we provide an expression for the CE of a coherent system’s lifetime when component lifetimes are independent and identically distributed, given that all components of the system have failed at time t by implementing the concept of system signature. In Section 3, some useful bounds are presented. A new criterion is represented to choose a preferable among coherent systems in Section 4. Some concluding remarks are also given in Section 5.
2. CE of the Past Lifetime
In this section, we present by applying the system signature concept to define the past lifetime CE of a coherent system, which can have an arbitrary structure. To this aim, we assume that at a specific time , all components of the system have failed and employ the concept of system signature, which is described by an n-dimensional vector = where the i-th element is defined as . (see [23]). Several recent papers have addressed the concept of survival signature. For example, Rusnak et al. [24] and Coolen et al. [25] have made notable contributions in this area.
Consider a coherent system whose component lifetimes are independent and identically distributed (i.i.d.), and whose signature vector = is known. Assuming that the coherent system has failed at time t, we can represent the past lifetime of the system as . Khaledi and Shaked [26] have established results that allow us to express the cumulative distribution function of in terms of their findings as
where
denotes the cdf of . It is important to note that represents the elapsed time since the failure of the component with a lifetime of in the system, given that the system has failed at or before time . Furthermore, according to Equation (6), corresponds to the ith order statistic of n i.i.d. components with a cumulative distribution function of . Hereafter, we provide a formula for computing the cumulative entropy of . For this purpose, we define , and use , which is essential to our approach. Using this transformation, we can express the cumulative entropy of in terms of V, as shown in the upcoming theorem.
Theorem 1.
We can express the CE of as follows
where for all and
represents the survival function of such that
is the survival function of i-th order statistics where lifetimes are uniformly distributed. Moreover, is the quantile function of .
Proof.
Substituting and using Equations (5) and (6), we obtain:
where the last equality is obtained by using the change in variables, . Furthermore, represents the survival function of , as given in Equation (9). By utilizing Equation (8), we can derive the relationship in Equation (7), which serves to conclude the proof. □
Suppose we examine an i-out-of-n system with a system signature of , where . Then, we obtain a special case of Equation (7), which reduces to
The following theorem is a direct consequence of Theorem 1 and characterizes the aging properties of the system’s components. It is noteworthy to mention that a random variable X is said to have a decreasing reversed hazard rate (DRHR) if its reversed hazard rate function, , declines for .
Theorem 2.
If X is DRHR, then is increasing in t.
Proof.
By noting that Equation (7) can be rewritten as
for all . We can easily confirm that holds for all Therefore, we obtain:
If , then . Therefore, if X has a DRHR property, then
By utilizing Equation (11), we can infer that for all , thus completing the proof. □
We provide an example to demonstrate the applications of Theorems 1 and 2 in engineering systems. This example highlights how these theorems can be utilized for analyzing the CE of a failed coherent system and for investigating the aging characteristics of a system.
Example 1.
To compute the precise value of using Equation (7), we require the lifetime distributions of the system components. For this purpose, let us assume the following lifetime distributions.
- (i)
- Let X follow the uniform distribution in . Since from Equation (7), we immediately obtainThe analysis indicates that the cumulative entropy of increases as time t increases, which aligns with previous research on the behavior of cumulative entropy for specific categories of random variables. For instance, it is established that the uniform distribution has a DRHR property, indicating that the CE of should increase as time t increases, as per Theorem 2.
- (ii)
- Let us examine a random variable X, whose cdf is defined as follows:After performing some algebraic manipulations, we haveCalculating this relationship explicitly is challenging; thus, we must rely on numerical methods to proceed. In Figure 2, we illustrate the cumulative entropy of for different values of k. It is evident that X exhibits a DRHR property for all . Referring back to Theorem 2, we can see that rises with increasing t when .
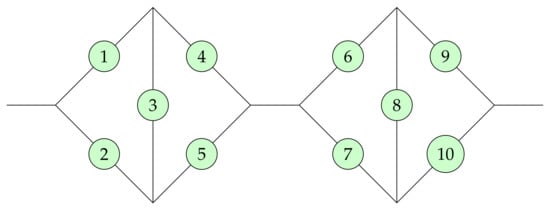
Figure 1.
A coherent system with signature = .
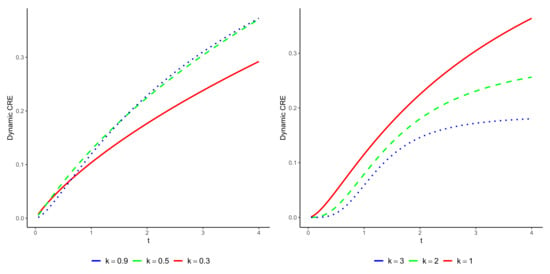
Figure 2.
Cumulative entropy of with respect to t for various values of , using the cdf Part (ii) from Example 1.
The example above provides insights into the complex interplay between the CE of a random variable and time, emphasizing the significance of accounting for the decreasing reversed hazard rate property when analyzing such systems. The results suggest that the DRHR property of X is a critical factor in determining the temporal dynamics of the CE of , which could have significant consequences in various areas of research, including the study of intricate systems and the development of efficient data compression methods.
The notion of duality is a valuable tool in engineering reliability to reduce the computational workload of computing the signatures of all coherent systems of a given magnitude by roughly half (as demonstrated, for instance, in Kochar et al. [27]). Particularly, if stands for lifetime of a coherent system with signature = then its dual system with lifetime has a signature . By utilizing the principle of duality, we have the following theorem, which facilitates the computational intricacy entailed in calculating the past cumulative entropy of .
Theorem 3.
If holds true for all and t, then, for all and , we can conclude that .
Proof.
It is crucial to emphasize that the equation is valid for all and . Furthermore, since holds for all , we can leverage Equation (7) to derive the subsequent expression:
and this completes the proof. □
Remark 1.
The aforementioned theorem explores a significant property of system components’ lifetimes, which has practical applications in various fields. Specifically, we consider the property where the component lifetimes satisfy the condition for all and . This property is particularly relevant in scenarios involving power distributions, uniform distributions, certain special cases of beta distributions, and other distributions that exhibit this behavior. Understanding and utilizing this property can yield valuable insights into and benefits in system reliability analysis. The practical implications of this property extend to diverse fields, including engineering, telecommunications, finance, and so on.
3. Bounding the Cumulative Entropy of Past Lifetime
When working with extremely intricate systems that consist of numerous components, calculating can be a difficult undertaking. To handle this difficulty, investigators have newly proposed uncertainty bounds for the component lifetimes in coherent systems. This approach is explored in works such as [18,21,22] and the related literature. In the next theorem, we obtain bounds for based on the CE of the parent distribution . These bounds can be useful in certain circumstances, particularly when calculating the precise cumulative past entropy is challenging.
Proposition 1.
If denotes the past lifetime of the system, then
where , and .
Proof.
The upper bound is given by:
The constant is dependent on the distribution of V. Using the same method, we can also derive a lower bound for . □
It is worth noting that in the aforementioned theorem is obtained by computing the infimum of for , and is obtained by computing the supremum of the same ratio. The given bounds offer valuable means of approximating based on .
Remark 2.
It is worth noting that the lower bound in Proposition 1 equals zero for all coherent systems that satisfy either or . This is especially true for coherent systems with more than one i.i.d. component, as outlined in [8].
Proposition 2.
The lower bound for the CE of is given by
where .
Proof.
Utilizing Equation (7) and the concavity of the function , we can derive the following lower bound:
where is the cumulative entropy of . □
Notice that equality in Equation (12) holds for i-out-of-n systems in the sense that we have , for and , for , and then . When the lower bounds in both parts of Theorems 1 and 2 can be computed, one may use the maximum of the two lower bounds.
Example 2.
In this example, we analyze a coherent system with the signature , consisting of i.i.d. component lifetimes drawn from a uniform distribution in the interval . If denotes the past lifetime of this system, Remark 2 yields , while and . As per Theorem 1, we deduce that is bounded accordingly:
Moreover, as , we can represent the lower bound provided in Equation (12) as:
4. Preferable System
Hereafter, we consider two nonnegative random variables, X and Y, that represent the lifetimes of two items having the same supports . For any given time , we define their respective past lifetimes as and . To this end, we also introduce the distribution functions of and by
respectively. In their groundbreaking work, Di Crescenzo and Longobardi [28] introduced a novel concept that utilizes the mean past lifetimes of nonnegative random variables X and Y with cdfs F and G, by and respectively. They proposed a past version of the cumulative Kullback–Leibler information measure that is defined as a function of the mean past lifetimes of X and Y as follows:
provided that whenever . In order to advance our findings, we define a novel measure of distance that is symmetric and applicable to two distributions. This measure is called symmetric past cumulative (SPC) Kullback–Leibler divergence and is denoted by the shorthand .
Definition 1.
Consider two non-negative past random variables, and , with shared support and cumulative distribution functions and , respectively. In this case, we introduce the SPC Kullback–Leibler divergence as a measure of distance between the two variables as follows:
for all .
The proposed measure, defined as Equation (17), possesses several desirable properties. First and foremost, it is nonnegative and symmetric. Moreover, the value of is equal to zero if, and only if, and are almost equal everywhere. In addition to these properties, we also observe the following.
Lemma 1.
Suppose we have three random variables, , , and , each with cumulative distribution functions , , and , respectively. If the stochastic ordering holds, then the following statement is true:
- (i)
- (ii)
for all .
Proof.
Given that the function is decreasing in the interval and increasing in , we can make an important inference from the condition for . Specifically, we can conclude that:
- (i)
- (ii)
- .
By integrating both sides of the descriptions (i) and (ii), we can obtain the desired result. □
As holds for any coherent system, from Lemma 1, we have the following theorem.
Theorem 4.
If is the lifetime of a coherent system based on , then:
- (i)
- (ii)
In the subsequent analysis, the implications of Theorem 3 lead us to propose a measure that allows for the selection of a system with superior reliability characteristics. Theorem 3 provides valuable insights into the reliability of systems and offers a framework for comparing different system configurations. Building upon this theorem, we introduce a novel measure that captures the reliability performance of various systems and aids in the selection process. Traditional stochastic ordering may not be sufficient for pairwise comparisons of system performance, particularly for certain system structures. In some cases, pairs of systems remain incomparable using stochastic orders. In this case, alternative metrics for comparing system performance are being explored. Hereafter, we will introduce a new method to choose a preferable system. It is worth noting that engineers typically favor those that offer extended operational time. As a result, it is crucial to ensure that the systems being compared possess comparable attributes. Furthermore, assuming that all other attributes are equal, we can choose parallel system lifetime since it has a longer past lifetime than alternative systems. In other words, from Equation (6), we have
Rather than relying on comparisons between two systems at a time we can explore a system that has a structure or distribution that is more similar to that of the parallel system. Essentially, our goal is to determine which of these systems is more similar or closer in configuration to the parallel system while also having a dissimilar configuration from that of the series system. To this aim, one can employ the idea of SPC given in Definition 1. Consequently, we put forth the following symmetric past divergence (SPD) measure for as
Theorem 3 establishes that . It is evident that if, and only if, and if and only if . Put simply, we can deduce that if is closer to 1, the distribution of is more akin to the parallel system’s distribution. On the other hand, if is closer to , the distribution of is more similar to the series system’s distribution. Based on this, we suggest the subsequent definition.
Definition 2.
Consider two coherent systems, each with n component lifetimes that are independent and identically distributed, alongside signatures and . Let and represent their respective past lifetimes. At time t, we assert that is more desirable than with regard to the symmetric past distance (SPD) measure, indicated by , if, and only if, for all .
It is important to note that the equivalence of and does not always mean that . In accordance with Definition 2, we can define . From Equation (17) and the aforementioned conversions, we obtain
for . Then, from (19), we obtain
If we assume that the components are i.i.d., we can derive the equations and . By referencing Theorem 3, we can arrive at an intriguing result.
Proposition 3.
If is the lifetime of a coherent system based on , then , for .
The next theorem is readily apparent.
Theorem 5.
Assuming the conditions outlined in Definition 2, if the is exponentially distributed, then the SPD measure is independent of time . In other words, holds true for all .
Proof.
Using the memoryless property, we can deduce that holds true for all . Consequently, we can conclude that the result holds true. □
Example 3.
Consider two coherent systems with past lifetimes and , in which the component lifetimes are exponentially distributed with cdf . The signatures of these systems are given by and respectively. Although these systems are not comparable using traditional stochastic orders, we can compare them using the SPD measure. By using numerical computation, we obtain and . This indicates that the system with lifetime is less similar to the parallel system than the system with lifetime .
Theorem 6.
Suppose that and denote the lifetimes of two coherent systems with signatures and , respectively, based on n i.i.d. components with the same cdf F. If , we can assert that .
Proof.
We can derive the desired outcome from Theorem 2.3 of Khaledi and Shaked [26]. Specifically, if we have two probability vectors denoted and , where , then we have . By applying Lemma 1, we can obtain and . These relations enable us to arrive at the desired outcome due to the relation defined in Equation (18). □
An exciting discovery is that the comparison based on SPD can perform as a necessary condition for the usual stochastic order. Let us assume we have two coherent systems, denoted by and , each composed of several components with lifetimes . If we find that is less reliable than in the stochastic order, denoted as , we can conclude that the system is also less reliable than in the SPD order, i.e., . This comparison of systems through the SPD order can be useful when comparing systems that are otherwise difficult to assess. It is worth noting that if we find that two systems and are equally reliable in the stochastic order, i.e., , then they are also equivalently reliable in the SPD order, i.e., . This highlights the potential power of the SPD order in system analysis.
5. Conclusions
In recent years, there has been a notable surge in interest surrounding the quantification of uncertainty associated with the lifetime of engineering systems. This criterion holds the potential to provide valuable insights into predicting and understanding the uncertainty surrounding system lifetimes. To address this need, the concept of cumulative entropy (CE) has emerged as an extension of Shannon’s entropy, offering a highly effective tool for analyzing and characterizing uncertainty in such scenarios. This paper has presented the application of CE to the lifetime of a system in which all components have failed at time t. By leveraging the concept of system signature, we have examined the properties of the proposed CE metrics, including their expressions and bounds in terms of CE uncertainties. Through a series of illustrative examples, we have effectively demonstrated the practical implications and findings of our research. In summary, this study has introduced criteria based on relative CE, enabling the identification of a preferred system that exhibits similarities to a parallel system. By utilizing CE to quantify uncertainty, we have provided a comprehensive framework for evaluating system lifetimes and making informed decisions regarding system design which can be seen as an advantage of the new measure. However, it can be somewhat difficult to compute the mentioned measure when the structure of the systems is complex or systems have large components. The insights gained from our research have the potential to contribute significantly to the field of engineering system reliability and offer valuable guidance for practical applications. As a whole, this paper has contributed to the ongoing exploration of uncertainty quantification in engineering systems by introducing and investigating the application of CE. By providing a solid foundation of theoretical analysis, examples, and criteria for system selection, our work aims to advance the understanding and utilization of CE in the context of system lifetime uncertainty. It is worth pointing out that the current analysis focuses on continuous-type random variables; however, we agree that exploring the application of RTE to discrete-type variables is an intriguing direction for future research. Discrete-time approaches, such as those used in telecommunication and networking systems where time slots are considered, indeed offer interesting opportunities to apply entropy-based measures. The concept of RTE can be extended to discrete-type variables by appropriately adapting the underlying probability models and considering the discrete nature of the observations. In such scenarios, the RTE for discrete-type variables can provide insights into the information content and uncertainty associated with the ordering of discrete observations within a given time slot or sequence. We hope to incorporate this suggestion in our future investigations.
Author Contributions
Conceptualization, M.S.; methodology, M.S.; software, M.K.; validation, M.S. and M.K.; formal analysis, M.S.; investigation, M.K.; resources, M.K.; writing—original draft preparation, M.S.; writing—review and editing, M.S. and M.K.; visualization, M.K.; supervision, M.K.; project administration, M.S.; funding acquisition, M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Researchers Supporting Project (number: RSP2023R464), King Saud University, Riyadh, Saudi Arabia.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
The authors acknowledge financial support from the Researchers Supporting Project (number: RSP2023R464), King Saud University, Riyadh, Saudi Arabia.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Rao, M.; Chen, Y.; Vemuri, B.C.; Wang, F. Cumulative residual entropy: A new measure of information. IEEE Trans. Inf. Theory 2004, 50, 1220–1228. [Google Scholar] [CrossRef]
- Rao, M. More on a new concept of entropy and information. J. Theor. Probab. 2005, 18, 967–981. [Google Scholar] [CrossRef]
- Asadi, M.; Zohrevand, Y. On the dynamic cumulative residual entropy. J. Stat. Plan. Inference 2007, 137, 1931–1941. [Google Scholar] [CrossRef]
- Baratpour, S. Characterizations based on cumulative residual entropy of first-order statistics. Commun. Stat. Methods 2010, 39, 3645–3651. [Google Scholar] [CrossRef]
- Baratpour, S.; Rad, A.H. Testing goodness-of-fit for exponential distribution based on cumulative residual entropy. Commun. -Stat.-Theory Methods 2012, 41, 1387–1396. [Google Scholar] [CrossRef]
- Navarro, J.; del Aguila, Y.; Asadi, M. Some new results on the cumulative residual entropy. J. Stat. Plan. Inference 2010, 140, 310–322. [Google Scholar] [CrossRef]
- Toomaj, A.; Zarei, R. Some new results on information properties of mixture distributions. Filomat 2017, 31, 4225–4230. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Longobardi, M. On cumulative entropies. J. Stat. Plan. Inference 2009, 139, 4072–4087. [Google Scholar] [CrossRef]
- Asadi, M.; Ebrahimi, N. Residual entropy and its characterizations in terms of hazard function and mean residual life function. Stat. Probab. Lett. 2000, 49, 263–269. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Longobardi, M. Entropy-based measure of uncertainty in past lifetime distributions. J. Appl. Probab. 2002, 39, 434–440. [Google Scholar] [CrossRef]
- Nair, N.U.; Sunoj, S. Some aspects of reversed hazard rate and past entropy. Commun. -Stat.-Theory Methods 2021, 32, 2106–2116. [Google Scholar] [CrossRef]
- Gupta, R.C.; Taneja, H.; Thapliyal, R. Stochastic comparisons of residual entropy of order statistics and some characterization results. J. Stat. Theory Appl. 2014, 13, 27–37. [Google Scholar] [CrossRef][Green Version]
- Abdolsaeed, T.; Doostparast, M. A note on signature-based expressions for the entropy of mixed r-out-of-n systems. Nav. Res. Logist. (NRL) 2014, 61, 202–206. [Google Scholar]
- Toomaj, A.; Doostparast, M. On the Kullback Leibler information for mixed systems. Int. J. Syst. Sci. 2016, 47, 2458–2465. [Google Scholar] [CrossRef]
- Asadi, M.; Ebrahimi, N.; Soofi, E.S.; Zohrevand, Y. Jensen–Shannon information of the coherent system lifetime. Reliab. Eng. Syst. Saf. 2016, 156, 244–255. [Google Scholar] [CrossRef]
- Toomaj, A. Renyi entropy properties of mixed systems. Commun. -Stat.-Theory Methods 2017, 46, 906–916. [Google Scholar] [CrossRef]
- Toomaj, A.; Chahkandi, M.; Balakrishnan, N. On the information properties of working used systems using dynamic signature. Appl. Stoch. Model. Bus. Ind. 2021, 37, 318–341. [Google Scholar] [CrossRef]
- Kayid, M.; Alshehri, M.A. Tsallis entropy of a used reliability system at the system level. Entropy 2023, 25, 550. [Google Scholar] [CrossRef]
- Mesfioui, M.; Kayid, M.; Shrahili, M. Renyi Entropy of the Residual Lifetime of a Reliability System at the System Level. Axioms 2023, 12, 320. [Google Scholar] [CrossRef]
- Kayid, M.; Shrahili, M. Rényi Entropy for Past Lifetime Distributions with Application in Inactive Coherent Systems. Symmetry 2023, 15, 1310. [Google Scholar] [CrossRef]
- Kayid, M.; Shrahili, M. On the Uncertainty Properties of the Conditional Distribution of the Past Life Time. Entropy 2023, 25, 895. [Google Scholar] [CrossRef]
- Samaniego, F.J. System Signatures and Their Applications in Engineering Reliability; Springer Science & Business Media: Boston, MA, USA, 2007; Volume 110. [Google Scholar]
- Rusnak, P.; Zaitseva, E.; Coolen, F.P.; Kvassay, M.; Levashenko, V. Logic differential calculus for reliability analysis based on survival signature. IEEE Trans. Dependable Secur. Comput. 2022, 20, 1529–1540. [Google Scholar] [CrossRef]
- Coolen, F.P.; Coolen-Maturi, T.; Al-Nefaiee, A.H. Nonparametric predictive inference for system reliability using the survival signature. Proc. Inst. Mech. Eng. Part J. Risk Reliab. 2014, 228, 437–448. [Google Scholar] [CrossRef]
- Khaledi, B.E.; Shaked, M. Ordering conditional lifetimes of coherent systems. J. Stat. Plan. Inference 2007, 137, 1173–1184. [Google Scholar] [CrossRef]
- Kochar, S.; Mukerjee, H.; Samaniego, F.J. The “signature” of a coherent system and its application to comparisons among systems. Nav. Res. Logist. (NRL) 1999, 46, 507–523. [Google Scholar] [CrossRef]
- Di Crescenzo, A.; Longobardi, M. Some properties and applications of cumulative Kullback–Leibler information. Appl. Stoch. Model. Bus. Ind. 2015, 31, 875–891. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).