Improvement in Some Inequalities via Jensen–Mercer Inequality and Fractional Extended Riemann–Liouville Integrals
Abstract
:1. Introduction
2. Trapezoid-Type Inequalities with Jensen–Mercer Inequality
3. Midpoint-Type Inequalities with Jensen–Mercer Inequality
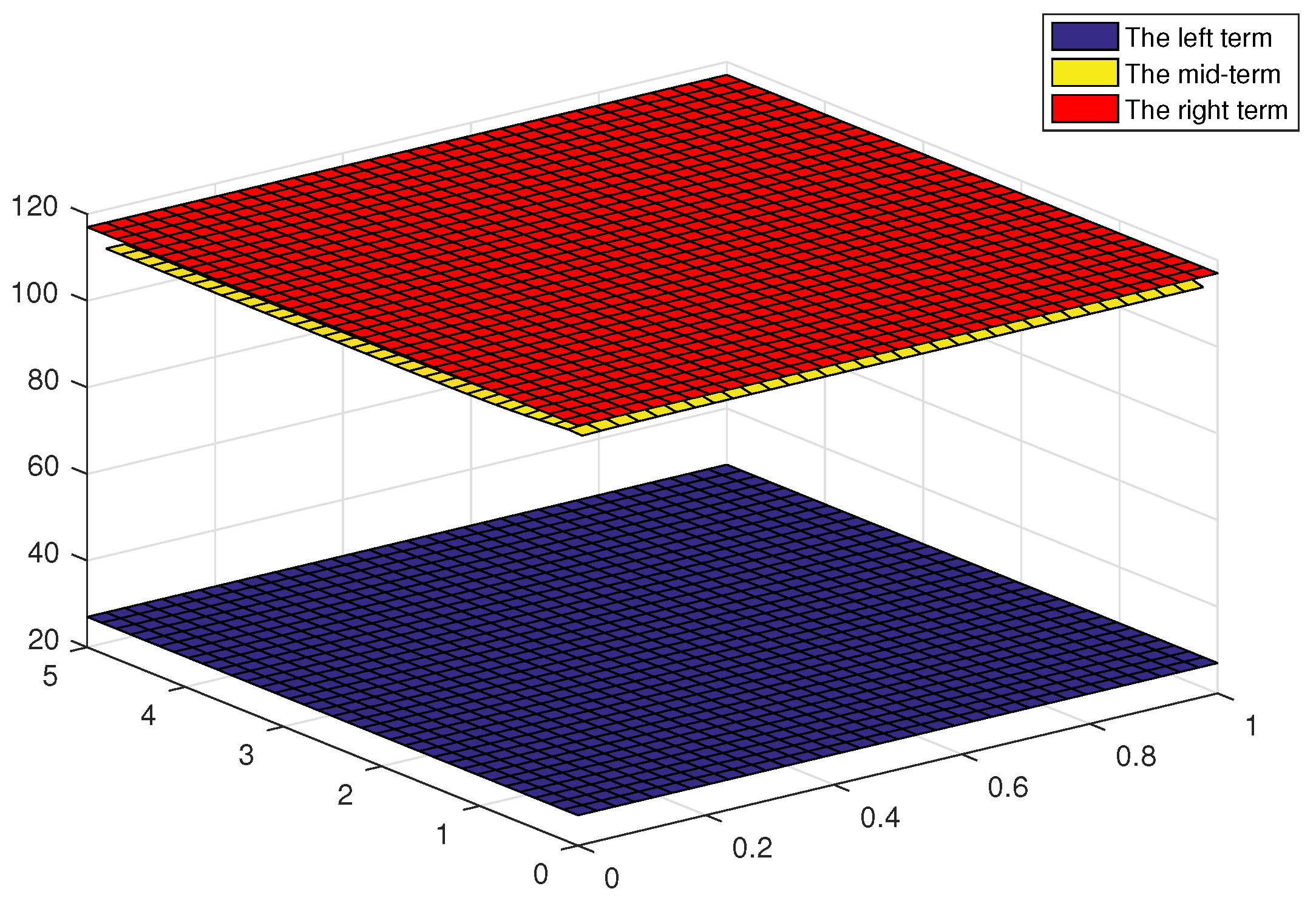
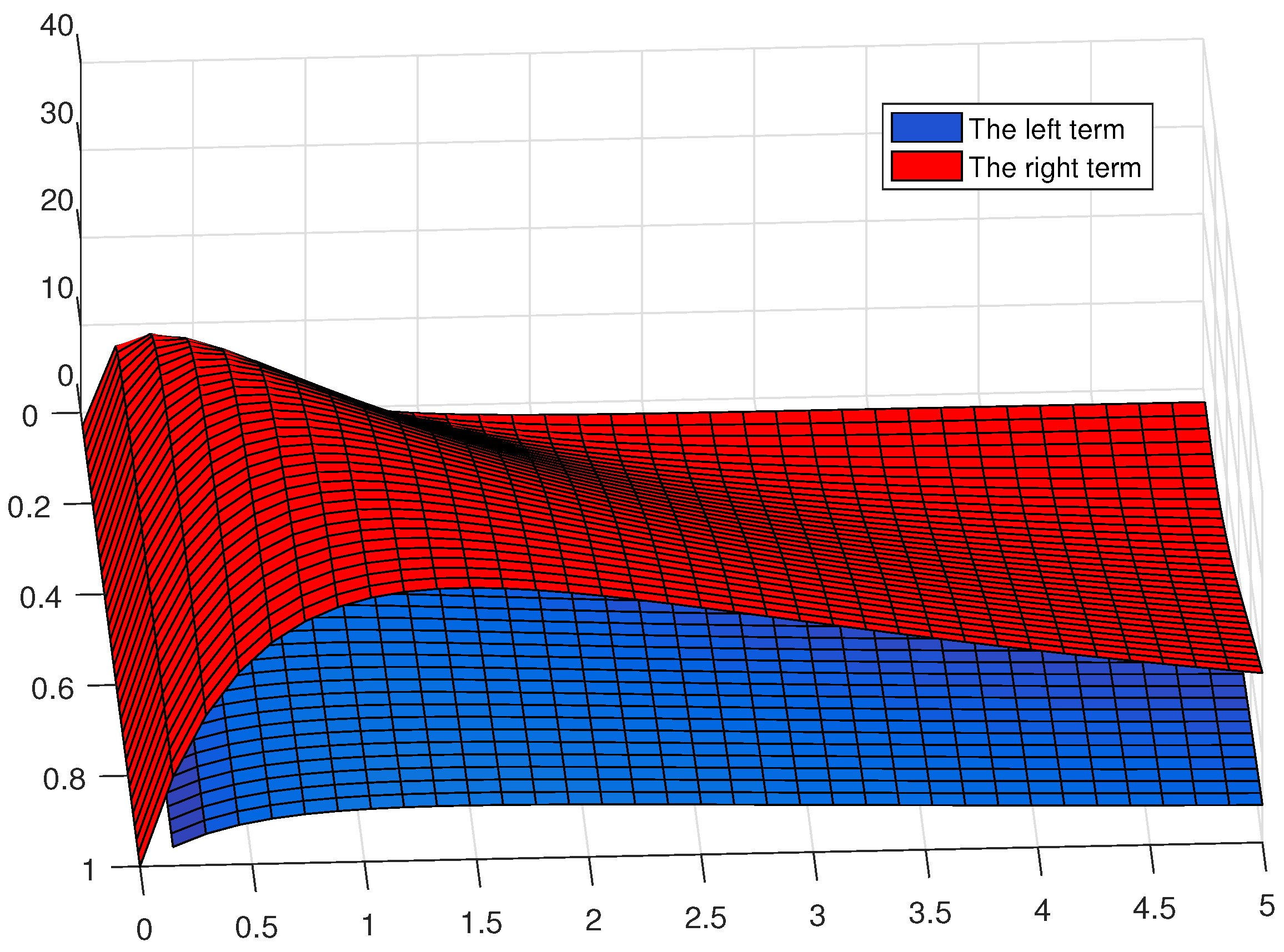
4. Some Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Panagiotopoulos, P.D. Nonconvex energy functions. Hemivariational inequalities and substationarity principles. Acta Mech. 1983, 48, 111–130. [Google Scholar] [CrossRef]
- Panagiotopoulos, P.D. Inequality Problems in Mechanics and Applications: Convex and Nonconvex Energy Functions; Birkhäuser: Boston, MA, USA, 1985. [Google Scholar]
- Panagiotopoulos, P.D. Hemivariational inequalities and their applications. In Topics in Nonsmooth Mechanics; Birkhäuser: Basel, Swizerland, 1988. [Google Scholar]
- Fan, K. Some properties of convex sets related to fixed point theorems. Math. Ann. 1984, 266, 519–537. [Google Scholar] [CrossRef]
- Gil, A.; Segura, J.; Temme, N.M. Evaluation of the Modified Bessel Function of the Third Kind of Imaginary Orders. J. Comput. Phys. 2002, 175, 398–411. [Google Scholar] [CrossRef]
- Rappoport, J.M. Tables of Modified Bessel Functions ; Nauka: Moscow, Russia, 1979. (In Russian) [Google Scholar]
- Abdeljawad, T.; Baleanu, D. Monotonicity results for fractional difference operators with discrete exponential kernels. Adv. Differ. Equ. 2017, 2017, 78. [Google Scholar] [CrossRef]
- Agarwal, R.; Purohit, S.D.; Kritika. A mathematical fractional model with nonsingular kernel for thrombin receptor activation in calcium signalling. Math. Methods Appl. Sci. 2019, 42, 7160–7171. [Google Scholar] [CrossRef]
- Agarwal, R.; Yadav, M.P.; Baleanu, D.; Purohit, S.D. Existence and uniqueness of miscible flow equation through porous media with a non singular fractional derivative. AIMS Math. 2020, 5, 1062–1073. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Purohit, S.D.; Swroop, R. A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math. Model. Nat. Phenom. 2019, 14, 304. [Google Scholar] [CrossRef]
- Katugampola, U.N. A new approach to generalized fractional derivatives. Bull. Math. Anal. Appl. 2014, 6, 1–15. [Google Scholar]
- Mishra, A.M.; Baleanu, D.; Tchier, F.; Purohit, S.D. Certain Results Comprising the Weighted Chebyshev Function Using Pathway Fractional Integrals. Mathematics 2019, 7, 896. [Google Scholar] [CrossRef]
- Mishra, A.M.; Kumar, D.; Purohit, S.D. Unified integral inequalities comprising pathway operators. AIMS Math. 2020, 5, 399–407. [Google Scholar] [CrossRef]
- Sarikaya, M.Z.; Set, E.; Yaldiz, H.; Basak, N. Hermite–Hadamard’s inequalities for fractional integrals and related fractional inequalities. Math. Comput. Model. 2013, 57, 2403–2407. [Google Scholar] [CrossRef]
- Set, E.; Çelik, B. On generalizations related to the left side of Fejer’s inequality via fractional integral operator. Miskolc Math. Notes 2017, 18, 1043–1057. [Google Scholar] [CrossRef]
- Set, E.; İşcan, İ.; Zeki Sarikaya, M.; Emin Özdemir, M. On new inequalities of Hermite–Hadamard–Fejér type for convex functions via fractional integrals. Appl. Math. Comput. 2015, 259, 875–881. [Google Scholar] [CrossRef]
- Abbas Baloch, I.; Chu, Y.-M. Petrović-type inequalities for harmonic h-convex functions. J. Funct. Spaces 2020, 2020, 3075390. [Google Scholar] [CrossRef]
- Adil Khan, M.; Mohammad, N.; Nwaeze, E.R.; Chu, Y.-M. Quantum Hermite–Hadamard inequality by means of a Green function. Adv. Differ. Equ. 2020, 2020, 99. [Google Scholar] [CrossRef]
- Rashid, S.; Abdeljawad, T.; Jarad, F.; Noor, M.A. Some Estimates for Generalized Riemann-Liouville Fractional Integrals of Exponentially Convex Functions and Their Applications. Mathematics 2019, 7, 807. [Google Scholar] [CrossRef]
- Butt, S.I.; Umar, M.; Rashid, S.; Akdemir, A.O.; Chu, Y.M. New Hermite–Jensen–Mercer-type inequalities via k-fractional integrals. Adv. Differ. Equ. 2020, 2020, 635. [Google Scholar] [CrossRef]
- Set, E.; Gözpinar, A.; Butt, S.I. A study on Hermite—Hadamard-type inequalities via new fractional conformable integrals. Asian-Eur. J. Math. 2021, 14, 2150016. [Google Scholar] [CrossRef]
- Hyder, A.-A.; Barakat, M.A.; Fathallah, A. Enlarged integral inequalities through recent fractional generalized operators. J. Inequalities Appl. 2022, 2022, 95. [Google Scholar] [CrossRef]
- Barakat, M.A.; Hyder, A.-A.; Rizk, D. New fractional results for Langevin equations through extensive fractional operators. AIMS Math. 2023, 8, 6119–6135. [Google Scholar] [CrossRef]
- Peajcariaac, J.E.; Tong, Y.L. Convex Functions, Partial Orderings, and Statistical Applications; Academic Press: Cambridge, MA, USA, 1992. [Google Scholar]
- Hadamard, J. Etude sur les propriétés des fonctions entières et en particulier d’une fonction considérée par Riemann. J. Mathématiques Pures Appliquées 1893, 58, 171–215. [Google Scholar]
- Mitrinović, D.S.; Pečarić, J.E.; Fink, A.M. On the Jensen inequality. Univ. Beograd. Publ. Elektrotehn Fak. Ser. Mat. Fis. 1979, 639–677, 50–54. [Google Scholar]
- Matković, A.; Pečarić, J.; Perić, I. A variant of Jensens inequality of Mercers type for operators with application. Linear Algebra Appl. 2006, 418, 551–564. [Google Scholar] [CrossRef]
- Dragomir, S.S.; Pearce, C.E.M. Selected Topics on Hermite-Hadamard Inequalities and Applications; RGMIA Monographs, Victoria University: Melbourne, VC, Canada, 2000. [Google Scholar]
- Kian, M.; Moslehian, M.S. Refinements of the operator Jensen-Mercer inequality. Electron. J. Linear Algebra 2013, 26, 50. [Google Scholar] [CrossRef]
- Mercer, A.M. A variant of Jensens inequality. J. Ineq. Pure Appl. Math. 2003, 4, 73. [Google Scholar]
- Fink, A.M.; Jodeit, M., Jr. Jensen inequalities for functions with higher monotonicities. Aequ. Math. 1990, 40, 26–43. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, North-Holland Mathematics Studies, 204; Elsevier Sci. B.V.: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Jarad, F.; Uğurlu, E.; Abdeljawad, T.; Baleanu, D. On a new class of fractional operators. Adv. Differ. Equ. 2017, 2017, 247. [Google Scholar] [CrossRef]
- Set, E.; Choi, J.; Gözpinar, A. Hermite-Hadamard type inequalities involving nonlocal conformable fractional integrals. Malays. J. Math. Sci. 2021, 15, 33–43. [Google Scholar]
- Hezenci, H.; Budak, H. A remark on midpoint-type inequalities for conformable fractional integrals. Miskolc Math. Notes, 2023; submitted. [Google Scholar]
- Öǧülmüs, H.; Sarikaya, M.Z. Hermite-Hadamard-Mercer type inequalities for fractional integrals. Filomat 2021, 35, 2425–2436. [Google Scholar] [CrossRef]
- Butt, S.I.; Akdemir, A.O.; Nasir, J.; Jarad, F. Some Hermite-Jensen-Mercer like inequalities for convex functions through a certain generalized fractional integrals and related results. Miskolc Math. Notes 2020, 21, 689–715. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hyder, A.-A.; Almoneef, A.A.; Budak, H. Improvement in Some Inequalities via Jensen–Mercer Inequality and Fractional Extended Riemann–Liouville Integrals. Axioms 2023, 12, 886. https://doi.org/10.3390/axioms12090886
Hyder A-A, Almoneef AA, Budak H. Improvement in Some Inequalities via Jensen–Mercer Inequality and Fractional Extended Riemann–Liouville Integrals. Axioms. 2023; 12(9):886. https://doi.org/10.3390/axioms12090886
Chicago/Turabian StyleHyder, Abd-Allah, Areej A. Almoneef, and Hüseyin Budak. 2023. "Improvement in Some Inequalities via Jensen–Mercer Inequality and Fractional Extended Riemann–Liouville Integrals" Axioms 12, no. 9: 886. https://doi.org/10.3390/axioms12090886
APA StyleHyder, A.-A., Almoneef, A. A., & Budak, H. (2023). Improvement in Some Inequalities via Jensen–Mercer Inequality and Fractional Extended Riemann–Liouville Integrals. Axioms, 12(9), 886. https://doi.org/10.3390/axioms12090886







