Abstract
Quantum Markov chains (QMCs) and open quantum random walks (OQRWs) represent different quantum extensions of the classical Markov chain framework. QMCs stand as a more profound layer within the realm of Markovian dynamics. The exploration of both QMCs and OQRWs has been a predominant focus over the past decade. Recently, a significant connection between QMCs and OQRWs has been forged, yielding valuable applications. This bridge is particularly impactful when studying QMCs on tree structures, where it intersects with the realm of phase transitions in models naturally arising from quantum statistical mechanics. Furthermore, it aids in elucidating statistical properties, such as recurrence and clustering. The objective of this paper centers around delving into the intricate structure of QMCs on Cayley trees in relation to OQRWs. The foundational elements of this class of QMCs are built upon using classical probability measures that encompass the hierarchical nature of Cayley trees. This exploration unveils the pivotal role that the dynamics of OQRWs play in shaping the behavior of the Markov chains under consideration. Moreover, the analysis extends to their classical counterparts. The findings are further underscored by the examination of notable examples, contributing to a comprehensive understanding of the outcomes.
MSC:
47N50; 81V25; 47L90
1. Introduction
QMCs were introduced by L. Accardi in [1,2], and subsequently, they have been studied by many authors in the 1D case [3,4,5,6,7,8]. Important applications of QMCs have been investigated [7,9,10,11,12]. Namely, significant use cases of Markov chains in modeling collaborative interactions for detecting proteins within biological systems have been explored in prior studies, as evidenced by research, such as [13,14,15,16,17].
Motivated by the theory of Dobrushin’s Markov random fields [18], several extensions of QMCs to graphs and trees have been suggested [19,20]. Namely, a quantum phase transitions approach to QMCs on Cayley trees has been investigated [21,22]. Quantum Markov states (QMSs) [3] are particular QMCs. The tree extension of QMSs has been described in detail [23].
Over the past few decades, quantum random walks [24,25,26,27,28,29,30,31] have been extensively studied due to their usefulness as powerful tools for constructing quantum algorithms. From a probabilistic perspective, open quantum random walks (OQRWs) [32,33,34,35,36,37] represent a natural and direct extension of classical Markov chains, exhibiting many interesting statistical and physical properties.
Recently, a significant connection between QMCs and OQRWs has been established [38,39,40]. In [41], the study focused on investigating QMCs on trees associated with OQRWs in relation to phase transition phenomena. Moreover, a mean entropy formulae for the associated tree-indexed QMS has been calculated (see also [42,43]). In addition, the concept of stopping rules for QMCs on trees has been explored in [44,45]. Additionally, in [46], the recurrence problem for a specific class of QMCs on trees was studied with a connection to phase transitions in an Ising-type model. In [47], the notion of recurrence was associated with QMCs on trees in conjunction with OQRWs.
In this paper, we explore a new class of quantum Markov chains (QMCs) on the semi-infinite Cayley tree of order. We express their correlations using classical probability measures that are not Markovian. For each density matrix , a probability measure is naturally assigned to the space of trajectories as follows:
for specific edge-paths in the Cayley tree.
The obtained characterization of a QMC extends the results of previous works [41,47,48]. We point out that the hierarchical structure of the Cayley tree is essentially used in expressing the considered QMCs, as well as in defining the associated classical probability measure.
It should be emphasized that this work opens up possibilities for further investigations on OQRWs. Potential future research directions include exploring the action of symmetry groups on general QMCs on Cayley trees, studying phase transitions, investigating recurrence in the sense of [47], examining ergodic properties, and exploring entropy for the class of QMCs studied in this paper. These topics will be the focus of forthcoming studies.
The structure of this paper is outlined as follows. After the preliminary Section 2, we proceed to Section 3 where we introduce QMCs on trees. Section 4 presents a structure theorem for generalized QMCs associated with OQRWs. Finally, Section 5 is dedicated to expressing the classical probability measures associated with the QMCs under consideration. Section 6 is devoted to some illustrative examples.
2. Preliminaries on Trees
By (), we denote the semi-infinite regular tree (Cayley tree) of order k. The vertex represents its root. The nearest-neighbor nodes are denoted as if and only if . A path on the tree is a finite list of pairwise distinct vertices , where m is referred to as the length of the path. The distance between two vertices is defined as the length of the unique path joining them.
A coordinate structure (see Figure 1) is naturally assigned to : each vertex is identified with an n-tuple , where for . The root o is represented as . The elements of the nth level can be listed as follows:
Put
To each vertex , we associate the unique path joining it to the root o as follows:
The direct successors set of u is defined by
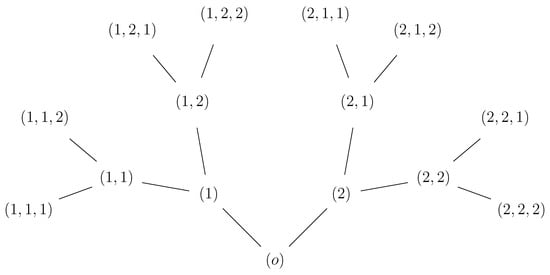
Figure 1.
Coordinate structure on .
For , we define
In particular, . Let be the set of vertices v whose unique path joining v to o contains . In other words,
Let The sub-tree , with vertex set , is isomorphic to . Define
The map defines a graph isomorphism [49] from into .
3. Quantum Markov Chains on Trees
For each , let be a C-algebra of observables on the site u with unit . Define for each n. We then have the embedding
where for each bounded region , we have . The local algebra associated with the increasing net is denoted as
and the associated quasi-local algebra is given by
For further details about quasi-local algebras, we refer to [50].
The set of states of a C-algebra is denoted as . Consider unital C-algebras and , where is a subset of , and is a subset of . It is important to note the following definitions:
- A quasi-conditional expectation [51] is a linear map that is completely positive and identity-preserving, satisfying the condition for all and .
- A (Markov) transition expectation is a linear map between two unitary -algebras that is completely positive and identity-preserving.
For a specific transition expectation denoted by from to , the map defined as
is a transition expectation with respect to the triplet .
The hierarchical structure of the Cayley tree is evident from the following equation:
This equation allows us to consider local transition expectations (see [23]), denoted by , from into . We then define the map
which provides a transition expectation from into .
Definition 1.
A (backward) quantum Markov chain (QMC) on is characterized by the triplet , where we have the following:
- is the initial state;
- For each n, the map is a transition expectation from into ;
- For each n, is a positive boundary condition.
Remark 1.
The definition above introduces quantum Markov chains on trees as a triplet that generalizes the definitions considered in [22] by incorporating boundary conditions. Additionally, it extends the recent unified definition of quantum Markov chains in the one-dimensional case [5] to trees.
Let be a unital C-algebra with identity . For each , we define . The graph isomorphism given by (4) can be extended to an isomorphism from to as follows:
Here, for each , we define , which means that a appears as the u-th component of the infinite tensor product. The notation represents the inverse isomorphism of , mapping to . Finally, let be the inverse isomorphism from to [48].
4. Main Result
Consider a connected graph with a countable vertex set . Let and be two separable Hilbert spaces. We define as an orthonormal basis of indexed by the graph . Furthermore, let .
For each vertex , we associate the C-algebra of observable . Additionally, for each pair , the transition from the state vector to the state vector is represented by an operator , satisfying the following:
Consider the density operator of the form
In the sequel, for the sake of simplicity of the calculations, it is assumed that for all (see [39], Remark 4.5 for other kinds of initial states).
Let us consider the following:
Following [39,41], one defines
For each , we set
Consider the symmetric group , which consists of permutations on the set . Each permutation defines an automorphism, denoted by , on . This automorphism can be represented as a linear extension of the following mapping:
Lemma 1.
Let . The map defined by
is a Markov transition expectation from into . Moreover,
for every Here,
Proof.
The map is completely positive from into itself. Moreover, the Kraus map and the partial trace are completely positive. Then,
is a composition of completely positive maps.
From (12) for each , one has
This leads to (16). On the other hand, because
Therefore, is a Markov transition expectation. This finishes the proof. □
For each , we consider the shifted transition expectation
from into . For and , one defines
The subsequent probability measure encompasses the open OQRW dynamics, taking into account the hierarchical structure of the Cayley trees via edge-paths.
For each , we introduce the following subsets of vertices:
Denote
In particular, for , we denote simply as . For each , we denote the largest integer such that . Specifically, if for some , then . Please refer to Figure 2 for an illustration of the elements of in the case of the Cayley tree with order 3.

Figure 2.
Coordinate structure on with highlight of elements of with .
The set of vertices in which the coordinates do not incorporate ℓ as an element is defined by
In particular, for each , we denote
For every we set
Theorem 1.
Proof.
Let us first prove the existence of the limit (8) for
and . Let . For and one has
It follows that
Then, the strongly finite limit defined by (8) exists and gives rise to a positive functional . Based on Lemma 1, the map is completely positive and implements a quantum channel with intermediate purification (CPIP). Therefore, represents a quantum Markov chain (QMC) on . Furthermore, we obtain the following:
One has
We are going to show by induction on p that
Starting with the case . For and . Let and , and for each , one has
One can see that . Then,
One has
It follows that
It follows that
Let us suppose that the induction hypothesis stated in (25) is valid for a specific value of p. In this case, it implies that
where
From the induction hypothesis (25), one finds
One has
and
Summing up, one gets
This proves that (25) holds for any integer . In particular, for , one obtains the expression of
By applying the initial state to the expression above, we obtain (22). This step concludes the proof. □
Remark 2.
In the notation of Theorem 1, the case has been studied in [41]. In that situation, the QMC φ is represented by
For any localized element , here
Meanwhile, the case leads to the QMC given by (22) which has a much more sophisticated structure.
Remark 3.
The equation (22) reveals that the essential constituents of the QMC are formed by the probability measures (1). Consequently, the correlations of the QMC under study are governed by the OQRW dynamics. In the subsequent section, we will observe that this substantial reliance of the QMC on the OQRW dynamics is further demonstrated by focusing on a diagonal subalgebra.
5. Classical Probability Associated with OQRW
In this section, we examine the classical probability measures associated with the quantum Markov chains described in Theorem 1. Consider the set equipped with the cylindrical -algebra . Let denote an orthonormal basis for . We define as the diagonal subalgebra of spanned by the projections .
Given a state on , we associate a classical probability measure on , which operates on atomic events as follows.
From (17) and (11), one finds
The classical probability associated with the QMC given by (26) is the following:
Remark 4.
The distinction between the two QMCs and becomes evident in the expressions of their corresponding classical probability measures and . Specifically, when restricted to the cylinder , the distribution focuses solely on the atomic events where for every . On the other hand, the distribution assigns probabilities to all atoms that satisfy the condition
as depicted in Figure 2.
6. Application to OQRW on
In this section, we consider , where is an integer. Let and be an infinite-dimensional Hilbert space with an orthonormal basis . We assume that satisfy . We define
In the following, we will represent as i for simplicity. We will maintain the same notations as in the previous sections and focus on the case where , specifically the Cayley tree . Let . The set consists of the vertices in the form , where and . It can be observed that . As a result, it divides the set .
6.1. Example 1
Let us consider as the complex vector space of dimension 2, denoted by . Let
be the transition operators. By performing a straightforward computation, we can establish that B and C satisfy the equation . By utilizing the identities , , and , it becomes evident that the only indices , where , for which the quantity
is non-zero correspond to for all .
More specifically, for each , we have
For , we have .
6.2. Example 2
Take as above and consider the transition operators
A simple calculation shows that B and C satisfy the identity . Using the identities, , and
We can easily deduce that the only non-zero words formed by picking letters from the alphabet are of the form
This leads us to consider two distinct cases, depending on whether m is even or odd. If m is odd, we have
Then, using , we obtain
If m is even, we have
and
7. Discussion
The complete understanding of the structure of general quantum Markov chain systems (QMCSs) associated with open quantum random walks (OQRWs) has been achieved. Contrary to the previous works, the correlation functions of the present QMCSs are heavily influenced by the dynamics of OQRWs. The probability measures defining these sequences establish potentially non-Markovian dynamics, which presents a significant avenue for future research. Exploring the entropy of this class of QMCSs and investigating their diagonalizability also pose intriguing questions for further exploration. Nevertheless, considering the recent advancements in this field, numerous other pertinent challenges are now approachable, including topics such as phase transitions, recurrence, clustering, and ergodic properties.
Author Contributions
Conceptualization, A.S. and F.M.; Methodology, A.S. and T.H.; Software, A.A. and T.H.; Validation, T.H.; Formal analysis, A.A.; Investigation, A.S., T.H., F.M. and A.A.; Data curation, T.H. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
The authors gratefully acknowledge Qassim University, represented by the Deanship of Scientific Research, for the financial support for this research under the number (cba-2020-1-3-I-10173) during the academic year 1442 AH/2020 AD.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Accardi, L. Noncommutative Markov chains. In Proceedings of the International School of Mathematical Physics, Camerino, Italy, 30 September–12 October 1974; pp. 268–295. [Google Scholar]
- Accardi, L. On noncommutative Markov property. Funct. Anal. Appl. 1975, 8, 1–8. [Google Scholar] [CrossRef]
- Accardi, L.; Frigerio, A. Markovian cocycles. Proc. R. Ir. Acad. 1983, 83A, 251–263. [Google Scholar]
- Accardi, L.; Khrennikov, A.; Ohya, M. Quantum Markov Model for Data from Shafir—Tversky Experiments in Cognitive Psychology. Open Syst. Inf. Dyn. 2009, 16, 371–385. [Google Scholar] [CrossRef]
- Accardi, L.; Souissi, A.; Soueidy, E.G. Quantum Markov chains: A unification approach. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 2020, 23, 2050016. [Google Scholar] [CrossRef]
- Gudder, S. Quantum Markov chains. J. Math. Phys. 2008, 49, 072105. [Google Scholar] [CrossRef]
- Lardizabal, C.F. A quantization procedure based on completely positive maps and Markov operators. Quantum Inf. Process. 2013, 12, 1033–1051. [Google Scholar] [CrossRef]
- Liu, C.; Petulante, N. On Limiting distributions of quantum Markov chains. Int. J. Math. Math. Sci. 2011, 2011, 740816. [Google Scholar] [CrossRef]
- Dhahri, A.; Fagnola, F. Potential theory for quantum Markov states and other quantum Markov chains. Anal. Math. Phys. 2023, 13, 31. [Google Scholar] [CrossRef]
- Fannes, M.; Nachtergaele, B.; Werner, R.F. Finitely correlated states on quantum spin chains. Commun. Math. Phys. 1992, 144, 443–490. [Google Scholar] [CrossRef]
- Feng, Y.; Yu, N.; Ying, M. Model checking quantum Markov chains. J. Comput. Syst. Sci. 2013, 79, 1181–1198. [Google Scholar] [CrossRef]
- Kümmerer, B. Quantum Markov processes and applications in physics. In Quantum Independent Increment Processes II; Lecture Notes in Mathematics; Springer: Berlin, Germany, 2006; Volume 1866, pp. 259–330. [Google Scholar]
- Abundo, M.; Accardi, L.; Rosato, N. A Markovian model for cooperative interactions in proteins. Math. Models Methods Appl. Sci. 1995, 6, 5. [Google Scholar] [CrossRef]
- Abundo, M.; Accardi, L.; Finazzi; Agrò, A.; Mei, G.; Rosato, N. A stochastic model for the sigmoidal behaviour of cooperative biological systems. Biophys. Chem. 1996, 58, 313–323. [Google Scholar] [CrossRef] [PubMed]
- Abundo, M.; Accardi, L.; Stella, L.; Rosato, N. A stochastic model for the cooperative relaxation of proteins, based on a hierarchy of interactions between amino acid residues. Math. Models Methods Appl. Sci. 1998, 8, 327–358. [Google Scholar] [CrossRef]
- Accardi, L.; Abundo, M. A stochastic model for the cooperative behaviour of biological systems. Amino Acids 1999, 17, 120–121. [Google Scholar]
- Accardi, L.; Abundo, M.; Rosato, N.; Stella, L. Analysing protein energy data by a stochastic model for cooperative interactions: Comparison and characterization of cooperativity. J. Math. Biol. 2002, 44, 341–359. [Google Scholar]
- Dobrushin, R.L. The description of a random field by means of conditional probabilities and conditions of its regularity. Theor. Probab. Appl. 1968, 13, 197–224. [Google Scholar] [CrossRef]
- Accardi, L.; Fidaleo, F. Quantum Markov fields. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 2003, 6, 123–138. [Google Scholar] [CrossRef]
- Liebscher, V. Markovianity of quantum random fields. In Quantum Probability and Infinite-Dimensional Analysis, Proceedings of the Burg Conference, Burg, Germany, 15–20 March 2001; Freudenberg, W., Ed.; QP-PQ Series; World Scientific: Singapore, 2003; Volume 15, pp. 151–159. [Google Scholar]
- Accardi, L.; Mukhamedov, F.; Saburov, M. On Quantum Markov Chains on Cayley tree II: Phase transitions for the associated chain with XY -model on the Cayley tree of order three. Ann. Henri Poincare 2011, 12, 1109–1144. [Google Scholar] [CrossRef]
- Mukhamedov, F.; Barhoumi, A.; Souissi, A. Phase transitions for quantum Markov chains associated with Ising type models on a Cayley tree. J. Stat. Phys. 2016, 163, 544–567. [Google Scholar] [CrossRef]
- Mukhamedov, F.; Souissi, A. Quantum Markov States on Cayley trees. J. Math. Anal. Appl. 2019, 473, 313–333. [Google Scholar] [CrossRef]
- Kempe, J. Quantum random walks: An introductory overview. Contemp. Phys. 2003, 44, 307–327. [Google Scholar] [CrossRef]
- Kitagawa, T. Topological phenomena in quantum walks: Elementary introduction to the physics of topological phases. Quantum Inf. Process. 2012, 11, 1107–1148. [Google Scholar] [CrossRef]
- Konno, N.; Yoo, H.J. Limit theorems for open quantum random walks. J. Stat. Phys. 2013, 150, 299–319. [Google Scholar] [CrossRef]
- Konno, N. A new type of limit theorems for one-dimensional quantum random walks. J. Math. Soc. Jpn. 2005, 57, 1179–1195. [Google Scholar] [CrossRef]
- Ohno, H. Unitary equivalent classes of one-dimensional quantum walks. Quantum Inf. Process. 2016, 15, 3599–3617. [Google Scholar] [CrossRef]
- Portugal, R. Quantum Walks and Search Algorithms; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Venegas-Andraca, S.E. Quantum walks: A comprehensive review. Quantum Inf. Process. 2012, 11, 1015–1106. [Google Scholar] [CrossRef]
- Accardi, L.; Watson, G.S. Quantum random walks. In Quantum Probability and Applications IV, Proceedings of the Year of Quantum Probability, Rome, Italy, 1987; Accardi, L., von Waldenfels, W., Eds.; LNM; 1989; Springer: Berlin/Heidelberg, Germany; Volume 1396, pp. 73–88.
- Lardizabal, C.F.; Souza, R.R. On a class of quantum channels, open random walks and recurrence. J. Stat. Phys. 2015, 159, 772–796. [Google Scholar] [CrossRef][Green Version]
- Attal, S.; Petruccione, F.; Sabot, C.; Sinayskiy, I. Open Quantum Random Walks. J. Stat. Phys. 2012, 147, 832–852. [Google Scholar] [CrossRef]
- Carbone, R.; Pautrat, Y. Homogeneous open quantum random walks on a lattice. J. Stat. Phys. 2015, 160, 1125–1152. [Google Scholar] [CrossRef]
- Carbone, R.; Pautrat, Y. Open quantum random walks: Reducibility, period, ergodic properties. Ann. Henri Poincaré 2016, 17, 99–135. [Google Scholar] [CrossRef]
- Goolam Hossen, Y.H.; Sinayskiy, I.; Petruccione, F. Non-reversal Open Quantum Walks. Open Syst. Inf. Dyn. 2018, 25, 1850017. [Google Scholar] [CrossRef]
- Machida, T. Phase transition of an open quantum walk. Int. J. Quantum Inf. 2021, 19, 2150028. [Google Scholar] [CrossRef]
- Dhahri, A.; Ko, C.K.; Yoo, H.J. Quantum Markov chains associated with open quantum random walks. J. Stat. Phys. 2019, 176, 1272–1295. [Google Scholar] [CrossRef]
- Dhahri, A.; Mukhamedov, F. Open quantum random walks, quantum Markov chains and recurrence. Rev. Math. Phys. 2019, 31, 1950020. [Google Scholar] [CrossRef]
- Ko, C.K.; Yoo, H.J. Quantum Markov chains associated with unitary quantum walks. J. Stoch. Anal. 2020, 1, 4. [Google Scholar] [CrossRef]
- Mukhamedov, F.; Souissi, A.; Hamdi, T. Open quantum random walks and quantum Markov chains on trees I: Phase transitions. Open Syst. Inf. Dyn. 2022, 29, 2250003. [Google Scholar] [CrossRef]
- Accardi, L.; Ohya, M.; Watanabe, N. Dynamical entropy through quantum Markov chains. Open Syst. Inf. Dyn. 1997, 4, 71–87. [Google Scholar] [CrossRef]
- Ohmura, K.; Watanabe, N. Quantum dynamical mutual entropy based on AOW entropy. Open Syst. Inf. Dyn. 2019, 26, 1950009. [Google Scholar] [CrossRef]
- Accardi, L.; Koroluk, D. Stopping times for quantum Markov chains. J. Theor. Probab. 1992, 5, 521–535. [Google Scholar] [CrossRef]
- Souissi, A. On Stopping Rules for Tree-indexed Quantum Markov chains. Infin. Dimens. Anal. Quantum Probab. Relat. Top. 2023, 2250030. [Google Scholar] [CrossRef]
- Barhoumi, A.; Souissi, A. Recurrence of a class of quantum Markov chains on trees. Chaos Solitons Fractals 2022, 164, 112644. [Google Scholar] [CrossRef]
- Mukhamedov, F.; Souissi, A.; Hamdi, T.; Andolsi, A. Open quantum random walks and quantum Markov Chains on trees II: The recurrence. Quantum Inf. Process. 2023, 22, 232. [Google Scholar] [CrossRef]
- Souissi, A.; Mukhamedov, F.; Barhoumi, A. Tree-Homogeneous Quantum Markov Chains. Int. J. Theor. Phys. 2023, 62, 19. [Google Scholar] [CrossRef]
- McKay, B.D.; Piperno, A. Practical graph isomorphism, II. J. Symb. Comput. 2014, 60, 94–112. [Google Scholar] [CrossRef]
- Bratteli, O.; Robinson, D.W. Operator Algebras and Quantum Statistical Mechanics I; Springer: New York, NY, USA, 1987. [Google Scholar]
- Accardi, L.; Cecchini, C. Conditional expectations in von Neumann algebras and a Theorem of Takesaki. J. Funct. Anal. 1982, 45, 245–273. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).