Quasi-Magical Fermion Numbers and Thermal Many-Body Dynamics
Abstract
1. Introduction
2. Statistical Notion of Order
3. SU2-Based Fermion Models
3.1. Lipkin Model
3.2. The AFP Model
3.3. Hamiltonian Matrices
4. Statistical Mechanics Indicators
Order Quantifiers
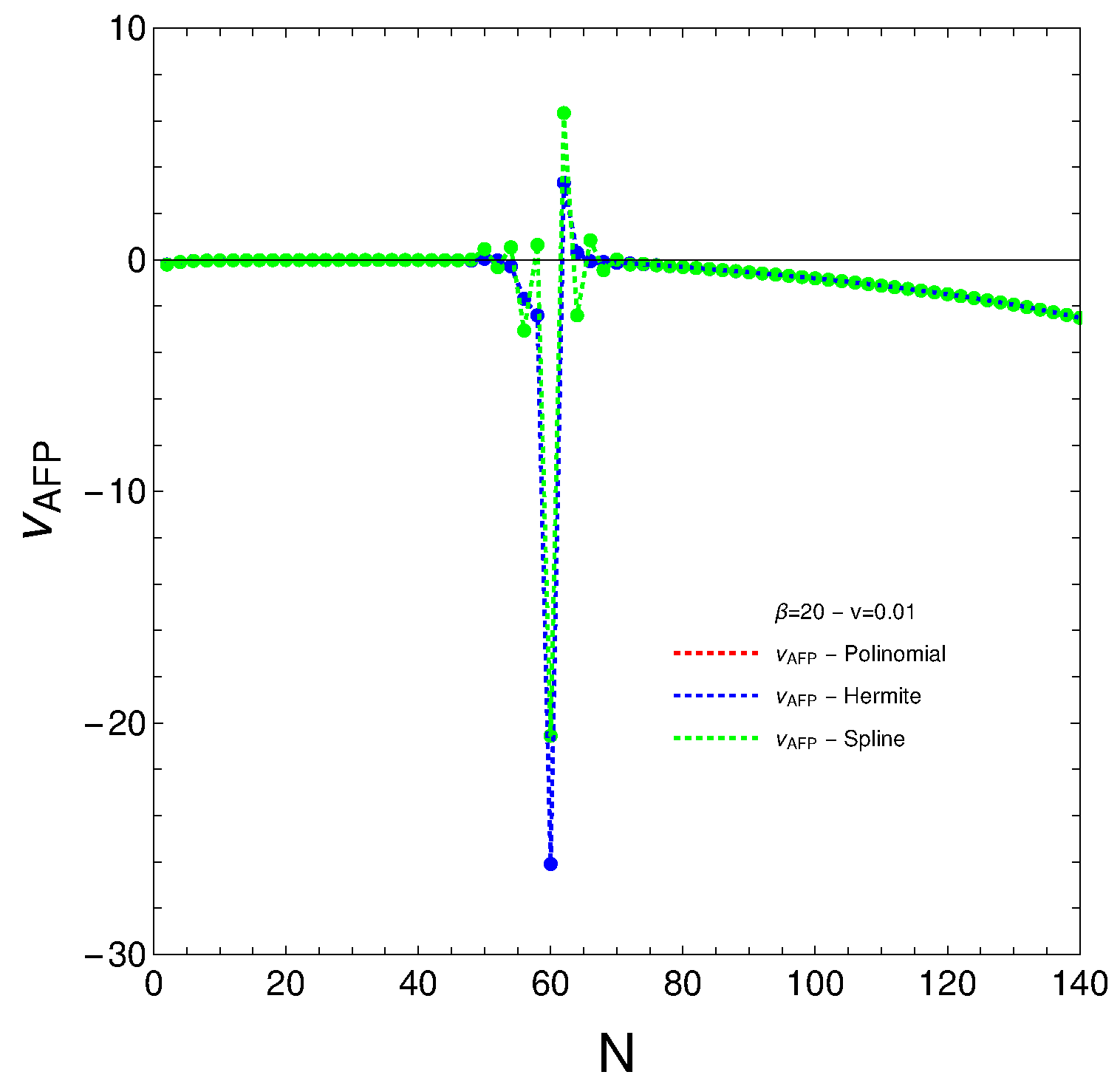
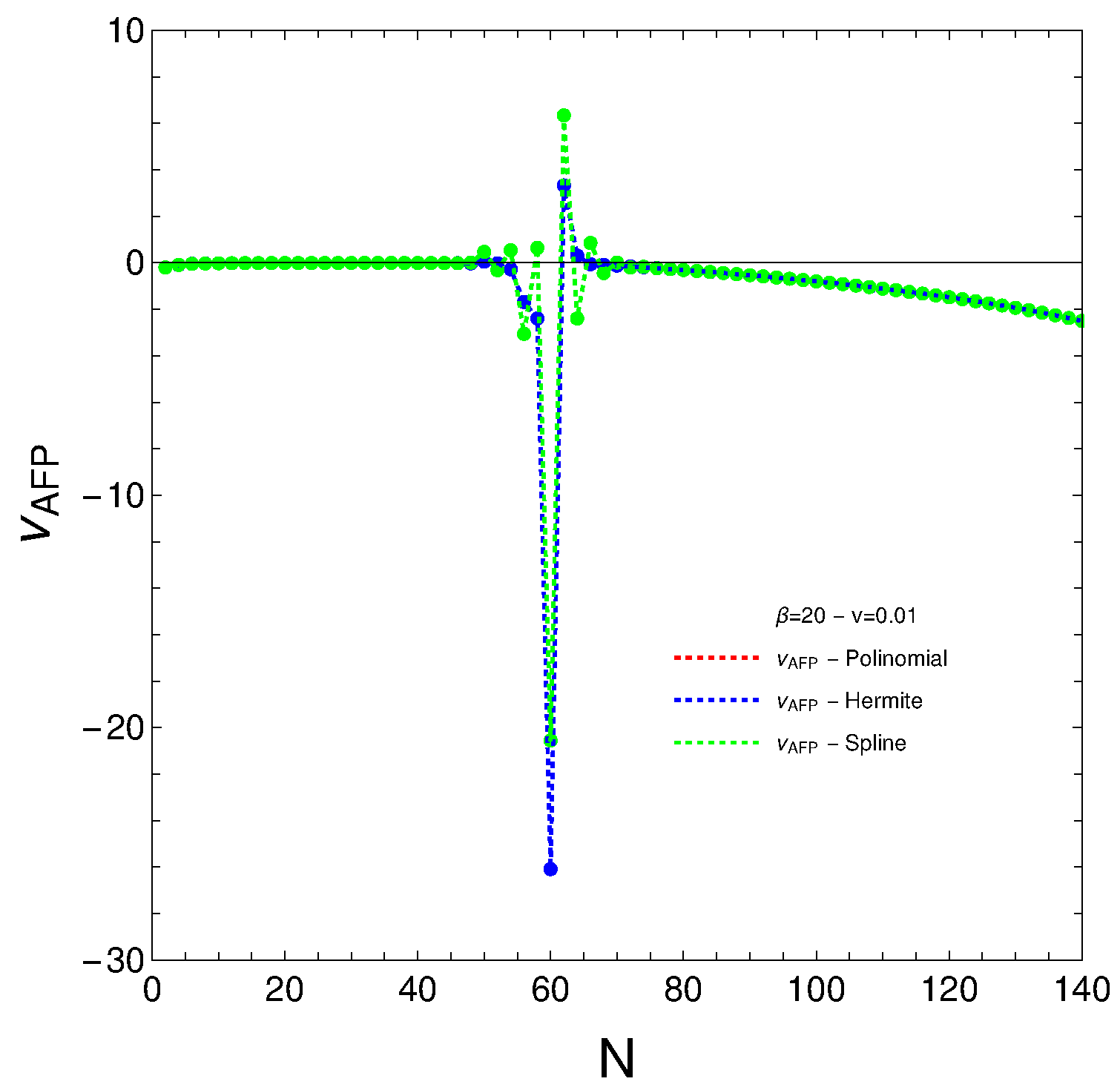
5. Singular Values for the Fermion Numbers
6. Conclusions
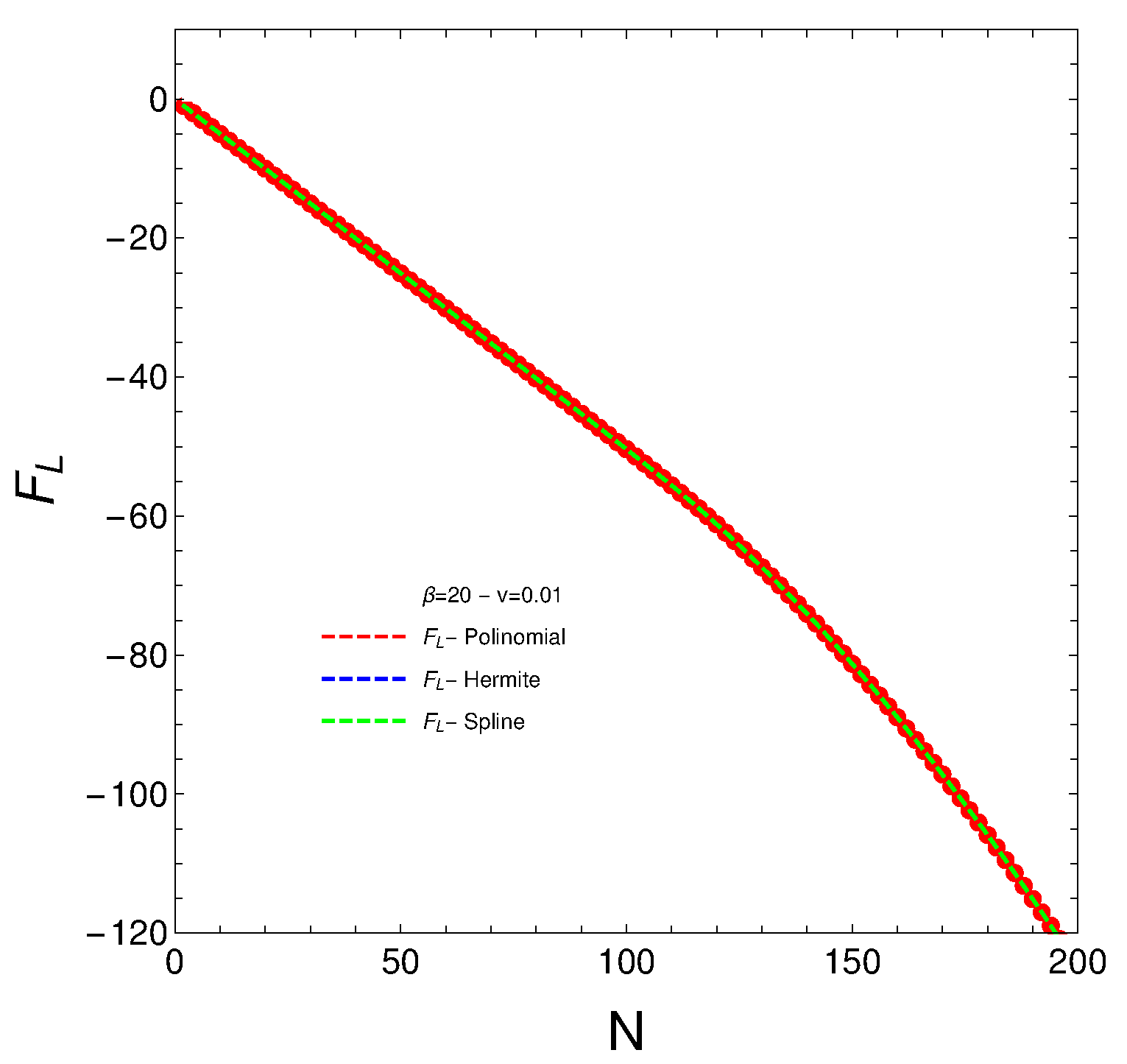
- The larger the value of N, the more stable the system becomes, as indicated by the behavior of the Lipkin free energy.
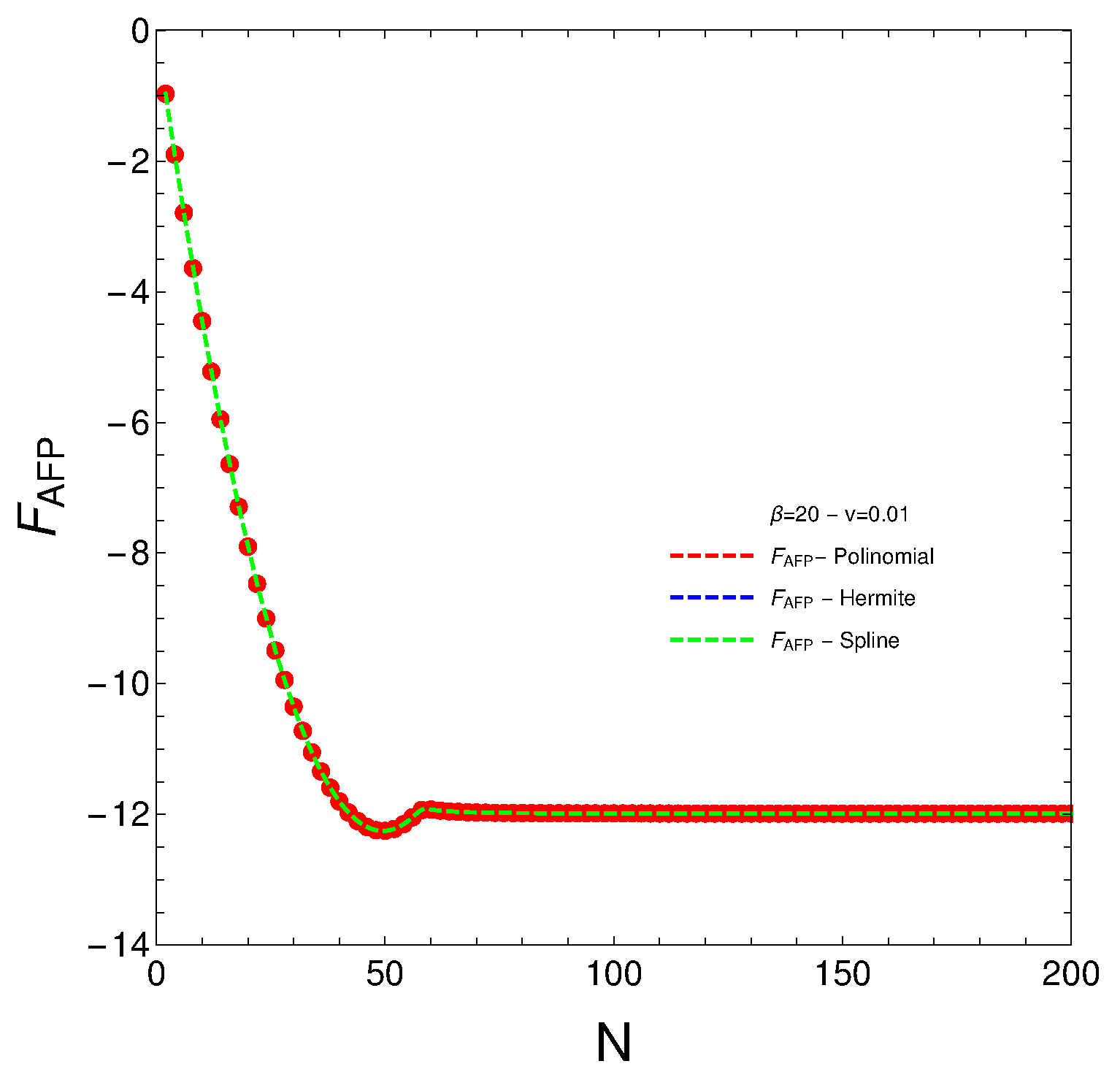
- This is not so in the AGFO case, where there is an absolute free energy minimum at a specific “magic” number.
- The main discovery with respect to the AFP entropy is the singular N value around N∼60 (the same as above). It signals not only stability but a loss of information.
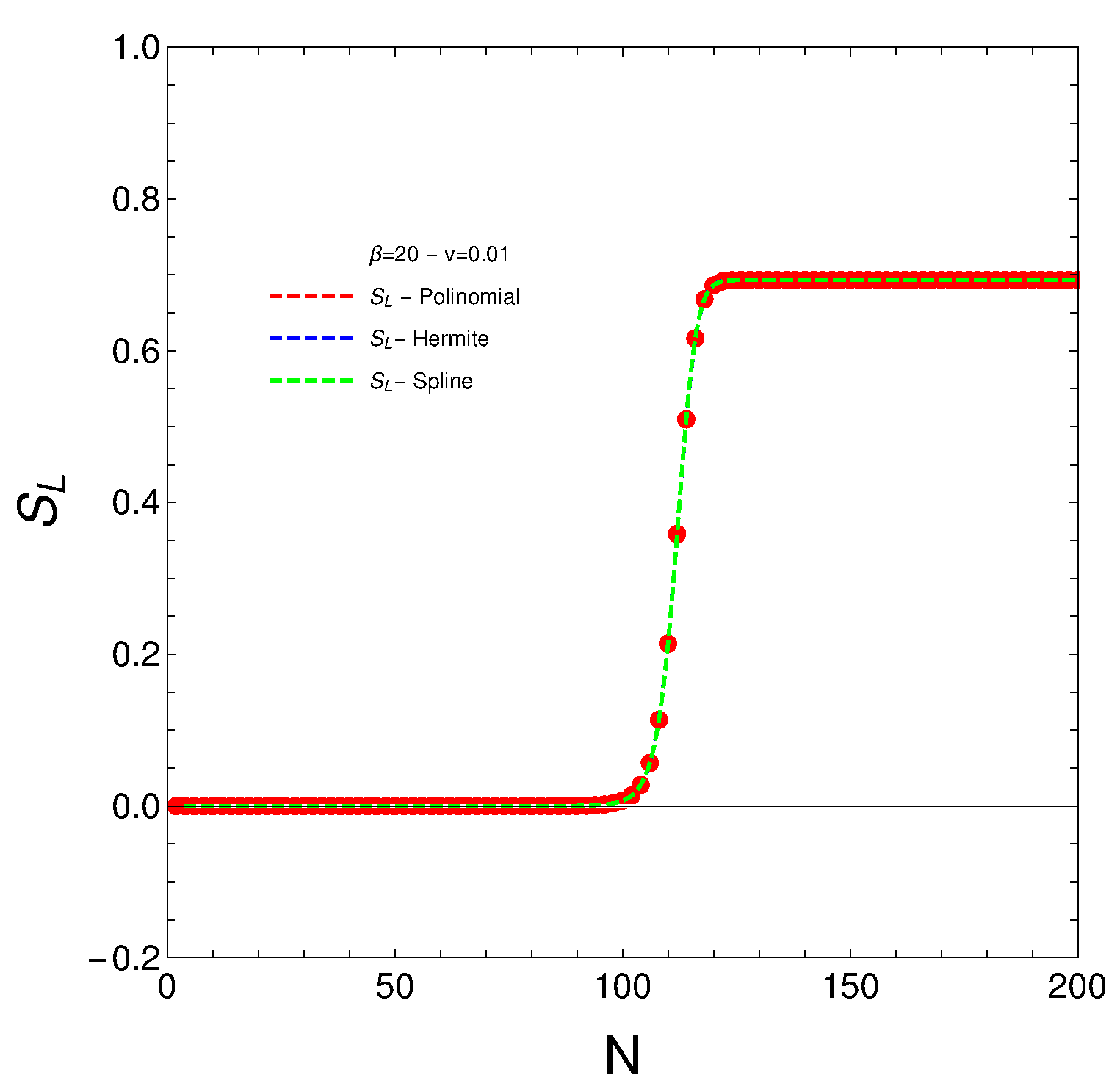
- As regards Lipkin’s entropy, we have rather a lot to say. For small N numbers, the entropy almost vanishes, indicating a system in a mixed state close to the ground state. Then, and rather suddenly (magic number), as N grows, the system leaves the state described above and passes to a much more mixed state, losing information. The new state, however, remains stable as N continues to increase.
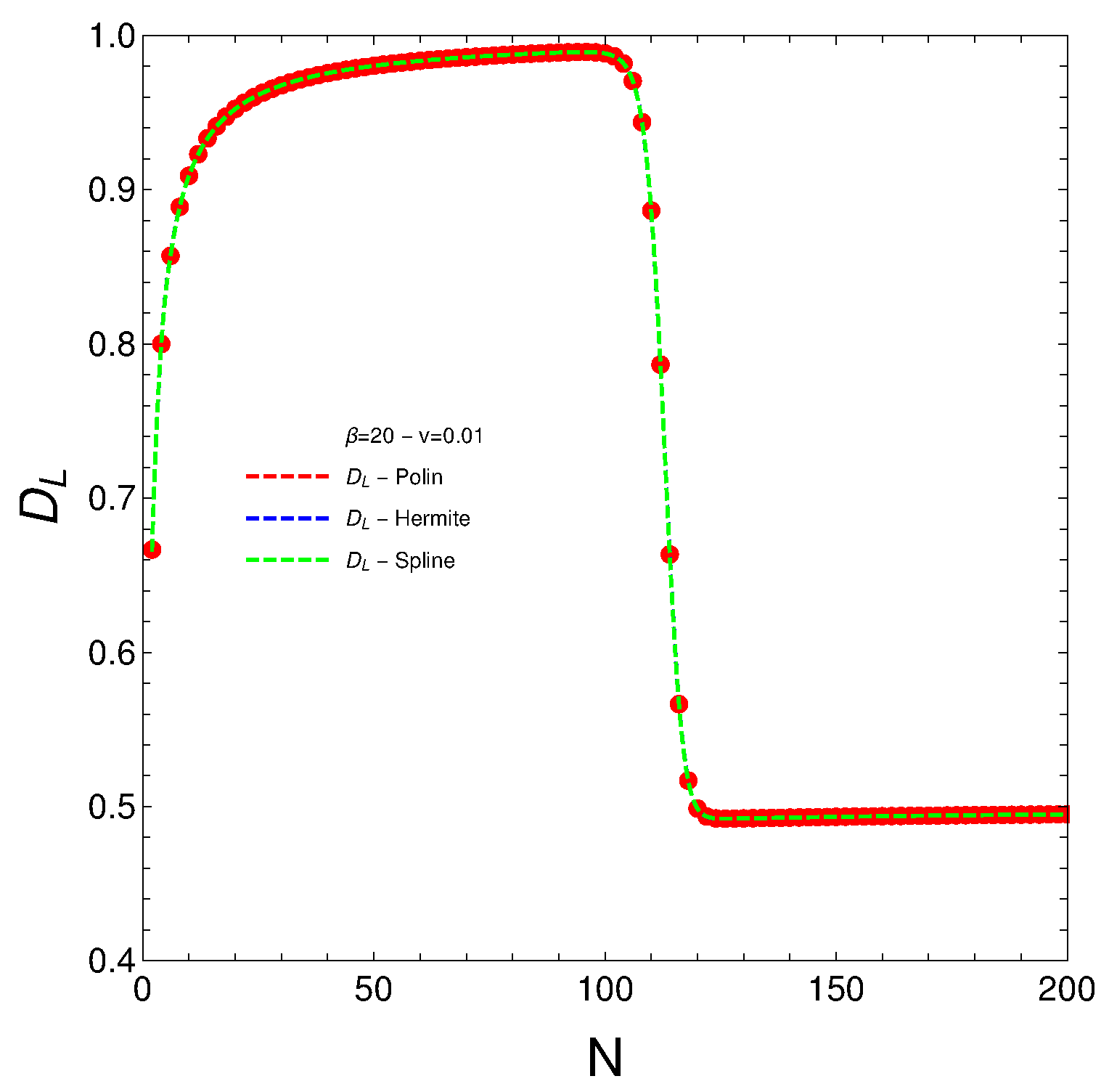
- AFPs D. The degree of order is large, in general, as the system lies in a state close to the ground state, as we saw above. However, for the same quasi-magic number N as above, the system abandons that state, passing to a much more mixed state and losing “order” as a consequence. This situation reverts back to the original one as N keeps growing.
- Lipkin’s D. The situation is much more complicated here than it was for the AFP model. For very small N values, this system lies in a disordered state. For moderate N values, a large degree of order is attained. Then, at the quasi-magic N value, the degree of order diminishes and then remains constant as N keeps increasing.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Frank, R. Quantum criticality and population trapping of fermions by non-equilibrium lattice modulations. New J. Phys. 2013, 15, 123030. [Google Scholar] [CrossRef]
- Lubatsch, A.; Frank, R. Evolution of Floquet topological quantum states in driven semiconductors. Eur. Phys. J. B 2019, 92, 215. [Google Scholar] [CrossRef]
- Otero, D.; Proto, A.; Plastino, A. Surprisal Approach to Cold Fission Processes. Phys. Lett. 1981, 98, 225. [Google Scholar] [CrossRef]
- Satuła, W.; Dobaczewski, J.; Nazarewicz, W. Odd-Even Staggering of Nuclear Masses: Pairing or Shape Effect? Phys. Rev. Lett. 1998, 81, 3599. [Google Scholar] [CrossRef]
- Dugett, T.; Bonche, P.; Heenen, P.H.; Meyer, J. Pairing correlations. II. Microscopic analysis of odd-even mass staggering in nuclei. Phys. Rev. 2001, 65, 014311. [Google Scholar] [CrossRef]
- Ring, P.; Schuck, P. The Nuclear Many-Body Problem; Springer: Berlin, Germany, 1980. [Google Scholar]
- Uys, H.; Miller, H.G.; Khanna, F.C. Generalized statistics and high-Tc superconductivity. Phys. Lett. A 2001, 289, 264. [Google Scholar] [CrossRef]
- Kruse, M.K.G.; Miller, H.G.; Plastino, A.R.; Plastino, A.; Fujita, S. Landau-Ginzburg method applied to finite fermion systems: Pairing in nuclei. Eur. J. Phys. 2005, 25, 339. [Google Scholar] [CrossRef]
- de Llano, M.; Tolmachev, V.V. Multiple phases in a new statistical boson fermion model of superconductivity. Physical A 2003, 317, 546. [Google Scholar] [CrossRef]
- Xu, F.R.; Wyss, R.; Walker, P.M. Mean-field and blocking effects on odd-even mass differences and rotational motion of nuclei. Phys. Rev. C 1999, 60, 051301. [Google Scholar] [CrossRef]
- Häkkinen, H.; Kolehmainen, J.; Koskinen, M.; Lipas, P.O.; Manninen, M. Universal Shapes of Small Fermion Clusters. Phys. Rev. Lett. 1997, 78, 1034. [Google Scholar] [CrossRef]
- Hubbard, J. Electron Correlations in Narrow Energy Bands. Proc. R. Soc. Lond. 1963, 276, 237. [Google Scholar]
- Liu, Y. Exact solutions to nonlinear Schrodinger equation with variable coefficients. Appl. Math. Comput. 2011, 217, 5866. [Google Scholar] [CrossRef]
- Lipkin, H.J.; Meshkov, N.; Glick, A.J. Validity of many-body approximation methods for a solvable model: (I). Exact solutions and perturbation theory. Nucl. Phys. 1965, 62, 188. [Google Scholar] [CrossRef]
- Co, G.; Leo, S.D. Analytical and numerical analysis of the complete Lipkin–Meshkov–Glick Hamiltonian. Int. J. Mod. Phys. E 2018, 27, 5. [Google Scholar]
- Reif, F. Fundamentals of Statistical Theoretic and Thermal Physics; McGraw Hill: New York, NY, USA, 1965. [Google Scholar]
- López Ruiz, R.; Mancini, H.L.; Calbet, X. A statistical measure of complexity. Phys. Lett. A 1995, 209, 321. [Google Scholar] [CrossRef]
- Arrachea, L.; Canosa, N.; Plastino, A.; Portesi, M.; Rossignol, R. Maximum Entropy Approach Crit. Phenom. Finite Quantum Systems. Phys. Rev. A 1992, 45, 44. [Google Scholar] [CrossRef]
- Abecasis, S.M.; Faessler, A.; Plastino, A. Appl. Multi Config. Hartree-Fock Theory A SimpleModel. Z. Phys. 1969, 218, 394. [Google Scholar] [CrossRef]
- Feng, D.H.; Gilmore, R.G. Phase transitions in nuclear matter described by pseudospin Hamiltonians. Phys. Rev. C 1992, 26, 1244. [Google Scholar] [CrossRef]
- Plastino, A.R.; Monteoliva, D.; Plastino, A. Information-theoretic features of many fermion systems: An exploration based on exactly solvable models. Entropy 2021, 23, 1488. [Google Scholar] [CrossRef]
- López-Ruiz, R. A information-theoretic Measure of Complexity. In Concepts and Recent Advances in Generalized Information Measures and Statistics; Kowalski, A., Rossignoli, R., Curado, E.M.C., Eds.; Bentham Science Books: New York, NY, USA, 2013; pp. 147–168. [Google Scholar]
- Martin, M.T.; Plastino, A.; Rosso, O.A. Generalized information-theoretic complexity measures: Geometrical and analytical properties. Physica A 2006, 369, 439. [Google Scholar] [CrossRef]
- Dehesa, J.S.; López-Rosa, S.; Manzano, D. Configuration complexities of hydrogenic atoms. Eur. Phys. J. D 2009, 55, 539. [Google Scholar] [CrossRef]
- Esquivel, R.O.; Molina-Espiritu, M.; Angulo, J.C.J.; Antoín, J.; Flores-Gallegos, N.; Dehesa, J.S. Information-theoretical complexity for the hydrogenic abstraction reaction. Mol. Phys. 2011, 109, 2353. [Google Scholar] [CrossRef]
- Nigmatullin, R.; Prokopenko, M. Thermodynamic efficiency of interactions in self-organizing systems. Entropy 2021, 23, 757. [Google Scholar] [CrossRef] [PubMed]
- Humpherys, J.; Jarvis, J.T. Interpolation. Foundations of Applied Mathematics Volume 2: Algorithms, Approximation, Optimization; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2020. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Plastino, A.; Monteoliva, D.; Plastino, A.R. Quasi-Magical Fermion Numbers and Thermal Many-Body Dynamics. Axioms 2023, 12, 493. https://doi.org/10.3390/axioms12050493
Plastino A, Monteoliva D, Plastino AR. Quasi-Magical Fermion Numbers and Thermal Many-Body Dynamics. Axioms. 2023; 12(5):493. https://doi.org/10.3390/axioms12050493
Chicago/Turabian StylePlastino, Angelo, Diana Monteoliva, and Angel Ricardo Plastino. 2023. "Quasi-Magical Fermion Numbers and Thermal Many-Body Dynamics" Axioms 12, no. 5: 493. https://doi.org/10.3390/axioms12050493
APA StylePlastino, A., Monteoliva, D., & Plastino, A. R. (2023). Quasi-Magical Fermion Numbers and Thermal Many-Body Dynamics. Axioms, 12(5), 493. https://doi.org/10.3390/axioms12050493






