Embedding Spanning Disjoint Cycles in Hypercube Networks with Prescribed Edges in Each Cycle

Abstract

One of the important issues in evaluating an interconnection network is to study the hamiltonian cycle embedding problems. A graph G is spanning k-edge-cyclable if for any k independent edges $e_1,e_2,\dots ,e_k$ of G, there exist k vertex-disjoint cycles $C_1,C_2,\dots ,C_k$ in G such that $V\left(C_1\right)\cup V\left(C_2\right)\cup \cdots \cup V\left(C_k\right)=V\left(G\right)$ and $e_i\in E\left(C_i\right)$ for all $1\le i\le k$. According to the definition, the problem of finding hamiltonian cycle focuses on $k=1$. The notion of spanning edge-cyclability can be applied to the problem of identifying faulty links and other related issues in interconnection networks. In this paper, we prove that the n-dimensional hypercube $Q_n$ is spanning k-edge-cyclable for $1\le k\le n-1$ and $n\ge 2$. This is the best possible result, in the sense that the n-dimensional hypercube $Q_n$ is not spanning n-edge-cyclable.

1. Introduction

Graph theory is a very important branch of discrete mathematics, and it mainly takes graph as the research object. This kind of graph is a mathematical model, using a graph as a model to represent the relationship between the real world, using the vertices of the graph to represent concrete things, and connecting the edges between the two vertices to indicate that there is a certain relationship between the two things. Graph theory is also applied to the many field such as chemistry, electrical, neural network and so on. Lu et al. used fuzzy molecular graphs to model chemical molecular structures with uncertainty information, where the vertex membership function and edge membership function describe the uncertainty of atoms and chemical bonds respectively [1]. In [2], Wang et al. used the relevant theories of graph theory to construct the electrical equipment control relations matrix of process enterprises based on analyzing the characteristics of electrical equipment faults and control relations. Li et al. proposed an ST-GCN based on node attention (NA-STGCN), so as to solve the problem of insufficient global information in ST-GCN by introducing node attention module to explicitly model the interdependence between global nodes [3]. Wang et al. focused on the research of industrial internet of things and power grid technology based on the knowledge graph and data asset relationship model [4]. Sun et al. proposed a semantic search KGSS algorithm based on the knowledge graph to explore the value of data resources of power grid enterprises [5].

In this paper, we study the architecture of an interconnection network which is always represented by a graph, where vertices represent processors and edges represent links between processors.

In recent years, the problem of embeddings in interconnection networks has attracted many researchers’ interest, especially the hamiltonian cycle and path embeddings [6,7]. Many parallel algorithms on hamiltonian cycles and paths are designed to solve various graph problems, algebraic problems, and problems in image and signal processing [8]. Consequently, embedding hamiltonian cycles (paths) into a network topology is crucial for the network simulation [9]. Thus, hamiltonicity and many variations on it have been widely studied, such as k-ordered hamiltonicity [10], hamiltonian decomposition [11], pancyclicity [12], spanning connectivity [13], and 2-factors (a 2-factor of a graph G is a spanning 2-regular subgraph of G) [14].

A graph G is Hamiltonian if it contains a Hamiltonian cycle, that is, a cycle containing all vertices of G. Let $H=(W,B;E)$ be a bipartite graph with bipartition W and B, then H is regarded as hamiltonian laceable if for any pair of vertices $w\in W$ and $b\in B$, there exists a hamiltonian path $P_{wb}$, i.e., a path containing all vertices of G, between w and b. In this paper, we study the spanning-edge-cyclability of the hypercube which is a strengthen of the hamiltonian property. We allow the graph to be spanned by a prescribed number of disjoint cycles. However, each must contain a prescribed edge. This concept can be applied to the problem of identifying faulty links and other related issues in interconnection networks. A graph G is spanning k-edge cyclable if for any k independent edges of G, there are k vertex disjoint cycles such that the union of these cycles cover $V\left(G\right)$ and each cylce contains exactly one edge. Blow, we give an example to clarify the notion.

Taking 3-dimentional hypercube $Q_3$ in Figure 1 as an example, we assume that $e_1=(000,001)$ and $e_2\in \{(100,101),(110,111),(100,110),(101,111),(010,011),(010,110),(011,111)\}$. We set $C_1=⟨000,001,011,010,000⟩$ and $C_2=⟨100,101,111,110,100⟩$ when $e_2\in \{(100,101),(110,111),(100,110),(101,111)\}$; we set $C_1=⟨000,001,101,100,000⟩$ and $C_2=⟨010,110,111,011,010⟩$ when $e_2\in \{(010,011),(010,110),(011,111)\}$. Then $C_1$ and $C_2$ are two disjoint spanning cycles of $Q_3$.

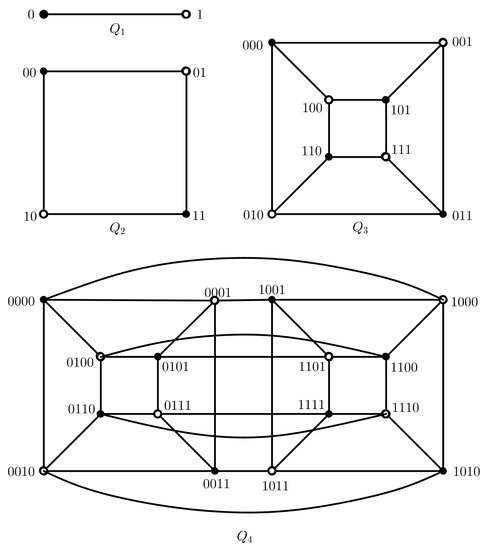
Figure 1. The hypercubes $Q_1$, $Q_2$, $Q_3$ and $Q_4$.

Wang proposed the following conjecture.

Conjecture 1

([15]). For each integer $k\ge 2$, there exists $N\left(k\right)$ such that if G is a graph of order $n\ge N\left(k\right)$ and $d_G\left(x\right)+d_G\left(y\right)\ge n+2k-2$ for each pair of nonadjacent vertices x and y of G, then G is spanning k-edge cyclable.

The conjecture was solved by Egawa et al. in [16]. Wang also posed the bipartite version of Conjecture 1, and the conjecture is partially solved by the author.

Conjecture 2

([17]). For each integer $k\ge 2$, there exists $N\left(k\right)$ such that if $G=(V_1,V_2;E)$ is a bipartite graph with $\mid V_1\mid =\mid V_2\mid =n\ge N\left(k\right)$ and $d_G\left(x\right)+d_G\left(y\right)\ge n+k$ for each pair of non-adjacent vertices x and y of G with $x\in V_1$ and $y\in V_2$, then G is spanning k-edge cyclable.

Recently, many researchers investigated the spanning cycles in a graph which contains prescribed vertices. Chronologically, in [18,19], the authors independently provided minimum degree sufficient conditions for a graph to be spanning k-cyclable. The problem of spanning k-cyclability of general graphs is well studied in the literature, see the survey article [20,21]. Besides, there are some results on spanning cyclability of special graph families. Lin et al. proved that the hypercube $Q_n$ with $n\ge 2$ is spanning k-cyclable for $1\le k\le n-1$ [14], and Kung et al. showed that the crossed cube $C{Q}_n$ is spanning k-cyclable for $1\le k\le n-1$ [22]. Shinde and Borse proved that the n-dimensional tori is spanning k-cyclable for $1\le k\le 2n-1$ [23]. Yang and Hsu proved that the generalized Petersen graph $GP(n,k)$ is spanning 2-cyclable for $k\le 4$ [24]. Recently, Qiao et al. proved that the enhanced hypercube $Q_{n,m}$ with $n\ge 4$ is spanning k-cyclable for $k\le n$ and $Q_{n,m}$ with $n=2,3$ is spanning k-cyclable for $k\le n-1$ [9]. Qiao et al. also proved that Cayley graph ${\Gamma }_n$ is spanning k-cyclable if $k\le n-2$ and $n\ge 3$ [25]. But up to date, no one has done anything about the spanning-edge-cyclability of specified networks. So it is reasonable and important to study the spanning-edge-cyclability of interconenction networks.

The hypercube $Q_n$ is one of the most popular and efficient interconnection networks. It possesses many excellent properties such as recursive structure, symmetry, small diameter, low degree, popular topological structure embedding, and easy routing. Because of such attractive properties, numerous topological properties of hypercubes have been extensively explored [26,27,28,29,30].

In this paper, we focus on the embedding spanning disjoint cycles in hypercubes with each cycle contains a prescribed edge. The main result of the paper is following:

Theorem 1.

The n-dimensional hypercube $Q_n$ is spanning r-edge-cyclable for $n\ge 2$ and $1\le r\le n-1$.

2. Preliminaries

First, we give the definition of spanning k-edge-cyclable graph as follows.

Definition 1

([15]). Let k be any positive integer, a graph G is called spanning k-edge-cyclable if, for any k independent edges $e_1,e_2,\dots ,e_k$, there exist k vertex-disjoint cycles $C_1,C_2,\dots ,C_k$ in G such that

(1) 

$V\left(C_1\right)\cup V\left(C_2\right)\cup \cdots \cup V\left(C_k\right)=V\left(G\right)$, and

(2) 

$e_i\in E\left(C_i\right)$ for all $1\le i\le k$.

In Definition 1, if $k=1$ then G is hamiltonian laceable. Thus, the spanning cycleability of a graph is a natural extension of hamiltonicity.

We use $P=⟨v_1,v_2,\dots ,v_m⟩$ and $C=⟨u_1,u_2,\dots ,u_m,u_1⟩$ to denote a path and a cycle, respectively. Let $G=(W,B;E)$ be a bipartite graph with bipartition W and B. Then G is $hamiltonian$ if it contains a hamiltonian cycle, i.e., a cycle containing all vertices of G. Moreover, G is regarded as hamiltonian laceable if for any pair of vertices $w\in W$ and $b\in B$, there exists a hamiltonian path $P_{wb}$, i.e., a path containing all vertices of G, between w and b.

Let n be a positive integer. The n-dimensional hypercube $Q_n$ is a graph with $2^n$ vertices, and its any vertex v is denoted by a unique n-bit binary string $v={\delta }_n{\delta }_{n-1}\cdots {\delta }_2{\delta }_1$, where ${\delta }_i\in \{0,1\}$ for $i=1,2,\dots ,n$. Two vertices of $Q_n$ are adjacent if and only if their binary strings differ in exactly one bit position. It is easy to show that $Q_n$ is an n-regular bipartite graph. Let B and W denote the two partite sets of $Q_n$. Assume that $(u,v)$ is an edge of $Q_n$. If the two binary strings of u and v differ in the i-th bit position, then the edge $(u,v)$ is called an edge of dimension i in $Q_n$. The set of all edges of dimension i in $Q_n$ is denoted by $E_i$. For any given h with $1\le h\le n$, let $Q_{n-1}^{0,h}$ and $Q_{n-1}^{1,h}$ be two $(n-1)$-dimensional subcubes of $Q_n$ induced by all vertices with the h-th bit being 0 and 1, respectively. By removing $E_h$, $Q_n$ is divided into $Q_{n-1}^{0,h}$ and $Q_{n-1}^{1,h}$, denoted by $Q_n-E_h=Q_{n-1}^{0,h}\cup Q_{n-1}^{1,h}$. For a given $\delta \in \{0,1\}$, if v is a vertex of $Q_{n-1}^{\delta ,h}$, then there is exactly one corresponding vertex in $Q_{n-1}^{1-\delta ,h}$, denoted by $v^{\prime }$, such that $(v,v^{\prime })\in E_h$. $Q_n$ is an n-connected Cayley graph and hence vertex-transitive, and also edge-transitive [31]. Examples of the hypercubes $Q_1$, $Q_2$, $Q_3$ and $Q_4$ are illustrated in Figure 1.

For any vertex $v\in V\left(Q_{n-1}^{i,h}\right)$ with $i=0$ or 1 and $1\le h\le n$, let $v^h$ be the copy vertex of v in $Q_{n-1}^{1-i,h}$ such that v and $v^h$ differ in the h-th coordinate. Let $P=⟨v_1,v_2,\dots ,v_x⟩$ be a path in $Q_{n-1}^{i,h}$, the copy path of P in $Q_{n-1}^{1-i,h}$ is denoted by $P^h=⟨v_1^h,v_2^h,\dots ,v_x^h⟩$. Similarly, let $C_t^i=⟨v_1,v_2,\dots ,v_x,v_1⟩$ be the cycle in $Q_{n-1}^{i,h}$ with $i=0$ or 1 and $1\le h\le n$, the copy cycle of $C_t^i$ in $Q_{n-1}^{1-i,h}$ is defined by $C_t^{1-i}=⟨v_1^h,v_2^h,\dots ,v_x^h,v_1^h⟩$. And $l\left(C\right)$ denotes the length of a cycle C.

The following are the related properties of the hypercube $Q_n$.

Lemma 1

([27]). Let $Q_n$ be the n-dimensional hypercube with bipartition W and B, and let $V_f$ be a set of all the end vertices of t independent edges in $Q_n$, where $t\le n-2$. Then the graph $H=Q_n-V_f$ is hamiltonian. Moreover, if $t\le n-3$, then $H=Q_n-V_f$ is hamiltonian laceable.

Lemma 2

([32]). Let n be any positive integer with $n\ge 4$. Let W and B form the bipartition of $Q_n$. Assume that x and w are any two different vertices in W, whereas y and b are any two different vertices in B. Then there exists a hamiltonian path of $Q_n-\{w,b\}$ joining x and y.

3. Proof of the Main Result

It is obvious that the 2-dimensional hypercube $Q_2$ is hamiltonian and the hamiltonian cycle contains every edge of $Q_2$. Thus $Q_2$ is spanning 1-edge-cyclable.

Lemma 3.

The 3-dimensional hypercube $Q_3$ is spanning t-edge-cyclable for $1\le t\le 2$.

Proof. 

Firstly, we will prove that $Q_3$ is spanning 1-edge-cyclable. By Lemma 1, $Q_3$ is hamilton laceable, thus for any edge $(u,v)$ of $Q_3$, there exists a hamiltonian path $HP$ between two end vertices u and v of the edge $(u,v)$. Then, there exists a hamiltonian cycle $C=⟨u,HP,v,u⟩$ containing the edge $(u,v)$. Thus $Q_3$ is spanning 1-edge-cyclable.

Next, we will prove that $Q_3$ is spanning 2-edge-cyclable. Because $Q_n$ is edge-transitive, we can fix one of the two prescribed edges as $(000,001)$. Then we can construct desired cycles as following, see Table 1.   □

Table 1. Spanning disjoint cycles in $Q_3$.

Prescribed Edges	Spanning Disjoint Cycles
$\left\{\right(000,001),(100,101\left)\right\}$ $\left\{\right(000,001),(110,111\left)\right\}$ $\left\{\right(000,001),(100,110\left)\right\}$ $\left\{\right(000,001),(101,111\left)\right\}$	$⟨000,001,011,010,000⟩$	$⟨100,101,111,110,100⟩$
$\left\{\right(000,001),(010,011\left)\right\}$ $\left\{\right(000,001),(010,110\left)\right\}$ $\left\{\right(000,001),(011,111\left)\right\}$	$⟨000,001,101,100,000⟩$	$⟨010,110,111,011,010⟩$

Lemma 4.

The 4-dimensional hypercube $Q_4$ is spanning t-edge-cyclable for $1\le t\le 3$.

Proof. 

By the hamiltonian laceability of $Q_4$, we can directly conclude that $Q_4$ is spanning 1-edge-cyclable. Thus, in the following, we only need to prove that $Q_4$ is spanning t-edge-cyclable for $2\le t\le 3$. Note that one can divide $Q_4$ into two 3-dimensional hypercubes $Q_3^{0,h}$ and $Q_3^{1,h}$ for $1\le h\le 4$.

Claim 1 The 4-dimensional hypercubes $Q_4$ is spanning 2-edge-cyclable.

We may suppose that $(u_1,v_1)$ and $(u_2,v_2)$ are any two independent edges in $Q_4$.

(1)

$(u_1,v_1)$ and $(u_2,v_2)$ are in different $Q_3^{(i,h)}$’s for $0\le i\le 1$ and $1\le h\le 4$.

We may suppose that $(u_1,v_1)\in E\left(Q_3^{0,h}\right)$ and $(u_2,v_2)\in E\left(Q_3^{1,h}\right)$. By Lemma 3, $Q_3^{0,h}$ and $Q_3^{1,h}$ are spanning 1-edge-cyclable, respectively. Thus, there exist two cycles $C_1$ and $C_2$ in $Q_3^{0,h}$ and $Q_3^{1,h}$, respectively, where $C_1$ contains $(u_1,v_1)$, $C_2$ contains $(u_2,v_2)$ and $C_1$ spans $Q_3^{0,h}$, $C_2$ spans $Q_3^{1,h}$. Then, $C_1\cup C_2$ spans $Q_4$ and each cycle contains exactly one of $(u_1,v_1)$ and $(u_2,v_2)$.

(2)

$(u_1,v_1)$ and $(u_2,v_2)$ are in the same $Q_3^{i,h}$ for $0\le i\le 1$ and $1\le h\le 4$.

We may suppose that both of $(u_1,v_1)$ and $(u_2,v_2)$ are in $E\left(Q_3^{0,h}\right)$. By Lemma 3, $Q_3$ is spanning 2-edge-cyclable. Thus there exist two cycles $C_1^0$ and $C_2^0$ in $Q_3^{0,h}$ such that $C_1^0$ contains $(u_1,v_1)$, $C_2^0$ contains $(u_2,v_2)$ and $C_1^0\cup C_2^0$ spans $Q_3^{0,h}$. Since $Q_n$ is triangle free, we can choose two adjacent vertices $a_1,b_1$ except $u_1,v_1$ on $C_1^0$. After removing the edge $(a_1,b_1)$, the cycle $C_1^0$ becomes a path $P_1$ which is between $a_1$ and $b_1$ and contains $(u_1,v_1)$. Moreover, we can take the neighbors $a_1^{\prime },b_1^{\prime }\in V\left(Q_3^{1,h}\right)$ of $a_1,b_1$, respectively. By definition of $Q_n$, $(a_1^{\prime },b_1^{\prime })\in E\left(Q_3^{1,h}\right)$. Furthermore, by the hamiltonian laceability of $Q_3$, there exists a hamiltonian path $HP$ between $a_1^{\prime }$ and $b_1^{\prime }$ in $Q_3^{1,h}$. Then we can construct two disjoint cycles as follows:

$$C_1=⟨a_1,P_1,b_1,b_1^{\prime },HP,a_1^{\prime },a_1⟩,C_2=C_2^0.$$

Clearly, $C_1\cup C_2$ spans $Q_4$ and $C_i$ contains $(u_i,v_i)$ for $i=1,2$.

Claim 2 The 4-dimensional hypercubes $Q_4$ is spanning 3-edge-cyclable.

Let $(u_1,v_1)$, $(u_2,v_2)$ and $(u_3,v_3)$ be three independent edges edges in $Q_4$.

(1)

Three prescribed edges $(u_1,v_1)$, $(u_2,v_2)$ and $(u_3,v_3)$ are not in the same $Q_3^{i,h}$ for $i=1,2$.

We may suppose that $(u_1,v_1),(u_2,v_2)\in E\left(Q_3^{0,h}\right)$ and $(u_3,v_3)\in E\left(Q_3^{1,h}\right)$. By Lemma 3, $Q_3^{0,h}$ is spanning 2-edge-cyclable. Thus, there exist two cycles $C_1^0$ and $C_2^0$ in $Q_3^{0,h}$ such that $C_1^0\cup C_2^0$ spans $Q_3^{0,h}$ and $C_i^0$ contains $(u_i,v_i)$ for $i=1,2$. By Lemma 1, $Q_3^{1,h}$ is hamiltonian laceable, thus there exists a hamiltonian path $HP$ between $u_3$ and $v_3$ in $Q_3^{1,h}$. Then we can construct three disjoint cycles as follows:

$$C_1=C_1^0,C_2=C_2^0,C_3=⟨u_3,HP,v_3,u_3⟩.$$

Then $C_1\cup C_2\cup C_3$ spans $Q_4$ and $(u_i,v_i)\in E\left(C_i\right)$ with $i=1,2,3$.

(2)

Three prescribed edges $(u_1,v_1)$, $(u_2,v_2)$ and $(u_3,v_3)$ are in the same $Q_3^{i,h}$ with $i=1,2$.

We may suppose that $(u_1,v_1)$, $(u_2,v_2)$ and $(u_3,v_3)$ are in $Q_3^{0,h}$. Because $Q_n$ is edge-transitive, we can fix one of the three prescribed edges $(u_1,v_1)$, $(u_2,v_2)$ and $(u_3,v_3)$ as $(000,001)$. Then we finish the remaining proof by brute force and the details can be seen in Table 2.

Table 2. Spanning disjoint cycles in $Q_4$.

Prescribed Edges	Spanning Disjoint Cycles
$\left\{\right(0000,0001),(0010,0011),(1000,1001\left)\right\}$ $\left\{\right(0000,0001),(0010,0011),(1000,1010\left)\right\}$ $\left\{\right(0000,0001),(0010,0011),(1001,1011\left)\right\}$ $\left\{\right(0000,0001),(0010,0011),(1010,1011\left)\right\}$	$⟨0000,0001,0101,0100,0000⟩$ $⟨1000,1001,1101,1100,1110,1111,1011,1010,1000⟩$	$⟨0010,0011,0111,0110,0010⟩$
$\left\{\right(0000,0001),(0010,1010),(1000,1001\left)\right\}$ $\left\{\right(0000,0001),(0011,1011),(1000,1001\left)\right\}$	$⟨0000,0001,0101,0100,0000⟩$ $⟨1000,1001,1101,1111,1110,1100,1000⟩$	$⟨0010,1010,1011,0111,0110,0010⟩$
$\left\{\right(0000,0001),(0010,1010),(1001,1011\left)\right\}$	$⟨0000,0001,0101,0100,0000⟩$ $⟨0010,1010,1110,0110,0111,0011,0010⟩$	$⟨1001,1011,1111,1101,1100,1000,1001⟩$
$\left\{\right(0000,0001),(0011,1011),(1000,1010\left)\right\}$	$⟨0000,0001,0101,0100,0000⟩$ $⟨0011,1011,1111,0111,0110,0010,0011⟩$	$⟨1000,1010,1110,1100,1101,1011,1000⟩$
$\left\{\right(0000,0001),(1000,1001),(1010,1011\left)\right\}$	$⟨1000,1001,1101,1100,1000⟩$ $⟨0000,0010,0011,0111,0110,0100,0101,0001,0000⟩$	$⟨1010,1011,1111,1110,1010⟩$
$\left\{\right(0000,0001),(1000,1010),(1001,1011\left)\right\}$	$⟨1000,1010,1110,1100,1000⟩$ $⟨0000,0001,0101,0100,0110,0111,0011,0010,0000⟩$	$⟨1001,1011,1111,1101,1001⟩$

Combining Claims 1 and 2, the lemma follows.   □

Proof of Theorem 1.

We prove the theorem by induction on n.

Base case As mentioned above, the theorem clearly holds for $n=2$, and for $n=3,4$ by Lemmas 3 and 4, resectively.

Induction hypothesis Assume that $Q_{n-1}$ is spanning r-edge-cyclable for $1\le r\le n-2$ and $n\ge 5$.

Inductive step Let $F=\{(u_1,v_1),(u_2,v_2),\dots ,(u_r,v_r)\}$ be a set of r independent edges of $Q_n$ for $1\le r\le n-1$.

Note that $Q_n$ can be divided into two ($n-1$)-dimensional hypercubes $Q_{n-1}^{0,h}$ and $Q_{n-1}^{1,h}$ for some h with $1\le h\le n$. Assume that $F_i=F\cap E\left(Q_{n-1}^{i,h}\right)$ for $i=0,1$.

Case 1. $1\le r\le n-2$.

Case 1.1. $1\le \mid F_0\mid \le n-3$.

We may suppose that $F_0=\{(u_1,v_1),\dots ,(u_s,v_s)\}$ and $F_1=\{(u_{s+1},v_{s+1}),\dots ,(u_r,v_r)\}$. By induction hypothesis, $Q_{n-1}$ is spanning r-edge-cyclable for $1\le r\le n-2$. Thus, there exist s disjoint cycles $C_1,C_2,\dots ,C_s$ in $Q_{n-1}^{0,h}$ such that the union of $C_1,\dots ,C_s$ spans $Q_{n-1}^{0,h}$ and $(u_i,v_i)\in E\left(C_i\right)$ with $i=1,2,\dots ,s$. Again by induction hypothesis, there also exist $r-s$ disjoint cycles $C_{s+1},C_{s+2},\dots ,C_r$ in $Q_{n-1}^{1,h}$ such that the union of $C_{s+1},\dots ,C_r$ spans $Q_{n-1}^{1,h}$ and $(u_i,v_i)\in E\left(C_i\right)$ with $i=s+1,\dots ,r$. Therefore, $C_1\cup C_2\cup \cdots \cup C_r$ spans $Q_n$ and $(u_i,v_i)\in E\left(C_i\right)$ with $1\le i\le r$.

Case 1.2. $\mid F_0\mid =0$.

Set $F_1=\{(u_1,v_1),(u_2,v_2),\dots ,(u_r,v_r)\}$. By induction hypothesis, $Q_{n-1}$ is spanning r-edge-cyclable for $1\le r\le n-2$. Thus, there exist r disjoint cycles $C_1^1,\dots ,C_r^1$ in $Q_{n-1}^{1,h}$ such that the union of $C_1^1,\dots ,C_r^1$ spans $Q_{n-1}^{1,h}$ and $(u_i,v_i)\in E\left(C_i\right)$ with $i=1,2,\dots ,r$. Then we can choose two adjacent vertices $a_1,b_1$ except from $u_1,v_1$ on $C_1^1$. After removing the edge $(a_1,b_1)$, the cycle $C_1^1$ becomes a path $P_1$ which containing $(u_1,v_1)$ is between $a_1$ and $b_1$. Moreover, we respectively can take neighbors $a_1^{\prime }$ and $b_1^{\prime }$ of $a_1$ and $b_1$ in $Q_{n-1}^{0,h}$. By Lemma 1, $Q_{n-1}$ is hamiltonian laceable for $n\ge 4$, thus there exists a hamiltonian path $HP$ between $a_1^{\prime }$ and $b_1^{\prime }$ in $Q_{n-1}^{0,h}$. Then we can construct r disjoint cycles as follows:

$$C_1=⟨a_1,P_1,b_1,b_1^{\prime },HP,a_1^{\prime },a_1⟩,C_x=C_x^1\mathrm{with}x=2,3,\dots ,r.$$

Thus $C_1\cup C_2\cup \cdots \cup C_r$ spans $Q_n$ and $(u_i,v_i)\in E\left(C_i\right)$ with $1\le i\le r$.

Case 2. $r=n-1$.

Case 2.1. $1\le \mid F_0\mid \le n-2$.

This case is similar to Case 1.1.

Case 2.2. $\mid F_0\mid =0$.

Set $F_1=\{(u_1,v_1),(u_2,v_2),\dots ,(u_{n-1},v_{n-1})\}$. By induction hypothesis, $Q_{n-1}$ is spanning $(n-2)$-edge cyclable. Thus, there exist $n-2$ disjoint cycles $C_1^1,C_2^1,\dots ,C_{n-2}^1$ in $Q_{n-1}^{1,h}$ such that the union of $C_1^1,C_2^1,\dots ,C_{n-2}^1$ spans $Q_{n-1}^{1,h}$ and each of them contains exactly one edge $(u_i,v_i)$ of $F_1$. Without lose of generality, we can suppose that $(u_i,v_i)\in E\left(C_i\right)$ for $i=1,2,\dots ,n-2$.

Case 2.2.1. $u_{n-1}$ and $v_{n-1}$ are in the same $C_i^1$.

(1)

$(u_{n-1},v_{n-1})\in E\left(C_i^1\right)$ with $i=1,2,\dots ,n-2$.

We may suppose that $(u_{n-1},v_{n-1})\in E\left(C_1^1\right)$. We can take neighbors $a,b\in V\left(C_1^1\right)$ of $u_1$ and $v_1$, respectively. After removing $(u_1,v_1)$, the cycle $C_1^1$ becomes a path $P_1$ containing the edge $(u_{n-1},v_{n-1})$. Furthermore, we can take the neighbors $a^{\prime }$, $b^{\prime }$, $u_1^{\prime }$ and $v_1^{\prime }$ of a, b, $u_1$ and $v_1$ in $Q_{n-1}^{0,h}$, respectively. By Lemma 2, there exists a hamiltonian path $HP$ between $a^{\prime }$ and $b^{\prime }$ in $Q_{n-1}^{0,h}-\{u_1^{\prime },v_1^{\prime }\}$. Then we can construct $n-1$ disjoint cycles as follows:

$$C_1=⟨v_1,u_1,u_1^{\prime },v_1^{\prime },v_1⟩,C_x=C_x^1\mathrm{with}x=2,3,\dots ,n-2,C_{n-1}=⟨a,P_1,b,b^{\prime },HP,a^{\prime },a⟩.$$

Then $C_1\cup C_2\cup \cdots \cup C_{n-1}$ spans $Q_n$ and $(u_i,v_i)\in E\left(C_i\right)$ with $1\le i\le n-1$.

(2)

$(u_{n-1},v_{n-1})\notin E\left(C_i^1\right)$ with $1\le i\le n-2$.

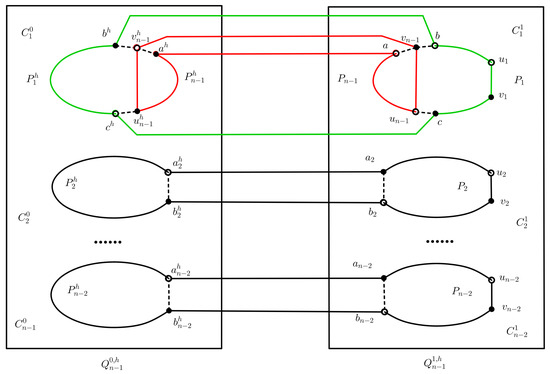
We may suppose that $u_{n-1},v_{n-1}\in V\left(C_1^1\right)$ and $(u_{n-1},v_{n-1})\notin E\left(C_1^1\right)$. Note that there exist copy cycles $C_1^0,C_2^0,\dots ,C_{n-2}^0$ in $Q_{n-1}^{0,h}$ of $C_1^1,C_2^1,\dots ,C_{n-2}^1$, respectively. In this situation, $l\left(C_1^1\right)\ge 6$ and there exist other vertices between $u_{n-1}$ and $v_{n-1}$. And then we may take neighbors a and b of $v_{n-1}$, where a is between $u_{n-1}$ and $v_{n-1}$, b is between $v_{n-1}$ and $u_1$. We also may take a neighbor c of $u_{n-1}$, where c is between $u_{n-1}$ and $v_1$. Let $P_1$ be a path joining b and c which contains $(u_1,v_1)$ and $P_{n-1}$ be a path joining $u_{n-1}$ and a. Furthermore, we may take the neighbors $u_{n-1}^h$, $v_{n-1}^h$, $a^h$, $b^h$ and $c^h$ in $C_1^0$ of $u_{n-1}$, $v_{n-1}$, a, b and c, respectively. Let $P_1^h$ and $P_{n-1}^h$ be two paths between $b^h,c^h$ and $a^h,u_{n-1}^h$, respectively. Thus we can construct two cycles $C_1$ and $C_{n-1}$ by using the vertices of $C_1^0$ and $C_1^1$ such that $(u_i,v_i)\in E\left(C_i\right)$ with $i=1,n-1$. For $2\le x\le n-2$, we may take a pair of adjacent vertices $a_x$ and $b_x$ on $C_x^1$ except $u_x$ and $v_x$. After removing the edge $(a_x,b_x)$, the cycle $C_x^1$ becomes a path $P_x$ which contains $(u_x,v_x)$ and joins $a_x$ and $b_x$. We also may take neighbors $a_x^h$ and $b_x^h$ in $C_x^0$ of $a_x$ and $b_x$, respectively. Moreover, after removing the edge $(a_x^h,b_x^h)$, the cycle $C_x^0$ becomes a path $P_x^h$ between $a_x^h$ and $b_x^h$. Thus we can construct $n-1$ disjoint cycles as follows (Figure 2):

$$\begin{array}{c}{C}_1=⟨b,P_1,c,c^h,P_1^h,b^h,b⟩,C_x=⟨a_x,P_x,b_x,b_x^h,P_x^h,a_x^h,a_x⟩\mathrm{with}2\le x\le n-2,\\ C_{n-1}=⟨v_{n-1},u_{n-1},P_{n-1},a,a^h,P_{n-1}^h,u_{n-1}^h,v_{n-1}^h,v_{n-1}⟩.\end{array}$$

Figure 2. Illustration of Case 2.2.1 (2).

Then $C_1\cup C_2\cup \cdots \cup C_{n-1}$ spans $Q_n$ and $(u_i,v_i)\in E\left(C_i\right)$ with $1\le i\le n-1$.

Case 2.2.2. $u_{n-1}$ and $v_{n-1}$ are in different $C_i^1$’s.

We may suppose that $u_{n-1}\in V\left(C_1^1\right)$ and $v_{n-1}\in V\left(C_2^1\right)$. Let $a_1$ and $b_1$ be neighbors of $u_1$ in $C_1^1$. Similarly, let $a_2$ and $b_2$ be neighbors of $v_1$ in $C_2^1$. After removing $u_{n-1}$ and $v_{n-1}$, the cycles $C_1^1$ and $C_2^1$ become two paths $P_1$ and $P_2$, where $P_1$ joins $a_1$ and $b_1$, $P_2$ joins $a_2$ and $b_2$. By definition of $Q_n$, there exist copy cycles $C_1^0,C_2^0,\dots ,C_{n-2}^0$ in $Q_{n-1}^{0,h}$ of $C_1^1,C_2^1,\dots ,C_{n-2}^1$, respectively. Further, there exist copy vertices $u_{n-1}^h\in V\left(C_1^0\right)$, $v_{n-1}^h\in V\left(C_2^0\right)$, $a_1^h\in V\left(C_1^0\right)$, $b_1^h\in V\left(C_1^0\right)$, $a_2^h\in V\left(C_2^0\right)$ and $b_2^h\in V\left(C_2^0\right)$ of $u_{n-1}$, $v_{n-1}$, $a_1$, $b_1$, $a_2$ and $b_2$, respectively. After removing $u_{n-1}^h$ and $v_{n-1}^h$, the cycles $C_1^0$ and $C_2^0$ become two paths $P_1^h$ and $P_2^h$, where $P_1^h$ joins $a_1^h$ and $b_1^h$, $P_2^h$ joins $a_2^h$ and $b_2^h$. For $3\le x\le n-1$, the method of constructing cycles $C_x$’s with $2\le x\le n-2$ is similar to Case 2.2.1 (2). Thus we can construct $n-1$ disjoint cycles as follows:

$$C_1=⟨a_1,P_1,b_1,b_1^h,P_1^h,a_1^h,a_1⟩,C_2=⟨a_2,P_2,b_2,b_2^h,P_2^h,a_2^h,a_2⟩,$$

$$C_x=⟨a_x,P_x,b_x,b_x^h,P_x^h,a_x^h,a_x⟩\mathrm{with}3\le x\le n-1.$$

Then $C_1\cup C_2\cup \cdots \cup C_{n-1}$ spans $Q_n$ and $(u_i,v_i)\in E\left(C_i\right)$ with $1\le i\le n-1$.   □

4. Discussion

Theorem 1 is optimal, i.e., $Q_n$ is not spanning n-edge cyclable. To see this, let u be any vertex of $Q_n$, and let $\{u_1,u_2,\dots ,u_n\}$ be the set of vertices adjacent to u. Set $(u_1,v_1),(u_2,v_2),\dots ,(u_n,v_n)$ be the n prescribed edges. If we can find n disjoint cycles $C_1,C_2,\dots ,C_n$ such that each cycle contains exactly one edge of $(u_1,v_1),(u_2,v_2),\dots ,(u_n,v_n)$, then $C_1\cup C_2\cup \cdots \cup C_n$ cannot contains u. Thus $Q_n$ is not spanning n-edge-cyclable.

5. Conclusions

Embedding cycles into a network is crucial for the network simulation. Especially, in designing effective interconnection networks, embedding hamiltonian cycles is a major requirement. This study investigates the spanning edge-cyclability problem (enhanced version of the hamiltonian problem) in the hypercube $Q_n$. We determine that the n-dimensional hypercube $Q_n$ is spanning r-edge-cyclable if $1\le r\le n-1$ and $n\ge 2$.