Process Capability Control Charts for Monitoring Process Accuracy and Precision

Abstract

Process capability index (PCI) is a convenient and useful tool of process quality evaluation that allows a company to have a complete picture of its manufacturing process in order to prevent defective products while ensuring the product quality is at the required level. The aim of this study was to develop a control chart for process incapability index $C_{pp}$, which differentiates between information related to accuracy and precision. Index $C_{ia}$ measures process inaccuracy as the degree to which the mean departs from the target value, while index $C_{ip}$ measures imprecision in terms of process variation. The most important advantage of using these control charts of $C_{pp}$, $C_{ia}$, and $C_{ip}$ is that practitioners can monitor and evaluate both the quality of the process and the differences in process capability. The $C_{ia}$ and $C_{ip}$ charts were instead of Shewhart’s $\overline{X}$ and $S$ chart since the process target values and tolerances can be incorporated in the charts for evaluation as a whole, which makes the charts capable of monitoring process stability and quality simultaneously. The proposed $C_{pp}$, $C_{ia}$, and $C_{ip}$ control charts enable practitioners to monitor and evaluate process quality as well as differences in process capability. The control charts are defined using probability limits, and operating characteristic (OC) curves used to detect shifts in process quality. The method proposed in this study can easily and accurately determine the process quality capability and a case is used to illustrate the application of control charts of $C_{pp}$, $C_{ia}$, and $C_{ip}$.

1. Introduction

A control chart is used to monitor the stability of product quality produced within a specific manufacturing process, rather than evaluating the quality of the process itself. The $\overline{X}$ and S control charts are commonly used in the industry; however, they are not applicable to the monitoring of process quality or estimating process capability in real time. In a fiercely competitive market, it is crucial for firms to prioritize the improvement of product quality and continually grasp the evolving needs of their customers. In other words, product specifications must be derived from the needs of customers and designers [1,2,3]. Determining the quality of a given process requires management to determine the corresponding target values and tolerances before assessing process capability, because products vary in specifications and units [4]. The process capability index (PCI) is the most widely used process quality evaluation tool in the industry [5].

The process capability indices $C_p$ and $C_{pk}$ are pivotal tools for characterizing a process’s capability to manufacture a product that conforms to specified requirements [6]. In [7], experts provided a detailed review of PCIs. More details on PCIs can be read in [8]. In addition, the PCI provides an easy-to-use criterion to evaluate the entire process. Kane [9] reported that the $C_p$ and $C_{pk}$ indices are the most widely used PCIs in industry. They are defined as follows:

$$C_p=\frac{USL-LSL}{6\sigma }=\frac{d}{3\sigma }$$

(1)

$$C_{pk}=\mathrm{m}\mathrm{i}\mathrm{n}\left\{\frac{USL-\mu }{3\sigma },\frac{\mu -LSL-\mu }{3\sigma }\right\}=\frac{d-|\mu -M|}{3\sigma }$$

(2)

where USL and LSL are the upper and lower specification limits, respectively, μ is the process mean, σ is the process standard deviation, $M=(USL+LSL)/2$ is the mid-point of the specification interval, and $d=(USL-LSL)/2$ is half the length of the specification interval. The author [6] pointed out that the definitions of $C_p$ and $C_{pk}$ are based on the process yield. However, the fact that neither is associated with target value T means that they are not able to reflect the degree to which a given process deviates from the target value. Based on the Taguchi loss function, experts [10] proposed $C_{pm}$, which is defined as follows:

$$C_{pm}=\frac{USL-LSL}{6\sqrt{{\sigma }^2+{(\mu -T)}^2}}=\frac{d}{3\sqrt{{\sigma }^2+{(\mu -T)}^2}}=\frac{D}{\sqrt{{\sigma }^2+{(\mu -T)}^2}}$$

(3)

where T is the target value, and $D=d/3$, ${\sigma }^2+{(\mu -T)}^2$ is the expected value of the Taguchi loss function. In [11], experts modified $C_{pm}$ in the development of process incapability index, $C_{pp}$, which is the square of the reciprocal of $C_{pm}$ expressed as $C_{pp}$ = (1/$C_{pm}$)². The definition is shown below:

$$C_{pp}={\left(\frac{\mu -T}{D}\right)}^2+{\left(\frac{\sigma }{D}\right)}^2$$

(4)

where ${(\mu -T/D)}^2$ is the inaccuracy index $C_{ia}$, and ${(\sigma /D)}^2$ is imprecision index $C_{ip}$. Thus, ${C_{pp}=C}_{ia}+C_{ip}$. In [12], the author proposed a loss ratio based on the same idea. Therefore, it is safe to say that $C_{pp}$ makes things easier for a company in terms of process management by assessing process precision and accuracy. Experts [13] argued that $C_{pp}$ is superior to $C_{pm}$.

Unfortunately, little research is available concerning capability indices. In [14], when $\overline{X}$ and S control charts are in statistical control, the control charts of process capability indices can be used to monitor the quality of process. It based the $C_{pm}$ chart on the conventional $\overline{X}$ and S charts and $\overline{X}$ and R charts for the monitoring of process variations during stable operating conditions [14]. Another expert [15] studied how to monitor the capability index $C_{pm}$ using an EWMA approach. Paper [16] optimally assesses the detection power between the $\overline{X}$ chart and the S chart while associating in-control and out-of-control process conditions with the process capability index, $C_{pk}$. A control chart using one-sided capability indices for the evaluation of process stability and capability was developed in [17]. The author proposed using the $C_p(u,v)$ family of capability indices with a logarithmic transformation in the form of an EWMA capability chart [18]. That system proved effective in the monitoring of unstable processes through the detection of variations in capability level. In [19], experts investigated the efficiency of the EWMA capability chart in terms of average run length (ARL). In [20], the process capability control charts used one-sided capability indices based on UMVUEs, using the estimators of the parameters of the quality characteristics obtained from the corresponding $\overline{X}-S$ and $\overline{X}-R$ charts.

The process incapability index, $C_{pp}$, includes $C_{ia}$ and $C_{ip}$ [11]. A statistical test for $C_{pp}$ is used to determine whether a given process is capable of meeting the demands of customers [13]; however, that method does not provide an effective means of monitoring actual processes. This fact was instrumental in the development of $C_{pp}$ estimation by [1] and process capability monitoring by [14]. $C_{pp}$, $C_{ia}$, and $C_{ip}$ were used to develop the upper control limits (UCL) and lower control limits (LCL) for the control chart in order to enable real-time monitoring of process capability. In this study, the software used is MATLAB, and the objective was to obtain a clear understanding of process quality and stability in order to initiate corrective actions and minimize occurrences of defective products.

The rest of this paper is organized as follows. In the next section, $C_{pp}$, $C_{ia}$, and $C_{ip}$ are used to develop control charts. Next, the proposed chart shows how this new approach efficiently monitors capable processes by detecting changes in the capability level, followed by an illustrative example in manufacturing. Then, operating characteristic (OC) curves of these control charts to detect shifts in process quality are evaluated. The last section contains some concluding remarks.

2. Process Capability Control Charts

Control charts are an important tool of statistical process control for monitoring the process mean, dispersion, or both to enhance customer confidence and the quality of the production process [21]. The fact that $C_{ia}$ is used for the evaluation of process accuracy and $C_{ip}$ is used for process precision makes it possible to incorporate $C_{ia}$ and $C_{ip}$ within a control chart simply by expanding the $\overline{X}$ and S control charts and introducing the idea of process capability. This allows for the direct monitoring of process stability as well as precision and accuracy.

Let X denote a process characteristic, let $\mu$ denote the process mean, and let ${\sigma }^2$ denote the process variance. Let $X_{ij}$, i = 1, 2, 3, …, m, be the m subgroups, and j = 1, 2, …, n, be the measurements of X arranged in sample size n. Assume that for each i, $X_{i1},X_{i2},...,X_{in}$ is a random sample from a normal distribution with the mean $\mu$ and standard deviation $\sigma$. Let ${\overline{X}}_i={\sum }_{j=1}^n{X}_{ij}/n$ be the mean of the ith sample, and let $S_i=\sqrt{{{\sum }_{j=1}^n(X_{ij}-{\overline{X}}_i)}^2/(n-1)}$ be the standard deviation of the ith sample. $\overline{\overline{X}}={\sum }_{i=1}^m{\overline{X}}_i/m$ denotes the average standard deviation of the m subgroups, and $\overline{S}={\sum }_{i=1}^m{S}_i/m$ the average of the m subgroups, are estimators of process mean $\mu$ and process standard deviation $\sigma$, respectively. The $\overline{X}$ and S control charts are based directly on ${\overline{X}}_i$ and $S_i$. For our purposes, it was necessary to use process capability indices $C_{pp}$, $C_{ia}$, and $C_{ip}$ as an alternative to classical sample statistics, such as ${\overline{X}}_i$ and $S_i$. For the estimation of indices $C_{pp}$, $C_{ia}$, and $C_{ip}$, Greenwich and Jahr-Schaffrath [11] considered unbiased, consistent point estimators for $C_{pp}$, $C_{ia}$, and $C_{ip}$, which are defined as follows:

$${\overline{C}}_{ppi}=\frac{{({\overline{X}}_i-T)}^2}{D^2}+\frac{S_i^2}{D^2}$$

(5)

$${\overline{C}}_{iai}=\frac{{({\overline{X}}_i-T)}^2}{D^2}$$

(6)

$${\overline{C}}_{ipi}=\frac{S_i^2}{D^2}.$$

(7)

Chen [1] developed ${\overline{C}}_{pp}$, ${\overline{C}}_{ia}$, and ${\overline{C}}_{ip}$ as uniformly minimum variance unbiased estimators (UMVUE) of $C_{pp}$, $C_{ia}$, and $C_{ip}$, respectively.

2.1. Process Capability Control Chart Based on $C_{pp}$

The $C_{ia}$ and $C_{ip}$ charts were introduced as an alternative to Shewhart’s $\overline{X}$ and S chart, due to their ability to incorporate process target values and tolerances and thereby enable the simultaneous monitoring of process stability and quality. In cases where the $C_{ia}$ and $C_{ip}$ charts indicate stable process quality, the implication is that the process mean and variance are stable. The $C_{ia}$ and $C_{ip}$ charts give no indication of how well a given process actually works. Therefore, we developed the $C_{pp}$ chart for the monitoring of process capability. Rewriting the expression of index $C_{pp}$, we obtain the following:

$$C_{pp}=\frac{{(\mu -T)}^2+{\sigma }^2}{D^2}=\frac{{(\mu -T)}^2+{\sigma }^2}{{\sigma }^2}\times \frac{{\sigma }^2}{D^2}=\left(\frac{{(\mu -T)}^2}{{\sigma }^2}+1\right)\frac{{\sigma }^2}{D^2}$$

Let $\lambda =n\frac{{(\mu -T)}^2}{{\sigma }^2}$, $C_{pp}=\left(\frac{\lambda }{n}+1\right)\frac{{\sigma }^2}{D^2}$, so $\frac{{\sigma }^2}{D^2}={\left(\frac{\lambda +n}{n}\right)}^{-1}{C}_{pp}$ and Greenwich and Jahr-Schaffrath [11] obtained ${\overline{C}}_{pp}={\sum }_{i=1}^n{(X_i-T)}^2/n{D}^2$. Hence, $W=(\lambda +n)\frac{{\overline{C}}_{pp}}{C_{pp}}=\frac{n{\overline{C}}_{pp}}{{\left[\right(\lambda +n)/n]}^{-1}{C}_{pp}}=\frac{{\sum }_{i=1}^n{(X_i-T)}^2/D^2}{{\sigma }^2/D^2}=\frac{{\sum }_{i=1}^n{(X_i-T)}^2}{{\sigma }^2}$.

Spiring [14] reported that $W={\sum }_{i=1}^n{(X_i-T)}^2/{\sigma }^2$ is distributed as ${{\chi }^{\prime }}_{(n;\lambda )}^2$, where ${{\chi }^{\prime }}_{(n;\lambda )}^2$ is non-central chi-square distribution with n degrees of freedom and $\lambda =n(C_{ia}/C_{ip})$ is a non-centrality parameter. Thus, the control limits of the process capability control chart of $C_{pp}$ are given by the following:

$$\begin{array}{ll}1-\alpha & =P\left({{\chi }^{\prime }}_{\alpha /2,(n;\lambda )}^2\le W\le {{\chi }^{\prime }}_{1-\alpha /2,(n;\lambda )}^2\right)\\ & =P\left({{\chi }^{\prime }}_{\alpha /2,(n;\lambda )}^2\le (\lambda +n)\frac{{\overline{C}}_{pp}}{C_{pp}}\le {{\chi }^{\prime }}_{1-\alpha /2,(n;\lambda )}^2\right)\\ & =P\left(\frac{{{\chi }^{\prime }}_{\alpha /2,(n;\lambda )}^2}{\left(\lambda +n\right)}\le \frac{{\overline{C}}_{pp}}{C_{pp}}\le \frac{{{\chi }^{\prime }}_{1-\alpha /2,(n;\lambda )}^2}{\left(\lambda +n\right)}\right)=P\left(I_1\le \frac{{\overline{C}}_{pp}}{C_{pp}}\le I_2\right)\\ & =P\left(\frac{{{\chi }^{\prime }}_{\alpha /2,(n;\lambda )}^2}{\left(\lambda +n\right)}{C}_{pp}\le {\overline{C}}_{pp}\le \frac{{{\chi }^{\prime }}_{1-\alpha /2,(n;\lambda )}^2}{\left(\lambda +n\right)}{C}_{pp}\right)=P\left(I_1{C}_{pp}\le {\overline{C}}_{pp}\le I_2{C}_{ip}\right).\end{array}$$

(8)

The control limits used with the control chart based on index $C_{pp}$ are obtained as follows:

$$UC{L}_{pp}=\frac{{{\chi }^{\prime }}_{1-\alpha /2,(n;\lambda )}^2}{(\lambda +n)}{C}_{pp}=I_1{C}_{pp}$$

(9)

$$C{L}_{pp}=C_{pp}$$

(10)

$$LC{L}_{pp}=\frac{{{\chi }^{\prime }}_{\alpha /2,(n;\lambda )}^2}{(\lambda +n)}{C}_{pp}=I_2{C}_{pp}$$

(11)

where $C_{pp}$ can be replaced by ${\overline{\overline{C}}}_{pp}$.

$${\overline{\overline{C}}}_{pp}=\frac{{(\stackrel{̿}{X}-T)}^2}{D^2}+\frac{{\overline{S}}^2}{D^2}.$$

(12)

To establish the constants $I_1$ and $I_2$, the value that convert according to $n=3\left(1\right)10$ and $\xi =0\left(0.1\right)1$. In addition, $\xi =C_{ia}/C_{ip}$ is set to α = 0.05 and 0.002 as shown in Table 1 and Table 2. It can be seen that when n and α are given, $I_1$ will increase as $\xi$ increases, but $I_2$ will decrease as $\xi$ increases. When n and $\xi$ are given, $I_1$ will increase as $\alpha$ increases, but $I_2$ will decrease as α increases.

Table 1. Values of the constants $I_1$ and $I_2$ for $\xi =0\left(0.1\right)1$, $n=3\left(1\right)10$, $\alpha =0.05$.

n		3		4		5		6		7		8		9		10
Constant		${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$
ξ	0.0	0.072	3.116	0.121	2.786	0.166	2.567	0.206	2.408	0.241	2.288	0.272	2.192	0.300	2.114	0.325	2.060
	0.1	0.072	3.105	0.122	2.776	0.167	2.558	0.207	2.400	0.242	2.280	0.273	2.185	0.301	2.107	0.326	2.054
	0.2	0.073	3.077	0.123	2.752	0.169	2.537	0.209	2.381	0.245	2.263	0.276	2.169	0.304	2.093	0.329	2.040
	0.3	0.075	3.040	0.125	2.721	0.172	2.510	0.212	2.357	0.248	2.241	0.28	2.149	0.308	2.074	0.333	2.022
	0.4	0.076	2.999	0.128	2.687	0.175	2.480	0.217	2.330	0.253	2.217	0.285	2.127	0.313	2.053	0.338	2.002
	0.5	0.078	2.957	0.131	2.651	0.179	2.448	0.221	2.303	0.258	2.192	0.290	2.104	0.318	2.032	0.343	1.982
	0.6	0.081	2.914	0.135	2.615	0.184	2.417	0.227	2.275	0.264	2.166	0.296	2.080	0.324	2.010	0.350	1.961
	0.7	0.084	2.872	0.139	2.58	0.189	2.387	0.232	2.248	0.27	2.142	0.302	2.058	0.331	1.989	0.356	1.941
	0.8	0.087	2.831	0.144	2.546	0.195	2.357	0.238	2.221	0.276	2.118	0.309	2.036	0.338	1.969	0.363	1.922
	0.9	0.090	2.791	0.149	2.513	0.200	2.329	0.245	2.196	0.283	2.095	0.316	2.015	0.344	1.949	0.370	1.903
	1.0	0.094	2.754	0.154	2.481	0.207	2.301	0.251	2.172	0.290	2.073	0.323	1.994	0.351	1.930	0.377	1.885

Table 2. Values of the constants $I_1$ and $I_2$ for $\xi =0\left(0.1\right)1$, $n=3\left(1\right)10$, $\alpha =0.002$.

n		3		4		5		6		7		8		9		10
Constants		${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$	${\mathit{I}}_1$	${\mathit{I}}_2$
ξ	0.0	0.038	3.782	0.074	3.319	0.111	3.017	0.145	2.802	0.177	2.639	0.206	2.511	0.232	2.407	0.256	2.321
	0.1	0.038	3.762	0.075	3.303	0.111	3.003	0.146	2.790	0.178	2.628	0.207	2.501	0.233	2.398	0.257	2.312
	0.2	0.039	3.717	0.076	3.266	0.113	2.972	0.148	2.762	0.180	2.603	0.209	2.479	0.235	2.377	0.259	2.293
	0.3	0.040	3.661	0.077	3.219	0.115	2.932	0.150	2.727	0.182	2.572	0.212	2.450	0.239	2.351	0.263	2.268
	0.4	0.041	3.599	0.079	3.169	0.117	2.889	0.153	2.689	0.186	2.538	0.216	2.419	0.243	2.322	0.267	2.242
	0.5	0.042	3.535	0.081	3.117	0.120	2.844	0.157	2.650	0.190	2.503	0.221	2.387	0.248	2.293	0.273	2.215
	0.6	0.043	3.473	0.084	3.066	0.124	2.801	0.161	2.612	0.195	2.468	0.226	2.356	0.253	2.264	0.278	2.188
	0.7	0.045	3.413	0.086	3.017	0.128	2.759	0.166	2.574	0.200	2.435	0.231	2.325	0.259	2.236	0.284	2.161
	0.8	0.047	3.354	0.090	2.969	0.132	2.718	0.171	2.538	0.206	2.403	0.237	2.296	0.265	2.208	0.291	2.136
	0.9	0.049	3.299	0.093	2.924	0.136	2.679	0.176	2.504	0.212	2.372	0.243	2.267	0.272	2.182	0.297	2.112
	1.0	0.051	3.246	0.097	2.881	0.141	2.642	0.182	2.471	0.218	2.342	0.250	2.240	0.278	2.157	0.304	2.088

2.2. Process Capability Control Chart Based on $C_{ia}$

The control limits for index $C_{ia}$ are based on the sample ${\overline{C}}_{iai}={({\overline{X}}_i-T)}^2/D^2$. Chen [1] showed that $Y=n{(\overline{X}-T)}^2/{\sigma }^2$ follows a non-central chi-square distribution ${{\chi }^{\prime }}_{(1;\lambda )}^2$ with one degree of freedom, and non-centrality parameter $\lambda =n(C_{ia}/C_{ip})$. To obtain the control limits for index $C_{ia}$, Y can be rewritten as

$$Y=\frac{n{(\overline{X}-T)}^2}{{\sigma }^2}=\frac{n{(\overline{X}-T)}^2/D^2}{{\sigma }^2/D^2}=\frac{n{\overline{C}}_{ia}}{C_{ip}}.$$

Similar to the method proposed by Spiring [14], the upper control limit (UCL) and lower control limit (LCL) for index $C_{ia}$ are as follows:

$$\begin{array}{ll}1-\alpha & =P\left({{\chi }^{\prime }}_{\alpha /2,(1;\lambda )}^2\le \frac{n{\overline{C}}_{ia}}{C_{ip}}\le {{\chi }^{\prime }}_{1-\alpha /2,(1;\lambda )}^2\right)\\ & =P\left(\frac{{{\chi }^{\prime }}_{\alpha /2,(1;\lambda )}^2}{n}\le \frac{{\overline{C}}_{ia}}{C_{ip}}\le \frac{{{\chi }^{\prime }}_{1-\alpha /2,(1;\lambda )}^2}{n}{C}_{ip}\right)=P\left(I_{a1}\le \frac{n{\overline{C}}_{ia}}{C_{ip}}\le I_{a2}\right)\\ & =P\left(\frac{{{\chi }^{\prime }}_{\alpha /2,(1;\lambda )}^2}{n}{C}_{ip}\le {\overline{C}}_{ia}\le \frac{{{\chi }^{\prime }}_{1-\alpha /2,(1;\lambda )}^2}{n}{C}_{ip}\right)=P\left(I_{a1}{C}_{ip}\le {\overline{C}}_{ia}\le I_{a2}{C}_{ip}\right).\end{array}$$

(13)

The control limits and centerline (CL) of the control chart of index $C_{ia}$ are defined as

$$UC{L}_{ia}=\frac{{{\chi }^{\prime }}_{1-\alpha /2,(1;\lambda )}^2}{n}{C}_{ip}=I_{a1}{C}_{ip}$$

(14)

$$C{L}_{ia}=C_{ia}$$

(15)

$$LC{L}_{ia}=\frac{{{\chi }^{\prime }}_{\alpha /2,(1;\lambda )}^2}{n}{C}_{ip}=I_{a2}{C}_{ip}$$

(16)

where $C_{ia}$ and $C_{ip}$ can be replaced by ${\overline{\overline{C}}}_{ia}$ and ${\overline{\overline{C}}}_{ip}$, respectively.

$${\overline{\overline{C}}}_{ia}=\frac{{(\stackrel{̿}{X}-T)}^2}{D^2}$$

(17)

$${\overline{\overline{C}}}_{ip}=\frac{{\overline{S}}^2}{D^2}$$

(18)

To establish the constants $I_{a1}$ and $I_{a2},$ the value that converts according to n = 3(1)10 and $\xi =0\left(0.1\right)1$ where $\xi =C_{ia}/C_{ip}$ is set to α = 0.05 and 0.002 as shown in Table 3 and Table 4. It can be seen that when n and α are given, $I_{a1}$ and $I_{a2}$ increase as $\xi$ increases. However, given arbitrary values for ξ and α, $I_{a1}$ will increase as n increases and $I_{a2}$ will decrease as n increases. When α = 0.002, $I_{a1}$ is close to 0 at any ξ and n.

Table 3. Values of the constants $I_{a1}$ and $I_{a2}$ for $\xi =0\left(0.1\right)1$, $n=3\left(1\right)10$, $\alpha =0.05$.

n		3		4		5		6		7		8		9		10
Constants		${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$
ξ	0.0	0.000	1.675	0.000	1.256	0.000	1.005	0.000	0.837	0.000	0.718	0.000	0.628	0.000	0.558	0.000	0.502
	0.1	0.000	2.127	0.000	1.694	0.000	1.429	0.000	1.250	0.000	1.119	0.000	1.020	0.000	0.941	0.000	0.877
	0.2	0.001	2.500	0.001	2.039	0.001	1.753	0.001	1.556	0.001	1.411	0.001	1.300	0.001	1.211	0.001	1.139
	0.3	0.001	2.822	0.001	2.334	0.001	2.029	0.001	1.817	0.001	1.660	0.001	1.539	0.002	1.443	0.002	1.363
	0.4	0.001	3.112	0.001	2.600	0.001	2.277	0.002	2.052	0.002	1.886	0.003	1.757	0.004	1.653	0.005	1.568
	0.5	0.001	3.381	0.002	2.846	0.002	2.508	0.003	2.272	0.005	2.096	0.006	1.960	0.009	1.851	0.012	1.761
	0.6	0.002	3.634	0.003	3.079	0.004	2.726	0.006	2.480	0.009	2.296	0.013	2.154	0.019	2.039	0.027	1.944
	0.7	0.003	3.874	0.004	3.300	0.006	2.935	0.010	2.679	0.016	2.488	0.025	2.340	0.036	2.220	0.048	2.121
	0.8	0.004	4.105	0.006	3.513	0.010	3.136	0.017	2.872	0.029	2.674	0.043	2.520	0.059	2.396	0.076	2.293
	0.9	0.005	4.328	0.009	3.720	0.016	3.331	0.029	3.058	0.046	2.854	0.066	2.695	0.088	2.566	0.108	2.460
	1.0	0.006	4.544	0.013	3.920	0.025	3.521	0.044	3.241	0.069	3.030	0.095	2.866	0.120	2.733	0.145	2.624

Table 4. Values of the constants $I_{a1}$ and $I_{a2}$ for $\xi =0\left(0.1\right)1$, $n=3\left(1\right)10$, $\alpha =0.002$.

n		3		4		5		6		7		8		9		10
Constants		${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$	${\mathit{I}}_{\mathit{a}1}$	${\mathit{I}}_{\mathit{a}2}$
ξ	0.0	0.000	3.609	0.000	2.707	0.000	2.166	0.000	1.805	0.000	1.547	0.000	1.353	0.000	1.203	0.000	1.083
	0.1	0.000	4.422	0.000	3.468	0.000	2.885	0.000	2.490	0.000	2.203	0.000	1.985	0.000	1.813	0.000	1.673
	0.2	0.000	4.980	0.000	3.970	0.000	3.346	0.000	2.920	0.000	2.609	0.000	2.371	0.000	2.182	0.000	2.029
	0.3	0.000	5.438	0.000	4.380	0.000	3.724	0.000	3.274	0.000	2.944	0.000	2.691	0.000	2.489	0.000	2.325
	0.4	0.000	5.840	0.000	4.742	0.000	4.058	0.000	3.587	0.000	3.242	0.000	2.976	0.000	2.764	0.000	2.591
	0.5	0.000	6.206	0.000	5.073	0.000	4.364	0.000	3.876	0.000	3.516	0.000	3.239	0.000	3.018	0.000	2.837
	0.6	0.000	6.547	0.000	5.381	0.000	4.651	0.000	4.146	0.000	3.774	0.000	3.486	0.000	3.257	0.000	3.069
	0.7	0.000	6.869	0.000	5.673	0.000	4.922	0.000	4.403	0.000	4.019	0.000	3.722	0.000	3.485	0.000	3.290
	0.8	0.000	7.175	0.000	5.951	0.000	5.182	0.000	4.648	0.000	4.254	0.000	3.948	0.000	3.704	0.000	3.503
	0.9	0.000	7.468	0.000	6.219	0.000	5.432	0.000	4.885	0.000	4.480	0.000	4.167	0.001	3.915	0.001	3.709
	1.0	0.000	7.751	0.000	6.478	0.000	5.674	0.000	5.115	0.000	4.700	0.001	4.379	0.001	4.121	0.003	3.909

2.3. Process Capability Control Chart Based on $C_{ip}$

The $C_{ip}$ control chart is used to monitor variations in process quality and precision. The centerline of the $C_{ip}$ control chart is designated as ${\overline{C}}_{ip}$, whereas the control limits are determined according to $K=n{\overline{C}}_{ip}/C_{ip}$.

$$K=\frac{n{\overline{C}}_{ip}}{C_{ip}}=\frac{n{S}^2/D^2}{{\sigma }^2/D^2}=\frac{n{S}^2}{{\sigma }^2}$$

Obviously, $K$ is distributed as ${\chi }_{(n-1)}^2$, where ${\chi }_{(n-1)}^2$ has a chi-square distribution with n−1 degrees of freedom. The control limits of the control chart of index $C_{ip}$ are obtained as follows:

$$\begin{array}{ll}1-\alpha & =P\left({\chi }_{\alpha /2,(n-1)}^2\le K\le {\chi }_{1-\alpha /2,(n-1)}^2\right)\\ & =P\left({\chi }_{\alpha /2,(n-1)}^2\le \frac{n{\overline{C}}_{ip}}{C_{ip}}\le {\chi }_{1-\alpha /2,(n-1)}^2\right)\\ & =P\left(\frac{{\chi }_{\alpha /2,(n-1)}^2}{n}\le \frac{{\overline{C}}_{ip}}{C_{ip}}\le \frac{{\chi }_{1-\alpha /2,(n-1)}^2}{n}\right)=P\left(I_{p1}\le \frac{{\overline{C}}_{ip}}{C_{ip}}\le I_{p2}\right)\\ & =P\left(\frac{{\chi }_{\alpha /2,(n-1)}^2}{n}{C}_{ip}\le {\overline{C}}_{ip}\le \frac{{\chi }_{1-\alpha /2,(n-1)}^2}{n}{C}_{ip}\right)=P\left(I_{p1}{C}_{ip}\le {\overline{C}}_{ip}\le I_{p2}{C}_{ip}\right).\end{array}$$

(19)

The control limits of the control chart of index $C_{ip}$ are given by

$$UC{L}_{ip}=\frac{{\chi }_{1-(\alpha /2),(n-1)}^2}{n}{C}_{ip}=I_{p1}{C}_{ip}$$

(20)

$$C{L}_{ip}=C_{ip}$$

(21)

$$LC{L}_{ip}=\frac{{\chi }_{\alpha /2,(n-1)}^2}{n}{C}_{ip}=I_{p2}{C}_{ip}$$

(22)

where $C_{ip}$ can be replaced by ${\overline{\overline{C}}}_{ip}$.

To establish the constants $I_{p1}$ and $I_{p2}$, the value converts according to $n=3\left(1\right)10$ where

α = 0.05 and 0.002 as shown in Table 5 and Table 6. It can be seen that given arbitrary values for α,$I_{p1}$ and $I_{p2}$ will increase as $n$ increases. However, giving arbitrary values for n, $I_1$ will increase as α increases and $I_2$ will decrease as α increases.

Table 5. Values of the constants $I_{p1}$ and $I_{p2}$ for n = 3(1)10, α = 0.05.

n		3		4		5		6		7		8		9		10
Constants		${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$
		0.017	2.459	0.054	2.337	0.097	2.229	0.139	2.139	0.177	2.064	0.211	2.002	0.242	1.948	0.270	1.902

Table 6. Values of the constants $I_{p1}$ and $I_{p2}$ for n = 3(1)10, α = 0.002.

n		3		4		5		6		7		8		9		10
Constants		${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$	${\mathit{I}}_{\mathit{p}1}$	${\mathit{I}}_{\mathit{p}2}$
		0.001	4.605	0.006	4.067	0.018	3.693	0.035	3.419	0.054	3.208	0.075	3.040	0.095	2.903	0.115	2.788

3. Capability indices for Process Monitoring

3.1. Model Schema for Process Monitoring

To evaluate the monitoring of process capability and performance, we outline the steps used in the implementation of $C_{ia}$, $C_{ip}$, and $C_{pp}$ charts in the following:

Step 1.

Collection of data

Select quality characteristic X; determine sample size, n, and number of subgroups, m; and determine the significance level $\alpha$.

Step 2.

Calculation of ${\overline{C}}_{ia}$, ${\overline{C}}_{ip}$, and ${\overline{C}}_{pp}$ and ${\overline{\overline{C}}}_{ia}$, ${\overline{\overline{C}}}_{ip}$, and ${\overline{\overline{C}}}_{pp}$

Tabulate the data, as shown in Table 7; and calculate ${\overline{C}}_{ia}$, ${\overline{C}}_{ip}$, and ${\overline{C}}_{pp}$.

Table 7. m subgroup observations with sample size n.

Subgroup	Observations			$\overline{\mathit{X}}$	$\mathit{S}$	${\overline{\mathit{C}}}_{\mathit{i}\mathit{a}}$	${\overline{\mathit{C}}}_{\mathit{i}\mathit{p}}$	${\overline{\mathit{C}}}_{\mathit{p}\mathit{p}}$
1	X11	X12	···X1n	${\overline{X}}_1$	$S_1$	${\overline{C}}_{ia1}$	${\overline{C}}_{ip1}$	${\overline{C}}_{pp1}$
2	X21	X22	···X2n	${\overline{X}}_2$	$S_2$	${\overline{C}}_{ia2}$	${\overline{C}}_{ip2}$	${\overline{C}}_{pp2}$
	·	·	·····	·	·	·	·	·
	·	·	·····	·	·	·	·	·
	·	·	·····	·	·	·	·	·
m	Xm1	Xm2	···Xmn	${\overline{X}}_m$	$S_m$	${\overline{C}}_{iam}$	${\overline{C}}_{ipm}$	${\overline{C}}_{ppm}$
						${\overline{\overline{C}}}_{ia}$	${\overline{\overline{C}}}_{ip}$	${\overline{\overline{C}}}_{pp}$

Step 3.

Calculation of control limits

Table 8 presents the equations used to determine the control limits for each of the charts. It is preferable to begin with the $C_{ip}$ chart when establishing the charts, due to the fact that the control limits of $C_{ia}$ are subject to process variance and $C_{pp}$ is subject to $C_{ia}$. $C_{ip}$. These limits are meaningful only when process variation is under control.

Table 8. Control limit equations and criteria used in process evaluation for index control charts.

Index	Control Limit	Process Evaluation Criteria
$C_{pp}$	$$\begin{gathered} LC{L}_{pp}=\frac{{{\chi }^{\prime }}_{\alpha /2,(n;\lambda )}^2}{(\lambda +n)}{C}_{pp} \\ C{L}_{pp}=C_{pp} \\ UC{L}_{pp}=\frac{{{\chi }^{\prime }}_{1-\alpha /2,(n;\lambda )}^2}{(\lambda +n)}{C}_{pp} \end{gathered}$$	1. $C_{pp}\ge 4$, the process capability is poor. 2. $C_{pp}=1$, the process s is typically called capable. 3. $C_{pp}=0.57$, the process s is typically called satisfactory. 4. $C_{pp}=0.44$, the process s is typically called good. 5. $C_{pp}=0.25$, the process s is typically called super.
$C_{ia}$	$$\begin{gathered} LC{L}_{ia}=\frac{{{\chi }^{\prime }}_{\alpha /2,(1;\lambda )}^2}{n}{C}_{ip} \\ C{L}_{ia}=C_{ia} \\ UC{L}_{ia}=\frac{{{\chi }^{\prime }}_{1-\alpha /2,(1;\lambda )}^2}{n}{C}_{ip} \end{gathered}$$	$C_{ia}=0$, the process accuracy is good.
$C_{ip}$	$$\begin{gathered} LC{L}_{ip}=\frac{{\chi }_{\alpha /2,(n-1)}^2}{n}{C}_{ip} \\ C{L}_{ip}=C_{ip} \\ UC{L}_{ip}=\frac{{\chi }_{1-(\alpha /2),(n-1)}^2}{n}{C}_{ip} \end{gathered}$$	1. $0.56\le C_{ip}\le$ 1.00, the process precision is capable. 2. $0.44\le C_{ip}\le$ 0.56, the process precision is satisfactory. 3. $0.36\le C_{ip}\le$ 0.44, the process precision is good. 4. $0.25\le C_{ip}\le$ 0.36, the process precision is excellent. 5. $C_{ip}\le$ 0.25, the process precision is super.

Step 4.

Plotting control limits and connecting the dots

Plot the values of ${\overline{C}}_{ia}$, ${\overline{C}}_{ip}$, and ${\overline{C}}_{pp}$ in the charts and connect the dots; and plot the control limits in the control charts.

Step 5.

Breakdown of control charts

After plotting the charts, the control status is evaluated based on analysis of any points that fall above or below a control limit as an indication of instability in the production process. Break down the $C_{ip}$ chart: The estimated variance of values within each sample. The $C_{ia}$ chart control limits are derived from the $C_{ip}$ values. If the $C_{ip}$ chart’s values are out of control, the $C_{ia}$ chart control limits are inaccurate. Thus, the stability of the $C_{ip}$ chart must be studied first. Break down the $C_{ia}$ chart: When the $C_{ip}$ chart is under control, the in-group variance is considered stable. The mean of each group can be analyzed to identify any significant time-dependent variations in the process center. In cases where the process is not under control, the source of instability in the process center must be identified. Break down the $C_{pp}$ chart: The control limits need to be recalculated in order to remove the (corrected) effects of process instability on the estimation of limits before seeking to verify whether the dots on the charts are under control. The steps of verification, correction, and recalculation are repeated as necessary.

Step 6.

Breakdown of the process

When the charts indicate that a process is under control (i.e., stable), it is necessary to evaluate the process capability in order to determine whether the specifications of the product and underlying process quality meet the needs of clients and designer. Limitations related to the control charts indicate whether the available processes can deliver sufficient precision consistently. Table 8 presents the criteria used in the evaluation of manufacturing processes by [13]. It is favorable to begin the evaluation of process capability using the $C_{pp}$ chart. In cases where process capability is poor, the $C_{ia}$ and $C_{ip}$ charts can be used to identify the causes. The $C_{ia}$ chart is used to determine the accuracy that can be achieved using a given process, while the $C_{ip}$ chart is used to determine precision and the reasons for process variation in order to formulate a plan for improvement.

Step 7.

Extension of control limits

If a process is under stable control and the processes are able to deliver the necessary accuracy and precision, the control limits can be extended to initiate control.

3.2. An Example

The data used in this example were obtained from a semiconductor manufacturer in Hsinchu, Taiwan. The wafer building process involves the placement of a large number of microcircuits on silicon-based wafers. The required critical dimension is 2 ± 0.4 μm; i.e., target value T = 2.00 μm with USL = 2.4 μm and LSL = 1.6 μm. Our objective was to build a model for monitoring adherence to the critical dimensions under mass production conditions. A breakdown of the steps is presented in the following:

Step 1.

Collection of data

Select quality characteristic X: the critical dimensions of the wafer (m) is a quality characteristic of this process. Determine the size of the sample (n = 5), and number of subgroups is 20, and determine the significance level ($\alpha$= 0.0027).

Step 2.

Calculation of ${\overline{C}}_{ia}$, ${\overline{C}}_{ip}$, and ${\overline{C}}_{pp}$

According to Formulas (12), (17), and (18), ${\overline{\overline{C}}}_{pp}=1.1139$,${\overline{\overline{C}}}_{ia}=0.3232$, and ${\overline{\overline{C}}}_{ip}=0.7907$ are calculated as shown in Table 9.

Table 9. Data and ${\overline{C}}_{ia}$, ${\overline{C}}_{ip}$, and ${\overline{C}}_{pp}$ values.

Subgroup		Observations				$\overline{\mathit{X}}$	S	${\overline{\mathit{C}}}_{\mathit{i}\mathit{a}}$	${\overline{\mathit{C}}}_{\mathit{i}\mathit{p}}$	${\overline{\mathit{C}}}_{\mathit{p}\mathit{p}}$	${\overline{\mathit{C}}}_{\mathit{p}\mathit{m}}$
1	1.81	2.21	2.06	1.96	2.11	2.030	0.1525	0.0506	1.3078	1.3584	0.8049
2	2.01	2.15	1.97	2.12	2.10	2.070	0.0765	0.2756	0.3291	0.6047	1.1810
3	2.16	2.17	2.00	2.04	2.08	2.090	0.0742	0.4556	0.3094	0.7650	1.0428
4	2.12	2.09	2.25	2.05	1.97	2.096	0.1029	0.5184	0.5951	1.1135	0.8699
5	2.15	2.11	1.76	1.82	2.11	1.990	0.1845	0.0056	1.9153	1.9209	0.6781
6	2.22	1.93	2.08	2.27	1.95	2.090	0.1538	0.4556	1.3303	1.7859	0.6942
7	1.98	2.19	2.02	1.96	1.95	2.020	0.0987	0.0225	0.5484	0.5709	1.2415
8	2.08	2.11	2.28	1.95	2.15	2.114	0.1193	0.7310	0.8004	1.5315	0.7413
9	2.01	2.05	2.11	2.10	1.91	2.036	0.0811	0.0729	0.3701	0.4430	1.4003
10	2.06	2.24	2.29	1.93	2.00	2.104	0.1550	0.6084	1.3517	1.9601	0.6608
11	2.29	2.25	2.11	2.09	2.15	2.178	0.0879	1.7822	0.4343	2.2165	0.6064
12	1.91	1.95	2.38	2.40	1.94	2.116	0.2507	0.7569	3.5342	4.2911	0.4497
13	2.22	2.20	2.05	1.98	1.81	2.052	0.1687	0.1521	1.6014	1.7535	0.7067
14	2.01	2.05	2.11	2.10	1.91	2.036	0.0811	0.0729	0.3701	0.4430	1.4003
15	2.12	2.09	2.25	2.05	1.97	2.096	0.1029	0.5184	0.5951	1.1135	0.8699
16	2.18	1.96	2.12	1.97	2.04	2.054	0.0953	0.1640	0.5108	0.6748	1.1301
17	2.16	2.04	2.13	1.91	1.97	2.042	0.1052	0.0992	0.6227	0.7219	1.0985
18	2.22	1.93	2.08	2.27	1.95	2.090	0.1538	0.4556	1.3303	1.7859	0.6942
19	2.18	2.20	2.07	2.29	2.11	2.170	0.0851	1.6256	0.4078	2.0334	0.6333
20	2.06	2.05	1.97	2.05	2.08	2.042	0.0421	0.0992	0.0996	0.1988	2.0554

Step 3.

Calculation of control limits

Using the data in Table 9, we obtained the following control limits for the $C_{pp}$ chart: $LC{L}_{pp}=0.0564$, $C{L}_{pp}=1.1139$, and $UC{L}_{pp}=4.1528$ The control limits for the $C_{ia}$ chart are as follows: $LC{L}_{ia}=0$, $C{L}_{ia}=0.3232$, and $UC{L}_{ia}=3.1029$. The control limits for the $C_{ip}$ chart are as follows: $LC{L}_{ip}=0.0167$, $C{L}_{ip}=0.7907$, and $UC{L}_{ip}=2.815$.

Step 4.

Plotting the control limits and connecting the dots

Figure 1 presents the control limits for the index control chart along with the ${\overline{C}}_{ia}$, ${\overline{C}}_{ip}$, and ${\overline{C}}_{pp}$ values obtained for various samples. Figure 1a,c indicates that point 12 exceeds the UCL, which necessitates an investigation into the assignable causes.

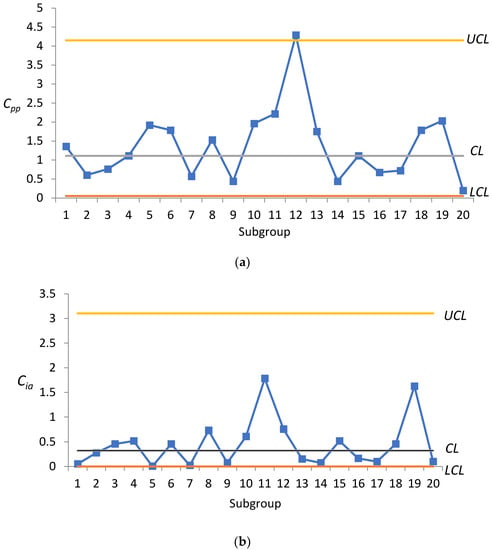
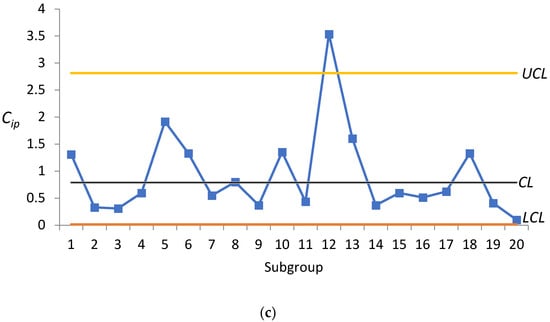
Figure 1. Process capability control charts for microcircuits. (a) C_pp chart. (b) C_ia chart. (c) C_ip chart.

Compared with [14], ${\overline{C}}_{pm}$ is presented in Table 9. The control limits of ${\overline{C}}_{pm}$ are drawn in Figure 2 where $LCL=0.4046$, $CL=0.8775$, and $UCL=3.7134$. It can be seen from Figure 2 that each ${\overline{C}}_{pm}$ is within the upper and lower limits of the control, indicating that there is no abnormality in this process. Compared with the control chart proposed by this study, it can be found that point 12 exceeds the UCL in Figure 1a,c, and the process can be improved immediately.

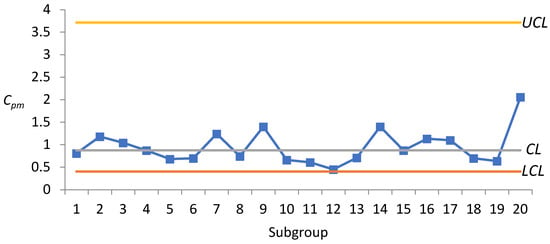
Figure 2. Process capability control charts of $C_{pm}$.

Step 5.

Breakdown of control charts

Figure 1 presents the $C_{pp}$, $C_{ia}$, and $C_{ip}$ charts. The C_ia chart presents all of the points located within the control limits in Figure 1b, indicating that the process accuracy is under control. The $C_{pp}$ and $C_{ip}$ charts indicate that point 12 exceeds the UCL in Figure 1a,c, thereby necessitating an investigation into assignable causes. Our subsequent investigation revealed that the problem with point 12 was a delay in the feeding of materials. We removed point 12 and re-calculated ${\overline{C}}_{ia}$, ${\overline{C}}_{ip}$, and ${\overline{C}}_{pp}$ which resulted in mean values of ${\overline{\overline{C}}}_{pp}=$1.0061, ${\overline{\overline{C}}}_{ia}=0.3064$, and ${\overline{\overline{C}}}_{ip}=0.7007$. The control limits for the $C_{pp}$ chart are as follows: $LC{L}_{pp}=0.0513$, $C{L}_{pp}=1.0061$, and $UC{L}_{pp}=3.7307$. The control limits for the $C_{ia}$ chart are as follows: $LC{L}_{ia}=0$, $C{L}_{ia}=0.3064$, and $UC{L}_{ia}=2.8054$. The control limits for the $C_{ip}$ chart are as follows: $LC{L}_{ip}=0.0148$, $C{L}_{ip}=0.7007$, and $UC{L}_{ip}=2.4923$. Figure 3 presents the control limits and the re-plotting of the charts. In Figure 3, all of the points fall within the control limits, thereby indicating that the process is under control.

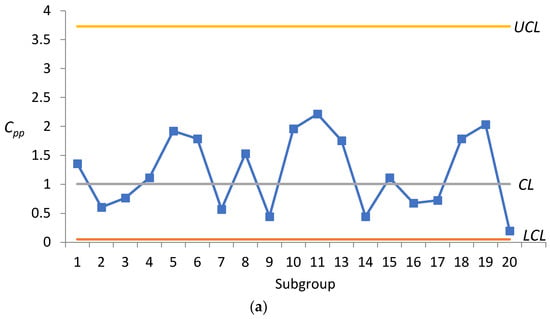
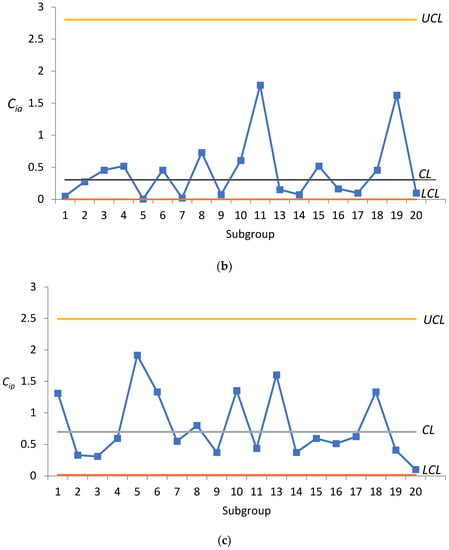
Figure 3. Improved process capability control charts for microcircuits. (a) $C_{pp}$ chart. (b) $C_{ia}$ chart. (c) $C_{ip}$ chart.

Step 6.

Breakdown of the process

The $C_{pp}$ chart clearly shows that the process capability for this product is substandard. The $C_{ia}$ and $C_{ip}$ charts provide a picture of process accuracy and precision. In Figure 3a, the plotted points 1, 5, 6, 8, 10, 11, 13, 18, and 19 are outside of $C_{pp}$ = 1, it indicates their $C_{pp}$ is higher than 1 but not more than 4, indicating the process capability is not poor. The rest of the points are all less than 1, which also means that the capabilities of these processes are considered to be satisfactory. If it is expected that the process capability can better meet the needs of the industry, researchers can learn from Figure 3b,c from the plotted points 1, 5, 6, 10, 13, and 18; they indicates that their $C_{ip}$ must be higher than their $C_{ia}$. When $C_{ip}>1$, the process precision is not capable. Thus, reducing their process variance has higher priority than reducing the process departure.

For the plotted points 11 and 19, their $C_{ia}$ must be higher than their $C_{ip}$. $C_{ia}>1$, the quality improvement efforts for these processes should be first focused on, reducing the departure of process mean from the target value.

In plotted point 8, the values of $C_{ia}$ and $C_{ip}$ are similar, which indicates that the variability of those processes is contributed equally by the mean departure and process variance.

Step 7.

Extension of control limits

The process was deemed to be under control and the process capability appeared to be up to standard. Thus, the control limits were extended to initiate control in order to enhance process stability and monitor process precision and accuracy.

The proposed model in this example allows businesses to have real-time understanding of the quality and stability of the manufacturing process. This enables real-time monitoring of process precision and accuracy. If the quality does not meet the standards or deteriorates, businesses can promptly make improvements to prevent the production of faulty products. This allows businesses to have continuous awareness of the quality and stability of the process. It eliminates the need for relying on control charts to determine process stability. The evaluation of process capability based on product specifications and target values can assess process drift and stability.

4. Operating Characteristic Curves for Control Charts for ${\mathit{C}}_{\mathit{p}\mathit{p}}$, ${\mathit{C}}_{\mathit{i}\mathit{a}}$, and ${\mathit{C}}_{\mathit{i}\mathit{p}}$

The efficacy of the $C_{pp}$, $C_{ia}$, and $C_{ip}$ charts to detect shifts in process quality is described by their OC curves. The OC curves for the process capability control charts of $C_{pp}$, $C_{ia}$, and $C_{ip}$ are as follows:

$$\begin{array}{ll}\mathrm{O}\mathrm{C}\left(C_{pp}\right)& =P(LC{L}_{pp}\le {\overline{C}}_{pp}\le UC{L}_{pp}|C_{pp},C_{ia},C_{ip})\\ & =F\left(u=\frac{\left(n+\frac{n\times C_{ia}}{C_{ip}}\right)\times UC{L}_{pp}}{C_{pp}},v=n,\lambda =\frac{n\times C_{ia}}{C_{ip}}\right)\\ & -F\left(u=\frac{\left(n+\frac{n\times C_{ia}}{C_{ip}}\right)\times LC{L}_{pp}}{C_{pp}},v=n,\lambda =\frac{n\times C_{ia}}{C_{ip}}\right)\end{array}$$

(23)

$$\begin{array}{ll}\mathrm{O}\mathrm{C}\left(C_{ia}\right)& =P(LC{L}_{ia}\le {\overline{C}}_{ia}\le UC{L}_{ia}|C_{ia},C_{ip})\\ & =F\left(u=\frac{n\times UC{L}_{ia}}{C_{ip}},v=1,\lambda =\frac{n\times C_{ia}}{C_{ip}}\right)\\ & -F\left(u=\frac{n\times UC{L}_{ia}}{C_{ip}},v=1,\lambda =\frac{n\times C_{ia}}{C_{ip}}\right)\end{array}$$

(24)

$$\begin{array}{ll}\mathrm{O}\mathrm{C}\left(C_{ip}\right)& =P(LC{L}_{ip}\le {\overline{C}}_{ip}\le UC{L}_{ip}|C_{ip})\\ & =F\left(u=\frac{n\times UC{L}_{ip}}{C_{ip}},v=n-1\right)-F\left(u=\frac{n\times LC{L}_{ip}}{C_{ip}},v=n-1\right).\end{array}$$

(25)

$F(u,v,\lambda )$ is the cumulative distribution function (cdf) of noncentral chi-square distribution for each of the values in u using the corresponding degrees of freedom in v and positive noncentrality parameters in $\lambda$. The noncentral chi-square cdf is rendered as follows:

$$F\left(u,v,\lambda \right)={\sum }_{j=0}^{\infty }\left(\frac{{\left(\frac{1}{2}\lambda \right)}^j}{j!}{e}^{\frac{-\frac{\lambda }{2}}{2}}\right)\mathrm{P}\mathrm{r}\left[{\chi }_{v+2j}^2\le u\right].$$

(26)

$F(u,v)$ is the cumulative distribution function (cdf) of a chi-square distribution for a given value u with v degrees of freedom: i.e.,

$$F(u,v)={\int }_0^u\frac{w^{(v-2)/2}\mathrm{e}\mathrm{x}\mathrm{p}(-w/2)}{{\left(2\right)}^{v/2}\Gamma (v/2)}dw$$

(27)

where $\Gamma (\cdot )$ is the Gamma function.

For these control charts, we assigned probability control limits of 0.00135 to each tail, such that the probability of a Type I error would be 0.0027 when the process is under control. Assume that the in-control process mean and variance are ${\mu }_0=10.6$ and ${\sigma }_0^2=0.64$, respectively, where USL = 13, LSL = 7, and T = 10. k is defined as the mean shift from ${\mu }_0$ to ${\mu }_1={\mu }_0+k{\sigma }_0$. If r is defined as the shift size of the standard deviation ${\sigma }_0$, then the shift amount of standard deviation is $r{\sigma }_0$. The following three cases make it possible to study shifts in process quality: (1) Only a shift in the mean values; (2) only a shift in the standard deviation; (3) shifts in both the mean values and standard deviation.

In case 1, the values of k are 0(0.5)3. The $C_{ip}$ chart could not determine the effects of different mean shifts. Thus, to construct the OC curve for the $C_{pp}$ and $C_{ia}$ charts, we plot the $\beta$-risk against the magnitude of the shift we wish to detect, as expressed in units of standard deviation for samples of various size $n=3\left(1\right)10$. The OC curves for the $C_{pp}$ and $C_{ia}$ charts are shown in Figure 4a and Figure 4b, respectively. As shown in Figure 4a, when k is fixed, an increase in n reduces the probability of Type II errors. When n is fixed, an increase in k reduces the probability of Type II errors. Consequently, similar results were obtained for the $C_{ia}$ chart (shown in Figure 4b). To summarize, an increase in n reduces the probability of Type II errors for the same k, whereas an increase in k reduces the probability of Type II errors for the same n.

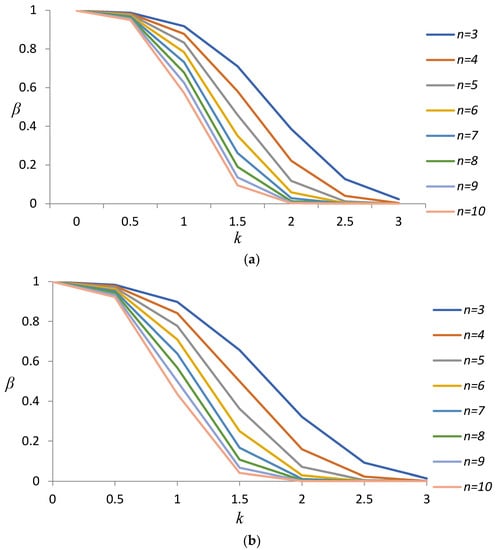
Figure 4. OC curves for index control charts, where process mean shifts by ${\mu }_0+k{\sigma }_0$. (a) $C_{pp}$ chart. (b) $C_{ia}$ chart.

In case 2, the value of r is 1(0.5)3. To construct OC curves for the $C_{pp}$, $C_{ia}$, and $C_{ip}$ charts, we plot the probability of Type II errors against the magnitude of the shift we wish to detect, which is expressed in units of standard deviation for samples of various size $n=3\left(1\right)10$. The OC curves for the $C_{pp}$, $C_{ia}$, and $C_{ip}$ are presented in Figure 5a, Figure 5b and Figure 5c, respectively. An examination of Figure 5b indicates that the $C_{ia}$ chart is not particularly effective in detecting process shifts when dealing with samples of various sizes. Furthermore, Figure 5a,c indicates that these $C_{pp}$ and $C_{ip}$ charts are not particularly effective in detecting process shifts in small samples due to a negligible shift in standard deviation.

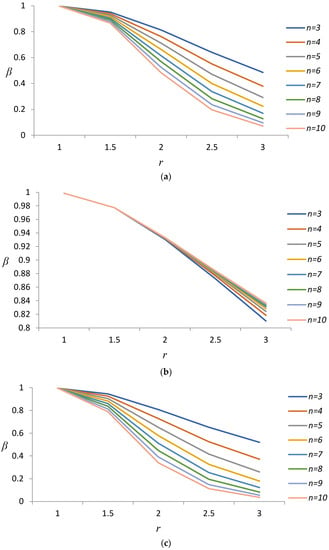
Figure 5. OC curves for index control charts, where process standard deviation shifts by $r{\sigma }_0$. (a) $C_{pp}$ chart. (b) $C_{ia}$ chart. (c) $C_{ip}$ chart.

Case 3 presents shifts in the mean as well as the standard deviation. The values of k are 0(0.5)3, and the values of r are 1(0.5)3. The OC curves for the control charts of $C_{pp}$, $C_{ia}$, and $C_{ip}$ with $n=5$ are presented in Figure 6a, Figure 6b and Figure 6c, respectively. As shown in Figure 6a,c, when mean shift k is fixed, $\beta$-risk decreases with an increase in r. As shown in Figure 6a,b, when r is fixed, the probability of Type II errors decreases with an increase in k. This indicates that the newly developed process capability control charts are more sensitive to larger shifts than to smaller ones. As shown in Figure 6c, when r is fixed, the probability of Type II errors does not vary with a change in k. As shown in Figure 6b, when mean shift k is fixed, the probability of Type II errors decreases with an increase in r when k ≤ 1, and the probability of Type II errors decreases with a decrease in r when k ≥ 1.5.

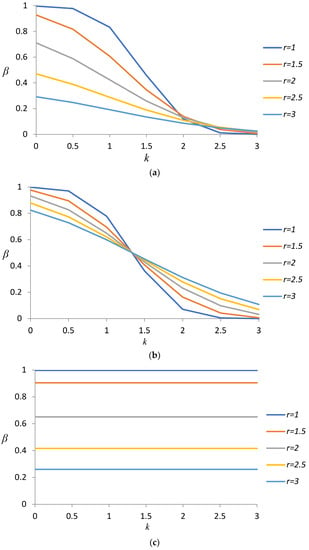
Figure 6. OC curves for index control charts with $n=5$, where both process the mean and standard deviation shifts. (a) $C_{pp}$ chart. (b) $C_{ia}$ chart. (c) $C_{ip}$ chart.

5. Conclusions

Manufacturers are constantly striving to improve process stability and quality in order to meet the evolving needs of clients. In the past, determining the stability of manufacturing processes involved the use of a control chart. Manufacturing processes must be kept under strict control in order to determine the capability of a given process in consistently achieving target specifications. In this study, we sought to combine control charts and process capability indices in the development of a monitoring model using indexed control charts to facilitate the control of system parameters in order to maintain a stable level of quality. We used the indices $C_{pp}$, $C_{ia}$, and $C_{ip}$ to establish upper and lower limits of control charts in order to facilitate the monitoring of process capability, accuracy, and precision. The objective was to provide a framework by which to guide actions aimed at improving manufacturing processes when quality fails to meet the set criteria, thereby minimizing the production of defective products. A practical example was outlined to illustrate the application of the proposed monitoring model. In this example, the $C_{pm}$ chart shows that the process is operating normally, without any unusual situation. However, both the $C_{pp}$ and $C_{ip}$ charts indicate that there is a problem with one of the processes, and it is important to investigate the specific reasons behind this issue. The proposed method aims to show how well a company’s processes meet customer needs. These charts not only highlight what customers want but also offer valuable information for process managers to make improvements.