1. Introduction
In this section, we provide some background information and terminology about the fixed point, coincidence point and dynamic markets, which will be helpful throughout the paper.
A mapping
on a complete metric space
is called a contraction if for some fixed
, the following condition is satisfied:
Banach [
1] considered such types of mappings on metric spaces and showed that if the metric space is complete, then such mappings have a unique fixed point. A natural and interesting case in the above inequality arises when
is taken to be equal to 1 and the inequality is taken to be strict, i.e., for
, the following strict inequality is satisfied:
In this case,
is called a contractive mapping. Rakotch [
2] by way of example showed that contractive mapping (even compact contractive mapping in a complete metric space) may not have a fixed point. Edelstein [
3] showed that a contractive mapping on a compact space must have a unique fixed point and this fixed point is the limit of an iterative sequence.
On the other hand, Kramosil and Michálek [
4] introduced the notion of fuzzy metric spaces. Grabiec [
5] extended the results of Banach [
1] and Edelstein [
3] in fuzzy metric spaces. The concept of Kramosil and Michálek [
4] was further extended by George and Veeramani [
6] so that they were able to obtain a Hausdorff induced topology by the fuzzy metric. Miheţ [
7] discussed the existence of fixed points of Edelstein fuzzy contractive mappings in the fuzzy metric spaces of George and Veeramani [
6].
Consider the mappings
ξ,
, where
is a nonempty set. A point
is a fixed point of
(♭) = ♭
♭
ξ and
if
and, in this case, the common value
is called the point of coincidence of
. For some
the sequence
given by
,
is called a Picard sequence
of
with an initial value
, while the sequence
given by
,
(provided it exists) is called a Jungck sequence (see [
8]) of the ordered pair
with an initial value
. Jungck first considered such sequences of ordered pairs of continuous mappings, and using this, he established the existence of fixed points of the mapping of the pair. Later, many authors used Jungck’s approach and extended his work to various spaces and for various types of mappings, see, e.g., [
9,
10,
11,
12,
13,
14]. Jungck’s sequence of an ordered pair of mappings plays an important role in establishing the existence of point of the coincidence of the mappings. We denote the class of all Jungck sequences of the ordered pair
with initial value in
by
.
In mathematical economics, a number of studies on economic models are subject to the analysis of the equilibrium states. A market that is continuously and rapidly changing (in terms of price of a commodity) over time is called a dynamic market, and the forces cause the change in price to represent the market dynamics. This dynamic is directly dependent on the variables (e.g., the supplied quantity of a commodity) associated with the market. The equilibrium of a dynamic market is a situation in which the market has a tendency to oppose the changes. The stability of a market is an important concept in the study of the equilibrium of a market. The price of the commodity at which the demanded and supplied quantities of the commodity becomes equal is called the equilibrium price, and at this stage, the market is said to be in equilibrium. A market can be temporarily at equilibrium without being stable (see, e.g., [
15] and the references therein). If a market is not in equilibrium, then changes in variables (on which the dynamics depends) may force the market (i.e., price of the commodity) towards its equilibrium, and if this is the case, then the market is called stable. We will see that in a stable market, the competitive market forces always bring the price of the commodity towards its equilibrium value.
The fixed point theory has numerous applications in various disciplines like science, engineering and economics; see, e.g., [
16,
17,
18,
19]. In particular, the stability of dynamic markets can be identified by the equilibrium point (price), and the equilibrium point is considered as a fixed point of some particular function associated with the demand and supply at successive stages of the market (see, e.g., [
20,
21,
22] and the references therein). Mezník [
22] showed that in a simple demand and supply model where the model is completely characterized by the demand function
and the supply function
(where
p stands for price and
q for the quantity; demanded or supplied), the equilibrium price
can be considered as a fixed point of the function
, where
represents the inverse function of
S. He proved that if
(where
and
are the derivatives of
D and
S), then the market is stable and the iterative sequence
of the market prices converges to the equilibrium price
which is a fixed point of
Indeed, the equilibrium price
is the point at which the demand and supply functions becomes equal, i.e.,
, where
is the equilibrium quantity. This state is called the equilibrium state of the market. Hence, we can say that the equilibrium quantity is a coincidence point of the demand and supply functions.
By keeping the definitions of a fixed point and a coincidence point in mind, it is more convenient and natural to consider the equilibrium point for a dynamic market as a coincidence point of the demand function D and the supply function S, and in this case, the equilibrium quantity will be the corresponding coincidence point and the equilibrium price will be the point of coincidence of D and S.
In this paper, we establish the existence of the equilibrium point of a market considered by Mezník [
22] with the help of a coincidence point theorem for the mappings satisfying Edelstein type contractive mappings in fuzzy metric spaces (in the sense of George and Veeramani [
6]). With this new approach, we do not need to find the derivatives of the demand and supply functions nor the inverse of the supply function. The iterative sequence used by Mezník [
22] was the Picard sequence, while we use the Jungck sequence to prove the existence of equilibrium prices and the stability of the market.
3. Main Result
In this section, we first introduce Edelstein ζ-contractive mappings on fuzzy metric spaces and prove a coincidence point result, as well as a common fixed point result.
Definition 6. Let be a fuzzy metric space, and be two mappings. Then, is called Edelstein -contractive on C if:It is obvious that every Edelstein contractive mapping on C is Edelstein -contractive on C with (the identity mapping of C). Example 1. Let , for all and the fuzzy metric be defined by:Then is a fuzzy metric space. Consider the mappings defined by and for all If , then , i.e., . Similar inequality holds if . Hence is Edelstein -contractive on Y. On the
other hand, is Edelstein contractive on Y since (2) does not hold for and .
From the above example, it is clear that ; therefore, it is always possible to construct a Jungck sequence of the ordered pair with some initial value (e.g., one can choose ), while have no coincidence point and no periodic
point (since for any , for all ). In the next proposition, we
establish the fact that if have no point of coincidence (therefore no coincidence
point), then they have no periodic point. Further, we will establish the conditions under
which will have point of coincidence.
Proposition 2. Let (Y, F, ∗) be a fuzzy metric space, C ⊆ Y and be two mappings
such that . If is Edelstein -contractive on C, then either and have a point of
coincidence or they have no periodic point.
Proof. Suppose that
with initial value
. Note that any periodic point of
order 1 is a point of coincidence of
. Hence, assume that there is no periodic point of
order 1. We claim that there is no
such that for a
p ≥ 2 we have
On the contrary, suppose that there exist
and
p ≥ 2 such that
. Then, since there is
no periodic point of order 1, by condition (2) we have: for all
τ > 0
Proceeding in similar way, we obtain
Again,
The above inequality with (3) yields a contradiction. This proves the claim. □
Lemma 1. Let (Y, F, ∗) be a fuzzy metric space, C ⊆ Y and be two mappings. If is Edelstein -contractive on C and is continuous on C, then is continuous on C.
Proof. If
C = Ø then the result is trivial. Suppose that ♭ ∈
C and {♭
n} is a sequence in
C
and converging to ♭. Then, by continuity of
, the sequence
converges to
, i.e., lim
n→∞ for all
τ > 0. Since
is Edelstein
-contractive on
C by (2), we
have:
for all
τ > 0. Hence, {
(♭
n)} converges to
(♭), and so,
is also continuous at ♭ ∈
C for all ♭ ∈
C. □
Theorem 1. Let be a fuzzy metric space, C be a nonempty compact subset of Y and be two mappings such that . If is an Edelstein -contractive mapping
and is continuous, then is singleton and for each initial value
there exists which converges to the unique element of .
Proof. For a
, we define a mapping
by:
Since ζ is continuous on
C, by Lemma 1,
is continuous on
C. Since
F is continuous on Y × Y × (0, ∞) (see [
31],
are continuous, then the function
φ is continuous and hence it attains its maximum value in
C. Suppose that
and for
there holds
We claim that
Co
. On the contrary, suppose that
As,
, there exists
such that
. Since
is Edelstein
-contractive, then for
each
τ > 0, we obtain
This is a contradiction with the definition of
α; hence, we must have
i.e.,
and
. The uniqueness of the point of coincidence
follows from
the contractive condition (2); hence,
Suppose that . By the steps given below, we construct a sequence with initial value such that converges to .
Since , there exists such that (say). Again, since , there exists such that (say). In a similar way, we obtain for all , i.e., with an initial value . Now, we consider the following cases I and II:
Case I: If at any stage of the process a term of the sequence is equal to , i.e., if for an we obtain , then since , the above process permits us to choose , so that . Again, since and Co (i.e., ) we choose , so that . Proceeding in a similar way, we observe that the sequence is an eventually constant sequence (i.e., for all ) converging to
Case II: Suppose that
for all
. Define
for all
and
. Then, for each
we have
Hence,
is an increasing sequence in
, and it is convergent. Let us suppose
Since
and
C is compact, there exists a subsequence
which converges to
and by continuity of
we obtain
and
as
. We show that
for all
. On the contrary, suppose that
for some
. Then, we have
Since
by (2) we obtain
This contradiction shows that
for all
, i.e.,
converges to
. □
Remark 1. If in the above theorem, the mappings are weakly compatible, then by Proposition 1
the mappings have a unique common fixed point.
Example 2. Let , where for all , for all and be defined by:Then, is a fuzzy metric space. Let , then C is a nonempty compact subset of Y. Consider the mappings defined by , for all and . Then, it is clear that . If , then we have
for all . Also:
for all . Therefore, is Edelstein -contractive on Y. It is easy to verify that is continuous.
We see that is singleton and for each initial value the Jungck sequence converges to 1.
We now state an application of the theorems stated above.
4. Application to a Stable Market
In this section, we apply Theorem 1 to prove that under some suitable conditions, a dynamic market is stable and an equilibrium state of the market is obtained as a limiting state.
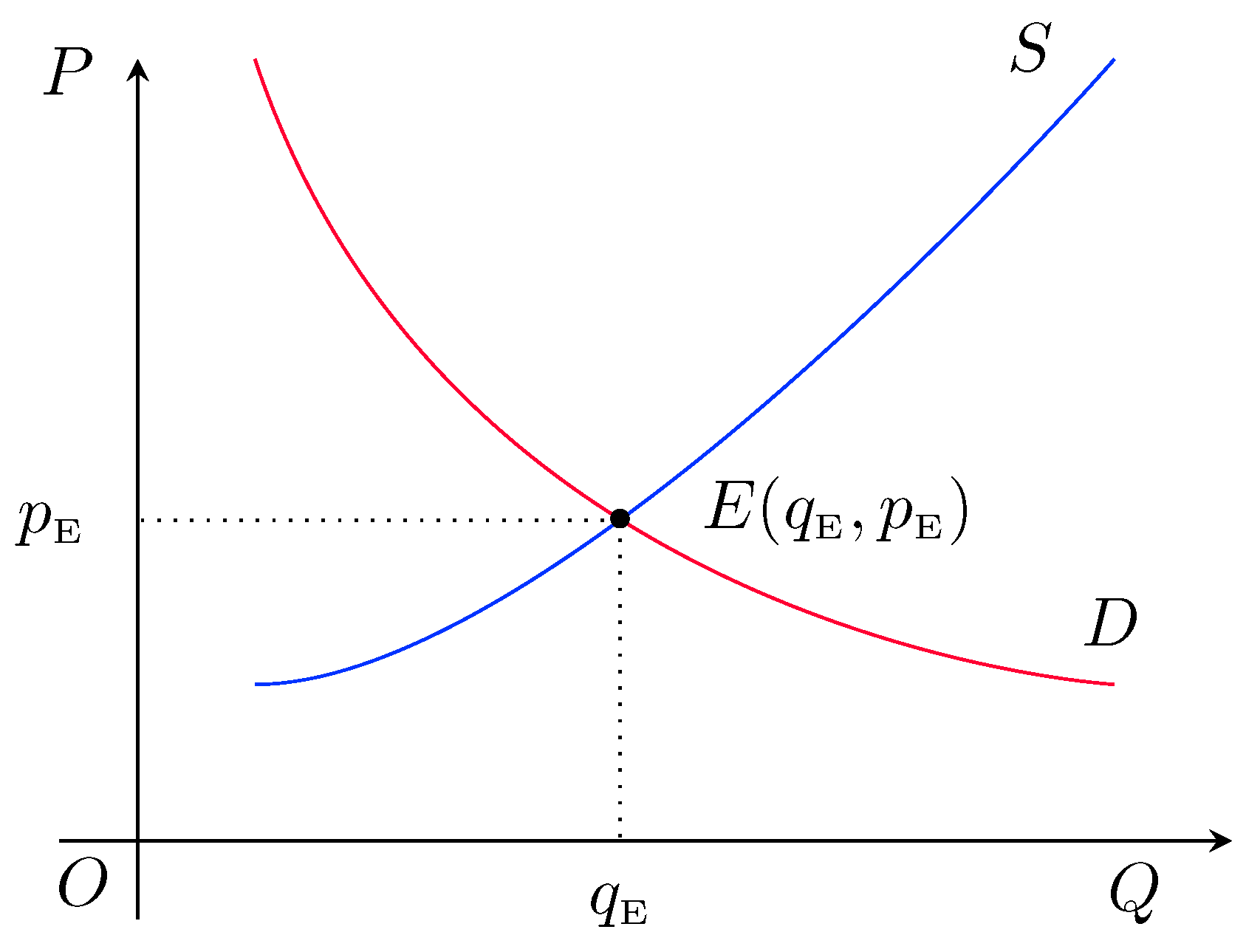
Consider a simple demand and supply model of a market. We represent various stages of the market graphically by taking the quantity (demanded or supplied) and the corresponding price of the commodity on the
Q (horizontal) and
P (vertical) axes, respectively. Such markets are completely characterized by the supply function (
S) and the demand function (
D) which express the price (
p) in terms of the supplied quantity and demanded quantity (
q), respectively. Under normal conditions of the market, the demand function
is decreasing, whereas the supply function
is increasing (see
Figure 1).
In practice, we assume that the price of a commodity and its demanded and supplied quantities are nonnegative finite quantities and the demand and supply functions are continuous functions of quantity q. We assume that the quantity (demanded or supplied) always lies in the interval , whereas the corresponding prices varies in the range for some . We also assume that for each price , there is a definite supplied quantity , and similar is true for demanded quantity as well. For application purpose, with suitable choice of functions, we can assume that the demanded and supplied quantities and the corresponding prices all lies in the interval (see Remark 2 below), and in the rest of discussion, we denote this interval by .
Definition 7. The sensitive index of a dynamic market in an interval is a positive number and it is defined byA dynamic market is said to be supply-sensitive if for all , i.e.,The above condition shows that corresponding to a definite change in the quantity, supply of commodity changes faster than the demand of commodity; hence, the market with such a nature will be called supply-sensitive. On the other hand, if corresponding to a definite change in the quantity, demand of commodity changes faster than the supply of commodity, then the market is called demand-sensitive. Mathematically, the market is said to be a demand-sensitive if for all
, i.e.,
Theorem 2. A supply-sensitive market is always stable and there exists a Jungck sequence of prices which converges to the equilibrium price .
Proof. Let , then consider the price corresponding to this demanded quantity, i.e., . Since for each price there is a definite supplied quantity, there exists such that . This shows that .
Since the market is supply-sensitive, we have
Note that the above inequality holds for all
with
Define a fuzzy set
F on
by:
Then, it is easy to see that
is a fuzzy metric space, where
for all
. Also, for
since
, we obtain
Note that I is compact in the usual metric space and if and only if for every sequence and q in . Therefore, I is a compact subset of the fuzzy metric space . Thus, with , , and , all the conditions of Theorem 1 are satisfied. Hence, by Theorem 1, for every initial value the Jungck sequence , , converges to the unique point of coincidence of D and S. Let be the unique point of coincidence of D and S. Obviously, is the equilibrium price of the market and the market is stable. □
Theorem 3. A demand-sensitive market is always stable and there exists a Jungck sequence of prices which converges to the equilibrium price .
Proof. Consider for . Since for each price there is a definite demanded quantity, there exists such that . This shows that .
Since the market is demand-sensitive, we have
Note that the above inequality holds for all
with
Consider the fuzzy set
F on
and the
t-norm ∗ defined in the proof of Theorem 2. Since
, for
we obtain
Thus, with , , and , all the conditions of Theorem 1 are satisfied. Hence, by Theorem 1, for every initial value , the Jungck sequence , , converges to the unique point of coincidence of D and S. Let is the unique point of coincidence of S and D. Obviously, is the equilibrium price of the market and the market is stable. □
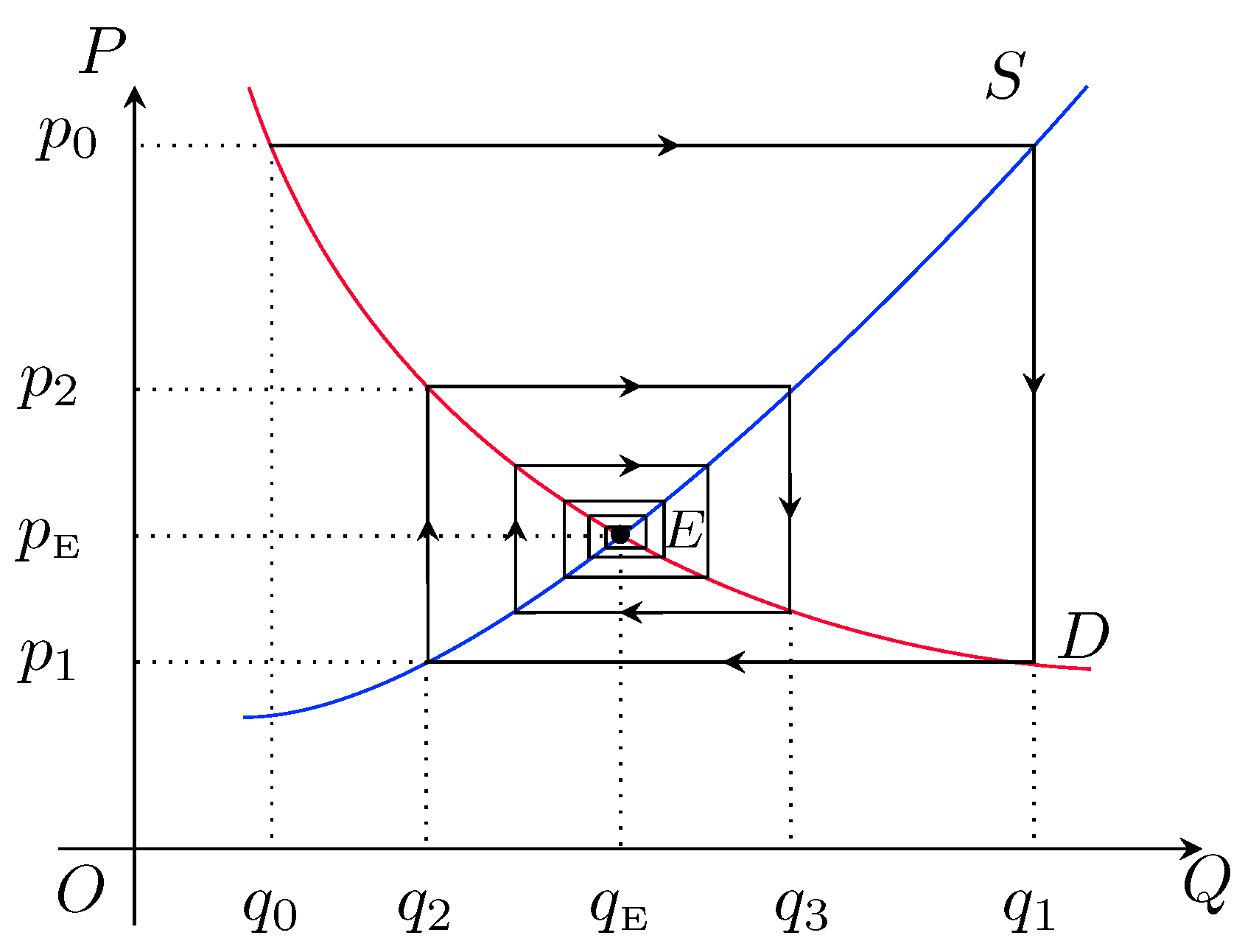
Convergence for supply and demand-sensitive markets: First consider a supply-sensitive market. In practice, the price of a commodity is not equal to the equilibrium price. Suppose initially the price is
, i.e.,
(if
, then a similar explanation will work). At this stage, suppose
. Since corresponding to this price
there is a definite supplied quantity, say
, the quantity
can be obtained by drawing a line passing from the point
and parallel to the
Q axis, see
Figure 2, i.e.,
.
Figure 2.
A supply-sensitive market.
Figure 2.
A supply-sensitive market.
From
Figure 2, it is clear that
; hence, at this stage the supplied quantity is higher than the demanded quantity of commodity and there is a surplus of the commodity
. The reaction of producers causes a decrement in the price of the commodity up to a value
such that for this price, the corresponding demanded quantity is
, i.e.,
. This process leads the market to the next (first) stage.
The price at first stage of the market is lower than the equilibrium price, i.e., . At this stage, the supplied quantity is and the demanded quantity is and , ; hence, there is shortage of commodity . Now producers increase the price up to a value such that for this price the corresponding demanded quantity is , i.e., . Since there is a definite supplied quantity corresponding to this price , say , i.e., . This process leads the market to the next (second) stage.
Similarly, for each stage of the market we obtain a sequence of prices
, where
Again, this sequence of prices is a Jungck sequence of the ordered pair
, i.e.,
, and the market is supply-sensitive; hence, the Jungck sequence is forced by Theorem 2 to be convergent, and the limit of the Jungck sequence is the point of coincidence of the functions
D and
S which is actually the equilibrium price for the market. Hence, the market is stable.
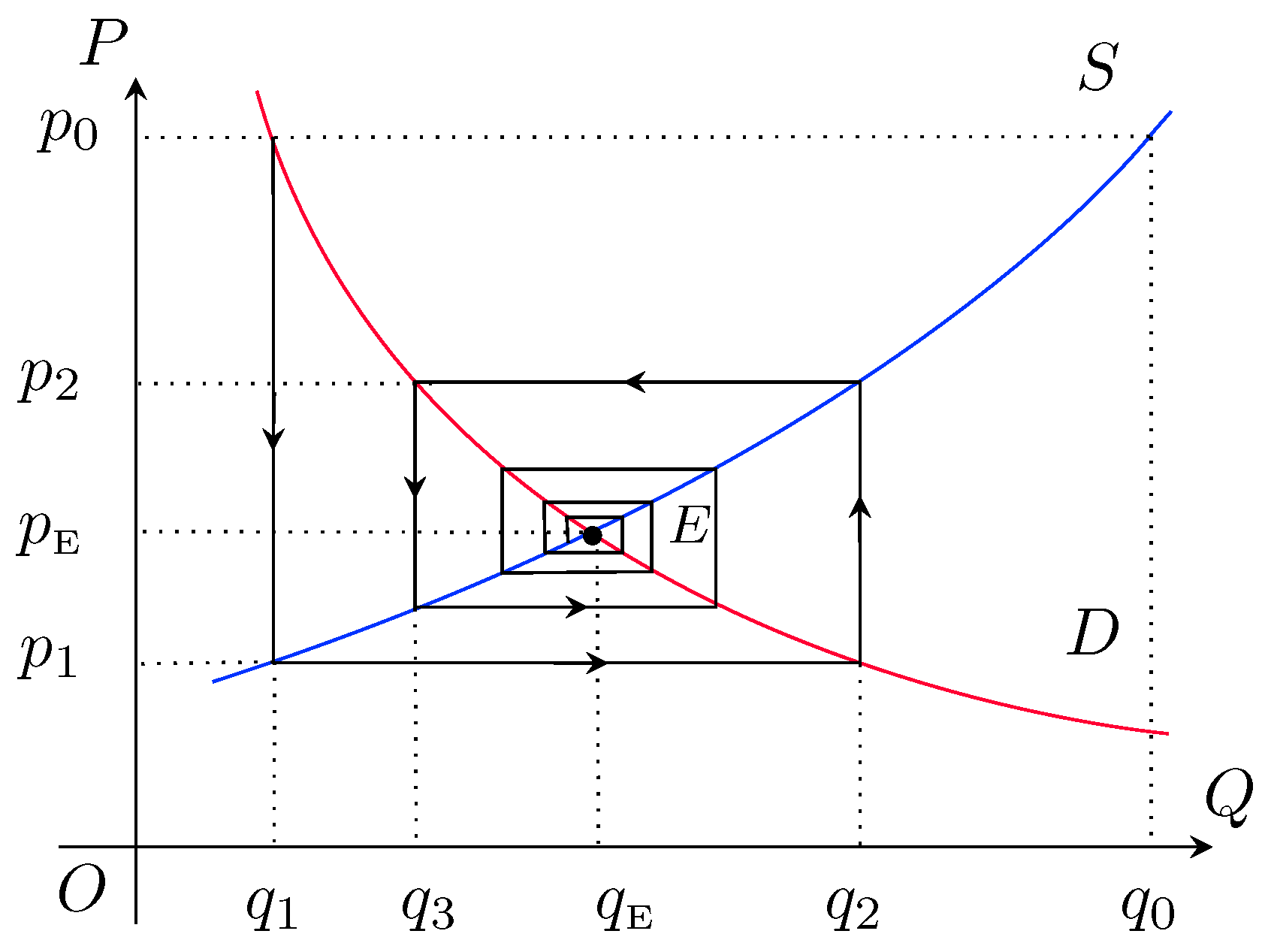
On the other hand, for a demand-sensitive market, if the initial price is
and
(if
, then a similar explanation will work). At this stage, suppose
. Since corresponding to this price
there is a definite demanded quantity, say
(the quantity
can be obtained by drawing a line which is parallel to the
P axis and passes through the point of intersection of: (i) demand curve; and (ii) the line parallel to
Q axis and passing through the point
; see
Figure 3), i.e.,
.
From
Figure 3 it is clear that
; hence, at this stage there is a surplus of the commodity
. The reaction of producers causes a decrement in the price of the commodity up to a value
such that for this price the corresponding supplied quantity is
, i.e.,
. This process leads the market to the next (first) stage.
The price at first stage of the market is lower than the equilibrium price, i.e., . At this stage, the supplied quantity is and the demanded quantity is and , ; hence, there is shortage of commodity . Now, producers increase the price up to a value such that for this price the corresponding supplied quantity is , i.e., . Since there is a definite demanded quantity corresponding to this price , say , i.e., , this process leads the market to the next (second) stage.
Similarly, for each stage of the market, we obtain a sequence of prices
, where
Obviously, this sequence of prices is a Jungck sequence of the ordered pair
, i.e.,
. Furthermore, since the market is demand-sensitive, the Jungck sequence is forced by Theorem 3 to be convergent, and the limit of the Jungck sequence is the point of coincidence of the functions
D and
S, which is actually the equilibrium price for the market. Hence, the market is stable.
Remark 2. In practical problems, it may happen that the demanded (supplied) quantities lie in an interval and the corresponding price of the commodity lies in the interval and . To overcome such situations, we use the method of “scaling”. We illustrate this method with the example of a supply-sensitive market as follows (the same can be conducted for a demand-sensitive market): consider the functions satisfying for all with . Suppose that and S is continuous. If , i.e., then are self-mappings of ; hence, by following a similar process to the proof of Theorem 2 one can ensure that have a point of coincidence, i.e., there exists such that . However, if , i.e., then are not self-mappings of , and so, the same procedure is not applicable and the existence of point of coincidence cannot be concluded.
To construct self-mappings on with the desired properties, we apply the process of “scaling” on such that the coincidence point can be concluded in a similar manner as we have conducted in the proof of Theorem 2. Suppose , and consider the functions:Then, we observe that Also, for we haveSince , we haveThus, . Hence, again following a similar process to the proof of Theorem 2, one can ensure the existence of the coincidence point of . Let Co . Note that Co if and only if Co ; hence, we are done. 5. Difference between the Two Strategies for Supply Sensitive and Demand-Sensitive Markets and Conclusions
In this section, we discuss two strategies for supply-sensitive and demand-sensitive markets and compare our approach with the approach of [
22].
It is clear from the above discussion that to examine stability of a market, it is sufficient to consider the convergence of the Jungck sequence
of prices, and if it is convergent, then it converges to the equilibrium price, and in this situation, the market is stable. It is also clear that in a supply-sensitive market, when the price of the commodity is not equal to the equilibrium price, at any stage of the market, producers reduce (or increase) the price until the demanded quantity becomes equal to the supplied quantity of the previous stage. Such a strategy is called a “demand-based” strategy. Hence, to control a supply-sensitive market, the producers strategy should be demand-based. On the other hand, in a demand-sensitive market, when the price of the commodity is not equal to the equilibrium price, at any stage of the market, producers reduce (or increase) the price until the supplied quantity becomes equal to the demanded quantity of the previous stage. Such a strategy is called a “supply-based” strategy. Hence, to control a demand-sensitive market, the producers strategy should be supply-based. The consequences of these two strategies can be seen in
Figure 2 and
Figure 3. In
Figure 2, for a supply-sensitive market, the convergence of the sequence of prices
is represented by a rectangular spiral that converges clockwise towards the equilibrium price
, while in
Figure 3, for a demand-sensitive market, it is represented by a rectangular spiral that converges anticlockwise towards the equilibrium price
. Also, if the producers do not follow the strategies suggested above, i.e., if a “demand-based” strategy is followed for a demand-sensitive market (or a “supply-based” strategy is followed for a supply-sensitive market), then the rectangular spiral diverges and the equilibrium state of the market cannot be reached.
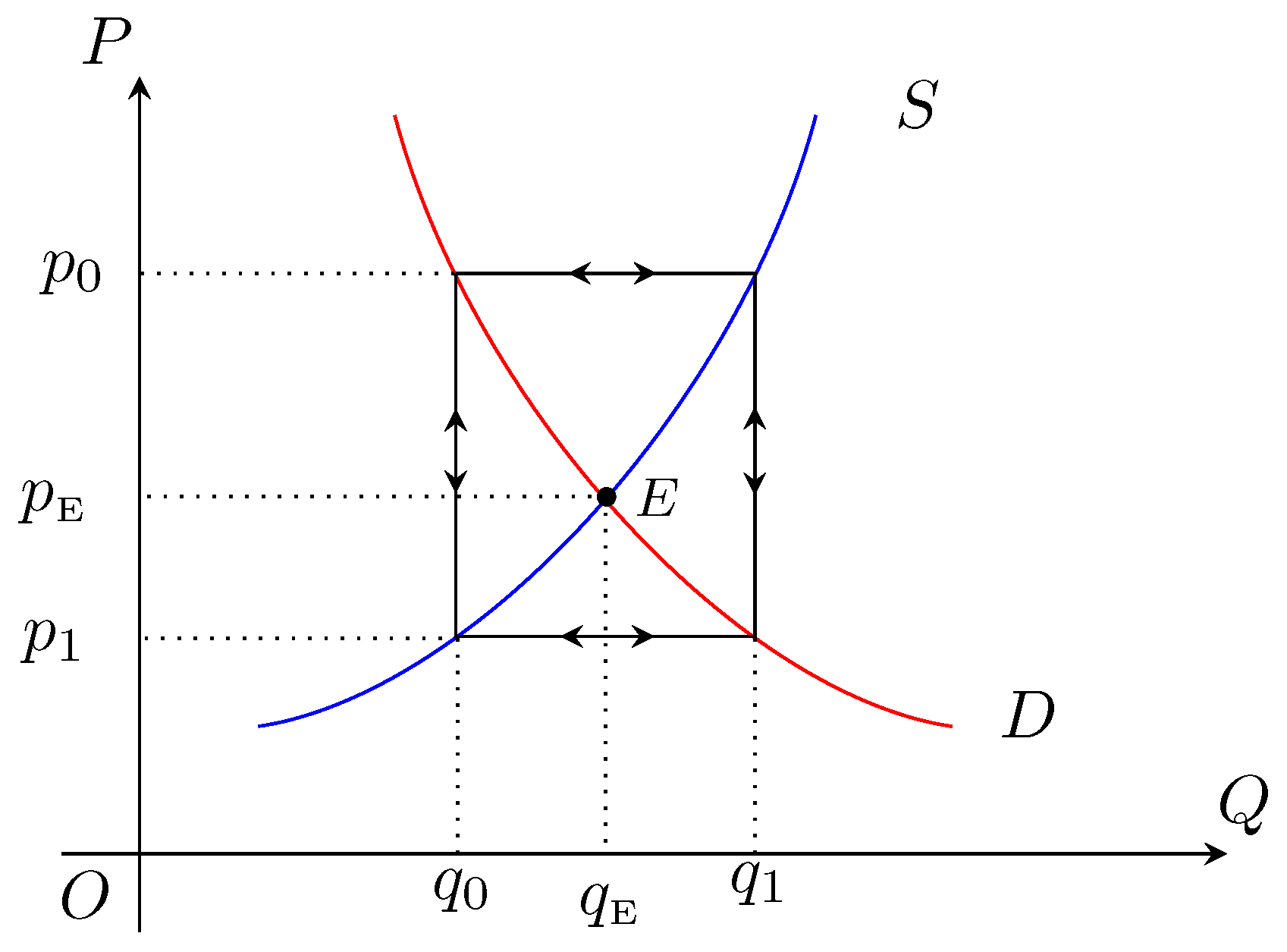
We see that if neither of the conditions (4) and (5) are satisfied for the market (i.e., if the market is neither supply-sensitive nor demand-sensitive), then the market may not be stable and the procedures discussed above (sequences of prices) may fail to converge and the equilibrium may be unreachable, e.g., at any stage, if
for some
(i.e., the sensitivity index
) with
then both the procedures discussed above fail to converge as shown in
Figure 4. As we can see in
Figure 4 for both strategies (supply-based and demand-based), the sequence of prices is represented by a rectangle through which we see repetition of price after each consecutive stage. Mathematically, in such cases, we see periodic points (prices) of the Jungck sequence, i.e.,
, which causes the prevention of the convergence of procedures. On the other hand, if any one of the conditions (4) and (5) is satisfied, then by Proposition 2, such a prevention is not possible and the market is stable.
Mezník’s [
22] approach is based on the existence of the fixed point of the mapping
(see [
22]) which involves the inverse of supply function S. Furthermore, the sufficient condition for convergence of sequence of prices involves the derivatives of the supply and demand functions. Further, the approach of Mezník [
22] is rooted in the cobweb theory (see [
32] and the references therein), which is based on the time leg between the supply and demand decision, and so, the demand of commodity is assumed to be a function of the current stage price and the supply of a commodity is a function of the previous stage. Hence, the suppliers control the demanded quantity (supplied quantity) by increasing or decreasing the price of the commodity for a current stage (e.g., in agricultural markets), i.e., by following the demand-based strategy. The drawback of this strategy is that in the case of a demand-sensitive market, the iteration procedure of Mezník [
22] diverges. Here, we have presented a generalized approach of the coincidence point to establish the stability of a demand–supply model without demanding the calculation of inverse functions or a derivative of the supply and demand function. Also, we suggest the theoretical possibility of convergence of the iteration procedure of a sequence of prices in the case of a demand-sensitive market by applying the supply-based strategy for the markets of a favorable nature.
In
Table 1, a comparison between these two approaches is provided.