Solution of a Half-Space in Generalized Thermoelastic Problem in the Context of Two Models Using the Homotopy Perturbation Method
Abstract
:1. Introduction
2. The Basic Models Used in the Problem
3. Basic Idea for the Technique of Homotopy Perturbation
4. Problem Formulation and the Fundamental Equations
5. Solution under the Homotopy Perturbation Technique
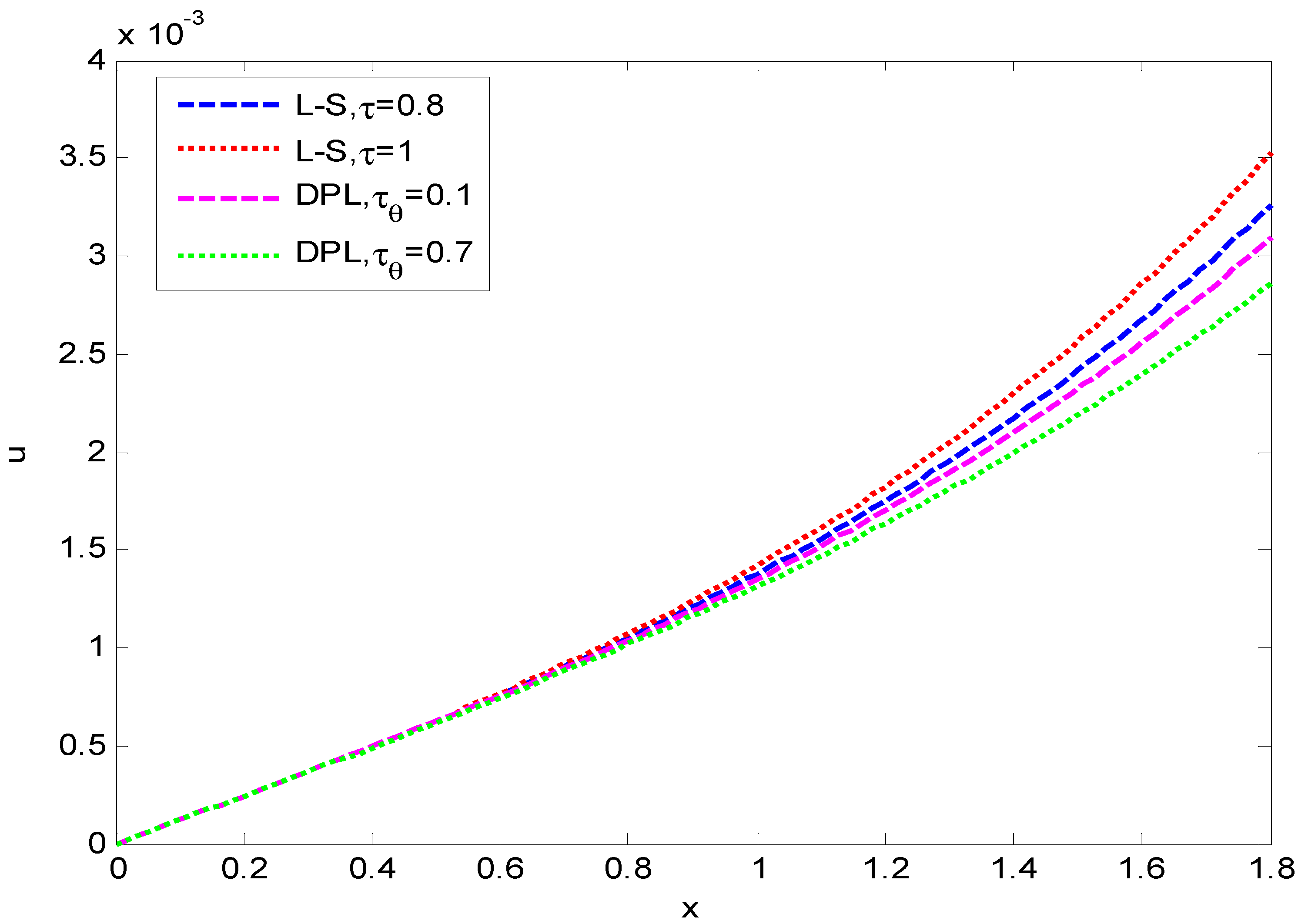
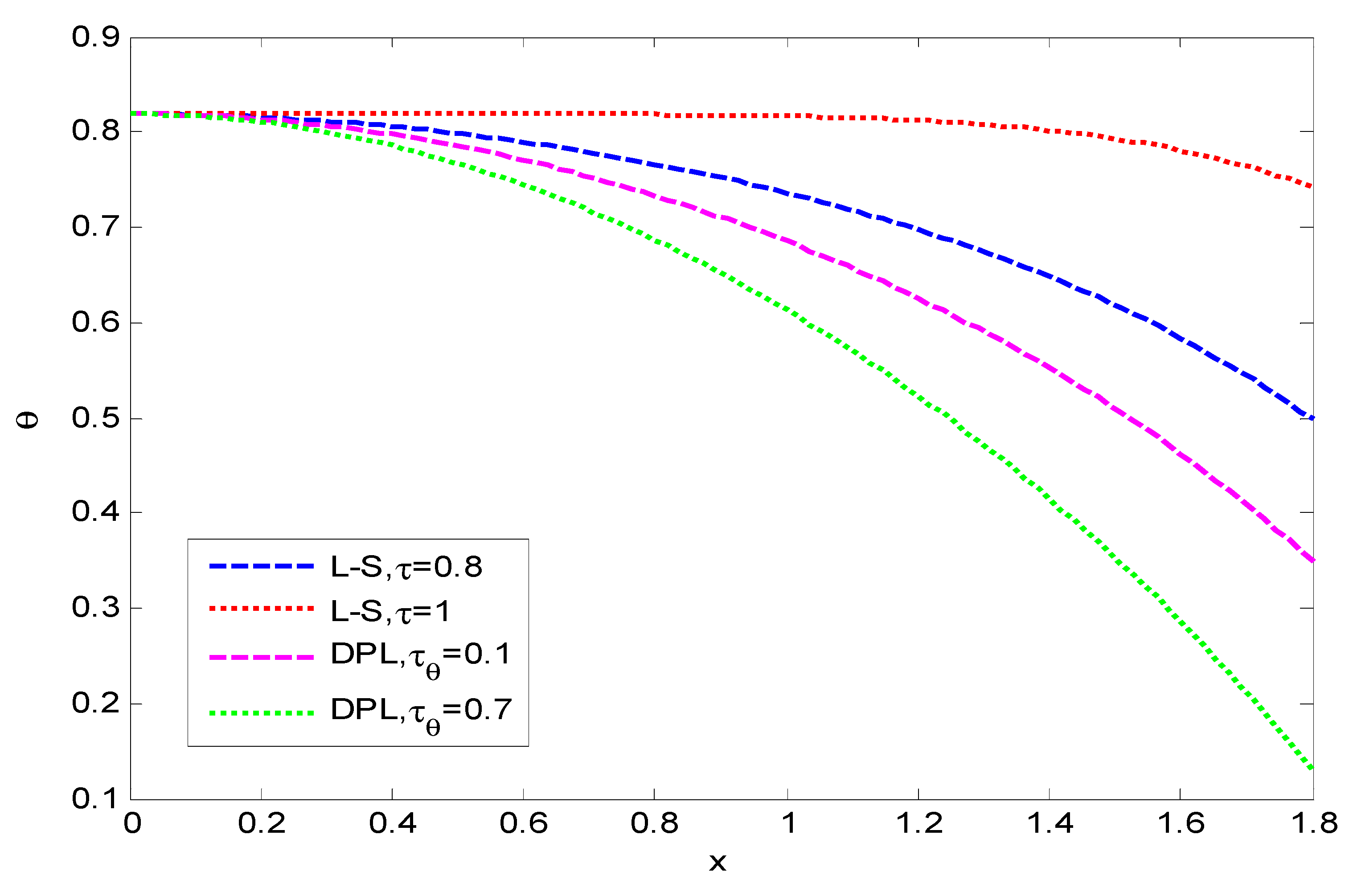
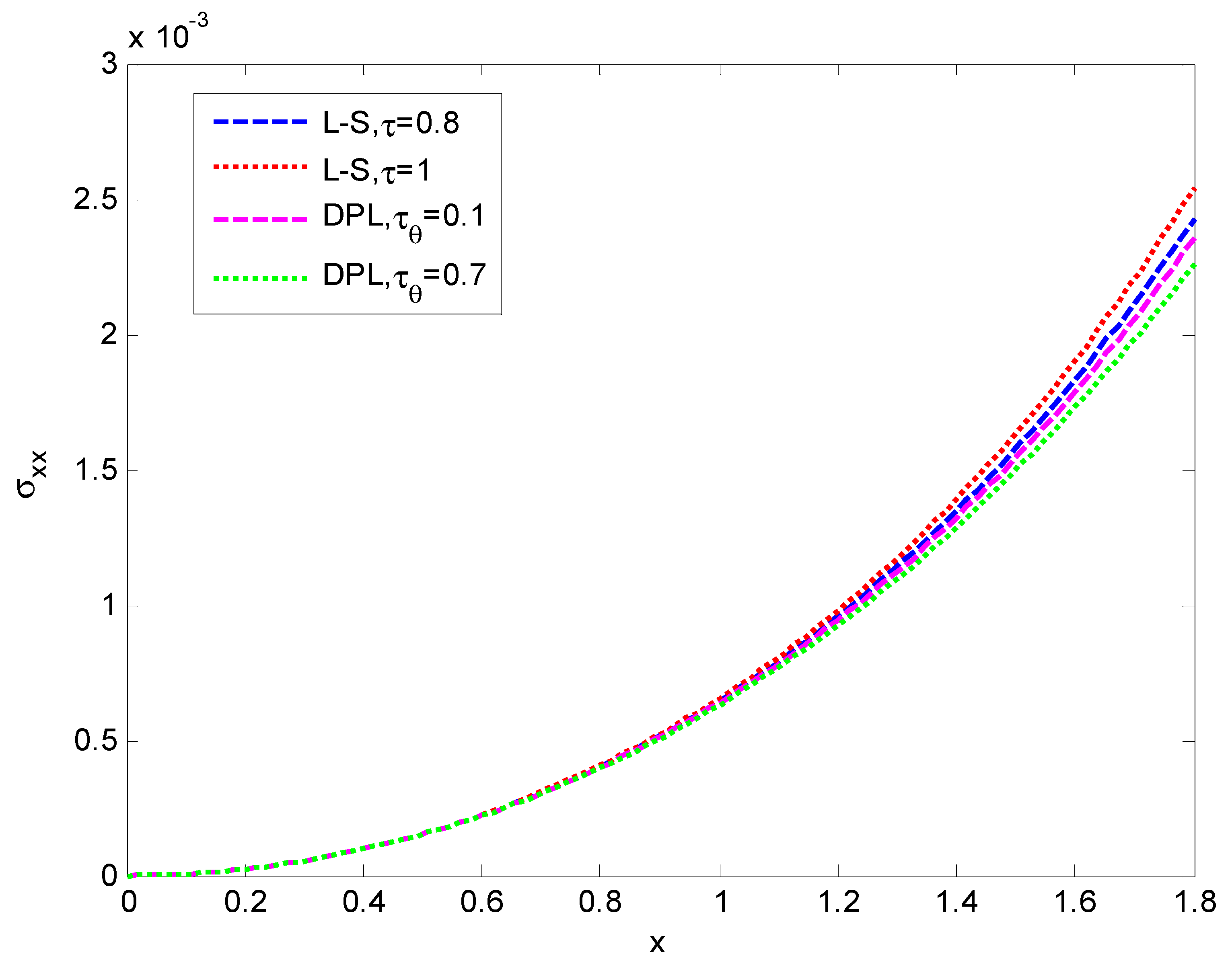
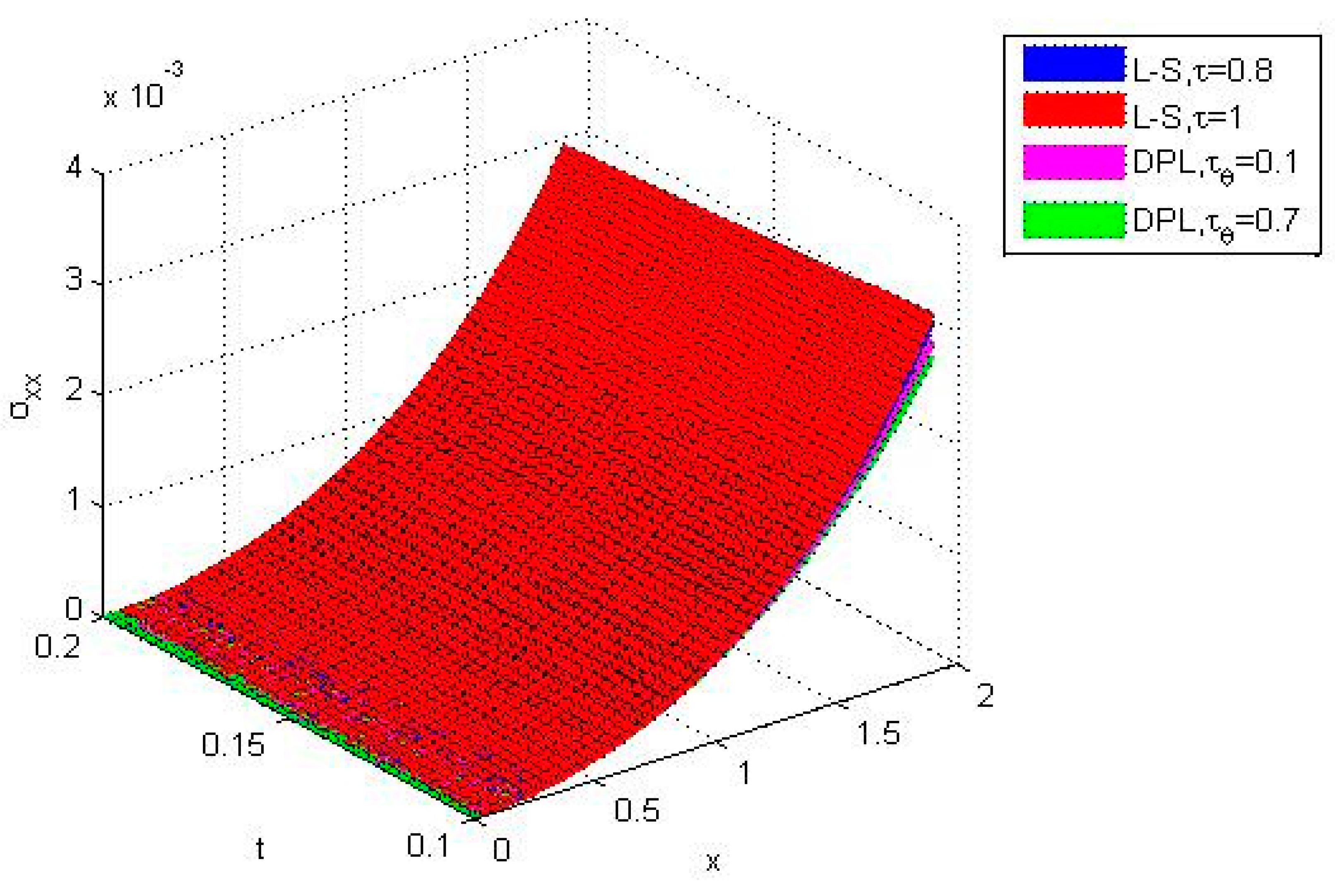
6. Numerical Results and Discussion
7. Conclusions
- The parameters have a significant effect on all the fields that have a good result due to the new external parameters.
- The comparison of different theories of thermoelasticity, namely the Lord and Shulman (LS) and Chandrasekharaiah and Tzou (DPL) models, is very clear and shows significantly different values between the two theories.
- All boundary conditions satisfy the physical quantities.
- The homotopy perturbation method (HPM) can be used to derive displacement, temperature, and stress analytically.
- The results obtained illustrate the strong impact on the displacement, temperature, and stress with the variations in the two models as well as the relaxation time parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Time | |
| Thermal conductivity | |
| An integral or differential operator | |
| Specific heat per unit mass | |
| Components of strain tensor | |
| The reference temperature | |
| The temperature distribution | |
| Coefficient of linear thermal expansion | |
| Kronecker delta | |
| and | Lame’s constants |
| Density | |
| Components of the stress vector | |
| The thermal relaxation time | |
| The phase-lag of temperature gradient | |
References
- Lord, H.W.; Shulman, Y. A generalized dynamical theory of thermo elasticity. J. Mech. Phys. Solids 1967, 15, 299–309. [Google Scholar] [CrossRef]
- Green, A.E.; Lindsay, A. Thermoelasticity. J. Elast. 1972, 2, 1–7. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S. One-dimensional wave propagation in the linear theory of thermoelasticity with energy dissipation. J. Therm. Stress. 1996, 19, 695–710. [Google Scholar] [CrossRef]
- Dhaliwal, R.S.; Singh, A. Dynamic Coupled Thermoelasticity; Hindustan Publishing Corporation: New Delhi, India, 1980; p. 726. [Google Scholar]
- Hetnarski, R.B.; Ignaczak, J. Generalized Thermoelasticity. J. Therm. Stress. 1999, 22, 451–476. [Google Scholar]
- Abo-Dahab, S.M.; Rida, S.Z.; Mohamed, R.A.; Kilany, A.A. Rotation, Initial Stress, Gravity and Electromagnetic Field Effect on P Wave Reflection from Stress-Free Surface Elastic Half-Space with Voids under Three Thermoelastic Models. Mech. Mech. Eng. 2018, 22, 313–328. [Google Scholar] [CrossRef]
- RoyChoudhuri, S.K. One-dimensional thermoelastic waves in elastic half-space with dual phase-lag effects. J. Mech. Mater. Struct. 2007, 2, 489–503. [Google Scholar] [CrossRef]
- Abouelregal, A.E. Rayleigh waves in a thermoelastic solid half space using dual-phase-lag model. Int. J. Eng. Sci. 2011, 49, 781–791. [Google Scholar] [CrossRef]
- Bayones, F.S.; Abo-Dahab, S.M.; Abd-Alla, A.M.; Kilany, A.A. Electromagnetic Field and Three-phase-lag in a Compressed Rotating Isotropic Homogeneous Micropolar Thermo-viscoelastic Half-space. Math. Methods Appl. Sci. 2021, 44, 9944–9965. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Kothari, S.; Kumar, R. On the Representation of Solutions for the Theory of Generalized Thermoelasticity with Three Phase Lags. Acta Mech. 2010, 214, 305–314. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S.; Srinath, K.S. One-dimensional Waves in a Thermoe-lastic Half-Space without Energy Dissipation. Int. J. Eng. Sci. 1996, 34, 1447–1455. [Google Scholar] [CrossRef]
- Chandrasekharaiah, D.S. Hyperbolic Thermoelasticity: A Review of Recent Literature. Appl. Mech. Rev. 1998, 51, 705–729. [Google Scholar] [CrossRef]
- Bayones, F.S.; Kilany, A.A.; Abouelregal, A.E.; Abo-Dahab, S.M. A rotational gravitational stressed and voids effect on an electromagnetic photothermal semiconductor medium under three models of thermoelasticity. Mech. Based Des. Struct. Mach. 2021, 51, 1115–1141. [Google Scholar] [CrossRef]
- Sudhakar, Y.; Kumar, A. A Homotopy Analysis Approach to Thermoelastic In-teractions under the Boundary Condition: Heat Source Varying Exponentially with Time and Zero Stress. Int. J. Sci. Res. 2015, 4, 2126–2129. [Google Scholar]
- Rashidi, M.M.; Mohimanian Pour, S.A. Analytic approximate solutions for un-steady boundary layer flow and heat transfer due to a stretching sheet by homotopy analysis method. Nonlinear Anal. Model. Control 2010, 15, 83–95. [Google Scholar] [CrossRef]
- Kilany, A.A.; Abo-Dahab, S.M.; Abd-Alla, A.M.; Abdel-Salam, E.A.-B. Non-integer order analysis of electro-magneto-thermoelastic with diffusion and voids considering Lord–Shulman and dual-phase-lag models with rotation and gravity. Waves Random Complex Media 2022, 1–31. [Google Scholar] [CrossRef]
- Behrouz, R.; Kuppalapalle, V. Homotopy analysis method for MHD viscoelastic fluid flow and heat transfer in a channel with a stretching wall. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4149–4162. [Google Scholar]
- Abo-Dahab, S.M.; Kilany, A.A.; Abdel-Salam, E.A.-B.; Hatem, A. Fractional derivative order analysis and temperature-dependent properties on p- and SV-waves reflection under initial stress and three-phase-lag model. Results Phys. 2020, 18, 103270. [Google Scholar] [CrossRef]
- Abd-Alla, A.-E.N.; Ghaleb, A.; Maugin, G. Harmonic wave generation in nonlinear thermoelasticity. Int. J. Eng. Sci. 1994, 32, 1103–1116. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Noor, M.A. Homotopy perturbation method for solving fourth-order boundary value problems. Math. Probl. Eng. 2007, 2007, 98602. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Noor, M.A. Homotopy perturbation method for solving partial differential equations. Z. Naturforschung 2009, 64, 157–170. [Google Scholar] [CrossRef]
- Kilany, A.; Abd-Alla, A.; Abo-Dahab, S.M. On thermoelastic problem based on four theories with the efficiency of the magnetic field and gravity. J. Ocean Eng. Sci. 2022. [Google Scholar] [CrossRef]
- Kilany, A.A.; Abo-Dahab, S.M.; Abd-Alla, A.M.; Abd-Alla, A.N. Photothermal and void effect of a semiconductor rotational medium based on Lord–Shulman theory. Mech. Based Des. Struct. Mach. 2020, 50, 2555–2568. [Google Scholar] [CrossRef]
- He, J.H. Approximate solution of nonlinear differential equations with convolution product nonlinearities. Comput. Methods Appl. Mech. Eng. 1998, 167, 69–73. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng. 1999, 178, 257–262. [Google Scholar] [CrossRef]
- Abo-Dahab, S.M.; Abd-Alla, A.M.; Kilany, A.A. Homotopy perturbation method on wave propagation in a transversely isotropic thermoelastic two-dimensional plate with gravity field. Numer. Heat Transf. Part A Appl. 2022, 82, 398–410. [Google Scholar] [CrossRef]
- Liao, S. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Roul, P. On the numerical solution of singular two-point boundary value problems: A domain decomposition homotopy perturbation approach. Math. Methods Appl. Sci. 2017, 40, 7396–7409. [Google Scholar] [CrossRef]
- Pinheiro, I.F.; Sphaier, L.A.; Alves, L.S.d.B. Integral transform solution of integro-differential equations in conduction-radiation problems. Numer. Heat Transf. Part A Appl. 2018, 73, 94–114. [Google Scholar] [CrossRef]
- Philipbar, B.M.; Waters, J.; Carrington, D.B. A finite element Menter Shear Stress turbulence transport model. Numer. Heat Transf. Part A Appl. 2020, 77, 981–997. [Google Scholar] [CrossRef]
- Abd-Alla, A.M.; Abo-Dahab, S.M.; Kilany, A.A. Finite difference technique to solve a problem of generalized thermoelasticity on an annular cylinder under the effect of rotation. Numer. Methods Partial. Differ. Equ. 2021, 37, 2634–2646. [Google Scholar] [CrossRef]
- Abdelhady, M.; Wood, D. Effect of thermal boundary condition on forced convection from circular cylinders. Numer. Heat Transf. Part A Appl. 2019, 76, 420–437. [Google Scholar] [CrossRef]
- Ahmad, F.; Gul, T.; Khan, I.; Saeed, A.; Selim, M.M.; Kumam, P.; Ali, I. MHD thin film flow of the Oldroyd-B fluid together with bioconvection and activationn energy. Case Stud. Therm. Eng. 2021, 27, 101218. [Google Scholar] [CrossRef]
- Dawar, A.; Islam, S.; Shah, Z.; Lone, S.A. A comparative analysis of the magnetized sodium alginate-based hybrid nanofluid flows through cone, wedge, and plate. ZAMM 2022, 103, e202200128. [Google Scholar] [CrossRef]
- Sedelnikov, A.; Serdakova, V.; Orlov, D.; Nikolaeva, A. Investigating the temperature shock of a plate in the framework of a static two-dimensional formulation of the thermoelasticity problem. Aerospace 2023, 10, 445. [Google Scholar] [CrossRef]
- Antaki, P.J. Effect of dual-phase-lag heat conduction on ignition of a solid. J. Thermophys. Heat Transf. 2000, 14, 276–278. [Google Scholar] [CrossRef]
- Marin, M. Cesaro means in thermoelasticity of dipolar bodies. Acta Mech. 1997, 122, 155–168. [Google Scholar] [CrossRef]
- Marin, M.; Ellahi, R.; Chirilă, A. On solutions of Saint-Venant’s problem for elastic dipolar bodies with voids. Carpathian J. Math. 2017, 33, 219–232. [Google Scholar] [CrossRef]
- Marin, M.; Nicaise, S. Existence and stability results for thermoelastic dipolar bodies with double porosity. Contin. Mech. Thermodyn. 2016, 28, 1645–1657. [Google Scholar] [CrossRef]
- Watts, H.A. Step size control in ordinary differential equation solvers. Trans. Soc. Comput. Simul. 1984, 1, 15–25. [Google Scholar]
- Loud, W.S. On the long-run error in the numerical solution of certain differential equations. J. Math. Phys. 1949, 28, 45–49. [Google Scholar] [CrossRef]
- Hammer, P.C.; Hollingsworth, J.W. Trapezoidal methods of approximating solutions of deferential equations. MTAC 1955, 9, 92–96. [Google Scholar]
- Lin, W. Global existence theory and chaos control of fractional differential equations. J. Math. Anal. Appl. 2007, 332, 709–726. [Google Scholar] [CrossRef]
- Kanth, A.R.; Aruna, K. Two-Dimensional Differential Transform Method for Solving Linear and Non-Linear Schrödinger Equation. Chaos Solitons Fractals 2009, 41, 2277–2281. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Rathore, S. Application of Homotopy Perturbation Transform Method for Solving Linear and Nonlinear Klein-Gordon Equations. Inf. Comput. 2012, 7, 131–139. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Althobaiti, N.; Abo-Dahab, S.M.; Kilany, A.A.; Abd-Aalla, A.M. Solution of a Half-Space in Generalized Thermoelastic Problem in the Context of Two Models Using the Homotopy Perturbation Method. Axioms 2023, 12, 827. https://doi.org/10.3390/axioms12090827
Althobaiti N, Abo-Dahab SM, Kilany AA, Abd-Aalla AM. Solution of a Half-Space in Generalized Thermoelastic Problem in the Context of Two Models Using the Homotopy Perturbation Method. Axioms. 2023; 12(9):827. https://doi.org/10.3390/axioms12090827
Chicago/Turabian StyleAlthobaiti, Nesreen, Sayed M. Abo-Dahab, Araby Atef Kilany, and Abdelmooty M. Abd-Aalla. 2023. "Solution of a Half-Space in Generalized Thermoelastic Problem in the Context of Two Models Using the Homotopy Perturbation Method" Axioms 12, no. 9: 827. https://doi.org/10.3390/axioms12090827
APA StyleAlthobaiti, N., Abo-Dahab, S. M., Kilany, A. A., & Abd-Aalla, A. M. (2023). Solution of a Half-Space in Generalized Thermoelastic Problem in the Context of Two Models Using the Homotopy Perturbation Method. Axioms, 12(9), 827. https://doi.org/10.3390/axioms12090827






