Optimal Auxiliary Function Method for Analyzing Nonlinear System of Belousov–Zhabotinsky Equation with Caputo Operator

Abstract

This paper introduces the optimal auxiliary function method (OAFM) for solving a nonlinear system of Belousov–Zhabotinsky equations. The system is characterized by its complex dynamics and is treated using the Caputo operator and concepts from fractional calculus. The OAFM provides a systematic approach to obtain approximate analytical solutions by constructing an auxiliary function. By optimizing the parameters of the auxiliary function, an approximate solution is derived that closely matches the behavior of the original system. The effectiveness and accuracy of the OAFM are demonstrated through numerical simulations and comparisons with existing methods. Fractional calculus enhances the understanding and modeling of the nonlinear dynamics in the Belousov–Zhabotinsky system. This study contributes to fractional calculus and nonlinear dynamics, offering a powerful tool for analyzing and solving complex systems such as the Belousov–Zhabotinsky equation.

1. Introduction

Fractional nonlinear systems of partial differential equations (PDEs) have garnered substantial research interest owing to their capacity to describe diverse phenomena across areas such as engineering, physics, and biology. Fractional derivatives, non-local operator that account for historical impacts, and complicated non-linearities are all part of these schemes. The usefulness of fractional calculus, which deals with fractional derivatives and integrals, has been demonstrated in real-world circumstances by simulating memory effects, long-range interactions, and anomalous diffusion. Simultaneously, nonlinear dynamics investigates the complicated behavior of complex systems that exhibit nonlinear interactions among their basic components [1,2,3]. The combination of these two domains has resulted in fractional nonlinear partial differential equation (PDE) systems capable of capturing the complicated dynamics found in several physical and biological systems. The analysis of fractional nonlinear PDE systems has provided a multitude of intriguing discoveries and practical applications within this rapidly developing field of study. Current research efforts are mostly focused on diving into the stability and bifurcation characteristics of solutions, as well as their uniqueness and existence, which is frequently supported by numerical simulations. These systems have been applied to a variety of disciplines, including fluid dynamics, electrochemistry, and population dynamics, each of which provides distinct insights and opportunities for investigation [4,5,6,7,8,9].

One class of nonlinear systems that has attracted significant attention is the nonlinear system of Belousov–Zhabotinsky equation (NSBZE). The NSBZE is a mathematical model that describes the complex behavior of reaction–diffusion systems exhibiting chemical oscillations and pattern formation. It finds applications in diverse areas such as chemistry, biology, and material science [10,11]. The nonlinear system of Belousov–Zhabotinsky equation, initially rooted in chemical reactions, has broadened its impact across multiple scientific domains. It is a cornerstone for understanding chemical kinetics, reaction–diffusion dynamics, and pattern formation. This equation finds applications in diverse fields, including materials science, biological systems, neural networks, artificial life, optics, and unconventional computing. Its insights inform the study of self-organizing materials, neural pattern formation, brain dynamics, and innovative information processing methods. Moreover, the equation’s visually captivating patterns and oscillations make it a valuable tool for educational outreach and fostering a deeper understanding of complex behaviors and nonlinear dynamics in various scientific contexts. To tackle the NSBZE, fractional calculus provides a powerful mathematical framework. Fractional calculus extends the concept of differentiation and integration to non-integer orders, allowing for analyzing systems with memory and long-range dependencies. The Caputo operator is commonly employed in fractional calculus, a fractional derivative operator widely used to describe the dynamics of physical systems governed by fractional differential equations [12,13,14,15,16,17].

The optimal auxiliary function method (OAFM) has proven to be a powerful tool for solving various types of nonlinear differential equations. This method introduces an auxiliary function that satisfies an ordinary differential equation optimized to yield approximate solutions for the original problem. The OAFM has been used effectively in various areas, including fluid dynamics, chemical reactions, and population dynamics [18,19,20,21]. In this paper, we aim to combine the optimal auxiliary function method with the Caputo operator in the context of the nonlinear system of Belousov–Zhabotinsky equation. We aim to develop an effective numerical technique for obtaining approximate solutions to this challenging nonlinear system. By utilizing the capabilities of the OAFM and the mathematical foundation provided by fractional calculus, we seek to enhance the accuracy and efficiency of the solution process.

2. Preliminaries

Definition 1.

The Caputo fractional derivative of a function $R(\zeta ,\tau )$ with a fractional order α is expressed as [18]

$${}^C{D}_t^{\alpha }R(\zeta ,t)=J_t^{m-\alpha }{R}^m(\zeta ,t),m-1<\alpha \le m,t>0.$$

(1)

Definition 2.

The expression for the Riemann fractional integral can be presented as follows [18]:

$$J_t^{\alpha }R(\zeta ,t)=\frac{1}{\mathsf{\Gamma }\left(\alpha \right)}{\int }_0^t{(t-r)}^{\alpha -1}R(\zeta ,r)dr$$

(2)

Lemma 1.

For $n-1<\alpha \le n$, $p>-1$, $t\ge 0$ and $\lambda \in R$, we have [18]:

1. 

$D_t^{\alpha }{t}^p=\frac{\mathsf{\Gamma }(\alpha +1)}{\mathsf{\Gamma }(p-\alpha +1)}{t}^{p-\alpha }$

2. 

$D_t^{\alpha }\lambda =0$

3. 

$D_t^{\alpha }{I}_t^{\alpha }R(\zeta ,t)=R(\zeta ,t)$

4. 

$I_t^{\alpha }{D}_t^{\alpha }R(\zeta ,t)=R(\alpha ,t)-{\sum }_{i=0}^{n-1}{\partial }^{i}R(\zeta ,0)\frac{t^i}{i!}$

3. General Procedure of OAFM

In this section, we consider the most general type of a nonlinear fractional order differential equation [18]:

$$\begin{array}{c}\hfill \frac{{\partial }^{\alpha }R(\xi ,\tau )}{\partial {\tau }^{\alpha }}=g(\xi ,\tau )+N\left(R(\xi ,\tau )\right)\end{array}$$

(3)

with the initial condition

$$\begin{array}{c}\hfill \frac{{\partial }^{k}R(\xi ,0)}{\partial {\tau }^k}=h_k\left(\xi \right),k=0, 1, 2, \cdots .\end{array}$$

(4)

where $\frac{{\partial }^{\alpha }}{\partial {\tau }^{\alpha }}$ represents the fractional derivative of order $\alpha$, $g(\xi ,\tau )$ is the unknown function, and $N\left(R\right(\xi ,\tau \left)\right)$ is the nonlinear function involving R, spatial variable $\xi$, and time variable $\tau$.

• Step 1: To solve Equation (3), we will use an approximate solution that has two components, such as:

  $$R(\xi ,\tau )=R_0(\xi ,\tau )+R_1(\xi ,\tau ,C_i),i=1, 2, 3, \dots , p$$

  (5)
• Step 2: To determine the zero and first-order solutions, we substitute Equation (5) into Equation (3), which results in:

  $$\frac{{\partial }^{\alpha }{R}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }}+\frac{{\partial }^{\alpha }{R}_1(\xi ,\tau )}{\partial {\tau }^{\alpha }}+g(\xi ,\tau )+N\left[\frac{{\partial }^{\alpha }{R}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }}+\frac{{\partial }^{\alpha }{R}_1(\xi ,\tau ,C_i)}{\partial {\tau }^{\alpha }}\right]=0$$

  (6)
• Step 3: For the purpose of determining the first approximation $R_0(\xi ,\tau )$ based on the linear equation.

  $$\frac{{\partial }^{\alpha }{R}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }}+g(\xi ,\tau )=0$$

  (7)

Using the inverse operator, we arrive at $R_0(\xi ,\tau )$, which is expressed as follows:

$$R_0(\xi ,\tau )=g(\xi ,\tau )$$

(8)

• Step 4: The nonlinear term seen in expanding form (6) is,

  $$N\left[\frac{{\partial }^{\rho }{R}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }}+\frac{\partial R_1^{\alpha }(\xi ,\tau ,C_i)}{\partial t^{\alpha }}\right]=N\left[R_0(\xi ,\tau )\right]+\sum _{k=1}^{\infty }\frac{R_1^k}{k!}{N}^{\left(k\right)}\left[R_0(\xi ,\tau )\right]$$

  (9)
• Step 5: To quickly solve Equation (9) and accelerate the convergence of the first-order approximations $R(\xi ,\tau )$, we propose the following alternative equation:

  $$\frac{{\partial }^{\alpha }{R}_1(\xi ,\tau ,C_i)}{\partial {\tau }^{\alpha }}=A_1\left[R_0(\xi ,\tau )\right]N\left[R_0(\xi ,\tau )\right]+A_2\left[R_0(\xi ,\tau ),C_j\right].$$

  (10)
• Step 6: We find a first-order solutions $R_1(\xi ,\tau )$ by using the inverse operator after putting the Auxiliary function into Equation (10).
• Step 7: Several methods are used to find the numerical values of the convergence control parameters $C_i$, including least squares, Galerkin’s, Ritz, and collocation. To eliminate mistakes, we employ the least squares approach.

  $$J(C_i,C_j)={\int }_0^t{\int }_{\mathsf{\Omega }}{\Re }^2(y,t;C_i,C_j)d\xi d\tau .$$

  (11)

  where ℜ denotes the residual,

  $$\begin{array}{cc}\hfill & \Re (\xi ,\tau ,C_i,C_j)=\frac{\partial R(\xi ,\tau ,C_i,C_j)}{\partial \tau }+g(\xi ,\tau )+N\left[R(\xi ,\tau ,C_i,C_j)\right],\hfill \\ \hfill & i=1, 2, \dots , s,j=S+1, S+2, \dots , p\hfill \end{array}$$

  (12)

4. Applications

4.1. Problem 1

Let us consider the Belousov–Zhabotinsky System of fractional order, which is represented by

$$\begin{array}{cc}\hfill & D_{\tau }^{\alpha }R(\xi ,\tau )-R(\xi ,\tau )-\frac{{\partial }^{2}R(\xi ,\tau )}{\partial {\xi }^2}+R^2(\xi ,\tau )+\lambda T(\xi ,\tau )=0,\hfill \\ \hfill & D_{\tau }^{\alpha }T(\xi ,\tau )-\frac{{\partial }^{2}T(\xi ,\tau )}{\partial {\xi }^2}+\gamma T(\xi ,\tau )T(\xi ,\tau )=0,\mathrm{where},0<\alpha \le 1\hfill \end{array}$$

(13)

Subject to the following IC’s:

$$\begin{array}{cc}\hfill & R(\xi ,0)=-\frac{1}{2}\left(1-tan{h}^2\left(\frac{\xi }{2}\right)\right),\hfill \\ \hfill & T(\xi ,0)=-\frac{1}{2}+tanh\left(\frac{\xi }{2}\right)+\frac{1}{2}tan{h}^2\left(\frac{\xi }{2}\right)\hfill \end{array}$$

(14)

Consider linear terms in Equation (13)

$$\begin{array}{cc}\hfill & L\left(R_0(\xi ,\tau )\right)=\frac{{\partial }^{\alpha }{R}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }},\hfill \\ \hfill & L\left(T_0(\xi ,\tau )\right)=\frac{{\partial }^{\alpha }{T}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }}\hfill \end{array}$$

(15)

Consider nonlinear terms in Equation (13)

$$\begin{array}{cc}\hfill & N\left(R_0(\xi ,\tau )\right)=-R_0(\xi ,\tau )-\frac{{\partial }^2{R}_0(\xi ,\tau )}{\partial {\xi }^2}+R_0^2(\xi ,\tau )+\lambda T_0(\xi ,\tau ),\hfill \\ \hfill & N\left(T_0(\xi ,\tau )\right)=-\frac{{\partial }^2{T}_0(\xi ,\tau )}{\partial {\xi }^2}+\gamma T_0(\xi ,\tau )R_0(\xi ,\tau )\hfill \end{array}$$

(16)

Zeroth-order approximation

$$\begin{array}{cc}\hfill & \frac{{\partial }^{\alpha }{R}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }}=0\hfill \\ \hfill & \frac{{\partial }^{\alpha }{T}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }}=0\hfill \end{array}$$

(17)

By apply of the inverse operator, we obtain result as:

$$\begin{array}{cc}\hfill & R_0(\xi ,\tau )=-\frac{1}{2}\left(1-tan{h}^2\left(\frac{\xi }{2}\right)\right),\hfill \\ \hfill & T_0(\xi ,\tau )=-\frac{1}{2}+tanh\left(\frac{\xi }{2}\right)+\frac{1}{2}tan{h}^2\left(\frac{\xi }{2}\right)\hfill \end{array}$$

(18)

By making use of Equation (18) in Equation (16), the system of nonlinear terms becomes

$$\begin{array}{cc}\hfill & N\left[R_0(\xi ,\tau )\right]=\frac{1}{14}{\mathrm{sech}}^4\left(\frac{\xi }{2}\right)(\lambda (2\sinh \left(\xi \right)+\sinh \left(2x\right)-2)-2(\lambda -2)\cosh \left(\xi \right))\hfill \\ \hfill & N\left[T_0(\xi ,\tau )\right]=\frac{1}{4}{\mathrm{sech}}^4\left(\frac{\xi }{2}\right)(\gamma (-\sinh \left(\xi \right))+\gamma +\sinh \left(\xi \right)+\cosh \left(\xi \right)-2)\hfill \end{array}$$

(19)

We choose the auxiliary function as:

$$\begin{array}{cc}\hfill & A_1=c_1\left(-\frac{1}{2}\left(1-tan{h}^2\left(\frac{\xi }{2}\right)\right)\right),\hfill \\ \hfill & A_2=c_2{\left(-\frac{1}{2}\left(1-tan{h}^2\left(\frac{\xi }{2}\right)\right)\right)}^3,\hfill \\ \hfill & A_3=c_3{\left(-\frac{1}{2}+tanh\left(\frac{\xi }{2}\right)+\frac{1}{2}tan{h}^2\left(\frac{\xi }{2}\right)\right)}^5\hfill \\ \hfill & A_4=c_4{\left(-\frac{1}{2}+tanh\left(\frac{\xi }{2}\right)+\frac{1}{2}tan{h}^2\left(\frac{\xi }{2}\right)\right)}^7\hfill \end{array}$$

(20)

First-order approximation using the OAFM approach, as described in Section 3.

$$\begin{array}{cc}\hfill & \frac{{\partial }^{\alpha }{R}_1(\xi ,\tau )}{\partial {\tau }^{\alpha }}=-\left(A_1[R_0(\xi ,\tau )N\left[R_0(\xi ,\tau )\right]+A_2[R_0(\xi ,\tau );c_j]\right)\hfill \\ \hfill & \frac{{\partial }^{\alpha }{T}_1(\xi ,\tau )}{\partial {\tau }^{\alpha }}=-\left(A_3[T_0(\xi ,\tau )N\left[T_0(\xi ,\tau )\right]+A_4[T_0(\xi ,\tau );c_j]\right)\hfill \end{array}$$

(21)

using Equations (19) and (20) in Equation (21).

$$\begin{array}{cc}\hfill & \frac{{\partial }^{\alpha }{R}_1(\xi ,\tau )}{\partial {\tau }^{\rho }}=\frac{1}{8}{\mathrm{sech}}^6\left(\frac{\xi }{2}\right)(c_1\lambda \sinh \left(\xi \right)+c_1\cosh \left(\xi \right)(\lambda \sinh \left(\xi \right)-\lambda +2)-c_1\lambda +c_2)\hfill \\ \hfill & \frac{{\partial }^{\alpha }{T}_1(\xi ,\tau )}{\partial {\tau }^{\rho }}=-\frac{1}{256}{(\sinh \left(\xi \right)-1)}^5{\mathrm{sech}}^{14}\left(\frac{\xi }{2}\right)(2\sinh \left(\xi \right)(-c_3\gamma +c_3-2c_4)+2c_3(\gamma -2)\hfill \\ & + 2c_3\cosh \left(\xi \right)c_4\cosh \left(2\xi \right)+c_4)\hfill \end{array}$$

(22)

Using the inverse operator to Equation (22) we get

$$\begin{array}{cc}\hfill & R_1(\xi ,\tau )=\frac{{\tau }^{\alpha }{\mathrm{sech}}^6\left(\frac{\xi }{2}\right)(c_1\lambda \sinh \left(\xi \right)+c_1\cosh \left(\xi \right)(\lambda \sinh \left(\xi \right)-\lambda +2)-c_1\lambda +c_2)}{8\mathsf{\Gamma }(1+\alpha )}\hfill \\ \hfill & T_1(\xi ,\tau )=-\frac{{\tau }^{\alpha }{\mathrm{sech}}^{14}\left(\frac{\xi }{2}\right){(\sinh \left(\xi \right)-1)}^5(2c_3(\gamma -2)+2c_3\cosh \left(x\right)+c_4\cosh \left(2\xi \right)+\mathrm{c}4)}{256\mathsf{\Gamma }(\alpha +1)}\hfill \\ & - \frac{{\tau }^{\alpha }{(\sinh \left(\xi \right)-1)}^5{\mathrm{sech}}^{14}\left(\frac{\xi }{2}\right)\left(2\sinh \left(\xi \right)(-c_3\gamma +c_3-2c_4)\right)}{256\mathsf{\Gamma }(\alpha +1)}\hfill \end{array}$$

(23)

According to the OAFM procedure

$$\begin{array}{cc}\hfill & R(\xi ,\tau )=R_0(\xi ,\tau )+R_1(\xi ,\tau )\hfill \\ \hfill & T(\xi ,\tau )=T_0(\xi ,\tau )+T_1(\xi ,\tau )\hfill \end{array}$$

(24)

In this discussion, we analyze the behavior of the Belousov–Zhabotinsky (BZ) system, as shown in Figure 1 and Figure 2. The BZ system is an example of a nonlinear chemical oscillator and is widely studied due to its oscillatory behavior, which can be observed in various fields such as biology, chemistry, and physics. We focus on the response functions $R(\xi ,\tau )$ and $T(\xi ,\tau )$, which describe the behavior of the system under varying conditions. The parameter $\alpha$ plays a crucial role in these response functions and is investigated in this discussion. Figure 1a presents a 2D plot of the response function $R(\xi ,\tau )$ at different values of the parameter $\alpha$. As the parameter $\alpha$ increases, the plot illustrates the change in the oscillatory behavior of the BZ system. The response function exhibits more complex oscillatory patterns with increasing values of $\alpha$. This suggests that the parameter $\alpha$ has a significant impact on the system’s response and can be used to control its behavior. Similarly, Figure 1b shows a 2D plot of the response function $T(\xi ,\tau )$ at different values of the parameter $\alpha$. The plot reveals that the oscillatory behavior of the BZ system also changes with varying values of $\alpha$ in the case of $T(\xi ,\tau )$. This further supports the idea that the parameter $\alpha$ is a key factor in determining the overall behavior of the BZ system. To provide a more comprehensive understanding of the BZ system, Figure 2a,b display 3D plots of the response functions $R(\xi ,\tau )$ and $T(\xi ,\tau )$, respectively, at different values of the parameter $\alpha$. These 3D plots offer a more detailed perspective on the complex oscillatory behavior of the BZ system. Figure 2a demonstrates how the 3D plot of the response function $R(\xi ,\tau )$ changes as the parameter $\alpha$ is varied. The plot exhibits intricate patterns, indicating the complex relationship between $\xi$, $\tau$, and $\alpha$. Similarly, Figure 2b showcases a 3D plot of the response function $T(\xi ,\tau )$ at different values of $\alpha$. This plot also displays intricate patterns, further highlighting the significance of the parameter $\alpha$ in the BZ system’s behavior. In Table 1 and Table 2, a comparison of the $R(\xi ,\tau )$ and $T(\xi ,\tau )$ OAFM solution and exact solution and their corresponding absolute error at fractional order $\alpha =1$ where $\lambda =2$ and $\gamma =3$ for Problem 1. In conclusion, the graphical analysis of Figure 1 and Figure 2 clearly demonstrates that the parameter $\alpha$ plays a crucial role in determining the behavior of the BZ system. The response functions $R(\xi ,\tau )$ and $T(\xi ,\tau )$ exhibit complex oscillatory patterns that change with varying values of $\alpha$. This analysis is beneficial for understanding and controlling the oscillatory behavior of the BZ system and other similar nonlinear chemical oscillators.

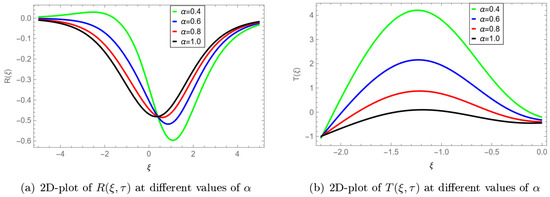
Figure 1. The 2D-plots of $R(\xi ,\tau )$ and $T(\xi ,\tau )$ using the OAFM solution where $\lambda =1.5$ and $\gamma =2.5$.

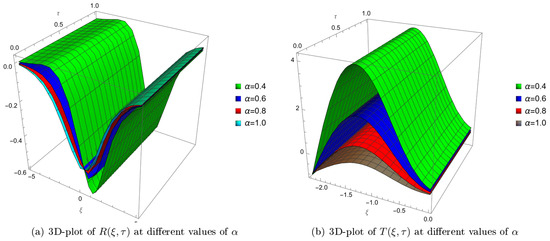
Figure 2. The 3D-plots of $R(\xi ,\tau )$ and $T(\xi ,\tau )$ using OAFM solution where the values $\lambda =1.5$ and $\gamma =2.5$.

Table 1. A comparison of the $R(\xi ,\tau )$ OAFM solution and exact solution and their corresponding absolute error at fractional order $\alpha =1$ where $\lambda =2$ and $\gamma =3$ for Problem 1.

$\mathit{\xi }$	$\mathit{R}(\mathit{\xi },\mathit{\tau })$ OAFM	$\mathit{R}(\mathit{\xi },\mathit{\tau })$ Exact	Abs.error
0.1	−0.4987	−0.4987	5.1$\times {10}^{-5}$
0.2	−0.495	−0.4950	3.3$\times {10}^{-5}$
0.3	−0.4889	−0.4889	1.5$\times {10}^{-5}$
0.4	−0.4805	−0.4805	2.7$\times {10}^{-6}$
0.5	−0.470	−0.4700	2.0$\times {10}^{-5}$
0.6	−0.4576	−0.4575	3.7$\times {10}^{-5}$
0.7	−0.4434	−0.4434	5.2$\times {10}^{-5}$
0.8	−0.4279	−0.4278	6.6$\times {10}^{-5}$
0.9	−0.411	−0.411	7.8$\times {10}^{-5}$
1	−0.3933	−0.3932	8.9$\times {10}^{-5}$

Table 2. Comparison of the $T(\xi ,\tau )$ OAFM solution and exact solution and their corresponding absolute error at fractional order $\alpha =1$ for Problem 1.

$\mathit{\xi }$	$\mathit{T}(\mathit{\xi },\mathit{\tau })$ OAFM	$\mathit{T}(\mathit{\xi },\mathit{\tau })$ Exact	Abs.error
0.1	−0.4487	−0.4487	4.9$\times {10}^{-5}$
0.2	−0.3953	−0.3953	8.2$\times {10}^{-5}$
0.3	−0.34	−0.3399	1.0 $\times {10}^{-4}$
0.4	−0.2831	−0.283	1.1$\times {10}^{-4}$
0.5	−0.2251	−0.225	1.2$\times {10}^{-4}$
0.6	−0.1663	−0.1661	1.2 $\times {10}^{-4}$
0.7	−0.1071	−0.1069	1.2 $\times {10}^{-4}$
0.8	−0.0479	−0.0478	1.2 $\times {10}^{-4}$
0.9	0.0109	0.01102	1.2 $\times {10}^{-4}$
1	0.06889	0.06901	1.1$\times {10}^{-4}$

The values of auxiliary constant obtained by collocation method.

$c_1=-2.358192481417809$, $c_2=0.7753100423748968$, $c_3=83.49971233901873$ and $c_4=-33.24684800337086$

4.2. Problem 2

Let us consider the system of a nonlinear fractional-order equation, which is represented by

$$\begin{array}{cc}\hfill & D_{\tau }^{\alpha }R(\xi ,\tau )-T(\xi ,\tau )\frac{{\partial }^{2}R(\xi ,\tau )}{\partial {\xi }^2}-R(\xi ,\tau )\frac{{\partial }^{2}T(\xi ,\tau )}{\partial {\xi }^2}-2+2{\xi }^2+2{\tau }^2=0,\hfill \\ \hfill & D_{\tau }^{\alpha }T(\xi ,\tau )-T(\xi ,\tau )\frac{{\partial }^{2}T(\xi ,\tau )}{\partial {\xi }^2}+R(\xi ,\tau )\frac{{\partial }^{2}R(\xi ,\tau )}{\partial {\xi }^2}-1-\frac{3}{2}{\xi }^2-\frac{3}{2}{\tau }^2=0,\mathrm{where},1<\alpha \le 2\hfill \end{array}$$

(25)

Subject to the following IC’s:

$$\begin{array}{cc}\hfill & R(\xi ,0)={\xi }^2,{\partial }_{\tau }R(\xi ,0)=0\hfill \\ \hfill & T(\xi ,0)=\frac{1}{2}{\xi }^2,{\partial }_{\tau }T(\xi ,0)=0\hfill \end{array}$$

(26)

Consider linear terms in Equation (25)

$$\begin{array}{cc}\hfill & L\left(R_0(\xi ,\tau )\right)=\frac{{\partial }^{\alpha }{R}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }},\hfill \\ \hfill & L\left(T_0(\xi ,\tau )\right)=\frac{{\partial }^{\alpha }{T}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }}\hfill \end{array}$$

(27)

Consider nonlinear terms in Equation (25)

$$\begin{array}{cc}\hfill & N\left(R_0(\xi ,\tau )\right)=-T_0(\xi ,\tau )\frac{{\partial }^2{R}_0(\xi ,\tau )}{\partial {\xi }^2}-R_0(\xi ,\tau )\frac{{\partial }^2{T}_0(\xi ,\tau )}{\partial {\xi }^2},\hfill \\ \hfill & N\left(T_0(\xi ,\tau )\right)=-T_0(\xi ,\tau )\frac{{\partial }^2{T}_0(\xi ,\tau )}{\partial {\xi }^2}+R_0(\xi ,\tau )\frac{{\partial }^2{R}_0(\xi ,\tau )}{\partial {\xi }^2}\hfill \end{array}$$

(28)

Zeroth-order approximation

$$\begin{array}{cc}\hfill & \frac{{\partial }^{\alpha }{R}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }}=0\hfill \\ \hfill & \frac{{\partial }^{\alpha }{T}_0(\xi ,\tau )}{\partial {\tau }^{\alpha }}=0\hfill \end{array}$$

(29)

By applying of the inverse operator, we obtain result as:

$$\begin{array}{cc}\hfill & R_0(\xi ,\tau )={\xi }^2,\hfill \\ \hfill & T_0(\xi ,\tau )=\frac{1}{2}{\xi }^2\hfill \end{array}$$

(30)

By making use of Equation (30) in Equation (28), the system of nonlinear terms becomes

$$\begin{array}{cc}\hfill & N\left[R_0(\xi ,\tau )\right]=-2{\xi }^2\hfill \\ \hfill & N\left[T_0(\xi ,\tau )\right]=\frac{3}{2}{\xi }^2\hfill \end{array}$$

(31)

We choose the auxiliary function as:

$$\begin{array}{cc}\hfill & A_1=(c_1+\xi c_2){\xi }^2,A_2=c_3{\left({\xi }^2\right)}^3,\hfill \\ \hfill & A_3=(c_4+\xi c_5){\left(\frac{3}{2}{\xi }^2\right)}^4,A_4=c_6{\left(\frac{3}{2}{\xi }^2\right)}^7\hfill \end{array}$$

(32)

First-order approximation using the OAFM approach, as described in Section 3.

$$\begin{array}{cc}\hfill & \frac{{\partial }^{\alpha }{R}_1(\xi ,\tau )}{\partial {\tau }^{\alpha }}=-\left(A_1[R_0(\xi ,\tau )N\left[R_0(\xi ,\tau )\right]+A_2[R_0(\xi ,\tau );c_j]\right)\hfill \\ \hfill & \frac{{\partial }^{\alpha }{T}_1(\xi ,\tau )}{\partial {\tau }^{\alpha }}=-\left(A_3[T_0(\xi ,\tau )N\left[T_0(\xi ,\tau )\right]+A_4[T_0(\xi ,\tau );c_j]\right)\hfill \end{array}$$

(33)

using Equations (30) and (32) in Equation (33)

$$\begin{array}{cc}\hfill & \frac{{\partial }^{\alpha }{R}_1(\xi ,\tau )}{\partial {\tau }^{\rho }}=2{\xi }^4(c_1+\mathrm{c}2\xi )-c_3{\xi }^6\hfill \\ \hfill & \frac{{\partial }^{\alpha }{T}_1(\xi ,\tau )}{\partial {\tau }^{\rho }}=-\frac{3}{32}{\xi }^{10}(c_4+c_5\xi )-\frac{c_6{\xi }^{14}}{128}\hfill \end{array}$$

(34)

applying inverse operator to Equation (34) we get

$$\begin{array}{cc}\hfill & R_1(\xi ,\tau )=\frac{{\xi }^4{\tau }^{\alpha }(2c_1+\xi (2c_2-c_3\xi ))}{\mathsf{\Gamma }(\alpha +1)}\hfill \\ \hfill & T_1(\xi ,\tau )=-\frac{{\xi }^{10}{\tau }^{\alpha }\left(12c_4+12c_5\xi +c_6{\xi }^4\right)}{128\mathsf{\Gamma }(\alpha +1)}\hfill \end{array}$$

(35)

According to the OAFM procedure

$$\begin{array}{cc}\hfill & R(\xi ,\tau )=R_0(\xi ,\tau )+R_1(\xi ,\tau )\hfill \\ \hfill & T(\xi ,\tau )=T_0(\xi ,\tau )+T_1(\xi ,\tau )\hfill \end{array}$$

(36)

The values of auxiliary constant obtained by collocation method.

$c_1=\mathrm{31,430.6586668333}$, $c_2=-\mathrm{110,362.31997412356}$, $c_3=-\mathrm{182,153.25836719057}$, $c_4=\mathrm{125,830.5231198654}$, $c_5=\mathrm{41,444.51349867818}$ and $c_6=-2.0600130170669805\times {10}^{-6}$

Figure 3 and Figure 4 present the graphical representations of the reflection, $R(\xi ,\tau )$, and transmission, $T(\xi ,\tau )$, coefficients obtained for a nonlinear fractional system of partial differential equations using the optimal amplitude frequency modulation (OAFM) method. Figure 3 illustrates the 2D plots of the coefficients: (a) represents the 2D plot of the reflection coefficient, $R(\xi ,\tau )$, and (b) displays the 2D plot of the transmission coefficient, $T(\xi ,\tau )$. The horizontal axis in both plots represents the spatial variable, $\xi$, while the vertical axis represents the temporal variable, $\tau$. The variation in color intensity indicates the magnitude of the coefficients. The 2D plots enable a clear visualization of the coefficients’ behavior with respect to the spatial and temporal variables, as well as how they change in the presence of nonlinearities. Figure 4, on the other hand, provides a more comprehensive representation of the coefficients through 3D plots. In this figure, (a) is the 3D plot of the reflection coefficient, $R(\xi ,\tau )$, while (b) is the 3D plot of the transmission coefficient, $T(\xi ,\tau )$. The horizontal plane represents the spatial variable, $\xi$, and the temporal variable, $\tau$. The vertical axis illustrates the magnitude of the coefficients. By using a 3D representation, it becomes easier to visualize the distribution of the coefficients and how they evolve in the nonlinear fractional system. Table 3 and Table 4 are a comparison of the OAFM solution and exact solution and their corresponding absolute error at fractional order $\alpha =2$ for $R(\xi ,\tau )$ and $T(\xi ,\tau )$ for Problem 2. In conclusion, Figure 3 and Figure 4 offer a graphical representation of the reflection and transmission coefficients, $R(\xi ,\tau )$ and $T(\xi ,\tau )$, for a nonlinear fractional system of partial differential equations using the OAFM method. The 2D and 3D plots allow for an in-depth understanding of the coefficients’ behavior and how they are affected by the nonlinearities present in the system.

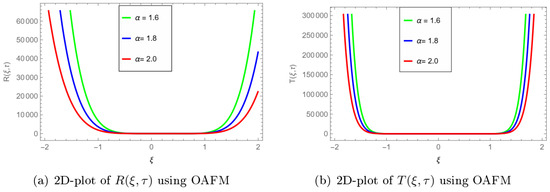
Figure 3. The 2D-plots of $R(\xi ,\tau )$,$T(\xi ,\tau )$ using OAFM solution at different values of fractional order.

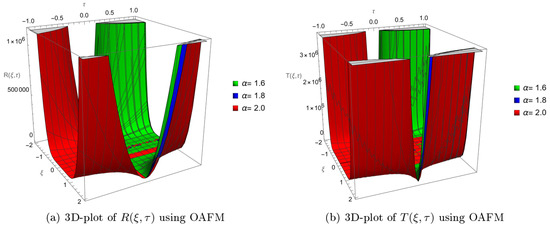
Figure 4. The 3D-plots of $R(\xi ,\tau )$,$T(\xi ,\tau )$ using OAFM solution at different values of fractional order.

Table 3. A comparison of the OAFM solution and exact solution and their corresponding absolute error at fractional order $\alpha =2$ for Problem 2.

$\mathit{\xi }$	$\mathit{R}(\mathit{\xi },\mathit{\tau })$ OAFM	$\mathit{R}(\mathit{\xi },\mathit{\tau })$ Exact	Abs.error
0.1	0.01	0.01	4.06$\times {10}^{-7}$
0.15	0.0225	0.0225	2.72$\times {10}^{-6}$
0.2	0.04001	0.04	7.12$\times {10}^{-6}$
0.25	0.06251	0.0625	1.30$\times {10}^{-5}$
0.3	0.09002	0.09	1.90$\times {10}^{-5}$
0.35	0.12252	0.1225	2.10$\times {10}^{-5}$
0.4	0.16002	0.16	1.70$\times {10}^{-5}$
0.45	0.2025	0.2025	2.74$\times {10}^{-6}$
0.5	0.24998	0.25	2.20$\times {10}^{-5}$

Table 4. A comparison of the OAFM solution and exact solution and their corresponding absolute error at fractional order $\alpha =2$ for Problem 2.

$\mathit{\xi }$	$\mathit{T}(\mathit{\xi },\mathit{\tau })$ OAFM	$\mathit{T}(\mathit{\xi },\mathit{\tau })$ Exact	Abs.error
0.10	0.005	0.005	2.000$\times {10}^{-8}$
0.15	0.01125	0.01125	2.0001$\times {10}^{-8}$
0.20	0.0200	0.0200	2.0025$\times {10}^{-8}$
0.25	0.03125	0.03125	2.0242$\times {10}^{-8}$
0.30	0.0450	0.04500	2.1515$\times {10}^{-8}$
0.35	0.06125	0.06125	2.7125$\times {10}^{-8}$
0.40	0.0800	0.0800	4.7134$\times {10}^{-8}$
0.45	0.10125	0.10125	1.0770$\times {10}^{-7}$
0.50	0.1250	0.12500	2.6870$\times {10}^{-7}$

5. Conclusions

In conclusion, the optimal Auxiliary function method (OAFM) has proven to be a powerful and effective technique for analyzing nonlinear systems, as demonstrated in this paper by applying it to the nonlinear system of the Belousov–Zhabotinsky equation. By utilizing the Caputo operator and concepts from fractional calculus, the OAFM provides a valuable approach to solving and understanding complex dynamic systems. The integration of Caputo operators further enhances the accuracy and authenticity of the model, enabling a more faithful representation of the underlying physical phenomena. The OAFM not only allows for accurate and efficient computations but also offers insights into the behavior and stability of the system. The results obtained using the OAFM highlight its effectiveness in addressing challenging problems in nonlinear dynamics. The combination of the OAFM, nonlinear systems, and fractional calculus opens up new avenues for future research, paving the way for further advancements and applications in various scientific and engineering domains.