The FitzHugh–Nagumo Model Described by Fractional Difference Equations: Stability and Numerical Simulation

Abstract

The aim of this work is to describe the dynamics of a discrete fractional-order reaction–diffusion FitzHugh–Nagumo model. We established acceptable requirements for the local asymptotic stability of the system’s unique equilibrium. Moreover, we employed a Lyapunov functional to show that the constant equilibrium solution is globally asymptotically stable. Furthermore, numerical simulations are shown to clarify and exemplify the theoretical results.

1. Introduction

Fractional calculus has been around for three centuries, and recently, it has become more frequently utilized in the scientific and technical fields. It investigates extensions of the basic calculus operators, differentiation and integration, defined by letting their order to roam outside of Z to more extended domains [1,2,3]. Such extensions are not only a mathematical novelty; differential equations containing the generalized operators have been employed in a wide range of scientific domains [4,5], from viscoelasticity [6] to epidemiology [7], economics [8,9], and electrical circuits [10].

Almost every mathematical theory has a discrete equivalent that enables it to be comprehended theoretically and practically in the modeling process of real-world issues. Owing to the availability of a coherent mathematical framework for continuous fractional calculus, the potential advancement of discrete fractional calculus has been inadequate until recently. However, there has been significant progress in the development of discrete fractional calculus. For example, Atici and Eloe [11] implemented a discrete Laplace transform technique for solving a series of fractional difference equations. Atici and Eloe [12] developed the triggers for the beginning value in discrete fractional calculus. With the nabla operator, Atici and Eloe [13] investigated the structure of a discrete fractional calculus. For additional information on recent advances in fractional discrete calculus, see [14,15,16,17,18,19].

Reaction–diffusion systems have acquired great theoretical attention and are of tremendous utility in many scientific and technical disciplines due to their capacity to simulate a range of real-world events and the intricacy of their solutions (see [20,21,22,23]). Meanwhile, the fractional partial differential equation is widely used in practice. Several papers on the subject have recently been published [24,25,26,27]. An effective and common application of fractional diffusion equations is the simulation of anomalous diffusion in porous media with rich nano–micro-size characteristics. However, many nonlinear systems in nature have discrete qualities, such as population models, brain networks, and gene information. Discrete models may be used to successfully identify parameters from experimental data. Fractional partial difference equations offer a separate time-discretization model, particularly for anomalous diffusion, or a time-discretization difference technique, which was recently described as a discrete fractional modeling [28]. The authors of [29] established a fractional time discretization diffusion model in the Caputo-like delta interpretation, and addressed diffusion concentration for various fractional difference orders. Alternatively, the authors of [30] proposed a variable-order fractional diffusion equation on discrete periods and created a variable-order function using a chaotic map.

Several neuron models have recently been proposed in the literature to describe neural dynamics. Among these models, one can find the reaction diffusion FitzHugh–Nagumo model, which is a classic standard model in neuroscience that has been extensively examined in periodical literature [31]. This model is a simplified variant of the well-known Hodgkin–Huxley model, which captures neuron dynamics and, more broadly, the dynamics of excitable systems in several domains such as chemical reaction kinetics and solid state physics [32,33,34]. It is made up of two differential equations that describe the voltage variable’s temporal evolution. In recent years, FitzHugh–Nagumo has received a lot of attention, and several notable studies have been conducted to examine this system. For example, in [35], the global existence and asymptotic stability of solutions for a generalized Lengyel–Epstein and FitzHugh–Nagumo reaction–diffusion system were explored. In [36], synchronization and control of FitzHugh–Nagumo coupled reaction–diffusion systems are addressed. In addition, synchronization of the reaction–diffusion FitzHugh–Nagumo systems using a one-dimensional linear control law was investigated in [37]. Finite element analysis of a FitzHugh–Nagumo reaction–diffusion system with Robin boundary conditions was explored in [38]. Moreover, many papers examined the influence of the fractional derivative on the FitzHugh–Nagumo model. For example, in [39] the low-voltage, low-power sinh-domain implementations of the fractional-order FitzHugh–Nagumo neuron model have been presented, as well as the influence of fractional orders on the neuron’s external excitation current and dynamics. In [40], the effect of the fractional order on the dynamics of action potentials in the FitzHugh–Nagumo model is discussed.

The goal of this paper is to study the stability of the equilibrium state of a discrete fractional-order reaction–diffusion FitzHugh–Nagumo model. Both local and global stability are explored for applicability in the above-mentioned neural model research. To the best of our knowledge, this is the first time a full theoretical stability study for a discrete fractional-order reaction–diffusion FitzHugh–Nagumo model has been conducted in which the effect of the fractional order on the dynamics of the model is investigated and discussed.

The paper is structured as follows. Section 2 is intended to provide some preliminary results as well as the discrete fractional-order dependent and independent outcomes. Section 3 describes the main findings of the study; the mathematical model is presented, the local stability of the equilibrium state is addressed, and global stability of the equilibrium state is examined, both dependently on the fractional orders of the considered model. The findings are corroborated by numerical simulations. Section 5 draws conclusions from the findings.

2. Preliminaries

This section begins by introducing the subject’s required nomenclature and stability theory.

Definition 1

([41]). Assume $\mathrm{x}:\mathbb{N}\to \mathbb{R},$ the forward difference operator Δ is then defined by

$$\Delta \mathrm{x}(\ell )=\mathrm{x}(\ell +1)-\mathrm{x}(\ell );\ell \in \mathbb{N}.$$

(1)

Next, the operators ${\Delta }^n,n=1,2,3,\dots ,$ are recursively identified by

$${\Delta }^n\mathrm{x}(\ell )=\Delta \left({\Delta }^{n-1}\mathrm{x}\right)(\ell ),\ell \in \mathbb{N}.$$

(2)

In particular, the second order difference operator of function $\mathrm{x}\left(t\right)$ is given by

$${\Delta }^2\mathrm{x}(\ell )=\mathrm{x}(\ell +2)-2\mathrm{x}(\ell +1)+\mathrm{x}(\ell ).$$

(3)

Lemma 1

([41]). Here we give some properties of the difference operator Δ,

• $\Delta c=0,$ where c is a constant.
• $\Delta (\mathrm{x}+\kappa )(\ell )=\Delta \mathrm{x}(\ell )+\Delta \kappa (\ell )$.
• $\Delta \left(\mathrm{x}\kappa \right)(\ell )=\mathrm{x}(\ell )\Delta \kappa (\ell )+\kappa (\ell +1)\Delta \mathrm{x}(\ell )$.

Theorem 1

([41]). Given two functions $\mathrm{x};\kappa :\mathbb{R}\to \mathbb{R}$ and $a;b\in \mathbb{N};a<b;$ we have the summation by parts’ formulas:

$$\begin{array}{cc}\hfill & \sum _{𝚥=a}^{b-1}{\mathrm{x}\left(𝚥\right)\Delta \kappa \left(𝚥\right)=\mathrm{x}\left(𝚥\right)\kappa \left(𝚥\right)|}_a^b-\sum _{𝚥=a}^{b-1}\kappa (𝚥+1)\Delta \mathrm{x}\left(𝚥\right),\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & \sum _{𝚥=a}^{b-1}{\mathrm{x}(𝚥+1)\Delta \kappa \left(𝚥\right)=\mathrm{x}\left(𝚥\right)\kappa \left(𝚥\right)|}_a^b-\sum _{𝚥=a}^{b-1}\kappa \left(𝚥\right)\Delta \mathrm{x}\left(𝚥\right).\hfill \end{array}$$

(5)

Definition 2

([42,43]). Let $\mathrm{x}\in {\left(h\mathbb{N}\right)}_a\to \mathbb{R}$. For given $\vartheta >0,$ the ϑ-th order h-sum is given by

$${}_h{\Delta }_a^{-\vartheta }\mathrm{x}\left(t\right)={\displaystyle \frac{h}{\Gamma \left(\vartheta \right)}}\sum _{\frac{t}{h}-\vartheta }^{s=\frac{a}{h}}{(t-\sigma \left(sh\right))}^{(\vartheta -1)}\mathrm{x}\left(sh\right),\sigma \left(sh\right)=(s+1)h,t\in {\left(h\mathbb{N}\right)}_{a+\vartheta h},$$

(6)

with $a\in \mathbb{R}$ as the initial value and the ℏ-falling factorial function described by

$$t_{\hslash }^{\left(\vartheta \right)}={\hslash }^{\vartheta }{\displaystyle \frac{\Gamma (\frac{t}{\hslash }+1)}{\Gamma (\frac{t}{\hslash }+1-\vartheta )}},$$

(7)

while

$${\left(h\mathbb{N}\right)}_{a+\vartheta \hslash }=\{a+(1-\vartheta )\hslash ,a+(2-\vartheta )\hslash ,\dots \}.$$

(8)

Definition 3

([43,44]). For a function $\mathrm{x}\left(t\right)$ defined on ${\left(h\mathbb{N}\right)}_a$ and for a certain $\vartheta >0$, so that $\vartheta \in \mathbb{N}$ the Caputo ℏ-difference operator is expressed by

$${}_{\hslash }^C{\Delta }_a^{\vartheta }\mathrm{x}\left(t\right){=}_{\hslash }{\Delta }_a^{-(n-\vartheta )}{\Delta }_{\hslash }^n\mathrm{x}\left(t\right),$$

(9)

where ${\Delta }_{\hslash }^n\mathrm{x}\left(t\right)={\displaystyle \frac{\mathrm{x}(t+\hslash )-\mathrm{x}\left(t\right)}{\hslash }}.$

Lemma 2

([42]). Here are some important properties employed in this work:

• Discrete Leibniz integral law:

  $${}_{\hslash }{\Delta }_{a+(1-\vartheta )\hslash }^{-\vartheta }{}_{\hslash }^C{\Delta }^{\vartheta }\mathrm{x}\left(t\right)=\mathrm{x}\left(t\right)-\mathrm{x}\left(a\right),0<\vartheta \le 1,t\in {(\hslash \mathbb{N})}_{a+\hslash }.$$

  (10)
• Caputo fractional difference of a constant x:

  $${}_{\hslash }^C{\Delta }^{\vartheta }x=0,0<\vartheta \le 1.$$

  (11)

Lemma 3

([42]). The following inequality holds:

$${}_h^C{\Delta }_a^{\vartheta }{\mathrm{x}}^2\left(t\right)\le 2\mathrm{x}{(t+\vartheta \hslash )}_h^C{\Delta }_a^{\vartheta }\mathrm{x}\left(t\right),t\in {(\hslash \mathbb{N})}_{a+\vartheta \hslash },$$

(12)

where $0<\vartheta \le 1.$

Let us consider the nonlinear fractional-order difference system.

$${}_{\hslash }^C{\Delta }_a^{\vartheta }\mathrm{x}\left(t\right)=\psi (t+\hslash \vartheta ,\mathrm{x}(t+\hslash \vartheta )),t\in {\left(h\mathbb{N}\right)}_{a+\vartheta h}.$$

(13)

Theorem 2

([42]). Let $\mathrm{x}=0$ be the system’s equilibrium point (13). The equilibrium point is asymptotically stable if there exists a positive, definite, and declining scalar function. If all the eigenvalues of ${\psi }^{\prime }\left({\mathrm{x}}^{*}\right)$ are located in $S_{\hslash }^{\vartheta }$, then ${\mathrm{x}}^{*}$ is asymptotically stable, where ${}_{\hslash }^C{\Delta }_a^{\vartheta }V(t,\mathrm{x}\left(t\right))\le 0$.

Theorem 3

([45]). Let ${\mathrm{x}}^{*}$ be an equilibrium point of (13). If all the eigenvalues of ${\psi }^{\prime }\left({\mathrm{x}}^{*}\right)$ are located in $S_{\hslash }^{\vartheta }$, then ${\mathrm{x}}^{*}$ is asymptotically stable,

where

$$S_{\hslash }^{\vartheta }=\left\{w\in \mathbb{C}:\left|Arg\left(w\right)\right|>{\displaystyle \frac{\vartheta \pi }{2}}\mathit{or}\left|w\right|>{\displaystyle \frac{2^{\vartheta }}{{\hslash }^{\vartheta }}}{cos}^{\vartheta }\left({\displaystyle \frac{Arg\left(w\right)}{\vartheta }}\right)\right\}.$$

(14)

3. The Discrete Fractional-Order FitzHugh–Nagumo Reaction–Diffusion System

In this section, we present the model under discussion, which is approximated using two well-known approaches. This discrete model is, to the best of our knowledge, the first in the literature.

The FitzHugh–Nagumo reaction–diffusion system, as is well known, was proposed in [46] as follows:

$$\left\{\begin{array}{c}{\displaystyle \frac{\partial u}{\partial t}}=d_1\Delta u-u^3+(\beta +1)u^2-\beta u-v,x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial v}{\partial t}}=d_2\Delta v+ϵu-ϵ\gamma v,x\in \Omega ,t>0,\hfill \\ {\partial }_u={\partial }_v=0,x\in \partial \Omega ,t>0,\hfill \\ u(x,0)=u_0\left(x\right)>0,v(x,0)=v_0\left(x\right)>0,x\in \Omega .\hfill \end{array}\right.$$

(15)

where $\Omega$ is a bounded domain in ${\mathbb{R}}^n,n=1$, with sufficiently smooth boundary $\partial \Omega$, $\Delta ={\sum }_{i=1}^n{\displaystyle \frac{{\partial }^2}{\partial x_i^2}}$. The state u corresponds to the membrane potential in this spatially extended system, whereas v reflects a combination of potassium activation and sodium inactivation at point $(x,t)\in \Omega \times (0,\infty )$. The parameters $\beta ,ϵ$ and $\gamma$ are positive constants with values of $0<\beta <{\displaystyle \frac{1}{2}}$ and $ϵ<<1$.

Since time fractional systems have been extensively studied by researchers, the following time fractional FitzHugh–Nagumo reaction–diffusion system was presented in [47] as follows:

$$\left\{\begin{array}{c}{}_0^C{D}_t^{\delta }u-d_1\Delta u=-u^3+(\beta +1)u^2-\beta u-v,\hfill \\ {}_0^C{D}_t^{\delta }v-d_2\Delta v=ϵu-ϵ\gamma v.\hfill \end{array}\right.$$

(16)

where $0<\delta \le 1$ is the fractional order and ${}_0^C{D}_t^{\delta }$ describes the Caputo fractional derivative, $d_1,d_2$ and $\sigma$ are strictly positive constants with the same initial conditions and Neumann boundary conditions.

Based on the model (16) and with the discretization used in [29,48], and assuming that $x\in [0,L]$, we have $x_{i+1}=x_i+k,i=0,\dots ,m$, and using the central difference formula concerning x, ${\displaystyle \frac{{\partial }^{2}u(x,t)}{\partial x^2}}$ and ${\displaystyle \frac{{\partial }^{2}v(x,t)}{\partial x^2}}$ can be approximately expanded as

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{2}u(x,t)}{\partial x^2}}\approx {\displaystyle \frac{u_{i+1}\left(t\right)-2u_i\left(t\right)+u_{i-1}\left(t\right)}{k^2}},\hfill \\ {\displaystyle \frac{{\partial }^{2}v(x,t)}{\partial x^2}}\approx {\displaystyle \frac{v_{i+1}\left(t\right)-2v_i\left(t\right)+v_{i-1}\left(t\right)}{k^2}}.\hfill \end{array}\right.$$

Using the definition of the second order difference operator of $u_i$ and $v_i$ we obtain

$$\left\{\begin{array}{c}{\displaystyle \frac{{\partial }^{2}u(x,t)}{\partial x^2}}\approx {\displaystyle \frac{{\Delta }^2{u}_{i-1}\left(t\right)}{k^2}},\hfill \\ {\displaystyle \frac{{\partial }^{2}v(x,t)}{\partial x^2}}\approx {\displaystyle \frac{{\Delta }^2{v}_{i-1}\left(t\right)}{k^2}}.\hfill \end{array}\right.$$

Therefore, we consider the following discrete-time reaction–diffusion fractional FitzHugh–Nagumo system

$$\left\{\begin{array}{c}{}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }{u}_i\left(t\right)={\displaystyle \frac{d_1}{k^2}}{\Delta }^2{u}_{i-1}(t+\hslash \vartheta )-u^3(t+\hslash \vartheta )+(\beta +1)u^2(t+\hslash \vartheta )-\beta u(t+\hslash \vartheta )-v_i(t+\hslash \vartheta ),\hfill \\ {}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }{v}_i\left(t\right)={\displaystyle \frac{d_2}{k^2}}{\Delta }^2{v}_{i-1}(t+\hslash \vartheta )+ϵu_i(t+\hslash \vartheta )-ϵ\gamma v_i(t+\hslash \vartheta ).\hfill \end{array}\right.$$

(17)

where ${}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }$ is the Caputo-like difference, $0<\vartheta \le 1,$ $t\in {(\hslash \mathbb{N})}_{t_0}$.

With the periodic boundary conditions

$$\left\{\begin{array}{c}{u}_0\left(t\right)=u_m\left(t\right),u_1\left(t\right)=u_{m+1}\left(t\right),\hfill \\ v_0\left(t\right)=v_m\left(t\right),v_1\left(t\right)=v_{m+1}\left(t\right),\hfill \end{array}\right.$$

(18)

and the initial condition

$$u_i\left(t_0\right)={\varphi }_1\left(x_i\right)\ge 0,v_i\left(t_0\right)={\varphi }_2\left(x_i\right)\ge 0.$$

4. Local Stability

In order to investigate the asymptotic stability of the considered discrete-time fractional FitzHugh–Nagumo system, we consider the unique equilibrium point, which is the solution of the following system:

$$\left\{\begin{array}{c}{\displaystyle \frac{d_1}{k^2}}{\Delta }^2{u}^{*}-u^{*3}+(\beta +1)u^{*2}-\beta u^{*}-v^{*}=0,\hfill \\ {\displaystyle \frac{d_2}{k^2}}{\Delta }^2{v}^{*}+ϵu^{*}-ϵ\gamma v^{*}=0.\hfill \end{array}\right.$$

(19)

As previously stated in [49], the system (17) may have many equilibriums depending on the sign of $\xi$, where $\xi$ is determined by

$$\xi ={(1-\beta )}^2-{\displaystyle \frac{4}{\gamma }}.$$

(20)

Thus, we may have the three cases listed below:

• If $\xi <0,$ system (17) has the origin $(u_0^{*},v_0^{*})=(0,0)$ as its only fixed point.
• If $\xi =0,$ system (17) has two fixed points; the origin and $(u_1^{*},v_1^{*})=\left(-{\displaystyle \frac{\beta +1}{2}},{\displaystyle \frac{u_1^{*}}{\gamma }}\right)$.
• If $\xi >0,$ system (17) has three fixed points; the origin,

  $$(u_2^{*},v_2^{*})=\left(-{\displaystyle \frac{\beta }{2}}-\sqrt{\xi },{\displaystyle \frac{u_2^{*}}{\gamma }}\right)\mathrm{and}(u_3^{*},v_3^{*})=\left(-{\displaystyle \frac{\beta }{2}}+\sqrt{\xi },{\displaystyle \frac{u_3^{*}}{\gamma }}\right).$$

4.1. Local Stability of the Free Diffusions System

In this part, we develop suitable requirements for the local asymptotic stability of the following system:

$$\left\{\begin{array}{c}{}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }u\left(t\right)=-u^3(t+\hslash \vartheta )+(\beta +1)u^2(t+\hslash \vartheta )-\beta u(t+\hslash \vartheta )-v(t+\hslash \vartheta ),\hfill \\ {}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }v\left(t\right)=ϵu(t+\hslash \vartheta )-ϵ\gamma v(t+\hslash \vartheta ).\hfill \end{array}\right.$$

(21)

The characteristic equation for the eigenvalues is obtained using linear stability analysis around the stable state:

$$J=\left(\begin{array}{c}{\displaystyle \frac{\partial \psi }{\partial u}}{\displaystyle \frac{\partial \psi }{\partial v}}\\ {\displaystyle \frac{\partial \Psi }{\partial u}}{\displaystyle \frac{\partial \Psi }{\partial v}}\end{array}\right)=\left(\begin{array}{cc}-3u^2+2(\beta +1)u-\beta & -1\\ ϵ\gamma & -ϵ\end{array}\right),$$

(22)

where

$$\psi (u,v)=-u^3(t+\hslash \vartheta )+(1+\beta )u^2(t+\hslash \vartheta )-\beta u(t+\hslash \vartheta )-v(t+\hslash \vartheta ),$$

(23)

and

$$\Psi (u,v)=ϵ\gamma u(t+\hslash \vartheta )-ϵv(t+\hslash \vartheta ).$$

(24)

We may deduce the following:

Theorem 4.

System (21) is locally asymptotically stable at the steady state according to the following cases:

• If $\xi =0$, the equilibrium point $(u_0^{*},v_0^{*})$ is locally asymptotically stable.
• If $\xi =0,$ the equilibrium points $(u_0^{*},v_0^{*})$ and $(u_1^{*},v_1^{*})$ are locally asymptotically stable.
• If $\xi >0$, the equilibrium points $(u_0^{*},v_0^{*})$ and $(u_2^{*},v_2^{*})$ are locally asymptotically stable, and $(u_3^{*},v_3^{*})$ is stable if the following hold true:

  $$\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)-\sqrt{\xi }(5\beta +2)+3\xi >0.$$

Proof. 

Since the system (21) might have many equilibriums depending on the sign of $\xi$, we shall analyze each one separately.

• Given that the origin $(u_0^{*},v_0^{*})$ always represents an equilibrium point, we shall investigate the stability of the system (21) regardless of the sign of $\xi$.
  The Jacobian matrix of the equilibrium point $(u_0^{*},v_0^{*})$ may be expressed as follows:

  $$J_{(u_0^{*},v_0^{*})}=\left(\begin{array}{c}-\beta -1\\ ϵ\gamma -ϵ\end{array}\right),$$

  (25)
  The Jacobian matrix $J_{(u_0^{*},v_0^{*})}$ has the following characteristic equation:

  $${\Lambda }^2-\mathrm{tr}(J_{(u_3^{*},v_3^{*})})\Lambda +\det (J_{(u_3^{*},v_3^{*})})=0,$$

  (26)

  where

  $$\mathrm{tr}(J_{(u_0^{*},v_0^{*})})=-\beta -ϵ,\det (J_{(u_0^{*},v_0^{*})})=\beta ϵ+ϵ\gamma .$$

  (27)
  This might lead to the following discriminant

  $$\begin{array}{cc}\hfill {\Delta }_{\Lambda }& ={\mathrm{tr}}^2(J_{(u_0^{*},v_0^{*})})-4\det (J_{(u_0^{*},v_0^{*})})={(\beta +ϵ)}^2-4\left(\beta ϵ+ϵ\gamma \right)={(\beta -ϵ)}^2-4ϵ\gamma .\hfill \end{array}$$
  The solutions of (26) are obviously dependent on the sing of ${\Delta }_{\Lambda }$; therefore, we may analyze the stability in the following situations.

  -

  If $(\beta -ϵ)2>4ϵ\gamma$, and since $\beta ϵ+ϵ\gamma >0$, the negativity of the eigenvalues is determined by the sign of $\mathrm{tr}(J_{(u_0^{*},v_0^{*})})$. Furthermore, as $-\beta -ϵ<0$, and the eigenvalues ${\Lambda }_1$ and ${\Lambda }_2$ are real, thus we have

  $${\Lambda }_1={\displaystyle \frac{\mathrm{tr}(J_{(u_0^{*},v_0^{*})})-\sqrt{{\Delta }_{\Lambda }}}{2}}<0.$$

  (28)

  As a consequence of this, $Arg\left({\Lambda }_1\right)=\pi$. It is self-evident that $Arg\left({\Lambda }_1\right)=Arg\left({\Lambda }_2\right)=\pi .$ As a result, according to Theorem 3, the equilibrium $(u_0^{*},v_0^{*})$ is asymptotically stable.

  -

  If ${(\beta -ϵ)}^2<4ϵ\gamma$, then

  $${\Lambda }_1={\displaystyle \frac{\mathrm{tr}(J_{(u_0^{*}{v}_0^{*})})-i\sqrt{-{\Delta }_{\Lambda }}}{2}},{\Lambda }_2={\displaystyle \frac{\mathrm{tr}(J_{(u_0^{*}{v}_0^{*})})+i\sqrt{-{\Delta }_{\Lambda }}}{2}}.$$

  (29)

  Since $-\beta -ϵ<0$, the system (21) is then asymptotically stable, based on the identical situation studied before.

  -

  If ${(\beta -ϵ)}^2=4ϵ\gamma$, $\mathrm{tr}(J_{(u_0^{*},v_0^{*})})$ cannot be equal to zero. The sign of the eigenvalues is the same as the sign of $\mathrm{tr}(J_{(u_0^{*},v_0^{*})})$. As a result, $(u_0^{*},v_0^{*})$ is asymptotically stable for all $\vartheta \in (0,1]$.

  We may deduce that the origin is locally asymptotically stable, regardless of the sing of ${\Delta }_{\Lambda }.$
• Now, assuming that $\xi =0$, and the origin is clearly stable according to the previous investigations, we can thus investigate the stability of the equilibrium point $(u_1^{*},v_1^{*})$.
  In this case, we have the Jacobian matrix of the equilibrium point $(u_1^{*},v_1^{*})$ defined by

  $$J_{(u_1^{*},v_1^{*})}=\left(\begin{array}{c}-3{\left({\displaystyle \frac{\beta +1}{2}}\right)}^2-2{\displaystyle \frac{{(\beta +1)}^2}{2}}-\beta -1\\ ϵ\gamma -ϵ\end{array}\right),$$

  (30)

  and we also have:

  $$\mathrm{tr}(J_{(u_1^{*},v_1^{*})})={\displaystyle \frac{-7{(\beta +1)}^2}{4}}-\beta -ϵ,\det (J_{(u_1^{*},v_1^{*})})=\left({\displaystyle \frac{7{(\beta +1)}^2}{4}}+\beta \right)ϵ+ϵ\gamma .$$

  (31)
  This may lead us to the discriminant of the eigenvalue problem (26):

  $$\begin{array}{cc}\hfill {\Delta }_{\Lambda }& ={\displaystyle \frac{7}{2}}{(\beta +1)}^2\left({\displaystyle \frac{7}{8}}{(\beta +1)}^2-ϵ+\beta \right)-4ϵ(\beta +\gamma )+{(\beta +ϵ)}^2.\hfill \end{array}$$
  We notice that $\det (J_{(u_1^{*},v_1^{*})})>0$ and $\mathrm{tr}(J_{(u_1^{*},v_1^{*})})<0$, which indicates that, based on the results we have reached about the stability of the equilibrium point, $(u_0^{*},v_0^{*})$, $(u_1^{*},v_1^{*})$ is asymptotically stable.
• In the last case, we suppose that $\xi >0$; thus, the equilibrium point $(u_0^{*},v_0^{*})$ remains stable, and we will discuss the stability of the two other equilibriums.

  -

  Concering the equilibrium $(u_2^{*},v_2^{*})$ we have

  $$J_{(u_2^{*},v_2^{*})}=\left(\begin{array}{c}-3{\left(-{\displaystyle \frac{\beta }{2}}-\sqrt{\xi }\right)}^2+2(\beta +1)\left(-{\displaystyle \frac{\beta }{2}}-\sqrt{\xi }\right)-\beta -1\\ ϵ\gamma -ϵ\end{array}\right).$$

  (32)

  This leads us to:

  $$\begin{array}{cc}\hfill \mathrm{tr}(J_{(u_2^{*},v_2^{*})})& =-3{\left(-{\displaystyle \frac{\beta }{2}}-\sqrt{\xi }\right)}^2+2(\beta +1)\left(-{\displaystyle \frac{\beta }{2}}-\sqrt{\xi }\right)-\beta -ϵ,\hfill \\ \hfill & =-\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)-\sqrt{\xi }(5\beta +2)-3\xi -ϵ,\hfill \end{array}$$

  $$\begin{array}{cc}\hfill \det (J_{(u_2^{*},v_2^{*})})& =-ϵ\left(-3{\left(-{\displaystyle \frac{\beta }{2}}-\sqrt{\xi }\right)}^2+2(\beta +1)\left(-{\displaystyle \frac{\beta }{2}}-\sqrt{\xi }\right)-\beta \right)+ϵ\gamma ,\hfill \\ \hfill & =-ϵ(\mathrm{tr}(J_{(u_2^{*},v_2^{*})})+ϵ)+ϵ\gamma .\hfill \\ \hfill & =ϵ\left(\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(5\beta +2)+3\xi +\gamma \right).\hfill \end{array}$$

  The discriminant of the eingenvalue problem (26) is as follows:

  $$\begin{array}{cc}\hfill {\Delta }_{\Lambda }& ={\left(-\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(-3\beta +2)-3\xi +ϵ\right)}^2-4ϵ\gamma .\hfill \end{array}$$

  This case is identical to the case of the equilibrium point $(u_1^{*},v_1^{*})$, since $\det (J_{(u_2^{*},v_2^{*})})>0$ and $\mathrm{tr}(J_{(u_2^{*},v_2^{*})})<0$, which leads us to the same results as the first and second cases of the demonstration. As a result, $(u_2^{*},v_2^{*})$ is locally asymptotically stable.

  -

  Finally, we investigate the stability of the equilibrium $(u_3^{*},v_3^{*})$, and we have

  $$J_{(u_3^{*},v_3^{*})}=\left(\begin{array}{c}-3{\left(-{\displaystyle \frac{\beta }{2}}+\sqrt{\xi }\right)}^2+2(\beta +1)\left(-{\displaystyle \frac{\beta }{2}}+\sqrt{\xi }\right)-\beta -1\\ ϵ\gamma -ϵ\end{array}\right).$$

  (33)

  We might observe from the Jacobian matrix that

  $$\begin{array}{cc}\hfill \mathrm{tr}(J_{(u_3^{*},v_3^{*})})& =-3{\left(-{\displaystyle \frac{\beta }{2}}+\sqrt{\xi }\right)}^2+2(\beta +1)\left(-{\displaystyle \frac{\beta }{2}}+\sqrt{\xi }\right)-\beta -ϵ,\hfill \\ \hfill & =-\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(5\beta +2)-3\xi -ϵ,\hfill \\ \hfill \det (J_{(u_3^{*},v_3^{*})})& =-ϵ\left(-3{\left(-{\displaystyle \frac{\beta }{2}}+\sqrt{\xi }\right)}^2+2(\beta +1)\left(-{\displaystyle \frac{\beta }{2}}+\sqrt{\xi }\right)-\beta \right)+ϵ\gamma ,\hfill \\ \hfill & =-ϵ(\mathrm{tr}(J_{(u_3^{*},v_3^{*})})+ϵ)+ϵ\gamma .\hfill \\ \hfill & =ϵ\left(\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)-\sqrt{\xi }(5\beta +2)+3\xi +\gamma \right).\hfill \end{array}$$

  The characteristic equation (26) has the following discriminant

  $$\begin{array}{cc}\hfill {\Delta }_{\Lambda }& ={\left(-\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(5\beta +2)-3\xi +ϵ\right)}^2-4ϵ\gamma .\hfill \end{array}$$

  (34)

  Based on (34), we investigate each case independently.

  ∗

  If ${\Delta }_{\Lambda }>0$ and if $\det (J_{(u_3^{*},v_3^{*})})>0$, as a result, the eigenvalues’ negativity is dependent on the sign of $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})$, and the eigenvalues ${\Lambda }_1$ and ${\Lambda }_2$ are real and may be represented as

  $${\Lambda }_1={\displaystyle \frac{\mathrm{tr}(J_{(u_3^{*},v_3^{*})})-\sqrt{{\Delta }_{\Lambda }}}{2}},{\Lambda }_2={\displaystyle \frac{\mathrm{tr}(J_{(u_3^{*},v_3^{*})})+\sqrt{{\Delta }_{\Lambda }}}{2}}.$$

  (35)

  ·

  If $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})<0$, then we have

  $${\Lambda }_1={\displaystyle \frac{\mathrm{tr}(J_{(u_3^{*},v_3^{*})})-\sqrt{{\Delta }_{\Lambda }}}{2}}<0.$$

  (36)

  As a result, $Arg\left({\Lambda }_1\right)=\pi$. Since both eigenvalues are real, it is obvious that $Arg\left({\Lambda }_1\right)=Arg\left({\Lambda }_2\right)=\pi .$ As a consequence, based on Theorem 3, the equilibrium $\left(u_3^{*}{,}^v{\ast }_3\right)$ is asymptotically stable.

  ·

  If $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})>0$, then we have

  $${\Lambda }_2={\displaystyle \frac{\mathrm{tr}(J_{(u_3^{*},v_3^{*})})+\sqrt{{\Delta }_{\Lambda }}}{2}}>0.$$

  (37)

  Therefore, $Arg\left({\Lambda }_2\right)=0$, and based on Theorem 3, system (21) is unstable.

  ∗

  If ${\Delta }_{\Lambda }<0$ and if $\det (J_{(u_3^{*},v_3^{*})})>0$, then

  $${\Lambda }_1={\displaystyle \frac{\mathrm{tr}(J_{(u_3^{*},v_3^{*})})-i\sqrt{-{\Delta }_{\Lambda }}}{2}},{\Lambda }_2={\displaystyle \frac{\mathrm{tr}(J_{(u_3^{*},v_3^{*})})+i\sqrt{-{\Delta }_{\Lambda }}}{2}}.$$

  (38)

  We may discuss the solutions based on the sign of $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})$.

  ·

  If $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})<0$ or $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})>0$, then, following the same case investigated previously, system (21) is asymptotically stable.

  ·

  If $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})=0$, then

  $$Arg\left({\displaystyle \frac{-i\sqrt{-{\Delta }_{\Lambda }}}{2}}\right)=Arg\left({\displaystyle \frac{i\sqrt{-{\Delta }_{\Lambda }}}{2}}\right)={\displaystyle \frac{\pi }{2}},$$

  and system (21) is asymptotically stable.

  ∗

  If ${\Delta }_{\Lambda }=0$, and $\det (J_{(u_3^{*},v_3^{*})})>0$, $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})$ cannot be equal to zero. The sign of the eigenvalues is the same as the sign of $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})$. As a result, $(u_3^{*},v_3^{*})$ is asymptotically stable for all $\vartheta \in (0,1]$ if $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})<0$ and unstable if $\mathrm{tr}(J_{(u_3^{*},v_3^{*})})>0$.

The proof is completed. □

4.2. Local Stability of the Diffusion System

We shall now show that in the presence of diffusion, the steady state $(u^{*},v^{*})$ can be stable under certain parameter circumstances. We will adopt the same approach as in [50], first considering the eigenvalues of the following equation:

$${\Delta }^2{\mathrm{x}}_{i-1}(t+h\vartheta )+{\Lambda }_i{\mathrm{x}}_i(t+h\vartheta )=0,$$

(39)

with the periodic boundary conditions:

$${\mathrm{x}}_0\left(t\right)={\mathrm{x}}_m\left(t\right),{\mathrm{x}}_1\left(t\right)={\mathrm{x}}_{m+1}\left(t\right).$$

(40)

We obtain

$$\left\{\begin{array}{c}{}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }{u}_i\left(t\right)=-{\displaystyle \frac{d_1}{k^2}}{\Lambda }_i{u}_i(t+\hslash \vartheta )-u_i^3(t+\hslash \vartheta )+(\beta +1)u_i^2(t+\hslash \vartheta )-\beta u_i(t+\hslash \vartheta )-v_i(t+\hslash \vartheta ),\hfill \\ {}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }{v}_i\left(t\right)=-{\displaystyle \frac{d_2}{k^2}}{\Lambda }_i{v}_i(t+\hslash \vartheta )+ϵu_i(t+\hslash \vartheta )-ϵ\gamma v_i(t+\hslash \vartheta ).\hfill \end{array}\right.$$

(41)

To explore the system’s local asymptotic stability, we will linearize it. If the eigenvalues of the linearized system fulfill the conditions of Theorem 3, using fundamental linear operator theory and keeping the system’s fractional structure in mind, we might state that $(u^{*},v^{*})$ is asymptotically stable.

We derive the following by linearizing the reaction diffusion system (41) about the steady state, and we obtain

$$J_i=\left(\begin{array}{c}-{\displaystyle \frac{d_1}{k^2}}{\Lambda }_i-3u_i^2(t+\hslash \vartheta )+2(\beta +1)u_i(t+\hslash \vartheta )-\beta -1\\ ϵ\gamma -{\displaystyle \frac{d_2}{k^2}}{\Lambda }_i-ϵ\end{array}\right).$$

(42)

The following result is conducted.

Theorem 5.

System (17) is asymptotically stable if the following hold:

• We suppose that $\xi <0$ and ${(\beta -ϵ)}^2>4ϵ\gamma .$ System (17) is asymptotically stable at the steady state $(u_0^{*},v_0^{*})$ if the following hold:

  -

  If $d_1<d_2$ and $\frac{d_1}{k^2}{\Lambda }_i\le -\beta .$

  -

  If $d_1>d_2$ and $\frac{d_1}{k^2}{\Lambda }_i\le -\beta$, and in addition, the eigenvalues

  $${\mu }_j\left({\Lambda }_i\right)={\displaystyle \frac{\mathrm{tr}(J_{i(u_0^{*},v_0^{*})}){}_{\underline{+-}}\sqrt{\mathrm{tr}{(J_{i(u_0^{*},v_0^{*})})}^2-4\det (J_{i(u_0^{*},v_0^{*})})}}{2}},j=1,2,$$

  satisfy $Arg\left({\mu }_j\left({\Lambda }_i\right)\right)>{\displaystyle \frac{\vartheta \pi }{2}}.$

• We suppose that $\xi =0$ and $({\displaystyle \frac{7}{2}}{(\beta +1)}^2\left({\displaystyle \frac{7}{8}}{(\beta +1)}^2-ϵ+\beta \right)>4ϵ(\beta +\gamma )-{(\beta +ϵ)}^2.$ System (17) is asymptotically stable at the steady state $(u_1^{*},v_1^{*})$ if the following hold:

  -

  If $d_1<d_2$ and $-\frac{d_1}{k^2}{\Lambda }_i\ge {\displaystyle \frac{7}{4}}{(\beta +1)}^2+\beta .$

  -

  If $d_1>d_2$ and $-\frac{d_1}{k^2}{\Lambda }_i\ge {\displaystyle \frac{7}{4}}{(\beta +1)}^2+\beta$, and in addition, the eigenvalues

  $${\mu }_j\left({\Lambda }_i\right)={\displaystyle \frac{\mathrm{tr}(J_{i(u_1^{*},v_1^{*})}){}_{\underline{+-}}\sqrt{\mathrm{tr}{(J_{i(u_1^{*},v_1^{*})})}^2-4\det (J_{i(u_1^{*},v_1^{*})})}}{2}},j=1,2,$$

  satisfy $Arg\left({\mu }_j\left({\Lambda }_i\right)\right)>{\displaystyle \frac{\vartheta \pi }{2}}.$

• We suppose that $\xi >0$ and we have two cases:

  -

  If ${\left(-\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)-\sqrt{\xi }(3\beta +2)-3\xi +ϵ\right)}^2>4ϵ\gamma$, system (17) is asymptotically stable at the steady state $(u_2^{*},v_2^{*})$ if the following hold:

  ∗

  If $d_1<d_2$ and $-\frac{d_1}{k^2}{\Lambda }_i\ge \beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(5\beta +2)+3\xi .$

  ∗

  If $d_1>d_2$ and $-\frac{d_1}{k^2}{\Lambda }_i\ge \beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(5\beta +2)+3\xi$, and in addition, the eigenvalues

  $${\mu }_j\left({\Lambda }_i\right)={\displaystyle \frac{\mathrm{tr}(J_{i(u_2^{*},v_2^{*})}){}_{\underline{+-}}\sqrt{\mathrm{tr}{(J_{i(u_2^{*},v_2^{*})})}^2-4\det (J_{i(u_2^{*},v_2^{*})})}}{2}},j=1,2,$$

  satisfy $Arg\left({\mu }_j\left({\Lambda }_i\right)\right)>{\displaystyle \frac{\vartheta \pi }{2}}.$

  -

  If ${\left(-\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(3\beta +2)-3\xi +ϵ\right)}^2>4ϵ\gamma$, system (17) is asymptotically stable at the steady state $(u_3^{*},v_3^{*})$ if the following hold:

  ∗

  If $d_1<d_2$ and $-\frac{d_1}{k^2}{\Lambda }_i\ge \beta \left({\displaystyle \frac{7}{4}}\beta +2\right)-\sqrt{\xi }(5\beta +2)+3\xi .$

  ∗

  If $d_1>d_2$ and $-\frac{d_1}{k^2}{\Lambda }_i\ge \beta \left({\displaystyle \frac{7}{4}}\beta +2\right)-\sqrt{\xi }(5\beta +2)+3\xi$, and in addition, the eigenvalues

  $${\mu }_j\left({\Lambda }_i\right)={\displaystyle \frac{\mathrm{tr}(J_{i(u_3^{*},v_3^{*})}){}_{\underline{+-}}\sqrt{\mathrm{tr}{(J_{i(u_3^{*},v_3^{*})})}^2-4\det (J_{i(u_3^{*},v_3^{*})})}}{2}},j=1,2,$$

  satisfy $Arg\left({\mu }_j\left({\Lambda }_i\right)\right)>{\displaystyle \frac{\vartheta \pi }{2}}.$

Proof. 

The proof will be conducted following the same cases investigated in the free diffusion section.

• We first start with the origin $(u_0^{*},v_0^{*})$, and we have

  $$\begin{array}{cc}\hfill & \left(\begin{array}{c}-\frac{d_1}{k^2}{\Lambda }_i-\beta -1\\ ϵ\gamma -\frac{d_2}{k^2}{\Lambda }_i-ϵ\end{array}\right)=J_{i(u_0^{*},v_0^{*})}-\lambda \left({\Lambda }_i\right)I,\hfill \end{array}$$

  which has the eigenvalue equation

  $${\mu }^2\left({\Lambda }_i\right)-\mathrm{tr}(J_{i(u_0^{*},v_0^{*})})\mu \left({\Lambda }_i\right)+\det (J_{i(u_0^{*},v_0^{*})})=0,$$

  (43)

  where

  $$\mathrm{tr}(J_{i(u_0^{*},v_0^{*})})=-\left(\frac{d_1}{k^2}+\frac{d_2}{k^2}\right){\Lambda }_i+\mathrm{tr}(J_{(u_0^{*},v_0^{*})}),$$

  (44)

  and

  $$\begin{array}{cc}\hfill \det (J_{i(u_0^{*},v_0^{*})})=& {\displaystyle \frac{d_1}{k^2}}{\displaystyle \frac{d_2}{k^2}}{\Lambda }_i^2+\left({\displaystyle \frac{d_1}{k^2}}ϵ+{\displaystyle \frac{d_2}{k^2}}\beta \right){\Lambda }_i+\det (J_{(u_0^{*},v_0^{*})}),\hfill \end{array}$$

  and its discriminant is

  $$\begin{array}{cc}\hfill {\Delta }_i& ={\mathrm{tr}}^2(J_{i(u_0^{*},v_0^{*})})-4\det (J_{i(u_0^{*},v_0^{*})})={\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)}^2{\Lambda }_i^2+2\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)(\beta -ϵ){\Lambda }_i+{\Delta }_{\Lambda }.\hfill \end{array}$$
  The sign of ${\Delta }_i$ is important to the stability of $(u_0^{*},v_0^{*})$. The discriminant of ${\Delta }_i$ in relation to ${\Lambda }_i$ is

  $$\begin{array}{cc}\hfill {\Delta }_{{\Lambda }_i}& ={\left(\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)(\beta -ϵ){\Lambda }_i\right)}^2-{\left(\frac{d_1}{k^2}-\frac{d_2}{k^2}\right)}^2{\Lambda }_i^2{\Delta }_{\Lambda }=4{\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)}^2ϵ\gamma .\hfill \end{array}$$
  Clearly, ${\Delta }_{{\Lambda }_i}>0$, because with $d_1\ne d_2$ we distinguish two cases:

  -

  If $d_1<d_2$, then ${(\beta -ϵ)}^2>4ϵ\gamma$, and the two solutions of the equation ${\Delta }_{{\Lambda }_i}=0$ are both negative. Thus, ${\Delta }_i>0$ and the roots of (43) are

  $$\left\{\begin{array}{c}{\mu }_1\left({\Lambda }_i\right)={\displaystyle \frac{\mathrm{tr}(J_{i(u_0^{*},v_0^{*})})+\sqrt{\mathrm{tr}{(J_i)}^2-4\det (J_{i(u_0^{*},v_0^{*})})}}{2}},\hfill \\ {\mu }_2\left({\Lambda }_i\right)={\displaystyle \frac{\mathrm{tr}(J_{i(u_0^{*},v_0^{*})})-\sqrt{\mathrm{tr}{(J_{i(u_0^{*},v_0^{*})})}^2-4\det (J_{i(u_0^{*},v_0^{*})})}}{2}}.\hfill \end{array}\right.$$

  (45)

  Note that the solutions are real, and also $\mu {\left({\Lambda }_i\right)}_1<0.$ In addition, if $-\frac{d_1}{k^2}{\Lambda }_1\ge \beta$, then $\mu {\left({\Lambda }_i\right)}_2<0.$ This leads to

  $$\left|Arg\left({\mu }_1\left({\Lambda }_i\right)\right)\right|=\left|Arg\left({\mu }_2{\left({\Lambda }_i\right)}_2\right)\right|=\pi ,$$

  (46)

  which ensures the asymptotic stability of $(u_0^{*},v_0^{*})$.

  -

  If $d_1>d_2$, we have ${(\beta -ϵ)}^2>4ϵ\gamma .$ This returns us to the previous scenario. Again, for $\frac{d_1}{k^2}{\Lambda }_1\ge \beta ,$ $det\left(J_{i(u_0^{*},v_0^{*})}\right)>0$; thus, ${\mu }_1\left({\Lambda }_i\right)$ and ${\mu }_2\left({\Lambda }_i\right)$ are negative and must meet the conditions of Theorem 3.

• Moving on to the second case where $\xi =0$, we will investigate the stability of the equilibrium point $(u_1^{*},v_1^{*})$, and in order to do so we consider the following:

  $$\begin{array}{cc}\hfill & \left(\begin{array}{c}-\frac{d_1}{k^2}{\Lambda }_i-{\displaystyle \frac{7}{4}}{(\beta +1)}^2-\beta -1\\ ϵ\gamma -\frac{d_2}{k^2}{\Lambda }_i-ϵ\end{array}\right)=J_{i(u_1^{*},v_1^{*})}-\lambda \left({\Lambda }_i\right)I,\hfill \end{array}$$

  where

  $$\mathrm{tr}(J_{i(u_1^{*},v_1^{*})})=-\left(\frac{d_1}{k^2}+\frac{d_2}{k^2}\right){\Lambda }_i+\mathrm{tr}(J_{(u_1^{*},v_1^{*})}),$$

  (47)

  and

  $$\begin{array}{cc}\hfill \det (J_{i(u_1^{*},v_1^{*})})=& {\displaystyle \frac{d_1}{k^2}}{\displaystyle \frac{d_2}{k^2}}{\Lambda }_i^2+\left({\displaystyle \frac{d_1}{k^2}}ϵ+{\displaystyle \frac{d_2}{k^2}}\left({\displaystyle \frac{7}{4}}(\beta +1)+\beta \right)\right){\Lambda }_i+\det (J_{(u_1^{*},v_1^{*})}),\hfill \end{array}$$

  and its discriminant is

  $$\begin{array}{cc}\hfill {\Delta }_i& ={\mathrm{tr}}^2(J_{i(u_0^{*},v_0^{*})})-4\det \left(J_{i(u_0^{*},v_0^{*})}\right)={\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)}^2{\Lambda }_i^2+2\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)(\beta -ϵ){\Lambda }_i+{\Delta }_{\Lambda }.\hfill \end{array}$$
  In this case, we have the discriminant of ${\Delta }_i$ in relation to ${\Lambda }_i$, defined by

  $$\begin{array}{cc}\hfill {\Delta }_{{\Lambda }_i}& ={\left(\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)(\beta -ϵ){\Lambda }_i\right)}^2-{\left(\frac{d_1}{k^2}-\frac{d_2}{k^2}\right)}^2{\Lambda }_i^2{\Delta }_{\Lambda }=4{\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)}^2ϵ\gamma .\hfill \end{array}$$
  We can clearly notice that the discriminant in this case is identical to the one calculated previously; therefore, we summarized the dynamics of the system concerning the $(u_1^{*},v_1^{*})$ in Theorem 5.
• Moving on to the last case where $\xi >0$, we will investigate the stability of the equilibrium points $(u_2^{*},v_2^{*})$ and $(u_3^{*},v_3^{*})$.

  -

  We start by considering the Jacobian matrix of $(u_2^{*},v_2^{*})$, and we have

  $$\begin{array}{cc}\hfill & \left(\begin{array}{c}-\frac{d_1}{k^2}{\Lambda }_i-\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)-\sqrt{\xi }(5\beta +2)-3\xi -1\\ ϵ\gamma -\frac{d_2}{k^2}{\Lambda }_i-ϵ\end{array}\right)=J_{i(u_2^{*},v_2^{*})}-\lambda \left({\Lambda }_i\right)I,\hfill \end{array}$$

  where

  $$\mathrm{tr}(J_{i(u_2^{*},v_2^{*})})=-\left(\frac{d_1}{k^2}+\frac{d_2}{k^2}\right){\Lambda }_i+\mathrm{tr}(J_{(u_2^{*},v_2^{*})}),$$

  (48)

  and

  $$\begin{array}{cc}\hfill \det \left(J_{i(u_2^{*},v_2^{*})}\right)=& {\displaystyle \frac{d_1}{k^2}}{\displaystyle \frac{d_2}{k^2}}{\Lambda }_i^2+{\displaystyle \frac{d_1}{k^2}}ϵ+{\displaystyle \frac{d_2}{k^2}}\left(\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(5\beta +2)+3\xi \right){\Lambda }_i+\det (J_{(u_2^{*},v_2^{*})}),\hfill \end{array}$$

  and its discriminant is

  $$\begin{array}{cc}\hfill {\Delta }_i& ={\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)}^2{\Lambda }_i^2+2\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)\left(\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(5\beta +2)+3\xi -ϵ\right){\Lambda }_i+{\Delta }_{\Lambda }.\hfill \end{array}$$

  The discriminant of ${\Delta }_i$ in relation to ${\Lambda }_i$ is

  $$\begin{array}{cc}\hfill {\Delta }_{{\Lambda }_i}& ={\left(\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)\left(\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(5\beta +2)+3\xi -ϵ\right)\right)}^2-{\left(\frac{d_1}{k^2}-\frac{d_2}{k^2}\right)}^2{\Lambda }_i^2{\Delta }_{\Lambda },\hfill \\ \hfill & =4{\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)}^2ϵ\gamma .\hfill \end{array}$$

  The discriminant in this situation is obviously similar to the one determined previously; therefore, we summarized the dynamics of the system concerning the $(u_2^{*},v_2^{*})$ in Theorem 5.

  -

  Finally, let us consider the equilibrium point $(u_3^{*},v_3^{*})$

  $$\begin{array}{cc}\hfill & \left(\begin{array}{c}-\frac{d_1}{k^2}{\Lambda }_i-\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(5\beta +2)-3\xi -1\\ ϵ\gamma -\frac{d_2}{k^2}{\Lambda }_i-ϵ\end{array}\right)=J_{i(u_3^{*},v_3^{*})}-\lambda \left({\Lambda }_i\right)I,\hfill \end{array}$$

  where

  $$\mathrm{tr}(J_{i(u_3^{*},v_3^{*})})=-\left(\frac{d_1}{k^2}+\frac{d_2}{k^2}\right){\Lambda }_i+\mathrm{tr}(J_{(u_3^{*},v_3^{*})}),$$

  (49)

  and

  $$\begin{array}{cc}\hfill \det (J_{i(u_3^{*},v_3^{*})})=& {\displaystyle \frac{d_1}{k^2}}{\displaystyle \frac{d_2}{k^2}}{\Lambda }_i^2+{\displaystyle \frac{d_1}{k^2}}ϵ+{\displaystyle \frac{d_2}{k^2}}\left(\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)-\sqrt{\xi }(5\beta +2)+3\xi \right){\Lambda }_i+\det (J_{(u_3^{*},v_3^{*})}),\hfill \end{array}$$

  and its discriminant is

  $$\begin{array}{cc}\hfill {\Delta }_i& ={\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)}^2{\Lambda }_i^2+2\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)\left(\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)-\sqrt{\xi }(5\beta +2)+3\xi -ϵ\right){\Lambda }_i+{\Delta }_{\Lambda }.\hfill \end{array}$$

  The discriminant of ${\Delta }_i$ in relation to ${\Lambda }_i$ is

  $$\begin{array}{cc}\hfill {\Delta }_{{\Lambda }_i}& ={\left(\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right){\left(\beta \left({\displaystyle \frac{7}{4}}\beta +2\right)+\sqrt{\xi }(5\beta +2)+3\xi -ϵ\right)}^2-\left(\frac{d_1}{k^2}-\frac{d_2}{k^2}\right)\right)}^2{\Lambda }_i^2{\Delta }_{\Lambda },\hfill \\ \hfill & =4{\left({\displaystyle \frac{d_1}{k^2}}-{\displaystyle \frac{d_2}{k^2}}\right)}^2ϵ\gamma .\hfill \end{array}$$

  We can easily see that the discriminant in this case is also similar to the one determined previously; thus, we outlined the dynamics of the system concerning the $(u_3^{*},v_3^{*})$ in Theorem 5.

 □

5. Global Stability

In this part, we define the global asymptotic stability of the constant steady-state solution. It is possible to rewrite the discrete-time fractional FitzHugh–Nagumo system (17) as follows:

$$\left\{\begin{array}{c}{}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }{u}_i\left(t\right)={\displaystyle \frac{k_1}{{\Delta }_x^2}}{\Delta }^2{u}_{i-1}(t+\hslash \vartheta )+\left(f\left(u_i\right)-f\left(u^{*}\right)\right)-(v_i(t+\hslash \vartheta )-v^{*}),\hfill \\ {}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }{v}_i\left(t\right)={\displaystyle \frac{k_2}{{\Delta }_x^2}}{\Delta }^2{v}_{i-1}(t+\hslash \vartheta )+ϵ\gamma ({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\vartheta }}-{\displaystyle \frac{u^{*}}{\vartheta }}-(v_i(t+\hslash \vartheta )-v^{*})).\hfill \end{array}\right.$$

(50)

We define the variables $U_i=u_i-u*$ and $V_i=v_i-v*$, such that the function $f\left(u_i\right)$ is defined as follows:

$$f\left(u_i\right)=-u_i^3+(\beta +1)u_i^2-\beta u_i.$$

(51)

Theorem 6.

System (17) is globally asymptotically stable if the following holds:

$$(u_i\left(t\right)-u^{*})\left(f\left(u_i\right)-f\left(u^{*}\right)\right)>0,1\le i\le m.$$

(52)

Proof. 

To achieve the unique equilibrium point’s global asymptotic stability $(u^{*},v^{*})$, we evaluate the following function:

$$L\left(t\right)={\displaystyle \frac{1}{2}}\sum _{i=1}^m\left({\left({\displaystyle \frac{u_i\left(t\right)}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right)}^2+{(v_i\left(t\right)-v^{*})}^2\right).$$

(53)

Taking the Caputo h-difference operator and using Lemma 3, we have

$$\begin{array}{cc}\hfill {}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }L\left(t\right)& ={\displaystyle \frac{1}{2}}\sum _{i=1}^m\left({}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }{\left({\displaystyle \frac{u_i\left(t\right)}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right)}^2{+}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }{(v_i\left(t\right)-v^{*})}^2\right),\hfill \\ \hfill & \le \sum _{i=1}^m\left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right){}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }\left({\displaystyle \frac{u_i\left(t\right)}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right)+{(v_i(t+\hslash \vartheta )-v^{*})}_{\hslash }^C{\Delta }_{t_0}^{\vartheta }(v_i\left(t\right)-v^{*}),\hfill \\ \hfill & \le \sum _{i=1}^m\left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right)({\displaystyle \frac{k_1}{{\Delta }_x^2}}{\Delta }^2{u}_{i-1}(t+\hslash \vartheta )+(f\left(u_i\right)-f\left(u^{*}\right))\hfill \\ \hfill & -(v_i(t+\hslash \vartheta )-v^{*}))+(v_i(t+\hslash \vartheta )-v^{*})({\displaystyle \frac{k_2}{{\Delta }_x^2}}{\Delta }^2{v}_{i-1}(t+\hslash \vartheta )\hfill \\ \hfill & +ϵ\gamma \left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}-(v_i(t+\hslash \vartheta )-v^{*})\right),\hfill \\ \hfill & \le \sum _{i=1}^m{\displaystyle \frac{k_1}{{\Delta }_x^2}}\left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right){\Delta }^2{u}_{i-1}(t+\hslash \vartheta )+{\displaystyle \frac{k_2}{{\Delta }_x^2}}(v_i(t+\hslash \vartheta )-v^{*}){\Delta }^2{v}_{i-1}(t+\hslash \vartheta )\hfill \\ \hfill & +\sum _{i=1}^m\left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right)((f\left(u_i\right)-f\left(u^{*}\right))-(v_i(t+\hslash \vartheta )-v^{*}))\hfill \\ \hfill & +\sum _{i=1}^m(v_i(t+\hslash \vartheta )-v^{*})(ϵ\gamma ({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}-(v_i(t+\hslash \vartheta )-v^{*}))),\hfill \\ \hfill & =J_1\left(t\right)+J_2\left(t\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill J_1\left(t\right)& =\sum _{i=1}^m{\displaystyle \frac{k_1}{{\Delta }_x^2}}\left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right){\Delta }^2{u}_{i-1}(t+\hslash \vartheta )+{\displaystyle \frac{k_2}{{\Delta }_x^2}}(v_i(t+\hslash \vartheta )-v^{*}){\Delta }^2{v}_{i-1}(t+\hslash \vartheta ),\hfill \end{array}$$

(54)

$$\begin{array}{cc}\hfill J_2\left(t\right)& =\sum _{i=1}^m\left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right)(\left(f\left(u_i\right)-f\left(u^{*}\right)\right)\hfill \end{array}$$

(55)

$$\begin{array}{cc}\hfill & -(v_i(t+\hslash \vartheta )-v^{*}))+(v_i(t+\hslash \vartheta )-v^{*})\left(ϵ\gamma \left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}-(v_i(t+\hslash \vartheta )-v^{*})\right)\right).\hfill \end{array}$$

(56)

We then examine the $J_1$ and $J_2$ signs:

$$\begin{array}{cc}\hfill J_1\left(t\right)& =\sum _{i=1}^m{\displaystyle \frac{k_1}{{\Delta }_x^2}}\left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right){\Delta }^2{u}_{i-1}(t+\hslash \vartheta )+{\displaystyle \frac{k_2}{{\Delta }_x^2}}(v_i(t+\hslash \vartheta )-v^{*}){\Delta }^2{v}_{i-1}(t+\hslash \vartheta ),\hfill \\ \hfill & =\sum _{i=1}^m{\displaystyle \frac{k_1}{\gamma {\Delta }_x^2}}(u_i(t+\hslash \vartheta )-u^{*}){\Delta }^2(u_{i-1}(t+\hslash \vartheta )-u^{*})+{\displaystyle \frac{k_2}{{\Delta }_x^2}}(v_i(t+\hslash \vartheta )-v^{*}){\Delta }^2(v_{i-1}(t+\hslash \vartheta )-v^{*})\hfill \\ \hfill & =\sum _{i=1}^m{\displaystyle \frac{k_1}{\gamma {\Delta }_x^2}}(u_i(t+\hslash \vartheta )-u^{*})\Delta (u_{i-1}(t+\hslash \vartheta )-u^{*}){|}_1^{m+1}\hfill \\ \hfill & +{\displaystyle \frac{k_2}{{\Delta }_x^2}}(v_i(t+\hslash \vartheta )-v^{*})\Delta (v_{i-1}(t+\hslash \vartheta )-v^{*}){|}_1^{m+1}-\sum _{i=1}^m{\displaystyle \frac{k_1}{\gamma {\Delta }_x^2}}{(\Delta (u_{i-1}(t+\hslash \vartheta )-u^{*}))}^2\hfill \\ \hfill & -{\displaystyle \frac{k_2}{{\Delta }_x^2}}{(\Delta (v_{i-1}(t+\hslash \vartheta )-v^{*}))}^2<0.\hfill \end{array}$$

$$\begin{array}{cc}\hfill J_2\left(t\right)& =\sum _{i=1}^m\left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right)(\left(f\left(u_i\right)-f\left(u^{*}\right)\right)-(v_i(t+\hslash \vartheta )-v^{*}))\hfill \\ \hfill & +(v_i(t+\hslash \vartheta )-v^{*})(ϵ\gamma ({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}-(v_i(t+\hslash \vartheta )-v^{*}))),\hfill \\ \hfill & \le \sum _{i=1}^m\left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\gamma }}\right)\left(f\left(u_i\right)-f\left(u^{*}\right)\right)-{\displaystyle \frac{ϵ}{\gamma }}\left(u_i(t+\hslash \vartheta )-u^{*}\right)(v_i(t+\hslash \vartheta )-v^{*})\hfill \\ \hfill & +{\displaystyle \frac{ϵ}{\gamma }}(v_i(t+\hslash \vartheta )-v^{*})(u_i(t+\hslash \vartheta )-u^{*})-{(v_i(t+\hslash \vartheta )-v^{*})}^2,\hfill \\ \hfill & \le \sum _{i=1}^m\left({\displaystyle \frac{u_i(t+\hslash \vartheta )}{\gamma }}-{\displaystyle \frac{u^{*}}{\vartheta }}\right)\left(f\left(u_i\right)-f\left(u^{*}\right)\right)-{(v_i(t+\hslash \vartheta )-v^{*})}^2.\hfill \end{array}$$

Now, the following hold:

• If $u_i(t+\hslash \vartheta )\le u^{*}$, then $(u_i(t+\hslash \vartheta )-u^{*})\left(f\left(u_i\right)-f(u*)\right)<0.$
• If $u_i(t+\hslash \vartheta )\ge u^{*}$, then $(u_i(t+\hslash \vartheta )-u^{*})\left(f\left(u_i\right)-f(u*)\right)<0.$

This means that $L\left(t\right)<0$, and according to Theorem 2, the system is globally asymptotically stable. □

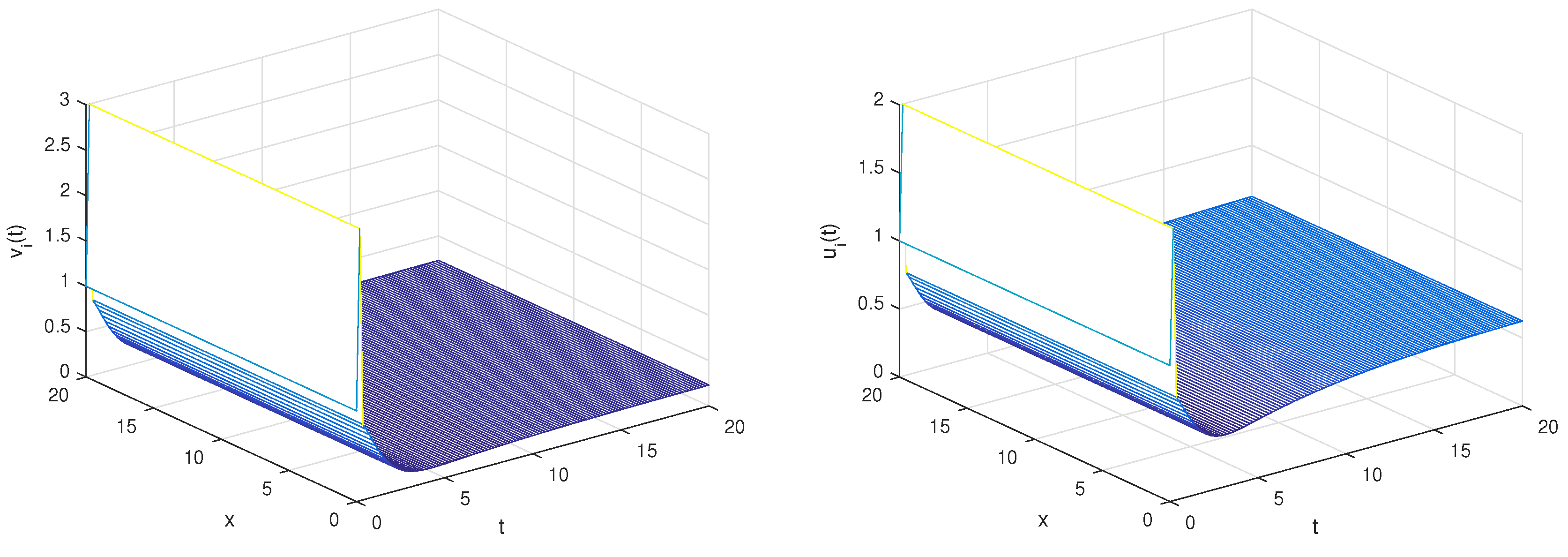
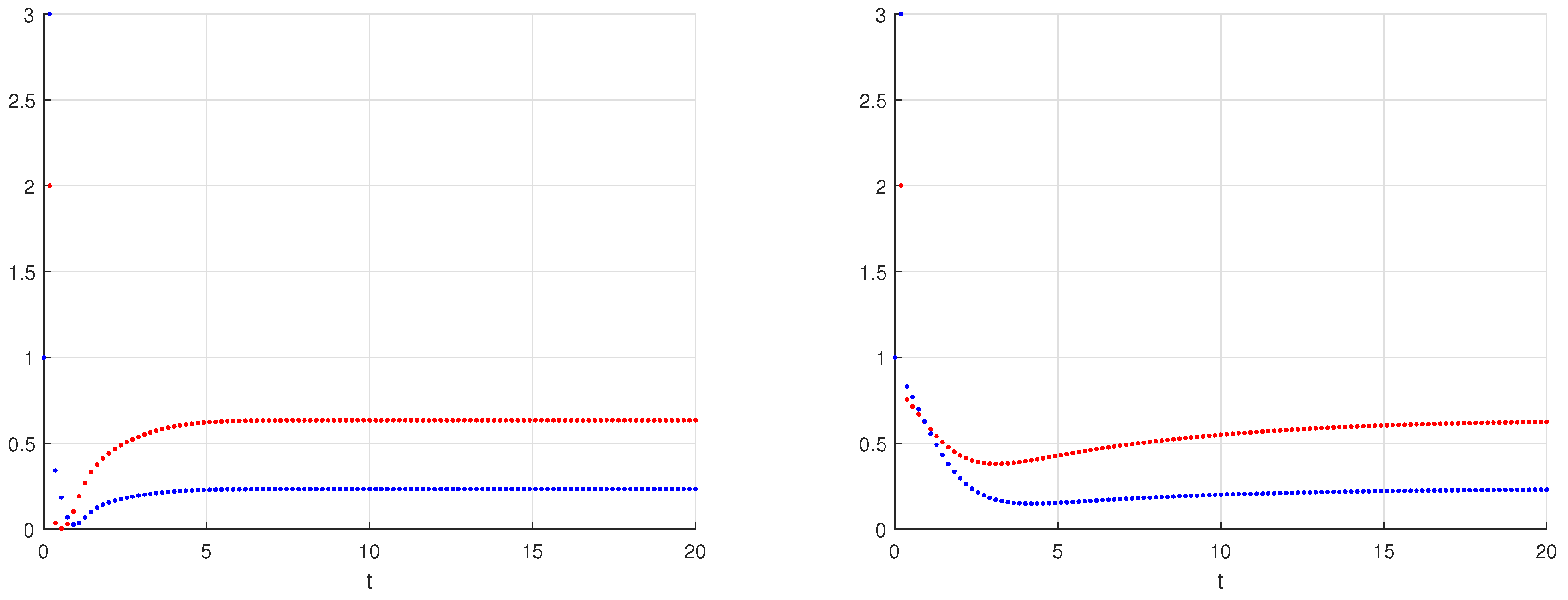
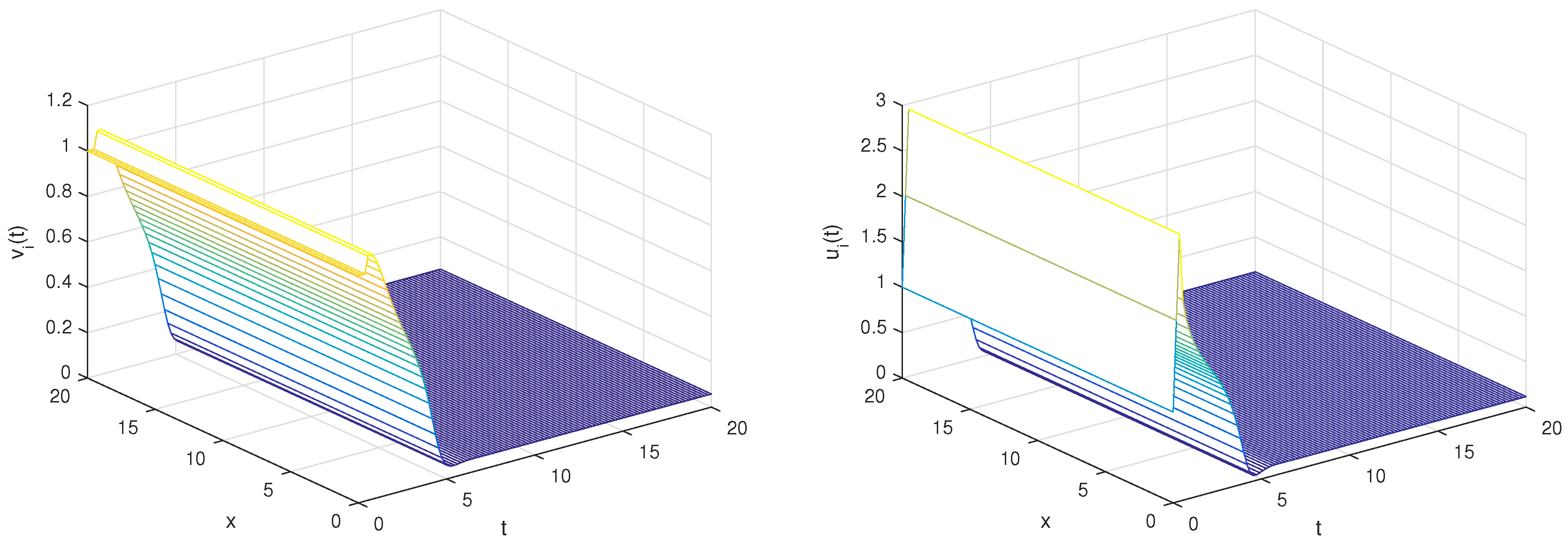
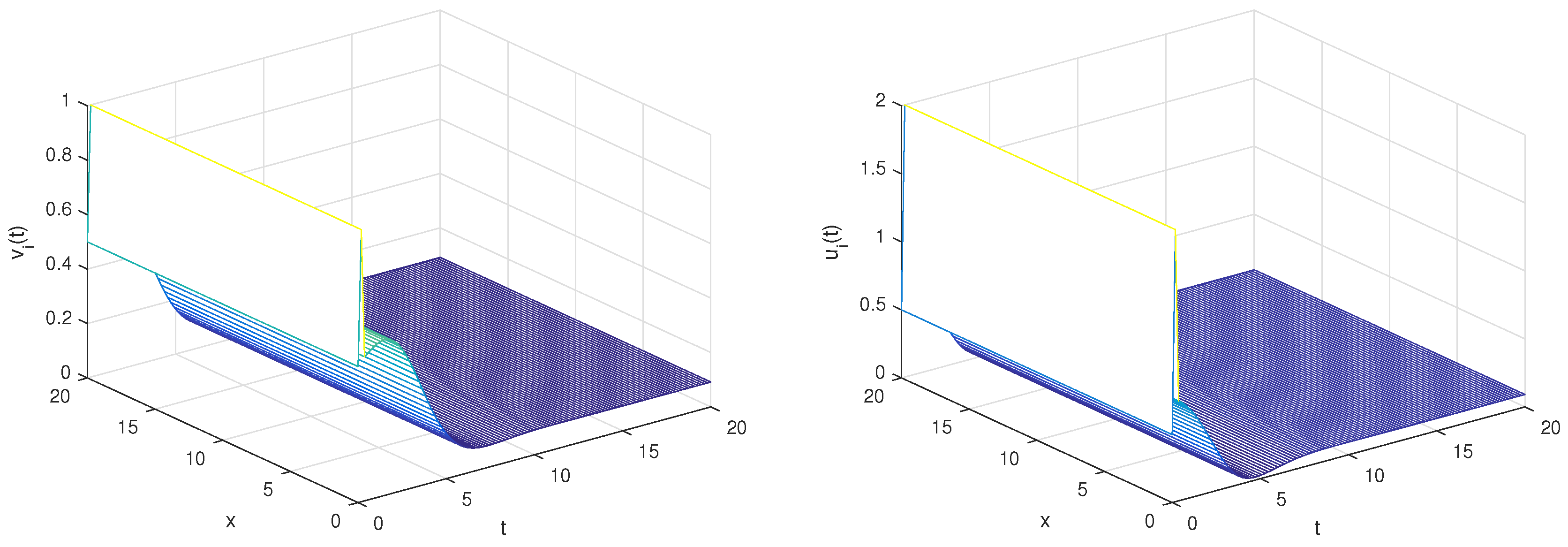
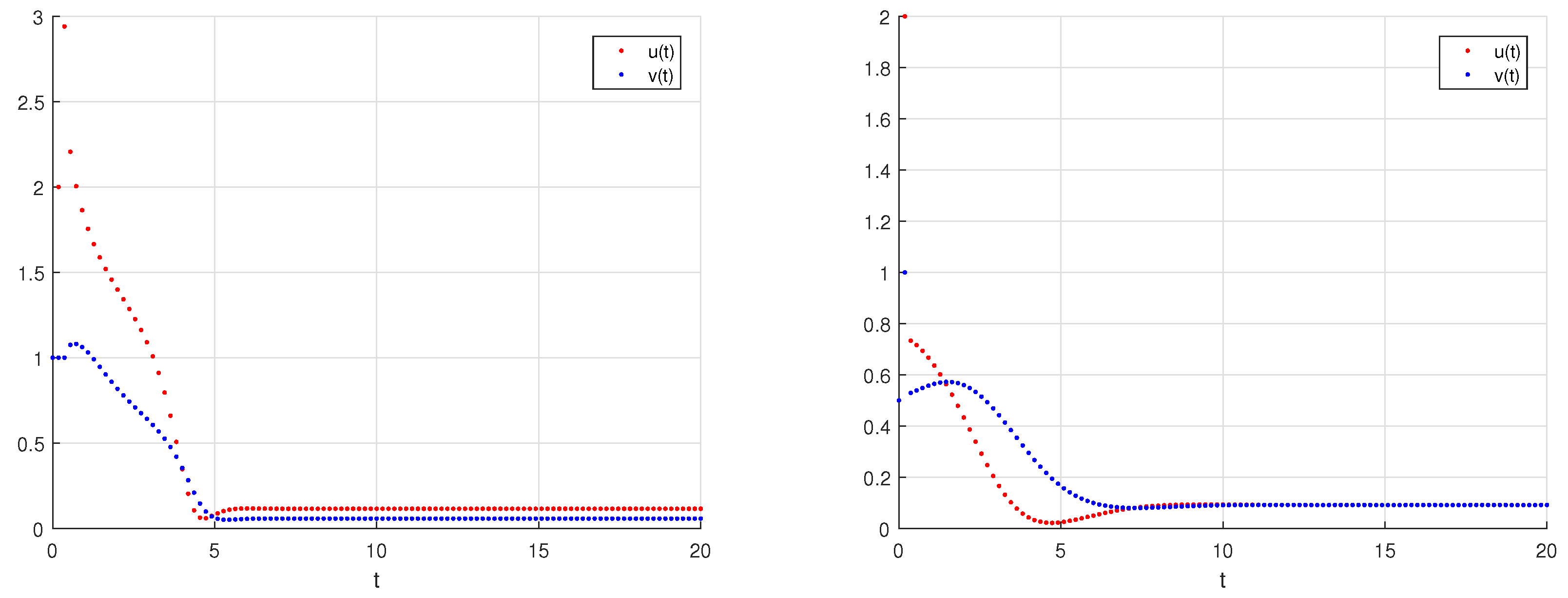
6. Numerical Simulations

In this part, we show some exemplary simulations of the theoretical properties of the stability of the discrete-time fractional FitzHugh–Nagumo reaction–diffusion system. We can observe the behavior of the system by modifying its parameters and order. We use the following numerical solution, and the system (17) appears as follows:

$$\left\{\begin{array}{c}{u}_i(n\hslash )={\varphi }_1\left(x_i\right)+{\displaystyle \frac{{\hslash }^{\vartheta }}{\Gamma \left(\vartheta \right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+\vartheta )}{\Gamma (n-j+1)}}[s{\displaystyle \frac{u_{i+1}((j-1)\hslash )-2u_i((j-1)\hslash )+u_{i-1}((j-1)\hslash )}{k^2}}\hfill \\ -u^3((j-1)\hslash )+(\beta +1)u^2((j-1)\hslash )-\beta u((j-1)\hslash )-v_i((j-1)\hslash )],\hfill \\ v_i(n\hslash )={\varphi }_2\left(x_i\right)+{\displaystyle \frac{{\hslash }^{\vartheta }}{\Gamma \left(\vartheta \right)}}\sum _{j=1}^n{\displaystyle \frac{\Gamma (n-j+\vartheta )}{\Gamma (n-j+1)}}[{\displaystyle \frac{v_{i+1}((j-1)\hslash )-2v_i((j-1)\hslash )+v_{i-1}((j-1)\hslash )}{k^2}}\hfill \\ +ϵu_i((j-1)\hslash )-ϵ\gamma v_i((j-1)\hslash )],\hfill \\ 1\le i\le m,\hfill \\ n>0.\hfill \end{array}\right.$$

(57)

Example 1.

Consider the following parameter values of model (17): $N=110,$ $(\beta ,ϵ,\gamma ,d_1,d_2)=(0.139,0.7,0.18,2,3)$ $\hslash =0.18,$ $t\in [0,20],$ $x\in [0,20]$ and the boundary conditions $(u_0\left(t\right),v_0\left(t\right))=(2,3),(u_1\left(t\right),v_1\left(t\right))=(2,3)$, with the initial conditions

$$\left\{\begin{array}{c}{\varphi }_1\left(x_i\right)=1-sin\left(\pi x_i\right),\hfill \\ {\varphi }_2\left(x_i\right)=3-sin\left(\pi x_i\right).\hfill \end{array}\right.$$

We see that all of our model’s solutions converge at some point to the equilibrium point $(u^{*},v^{*})=(0.64,0.12)$. The unique equilibrium is thus asymptotically stable. This numerical conclusion is consistent with our earlier theoretical results. Figure 1, Figure 2 and Figure 3 display the results mentioned earlier for different orders.

Example 2.

In this example, we set the following parameter of the model (17): $N=110,$ $(\beta ,ϵ,\gamma ,d_1,d_2)=(0.3,0.01,0.1,0.1,0.7)$ $\hslash =0.4,$ $t\in [0,20],$ $x\in [0,20]$ and the boundary conditions $(u_0\left(t\right),v_0\left(t\right))=(1,3),(u_1\left(t\right),v_1\left(t\right))=(1,3)$, with the initial conditions

$$\left\{\begin{array}{c}{\varphi }_1\left(x_i\right)=3+cos\left({\displaystyle \frac{\pi x_i}{2}}\right),\hfill \\ {\varphi }_2\left(x_i\right)=2+cos\left({\displaystyle \frac{\pi x_i}{2}}\right).\hfill \end{array}\right.$$

We can observe that the solutions of the model converge to the equilibrium point $(u^{*},v^{*})=(0,0)$. As a result, the unique equilibrium is asymptotically stable. This numerical solution agrees with the theories provided in the previous sections, as displayed in Figure 4, Figure 5 and Figure 6 for different fractional orders.

7. Conclusions

In this paper, we looked at a discrete-time fractional-order variant of the reaction diffusion FitzHugh–Nagumo system. We provided adequate constraints for the unique equilibrium’s local asymptotic stability. Moreover, with the help of the direct Lyapunov technique, the steady-state solution’s global asymptotic stability was established. Finally, the simulation results illustrate all of the theoretical investigations’ results. In the future, further research will be performed to examine this kind of discrete-time reaction–diffusion system.

Moreover, the linearization approach and the Lyapunov functional may be utilized to solve the issue of stability in discrete fractional reaction–diffusion models. In addition, the results of this study may be readily applicable to many various types of discrete fractional spatiotemporal systems with reaction–diffusion terms, as well as to other dynamical issues, such as chaos and synchronization control.