Sturm-Liouville Problem with Mixed Boundary Conditions for a Differential Equation with a Fractional Derivative and Its Application in Viscoelasticity Models
Abstract
1. Introduction
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Nauka i Tekhnika, M., Ed.; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1988. (In Russian) [Google Scholar]
- Machado, J.A.T. Handbook of Fractional Calculus with Applications; De Gruyter GmbH: Berlin, Germany; Boston, MA, USA, 2019; Volume 1–8. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, A.T. Advances in Fractional Calculus. In Theoretical Developments and Applications in Physics and Engineering; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010; 314p. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Wave Propagation, Impact and Variational Principles; Wiley: London, UK, 2014; 406p. [Google Scholar]
- Sandev, T.; Tomovshi, Z. Fractional Equations and Models: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Alotta, G.; Barrera, O.; Cocks, A.; Di Paola, M. The finite element implementation of 3D fractional viscoelastic constitutive models. Finite Elements Anal. Des. 2018, 146, 28–41. [Google Scholar] [CrossRef]
- Alotta, G.; Barrera, O.; Pegg, E.C. Viscoelastic material models for more accurate polyethylene wear estimation. J. Strain Anal. Eng. Des. 2018, 53, 302–312. [Google Scholar] [CrossRef]
- Shitikova, M.V. Fractional Operator Viscoelastic Models in Dynamic Problems of Mechanics of Solids: A Review. Mech. Solids 2022, 57, 1–33. [Google Scholar] [CrossRef]
- Shitikova, M.V.; Krusser, A.I. Models of viscoelastic materials: A review on historical development and formulation. Adv. Struct. Mater. 2022, 175, 285–326. [Google Scholar] [CrossRef]
- Shabani, M.; Jahani, K.; Di Paola, M.; Sadeghi, M.H. Frequency domain identification of the fractional Kelvin-Voigt’s parameters for viscoelastic materials. Mech. Mater. 2019, 137, 103099. [Google Scholar] [CrossRef]
- Lewandowski, R.; Chorazyczewski, B. Identification of the parameters of the Kelvin-Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comput. Struct. 2010, 88, 1–17. [Google Scholar] [CrossRef]
- Di Paola, M.; Pirrotta, A.; Valenza, A. Visco-elastic behavior through fractional calculus: An easier method for best fitting ex-perimental results. Mech. Mat. 2011, 43, 799–806. [Google Scholar] [CrossRef]
- Popov, I.I.; Chang, T.-P.; Rossikhin, Y.A.; Shitikova, M.V. Experimental Study of Concrete Aging Effect on the Contact Force and Contact Time During the Impact Interaction of an Elastic Rod with a Viscoelastic Beam. J. Mech. 2016, 33, 317–322. [Google Scholar] [CrossRef]
- Lagos-Varas, M.; Movilla-Quesada, D.; Arenas, J.; Raposeiras, A.; Castro-Fresno, D.; Calzada-Perez, M.A.; Vega-Zamanillo, A.; Maturana, J. Study of the mechanical behavior of asphalt mixtures using fractional rheology to model their viscoelasticity. Constr. Build. Mater. 2018, 200, 124–134. [Google Scholar] [CrossRef]
- Wang, Y.; Harris, J.M. Seismic attenuation models: Multiple and fractional generalizations. In SEG Technical Program Expanded Abstracts; SEG: Houston, TX, USA, 2020; pp. 2754–2758. [Google Scholar]
- Popov, I.I.; Shitikova, M.V.; Levchenko, A.V.; Zhukov, A.D. Experimental identification of the fractional parameter of the fractional derivative standard linear solid model for fiber-reinforced rubber concrete. Mech. Adv. Mater. Struct. 2023, 30, 1–9. [Google Scholar] [CrossRef]
- Popov, I.I.; Shitikova, M.V. Impulse excitation technique and its application for identification of material damping: An over-view. IOP Conf. Ser. Mater. Sci. Eng. 2020, 962, 022025. [Google Scholar] [CrossRef]
- Erokhin, S.V.; Aleroev, T.S. Parametric identification of the order of a fractional derivative in the Begley–Torvik model. Math. Model. 2018, 30, 93–102. [Google Scholar]
- Ungarova, L.G.; Ogorodnikov, E.N. Identification of the parameters of non-linear fractional mathematical models of a hered-itarily elastic body based on experimental data on the creep of PVC-compound samples. In Proceedings of the XI All-Russian Scientific Conference “Mathematical Modeling and Boundary Value Problems”, Samara, Russia, 27–30 May 2019; Volume 1, pp. 359–363. [Google Scholar]
- Xu, Y.; He, Q.; Guo, Y.-Q.; Huang, X.-H.; Dong, Y.-R.; Hu, Z.-W.; Kim, J. Experimental and Theoretical Investigation of Viscoelastic Damper by Applying Fractional Derivative Method and Internal Variable Theory. Buildings 2023, 13, 239. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional Calculus—A Different Approach to the Analysis of Viscoelastically Damped Struc-tures. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J. 1985, 23, 918–925. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the Fractional Calculus Model of Viscoelastic Behavior. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Caputo, M. Vibrations of an infinite viscoelastic layer with a dissipative memory. J. Acoust. Soc. Am. 1974, 56, 897–904. [Google Scholar] [CrossRef]
- Ingman, D.; Suzdalnitsky, J. Control of damping oscillations by fractional differential operator with time-dependent order. Comput. Methods Appl. Mech. Eng. 2004, 193, 5585–5595. [Google Scholar] [CrossRef]
- Naber, M. Linear Fractionally Damped Oscillator. Int. J. Differ. Equ. 2010, 2010, 197020. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications; Academic Press: London, UK, 1999; 340p. [Google Scholar]
- Watanabe, S. An Approach to Visco-Elastic Behaviors with a Mathematical Method. J. Text. Mach. Soc. Jpn. 1959, 5, 10–13. [Google Scholar] [CrossRef]
- Gerasimov, A.N. Generalisation of linear laws of deformation and its application to internal friction problems. PMM 1948, 12, 251–260. [Google Scholar]
- Aleroev, T.; Aleroeva, H. Problems of Sturm-Liouville type for diferential equations with fractional derivatives. In Fractional Diferential Equations; Kochubei, A., Luchko, Y., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019; pp. 21–46. [Google Scholar]
- Kirianova, L. The fractional derivative type identification for the modelling deformation and strength characteristics of polymer concrete. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1030, 012094. [Google Scholar] [CrossRef]
- Aleroev, T.S.; Kirane, M.; Tang, Y.F. Boundary-value problems for dirential equations of fractional order. J. Math. Sci. 2013, 10, 158–175. [Google Scholar]
- Nashif, A.D.; Jones, D.I.G.; Henderson, J.P. Vibration Damping; John Wiley & Sons: Hoboken, NJ, USA, 1991; 472p, ISBN 978-0-471-86772-2. [Google Scholar]

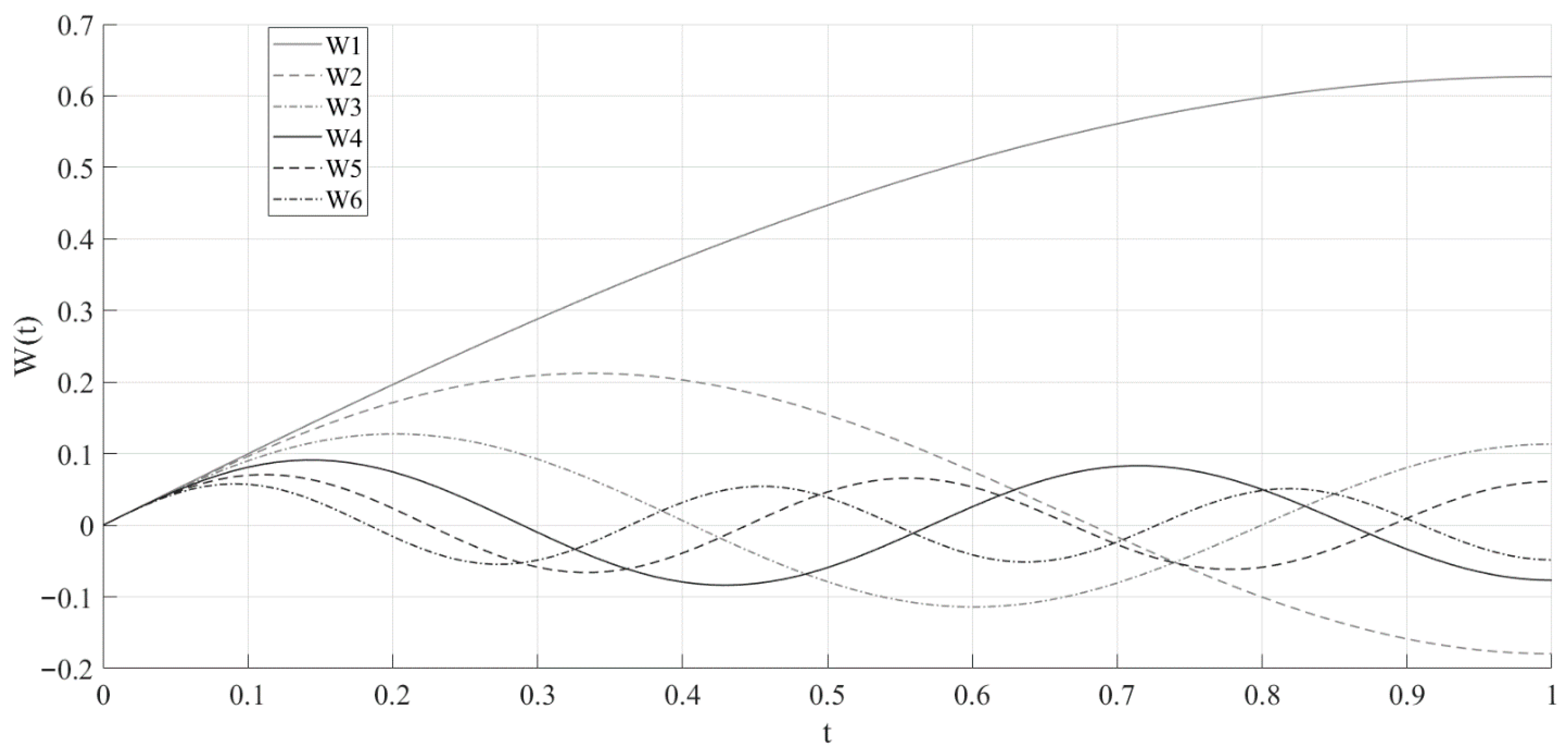
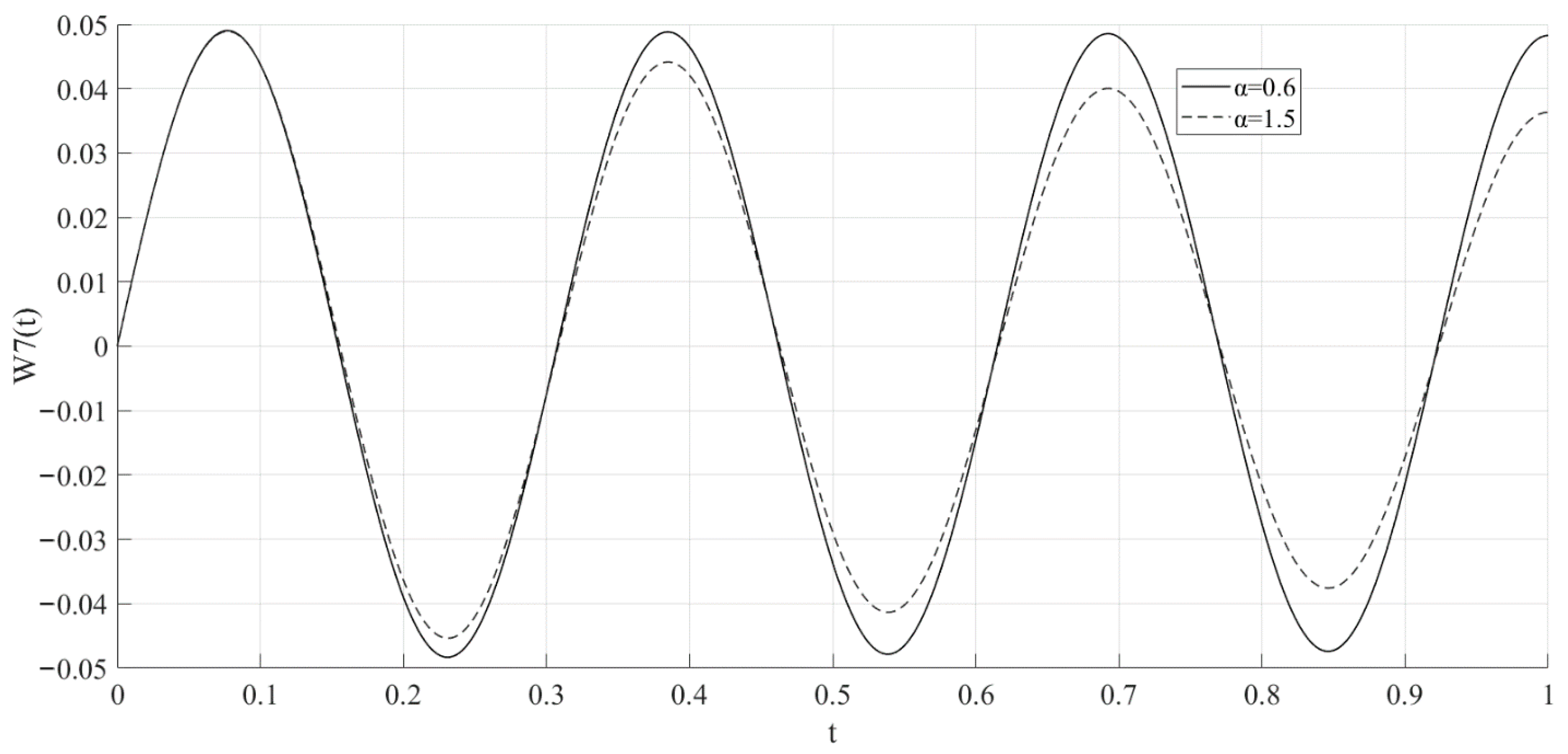

| 2.59 | 21.99 | 61.41 | 120.47 | 199.37 | 297.97 | 416.35 | 554.43 | 712.29 | 890.15 | |
| 2.65 | 22.27 | 61.67 | 120.81 | 199.69 | 298.31 | 416.69 | 554.79 | 712.63 | 890.37 | |
| 2.73 | 22.85 | 62.67 | 122.29 | 201.63 | 300.75 | 419.61 | 558.23 | 716.59 | 894.83 | |
| 2.81 | 23.87 | 65.05 | 126.41 | 207.77 | 309.17 | 430.55 | 571.91 | 733.21 | 914.29 |
| 2.23 | 21.87 | 61.27 | 120.41 | 199.31 | 297.95 | 416.33 | 554.47 | 712.33 | 890.12 | |
| 2.27 | 22.01 | 61.49 | 120.71 | 199.67 | 298.37 | 416.81 | 554.97 | 712.89 | 890.73 | |
| 2.51 | 23.23 | 64.27 | 125.45 | 206.71 | 307.99 | 427.27 | 570.53 | 731.75 | 912.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kiryanova, L.; Matseevich, T. Sturm-Liouville Problem with Mixed Boundary Conditions for a Differential Equation with a Fractional Derivative and Its Application in Viscoelasticity Models. Axioms 2023, 12, 779. https://doi.org/10.3390/axioms12080779
Kiryanova L, Matseevich T. Sturm-Liouville Problem with Mixed Boundary Conditions for a Differential Equation with a Fractional Derivative and Its Application in Viscoelasticity Models. Axioms. 2023; 12(8):779. https://doi.org/10.3390/axioms12080779
Chicago/Turabian StyleKiryanova, Ludmila, and Tatiana Matseevich. 2023. "Sturm-Liouville Problem with Mixed Boundary Conditions for a Differential Equation with a Fractional Derivative and Its Application in Viscoelasticity Models" Axioms 12, no. 8: 779. https://doi.org/10.3390/axioms12080779
APA StyleKiryanova, L., & Matseevich, T. (2023). Sturm-Liouville Problem with Mixed Boundary Conditions for a Differential Equation with a Fractional Derivative and Its Application in Viscoelasticity Models. Axioms, 12(8), 779. https://doi.org/10.3390/axioms12080779





