Abstract
In this study, we obtained a system of eigenfunctions and eigenvalues for the mixed homogeneous Sturm-Liouville problem of a second-order differential equation containing a fractional derivative operator. The fractional differentiation operator was considered according to two definitions: Gerasimov-Caputo and Riemann-Liouville-Visualizations of the system of eigenfunctions, the biorthogonal system, and the distribution of eigenvalues on the real axis were presented. The numerical behavior of eigenvalues was studied depending on the order of the fractional derivative for both definitions of the fractional derivative.
Keywords:
fractional differentiation operator; Sturm-Liouville problem; mixed boundary conditions; mathematical models of viscoelasticity MSC:
34A08; 34B09; 34K10; 93A30
1. Introduction
Differential equations containing fractional derivatives are actively used in constructing mathematical models for various phenomena and processes, followed by studying the properties and behavior of the solutions of these equations. Such processes include research on continuous media with memory, filtration of fluids in fractal geometries, physical aspects of stochastic transport and diffusion, mathematical models of viscoelastic materials, models of damped oscillations with fractional damping (e.g., vibrations of rock formations during earthquakes or vibrations of nanoscale sensors), models of nonlocal physical processes and fractal phenomena, climate models, and so on. For a long time, the encyclopedia of fractional calculus was the monograph [1]. Currently, the most detailed publication, presenting the fundamental theoretical principles of fractional calculus and various examples of its practical applications, can be considered [2]. Monographs [3,4,5,6,7,8,9] are also devoted to the application of differential equations with fractional derivatives in constructing models of physical processes.
Especially intensively developed at present is the direction related to the use of differential equations containing fractional differentiation operators in constructing viscoelastic models of solid bodies (for example, [10,11]). A detailed review of viscoelastic models with fractional derivatives and their historical development is given in [12,13].
In addition to direct problems—the study of the properties of solutions of differential equations containing fractional derivatives—inverse problems are always relevant—determining the type of equation that serves as the best mathematical model for the studied process. In particular, the problem of selecting the order of the fractional derivative included in differential equations used as rheological models is addressed in works [14,15,16,17,18,19,20,21,22,23,24].
2. Materials and Methods
Let us consider a differential equation containing a fractional-order operator used as a model for viscoelasticity (a Linear Fractionally Damped Oscillator). Such an equation is used [25,26,27,28,29,30] for modeling the changes in deformational and strength characteristics of various viscoelastic materials. This second-order equation contains a fractional derivative of order less than two:
Here represents the displacement of a fixed point (construction material) at a given time ;
—end of the time period under consideration;
—represents the Gerasimov-Caputo or Riemann-Liouville fractional differentiation operator of order α.
c, , and —constants. In [22], the following physical interpretation is proposed for these constants:
c—represents the material’s viscosity modulus,
—represents the material’s stiffness modulus,
—represents the viscoelasticity parameter of the material.
The fractional differentiation operators are defined as follows [31,32,33]. The left-sided Gerasimov-Caputo fractional derivative:
The left-sided Riemann-Liouville fractional derivative:
Here represents the Euler gamma function.
We will consider the behavior of a fixed point in a viscoelastic material subjected to an impulsive load at the initial moment of time. Therefore, we impose the following mixed, homogeneous boundary conditions:
which means that the displacement of the point is zero at the initial moment of time, and it is given an initial velocity upon impact. The velocity of the point becomes zero at the final moment of time (at the moment of cessation of oscillation).
The solution to problems (1)–(2) with homogeneous first-type boundary conditions (Dirichlet problem) is provided in [34].
The general solution of Equation (1) can be found, as in [35], by solving a second-order Volterra equation using a sequence of recursive kernels and expressing it as a power series.
3. Results
The general solution of Equation (1) in the case of the Gerasimov-Caputo fractional derivative, in the form of a power series, is given by:
Here represents a binomial coefficient.
Using the boundary conditions, it follows: from the first that and from the second that the eigenvalues of the problems (1)–(2) are the zeros of the function :
Figure 1 shows the graph of the function for various values of the fractional derivative order with T = 1 and c = 0.2.

Figure 1.
Graphs of the function with T = 1 and c = 0.2 for α = 0.5, α = 1, and α = 1.5.
Table 1 presents the first ten eigenvalues of the problems (1)–(2) for T = 1 and c = 0.2 obtained through numerical simulation using MATLAB.

Table 1.
Eigenvalues of the problems (1)–(2) for T = 1 and c = 0.2 with various values of the fractional derivative order according to Gerasimov-Caputo.
According to the values in Table 1, as the fractional derivative order increases, the eigenvalues increase slightly. The maximum relative deviation is observed in the second eigenvalue:
The system of eigenfunctions for the problems (1)–(2) with the Gerasimov-Caputo fractional derivative is given by:
represents the eigenvalues with
Thus, solutions to problem (1) satisfying boundary conditions (2) are found. That is, we obtain the equations of motion of a fixed point of a viscoelastic body to which a non-zero velocity is given at the initial moment (rest position) of time, and at the final moment of time T, the velocity is zero.
Figure 2 illustrates the graphs of the first 6 eigenfunctions for the problems (1)–(2) with a fractional derivative order of α = 1.2 according to Gerasimov-Caputo, with T = 1 and c = 0.2. The values of functions ÷ were computed using numerical simulation in MATLAB, where a partial sum of the series was taken instead of the full sum.

Figure 2.
Graphs of the first 6 eigenfunctions for the problems (1)–(2) with a fractional derivative order of α = 1.2 according to Gerasimov-Caputo, with T = 1 and c = 0.2.
Figure 3 displays the graphs of the seventh eigenfunction for the problems (1)–(2) with fractional derivative orders of α = 0.6 (solid line) and α = 1.5 (dashed line) according to Gerasimov-Caputo, with T = 1 and c = 0.2. From the figure, it can be observed that the eigenfunction corresponding to a higher fractional derivative order decays faster at local maxima and minima. It is worth noting that similar conclusions hold for all the cases studied by the authors with T = 1, c ∈ [0.1; 1.0], and α ∈ [0.1; 1.8].
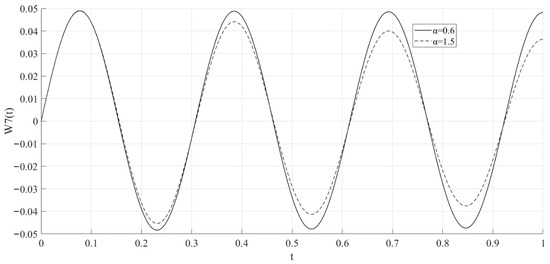
Figure 3.
Graphs of the seventh eigenfunction for the problems (1)–(2) with fractional derivative orders of α = 0.6 and α = 1.5 according to Gerasimov-Caputo with T = 1 and c = 0.2.
The system of eigenfunctions is complete in , but not orthogonal [34]. Let us construct a biorthogonal system for it using the approach from [36]. To obtain a biorthogonal system for the system , we consider the adjoint equation to (1). For this purpose, we examine the operator:
Then, the adjoint operator to is denoted as , such that:
where the scalar product is defined as:
Assuming the functions f and g satisfy the boundary conditions (2), we have:
Using the self-adjointness of the repeated differentiation operator, we have:
The linearity of the fractional differentiation operator gives:
By changing the integration limits in the double integral, we have
Let us denote:
then, using the boundary conditions,
Furthermore, by using the relation between the right-sided fractional derivatives according to Gerasimov-Caputo and Riemann-Liouville derivatives, we obtain:
Therefore,
Thus, the adjoint operator takes the following form:
The adjoint boundary value problem on the interval t ∈ [0; T] for the Gerasimov-Caputo fractional derivative definition of (1)–(2) is given by:
The general solution of Equation (5), obtained through the solution of the second-kind Volterra equation using a sequence of recurrent kernels, is given by:
Substituting and using (6), we have .
Differentiating the obtained series, we have:
Next, we use the second boundary condition:
Hence, the eigenvalues coincide, and the eigenfunctions of the adjoint problem have the form:
Figure 4 shows the graphs of —the first four eigenfunctions of the problems (1)–(2) in black, and the graphs of —the first four eigenfunctions of the adjoint problem (5)–(6) in gray for the fractional derivative with order α = 1.2 according to Gerasimov-Caputo with T = 1 and c = 0.2.
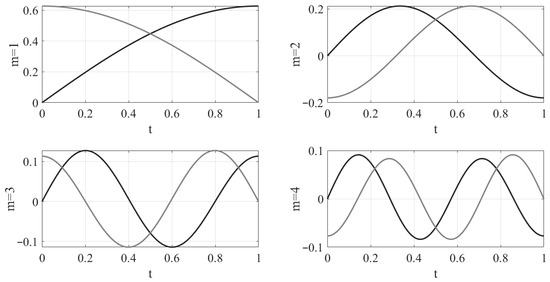
Figure 4.
Graphs of (black) и (gray) for the fractional derivative with order α = 1.2 according to Gerasimov-Caputo with T = 1 and c = 0.2.
To prove the orthogonality of the systems and let us consider two eigenfunctions and their corresponding (non-equal) eigenvalues :
Therefore, for any , which means that —are the functions from the system that are biorthogonal to the system .
The solution of problems (1)–(2) is given by:
The coefficients can be found using the standard approach, employing the inner product in :
Thus, we have the representation:
Similar calculations can be carried out if the fractional differentiation operator is defined according to Riemann-Liouville. In this case, the eigenvalues are zeros of the function:
Table 2 presents the first ten eigenvalues of the problem (1)–(2) for T = 1, c = 0.2, and various values of the order of the fractional derivative according to Riemann-Liouville.

Table 2.
Eigenvalues of problems (1)–(2) for T = 1, c = 0.2 at various values of the order of the fractional derivative according to Riemann-Liouville.
According to the values in Table 2, as the order of the fractional derivative increases, the eigenvalues slightly increase. The maximum relative deviation is observed in the first eigenvalue:
It should be noted that according to the values from Table 1 and Table 2, the eigenvalues corresponding to different fractional differentiation operators with the same order of the fractional derivative (specifically, α = 1.5) do not coincide. The maximum relative deviation is observed in the first eigenvalue and amounts to 11%.
Next, the system of eigenfunctions of problems (1)–(2) in the case of defining the fractional differentiation operator according to Riemann-Liouville takes the form:
In conclusion, let us consider the classical particular case: when α = 1, problems (1)–(2) transform into Sturm-Liouville problems for a second-order equation containing the first derivative:
The eigenvalues of problems (8)–(9) are zeros of the function:
The eigenfunctions of problems (8)–(9) are given by:
It should be noted that the eigenvalues calculated in the MATLAB software using the function for the values with a step of 0.1 coincide with the eigenvalues calculated using the function
4. Discussion
In viscoelasticity models (see, for example, [37]), the quantity is referred to as the coefficient of relative damping (over one period of the trigonometric component, the natural logarithm of the eigenfunction decreases times ), —is the coefficient of losses, and —is the (circular) frequency of damped eigenoscillations (the quantity divided by is inversely proportional to the period of the trigonometric component of the eigenfunction). When building mathematical models of viscoelasticity using the apparatus of fractional differentiation, it is clear that both the damping coefficient and the frequency of damped eigenoscillations should contain the order of the fractional derivative. In our view, the relative damping depends on two parameters, c and , and the frequency of damped eigenoscillations on three parameters, (eigenvalues), c and .Therefore, the physical meaning of the coefficients in Equation (1) used in [22] appears to be justified by the authors.
5. Conclusions
In this study, a mixed homogeneous Sturm-Liouville problem for a second-order differential equation containing a fractional differentiation operator was analyzed, considering two definitions: Gerasimov-Caputo and Riemann-Liouville.
A system of eigenfunctions and eigenvalues for the considered mixed boundary value problem was obtained.
A conjugate boundary value problem for the fractional derivative according to Gerasimov-Caputo was constructed.
A system biorthogonal to the found system of eigenfunctions was constructed in the case when the fractional derivative is defined according to Gerasimov-Caputo.
The numerical behavior of eigenvalues was studied depending on the order of the fractional derivative for both definitions of the fractional derivative.
Visualizations of the system of eigenfunctions, the biorthogonal system, and the distribution of eigenvalues on the real axis were presented.
Author Contributions
Conceptualization, L.K. and T.M.; methodology, L.K.; software, L.K. and T.M.; validation, L.K. and T.M.; formal analysis, L.K. and T.M.; investigation, L.K. and T.M.; resources, L.K. and T.M.; data curation, L.K. and T.M.; writing—original draft preparation, L.K. and T.M.; writing—review and editing, L.K.; visualization, L.K. and T.M.; supervision, L.K.; project administration, L.K. and T.M.; funding acquisition, L.K. and T.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
The authors are sincerely grateful to Temirkhan S. Aleroyev for useful discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Nauka i Tekhnika, M., Ed.; Gordon and Breach Science Publishers: Philadelphia, PA, USA, 1988. (In Russian) [Google Scholar]
- Machado, J.A.T. Handbook of Fractional Calculus with Applications; De Gruyter GmbH: Berlin, Germany; Boston, MA, USA, 2019; Volume 1–8. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Sabatier, J.; Agrawal, O.P.; Machado, A.T. Advances in Fractional Calculus. In Theoretical Developments and Applications in Physics and Engineering; Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Mainardi, F. Fractional Calculus and Waves in Linear Viscoelasticity: An Introduction to Mathematical Models; Imperial College Press: London, UK, 2010; 314p. [Google Scholar]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists, 2nd ed.; World Scientific: Singapore, 2014. [Google Scholar]
- Atanacković, T.M.; Pilipović, S.; Stanković, B.; Zorica, D. Fractional Calculus with Applications in Mechanics: Wave Propagation, Impact and Variational Principles; Wiley: London, UK, 2014; 406p. [Google Scholar]
- Sandev, T.; Tomovshi, Z. Fractional Equations and Models: Theory and Applications; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Alotta, G.; Barrera, O.; Cocks, A.; Di Paola, M. The finite element implementation of 3D fractional viscoelastic constitutive models. Finite Elements Anal. Des. 2018, 146, 28–41. [Google Scholar] [CrossRef]
- Alotta, G.; Barrera, O.; Pegg, E.C. Viscoelastic material models for more accurate polyethylene wear estimation. J. Strain Anal. Eng. Des. 2018, 53, 302–312. [Google Scholar] [CrossRef]
- Shitikova, M.V. Fractional Operator Viscoelastic Models in Dynamic Problems of Mechanics of Solids: A Review. Mech. Solids 2022, 57, 1–33. [Google Scholar] [CrossRef]
- Shitikova, M.V.; Krusser, A.I. Models of viscoelastic materials: A review on historical development and formulation. Adv. Struct. Mater. 2022, 175, 285–326. [Google Scholar] [CrossRef]
- Shabani, M.; Jahani, K.; Di Paola, M.; Sadeghi, M.H. Frequency domain identification of the fractional Kelvin-Voigt’s parameters for viscoelastic materials. Mech. Mater. 2019, 137, 103099. [Google Scholar] [CrossRef]
- Lewandowski, R.; Chorazyczewski, B. Identification of the parameters of the Kelvin-Voigt and the Maxwell fractional models, used to modeling of viscoelastic dampers. Comput. Struct. 2010, 88, 1–17. [Google Scholar] [CrossRef]
- Di Paola, M.; Pirrotta, A.; Valenza, A. Visco-elastic behavior through fractional calculus: An easier method for best fitting ex-perimental results. Mech. Mat. 2011, 43, 799–806. [Google Scholar] [CrossRef]
- Popov, I.I.; Chang, T.-P.; Rossikhin, Y.A.; Shitikova, M.V. Experimental Study of Concrete Aging Effect on the Contact Force and Contact Time During the Impact Interaction of an Elastic Rod with a Viscoelastic Beam. J. Mech. 2016, 33, 317–322. [Google Scholar] [CrossRef]
- Lagos-Varas, M.; Movilla-Quesada, D.; Arenas, J.; Raposeiras, A.; Castro-Fresno, D.; Calzada-Perez, M.A.; Vega-Zamanillo, A.; Maturana, J. Study of the mechanical behavior of asphalt mixtures using fractional rheology to model their viscoelasticity. Constr. Build. Mater. 2018, 200, 124–134. [Google Scholar] [CrossRef]
- Wang, Y.; Harris, J.M. Seismic attenuation models: Multiple and fractional generalizations. In SEG Technical Program Expanded Abstracts; SEG: Houston, TX, USA, 2020; pp. 2754–2758. [Google Scholar]
- Popov, I.I.; Shitikova, M.V.; Levchenko, A.V.; Zhukov, A.D. Experimental identification of the fractional parameter of the fractional derivative standard linear solid model for fiber-reinforced rubber concrete. Mech. Adv. Mater. Struct. 2023, 30, 1–9. [Google Scholar] [CrossRef]
- Popov, I.I.; Shitikova, M.V. Impulse excitation technique and its application for identification of material damping: An over-view. IOP Conf. Ser. Mater. Sci. Eng. 2020, 962, 022025. [Google Scholar] [CrossRef]
- Erokhin, S.V.; Aleroev, T.S. Parametric identification of the order of a fractional derivative in the Begley–Torvik model. Math. Model. 2018, 30, 93–102. [Google Scholar]
- Ungarova, L.G.; Ogorodnikov, E.N. Identification of the parameters of non-linear fractional mathematical models of a hered-itarily elastic body based on experimental data on the creep of PVC-compound samples. In Proceedings of the XI All-Russian Scientific Conference “Mathematical Modeling and Boundary Value Problems”, Samara, Russia, 27–30 May 2019; Volume 1, pp. 359–363. [Google Scholar]
- Xu, Y.; He, Q.; Guo, Y.-Q.; Huang, X.-H.; Dong, Y.-R.; Hu, Z.-W.; Kim, J. Experimental and Theoretical Investigation of Viscoelastic Damper by Applying Fractional Derivative Method and Internal Variable Theory. Buildings 2023, 13, 239. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional Calculus—A Different Approach to the Analysis of Viscoelastically Damped Struc-tures. AIAA J. 1983, 21, 741–748. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J. 1985, 23, 918–925. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. On the Fractional Calculus Model of Viscoelastic Behavior. J. Rheol. 1986, 30, 133–155. [Google Scholar] [CrossRef]
- Caputo, M. Vibrations of an infinite viscoelastic layer with a dissipative memory. J. Acoust. Soc. Am. 1974, 56, 897–904. [Google Scholar] [CrossRef]
- Ingman, D.; Suzdalnitsky, J. Control of damping oscillations by fractional differential operator with time-dependent order. Comput. Methods Appl. Mech. Eng. 2004, 193, 5585–5595. [Google Scholar] [CrossRef]
- Naber, M. Linear Fractionally Damped Oscillator. Int. J. Differ. Equ. 2010, 2010, 197020. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and some of their Applications; Academic Press: London, UK, 1999; 340p. [Google Scholar]
- Watanabe, S. An Approach to Visco-Elastic Behaviors with a Mathematical Method. J. Text. Mach. Soc. Jpn. 1959, 5, 10–13. [Google Scholar] [CrossRef]
- Gerasimov, A.N. Generalisation of linear laws of deformation and its application to internal friction problems. PMM 1948, 12, 251–260. [Google Scholar]
- Aleroev, T.; Aleroeva, H. Problems of Sturm-Liouville type for diferential equations with fractional derivatives. In Fractional Diferential Equations; Kochubei, A., Luchko, Y., Eds.; De Gruyter: Berlin, Germany; Boston, MA, USA, 2019; pp. 21–46. [Google Scholar]
- Kirianova, L. The fractional derivative type identification for the modelling deformation and strength characteristics of polymer concrete. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1030, 012094. [Google Scholar] [CrossRef]
- Aleroev, T.S.; Kirane, M.; Tang, Y.F. Boundary-value problems for dirential equations of fractional order. J. Math. Sci. 2013, 10, 158–175. [Google Scholar]
- Nashif, A.D.; Jones, D.I.G.; Henderson, J.P. Vibration Damping; John Wiley & Sons: Hoboken, NJ, USA, 1991; 472p, ISBN 978-0-471-86772-2. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).