A Method for Extrapolating Continuous Functions by Generating New Training Samples for Feedforward Artificial Neural Networks
Abstract
1. Introduction
- Increased uncertainty: the larger time horizon implies the possibility of more numerous and more significant changes in the environment, objects and subjects, phenomena and processes, etc.
- Variability of trends: Long-term forecasts are based on the assumption that current trends will continue in the future. However, over longer periods, significant changes can occur and alter existing trends.
- Insufficient historical data: long-term forecasts often rely on historical data, but in some cases, the available historical data may not be sufficient.
- Unknown or unforeseen events: unknown or unforeseen events, such as natural disasters, economic crises, or pandemics, can have a significant impact on long-term forecasts.
- Complexity of the models: for long-term forecasts, more complex models are often created, and these can be difficult to build, parameterize, interpret, and manage, and may produce results with high error rates.
2. State of the Art
- Polynomial or function extrapolation: A polynomial (quadratic, cubic, etc.) or specific function (logarithmic, exponential, sinusoidal, etc.) is sought that fits the existing data. The found function is then used to compute forecast values outside the range of available data.
- Regression models: These are used to predict a dependent variable based on one or more independent variables. A regression model is suitable when there is a linear or nonlinear dependence between the variables. Forecasts are based on the assumption that the relationship discovered in the available data will continue to be valid in the future. There are different types of models—linear, polynomial, logistic, multiple, etc.
- Time series models: These statistical methods analyze data collected sequentially over specified time intervals to predict future values. These models discover patterns and trends and extrapolate them into the future. The following models are more commonly used: auto-regressive, moving average, ARIMA, deep learning with recurrent neural networks (RNNs) and long short-term memory (LSTM), STL (seasonal and trend decomposition using loess), and others.
- Neural networks: Neural networks, particularly recurrent neural networks (RNNs) and long short-term memory (LSTM) networks, are used for extrapolation tasks, especially with time series data. They can model complex nonlinear relationships, but they require large amounts of data and can be computationally intensive.
- Capacity to capture complex nonlinear dependencies: neural networks can model complex nonlinear relationships between variables, which can be challenging with traditional mathematical and statistical methods.
- Ability to handle large volumes of data: neural networks can handle large amounts of data, and this makes them suitable for extrapolation based on large data sets.
- Adaptability: neural networks can learn and adapt based on new data, which means they can adjust to changes in the data or observed patterns.
3. Issues with Long-Term Forecasting via ANNs
- (1)
- Training Set:
- This is the largest data subset, and it is used to train the neural network.
- The data in this subset are diverse and representative of the approximation task.
- The training subset consists of 70% of all the data.
- (2)
- Validation Set:
- These data are used to estimate and tune the hyperparameters of the model during training.
- We use the validation set to control the overfitting of the model and to make decisions concerning potential changes in the hyperparameters (e.g., learning rate, number of epochs).
- The data in this subset are representative of the overall data, but they are not involved in the direct training of the model.
- The validation subset consists of 15% of all the data.
- (3)
- Test Set:
- This is the data set used for the final assessment of the trained model. These data are used in the final stage of the model assessment after all adjustments and optimizations have been made.
- The test set is used to measure the generalization ability of the model after the training is complete.
- The data in this subset are independent of the training and validation data and are representative of real situations.
- The test set consists of 15% of all the data.
4. New Concepts and Definitions Needed to Describe the Iterative Algorithm
- (1)
- is perfectly trained on , i.e., condition (4) is satisfied, and
- (2)
- ,
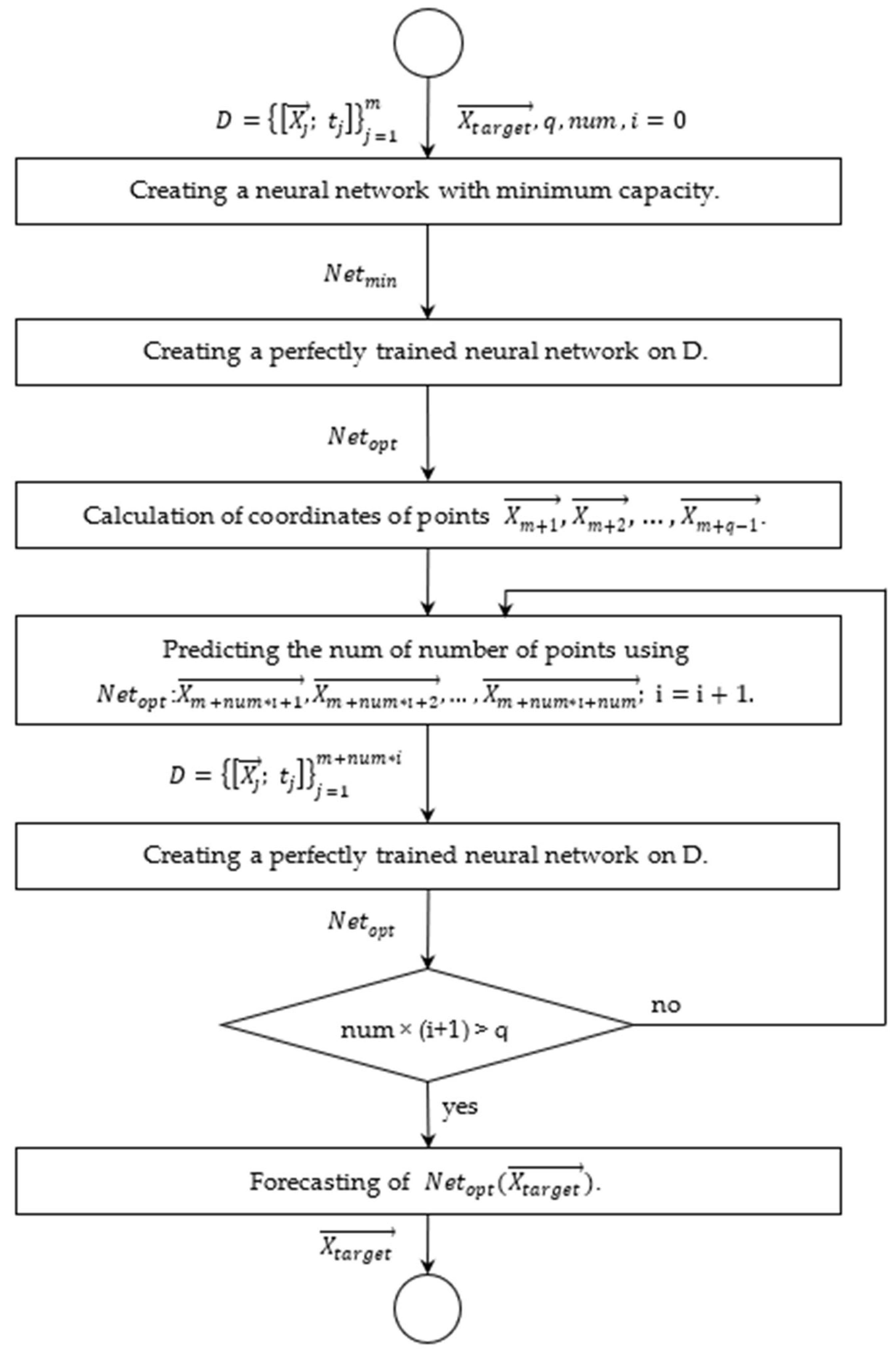
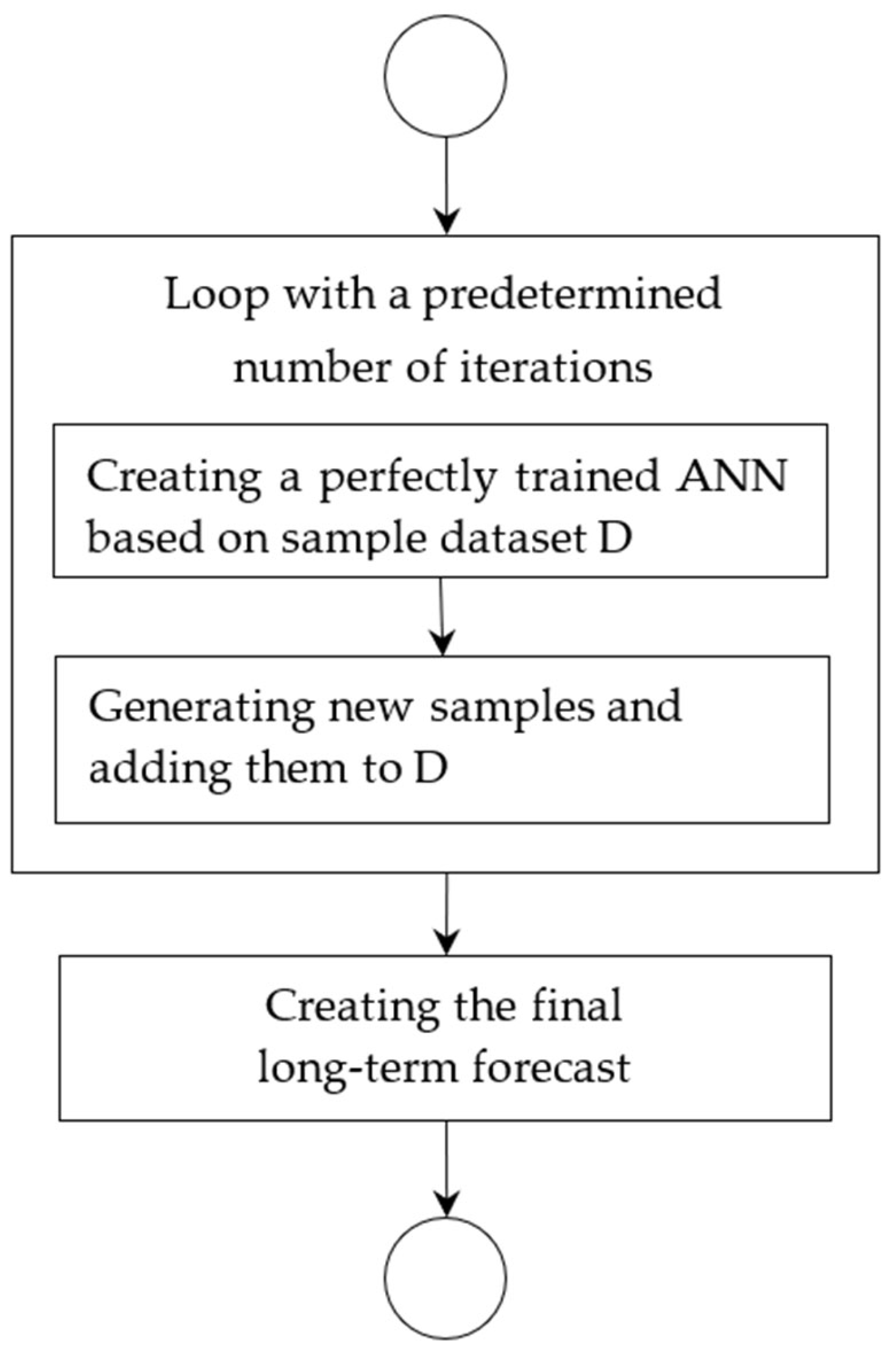
5. A Method for Extrapolating Continuous Functions with Artificial Neural Networks by Generating New Training Samples
- (1)
- Creating an efficient artificial neural network with minimum capacity on the initial sample
- (2)
- Creating a perfectly trained artificial neural network
- (3)
- Generating new samples outside the initial sampling
- The number of prediction points that lie between the sample boundaries and the target prediction point is determined. The available computing resources and time, as well as the user settings, are important for determining the number of points . A greater number of points leads to more accurate prediction results.
- The intermediate points which are evenly spaced between and are calculated. With different modifications to the algorithm, these points may be calculated differently and therefore they may not be evenly distributed.
- The following activities are performed iteratively until the target point is reached:
- ◦
- Using the current AN, one or more points are predicted, successively taking the points closest to the boundary. The number of these points is set by the user.
- ◦
- The newly obtained input–output samples are added to the neural network training dataset.
- ◦
- A neural network is perfectly trained on the updated dataset.
- (4)
- Prediction
6. Experiments and Discussion
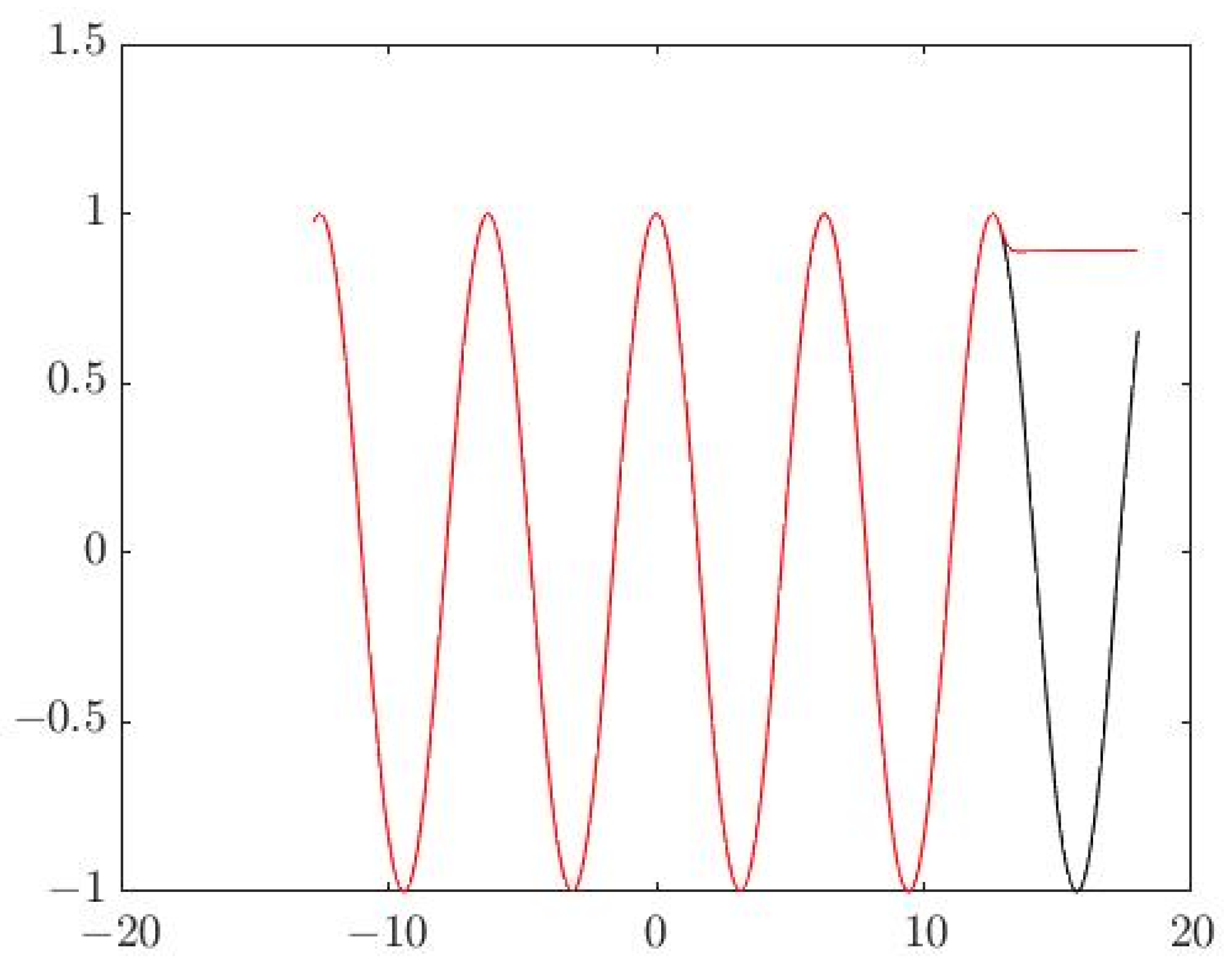
 | Represents the graph of the real target function F. The algorithms have not yet been started and the network Net has not been created. |
 | The algorithm has completed stage (1) and a minimum capacity approximating the neural network Net trained on the original sample is created. |
 | Represents the graph of the approximating neural network Net after the algorithm has completed step (2) and the network has been optimized, i.e., after it has been perfectly trained on the sample and the minimum capacity has been obtained. |
 | Represents the graph of the approximating neural network Net after the algorithm has completed stage (3). The network is perfectly trained on the samples outside the initial dataset. |
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Celik, S.; Inci, H.; Sengul, T.; Sogut, B.; Sengul, A.; Taysi, M. Interpolation method for live weight estimation based on age in Japanese quails. Rev. Bras. Zootec. 2016, 45, 445–450. [Google Scholar] [CrossRef]
- Burden, R.L.; Faires, J.D. Interpolation & Polynomial Approximation/Lagrange Interpolating Polynomials II. In Numerical Analysis, 9th ed.; Faires, R.L., Ed.; Brooks/Cole, Cengage Learning: Dublin, Ireland, 2011. [Google Scholar]
- Mutombo, N.M.-A.; Numbi, B.P. Development of a Linear Regression Model Based on the Most Influential Predictors for a Research Office Cooling Load. Energies 2022, 15, 5097. [Google Scholar] [CrossRef]
- Guerard, J. Regression Analysis and Forecasting Models. In Introduction to Financial Forecasting in Investment Analysis; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Schleifer, A. Forecasting with Regression Analysis; Product #: 894007-PDF-ENG; Harvard Business Publishing: Harvard, MA, USA, 1993. [Google Scholar]
- Peña, D.; Tiao, G.; Tsay, R.A. Course in Time Series Analysis; Wiley: Hoboken, NJ, USA, 2000; ISBN 978-0-471-36164-0. [Google Scholar]
- Yaffee, R.; McGee, M. Introduction to Time Series Analysis and Forecasting with Applications of SAS and SPSS; Academic Press: Cambridge, MA, USA, 2000; ISBN 0127678700. [Google Scholar]
- Brockwell, P.; Davis, R. Introduction to Time Series and Forecasting; Springer: Berlin/Heidelberg, Germany, 2002; ISBN 0-387-95351-5. [Google Scholar]
- Zhou, H.; Wang, T.; Zhao, H.; Wang, Z. Updated Prediction of Air Quality Based on Kalman-Attention-LSTM Network. Sustainability 2023, 15, 356. [Google Scholar] [CrossRef]
- Ly, R.; Traore, F.; Dia, K. Forecasting commodity prices using long-short-term memory neural networks. IFPRI Discuss. Pap. 2021, 2000, 26. [Google Scholar] [CrossRef]
- Zhang, K.; Hong, M. Forecasting crude oil price using LSTM neural networks. Data Sci. Financ. Econ. 2022, 2, 163–180. [Google Scholar] [CrossRef]
- Wei, J.; Zou, K. EDA: Easy Data Augmentation Techniques for Boosting Performance on Text Classification. In Proceedings of the ICLR 2019-7th International Conference on Learning Representations, Hong Kong, China, 3–7 November 2019; pp. 6382–6388. [Google Scholar] [CrossRef]
- Şahin, G.G.; Steedman, M. Data Augmentation via Dependency Tree Morphing for Low-Resource Languages. In Proceedings of the 2018 Conference on Empirical Methods in Natural Language Processing, Brussels, Belgium, 31 October–4 November 2018; pp. 5004–5009. [Google Scholar] [CrossRef]
- Fadaee, M.; Bisazza, A.; Monz, C. Data Augmentation for Low-Resource Neural Machine Translation. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, Vancouver, BC, Canada, 30 July–4 August 2017; pp. 567–573. [Google Scholar] [CrossRef]
- Sugiyama, A.; Yoshinaga, N. Data augmentation using back-translation for context-aware neural machine translation. In Proceedings of the Fourth Workshop on Discourse in Machine Translation (DiscoMT 2019), Hong Kong, China, 6–9 November 2019; pp. 35–44. [Google Scholar] [CrossRef]
- Shorten, C.; Khoshgoftaar, T.M.; Furht, B. Text data augmentation for deep learning. J. Big Data 2021, 8, 101. [Google Scholar] [CrossRef] [PubMed]
- Abdali, S.; Mukherjee, S.; Papalexakis, E. Vec2Node: Self-Training with Tensor Augmentation for Text Classification with Few Labels. Mach. Learn. Knowl. Discov. Databases 2023, 13714, 571–587. [Google Scholar] [CrossRef]
- Kwon, S.; Lee, Y. Explainability-Based Mix-Up Approach for Text Data Augmentation. ACM Trans. Knowl. Discov. Data 2023, 17, 13. [Google Scholar] [CrossRef]
- Saha, P.; Logofatu, D. Efficient Approaches for Data Augmentation by Using Generative Adversarial Networks. Eng. Appl. Neural Netw. 2022, 1600, 386–399. [Google Scholar] [CrossRef]
- Summers, C.; Dinneen, M.J. Improved mixed-example data augmentation. In Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 7–11 January 2019; pp. 1262–1270. [Google Scholar] [CrossRef]
- Kaur, P.; Khehra, B.S.; Mavi, E.B.S. Data augmentation for object detection: A review. In Proceedings of the 2021 IEEE International Midwest Symposium on Circuits and Systems (MWSCAS), Lansing, MI, USA, 9–11 August 2021; pp. 537–543. [Google Scholar] [CrossRef]
- Zoph, B.; Cubuk, E.D.; Ghiasi, G.; Lin, T.Y.; Shlens, J.; Le, Q.V. Learning Data Augmentation Strategies for Object Detection. In Proceedings of the 16th European Conference, Glasgow, UK, 23–28 August 2020; Lecture Notes in Computer Science; Vedaldi, A., Bischof, H., Brox, T., Frahm, J.M., Eds.; Springer: Cham, Switzerland, 2020; Volume 12372, pp. 566–583. [Google Scholar] [CrossRef]
- Fawzi, A.; Samulowitz, H.; Turaga, D.; Frossard, P. Adaptive data augmentation for image classification. In Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25–28 September 2016; pp. 3688–3692. [Google Scholar] [CrossRef]
- Chlap, P.; Min, H.; Vandenberg, N.; Dowling, J.; Holloway, L.; Haworth, A. A review of medical image data augmentation techniques for deep learning applications. J. Med. Imaging Radiat. Oncol. 2021, 65, 545–563. [Google Scholar] [CrossRef]
- Nalepa, J.; Marcinkiewicz, M.; Kawulok, M. Data augmentation for brain-tumor segmentation: A review. Front. Comput. Neurosci. 2019, 13, 83. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, X.-H.; Wei, Z.; Heidari, A.A.; Zheng, N.; Li, Z.; Chen, H.; Hu, H.; Zhou, Q.; Guan, Q. Generative adversarial networks in medical image augmentation: A review. Comput. Biol. Med. 2022, 144, 105382. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, Y.; Cheng, Y.; Yang, Y.; Zhao, F.; Li, J.; Liu, H.; Yan, S.; Feng, J. Look across elapse: Disentangled representation learning and photorealistic cross-age face synthesis for age-invariant face recognition. Proc. AAAI Conf. Artif. Intell. 2019, 33, 9251–9258. [Google Scholar] [CrossRef]
- Zhao, J.; Cheng, Y.; Xu, Y.; Xiong, L.; Li, J.; Zhao, F.; Jayashree, K.; Pranata, S.; Shen, S.; Xing, J.; et al. Towards pose invariant face recognition in the wild. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 2207–2216. [Google Scholar] [CrossRef]
- Tran, L.; Yin, X.; Liu, X. Disentangled representation learning gan for pose-invariant face recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 1415–1424. [Google Scholar] [CrossRef]
- Chen, X.; Wang, G.; Guo, H.; Zhang, C. Pose guided structured region ensemble network for cascaded hand pose estimation. Neurocomputing 2020, 395, 138–149. [Google Scholar] [CrossRef]
- Baek, S.; Kim, K.I.; Kim, T.K. Augmented skeleton space transfer for depth-based hand pose estimation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 8330–8339. [Google Scholar] [CrossRef]
- Chen, L.; Lin, S.Y.; Xie, Y.; Lin, Y.Y.; Fan, W.; Xie, X. DGGAN: Depth-image guided generative adversarial networks for disentangling RGB and depth images in 3D hand pose estimation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision, Village, CO, USA, 1–5 March 2020; pp. 411–419. [Google Scholar] [CrossRef]
- He, W.; Xie, Z.; Li, Y.; Wang, X.; Cai, W. Synthesizing depth hand images with GANs and style transfer for hand pose estimation. Sensors 2019, 19, 2919. [Google Scholar] [CrossRef] [PubMed]
- Cader, A. The Potential for the Use of Deep Neural Networks in e-Learning Student Evaluation with New Data Augmentation Method. Artif. Intell. Educ. 2020, 12164, 37–42. [Google Scholar] [CrossRef]
- Cochran, K.; Cohn, C.; Hutchins, N.; Biswas, G.; Hastings, P. Improving Automated Evaluation of Formative Assessments with Text Data Augmentation. Artif. Intell. Educ. 2022, 13355, 390–401. [Google Scholar] [CrossRef]
- Maharana, K.; Mondal, S.; Nemade, B. A review: Data pre-processing and data augmentation techniques. Glob. Transit. Proc. 2022, 3, 91–99. [Google Scholar] [CrossRef]
- Ostertagova, E. Modelling Using Polynomial Regression. Procedia Eng. 2012, 48, 500–506. [Google Scholar] [CrossRef]
- Hyndman, R.; Athanasopoulos, G. Forecasting: Principles and Practice; OTexts: Melbourne, VI, Australia, 2013; ISBN 0987507109. [Google Scholar]
- Chollet, F. Deep Learning with Python; Manning: Shelter Island, NY, USA, 2021; ISBN 1617296864. [Google Scholar]
- Bandara, K.; Bergmeir, C.; Smyl, S. Forecasting across time series databases using recurrent neural networks on groups of similar series: A clustering approach. Expert Syst. Appl. 2020, 140, 112896. [Google Scholar] [CrossRef]
- Taylor, S.; Letham, B. Forecasting at Scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Bandara, K.; Hewamalage, H.; Liu, Y.-H.; Kang, Y.; Bergmeir, C. Improving the accuracy of global forecasting models using time series, data augmentation. Pattern Recognit. 2021, 120, 108148. [Google Scholar] [CrossRef]
- Goodfellow, I.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative adversarial networks. Commun. ACM 2020, 63, 139–144. [Google Scholar] [CrossRef]
- Mumuni, A.; Mumuni, F. Data augmentation: A comprehensive survey of modern approaches. Array 2022, 16, 100258. [Google Scholar] [CrossRef]
- Yoon, J.; Jordon, J.; Schaar, M. GAIN: Missing Data Imputation using Generative Adversarial Nets. arXiv 2018, arXiv:1806.02920. [Google Scholar] [CrossRef]
- Aziira, A.; Setiawan, N.; Soesanti, I. Generation of Synthetic Continuous Numerical Data Using Generative Adversarial Networks. J. Phys. Conf. Ser. 2020, 1577, 012027. [Google Scholar] [CrossRef]
- Yean, S.; Somani, P.; Lee, B.; Oh, H. GAN+: Data Augmentation Method using Generative Adversarial Networks and Dirichlet for Indoor Localisation. In Proceedings of the IPIN 2021 WiP Proceedings, Lloret de Mar, Spain, 12–13 September 2021. [Google Scholar]
- Yean, S.; Somani, P.; Lee, B.; Oh, H. Numeric Data Augmentation using Structural Constraint Wasserstein Generative Adversarial Networks. In Proceedings of the 2020 IEEE International Symposium on Circuits and Systems (ISCAS), Seville, Spain, 12–14 October 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Moreno-Barea, F.; Jerez, J.; Franco, L. Improving classification accuracy using data augmentation on small data sets. Expert Syst. Appl. 2020, 161, 113696. [Google Scholar] [CrossRef]
- Moreno-Barea, F.J.; Jerez, J.M.; Franco, L. A Parallel Hybrid Neural Network with Integration of Spatial and Temporal Features for Remaining Useful Life Prediction in Prognostics. IEEE Trans. Instrum. Meas. 2023, 72, 3501112. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Tian, J.; Luo, H.; Yin, S. An integrated multi-head dual sparse self-attention network for remaining useful life prediction. Reliab. Eng. Syst. Saf. 2023, 233, 109096. [Google Scholar] [CrossRef]
- Zhang, J.; Jiang, Y.; Li, X.; Luo, H.; Yin, S.; Kaynak, O. Remaining Useful Life Prediction of Lithium-Ion Battery with Adaptive Noise Estimation and Capacity Regeneration Detection. IEEE/ASME Trans. Mechatron. 2023, 28, 632–643. [Google Scholar] [CrossRef]
- Yotov, K.; Hadzhikolev, E.; Hadzhikoleva, S.; Cheresharov, S. Finding the Optimal Topology of an Approximating Neural Network. Mathematics 2023, 11, 217. [Google Scholar] [CrossRef]


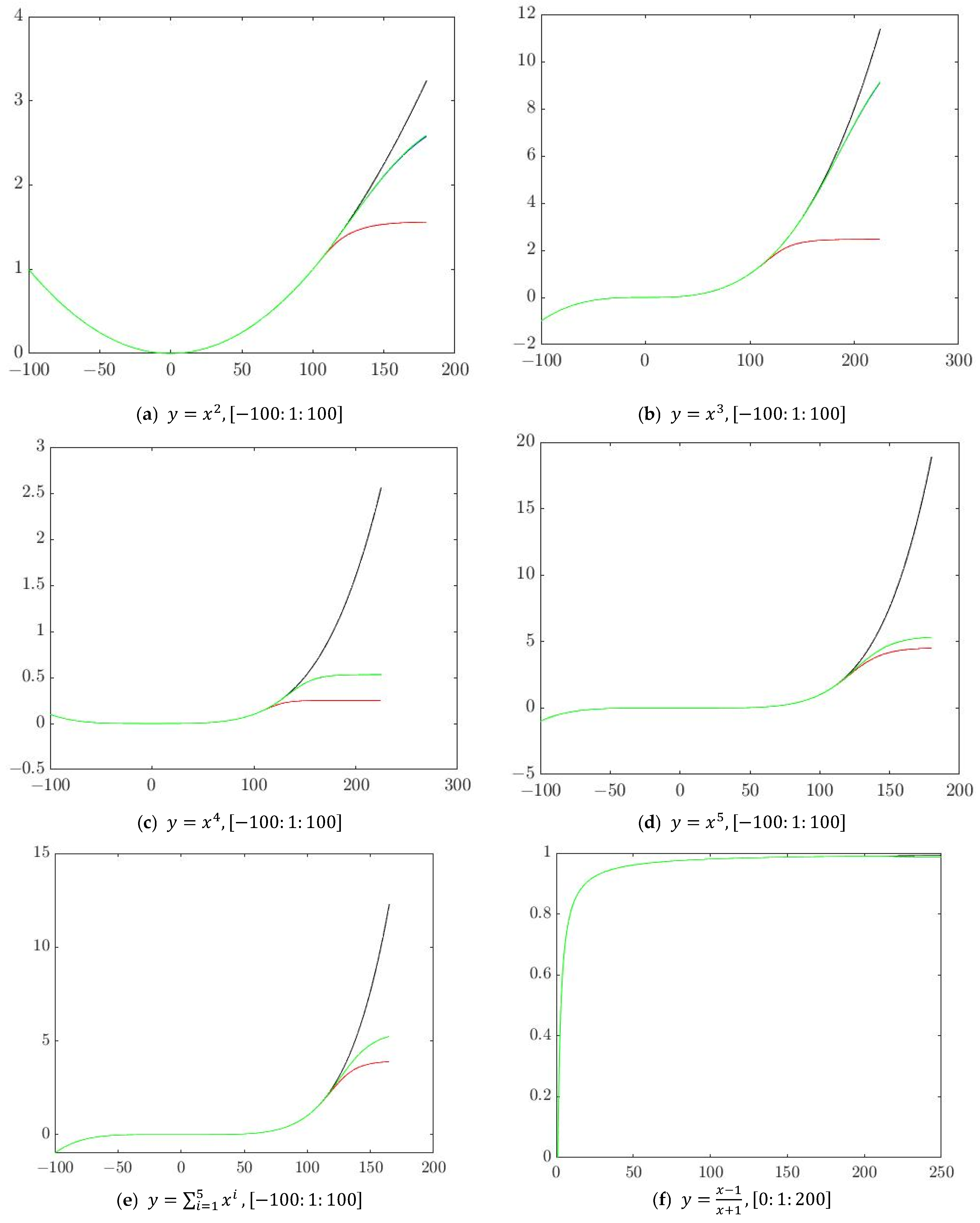

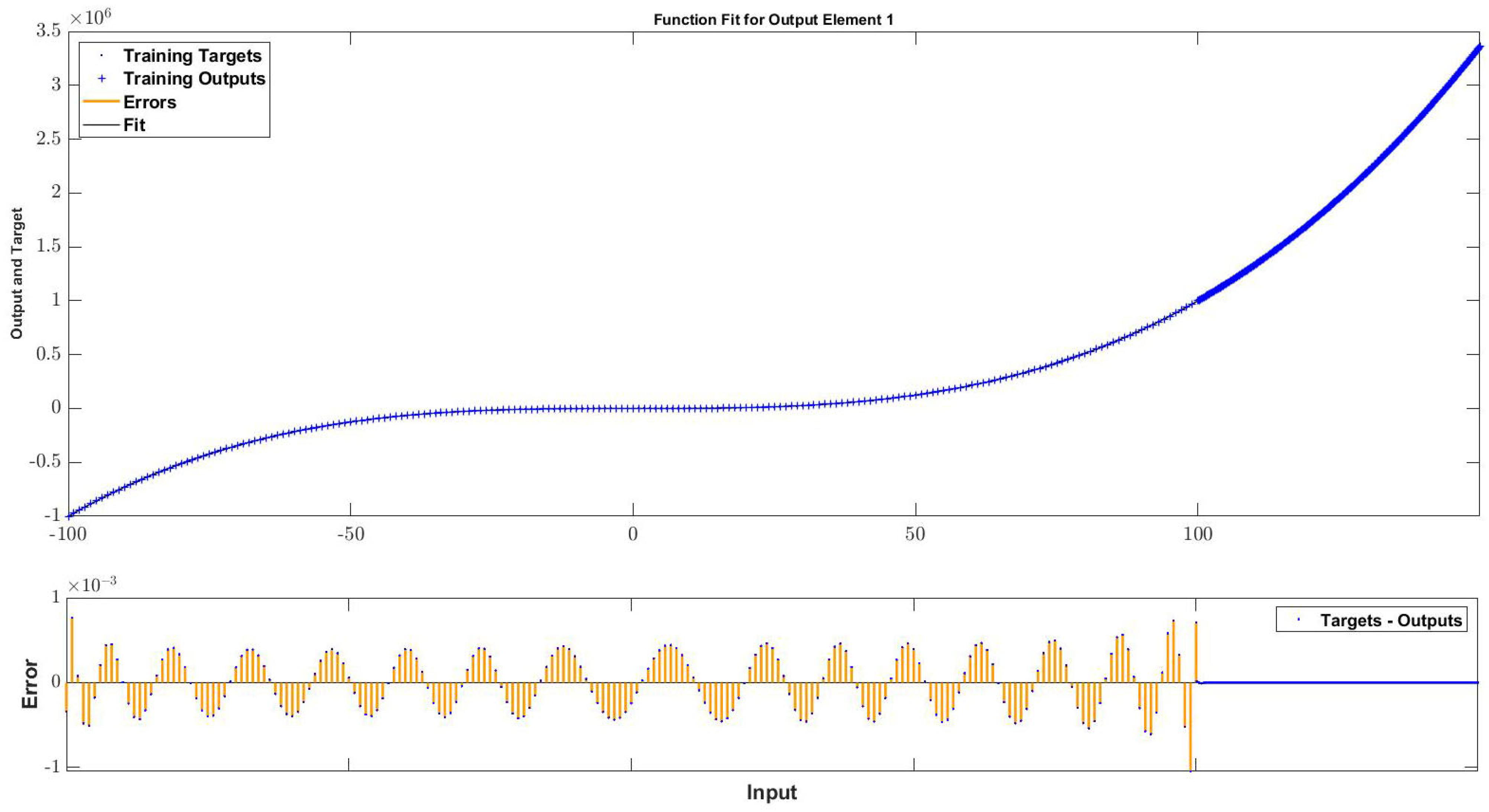
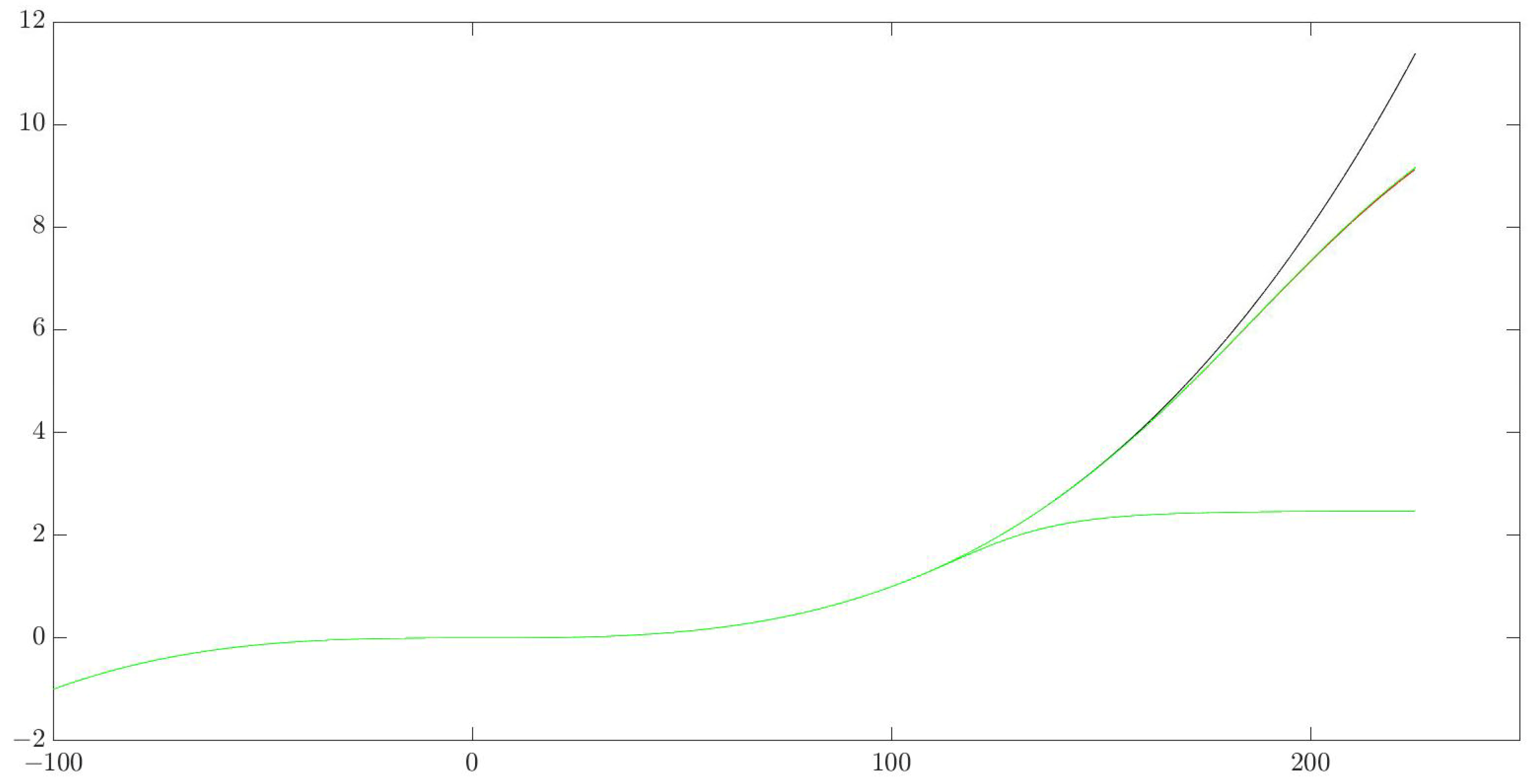

| Function | Training Sample Interval | Absolute Error at | Absolute Error at | Absolute Error at | Absolute Error at | Absolute Error at | Absolute Error at |
|---|---|---|---|---|---|---|---|
| [−100:1:100] | 2.4 × 10−1 | 1.79 × 10−4 | 1.41 × 10−4 | 1.81 × 10−4 | 3.96 | 6.85 × 101 | |
| [−100:1:100] | 1.59 × 104 | 1 × 10−2 | 1 × 10−3 | 1 × 10−2 | 7.35 × 104 | 2.34 × 105 | |
| [−100:1:100] | 5.8 × 106 | 4.84 | 4.3 × 10−1 | 3.85 | 2.35 × 107 | 1.21 × 108 | |
| [−100:1:100] | 1.43 × 109 | 1.22 × 104 | 1.92 × 102 | 2.58 × 103 | 7.86 × 109 | 6.23 × 1010 | |
| [−100:1:100] | 2.9 × 1011 | 7.21 × 105 | 3.54 × 104 | 4.12 × 105 | 2.4 × 1012 | 3.12 × 1013 | |
| [−100:1:100] | 3.06 × 1011 | 3.54 × 109 | 2.3 × 107 | 2.77 × 109 | 3.24 × 1011 | 3.13 × 1013 | |
| [0:1:200] | 3.68 | 1.96 | 3.29 × 10−6 | 3.62 × 10−6 | 5.3 × 10−1 | 4.08 | |
| [1:0.5:100] | - | - | 3 × 10−3 | 1.1 × 10−2 | 1.1 | 1.61 | |
| [−100:1:100] | 1.08 × 1034 | 6.62 × 1033 | 2.67 × 1015 | 7.1 × 1043 | 1.94 × 10130 | 1.4 × 10217 |
| Function | Training Sample Interval | Absolute Error at | Absolute Error at | Absolute Error at | Absolute Error at | Absolute Error at | Absolute Error at |
|---|---|---|---|---|---|---|---|
| [−12.8:0.1:12.8] | 0.7 | 7.77 × 10−4 | 3.06 × 10−5 | 0.78 | 2.34 | 0.67 | |
| [−12.8:0.1:12.8] | 0.42 | 0.01 | 3.49 × 10−4 | 1.52 | 0.1 | 0.35 |
| Function | Training Sample Interval | Efficiency of the Original Network | Efficiency of after Passing through the Stages of the Algorithm | MAPE of the Initial | MAPE of
after Passing through the Stages of the Algorithm |
|---|---|---|---|---|---|
| [−100:1:100] | 5.88 × 109 | 3.2 × 1012 | 0.029% | 0.00024% | |
| [−100:1:100) | 7.4 × 104 | 8.8 × 1010 | 31.8149% | 6.3355% | |
| [−100:1:100] | 7.8 × 10−1 | 3 × 107 | 31.1204% | 0.2488% | |
| [−100:1:100] | 1.03 × 10−3 | 2.73 × 103 | 51.20% | 13.79% | |
| [−100:1:100] | 1.8 × 10−8 | 1.94 × 10−7 | 44.85% | 37.54% | |
| [−100:1:100] | 2.23 × 10−8 | 1.94 × 10−7 | 50.61% | 37.34% | |
| [0:1:200] | 9.25 × 1010 | 1.79 × 1015 | 0.51% | 0.14% | |
| [1:0.5:100] | 1.32 × 1010 | 1.35 × 1013 | 7.51% | 2.56% |
| Function | Training Sample Interval | Efficiency of the Original Network | Efficiency of after Passing through the Stages of the Algorithm | MAPE of the Initial | MAPE of
after Passing through the Stages of the Algorithm |
|---|---|---|---|---|---|
| [−12.8:0.1:12.8] | 5.64 × 10−6 | 3.84 × 10−3 | 98.11% | 65.33% | |
| [−12.8:0.1:12.8] | 2.51 × 10−5 | 2.44 × 10−2 | 74.20% | 32.92% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yotov, K.; Hadzhikolev, E.; Hadzhikoleva, S.; Cheresharov, S. A Method for Extrapolating Continuous Functions by Generating New Training Samples for Feedforward Artificial Neural Networks. Axioms 2023, 12, 759. https://doi.org/10.3390/axioms12080759
Yotov K, Hadzhikolev E, Hadzhikoleva S, Cheresharov S. A Method for Extrapolating Continuous Functions by Generating New Training Samples for Feedforward Artificial Neural Networks. Axioms. 2023; 12(8):759. https://doi.org/10.3390/axioms12080759
Chicago/Turabian StyleYotov, Kostadin, Emil Hadzhikolev, Stanka Hadzhikoleva, and Stoyan Cheresharov. 2023. "A Method for Extrapolating Continuous Functions by Generating New Training Samples for Feedforward Artificial Neural Networks" Axioms 12, no. 8: 759. https://doi.org/10.3390/axioms12080759
APA StyleYotov, K., Hadzhikolev, E., Hadzhikoleva, S., & Cheresharov, S. (2023). A Method for Extrapolating Continuous Functions by Generating New Training Samples for Feedforward Artificial Neural Networks. Axioms, 12(8), 759. https://doi.org/10.3390/axioms12080759






