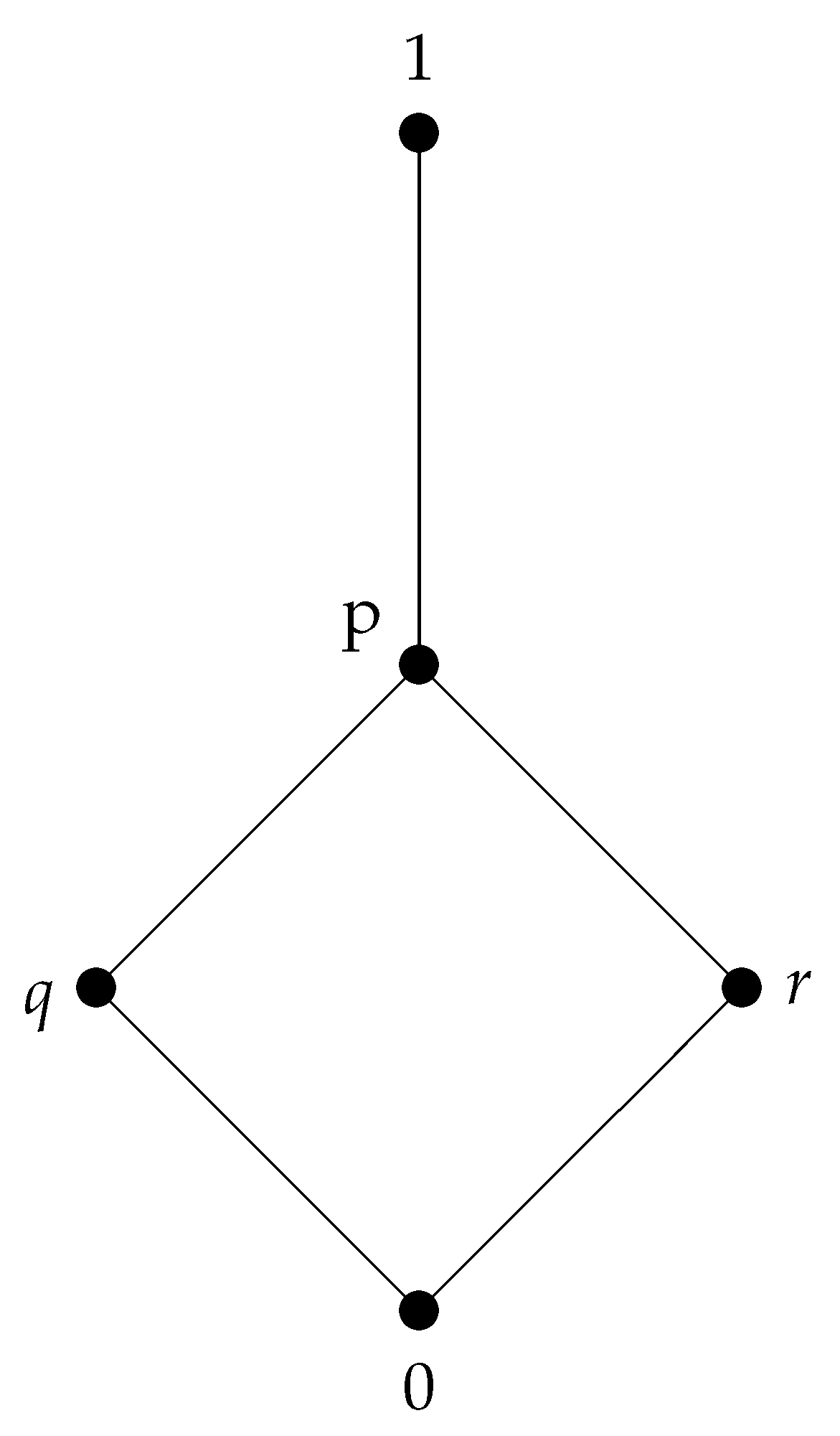
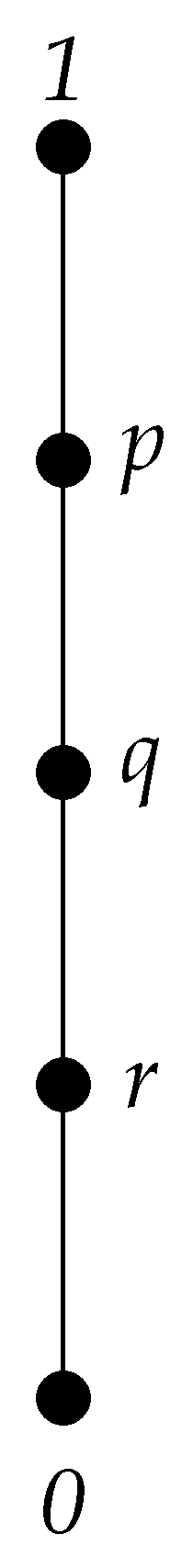3.1. -Congruences and -Ideals
Let be an -ring. Knowing the well-known connection between congruences and ideals in crisp algebras, first we define -congruences and then -ideals using this notion.
An -valued congruence on is an -valued relation on R, which is -reflexive (for every , ), symmetric, transitive and compatible with the operations in , and for all fulfills .
The following proposition yields directly from the definition.
Proposition 3. Let Θ be an Ω-valued congruence on an Ω-ring . Then, for every , such that , is a congruence relation on , and the algebra is a ring.
If
is a congruence on an
-ring
, we define
by
where
o is a nullary operation in
. Next, we define
by
Analyzing the -valued set , we can see that it “measures” the grade to which an element is equal to the constant o. Taking into account the definition of crisp two-sided ideals in the ring, it corresponds to a congruence on the ring and it consists of all elements which are congruent with o. Hence, we introduce a notion of the -two-sided ideal in -ring, as follows.
If on R is an -valued congruence on an -ring , then , where is an -valued two-sided ideal on an -ring (or -valued ideal).
There is the smallest and the greatest congruence on every -ring, and the related -ideals are described in the sequel.
The smallest congruence on an -ring is . Then, and .
The greatest congruence is , for all . Then, for all and .
In the following part, we prove that the -valued ideal is an -subring of .
Proposition 4. If is an Ω-ring, then the Ω-valued ideal is an Ω-subring of .
Proof. First, we have to prove that is compatible with the nullary, unary and two binary operations.
That is,
,
,
and
.
By being an -congruence, we have that .
By Proposition 1, we have that , and .
Hence, we have the following:
Using transitivity from the previous three formulas, we have
. Since it is valid for every
x, it is also valid for
o, so we have that
Further, by Proposition 1, we have that
and hence
. Therefore,
Finally, by
, we have that
Finally, the condition that
is a restriction to
is fulfilled:
by the definition of
, since
, and similarly for
.
Therefore, is an -subring of . □
Remark 2. Note that in the case of classical (crisp) rings, an Ω-ideal gives a characteristic function of an ideal. Indeed, since in a crisp case Ω is the chain , Θ is a weak-congruence relation (weakly reflexive, symmetric, transitive and compatible with operations). In this case, an ideal is a characteristic function with values 1 in case an element is in relation with o under Θ, which characterizes an ideal.
Since we first defined -ideals independently of the notion of -subrings and later proved that every -ideal is an -subring, in the following we give a necessary and sufficient condition for an -subring to be an -ideal.
Proposition 5. Let be an Ω-ring and an Ω-subring of . Then, the necessary and sufficient condition that is an Ω-ideal of is that there is an Ω-valued congruence Θ on , such that for all , Proof. The proof is obvious by the definition of an -ideal. □
In the following, we prove that the notion of the -ideal introduced above is cutworthy, in the sense that -ring is an -ideal if and only if all cut sets over related cut equalities are ideals of the corresponding cut-factor ring.
Theorem 4. An Ω-subring of an Ω-ring is an Ω-ideal of if and only if for every , is an ideal of the ring .
Proof. If
is an
-ideal of an
-ring
, then by the definition there is an
-valued congruence
on
, such that for all
,
and
By the cutworthy properties of -congruences, the cut for is a congruence on the subalgebra of , by -reflexivity and the fact that .
The relation
, naturally defined on classes by
is a congruence on
.
By Theorem 1,
where
is a ring and
is a congruence on it; hence,
is a ring as well.
By the definition of , for all , and looking at the cuts, for , if and only if .
It is already proved in Theorem 3 that is a subring of .
Now we show that is an ideal of . By the definition, we should prove that is a class of a congruence on , containing o.
We have that is a congruence on and the class of this congruence containing o is exactly (since for every p).
To prove the converse, let be an -subring of an -ring . Now, we have the assumption on cuts, and we have to prove that is an ideal on .
Since for every
,
is an ideal of
, elements in
are exactly some classes of
. Now we can look at the related congruences. For every
,
on
is defined by
Since
is an ideal,
is a congruence on
if and only if
if and only if
if and only if
Starting from a family of congruences
,
if and only if
Further,
if and only if
for every
if and only if
The family
is closed under intersections, since
Next, by the synthesis of this family, we define a relation
by
The supremum of ∅ in the complete lattice is 0; hence, in the case that does not belong to any for , we have that
Now,
is a symmetric, transitive and compatible
-valued relation on
(being a synthesis of the family of the relations of analogous crisp properties). It is also
-reflexive: for
,
since
is one of the values over which the supremum runs.
Finally, we prove the condition that for all , as follows. If , then and hence . Since is a congruence on , we have that and .
Hence, is an -valued congruence on , and by the construction . Therefore, is an -ideal of . □
Remark 3. If is an Ω-ideal of an Ω-ring , then the congruence Θ related to the ideal is unique. This follows from the proof of the previous theorem. Indeed, if θ is an Ω-congruence, then the unique Ω-ideal is obtained by the definition. On the other hand, if is an Ω-ideal, then the congruences obtained on all cuts , on , defined byare unique (due to the fact that ideals and congruences are in 1-1 correspondence in rings). Now the Ω-congruence θ is uniquely obtained from the family of cuts on , as in the proof of Theorem 4. By the previous remark, the -ideals and -congruences are in 1-1 correspondence in -rings.
Now, adapting the definition of
-homomorphisms in algebras from [
33], we formulate the definition of
-homomorphisms and introduce the relationship among the
-ideals,
-congruences and
-homomorphisms in
-rings.
Let and be two algebras, and and two -rings.
A function
is an
-homomorphism from
to
if for all
, and the following conditions hold:
By the general result about
-algebras (Theorem 8 in [
33]), we have the following cutworthy property of
-homomorphisms.
Proposition 6. If the function from an Ω-ring to an Ω-ring is an Ω-homomorphism, then the mapping , such that is a classical homomorphism.
Let
be an
-homomorphism from
to
. Then, an
-valued relation
defined by
is called an
-valued kernel of
.
The following proposition are here formulated for rings and follow directly from the analogous result in general algebras that are proved in [
33].
Proposition 7. Let φ be an Ω-homomorphism from Ω-ring to Ω-ring . Then, the Ω-valued kernel of φ is an Ω-valued congruence on the Ω-ring .
3.2. Structure of -Ideals
Now we look at the family of all -ideals on an -ring and we prove that it is a complete lattice.
We define a natural ordering ⩽ on the family of all -ideals:
Given two -ideals and ,
if and only if for every , .
Proposition 8. The family of all ideals on an Ω-ring is a complete lattice under ⩽.
Proof. Let be an -ring. We can note that that the relation , defined by for all , is an -congruence. Hence, the mapping for all is an -ideal, and the family of all ideals on any -ring is nonempty. Moreover, it is obvious that is the greatest of all ideals under the ordering ⩽.
Now we have to prove that the infimum of every family of -ideals on the -ring is again an ideal.
Let be a family of -ideals on the -ring. Now, we prove that the intersection of fuzzy sets is an -ideal and it is the infimum of the family . Indeed, it is easy to check that for every where for every , is the corresponding congruence to . Since is also an -congruence on , we have that is an -ideal.
Hence, the family of all -ideals on is a complete lattice. □
It is easy to check that for two congruences and , such that and , and , and for two corresponding functions and and relations determining -ideals , respectively,
if and only if if and only if .
Keeping this in mind, and the fact that , we have the following corollary.
Corollary 1. The smallest element of the family of all ideals on an Ω-ring is the ideal defined by In the following, we prove that an -valued congruence on an -ring , such that , can be regarded as an -valued equality, and can generate another -ring.
Theorem 5. Let be an Ω-valued congruence on an Ω-ring , such that . Then, is an Ω-ring as well. Moreover, for every , the mapping , defined by , is a surjective ring homomorphism.
Proof. We prove that the ring identities in the sense of the
-ring are fulfilled. For instance, to prove the distributivity on
R, using
and
, we have
Analogously, we check all other
-ring identities.
To prove that for
,
, defined by
, is a homomorphism, let
. Then,
Analogously, we check that
f is compatible with all other operations. The homomorphism is surjective, since every class
is the image of
under
f. □
Example 4. Let be a commutative Ω-ring from [1], with lattice Ω given in Figure 2, where is an algebra with , operations + and presented in Table 3 and a unary operation − defined by . The Ω-valued equality is given in Table 4. The function is determined by : .| x | o | a | b | c |
| 1 | p | u | q |
We give a construction of an Ω-ideal starting from an Ω-valued congruence Θ on R in Table 5. One could easily check that θ is an Ω-valued congruence on R satisfying for all .
Now, we define an Ω-ideal on R, by .
In the following, we give the table for (Table 6). Now, is an Ω-valued ideal.
The cuts of ν and are as follows: Now we can check the results of Theorem 4, and we obtain that for every , is an ideal of the ring .