Omega Ideals in Omega Rings and Systems of Linear Equations over Omega Fields

Abstract

Omega rings ($\mathsf{\Omega }$-rings) (and other related structures) are lattice-valued structures (with $\mathsf{\Omega }$ being the codomain lattice) defined on crisp algebras of the same type, with lattice-valued equality replacing the classical one. In this paper, $\mathsf{\Omega }$-ideals are introduced, and natural connections with $\mathsf{\Omega }$-congruences and homomorphisms are established. As an application, a framework of approximate solutions of systems of linear equations over $\mathsf{\Omega }$-fields is developed.

1. Introduction

An algebraic structure of a ring in the framework of $\mathsf{\Omega }$-structures, where $\mathsf{\Omega }$ is a complete lattice, is introduced in [1]. Therein some basic properties of $\mathsf{\Omega }$-rings are investigated and some related structures are introduced and investigated as well.

In the present paper, we develop this study further, introducing $\mathsf{\Omega }$-ideals, connecting them with $\mathsf{\Omega }$-congruences and $\mathsf{\Omega }$-homomorphisms and continuing our investigation towards the theory of solving systems of equations on $\mathsf{\Omega }$-rings, in particular on $\mathsf{\Omega }$-fields.

$\mathsf{\Omega }$-algebras are classical algebras characterized by a particular lattice-valued relation, so-called $\mathsf{\Omega }$-equality, which replaces the ordinary one; according to this generalized equality, $\mathsf{\Omega }$-algebras fulfill identities as lattice formulas.

Since $\mathsf{\Omega }$-equality is a lattice-valued function, $\mathsf{\Omega }$-algebras are objects in the lattice-valued fuzzy framework. Fuzzy algebraic structures are one of the most established topics in the theoretical research of fuzziness. Almost all aspects of classical algebraic structures are “fuzzified”. Besides fuzzy groups, which were studied by hundreds of investigators (e.g., [2,3,4,5,6]), various aspects of fuzzy rings are also investigated (e.g., [7,8,9,10,11]).

The classical framework of fuzzy algebraic structures is based on classical algebras of the corresponding types (e.g., fuzzy groups are constructed by groups, similarly fuzzy rings, etc).

Our framework is different in several aspects. First, we use a lattice as a codomain of functions representing fuzzy sets; therefore, we say that they are lattice-valued [12,13]. Further, $\mathsf{\Omega }$-algebras by definition can use wider classes of classical algebras of the corresponding type. Moreover, in the present research, we use $\mathsf{\Omega }$-valued equality which does not necessarily fulfill the separability property [1,14]. This enables us to extend our framework more, using full classes of underlying algebras of the given type, as proved in our previous study [1]. However, in general, our study follows the others with various types of $\mathsf{\Omega }$-algebras with separability [15,16].

Historically, we have to mention that this type of lattice-valued equality was first introduced by Fourman and Scott [17] for investigations in logic and set theory and later by Höhle [17,18,19,20] in the theoretical development of fuzziness; this framework also contained a separability condition and it was based on a complete Heyting algebra. Demirci, Bělohlávek and Vychodil also conducted research on algebraic structures that were equipped with a concept of similar fuzzy equality (see e.g., [21,22,23,24,25,26,27,28,29]). In this approach, traditional algebras are utilized, but instead of employing strict equality, fuzzy equality compatible with the algebra’s fundamental operations is employed.

To sum up, let us clearly underline the motivating reasons for dealing with $\mathsf{\Omega }$-algebraic structures. The first is the usage of generalized, $\mathsf{\Omega }$-valued equality instead of the classical “being equal” relation.. Indeed, in many real-life situations, data are corrupted, or they are missing, or simply there is noise in the communication. Then, being equal is often replaced by equal to some extent, and an appropriate many-valued equality can establish a connection among similar objects. In addition, the level of equality of an object to itself is understood as the belonging of this object to a domain with non-sharp boundaries. Finally, in reality, a set of equality levels for different objects need not be linearly ordered, which leads to a complete lattice as a codomain. This points to the second reason for introducing $\mathsf{\Omega }$-algebras. They are constructed on classical basic algebras, which are equipped with an $\mathsf{\Omega }$-equality. Depending on the identities that they satisfy with respect to this generalized equality, they may be, e.g., $\mathsf{\Omega }$-groups, $\mathsf{\Omega }$-quasigroups, $\mathsf{\Omega }$-rings, etc. Still, the mentioned basic algebras need not be groups, quasigroups, rings, etc. However, an essential property of $\mathsf{\Omega }$-algebras is that particular quotient structures of level subalgebras over the levels of $\mathsf{\Omega }$-equality are classical algebras fulfilling the mentioned equalities! In other words, classical groups, quasigroups, rings, etc., are hidden as quotient algebras of $\mathsf{\Omega }$-groups, $\mathsf{\Omega }$-quasigroups, $\mathsf{\Omega }$-rings, etc., respectively. Therefore, when dealing with a generalized $\mathsf{\Omega }$-structure obtained from a real situation, we can use many suitable features of the corresponding classical structure, which is present in the form of quotients.

2. Preliminaries

2.1. Some Basic Notions from Ordered and Algebraic Structures

In our approach, we mostly deal with functions whose codomain is a complete lattice, which is a partially ordered set $(\mathsf{\Omega },⩽)$ in which there are infima (the greatest lower bounds meet) and suprema (the lowest upper bounds join) for all subsets (denoted by ∧ and ∨, respectively) ([30]). The greatest (top) element is denoted by 1 and the lowest (bottom) element by 0.

In the following, we recall some well-known algebraic notions.

We consider a ring to be an algebraic structure of the type $(R,+,·,-,o)$, where R is a nonempty set, + and $·$ are binary operations, − is a unary operation and o is a constant (nullary operation), such that $(R,+,-,o)$ is a commutative group and $(R,·)$ is a semigroup and the second binary operation, $·$, is distributive with respect to the first, $+$.

We also consider algebras $(R,+,·,-,o)$ where $(+,·,-,o)$ are operations of the same type (as for rings) without special properties.

A homomorphism of two algebras of the same type $(R,+,·,-,o)$ and $(T,+$$,·,-,o)$ is a mapping $f:S\to T$, such that for all $x,y\in R$,

$f(x+y)=f\left(x\right)+f\left(y\right)$, $f(x·y)=f\left(x\right)·f\left(y\right)$, $f(-x)=-f\left(x\right)$ and $f\left(o\right)=o$.

(Although the operations on S and T are different, for simplicity we use the same symbol for the corresponding operations.)

A kernel of the homomorphism is a relation $kerf$ on R, such that $(x,y)\in kerf$ if and only if $f\left(x\right)=f\left(y\right)$.

A congruence on $\mathcal{R}$ is an equivalence relation, $\rho$ on R, which is compatible with all operations:

For $x,y,z,t\in R$, if $x\rho y$ and $z\rho t$, then $(x+z)\rho (y+t)$, $(x·z)\rho (y·t)$ and $(-x)\rho (-y)$.

The congruence class of a is defined by ${\left[a\right]}_{\rho }:=\{x\in R\mid (a,x)\in \rho \}$ as usual. The quotient ring $\mathcal{R}/\rho$ is the ring on the set of all congruence classes, where the operations are naturally defined by representatives.

A kernel of a homomorphism is a congruence relation on the domain algebra.

We formulate here the Second Isomorphism Theorem for rings [31]. Since we require it for certain proofs, it is necessary to mention it.

Theorem 1.

If ϕ and θ are congruences on a ring $\mathcal{R}$ and $\theta \subseteq \varphi$, then $\varphi /\theta$ is a congruence on $\mathcal{R}/\theta$.

2.2. $\mathsf{\Omega }$-Valued Sets and Relations

As mentioned, the main objects of this research are functions from various sets in a lattice, named in several ways throughout the literature: fuzzy sets and fuzzy relations (if the domain is a square of a set); also lattice-valued sets and relations; finally, $\mathsf{\Omega }$-valued sets and $\mathsf{\Omega }$-valued relations, if the codomain lattice is denoted by $\mathsf{\Omega }$. In order to unify the notation, throughout the text we use the last version of these, sometimes replacing $\mathsf{\Omega }$-valued with lattice valued, for the most general notions. Moreover, for several notions, we use only the prefix $\mathsf{\Omega }$ (without the word “valued”).

An $\mathsf{\Omega }$-valued set $\mu$ on a nonempty set A is a function $\mu :A\to \mathsf{\Omega }$, where $(\mathsf{\Omega },⩽)$ is a complete lattice.

If $\mu$ and $\nu$ are $\mathsf{\Omega }$-valued sets, then $\mu$ is an $\mathsf{\Omega }$-valued subset of $\nu$ (denoted by $\mu \subseteq \nu$), if for every $x\in A$, $\mu \left(x\right)⩽\nu \left(x\right)$.

For $p\in \mathsf{\Omega }$, a cut set (p-cut) of $\mu :A\to \mathsf{\Omega }$ is defined by

$${\mu }_p=\{x\in A\mid \mu \left(x\right)⩾p\}.$$

Example 1.

Let Ω be a lattice in Figure 1, and let $A=\{a,b,c,d\}$ be a set. Then, $\mu :A\to \mathsf{\Omega }$ defined by

x	a	b	c	d
$\mu \left(x\right)$	p	1	r	r

is an Ω-valued set on A.

Figure 1. Lattice $\mathsf{\Omega }$.

The cut sets of μ are ${\mu }_1=\left\{b\right\}$, ${\mu }_p={\mu }_q=\{a,b\}$ and ${\mu }_r={\mu }_0=\{a,b,c,d\}$.

An $\mathsf{\Omega }$-valued relation $\rho$ on A is an $\mathsf{\Omega }$-valued set on $A^2$.

As usual, $\rho$ is symmetric if $\rho (x,y)=\rho (y,x)$ and $\rho$ is transitive if $(x,z)\wedge \rho (z,y)⩽\rho (x,y)$ for all $x,y,z\in A$.

A symmetric and transitive $\mathsf{\Omega }$-valued relation $\rho$ on A is called an $\mathsf{\Omega }$-valued equality on A.

Let $\mu :A\to \mathsf{\Omega }$ be an $\mathsf{\Omega }$-valued set and $\rho :A^2\to \mathsf{\Omega }$ an $\mathsf{\Omega }$-valued relation on A. If for $x,y\in A$, $\rho$ and $\mu$ satisfy

$$\rho (x,y)⩽\mu \left(x\right)\wedge \mu \left(y\right),$$

(1)

then we say that $\rho$ is an $\mathsf{\Omega }$-valued relation on $\mu$ (see, e.g., [32]).

The $\mathsf{\Omega }$-valued relation $\rho$ is reflexive on $\mu$ if

$$\rho (x,x)=\mu \left(x\right) \mathrm{f}\mathrm{o}\mathrm{r} \mathrm{e}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{y} x\in A.$$

(2)

Example 2.

Let Ω be a lattice in Figure 1, and let $A=\{a,b,c,d\}$ as in Example 1. Let $E:A^2\to \mathsf{\Omega }$ be an Ω-valued relation defined in Table 1.

Table 1. $\mathsf{\Omega }$-valued equality on A.

E	a	b	c	d
a	p	q	0	0
b	q	1	0	0
c	0	0	r	r
d	0	0	r	r

One can easily check that E is an Ω-valued equality on A. It is also a reflexive Ω-valued relation on the Ω-valued set μ from Example 1.

Let $\nu :A\to \mathsf{\Omega }$ be a nonempty $\mathsf{\Omega }$-valued subset of an $\mathsf{\Omega }$-valued set $\mu :A\to \mathsf{\Omega }$, R an $\mathsf{\Omega }$-valued relation on $\mu$ and $S:A^2\to \mathsf{\Omega }$ an $\mathsf{\Omega }$-valued relation on A. Then, S is a restriction of R to $\nu$ if

$$S(x,y)=R(x,y)\wedge \nu \left(x\right)\wedge \nu \left(y\right).$$

(3)

In the following, we introduce the (known) concept of lattice-valued compatibility.

If $\mathsf{\Omega }$ is a complete lattice and $\mathcal{R}=(R,F)$ is an algebra, then the function $\mu :R\to \mathsf{\Omega }$ is said to be compatible with the operations in F if for any $f\in F$, $f:R^n\to R,n\in \mathbb{N}$, for all $a_1,\dots ,a_n\in R$ and for a nullary operation $o\in F$,

$${\displaystyle \underset{i=1}{\overset{n}{\bigwedge }}\mu \left(a_i\right)⩽\mu \left(f(a_1,\dots ,a_n)\right),\mu \left(o\right)=1.}$$

(4)

Analogously, an $\mathsf{\Omega }$-valued relation $E:R^2\to \mathsf{\Omega }$ on $\mathcal{R}$ is compatible with the operations in F if the following holds: for every n-ary operation $f\in F$, for all $a_1,\dots ,a_n,b_1,\dots ,b_n\in R$, and for constant $o\in F$,

$$\underset{i=1}{\overset{n}{\bigwedge }}E(a_i,b_i)⩽E(f(a_1,\dots ,a_n),f(b_1,\dots ,b_n));E(o,o)=1.$$

(5)

Throughout the text, we relate some algebraic properties of lattice-valued objects with their cuts, as follows: a property $\mathfrak{P}$ of an $\mathsf{\Omega }$-valued structure A is said to be cutworthy if the analog crisp property holds for every cut-structure $A_p$, $p\in \mathsf{\Omega }$.

2.3. $\mathsf{\Omega }$-Rings

An $\mathsf{\Omega }$-set is an ordered pair $(R,E)$, where R is a nonempty set and E an $\mathsf{\Omega }$-valued equality on A [17].

Remark 1.

There is a difference between an $\mathsf{\Omega }$-valued set defined in the previous section and an $\mathsf{\Omega }$-set as defined here. The former is only a function from a set on a lattice Ω and the latter is a pair consisting of a set and a particular lattice-valued relation on this set.

If $(R,E)$ is an $\mathsf{\Omega }$-set, the related $\mathsf{\Omega }$-valued set on R, denoted by $\mu$, is defined by

$$\mu \left(x\right):=E(x,x).$$

(6)

E is an $\mathsf{\Omega }$-valued reflexive relation on $\mu$, as defined by (1) (to be more precise, E is an $\mathsf{\Omega }$-valued equality on $\mu$.

If $\mathcal{R}=(R,F)$ is an algebra and $E:R^2\to \mathsf{\Omega }$ an $\mathsf{\Omega }$-valued equality on R compatible with the operations in F, then $\overline{\mathcal{R}}=(\mathcal{R},E)$ is an $\mathsf{\Omega }$-algebra. Algebra $\mathcal{R}$ is called the underlying, basic algebra of $\overline{\mathcal{R}}$.

Let $(\mathcal{R},E)$ be an $\mathsf{\Omega }$-algebra and $t_1(x_1,\dots ,x_n)\approx t_2(x_1,\dots ,x_n)$, and briefly let $t_1\approx t_2$ be an identity in the type of $\mathcal{R}$. Then, we can state that $(\mathcal{R},E)$ satisfies identity $t_1\approx t_2$ if

$$\underset{i=1}{\overset{n}{\bigwedge }}\mu \left(b_i\right)⩽E(t_1(b_1,\dots ,b_n),t_2(b_1,\dots ,b_n)),$$

(7)

for all $b_1,\dots ,b_n\in A$ and the term operations on $\mathcal{R}$ corresponding to terms $t_1$ and $t_2$, respectively.

We continue with the main structure of the present research. An $\mathsf{\Omega }$-ring is an $\mathsf{\Omega }$-algebra $\overline{\mathcal{R}}=(\mathcal{R},E)$, where $\mathcal{R}=(R,+,·,-,o)$ is an algebra with two binary operations ($·,+$), a unary operation (−) and a constant (o), so that the following identities hold in the sense of (7):

$$u+(v+w)\approx (u+v)+w$$

$$u+o\approx u,o+u\approx u$$

$$u+(-u)\approx o,(-u)+u\approx o$$

$$u+v\approx v+u$$

$$u·(v·w)\approx (u·v)·w$$

$$u·(v+w)\approx (u·v)+(u·w)$$

$$(v+w)·u\approx (v·u)+(w·u).$$

We have $E(o,o)=\mu \left(o\right)=1$.

Next, we present some cut properties of $\mathsf{\Omega }$-rings. These also hold for $\mathsf{\Omega }$-groups and generally for all $\mathsf{\Omega }$-algebras as well [14].

Theorem 2.

Let $\overline{\mathcal{R}}=(\mathcal{R},E)$ be an Ω-algebra of the type $(+,·,-,o)$. Then, $\overline{\mathcal{R}}$ is an Ω-ring if and only if for every $p\in \mathsf{\Omega }$ the quotient structure ${\mu }_p/E_p$ is a ring.

Example 3.

Let $A=\{a,b,c,d\}$, operations + and $·$ be as presented in Table 2 and the unary operation − defined by $-x:=x$, and let b be a constant (nullary operation). Let $E:A^2\to \mathsf{\Omega }$ be the Ω-relation defined in Example 2 (Table 1), where Ω is a lattice in Figure 1. μ is Ω-set from Example 2 and E is symmetric, transitive and reflexive on μ.

Table 2. (a) Binary operation + on A. (b) Binary operation $·$ on A.

(a)
+	a	b	c	d
a	b	a	d	c
b	a	b	d	d
c	c	d	b	b
d	d	c	a	a
(b)
$·$	a	b	c	d
a	a	b	a	b
b	b	b	b	a
c	a	a	d	c
d	b	b	c	d

The Ω-relation E is compatible since all the cuts are congruence relations on cuts of μ.

All the factor cuts are rings. Indeed, ${\mu }_1/E_1$ is a one-element ring, isomorphic to $\left\{b\right\}$, ${\mu }_p/E_p$ is a two-element ring isomorphic to subring $\{a,b\}$. ${\mu }_q/E_q$ is also a one-element ring. ${\mu }_r/E_r$ is a two-element ring $\left\{\right\{a,b\},\{c,d\left\}\right\}$. Finally, ${\mu }_0/E_0$ is also a one-element ring with one element being the class $\{a,b,c,d\}$.

Hence, the structure $(A,E)$ is an Ω-ring by Theorem 2.

We mention some basic properties of $\mathsf{\Omega }$-rings (proved in [1]) that we shall need in some proofs.

Proposition 1

([1]). Let $\overline{\mathcal{R}}=(\mathcal{R},E)$ be an Ω-ring where $\mathcal{R}=(R,+,·,-,o)$.

Then, the following hold in the sense of (7):

(i)

$u·o\approx o$, $o·u\approx o$;

(ii)

$u·(-v)\approx -(v·u)$;

(iii)

$(-u)·v\approx -(v·u)$.

An $\mathsf{\Omega }$-ring is commutative if $u·v\approx v·u$.

If ${\mathcal{R}}_{\iota }=(R,+,·,-,o,\iota )$ is an algebra with two binary, one unary and two nullary operations o and $\iota$, then $({\mathcal{R}}_{\iota },E)$ is an $\mathsf{\Omega }$-ring with identity if $\left(\right(R,+,·,-,o),E)$ is an $\mathsf{\Omega }$-ring and if $u·\iota \approx u,\iota ·u\approx u$. An $\mathsf{\Omega }$-ring with identity is called an $\mathsf{\Omega }$-field if ${\mathcal{R}}^o=(R\setminus \left\{o\right\},·{,}^{-1},\iota )$ (where ${}^{-1}$ is a unary operation) is an $\mathsf{\Omega }$-group, where $E^o$ is the restriction of E to $R\setminus \left\{o\right\}$.

The following proposition is proved in [1].

Proposition 2

([1]). An Ω-ring with identity ${\mathcal{R}}_{\iota }=((R,+,·,-,o,\iota ),E)$ is an Ω-field if and only if for every $p\in \mathsf{\Omega }$, the factor ${\mu }_p/E_p$ is a field.

If $\overline{\mathcal{R}}=(\mathcal{R},E)$ and ${\overline{\mathcal{R}}}_1=(\mathcal{R},E^{{\mu }_1})$ are $\mathsf{\Omega }$-rings, we say that ${\overline{\mathcal{R}}}_1$ is an $\mathsf{\Omega }$-subring of the $\mathsf{\Omega }$-ring $\overline{\mathcal{R}}$ if $E^{{\mu }_1}$ is a restriction of E to the $\mathsf{\Omega }$-valued function ${\mu }_1$ of $\mathcal{R}$, determined by $E^{{\mu }_1}$.

Hence, $E^{{\mu }_1}(x,y)=E(x,y)\wedge {\mu }_1\left(x\right)\wedge {\mu }_1\left(y\right)$ for all $x,y\in R$.

Theorem 3

([1]). Let $\overline{\mathcal{R}}=(\mathcal{R},E)$ be an Ω-ring and $\overline{\mathcal{S}}=(\mathcal{R},E^{\nu })$ an Ω-subring of $\overline{\mathcal{R}}$. Then, for every $p\in \mathsf{\Omega }$, the ring ${\nu }_p/E_p^{\nu }$ is, up to an isomorphism, a subring of the ring ${\mu }_p/E_p$.

3. Results

3.1. $\mathsf{\Omega }$-Congruences and $\mathsf{\Omega }$-Ideals

Let $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$ be an $\mathsf{\Omega }$-ring. Knowing the well-known connection between congruences and ideals in crisp algebras, first we define $\mathsf{\Omega }$-congruences and then $\mathsf{\Omega }$-ideals using this notion.

An $\mathsf{\Omega }$-valued congruence on $\overline{\mathcal{R}}$ is an $\mathsf{\Omega }$-valued relation $\mathsf{\Theta }:R^2\to \mathsf{\Omega }$ on R, which is $\mu$-reflexive (for every $x\in R$, $\mathsf{\Theta }(x,x)=E^{\mu }(x,x)$), symmetric, transitive and compatible with the operations in $\mathcal{R}$, and for all $x,y\in R$ fulfills $\mathsf{\Theta }(x,y)⩾E^{\mu }(x,y)$.

The following proposition yields directly from the definition.

Proposition 3.

Let Θ be an Ω-valued congruence on an Ω-ring $\overline{\mathcal{R}}$. Then, for every $p\in \mathsf{\Omega }$, such that ${\mu }_p\ne \varnothing$, ${\mathsf{\Theta }}_p$ is a congruence relation on ${\mu }_p$, and the algebra ${\mu }_p/{\mathsf{\Theta }}_p$ is a ring.

If $\mathsf{\Theta }$ is a congruence on an $\mathsf{\Omega }$-ring $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$, we define $\nu :R\to \mathsf{\Omega }$ by

$$\nu \left(x\right):=\mathsf{\Theta }(o,x),$$

(8)

where o is a nullary operation in $\mathcal{R}$. Next, we define $E^{\nu }:R^2\to \mathsf{\Omega }$ by

$$E^{\nu }(x,y):=E^{\mu }(x,y)\wedge \nu \left(x\right)\wedge \nu \left(y\right).$$

(9)

Analyzing the $\mathsf{\Omega }$-valued set $\nu$, we can see that it “measures” the grade to which an element is equal to the constant o. Taking into account the definition of crisp two-sided ideals in the ring, it corresponds to a congruence on the ring and it consists of all elements which are congruent with o. Hence, we introduce a notion of the $\mathsf{\Omega }$-two-sided ideal in $\mathsf{\Omega }$-ring, as follows.

If $\mathsf{\Theta }:R^2\to \mathsf{\Omega }$ on R is an $\mathsf{\Omega }$-valued congruence on an $\mathsf{\Omega }$-ring $\overline{\mathcal{R}}$, then $\overline{\mathcal{P}}=(\mathcal{R},E^{\nu })$, where $\nu \left(x\right):=\mathsf{\Theta }(o,x)$ is an $\mathsf{\Omega }$-valued two-sided ideal on an $\mathsf{\Omega }$-ring (or $\mathsf{\Omega }$-valued ideal).

There is the smallest and the greatest congruence on every $\mathsf{\Omega }$-ring, and the related $\mathsf{\Omega }$-ideals $\overline{\mathcal{P}}=(\mathcal{R},E^{\nu })$ are described in the sequel.

The smallest congruence on an $\mathsf{\Omega }$-ring is $\mathsf{\Theta }(x,y)=E^{\mu }(x,y)$. Then, $\nu \left(x\right):=E^{\mu }(o,x)$ and $E^{\nu }(x,y):=E^{\mu }(x,y)\wedge E^{\mu }(o,x)\wedge E^{\mu }(o,y)$.

The greatest congruence is $\mathsf{\Theta }(x,y)=1$, for all $x,y\in R$. Then, $\nu \left(x\right)=1$ for all $x\in R$ and $E^{\nu }(x,y):=E^{\mu }(x,y)$.

In the following part, we prove that the $\mathsf{\Omega }$-valued ideal is an $\mathsf{\Omega }$-subring of $\overline{\mathcal{R}}$.

Proposition 4.

If $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$ is an Ω-ring, then the Ω-valued ideal $\overline{\mathcal{P}}=(\mathcal{R},E^{\nu })$ is an Ω-subring of $\overline{\mathcal{R}}$.

Proof. 

First, we have to prove that $\nu :R\to \mathsf{\Omega }$ is compatible with the nullary, unary and two binary operations.

That is, $\nu (x+y)⩾\nu \left(x\right)\wedge \nu \left(y\right)$, $\nu (x·y)⩾\nu \left(x\right)\wedge \nu \left(y\right)$, $\nu (-x)⩾\nu \left(x\right)$ and $\nu \left(o\right)=1$.

$$\nu \left(o\right)=\mathsf{\Theta }(o,o)=\mu \left(o\right)=1.$$

By $\mathsf{\Theta }$ being an $\mathsf{\Omega }$-congruence, we have that $\mathsf{\Theta }(x,o)⩽\mathsf{\Theta }(-x,-o)$.

By Proposition 1, we have that $\mu \left(x\right)\wedge \mu \left(o\right)⩽E^{\mu }(-(x·o),(-x)·o)$, $\mu \left(x\right)\wedge \mu \left(o\right)⩽E^{\mu }(-(x·o),x·(-o))$ and $\mu \left(x\right)⩽E^{\mu }(x·o,o)$.

Hence, we have the following:

$$\mu \left(x\right)⩽E(x·o,o)⩽E(-(x·o),-o)$$

$$\mu \left(x\right)⩽\mu (-x)⩽E\left(\right(-x)·o,o)$$

$$\mu \left(x\right)⩽\mu (-x)⩽E(-(x·o),(-x)·o).$$

Using transitivity from the previous three formulas, we have

$\mu \left(x\right)⩽E(o,-o)$. Since it is valid for every x, it is also valid for o, so we have that

$$E(o,-o)=1.$$

Since

$$E⩽\mathsf{\Theta },$$

we have that

$$\mathsf{\Theta }(o,-o)=1$$

Now,

$$\mathsf{\Theta }(x,o)⩽\mathsf{\Theta }(-x,-o)\wedge \mathsf{\Theta }(-o,o)⩽\mathsf{\Theta }(-x,o).$$

Hence,

$$\nu \left(x\right)⩽\nu (-x).$$

Further, by Proposition 1, we have that $E(o·o,o)=1$ and hence $\mathsf{\Theta }(o·o,o)=1$. Therefore,

$$\nu \left(x\right)\wedge \nu \left(y\right)=\mathsf{\Theta }(x,o)\wedge \mathsf{\Theta }(y,o)⩽\mathsf{\Theta }(x·y,o·o)\wedge 1=\mathsf{\Theta }(x·y,o·o)\wedge \mathsf{\Theta }(o·o,o)⩽\mathsf{\Theta }(x·y,o)=\nu (x·y).$$

Finally, by $1=E(o+o,o)⩽\mathsf{\Theta }(o+o,o)$, we have that

$$\nu \left(x\right)\wedge \nu \left(y\right)=\mathsf{\Theta }(x,o)\wedge \mathsf{\Theta }(y,o)⩽\mathsf{\Theta }(x+y,o+o)\wedge \mathsf{\Theta }(o+o,o)⩽\mathsf{\Theta }(x+y,o)=\nu (x+y).$$

Finally, the condition that $E^{\nu }(x,y)$ is a restriction to $E^{\mu }(x,y)$ is fulfilled:

$$E^{\nu }(x,y)=E^{\mu }(x,y)\wedge E^{\nu }(x,x)\wedge E^{\nu }(y,y),$$

by the definition of $E^{\nu }$, since $E^{\nu }(x,x)=E^{\mu }(x,x)\wedge \mathsf{\Theta }(o,x)=\mathsf{\Theta }(o,x)$, and similarly for $E^{\nu }(y,y)$.

Therefore, $\overline{\mathcal{P}}$ is an $\mathsf{\Omega }$-subring of $\overline{\mathcal{R}}$. □

Remark 2.

Note that in the case of classical (crisp) rings, an Ω-ideal gives a characteristic function of an ideal. Indeed, since in a crisp case Ω is the chain $\{0,1\}$, Θ is a weak-congruence relation (weakly reflexive, symmetric, transitive and compatible with operations). In this case, an ideal is a characteristic function with values 1 in case an element is in relation with o under Θ, which characterizes an ideal.

Since we first defined $\mathsf{\Omega }$-ideals independently of the notion of $\mathsf{\Omega }$-subrings and later proved that every $\mathsf{\Omega }$-ideal is an $\mathsf{\Omega }$-subring, in the following we give a necessary and sufficient condition for an $\mathsf{\Omega }$-subring to be an $\mathsf{\Omega }$-ideal.

Proposition 5.

Let $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$ be an Ω-ring and $\overline{\mathcal{I}}=(\mathcal{R},E^{\nu })$ an Ω-subring of $\overline{\mathcal{R}}$. Then, the necessary and sufficient condition that $\overline{\mathcal{I}}$ is an Ω-ideal of $\overline{\mathcal{R}}$ is that there is an Ω-valued congruence Θ on $\overline{\mathcal{R}}$, such that for all $x,y\in R$,

$$E^{\nu }(x,y)=E^{\mu }(x,y)\wedge \mathsf{\Theta }(o,x)\wedge \mathsf{\Theta }(o,y).$$

(10)

Proof. 

The proof is obvious by the definition of an $\mathsf{\Omega }$-ideal. □

In the following, we prove that the notion of the $\mathsf{\Omega }$-ideal introduced above is cutworthy, in the sense that $\mathsf{\Omega }$-ring is an $\mathsf{\Omega }$-ideal if and only if all cut sets over related cut equalities are ideals of the corresponding cut-factor ring.

Theorem 4.

An Ω-subring $\overline{\mathcal{I}}=(\mathcal{R},E^{\nu })$ of an Ω-ring $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$ is an Ω-ideal of $\overline{\mathcal{R}}$ if and only if for every $p\in \mathsf{\Omega }$, ${\nu }_p/E_p^{\nu }$ is an ideal of the ring ${\mu }_p/E_p^{\mu }$.

Proof. 

If $\overline{\mathcal{I}}=(\mathcal{R},E^{\nu })$ is an $\mathsf{\Omega }$-ideal of an $\mathsf{\Omega }$-ring $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$, then by the definition there is an $\mathsf{\Omega }$-valued congruence $\mathsf{\Theta }$ on $\overline{\mathcal{R}}$, such that for all $x,y\in R$, $E^{\mu }(x,y)⩽\mathsf{\Theta }(x,y)$ and

$$E^{\nu }(x,y)=E^{\mu }(x,y)\wedge \mathsf{\Theta }(o,x)\wedge \mathsf{\Theta }(o,y).$$

By the cutworthy properties of $\mathsf{\Omega }$-congruences, the cut ${\mathsf{\Theta }}_p$ for $p\in \mathsf{\Omega }$ is a congruence on the subalgebra ${\mu }_p$ of $\mathcal{R}$, by $\mu$-reflexivity and the fact that $E_p^{\mu }\subseteq {\mathsf{\Theta }}_p$.

The relation ${\mathsf{\Theta }}_p/E_p^{\mu }$, naturally defined on classes by

$$({\left[x\right]}_{E_p^{\mu }},{\left[y\right]}_{E_p^{\mu }})\in {\mathsf{\Theta }}_p/E_p^{\mu }\mathrm{i}\mathrm{f} \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{o}\mathrm{n}\mathrm{l}\mathrm{y} \mathrm{i}\mathrm{f}(x,y)\in {\mathsf{\Theta }}_p,$$

(11)

is a congruence on ${\mu }_p/E_p^{\mu }$.

By Theorem 1,

$${\mu }_p/E_p^{\mu }/{\mathsf{\Theta }}_p/E_p^{\mu }\cong {\mu }_p/{\mathsf{\Theta }}_p,$$

where ${\mu }_p/E_p^{\mu }$ is a ring and ${\mathsf{\Theta }}_p/E_p^{\mu }$ is a congruence on it; hence, ${\mu }_p/{\mathsf{\Theta }}_p$ is a ring as well.

By the definition of $\nu$, $\nu \left(x\right)=\mathsf{\Theta }(o,x)$ for all $x\in R$, and looking at the cuts, for $p\in \mathsf{\Omega }$, $x\in {\nu }_p$ if and only if $\mathsf{\Theta }(o,x)⩾p$.

It is already proved in Theorem 3 that ${\nu }_p/E_p^{\nu }$ is a subring of ${\mu }_p/E_p^{\mu }$.

Now we show that ${\nu }_p/E_p^{\nu }$ is an ideal of ${\mu }_p/E_p^{\mu }$. By the definition, we should prove that ${\nu }_p/E_p^{\nu }$ is a class of a congruence on ${\mu }_p/E_p^{\mu }$, containing o.

We have that ${\mathsf{\Theta }}_p/E_p^{\mu }$ is a congruence on ${\mu }_p/E_p^{\mu }$ and the class of this congruence containing o is exactly ${\nu }_p/E_p^{\nu }$ (since $o\in {\nu }_p$ for every p).

To prove the converse, let $\overline{\mathcal{P}}=(\mathcal{P},E^{\nu })$ be an $\mathsf{\Omega }$-subring of an $\mathsf{\Omega }$-ring $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$. Now, we have the assumption on cuts, and we have to prove that $\overline{\mathcal{P}}$ is an ideal on $\overline{\mathcal{R}}$.

Since for every $p\in \mathsf{\Omega }$, ${\nu }_p/E_p^{\nu }$ is an ideal of ${\mu }_p/E_p^{\mu }$, elements in ${\nu }_p/E_p^{\nu }$ are exactly some classes of ${\mu }_p/E_p^{\mu }$. Now we can look at the related congruences. For every $p\in \mathsf{\Omega }$, ${\mathsf{\Theta }}_p$ on ${\mu }_p/E_p^{\mu }$ is defined by

$${\left[x\right]}_{E_p^{\mu }}{\mathsf{\Theta }}_p{\left[y\right]}_{E_p^{\mu }}\mathrm{i}\mathrm{f} \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{o}\mathrm{n}\mathrm{l}\mathrm{y} \mathrm{i}\mathrm{f}{\left[x\right]}_{E_p^{\mu }}+(-{\left[y\right]}_{E_p^{\mu }})\in {\nu }_p/E_p^{\nu }.$$

Since ${\nu }_p/E_p^{\nu }$ is an ideal, ${\mathsf{\Theta }}_p$ is a congruence on ${\mu }_p/E_p^{\mu }.$

$${\left[x\right]}_{E_p^{\mu }}+(-{\left[y\right]}_{E_p^{\mu }})\in {\nu }_p/E_p^{\nu }$$

if and only if

$${[x+(-y)]}_{E_p^{\mu }}\in {\nu }_p/E_p^{\nu },$$

if and only if

$$x+(-y)\in {\nu }_p,$$

if and only if

$$\nu (x+(-y\left)\right)⩾p.$$

Starting from a family of congruences $\{{\mathsf{\Theta }}_i\mid i\in I\subseteq \mathsf{\Omega }\}$,

$${\left[x\right]}_{E_i^{\mu }}{\mathsf{\Theta }}_i{\left[y\right]}_{E_i^{\mu }}$$

if and only if

$$\nu (x+(-y\left)\right)⩾i.$$

Further,

$${\left[x\right]}_{E_i^{\mu }}{\mathsf{\Theta }}_i{\left[y\right]}_{E_i^{\mu }}$$

if and only if

$$\nu (x+(-y))⩾\underset{i\in I}{\bigvee }i,$$

for every $i\in I$ if and only if

$${\left[x\right]}_{E_i^{\mu }}{\mathsf{\Theta }}_{{\bigvee }_{i\in I}i}{\left[y\right]}_{E_i^{\mu }}.$$

The family $\{{\mathsf{\Theta }}_i\mid i\in \mathsf{\Omega }\}$ is closed under intersections, since

$$\bigcap _{i\in I}{\mathsf{\Theta }}_i={\mathsf{\Theta }}_{{\bigvee }_{i\in I}i.}$$

Next, by the synthesis of this family, we define a relation $\mathsf{\Theta }:R^2\to \mathsf{\Omega }$ by

$$\mathsf{\Theta }(x,y):=\bigvee \{p\mid ({\left[x\right]}_{E_p^{\mu }},{\left[y\right]}_{E_p^{\mu }})\in {\mathsf{\Theta }}_p\}.$$

The supremum of ∅ in the complete lattice $\mathsf{\Omega }$ is 0; hence, in the case that $(x,y)$ does not belong to any ${\mathsf{\Theta }}_p$ for $p\in \mathsf{\Omega }$, we have that $\mathsf{\Theta }(x,y)=0$

Now, $\mathsf{\Theta }$ is a symmetric, transitive and compatible $\mathsf{\Omega }$-valued relation on $\overline{\mathcal{R}}$ (being a synthesis of the family of the relations of analogous crisp properties). It is also $\mu$-reflexive: for $x\in R$,

$$\mathsf{\Theta }(x,x)=\bigvee \{p\mid ({\left[x\right]}_{E_p^{\mu }},{\left[x\right]}_{E_p^{\mu }})\in {\mathsf{\Theta }}_p\}=\bigvee \{p\mid x\in {\mu }_p\}=\mu \left(x\right)=E^{\mu }(x,x),$$

since $\mu \left(x\right)$ is one of the values over which the supremum runs.

Finally, we prove the condition that $E^{\mu }(x,y)⩽\mathsf{\Theta }(x,y)$ for all $x,y\in R$, as follows. If $E^{\mu }(x,y)=p$, then $(x,y)\in E_p$ and hence ${\left[x\right]}_{e_p^{\mu }}={\left[y\right]}_{e_p^{\mu }}$. Since ${\mathsf{\Theta }}_p$ is a congruence on ${\mu }_p/E_p^{\mu }$, we have that $({\left[x\right]}_{e_p^{\mu }},{\left[y\right]}_{e_p^{\mu }})\in {\mathsf{\Theta }}_p$ and $\mathsf{\Theta }(x,y)⩾p$.

Hence, $\mathsf{\Theta }$ is an $\mathsf{\Omega }$-valued congruence on $\overline{\mathcal{R}}$, and by the construction $\mathsf{\Theta }(x,o)=\nu \left(x\right)=E^{\nu }(x,x)$. Therefore, $\overline{\mathcal{I}}$ is an $\mathsf{\Omega }$-ideal of $\overline{\mathcal{R}}$. □

Remark 3.

If $\overline{\mathcal{I}}=(\mathcal{R},E^{\nu })$ is an Ω-ideal of an Ω-ring $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$, then the congruence Θ related to the ideal $\overline{\mathcal{I}}$ is unique. This follows from the proof of the previous theorem. Indeed, if θ is an Ω-congruence, then the unique Ω-ideal is obtained by the definition. On the other hand, if $\overline{\mathcal{I}}=(\mathcal{R},E^{\nu })$ is an Ω-ideal, then the congruences obtained on all cuts $p\in \mathsf{\Omega }$, ${\mathsf{\Theta }}_p$ on ${\mu }_p/E_p^{\mu }$, defined by

$${\left[x\right]}_{E_p^{\mu }}{\mathsf{\Theta }}_p{\left[y\right]}_{E_p^{\mu }}if and only if{\left[x\right]}_{E_p^{\mu }}+(-{\left[y\right]}_{E_p^{\mu }})\in {\nu }_p/E_p^{\nu }$$

are unique (due to the fact that ideals and congruences are in 1-1 correspondence in rings). Now the Ω-congruence θ is uniquely obtained from the family of cuts on ${\mu }_p/E_p^{\mu }$, as in the proof of Theorem 4.

By the previous remark, the $\mathsf{\Omega }$-ideals and $\mathsf{\Omega }$-congruences are in 1-1 correspondence in $\mathsf{\Omega }$-rings.

Now, adapting the definition of $\mathsf{\Omega }$-homomorphisms in algebras from [33], we formulate the definition of $\mathsf{\Omega }$-homomorphisms and introduce the relationship among the $\mathsf{\Omega }$-ideals, $\mathsf{\Omega }$-congruences and $\mathsf{\Omega }$-homomorphisms in $\mathsf{\Omega }$-rings.

Let $\mathcal{R}=(R,+,·,-,o)$ and $\mathcal{S}=(S,+,·,-,o)$ be two algebras, and $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$ and $\overline{\mathcal{S}}=(\mathcal{S},E^{\nu })$ two $\mathsf{\Omega }$-rings.

A function $\phi :R\to S$ is an $\mathsf{\Omega }$-homomorphism from $\overline{\mathcal{R}}$ to $\overline{\mathcal{S}}$ if for all $a,b\in R$, and the following conditions hold:

$$E^{\mu }(a,b)⩽E^{\nu }(\phi \left(a\right),\phi \left(b\right)),$$

$$E^{\mu }(a,a)=E^{\nu }(\phi \left(a\right),\phi \left(a\right));$$

$$\begin{array}{c}\hfill \mu \left(a\right)\wedge \mu \left(b\right)⩽E^{\nu }(\phi (a+b),\phi \left(a\right)+\phi \left(b\right));\\ \hfill \mu \left(a\right)\wedge \mu \left(b\right)⩽E^{\nu }(\phi (a·b),\phi \left(a\right)·\phi \left(b\right))\\ \hfill \mu \left(a\right)⩽E^{\nu }(\phi (-a),-\phi \left(a\right));\\ \hfill \mu \left(o\right)⩽E^{\nu }(\phi \left(o\right),o)\end{array}$$

$$\phi \left(a\right)+\phi \left(b\right)\in \phi \left(R\right);\phi \left(a\right)·\phi \left(b\right)\in \phi \left(R\right)\mathrm{a}\mathrm{n}\mathrm{d}-\phi \left(a\right)\in \phi \left(R\right).$$

By the general result about $\mathsf{\Omega }$-algebras (Theorem 8 in [33]), we have the following cutworthy property of $\mathsf{\Omega }$-homomorphisms.

Proposition 6.

If the function $\phi :R\to S$ from an Ω-ring $(\mathcal{R},E^{\mu })$ to an Ω-ring $(\mathcal{S},E^{\nu })$ is an Ω-homomorphism, then the mapping $\overline{\phi }:{\mu }_p^E/E_p\to {\mu }_p^G/G_p$, such that $\overline{\phi }\left({\left[x\right]}_{E_p}\right):={\left[\phi \left(x\right)\right]}_{G_p}$ is a classical homomorphism.

Let $\phi$ be an $\mathsf{\Omega }$-homomorphism from $(R,E^{\mu })$ to $(S,E^{\nu })$. Then, an $\mathsf{\Omega }$-valued relation ${\ker }_{\mathsf{\Omega }}\phi :R^2\to \mathsf{\Omega }$ defined by

$${\ker }_{\mathsf{\Omega }}\phi (a,b)=E^{\nu }(\phi \left(a\right),\phi \left(b\right))\wedge \mu \left(a\right)\wedge \mu \left(b\right),\mathrm{f}\mathrm{o}\mathrm{r} \mathrm{a}\mathrm{l}\mathrm{l} a,b\in R,$$

(12)

is called an $\mathsf{\Omega }$-valued kernel of $\phi$.

The following proposition are here formulated for rings and follow directly from the analogous result in general algebras that are proved in [33].

Proposition 7.

Let φ be an Ω-homomorphism from Ω-ring $(R,E^{\mu })$ to Ω-ring $(S,E^{\nu })$. Then, the Ω-valued kernel ${\ker }_{\mathsf{\Omega }}\phi :R^2\to \mathsf{\Omega }$ of φ is an Ω-valued congruence on the Ω-ring $(R,E^{\mu })$.

3.2. Structure of $\mathsf{\Omega }$-Ideals

Now we look at the family of all $\mathsf{\Omega }$-ideals on an $\mathsf{\Omega }$-ring and we prove that it is a complete lattice.

We define a natural ordering ⩽ on the family of all $\mathsf{\Omega }$-ideals:

Given two $\mathsf{\Omega }$-ideals ${\nu }_1$ and ${\nu }_2$,

${\nu }_1⩽{\nu }_2$ if and only if for every $x\in R$, ${\nu }_1\left(x\right)⩽{\nu }_2\left(x\right)$.

Proposition 8.

The family of all ideals $\mathcal{F}$ on an Ω-ring $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$ is a complete lattice under ⩽.

Proof. 

Let $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$ be an $\mathsf{\Omega }$-ring. We can note that that the relation $\mathsf{\Theta }:R^2\mapsto \mathsf{\Omega }$, defined by $\mathsf{\Theta }(x,y)=1$ for all $x,y\in R$, is an $\mathsf{\Omega }$-congruence. Hence, the mapping $\nu \left(x\right)=\mathsf{\Theta }(x,o)=1$ for all $x\in R$ is an $\mathsf{\Omega }$-ideal, and the family of all ideals on any $\mathsf{\Omega }$-ring is nonempty. Moreover, it is obvious that $\nu \left(x\right)=1$ is the greatest of all ideals under the ordering ⩽.

Now we have to prove that the infimum of every family of $\mathsf{\Omega }$-ideals on the $\mathsf{\Omega }$-ring is again an ideal.

Let $\{{\nu }_i\mid i\in I\}$ be a family of $\mathsf{\Omega }$-ideals on the $\mathsf{\Omega }$-ring. Now, we prove that the intersection of fuzzy sets ${\cap }_{i\in I}{\nu }_i$ is an $\mathsf{\Omega }$-ideal and it is the infimum of the family $\{{\nu }_i\mid i\in I\}$. Indeed, it is easy to check that ${\cap }_{i\in I}{\nu }_i\left(x\right)={\cap }_{i\in I}{\mathsf{\Theta }}_i(x,o)$ for every $x\in R$ where for every $i\in I$, ${\mathsf{\Theta }}_i$ is the corresponding congruence to ${\nu }_i$. Since ${\cap }_{i\in I}{\mathsf{\Theta }}_i$ is also an $\mathsf{\Omega }$-congruence on $(\mathcal{R},E^{\mu })$, we have that ${\cap }_{i\in I}{\nu }_i$ is an $\mathsf{\Omega }$-ideal.

Hence, the family of all $\mathsf{\Omega }$-ideals on $(\mathcal{R},E^{\mu })$ is a complete lattice. □

It is easy to check that for two congruences ${\mathsf{\Theta }}_1$ and ${\mathsf{\Theta }}_2$, such that ${\mathsf{\Theta }}_1⩾E^{\mu }$ and ${\mathsf{\Theta }}_2⩾E^{\mu }$, and ${\mathsf{\Theta }}_1⩽{\mathsf{\Theta }}_2$, and for two corresponding functions ${\nu }_1$ and ${\nu }_2$ and relations determining $\mathsf{\Omega }$-ideals $E^{{\nu }_1}⩽E^{{\nu }_2}$, respectively,

${\mathsf{\Theta }}_1⩽{\mathsf{\Theta }}_2$ if and only if ${\nu }_1⩽{\nu }_2$ if and only if $E^{{\nu }_1}⩽E^{{\nu }_2}$.

Keeping this in mind, and the fact that $E^{\mu }(o,x)\wedge E^{\mu }(o,y)⩽E^{\mu }(x,y)$, we have the following corollary.

Corollary 1.

The smallest element of the family of all ideals $\mathcal{F}$ on an Ω-ring $\overline{\mathcal{R}}=(\mathcal{R},E^{\mu })$ is the ideal $E^0:R^2\to \mathsf{\Omega }$ defined by

$$E^0(x,y)=E^{\mu }(o,x)\wedge E^{\mu }(o,y)$$

(13)

In the following, we prove that an $\mathsf{\Omega }$-valued congruence $\mathsf{\Theta }$ on an $\mathsf{\Omega }$-ring $(\mathcal{R},E^{\mu })$, such that $\mathsf{\Theta }⩾E^{\mu }$, can be regarded as an $\mathsf{\Omega }$-valued equality, and can generate another $\mathsf{\Omega }$-ring.

Theorem 5.

Let $\mathsf{\Theta }:R^2\to \mathsf{\Omega }$ be an Ω-valued congruence on an Ω-ring $(\mathcal{R},E^{\mu })$, such that $\mathsf{\Theta }\ge E^{\mu }$. Then, $(\mathcal{R},\mathsf{\Theta })$ is an Ω-ring as well. Moreover, for every $p\in \mathsf{\Omega }$, the mapping $f:{\mu }_p/E_p^{\mu }\to {\mu }_p/{\mathsf{\Theta }}_p$, defined by $f({\left[x\right]}_{E_p^{\mu }})={\left[x\right]}_{{\mathsf{\Theta }}_p}$, is a surjective ring homomorphism.

Proof. 

We prove that the ring identities in the sense of the $\mathsf{\Omega }$-ring are fulfilled. For instance, to prove the distributivity on R, using $\mu \left(x\right)=\mathsf{\Theta }(x,x)$ and $E^{\mu }\le \mathsf{\Theta }$, we have

$$\mu \left(x\right)\wedge \mu \left(y\right)\wedge \mu \left(z\right)⩽E^{\mu }(x·(y+z),(x·y)+(x·z))⩽\mathsf{\Theta }(x·(y+z),(x·y)+(x·z)).$$

Analogously, we check all other $\mathsf{\Omega }$-ring identities.

To prove that for $p\in \mathsf{\Omega }$, $f:{\mu }_p/E_p^{\mu }\to {\mu }_p/{\mathsf{\Theta }}_p$, defined by $f({\left[x\right]}_{E_p^{\mu }})={\left[x\right]}_{{\mathsf{\Theta }}_p}$, is a homomorphism, let $x,y\in {\mu }_p$. Then,

$$f({[x+y]}_{E_p^{\mu }})={[x+y]}_{{\mathsf{\Theta }}_p}={\left[x\right]}_{{\mathsf{\Theta }}_p}+{\left[y\right]}_{{\mathsf{\Theta }}_p}=f({\left[x\right]}_{E_p^{\mu }})+f({\left[y\right]}_{E_p^{\mu }}).$$

Analogously, we check that f is compatible with all other operations. The homomorphism is surjective, since every class ${\left[x\right]}_{{\mathsf{\Theta }}_p}$ is the image of ${\left[x\right]}_{E_p^{\mu }}$ under f. □

Example 4.

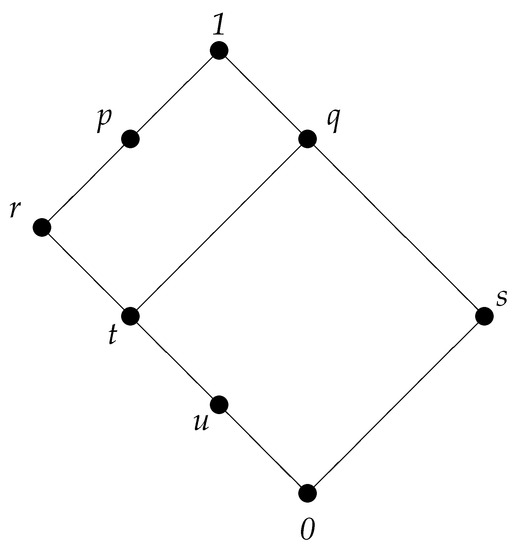
Let $(\mathcal{R},E^{\mu })$ be a commutative Ω-ring from [1], with lattice Ω given in Figure 2, where $\mathcal{R}=(R,+,·,-,o)$ is an algebra with $R=\{o,a,b,c\}$, operations + and $·$ presented in Table 3 and a unary operation − defined by $-x:=x$. The Ω-valued equality $E^{\mu }$ is given in Table 4.

Figure 2. Lattice $\mathsf{\Omega }$.

Table 3. (a) Binary operation + on R. (b) Binary operation $·$ on R.

(a)
+	o	a	b	c
o	o	a	c	c
a	a	o	b	c
b	c	b	o	a
c	c	c	a	o
(b)
$·$	o	a	b	c
o	o	o	a	o
a	o	o	o	a
b	a	a	c	b
c	o	o	b	c

Table 4. $\mathsf{\Omega }$-valued equality on R.

${\mathit{E}}^{\mathit{\mu }}$	o	a	b	c
o	1	r	0	s
a	r	p	0	0
b	0	0	u	u
c	s	0	u	q

The function $\mu :R\to \mathsf{\Omega }$ is determined by $E^{\mu }$: $\mu \left(x\right)=E^{\mu }(x,x)$.

x	o	a	b	c
$\mu \left(x\right)$	1	p	u	q

We give a construction of an Ω-ideal starting from an Ω-valued congruence Θ on R in Table 5.

Table 5. $\mathsf{\Omega }$-valued congruence on R.

$\mathbf{\Theta }$	o	a	b	c
o	1	p	0	s
a	p	p	0	0
b	0	0	u	u
c	s	0	u	q

One could easily check that θ is an Ω-valued congruence on R satisfying $\mathsf{\Theta }(x,y)⩾E^{\mu }(x,y)$ for all $x,y\in R$.

Now, we define an Ω-ideal on R, by $E^{\nu }(x,y):=E^{\mu }(x,y)\wedge \mathsf{\Theta }(o,x)\wedge \mathsf{\Theta }(o,y)$.

In the following, we give the table for $E^{\nu }$ (Table 6).

Table 6. The equality relation determining $\mathsf{\Omega }$-valued ideal.

${\mathit{E}}^{\mathit{\nu }}$	o	a	b	c
o	1	r	0	s
a	r	p	0	0
b	0	0	0	0
c	s	0	0	s

Now, $(\mathcal{R},E^{\nu })$ is an Ω-valued ideal.

The cuts of ν and $E^{\nu }$ are as follows:

$${\nu }_{\mathit{0}}=\{o,a,b,c\};E_{\mathit{0}}^{\nu }=\{(o,o),(o,a),(o,b),(o,c),(a,o),(a,a),(a,b),(a,c),(b,o),(b,a),(b,b),(b,c),(c,o),(c,a),(c,b),(c,c)\}.$$

$${\nu }_u={\nu }_t={\nu }_r=\{o,a\};$$

$$E_u^{\nu }=E_t^{\nu }=E_r^{\nu }=\{(o,o),(o,a),(a,o),(a,a)\}.$$

$${\nu }_s=\{o,c\};E_s^{\nu }=\{(o,o),(o,c),(c,o),(c,c)\}.$$

$${\nu }_p=\{o,a\};E_p^{\nu }=\{(o,o),(a,a)\}.$$

$${\nu }_1={\nu }_q=\left\{o\right\};E_1^{\nu }=E_q^{\nu }=\left\{(o,o)\right\}.$$

Now we can check the results of Theorem 4, and we obtain that for every $p\in \mathsf{\Omega }$, ${\nu }_p/E_p^{\nu }$ is an ideal of the ring ${\mu }_p/E_p^{\mu }$.

4. Systems of Linear Equations over $\mathsf{\Omega }$-Fields

Systems of linear equations with several unknowns are usually considered and solved over fields. Here, we show that $\mathsf{\Omega }$-fields can be used to deal with solutions of such systems over algebraic structures which are not necessarily fields. The technique we present in this section has the potential to expand the application of systems of linear equations to situations where specific data are organized in structures sharing the same type as a field. For this purpose, we use the following proposition, as a straightforward and obvious consequence of Proposition 2.

Proposition 9.

An Ω-algebra with identity ${\mathcal{R}}_i=((R,+,·,-,o,\iota ),E)$ is an Ω-field if and only if for every $p\in \mathsf{\Omega }$ the factor ${\mu }_p/E_p$ is a field.

Let $\overline{{\mathcal{R}}_{\iota }}=({\mathcal{R}}_{\iota },E)$ be an $\mathsf{\Omega }$-field, where ${\mathcal{R}}_{\iota }=(R,+,·,-,o,\iota )$ is the basic algebra as defined in Section 2.3. Also let

$$a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n=b,a_1,\dots ,a_n,b\in R$$

(14)

be a linear equation with n unknowns over ${\mathcal{R}}_{\iota }$. We say that an n-tuple $(c_1,\dots ,c_n)\in R^n$ is a solution of Equation (14) over $\overline{{\mathcal{R}}_{\iota }}$ if

$$\underset{i=1}{\overset{n}{\bigwedge }}\mu \left(a_i\right)\wedge \mu \left(b\right)⩽\underset{i=1}{\overset{n}{\bigwedge }}\mu \left(c_i\right)\wedge E(a_1{c}_1+\dots +a_n{c}_n,b).$$

(15)

Theorem 6.

Let $\overline{{\mathcal{R}}_{\iota }}$ be an Ω-field. Then, $(c_1,\dots ,c_n)$ is a solution of a linear equation $a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n=b$ over $\overline{{\mathcal{R}}_{\iota }}$ with $p={\bigwedge }_{i=1}^n\mu \left(a_i\right)\wedge \mu \left(b\right)$, if and only if $({\left[c_1\right]}_{E_p},\dots ,{\left[c_n\right]}_{E_p})$ is a classical solution of the linear equation ${\left[a_1\right]}_{E_p}{x}_1+{\left[a_2\right]}_{E_p}{x}_2+\dots +{\left[a_n\right]}_{E_p}{x}_n={\left[b\right]}_{E_p}$ over the cut-quotient field ${\mu }_p/E_p$, where $c_i$, $i=1,\dots ,n$ is an arbitrary representative of the class replacing the unknown $x_i$.

Proof. 

Suppose that $(c_1,\dots ,c_n)$ is a solution of a linear equation $a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n=b$ over the $\mathsf{\Omega }$-field $\overline{{\mathcal{R}}_{\iota }}$. Then, the formula (15) holds, i.e., for ${\bigwedge }_{i=1}^n\mu \left(a_i\right)\wedge \mu \left(b\right)=p$, ${\bigwedge }_{i=1}^n\mu \left(c_1\right)\wedge E(a_1{c}_1+\dots +a_n{c}_n,b)⩾p$. Hence, $a_1,\dots ,a_n,b,c_1,\dots ,c_n\in {\mu }_p$. The cut ${\mu }_p$ is a subalgebra of ${\mathcal{R}}_{\iota }$ and $E_p$ is a congruence on ${\mu }_p$. By Proposition 9, ${\mu }_p/E_p$ is an $\mathsf{\Omega }$-field. Since $E(a_1{c}_1+\dots +a_n{c}_n,b)⩾p$, we have $(a_1{c}_1+\dots +a_n{c}_n,b)\in E_p$. Hence, ${[a_1{c}_1+\dots +a_n{c}_n]}_{E_p}={\left[b\right]}_{E_p}$, i.e., ${\left[a_1\right]}_{E_p}{\left[c_1\right]}_{E_p}+\dots +{\left[a_n\right]}_{E_p}{\left[c_n\right]}_{E_p}={\left[b\right]}_{E_p}$, which proves that $({\left[c_1\right]}_{E_p},\dots ,{\left[c_n\right]}_{E_p})$ is a solution of the corresponding linear equation ${\left[a_1\right]}_{E_p}{x}_1+{\left[a_2\right]}_{E_p}{x}_2+\dots +{\left[a_n\right]}_{E_p}{x}_n={\left[b\right]}_{E_p}$ over the cut-quotient field ${\mu }_p/E_p$.

Conversely, assume that for a linear equation $a_1{x}_1+a_2{x}_2+\dots +a_n{x}_n=b$, the n-tuple $({\left[c_1\right]}_{E_p},\dots ,{\left[c_n\right]}_{E_p})$ of classes is a solution of the corresponding equation ${\left[a_1\right]}_{E_p}{x}_1+{\left[a_2\right]}_{E_p}{x}_2+\dots +{\left[a_n\right]}_{E_p}{x}_n={\left[b\right]}_{E_p}$ over the cut-quotient field ${\mu }_p/E_p$, where $p={\bigwedge }_{i=1}^n\mu \left(a_i\right)\wedge \mu \left(b\right)$; $c_i$, $i=1,\dots ,n$ is an arbitrary representative of the class replacing the unknown $x_i$. This means that ${\left[a_1\right]}_{E_p}{\left[c_1\right]}_{E_p}+\dots +{\left[a_n\right]}_{E_p}{\left[c_n\right]}_{E_p}={\left[b\right]}_{E_p}$, i.e., ${[a_1{c}_1+\dots +a_n{c}_n]}_{E_p}={\left[b\right]}_{E_p}$. Then, $(a_1{c}_1+\dots +a_n{c}_n,b)\in E_p$, i.e., $E(a_1{c}_1+\dots +a_n{c}_n,b)⩾p$. Since $c_i\in {\left[c_i\right]}_{E_p}$, we have that $\mu \left(c_i\right)⩾p$, and hence the formula (15) holds. This proves that every n-tuple $(c_1,\dots ,c_n)$ of elements from the corresponding classes forming a solution over the field ${\mu }_p/E_p$ is a solution in the sense of (15). □

Analogously, as for the single equation, we can deal with solutions of the system of linear equations over an $\mathsf{\Omega }$-field $\overline{{\mathcal{R}}_{\iota }}$. The system is given by

$$\begin{array}{c}{a}_{11}{x}_1+a_{12}{x}_2+\dots +a_{1n}{x}_n=b_1\\ a_{21}{x}_1+a_{22}{x}_2+\dots +a_{2n}{x}_n=b_2\\ \dots \dots \dots \dots \dots \\ a_{m1}{x}_1+a_{m2}{x}_2+\dots +a_{mn}{x}_n=b_m\end{array},$$

(16)

where $a_{ij},b_k\in R$. We say that an n-tuple $(c_1,\dots ,c_n)\in R^n$ is a solution of the system (16) if for every $i=1,\dots ,m$,

$$\underset{j=1}{\overset{n}{\bigwedge }}\mu \left(a_{ij}\right)\wedge \mu \left(b_i\right)⩽\underset{j=1}{\overset{n}{\bigwedge }}\mu \left(c_j\right)\wedge E(a_{i1}{c}_1+\dots +a_{in}{c}_n,b_i).$$

(17)

Dealing with systems of linear equations over an $\mathsf{\Omega }$-field, we formulate the result analogously to the one presented in Theorem 6 (for one linear equation). We omit the proof, since it is very similar to the one of the mentioned theorem.

Theorem 7.

Let $\overline{{\mathcal{R}}_{\iota }}$ be an Ω-field. The n-tuple $(c_1,\dots ,c_n)$ is a solution of a system of linear equations (16) over $\overline{{\mathcal{R}}_{\iota }}$, where for $i=1,\dots ,m$, $p_i={\bigwedge }_{j=1}^n\mu \left(a_{ij}\right)\wedge \mu \left(b_i\right)$ if and only if for $i\in \{1,\dots ,m\}$, $({\left[c_1\right]}_{E_{p_i}},\dots ,{\left[c_n\right]}_{E_{p_i}})$ is a classical solution of the linear equation

$${\left[a_{i1}\right]}_{E_{p_i}}{x}_1+{\left[a_{i2}\right]}_{E_{p_i}}{x}_2+\cdots +{\left[a_{in}\right]}_{E_{p_i}}{x}_n={\left[b_i\right]}_{E_{p_i}}$$

over the cut-quotient field ${\mu }_{p_i}/E_{p_i}$.

Remark 4.

Observe that the procedure presented in this section is a particular way of obtaining approximate solutions for systems of linear equations. Indeed, in real situations, data (numbers) often do not belong to the field of real or complex numbers, nor to some finite field. Such a structure may be a ring, or more generally, another algebraic structure of the same type. In these situations, a lattice Ω and the corresponding Ω-equality obtained from the properties of these data allow the construction of an Ω-field, as presented here. Then, we can obtain solutions of (systems of) linear equations. These solutions are approximate since the classical equality is replaced with an Ω-valued one. And this equality respects similarities in a collection of data.

Example 5.

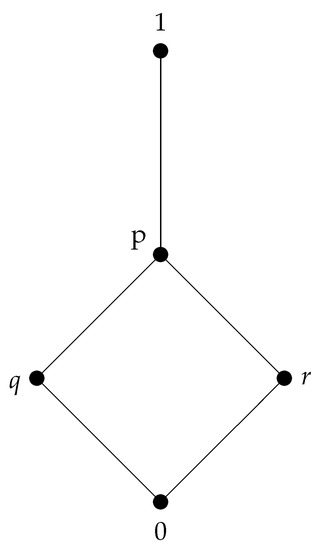
Let $(Z,+,·,-,0,1)$ be the ring of integers considered as an algebra with two binary, one unary and two nullary operations, and let Ω be a lattice in Figure 3. Let $E:Z\times Z\to \mathsf{\Omega }$ be defined as follows:

$$E(x,y)=\left\{\begin{array}{ccc}1\hfill & if\hfill & x=y=0\hfill \\ p\hfill & if\hfill & 10|x\&10|y\&x\equiv y\left(mod3\right)\hfill \\ q\hfill & if\hfill & 2|x\&2|y\&5\cancel{|}x\&5\cancel{|}y\&x\equiv y(mod3)\hfill \\ r\hfill & if\hfill & 5|x\&5|y\&2\cancel{|}x\&2\cancel{|}y\&x\equiv y(mod3)\hfill \\ 0\hfill & & otherwise\hfill \end{array}\right.$$

Figure 3. A lattice $\mathsf{\Omega }$.

One can easily check that E is an Ω-valued equality on Z.

The related Ω-set μ is defined as follows

$$\mu \left(x\right)=\left\{\begin{array}{ccc}1\hfill & if\hfill & x=0\hfill \\ p\hfill & if\hfill & 10|x\hfill \\ q\hfill & if\hfill & 2|x\&5\cancel{|}x\hfill \\ r\hfill & if\hfill & 5|x\&2\cancel{|}x\hfill \\ 0\hfill & & otherwise\hfill \end{array}\right.$$

Now, we look at the cuts:

${\mu }_1/E_1$ is a trivial, one-element algebra. ${\mu }_p/E_p$, ${\mu }_q/E_q$, ${\mu }_r/E_r$ consists of three classes and it is isomorphic with a three-element field. ${\mu }_0/E_0$ is also a trivial one-element algebra.

Now, lets look at a system of equations on $(Z,+,·,-,0,1)$:

$$\begin{array}{ccc}4x\hfill & +10y\hfill & =22\hfill \\ 10x\hfill & +12y\hfill & =26.\hfill \end{array}$$

It does not have solutions in $(Z,+,·,-,0,1)$. However, we can find approximate solutions by solving it in the cut structure.

We see that the value of a function μ of all coefficients is either p or q, so we can look at the solution in $p\wedge q$-cut (the q-cut), which is a three-element field.

In this field, considering the congruence relation module 3, the system is transformed to

$$\left[1\right]\left[x\right]+\left[1\right]\left[y\right]=\left[1\right].$$

$$\left[1\right]\left[x\right]+\left[0\right]\left[y\right]=\left[2\right].$$

This system of equations has the following solution in the three-element field:

$$\left[x\right]=\left[2\right],\left[y\right]=\left[2\right].$$

So, in this way, we obtain an approximate solution and we can take any element from these classes, so the solution can be, e.g., approximately $x=2$ and $y=2$.

5. Conclusions

Continuing our research of $\mathsf{\Omega }$-rings, here we have presented $\mathsf{\Omega }$-ideals and their connection to homomorphisms. We have also shown that systems of linear equations could be solved with data (numbers) which do not necessarily form a field, constructing an $\mathsf{\Omega }$-field over a basic structure which may be a ring, or some other structure of the same type.

$\mathsf{\Omega }$-structures turn out to be suitable for applications of known algebraic structures (groups, rings, fields…) in real problems, when not all properties of these structures are fulfilled. As shown in our research, particular quotient structures of $\mathsf{\Omega }$-algebras remain classical structures. Therefore, these quotients can be used as a tool for solving problems with corrupted or missing data. We shall continue our investigations in this direction, dealing particularly with real problems which could be solved in the framework of special $\mathsf{\Omega }$-rings and polynomials over finite $\mathsf{\Omega }$-fields.