Topological Comparison of Some Dimension Reduction Methods Using Persistent Homology on EEG Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Preliminaries
2.2. ISOMAP
- 1.
- For a fixed integer K and real number , perform an -nearest neighbor search using the fact that the geodesic distance between two points on is the same (by isometry) as their euclidian distance in . K is the number of data points selected within a ball of radius .
- 2.
- Having calculated the distance between points as above, the entire data set can be considered as a weighted graph with vertices and edges , where connects with with a distance , considered an associated weight. The geodesic distance between two data points and is estimated as the graph distance between the two edges, that is, the number of edges in the shortest path connecting them. We observe that this shortest path is found by minimizing the sum of the weights of its constituent edges.
- 3.
- Having calculated the geodesic distances as above, we observe that is a symmetric matrix, so we can apply the classical multidimensional scaling algorithm (MDS) (see [33]) to by mapping (embedding) them into a feature space of dimension d while preserving the geodesic distance on . is generated by a matrix whose i-th column represents the coordinates of in .
2.3. Laplacian Eigenmaps
- 1.
- For a fixed integer K and real number , perform a K-nearest neighbor search on symmetric neighborhoods. Note that given two points , their respective K-neighborhood and are symmetric if and only .
- 2.
- For a given real number and each pair of points , calculate the weight if and if . Obtain the adjacency matrix . The data now form a weighted graph with vertices , with edges , and weights , where connects with with distance .
- 3.
- Consider to be a diagonal matrix with and define the graph Laplacian as . Then, is positive definite so let be the matrix that minimizes . Then, can used to embed into a d-dimensional space , whose i-th column represents the coordinates of in .
2.4. Fast ICA
- 1.
- Data preparation: it consists of centering the data with respect to the column to obtain . That is, , for . The centered data are then whitened; that is, is linearly transformed into , a matrix of uncorrelated components. This is accomplished through an eigenvalue decomposition of the covariance matrix to obtain two matrices , respectively, of eigenvectors and eigenvalues so that . The whitened data are found as and simply referred to again as for simplicity.
- 2.
- Component extraction: Let for a given constant , where is the optimal weight matrix. Applying the Newton scheme () to the differentiable function , we
- Select a random starting vector .
- For , .
- Normalize as .
- Repeat until a suitable convergence level is reached.
- From the last matrix obtained, let .
2.5. Kernel Ridge Regression
2.6. t-SNE
- Calculate the asymmetrical probabilities as , where represents the dissimilarity between and , and is a parameter selected by the experimenter or by a binary search. represents the conditional probability that datapoint is the neighborhood of datapoint if neighbors were selected proportionally to their probability density under a normal distribution centered at and variance .
- Assuming that the low dimensional data are , the corresponding dissimilarity probabilities are calculated under constant variance as , where in the case of SNE, and for t-SNE.
- Then, we minimize the Kullback–Leibler divergence between and , given as , using the gradient descent method with a momentum term with the scheme for for some given T. Note that , where is the identity matrix, is a constant representing a learning rate, and is t-th momentum iteration. We note that for where
- Then, we use as the low dimensional representation of .
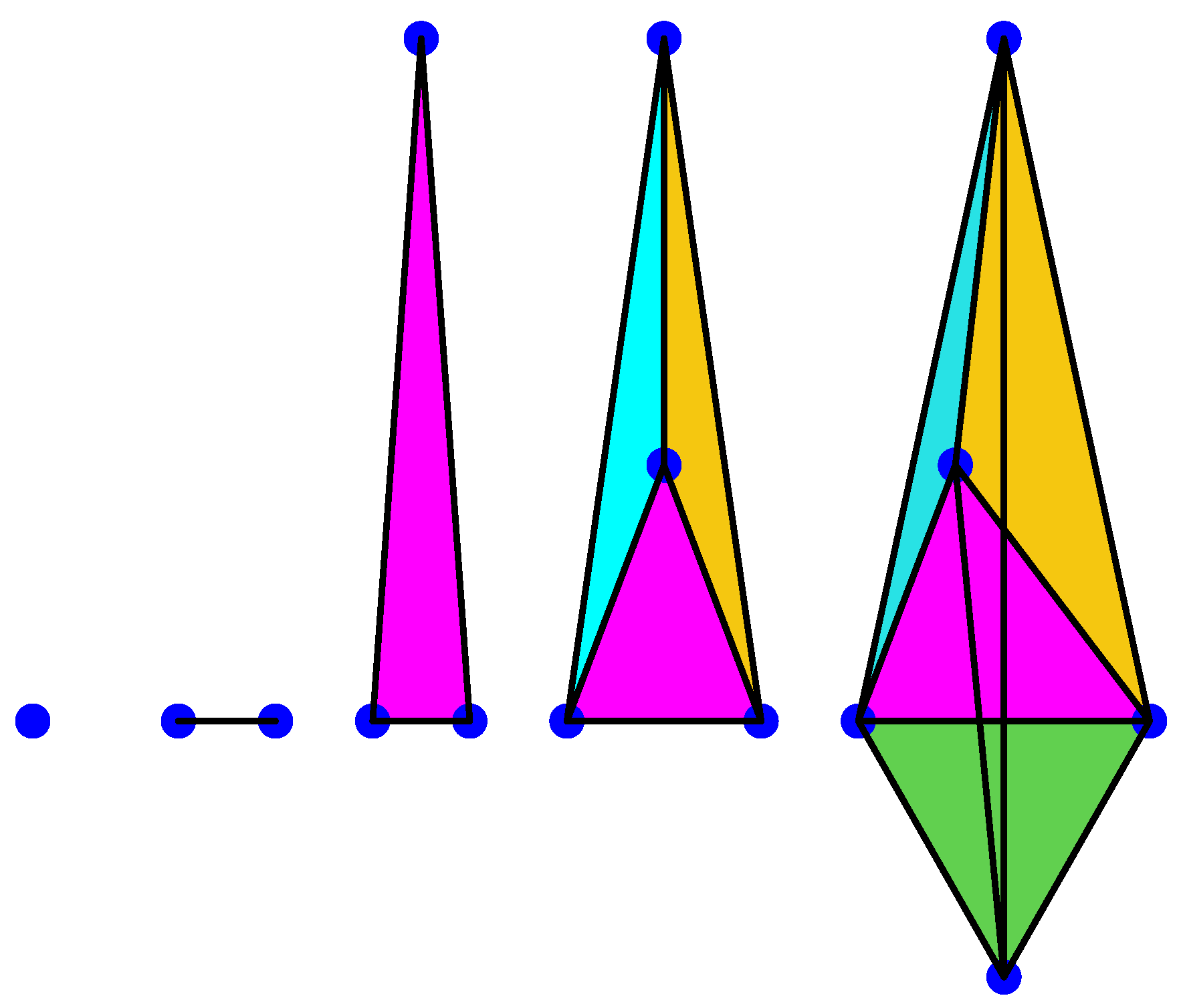
3. Persistent Homology
3.1. Simplex Complex
- 1.
- Given , its face .
- 2.
- Given , either or , the faces of and , respectively.
- 1.
- For all , then .
- 2.
- For any set U such that for some , then .
- 1.
- 2.
- , where is the set of all subsets of Ω.
3.2. Homology and Persistent Homology
- 1.
- is the number of connected components of the complex.
- 2.
- is the number of tunnels and holes.
- 3.
- is the number of shells around cavities or voids.
4. Results
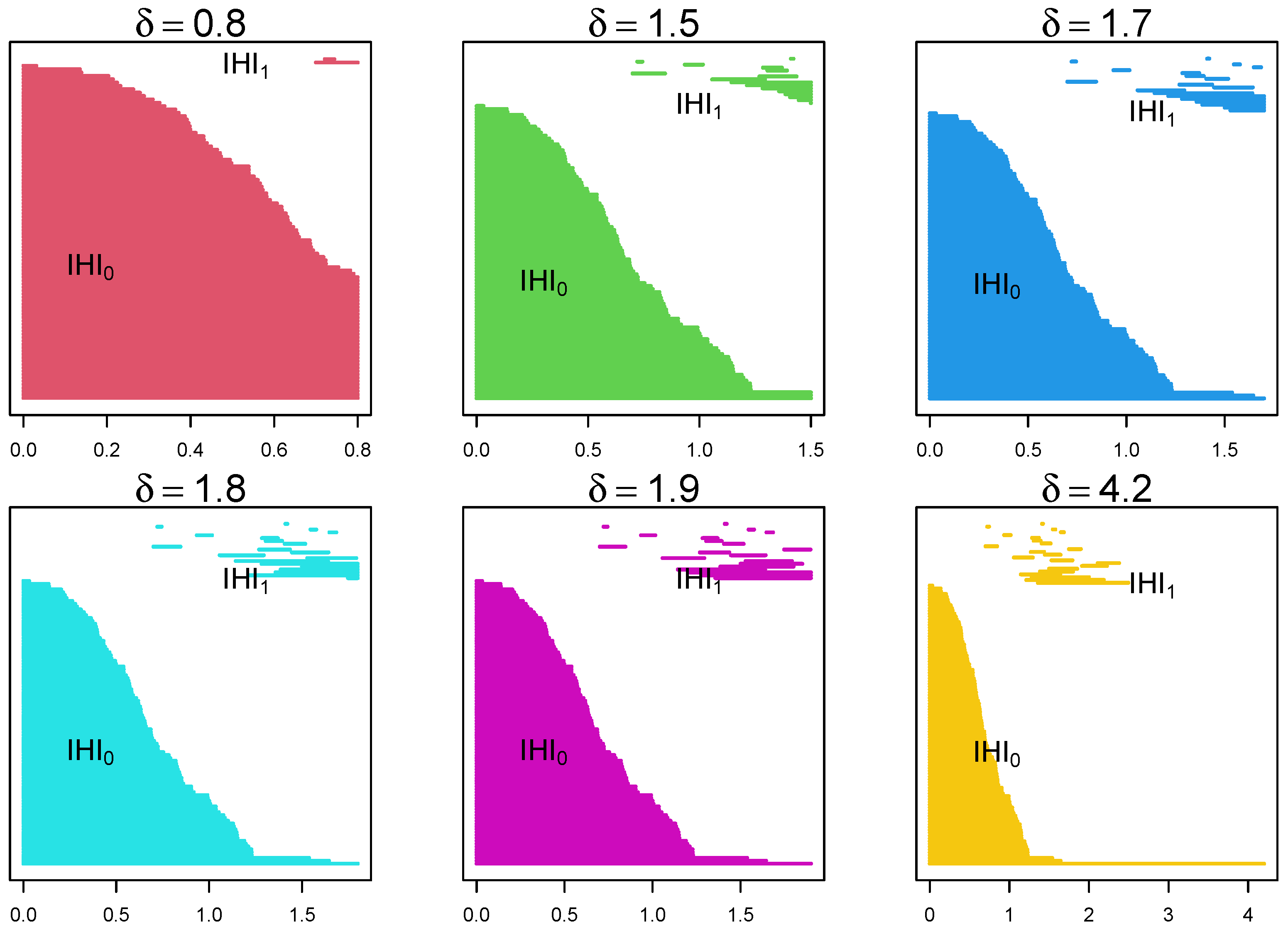
4.1. Randomly Generated Data
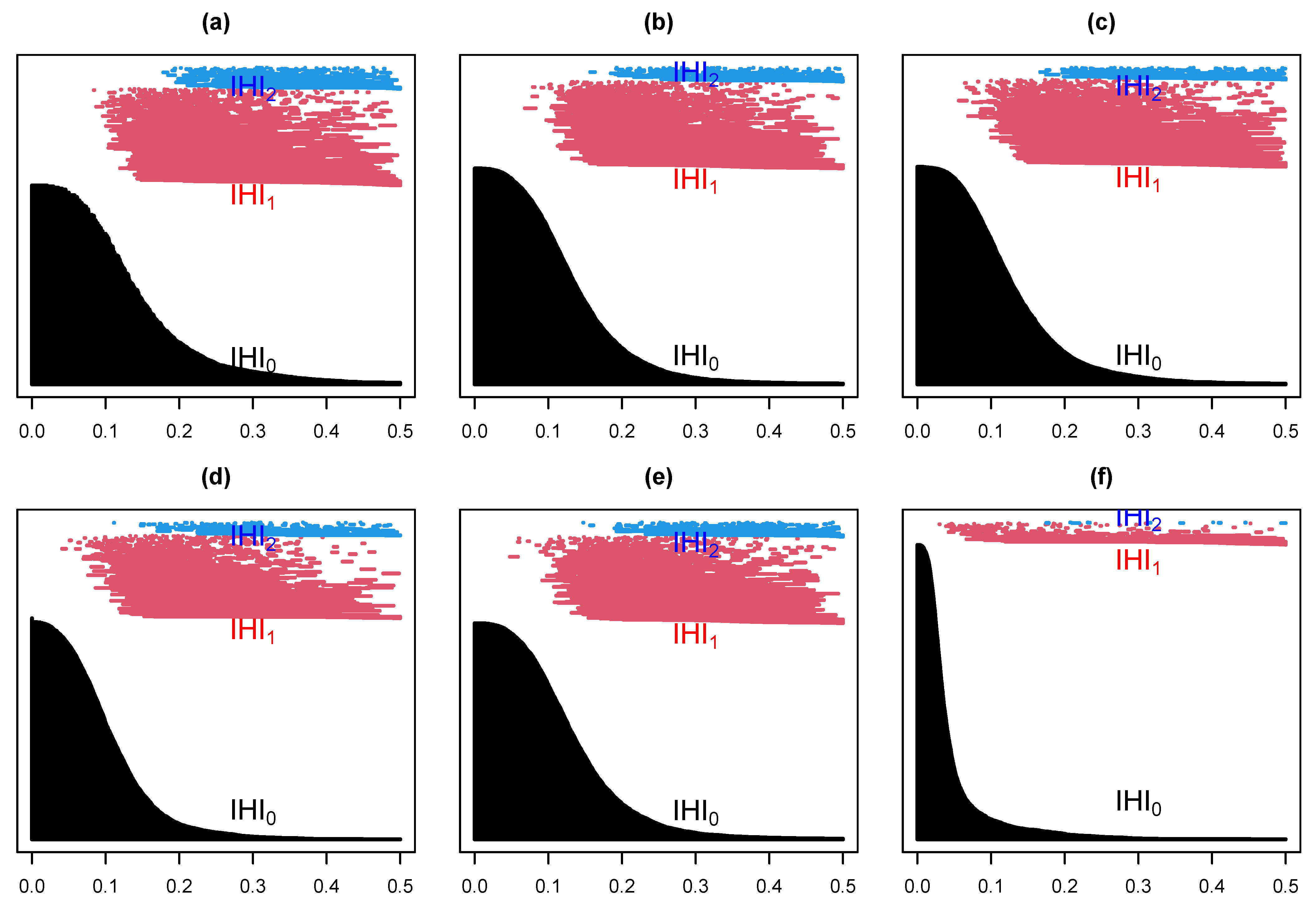
4.2. EEG Epilepsy Data
4.2.1. Data Description
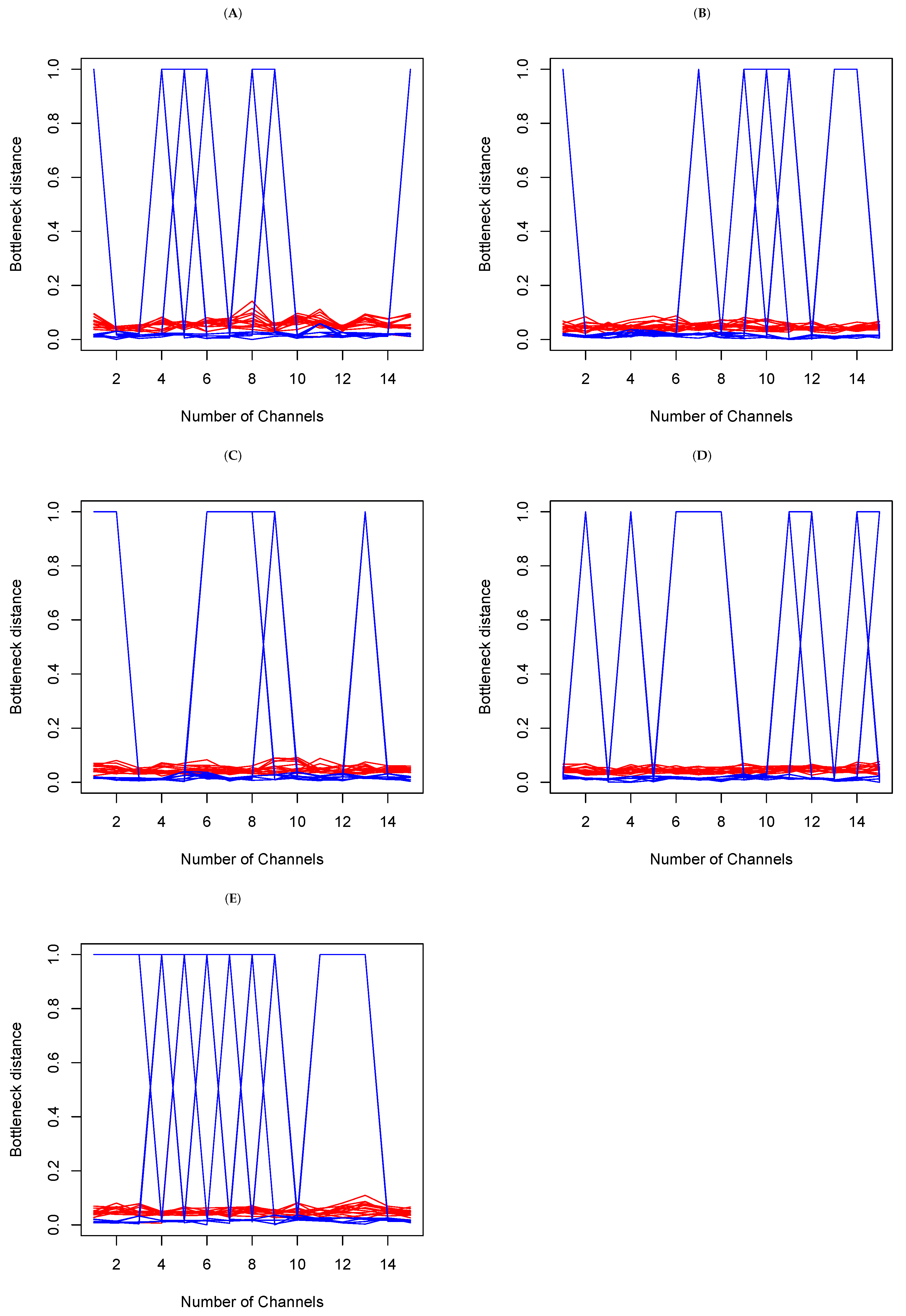
4.2.2. Data Analysis
- (a)
- Within set analysis
- (b)
- Between set analysis
5. Concluding Remarks
Funding
Data Availability Statement
Conflicts of Interest
References
- Whitney, H. Differentiable manifolds. Ann. Math. 1936, 37, 645–680. [Google Scholar] [CrossRef]
- Takens, F. Detecting strange attractors in turbulence dynamical systems and turbulence. Lect. Notes Math. 1981, 898, 366–381. [Google Scholar]
- Ma, Y.; Fu, Y. Manifold Learning: Theory and Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Hotelling, H. Analysis of a complex of statistical variables into principal components. J. Educ. Psychol. 1933, 24, 498–520. [Google Scholar] [CrossRef]
- Ramsay, J.O.; Silverman, B.W. Functional Data Analysis, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Cohen, J.; West, S.G.; Aiken, L.S. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3rd ed.; Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 2003. [Google Scholar]
- Friedman, J.H. Regularized discriminant analysis. J. Am. Stat. Assoc. 1989, 84, 165–175. [Google Scholar] [CrossRef]
- Yu, H.; Yang, J. A direct lda algorithm for high-dimensional data—With application to face recognition. Pattern Recognition 2001, 34, 2067–2069. [Google Scholar] [CrossRef]
- Tenenbaum, J.B.; de Siva, V.; Langford, J.C. A global geometric frameworkfor nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef]
- Belkin, M.; Niyogi, P. Laplacian eigenmaps and spectral techniques for embedding and clustering. In Advances in Neural Information Processing Systems 14; Dietterich, T.G., Becker, S., Ghahramani, Z., Eds.; MIT Press: Cambridge, MA, USA, 2002; pp. 585–591. [Google Scholar]
- Hyvärinen, A. Fast and robust fixed-point algorithms for independent component analysis. IEEE Trans. Neural Netw. 1999, 13, 411–430. [Google Scholar] [CrossRef]
- Theodoridis, S. (Ed.) Chapter 11—Learning in reproducing kernel hilbert spaces . In Machine Learning, 2nd ed.; Academic Press: Cambridge, MA, USA, 2020; pp. 531–594. Available online: https://www.sciencedirect.com/science/article/pii/B9780128188033000222 (accessed on 28 June 2023).
- Van der Maaten, L.J.P.; Hinton, G.E. Visualizing data using t-sne. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- Naizait, G.; Zhitnikov, A.; Lim, L.-H. Topology of deep neural networks. J. Mach. Learn. Res. 2020, 21, 7503–7542. [Google Scholar]
- Chan, J.M.; Carlsson, G.; Rabadan, R. Topology of viral evolution. Proc. Natl. Acad. Sci. USA 2013, 110, 18566–18571. [Google Scholar] [CrossRef]
- Otter, N.; Porter, M.A.; Tillman, U.; Grindrod, P.; Harrington, H.A. A roadmap for the computationof persistent homology. EPJ Data Sci. 2017, 6, 17. [Google Scholar] [CrossRef]
- De Silva, V.G.; Ghrist, R. Coverage in sensor networks via persistent homology. Algebr. Geom. Topol. 2007, 7, 339–358. [Google Scholar] [CrossRef]
- Gameiro, M.; Hiraoka, Y.; Izumi, S.; Mischaikow, K.M.K.; Nanda, K. A topological measurement of proteincompressibility. Jpn. J. Ind. Appl. Math. 2015, 32, 1–17. [Google Scholar] [CrossRef]
- Xia, K.; Wei, G.-W. Persistent homology analysis of protein structure, flexibility, and folding. Int. J. Numer. Methods Biomed. Eng. 2014, 30, 814–844. [Google Scholar] [CrossRef] [PubMed]
- Emmett, K.; Schweinhart, N.; Rabadán, R. Multiscale topology of chromatin folding. In Proceedings of the 9th EAIinternational Conference on Bio-Inspired Information and Communications Technologies, BICT’15, ICST 2016, New York City, NY, USA, 3–5 December 2015; pp. 177–180. [Google Scholar]
- Rizvi, A.; Camara, P.; Kandror, E.; Roberts, T.; Schieren, I.; Maniatis, T.; Rabadán, R. Single-cell topological rna-seqanalysis reveals insights into cellular differentiation and development. Nat. Biotechnol. 2017, 35, 551–560. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, S.; Ghrist, R.; Kumar, V. Persistent homology for path planning in uncertain environments. IEEE Trans. Robot. 2015, 31, 578–590. [Google Scholar] [CrossRef]
- Pokorny, F.T.; Hawasly, M.; Ramamoorthy, S. Topological trajectory classification with filtrations of simplicialcomplexes and persistent homology. Int. J. Robot. Res. 2016, 35, 204–223. [Google Scholar] [CrossRef]
- Vasudevan, R.; Ames, A.; Bajcsy, R. Persistent homology for automatic determination of human-data based costof bipedal walking. Nonlinear Anal. Hybrid Syst. 2013, 7, 101–115. [Google Scholar] [CrossRef]
- Chung, M.K.; Bubenik, P.; Kim, P.T. Persistence diagrams of cortical surface data. In Information Processing in Medical Imaging. Lecture Notes in Computer Science; Prince, J.L., Pham, D.L., Myers, K.J., Eds.; Springer: Berlin, Germany, 2009; Volume 5636, pp. 386–397. [Google Scholar]
- Guillemard, M.; Boche, H.; Kutyniok, G.; Philipp, F. Persistence diagrams of cortical surface data. In Proceedings of the 10th International Conference on Sampling Theory and Applications, Bremen, Germany, 1–5 July 2013; pp. 309–312. [Google Scholar]
- Taylor, D.; Klimm, F.; Harrington, H.A.; Kramár, M.; Mischaikow, K.; Porter, M.A.; Mucha, P.J. Topological data analysis ofcontagion maps for examining spreading processes on networks. Nat. Commun. 2015, 6, 7723. [Google Scholar] [CrossRef]
- Leibon, G.; Pauls, S.; Rockmore, D.; Savell, R. Topological structures in the equities market network. Proc. Natl. Acad. Sci. USA 2008, 105, 20589–20594. [Google Scholar] [CrossRef]
- Giusti, C.; Ghrist, R.; Bassett, D. Two’s company and three (or more) is a simplex. J. Comput. Neurosci. 2016, 41, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Sizemore, A.E.; Phillips-Cremins, J.E.; Ghrist, R.; Bassett, D.S. The importance of the whole: Topological data analysis for the network neuroscientist. Netw. Neurosci. 2019, 3, 656–673. [Google Scholar] [CrossRef]
- Maletić, S.; Zhao, Y.; Rajković, M. Persistent topological features of dynamical systems. Chaos 2016, 26, 053105. [Google Scholar] [CrossRef] [PubMed]
- Chung, M.K.; Ramos, C.G.; Paiva, J.; Mathis, F.B.; Prabharakaren, V.; Nair, V.A.; Meyerand, E.; Hermann, B.P.; Binder, J.R.; Struck, A.F. Unified topological inference for brainnetworks in temporal lobe epilepsy using thewasserstein distance. arXiv 2023, arXiv:2302.06673. [Google Scholar]
- Torgerson, W.S. Multidimensional scaling: I. theory and method. Psychometrika 1952, 17, 410–419. [Google Scholar] [CrossRef]
- Jäntschi, L. Multiple linear regressions by maximizing the likelihood under assumption of generalized gauss-laplace distribution of the error. Comput. Math. Methods Med. 2016, 2016, 8578156. [Google Scholar] [CrossRef] [PubMed]
- Jäntschi, L. Symmetry in regression analysis: Perpendicular offsets—The case of a photovoltaic cell. Symmetry 2023, 15, 948. [Google Scholar] [CrossRef]
- NSilver, The Signal and Noise: Why So Many Predictions Fail—But Some Dont; The Penguin Press: London, UK, 2012.
- Hinton, G.E.; Roweis, S. Stochastic neighbor embedding. In Advances in Neural Information Processing Systems; Becker, S., Thrun, S., Obermayer, K., Eds.; MIT Press: Cambridge, MA, USA, 2002; Volume 15. [Google Scholar]
- Ghrist, R. Barcodes: The persistent topology of data. Bull. Amer. Math. Soc. 2008, 45, 61–75. [Google Scholar] [CrossRef]
- Kwessi, E.; Edwards, L. Analysis of eeg time series data using complex structurization. Neural Comput. 2021, 33, 1942–1969. [Google Scholar] [CrossRef]
- Mileyko, Y.; Mukherjee, S.; Harer, J. Probability measures on the space of persistence diagrams. Inverse Probl. 2011, 27, 124007. [Google Scholar] [CrossRef]
- Berry, E.; Chen, Y.-C.; Cisewski-Kehe, J.; Fasy, B.T. Functional summaries of persistence diagrams. J. Appl. Comput. Topol. 2020, 4, 211–262. [Google Scholar] [CrossRef]



| (a) | ||||||
| Tak | Iso | KRR | ICA | LEIM | TSNE | |
| Tak | ||||||
| Iso | 0.0945019 | |||||
| KRR | 0.0957546 | 0.0200035 | ||||
| ICA | 0.0982795 | 0.0157002 | 0.0071899 | |||
| LEIM | 0.1678820 | 0.1182656 | 0.1247918 | 0.1205499 | ||
| TSNE | 0.2238167 | 0.1730406 | 0.1817924 | 0.1759454 | 0.1162392 | |
| (b) | ||||||
| / | Tak | Iso | KRR | ICA | LEIM | TSNE |
| Tak | 0.0363205 | 0.0301992 | 0.0292631 | 0.0291247 | 0.0551774 | |
| Iso | 0.0340282 | 0.0330687 | 0.0290406 | 0.0236890 | 0.0598517 | |
| KRR | 0.0317261 | 0.0279460 | 0.0207599 | 0.0212138 | 0.0647935 | |
| ICA | 0.0310771 | 0.0270919 | 0.0208086 | 0.0242277 | 0.0611090 | |
| LEIM | 0.0607389 | 0.0725585 | 0.0702695 | 0.0682761 | 0.0542615 | |
| TSNE | 0.0757815 | 0.0959521 | 0.0864587 | 0.0861522 | 0.0785030 | |
| / | A | B | C | D | E |
|---|---|---|---|---|---|
| A | 0.1975936 | 0.3049497 | 0.2467548 | 0.7432987 | |
| B | 0.3202554 | 0.3835209 | 0.5066311 | 0.1707835 | |
| C | 0.0832231 | 0.1322987 | 0.8356690 | 0.7088614 | |
| D | 0.2012797 | 0.6292608 | 0.6292608 | 0.5067258 | |
| E | 0.0049325 | 0.0157855 | 0.0157855 | 0.0114901 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kwessi, E. Topological Comparison of Some Dimension Reduction Methods Using Persistent Homology on EEG Data. Axioms 2023, 12, 699. https://doi.org/10.3390/axioms12070699
Kwessi E. Topological Comparison of Some Dimension Reduction Methods Using Persistent Homology on EEG Data. Axioms. 2023; 12(7):699. https://doi.org/10.3390/axioms12070699
Chicago/Turabian StyleKwessi, Eddy. 2023. "Topological Comparison of Some Dimension Reduction Methods Using Persistent Homology on EEG Data" Axioms 12, no. 7: 699. https://doi.org/10.3390/axioms12070699
APA StyleKwessi, E. (2023). Topological Comparison of Some Dimension Reduction Methods Using Persistent Homology on EEG Data. Axioms, 12(7), 699. https://doi.org/10.3390/axioms12070699






