Numerical Analysis of New Hybrid Algorithms for Solving Nonlinear Equations
Abstract
1. Introduction
2. Classical Methods
2.1. Bisection Method
2.2. Trisection Method
2.3. False Position (Regula Falsi) Method
2.4. Modified False Position Method
3. Hybrid Algorithms
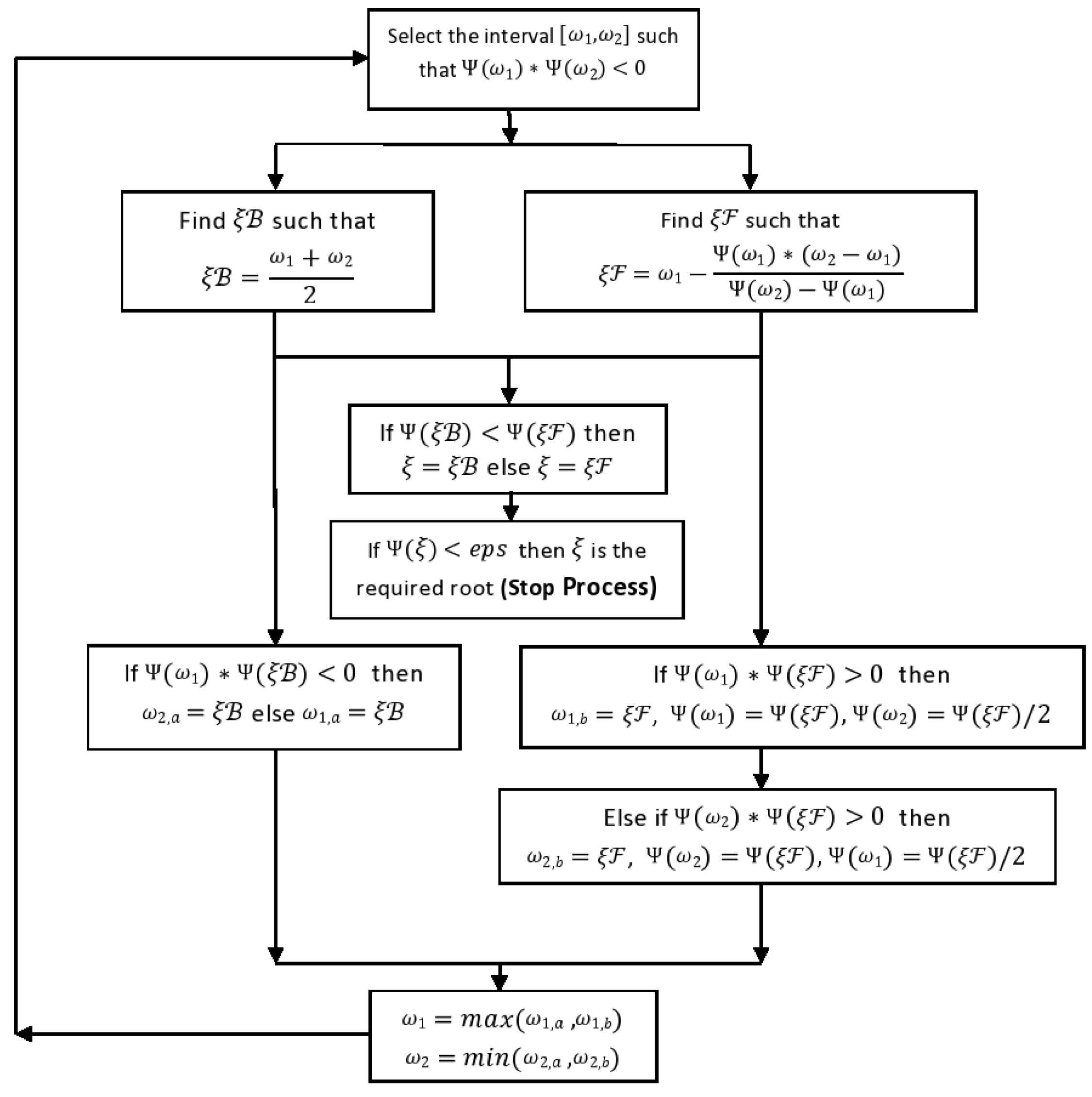
3.1. Bisection-Modified False Position Method
| Algorithm 1: Hybrid Bi-MRF . |
|
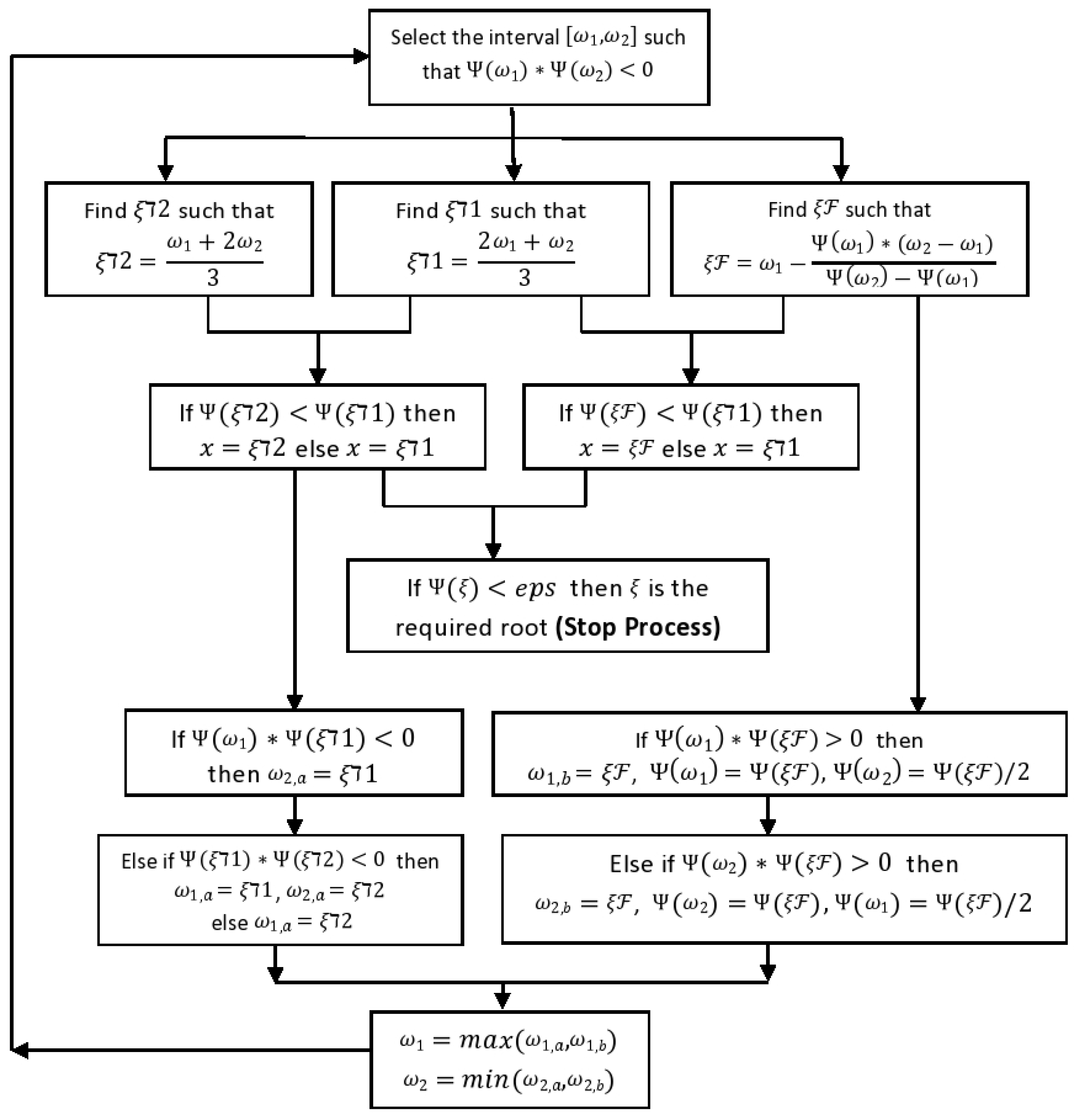
3.2. Trisection-Modified False Position Method
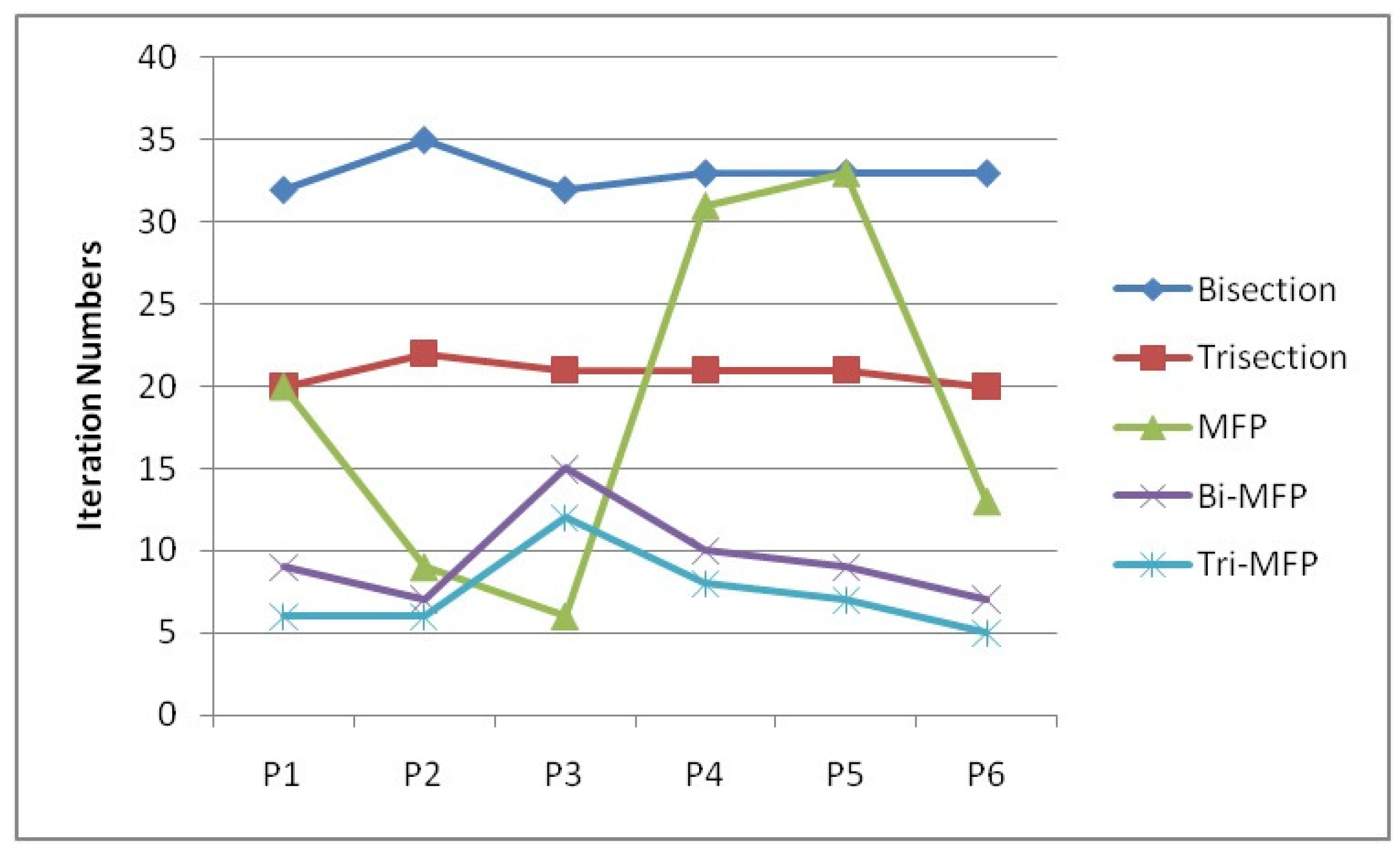
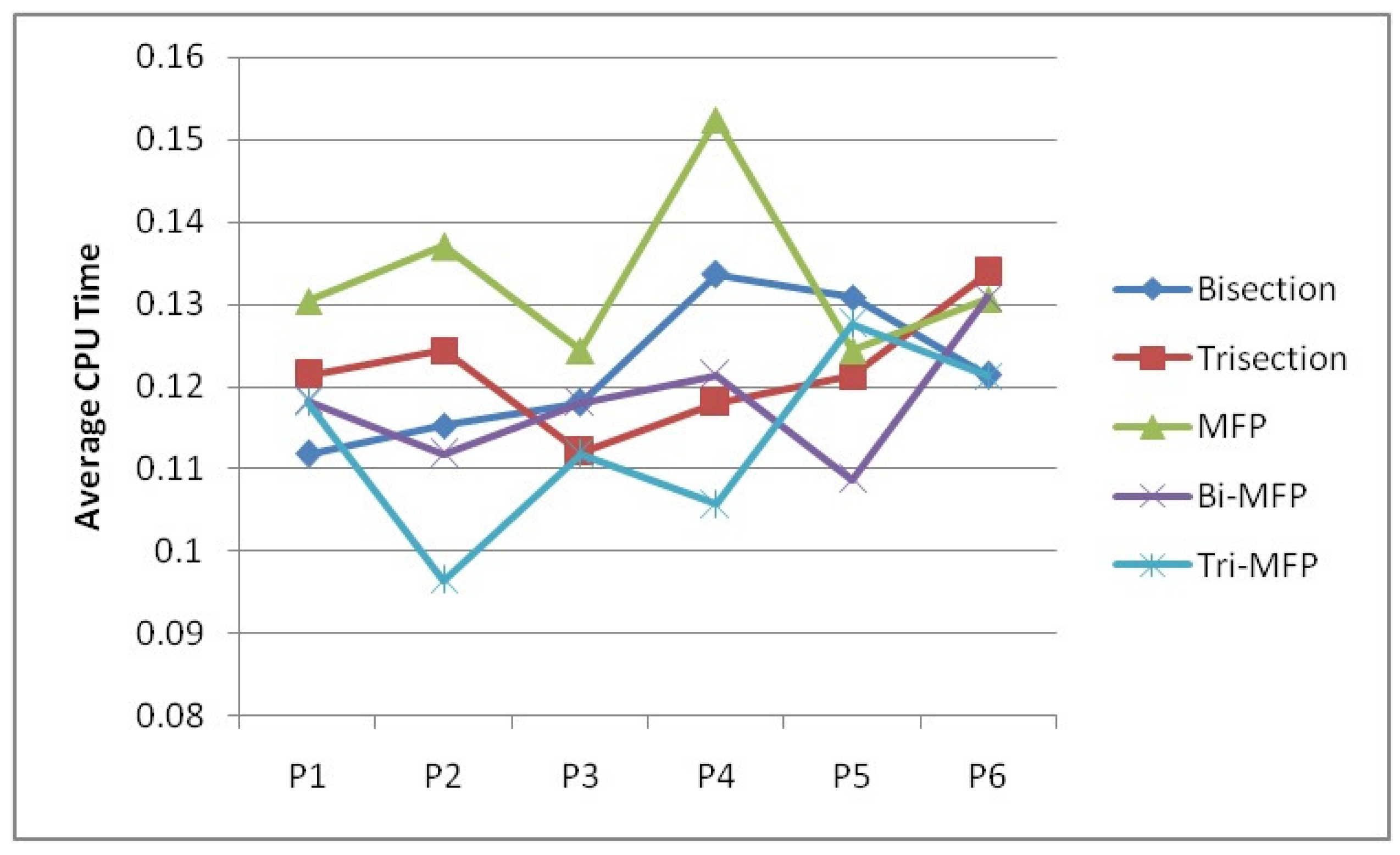
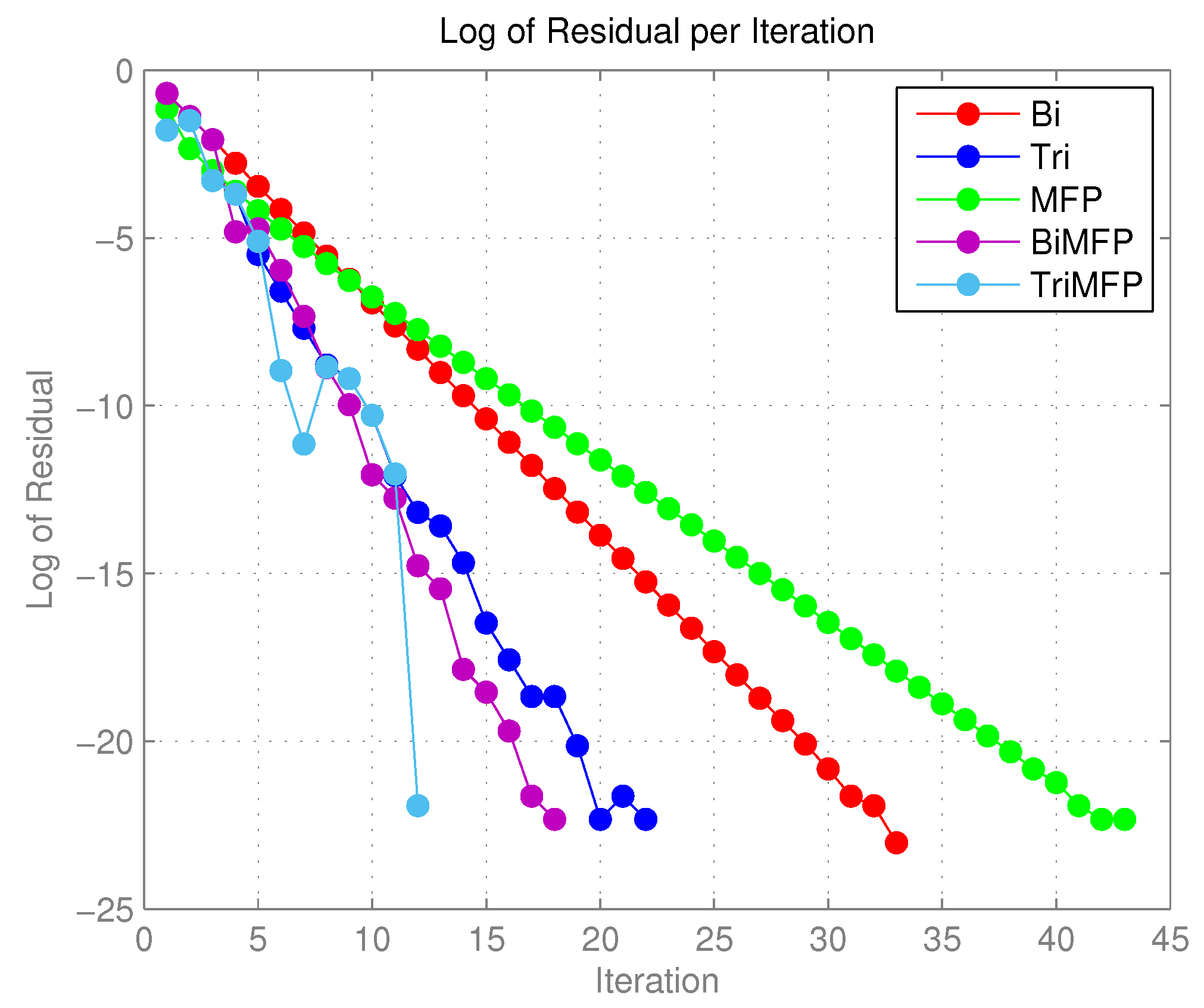
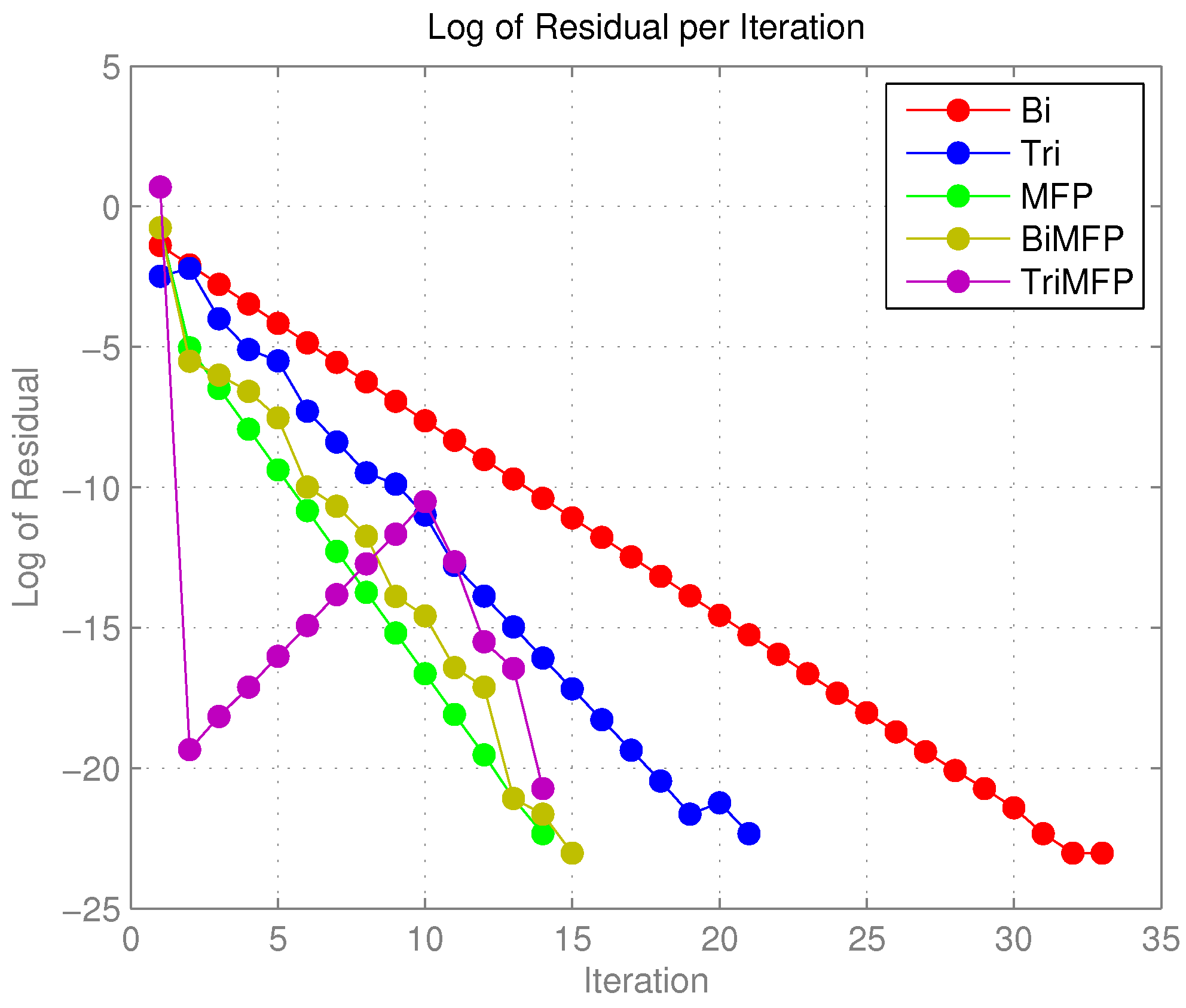
3.3. Empirical Study
| Algorithm 2: Hybrid Tri-MRF . |
|
3.4. Some New Numerical Experiments
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Burden, R.L.; Faires, J.D. Numerical Analysis, 9th ed.; Brooks/Cole, Cengage Learning: Boston, MA, USA, 2011. [Google Scholar]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers, 7th ed.; McGraw-Hill: Boston, MA, USA, 2015. [Google Scholar]
- Ehiwario, J.C.; Aghamie, S.O. Comparative Study of Bisection, Newton-Raphson and Secant Methods of Root-Finding Problems. IOSR J. Eng. 2014, 4, 1–7. [Google Scholar]
- Ernst, T. A method for q-calculus. J. Nonlinear Math. Phys. 2003, 10, 487–525. [Google Scholar] [CrossRef]
- Esfandiari, R.S. Numerical Methods for Engineers and Scientists Using MATLAB; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Harder, D.W.; Khoury, R. Numerical Methods and Modelling for Engineering; Springer International Publishing: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Joe, D.H. Numerical Methods for Engineers and Scientists, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Kac, V.; Cheung, P. Quantum Calculus; Springer: New York, NY, USA, 2002. [Google Scholar]
- Khan, A.G.; Ameen, F.; Awan, M.U.; Nonlaopon, K. Some new numerical schemes for finding the solutions to nonlinear equations. AIMS Math. 2022, 7, 18616–18631. [Google Scholar] [CrossRef]
- Mathews, J.H.; Fink, K.D. Numerical Methods Using Matlab, 4th ed.; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 2004; ISBN 0-13-065248-2. [Google Scholar]
- Nonlaopon, K.; Khan, A.G.; Ameen, F.; Awan, M.U.; Cesarano, C. Multi-Step Quantum Numerical Techniques for Finding the Solutions of Nonlinear Equations. Mathematics 2022, 10, 2595. [Google Scholar] [CrossRef]
- Nonlaopon, K.; Khan, A.G.; Ameen, F.; Awan, M.U.; Cesarano, C. Some New Quantum Numerical Techniques for Solving Nonlinear Equations. Symmetry 2022, 14, 1829. [Google Scholar] [CrossRef]
- Noor, M.A. Fifth-order convergent iterative method for solving nonlinear equations using quadrature formula. J. Math. Control Sci. Appl. 2018, 4, 95–104. [Google Scholar]
- Sana, G.; Mohammed, P.O.; Shin, D.Y.; Noor, M.A.; Oudat, M.S. On iterative methods for solving nonlinear equations in quantum calculus. Fractal Fract. 2021, 5, 60. [Google Scholar] [CrossRef]
- Srivastava, R.B.; Srivastava, S. Comparison of numerical rate of convergence of bisection, Newton and secant methods. J. Chem. Biol. Phys. Sci. 2011, 2, 472–479. [Google Scholar]
- Badr, E.; Almotairi, S.; Ghamry, A.E. A Comparative Study among New Hybrid Root Finding Algorithms and Traditional Methods. Mathematics 2021, 9, 1306. [Google Scholar] [CrossRef]
- Sabharwal, C.L. Blended root finding algorithm outperforms bisection and Regula Falsi Algorithms. Mathematics 2019, 7, 1118. [Google Scholar] [CrossRef]
- Novak, E.; Ritter, K.; Wozniakowski, H. Average-case ompitmality of a hybrid secant-bisection method. Math. Comput. 1995, 64, 1517–1539. [Google Scholar] [CrossRef]
- Badr, H.; Attiya, S.; Ghamry, A.E. Novel hybrid algorithms for root determining using advantages of open methods and bracketing methods. Alex. Eng. J. 2022, 61, 11579–11588. [Google Scholar] [CrossRef]
- Hasan, A.; Ahmad, N. Compartive study of a new iterative method with that Newtons Method for solving algebraic and transcesental equations. Int. J. Comput. Math. Sci. 2015, 4, 32–37. [Google Scholar]
- Fournier, R.L. Basic Transport Phenomena in Biomedical Engineering; Taylor and Francis: New York, NY, USA, 2007. [Google Scholar]
- Zafar, F.; Cordero, A.; Torregrosa, J.R. An efficient family of optimal eighth-order multiple root finders. Mathematics 2018, 6, 310. [Google Scholar] [CrossRef]

| No. | Problem | Interval | References |
|---|---|---|---|
| P1 | Calihoun [13] | ||
| P2 | Ehiworio [3] | ||
| P3 | Mathews [18] | ||
| P4 | Esfandiari [17] | ||
| P5 | Hoffman [14] | ||
| P6 | Chapra [11] |
| Problems | Bisection Method | |||||
|---|---|---|---|---|---|---|
| Iter | Average CPU Time | Approx Root | Function Value | Lower Bound | Upper Bound | |
| P1 | 32 | 0.1118 | 1.52434520468 | 1.52434520422 | 1.52434520515 | |
| P2 | 35 | 0.1152 | 0.739085134091 | 0.739085134062 | 0.739085134119 | |
| P3 | 32 | 0.1180 | 1.11415714072 | 1.11415714026 | 1.11415714119 | |
| P4 | 33 | 0.1336 | 3.22158839905 | 3.22158839876 | 3.22158839934 | |
| P5 | 33 | 0.1308 | 2.12539119889 | 2.12539119854 | 2.12539119923 | |
| P6 | 33 | 0.1214 | 0.876726215414 | 0.876726215355 | 0.876726215471 | |
| Problems | Trisection Method | |||||
|---|---|---|---|---|---|---|
| Iter | Average CPU Time | Approx Root | Function Value | Lower Bound | Upper Bound | |
| P1 | 20 | 0.1214 | 1.52434520541 | 1.52434520484 | 1.52434520656 | |
| P2 | 22 | 0.1244 | 0.739085133325 | 0.739085133262 | 0.739085133357 | |
| P3 | 21 | 0.1120 | 1.11415714133 | 1.11415714114 | 1.11415714171 | |
| P4 | 21 | 0.1180 | 3.22158839889 | 3.22158839841 | 3.22158839913 | |
| P5 | 21 | 0.1212 | 2.12539119879 | 2.12539119823 | 2.12539119908 | |
| P6 | 20 | 0.1338 | 0.876726215456 | 0.876726215170 | 0.876726215600 | |
| Problems | Modified Regula Falsi Method | |||||
|---|---|---|---|---|---|---|
| Iter | Average CPU Time | Approx Root | Function Value | Lower Bound | Upper Bound | |
| P1 | 20 | 0.1304 | 1.52434520493 | 1.52434520482 | 2.0000000000 | |
| P2 | 9 | 0.1370 | 0.739085133213 | 0.739085133171 | 1.0000000000 | |
| P3 | 6 | 0.1244 | 1.11415714087 | 1.11415714087 | 1.11415714304 | |
| P4 | 31 | 0.1524 | 3.22158839849 | 3.22158839777 | 4.0000000000 | |
| P5 | 33 | 0.1244 | 2.12539119823 | 2.12539119761 | 3.0000000000 | |
| P6 | 13 | 0.1306 | 0.876726215392 | 0.876726215372 | 1.0000000000 | |
| Problems | Bisection-Modified Regula Falsi Method | |||||
|---|---|---|---|---|---|---|
| Iter | Average CPU Time | Approx Root | Function Value | Lower Bound | Upper Bound | |
| P1 | 9 | 0.1182 | 1.52434520539 | 1.52434520445 | 1.52772146940 | |
| P2 | 7 | 0.1118 | 0.739085133226 | 0.739085129706 | 0.745369013289 | |
| P3 | 15 | 0.1180 | 1.11415714088 | 1.11414625500 | 1.11425614878 | |
| P4 | 10 | 0.1214 | 3.22158839955 | 3.22158839943 | 3.22238911820 | |
| P5 | 9 | 0.1086 | 2.12539119894 | 2.12539118521 | 2.12787084220 | |
| P6 | 7 | 0.1308 | 0.876726215441 | 0.876726210685 | 0.877268445426 | |
| Problems | Trisection-Modified Regula Falsi Method | |||||
|---|---|---|---|---|---|---|
| Iter | Average CPU Time | Approx Root | Function Value | Lower Bound | Upper Bound | |
| P1 | 6 | 0.1180 | 1.52434520508 | 1.52434520413 | 1.52441127915 | |
| P2 | 6 | 0.0964 | 0.739085133236 | 0.739085133117 | 0.739643235290 | |
| P3 | 12 | 0.1118 | 1.11415714132 | 1.11415714046 | 1.11415841776 | |
| P4 | 8 | 0.1056 | 3.22158839889 | 3.22158839878 | 3.22215305257 | |
| P5 | 7 | 0.1276 | 2.12539119914 | 2.12539119840 | 2.12548466697 | |
| P6 | 5 | 0.1212 | 0.876726215473 | 0.876726215114 | 0.876727040681 | |
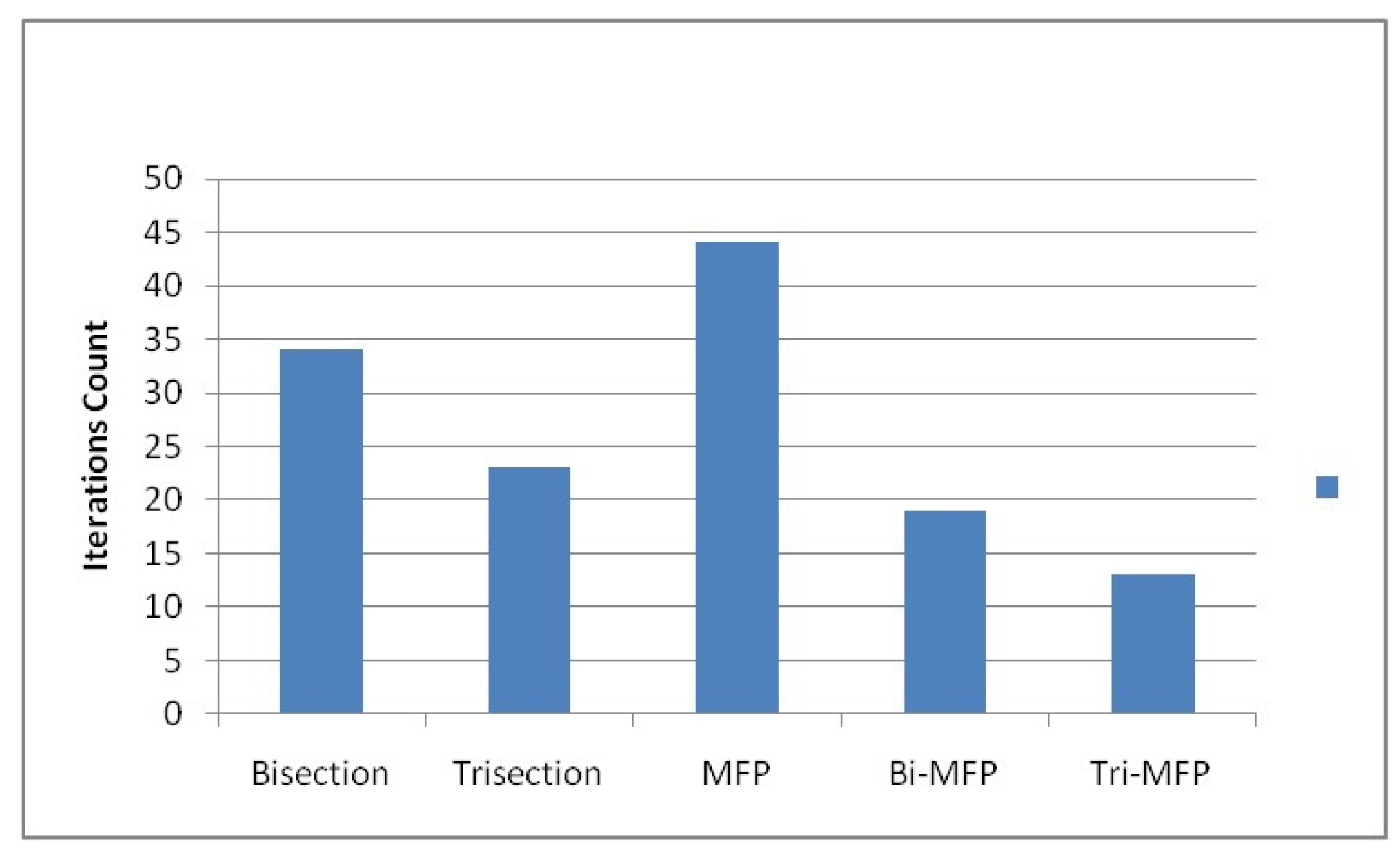
| Method | Blood Rheology and Fractional Nonlinear Equations Model | ||||
|---|---|---|---|---|---|
| Iter | Approx Root | Function Value | Lower Bound | Upper Bound | |
| Bisection | 34 | 0.104698652342 | 0.104698652284 | 0.104698652401 | |
| Trisection | 23 | 0.104698652104 | 0.104698652083 | 0.104698652115 | |
| MFP | 44 | 0.104698651667 | 0.000000000000 | 0.104698651748 | |
| Bi-MFP | 19 | 0.104698651542 | 0.104698181152 | 0.104701995849 | |
| Tri-MFP | 13 | 0.104698651485 | 0.104698357861 | 0.104700239538 | |
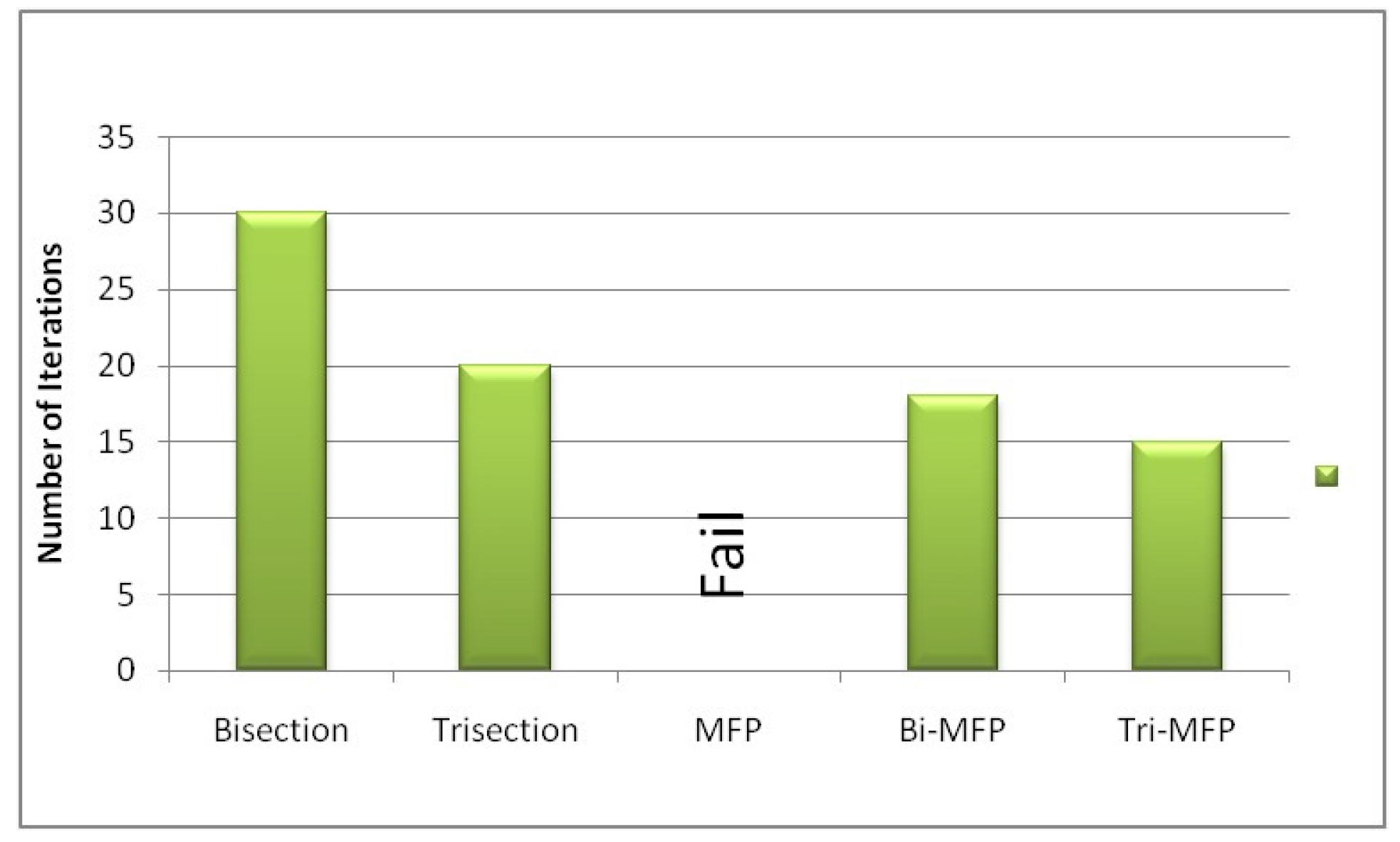
| Method | Fluid Permeability in Biogels | ||||
|---|---|---|---|---|---|
| Iter | Approx Root | Function Value | Lower Bound | Upper Bound | |
| Bisection | 30 | 1.00003698747 | 1.00003698654 | 1.00003698840 | |
| Trisection | 20 | 1.00003698880 | 1.00003698823 | 1.00003698909 | |
| MFP | Fail | ||||
| Bi-MFP | 18 | 1.00003698850 | 1.00003698808 | 1.00003699241 | |
| Tri-MFP | 15 | 1.00003698885 | 1.00003698848 | 1.00003699616 | |
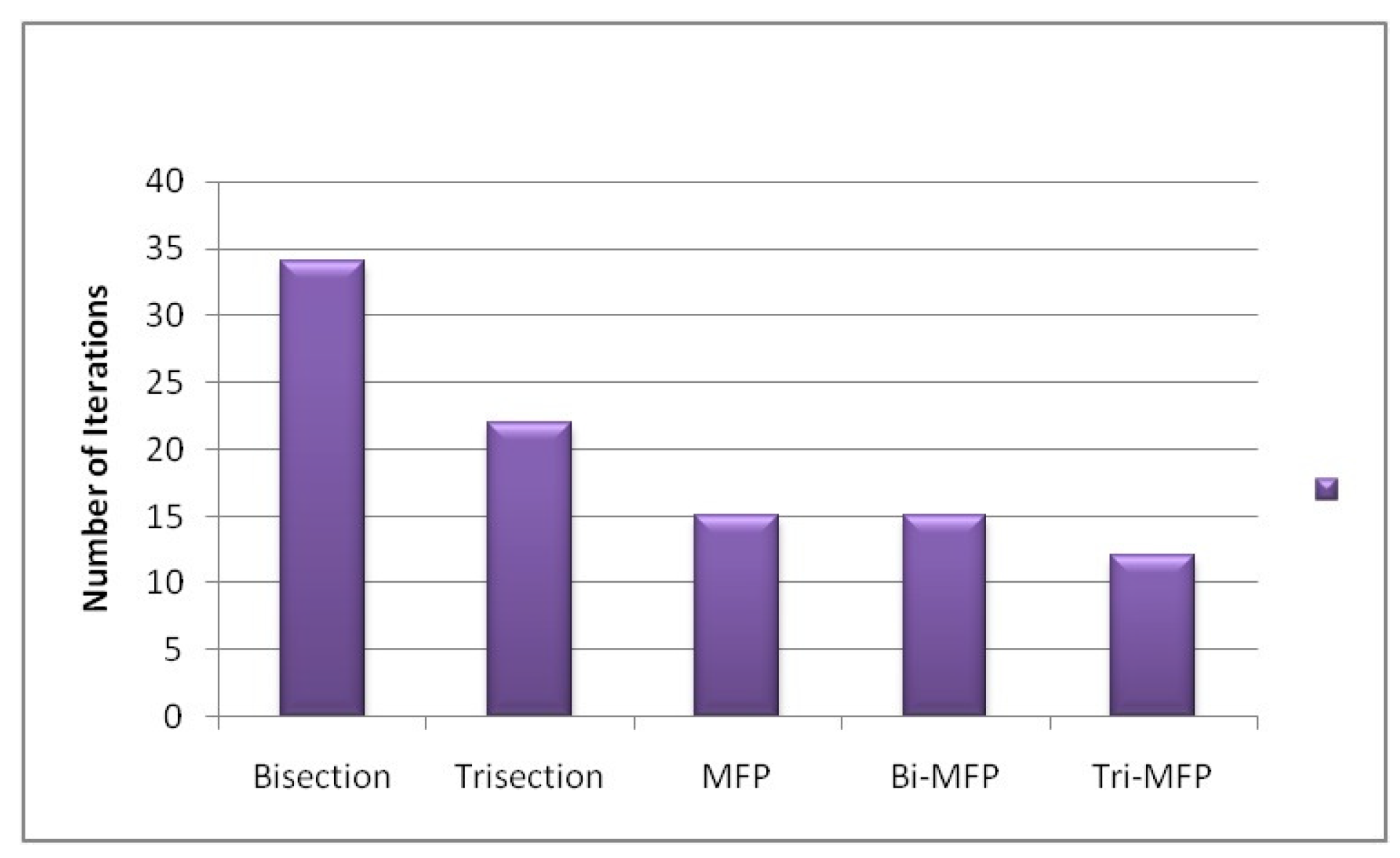
| Method | Beam Position Model | ||||
|---|---|---|---|---|---|
| Iter | Approx Root | Function Value | Lower Bound | Upper Bound | |
| Bisection | 34 | −0.535898384669 | −0.535898384698 | −0.535898384639 | |
| Trisection | 22 | −0.535898384057 | −0.535898384089 | −0.535898384042 | |
| MFP | 15 | −0.535898384849 | −1.000000000000 | −0.535898384808 | |
| Bi-MFP | 15 | −0.535898384738 | −0.535919189454 | −0.535888671875 | |
| Tri-MFP | 12 | −0.535898384898 | −0.535899563639 | −0.535896741125 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vivas-Cortez, M.; Ali, N.Z.; Khan, A.G.; Awan, M.U. Numerical Analysis of New Hybrid Algorithms for Solving Nonlinear Equations. Axioms 2023, 12, 684. https://doi.org/10.3390/axioms12070684
Vivas-Cortez M, Ali NZ, Khan AG, Awan MU. Numerical Analysis of New Hybrid Algorithms for Solving Nonlinear Equations. Axioms. 2023; 12(7):684. https://doi.org/10.3390/axioms12070684
Chicago/Turabian StyleVivas-Cortez, Miguel, Naseem Zulfiqar Ali, Awais Gul Khan, and Muhammad Uzair Awan. 2023. "Numerical Analysis of New Hybrid Algorithms for Solving Nonlinear Equations" Axioms 12, no. 7: 684. https://doi.org/10.3390/axioms12070684
APA StyleVivas-Cortez, M., Ali, N. Z., Khan, A. G., & Awan, M. U. (2023). Numerical Analysis of New Hybrid Algorithms for Solving Nonlinear Equations. Axioms, 12(7), 684. https://doi.org/10.3390/axioms12070684








