Abstract
A new fault detection and identification approach is proposed. The kernel principal component analysis (KPCA) is first applied to the data for reducing dimensionality, and the occurrence of faults is determined by means of two statistical indices, T2 and Q. The K-means clustering algorithm is then adopted to analyze the data and perform clustering, according to the type of fault. Finally, the type of fault is determined using a long short-term memory (LSTM) neural network. The performance of the proposed technique is compared with the principal component analysis (PCA) method in early detecting malfunctions on a continuous stirred tank reactor (CSTR) system. Up to 10 sensor faults and other system degradation conditions are considered. The performance of the LSTM neural network is compared with three other machine learning techniques, namely the support vector machine (SVM), K-nearest neighbors (KNN) algorithm, and decision trees, in determining the type of fault. The results indicate the superior performance of the suggested methodology in both early fault detection and fault identification.
Keywords:
fault detection and identification; kernel principal component analysis; artificial neural network MSC:
62M45; 62H30; 91C20; 94C12
1. Introduction
Fault detection and identification play a critical role in various fields, contributing to the overall safety, reliability, and efficiency of systems and processes. It is crucial across different domains, such as manufacturing, chemical processing, power generation, oil and gas distribution, transportation and automotive systems, energy and utilities, aerospace, defense, smart infrastructures, environmental monitoring, and medical devices and healthcare.
In modern industrial systems, fault detection and identification is a key requirement. Because control systems are becoming more complex and data dimensionality is growing, a fault can result in catastrophic harm. Indeed, in the worst circumstances, system failure may result in human injuries, as well as damage with significant economic impact, concerning production items, devices, and equipment. Control engineers are therefore focused on researching effective fault detection and identification techniques. Improving speed and efficiency, optimizing the management of systems and their maintenance, increasing the reliability and health of systems, maximizing production, and minimizing repair time, are additional reasons to address fault detection and identification.
Ensuring the system’s continuously safe or, at least, acceptable operation requires appropriate fault detection and isolation mechanisms, which are able to distinguish between non-faulty and faulty system behavior and find the location and nature of the fault in case some abnormal condition is signalized. Often, controller reconfiguration is required in response to the fault [1,2].
Several methods for detecting faults have been proposed. Finding or creating methods exhibiting high accuracy and speed for dealing with a system’s faults is the most crucial issue. Indeed, after a fault occurs, there is not much time to identify it, and thus, immediate actions are required to minimize the damage. In light of this, if the method chosen for fault detection and identification is not reliable, then incorrect actions may result, and the fault may spread to additional layers of the system. Even though the fault’s primary cause may be unknown, it is crucial that it can be determined through diagnosis. The sort of fault that occurred must also be identified after the issue has been located. To prevent the fault from spreading to higher levels, the system’s component where the problem occurred can be temporarily removed by identifying the type of fault [3].
A fault is defined by the International Federation of Automatic Control (IFAC) Technical Committee as an unapproved deviation of at least one characteristic or system parameter from the conditions that are considered acceptable/normal/standard. Such a problem can affect a single process, set of sensors, or set of actuators [1,2].
In general, three categories of faults have been taken into account in earlier studies [1]:
- (1)
- Process or component fault: Process faults arise when a system’s components behave negatively, affecting the dynamics of the system.
- (2)
- Actuator fault: An actuator fault is a discrepancy between the actuator’s input command and its actual output.
- (3)
- Sensor fault: Sensor faults result in discrepancies between the measured and real values of the system’s variables [1,4].
This article looks at approaches that are currently available for diagnosing and identifying faults in control systems, combining them to provide a new technique for accurate diagnosis and fault-type identification. In the devised approach, kernel principal component analysis (KPCA) is first used to minimize the dimensions of the data collected from the system. This streamlines computations and expedites the fault-finding procedure. Then, the presence of a fault in the system is detected using statistical indices, which are assigned threshold values in such a way that whenever the required statistical indices surpass some upper limits, a warning is sent, denoting that a fault has occurred. The K-means algorithm is adopted for data clustering as a step to determine the type of fault. The data are separated into three groups, and clustering is carried out for each category in accordance with the variation range of the variables. The type of fault is then determined using a long short-term memory (LSTM) artificial neural network, meaning a recurrent neural network with extremely high accuracy. The labeled data in the K-means algorithm is used to train the LSTM. The proposed technique is tested for detecting malfunctions on a continuous stirred tank reactor (CSTR) system when considering up to 10 sensor faults and other system abnormal conditions. The effectiveness of the method is compared with the principal component analysis (PCA) approach for fault detection, and with the support vector machine (SVM), K-nearest neighbors (KNN), and decision trees algorithms, for determining the type of fault. The results show the superior performance of the proposed methodology in both fault detection and fault identification.
The paper is structured as follows. Section 2 reviews prior studies on fault detection and identification. Section 3 introduces the proposed approach. Section 4 presents the CSTR system used as a test bed. Section 5 reports several simulation results to illustrate the effectiveness of the new method. Finally, Section 6 presents the main conclusions.
2. Literature Review
There are two primary categories of fault detection and identification approaches. These are statistical methods and machine learning techniques. A statistical method for fault detection and isolation utilizing inverse dynamic models for robot arms and partial least squares (PLS) was provided in [5]. The PLS is a linear process control technique used to locate and monitor industrial processes. The PCA employing a serial model structure, often known as serial PCA (SPCA), as a new linear-nonlinear statistical method for nonlinear process monitoring was reported in [6]. A machine learning approach based on the SVM for fault detection was employed in [7]. By categorizing the data linked to the fault and the data connected to the system’s typical operation period, the SVM could detect faults. This approach was thought to be a simple way to identify sensor failures. Using convolutional neural networks (CNN), a highly precise modular multilevel converter (MMC) circuit monitoring system for early failure detection and identification was proposed in [8]. Reference [9] described a technique using Bayesian networks to identify sensor and process faults, as well as faults involving several sensors or processes. A new hybrid system based on the Hilbert–Huang (HH) transform and the adaptive neuro-fuzzy inference system (ANFIS) with optimal parameters was proposed in [10]. As a detection index for the KNN-based fault detection approach, which could separate several sensor faults, a new separation index using KNN distance decomposition was provided in [11]. Reference [12] presented the development of two independent reduced kernel partial least squares (IRKPLS) regression models for fault detection in large-scale nonlinear and uncertain systems. The use of a weighted kernel independent component analysis (WKICA) based Gaussian mixed model (GMM) for monitoring and fault identification in nonlinear and non-Gaussian processes was proposed in [13]. The probabilities of KICA were estimated using GMM for the first time in the WKICA approach. A model for fault identification using a variational Bayesian Gaussian mixture model with canonical correlation analysis (VBGMM-CCA) was provided in [14]. In Reference [15], a method for fault detection and identification was suggested, which combined artificial neural networks (ANN) and the wavelet transform (WT) multi-loop analysis methodology. A novel method for fault identification was provided in [16], which was based on KPCA and SVM.
Motivated by the above discussion, the present paper proposes a novel method that integrates KPCA, K-means, and LSTM neural networks for detecting and identifying faults in multi-process systems. The method introduces several unique aspects that differentiate it from existing approaches and offers improved fault detection and identification performance.
The main contributions of this paper are:
- The KPCA is performed to decrease the dimension of the original data set while detecting the existence of potential faults. Thus, in subsequent fault identification steps, computational burden and transmission energy consumption is reduced, which is very important in wireless sensor networks.
- In the reduced data space, the K-means is used for clustering data into different groups and detecting faults using statistics. By using clustering, faults in different processes can be detected, which is an advantage typically overlooked in traditional approaches.
- An LSTM network is trained in order to identify faults by reconstruction. The LSTM excels at capturing temporal dependencies in sequential data, identifying fault patterns that unfold over time. This temporal modeling capability enhances fault identification and enables the detection of complex and dynamic fault scenarios.
- Simulations demonstrate the effectiveness of the method in the detection and identification of faults. Thus, based on measured data, the method can identify crashed sensors and actuators and components’ misbehavior.
By combining KPCA for fault detection, K-means for data preparation, and LSTM for fault identification, the proposed approach offers a unique and comprehensive solution to fault detection and identification. It surpasses the limitations of individual methods by integrating nonlinear feature extraction, clustering-based data preparation, and temporal modeling. This integration leads to improved fault detection and identification performance, enabling the system to handle complex fault dynamics, adapt to different fault types, and achieve accurate fault identification. To the best of the authors’ knowledge, the work proposed herein is the first to effectively combine those three algorithms together for the actual detection and identification of faults.
3. The Proposed Method
The new hybrid technique for detecting and identifying faults is illustrated in Figure 1. The KPCA is initially used for fault diagnosis, which may trigger subsequent fault identification. Thus, once a fault is detected, the data are tagged using K-means clustering, as a preparation for the next stage of fault identification, based on their embedded inter-distances. Finally, an LSTM neural network determines the type of fault. Thus, the method consists of three fundamental steps:
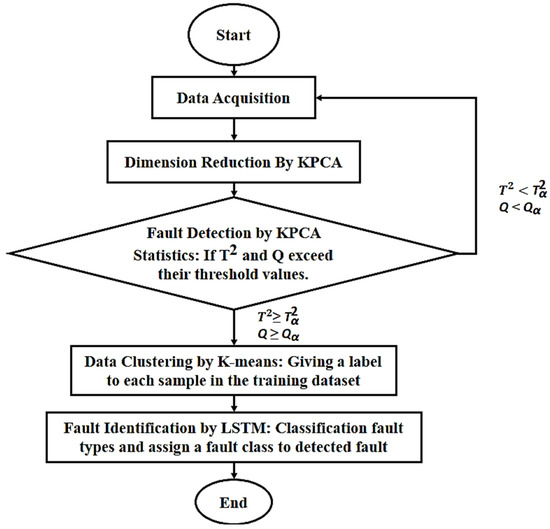
Figure 1.
Overview of the proposed method.
- The KPCA for fault detection.
- The K-means clustering for processing faulty data.
- The LSTM neural network for determining the fault type.
These steps are described in the next subsections.
3.1. Fault Detection by KPCA
This step results in data dimensionality reduction in addition to reliable and fast fault detection in nonlinear data. The KPCA is a generalization of the PCA method and one of the most cutting-edge approaches for leveraging kernel functions to monitor nonlinear systems [17,18]. The rationale of KPCA is to extract the nonlinear principal components from the PCA decomposition in the feature space after first mapping the original input data to a high-dimensional defined space using a nonlinear function. In other words, let us consider that the data consists of N observations, , k = 1, …, N, where u and y are the input and output of the process, respectively [18]. The data are normalized, yielding , so that their mean is zero and their variance is equal to one. In the PCA, features are extracted only in a linear space. Therefore, we must first use the nonlinear mapping Φ(·) to represent the data from the original nonlinear input space onto a linear feature one, F, assuming that is used [18].
The PCA seeks to solve the eigenvalue problem in the covariance matrix in the linear space F as given by [18]:
where is the sample covariance in the F space, w denotes the eigenvector, and λ is the eigenvalue. To avoid the explicit use of Φ(·), the kernel functions K are defined in the form [18]:
where w and:
where v is the eigenvector and is defined as [18]:
where and . Then, using the matrix obtained from Equation (4), the SVD decomposition is performed [18]:
where S contains N eigenvectors of v, and contains N eigenvalues of λ. Next, only r main components that contain 99% of the variances remain and are placed in the matrix such that [18]:
Each test data is normalized and converted into , and then it is mapped to the F space according to [18]:
where is the training data from j = 1, …, N and is normalized according to:
and, finally:
To identify the fault by KPCA, two statistical indices and Q are generally used [18]. The values of these two parameters are obtained by:
A threshold value is defined for each index. If and Q exceed their threshold values; then it means that there is a fault in the system.
The threshold values are defined as [18]:
where r is the number of remaining principal components, is the value of the F distribution corresponding to a significance level α, with degrees of freedom r and m − r for numerator and denominator, respectively, , and [17]. In this paper, the two statistical indices and Q are calculated, and then, by determining and , the occurrence of a fault is detected [18].
3.2. Faulty Data Labeling Using the K-Means Technique for Clustering
The faulty data must be labeled in a consistent manner after the fault has been found in order to enter and train the neural network. The data are labeled using the K-means clustering algorithm, a subset of machine learning. By giving a label to each sample in the training dataset, the approach simplifies the data for the neural network and improves network learning. Following data labeling, the LSTM network performs data classification among various types of faults by learning about the different types. In order to obtain insight into the structure of the data, one of the most popular exploratory data analysis approaches is clustering, which is in charge of identifying subgroups in the data so that that points can be grouped together. While data points in various clusters are highly varied, data points within a subgroup (cluster) are very similar. The unsupervised learning algorithm K-means divides unlabeled datasets into K groups, specifying in advance how many clusters will be produced. This approach enables the grouping of data into many categories and can be used to indicate the grouping of a set of unlabeled data. Each cluster has a center because it is a center-based algorithm. This algorithm’s major objective is to reduce the overall distance between data points and the clusters that correspond to those locations. This algorithm separates the input unlabeled dataset into K clusters and then iterates through the clusters until it finds the best ones. Essentially, the K-means clustering method does two things:
- Utilizes an iterative technique to choose the greatest value for K center points.
- Chooses the closest K center for each data point. A cluster is formed by the data points that are near the K’s center.
As a result, each cluster is distinct from the others while sharing some characteristics with the data [19]. K-means clustering is utilized in this paper to prepare the data before it is fed into the neural network.
3.3. Using an LSTM Neural Network to Identify the Type of Fault
When the KPCA detects a fault, its source must be quickly determined using a highly accurate procedure. This paper introduces a novel approach to fault detection using an LSTM neural network. This network has very high accuracy in fault identification because of its recursive structure. Additionally, compared to other machine learning techniques, the inclusion of long-term memory makes this network a powerful tool for fault identification. The K-means approach is used to train the LSTM network with clustered training data, which represent various kinds of faults. The network then assigns a category to any fault whenever new data arrives.
The LSTM is an improvement on the recurrent neural network, which is often applied to time series, such as speech recognition or natural language processing. Gradient vanishing is a problem in long time series, in which the weights of neural networks do not update well [20]. The LSTM can eliminate this problem by adjusting the amount of information within a cell through the forget gate, input gate, and output gate. A forget gate specifies how much information should be forgotten from previous cells. Input gates determine how much information the current input value will receive, whereas output gates determine how much information the cell should transmit. The useful information can be stored for a long time using these three gates, while the useless information can be forgotten [21].
In order to develop good LSTM models, the appropriate parameters must be found. The LSTM model for fault identification requires parameters such as hidden state dimension, optimizer type, regularization degree, and dropout rate. Training the LSTM models requires the first two parameters while avoiding overfitting requires the last two.
The dimensionality of hidden states refers to the size of the shared weight matrix, which should be determined by considering the training data size. The optimizer finds the global optimum of the loss function. Among the candidates for the proper optimizer are RMSprop, AdaGrad, and Adam. It is necessary to adjust the learning rate during the training process and check the trend of error decrease to prevent falling into a local optimum [22].
In the meantime, big neural network models often suffer from overfitting. Regularization, which gives penalties corresponding to the big weights, is helpful in preventing the issue. Regularization must be adjusted to the appropriate degree. The dropout method prevents overfitting by ignoring some weights randomly depending on the training dropout rate. In addition to improving the representation of training data, the method can also prevent overfitting [22].
In this paper, the LSTM network incorporates a hidden state with a dimension of 100. This hidden state allows the network to capture and remember relevant information from previous time steps, enabling it to learn long-term dependencies in the data. The Adam optimizer is selected to optimize the network’s performance during training, combining the benefits of adaptive learning rates and momentum-based updates. Additionally, a lambda value of 0.1 is set for kernel regularization, which helps to prevent overfitting by adding a penalty term to the loss function. Moreover, a dropout rate of 0.3 is implemented within the model. Dropout randomly sets a fraction of the LSTM units to zero during training, reducing the network’s reliance on specific units and improving its ability to generalize to unseen data. A minimum batch size of 32 is chosen, specifying the number of samples processed before the weights are updated. These configurations collectively contribute to the LSTM network’s ability to effectively capture complex temporal patterns and generalize well to new data.
There are also advanced models of LSTMs, which are briefly mentioned. The bidirectional LSTM (bi-LSTM) refers to a neural network that stores sequence information in both backward (future to past) and forward (past to present) directions. Thus, a bidirectional LSTM is characterized by input flowing in both directions. Standard LSTMs can only deal with input flow in one direction, either backward or forward. By contrast, bi-directional input can preserve past and future information by handling flowing in both directions [23,24]. Another advanced LSTM method is the dual-LSTM, which consists of two parallel LSTM networks. In the dual channel LSTM model, the loss is minimized with the objective of obtaining the optimum weights and biases [25].
In this paper, in order to determine the efficacy and accuracy of the proposed method for identifying faults in a CSTR system, conventional methods of fault identification provided by other researchers are used for comparison. Typical machine learning techniques, such as SVM, KNN, and decision trees, are considered.
3.4. SVM-Based Fault Type Identification
The SVM is a supervised machine learning technique that can be applied to problems involving classification or regression. Each data point is represented as a point in an n-dimensional space (n being the number of features), where each feature corresponds to a particular coordinate. After that, classification is carried out by locating a hyperplane that categorizes the data into various groups. Both linear and nonlinear issues can be resolved with SVM [26]. The SVM approach is used in this paper to identify the categories of faults while comparing it with the proposed approach.
3.5. KNN-Based Fault Type Identification
The KNN is a form of supervised learning algorithm that measures the distance between the test data and all training points in an effort to predict the right class of test data. The KNN method chooses K points that are relatively close to the test data. The test data are then assigned to the category with the highest probability out of the many training data categories that have been chosen after calculating their probabilities [11]. The KNN is used in this paper to identify faults and for comparison purposes.
3.6. Decision Trees Based Fault Type Identification
The supervised learning algorithm family includes the decision tree algorithm. There are roots, branches, nodes, and leaves in a decision tree. A batch of test data for prediction decision trees is started at the tree’s base. A feature whose value the test data is compared with is present at the root. The branch associated with that value is followed, and this branch finishes at a node based on the comparison. Every node has a feature, and the next branch is chosen by comparing the test data with that feature. The test data eventually reach a leaf that defines the test data’s category [27]. The decision tree is used in this study to identify the type of fault and compare its results with those of the proposed approach.
4. Description of the CSTR System
A CSTR is a type of reaction vessel where the products of the reaction simultaneously exit the vessel as reagents and reactants, and frequently solvents flow into the reactor. The tank reactor is regarded as a useful tool for continuous chemical processing. The composition of the material inside the reactor, which depends on residence time and reaction rate, should ideally match the composition of the exit. Several CSTRs may be joined together to form a parallel or linear series mode when the reaction is extremely slow or when there are two immiscible or viscous liquids that need high stirring speed [28].
A basic general model of a tank with a fixed cover, which continuously performs the first-order heat reaction, is shown in Figure 2 [29].
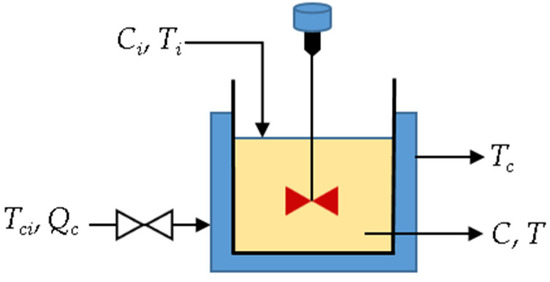
Figure 2.
Overview of the CSTR system [29].
The CSTR model when undergoing exothermic first-order reaction is given as [29]:
with inputs and outputs . Moreover, stands for the process noise, and is an Arrhenius rate constant. The parameters’ values in Equations (13)–(15), defined as in reference [29], are inlet flow rate Q = 100.0 L·min−1, tank volume V = 150.0 L, jacket volume Vc = 10.0 L, heat of reaction ∆Hr = −0.2 × 105 cal·mol−1, heat transfer coefficient UA = 7.0 × 105 cal·min−1·K−1, pre-exponential factor to k k0 = 7.2 × 1010 min−1, activation energy E/R = 104 K, fluid density ρ, ρc = 1000.0 g·L−1, and fluid heat capacity Cp, Cpc = 1.0 cal·g−1·K−1.
There are seven input and output variables in the system. Each variable is measured by a sensor properly located. In general, there are three types of variables: C, T, and Q, which are related to product concentration, reactor temperature, and inlet flow rate, respectively. For each sensor, there is a type of fault that can be considered. Due to the chemical nature of the system, it may also be subject to catalyst decay or fouling. As a result, component faults can also occur. Moreover, it is possible that input variables are noisy.
In this paper, we consider a total of 10 variables, including 7 input and output, as well as 3 noisy input variables. There is a wide range of data in this system, from very small to very large, depending on the variables. Considering this issue, besides reducing dimensions, the data need to be mapped. In order to improve training, 770 datasets from system faulty and regular operation data are used. Based on simulation experiments in MATLAB software and the lack of outliers, this number was found suitable for use.
A total of 10 categories of faults may exist in this system, where 7 are sensor faults corresponding to each input (4) and output (3) values, 1 is related to the degradation of the catalyst, and 1 is due to the buildup of heat transfer. The combination of these two also constitutes an additional fault. These last 3 faults are related to process faulty conditions and, thus, are considered the most critical ones. When there is no fault, the values of the parameters a and b in the CSTR system model (13)–(15) are equal to 1.00. It is feasible to replicate the deterioration of the catalyst and the deposition of heat transfer by reducing their values to zero. Table 1 summarizes the fault scenarios, as considered in reference [29]. The subscript 0 stands for nominal values and t is measured in minutes.

Table 1.
Scenarios of CSTR primary faults [29].
5. Simulation Results
The KPCA is used to find faults, as previously described. The method uses both faulty and normal system data. For this reason, samples from the CSTR were created, each having both normal and faulty data. The samples were prepared using the MATLAB software for simulating the CSTR system. For each type of fault, a data set of 300 samples was generated, which was sufficient for learning and characterizing the faults. To gather data for each fault, samples of normal operation were collected first in the simulation, followed by data of faulty operation, until the total number of samples reached 300. For example, in a dataset related to a particular type of fault, the normal data may be displayed from sample 1 to sample 120, while the faulty data appear from sample 121 onwards. Arranging the data in this way is arbitrary. The and Q indicators are used for fault detection. The simulation’s outcomes demonstrate how the first faulty sample was correctly identified. The simulation results for the second type of fault, which are present in samples 121 to 300, are shown in Figure 3.
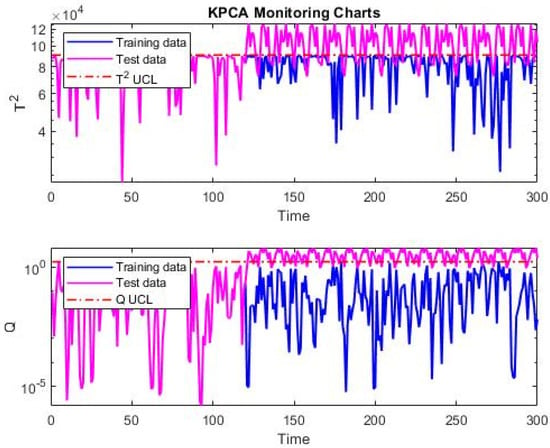
Figure 3.
Simulation results of fault detection by KPCA in the CSTR system.
As seen in Figure 3, sample 121 exhibits the occurrence of the fault. That is, in this kind of fault, the fault is found at the first occurrence it appears, demonstrating the method’s high degree of accuracy. Both the statistical indices and Q successfully identify this issue. Indeed, each of the 10 fault types is in a different range, as shown in Table 2, and is identified by the two indices. The results with the slightly differ from those with the Q index in terms of how well they identify the faults.

Table 2.
Fault sample detected by and Q for all fault types.
For comparison, the PCA approach was utilized for fault detection. Figure 4 depicts the results of the second kind of fault with PCA. We verify that the PCA approach does not effectively detect faults in nonlinear data.
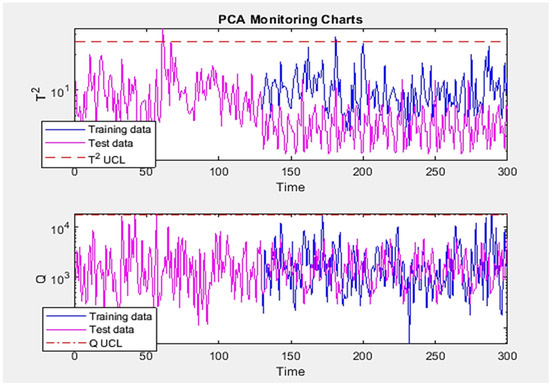
Figure 4.
Simulation results of fault detection by PCA in the CSTR system.
For fault identification, it is necessary to cluster or label the data in order to incorporate the values of the model variables for usage in the neural network. The initial values of these variables spread out over wide intervals and are not suited for use in neural networks. As a result, the K-means method is applied to create 64 initial clusters. In other words, each sample, which consists of 10 variables, is assigned a label from 1 to 64 and placed in one of these 64 clusters. The values of the samples are transformed into a label column using this clustering. The accuracy cannot be increased enough by utilizing these labels, so the variables are first divided into three groups, and separate clustering is carried out for each category. Three columns of labels are eventually produced for each sample, greatly enhancing the accuracy. The proposed approach was evaluated based on the common quality metrics of accuracy, recall, and precision, which are explained in Equations (16)–(18):
where tp, tn, fp, and fn stand for true positives, true negatives, false positives, and false negatives, respectively. A confusion matrix can be used to obtain these indices directly. Results obtained for various fault identification modes are shown in Table 3.

Table 3.
The accuracy, recall, and precision of different fault identification modes.
The method proposed in this study, which entails clustering data for each category of variables and then identifying the fault via the LSTM network, improves fault identification accuracy to nearly 99%, as shown in Table 3. Additionally, in the simulations, the third mode of the LSTM network, in which the variables are divided into three categories and clustered, operates at a significantly faster rate than the other two modes.
Due to its memory and recursion characteristics, the LSTM network appears to be an appropriate method for fault diagnosis. The sorts of faults have been determined by using this network and labels that are connected to 10 different types of faults that already exist. A total of 770 training examples, including 10 different fault types and a normal system operation, are used to train this network (11 categories in total). Once the network has been trained, test data from each of the 11 categories are fed into it, and the network then uses these data to identify which category each sample belongs. This network’s accuracy was estimated to be 99.09%. As a result, this method’s results for fault identification are highly accurate, and the method may be used to find many kinds of faults in actual systems.
Table 4 compares the accuracy, recall, and precision of fault identification using the LSTM, SVM, KNN, and decision tree approaches.

Table 4.
Comparing the accuracy, recall, and precision of different machine learning methods for fault identification.
We verify that the classification performance of different machine learning methods for different sorts of faults varies greatly. The SVM approach, with a 23% accuracy rate, the KNN, with a 27.5% accuracy rate, and the decision tree, with a 45.2% accuracy rate, are worse than the new method based on the LSTM network, with a 99.09% accuracy rate. Indeed, the LSTM demonstrates very good performance in identifying the CSTR system faults. As a result, the fault identification model by the LSTM network can be used in practice, as it enables precise identification of the type of fault that has occurred in the system. Industries place a high value on precision because this helps them to avoid expensive repairs and damages.
6. Conclusions
In this paper, a novel hybrid approach was used to address fault detection and identification in an industrial system by employing KPCA, K-means, and LSTM neural networks. The method was tested in a CSTR system. First, a dataset was created using both non-faulty and faulty data from the CSTR. Next, a fault detection stage was carried out using the KPCA method, and faults could be found in the datasets. In the following phase, the data were processed and labeled using the K-means approach. Finally, an LSTM neural network was used to identify fault types. The network was taught using the information on the names of 10 different types of system faults and the normal system condition. Then, the LSTM network carried out fault identification using testing data.
Apart from being effective and practical, the proposed approach can be applied to faults that occur across a variety of processes. The method can be used as an easily implementable generic fault detection procedure. Dimension reduction contributes to energy savings in data transmission, clustering allows fault detection in different processes, and ANN-based fault identification permits the isolation of malfunctioning sensors, actuators, and components. The advantages of this comprehensive method make it useful for industrial processes or other systems that produce large amounts of data and perform a variety of processes.
The following conclusions can be drawn from the overall findings using the suggested methodology:
- In the sample where the fault appears, the KPCA fault detection method finds the existing fault very well and with excellent accuracy.
- The KPCA approach minimizes the data dimensions, sometimes even to half of the real dimensions, which decreases the number of calculations and speeds up computer processing.
- Unlike the PCA approach, the KPCA method finds faults in all data and performs well for nonlinear data.
- When faults are classified using K-means clustering, the identification is substantially more accurate.
- Due to its recursion, the LSTM network produces relatively significant results when compared to other machine learning techniques.
- The LSTM network correctly identifies faults, and its accuracy is very high, reaching 99.09%.
- Naturally, the proposed approach can be applied to detect and identify faults in other types of equipment.
It is important to note that real-world data are affected by uncertainty, which can be aleatoric or epistemic. The first occurs due to the inherent randomness and variability that accompanies the data generation process, such as measurement errors and noise. The second originates from the incomplete knowledge or understanding of the underlying system or model parameters [30]. Neglecting these types of uncertainty in the context of fault detection and identification can limit the reliability and generalizability of the proposed method. Therefore, it is crucial to highlight that addressing and quantifying aleatoric and epistemic uncertainties in real-world data is an avenue for further research, which the author will pursue to improve the robustness and accuracy of fault detection and identification techniques.
Author Contributions
Conceptualization, N.J.; methodology, N.J. and A.M.L.; software, N.J.; validation, N.J. and A.M.L.; investigation, N.J. and A.M.L.; writing—original draft preparation, N.J.; writing—review and editing, A.M.L.; visualization, A.M.L.; funding acquisition, A.M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hwang, I.; Kim, S.; Kim, Y.; Seah, C.E. A survey of fault detection, isolation, and reconfiguration methods. IEEE Trans. Control Syst. Technol. 2010, 18, 636–653. [Google Scholar] [CrossRef]
- Thirumarimurugan, M.; Bagyalakshmi, N.; Paarkavi, P. Comparison of Fault Detection and Isolation Methods: A Review. In Proceedings of the IEEE 10th International Conference on Intelligent Systems and Control (ISCO), Coimbatore, India, 7–8 January 2016. [Google Scholar]
- Khalili, M.; Zhang, X.; Cao, Y.; Polycarpou, M.M.; Parisini, T. Distributed adaptive fault-tolerant control of nonlinear uncertain second-order multi-agent systems. In Proceedings of the IEEE Annual Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015. [Google Scholar]
- Kersten, J.; Rauh, A.; Aschemann, H. Analyzing Uncertain Dynamical Systems after State-Space Transformations into Cooperative Form: Verification of Control and Fault Diagnosis. Axioms 2021, 10, 88. [Google Scholar] [CrossRef]
- Muradore, R.; Fiorini, P. A PLS-Based Statistical Approach for Fault Detection and Isolation of Robotic Manipulators. IEEE Trans. Ind. Electron. 2012, 59, 3167–3175. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X.; Chen, S.J.; Harris, C. Nonlinear Process Fault Diagnosis Based on Serial Principal Component Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 560–572. [Google Scholar] [CrossRef] [PubMed]
- Zidi, S.; Moulahi, T.; Alaya, B. Fault detection in Wireless Sensor Networks through SVM classifier. IEEE Sens. J. 2017, 6, 340–347. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Gastli, A.; Ben-brahim, L. Real-Time Fault Detection and Identification for MMC using 1-D Convolutional Neural Networks. IEEE Trans. Ind. Electron. 2019, 66, 8760–8771. [Google Scholar] [CrossRef]
- Krishnamoorthy, G.; Ashok, P.; Tesar, D. Simultaneous Sensor and Process Fault Detection and Isolation in Multiple-Input—Multiple-Output Systems. IEEE Syst. J. 2015, 9, 335–349. [Google Scholar] [CrossRef]
- Rohani, R.; Koochaki, A. A Hybrid Method Based on Optimized Neuro-Fuzzy System and Effective Features for Fault Location in VSC-HVDC Systems. IEEE Access 2020, 8, 70861–70869. [Google Scholar] [CrossRef]
- Zhou, Z.; Wen, C.; Yang, C. Fault Isolation Based on K-Nearest Neighbor Rule for Industrial Processes. IEEE Trans. Ind. Electron. 2016, 63, 2578–2586. [Google Scholar] [CrossRef]
- Fezai, R.; Nounou, M.; Messaoud, H. Reliable Fault Detection and Diagnosis of Large-Scale Nonlinear Uncertain Systems Using Interval Reduced Kernel. IEEE Access 2020, 8, 78343–78353. [Google Scholar] [CrossRef]
- Cai, L.; Tian, X.; Chen, S. Monitoring Nonlinear and Non-Gaussian Processes Using Gaussian Mixture Model-Based Weighted Kernel Independent Component Analysis. IEEE Trans. Neural Netw. Learn. Syst. 2015, 28, 122–135. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X. Multimode Process Monitoring Using Variational Bayesian Inference and Canonical Correlation Analysis. IEEE Trans. Autom. Sci. Eng. 2019, 16, 1814–1824. [Google Scholar] [CrossRef]
- Li, W.; Monti, A.S.; Ponci, F. Fault Detection and Classification in Medium Voltage DC Shipboard Power Systems With Wavelets and Artificial Neural Networks. IEEE Trans. Instrum. Meas. 2014, 63, 2651–2665. [Google Scholar] [CrossRef]
- Ni, J.; Zhang, C.; Yang, S. An Adaptive Approach Based on KPCA and SVM for Real-Time Fault Diagnosis of HVCBs. IEEE Trans. Power Deliv. 2011, 26, 1960–1971. [Google Scholar] [CrossRef]
- Pilario, K.E.S.; Cao, Y.; Shafiee, M. Mixed kernel canonical variate dissimilarity analysis for incipient fault monitoring in nonlinear dynamic processes. Comput. Chem. Eng. 2019, 123, 143–154. [Google Scholar] [CrossRef]
- Lee, J.M.; Yoo, C.K.; Choi, S.W.; Vanrolleghem, P.A.; Lee, I.B. Nonlinear process monitoring using kernel principal component analysis. Chem. Eng. Sci. 2004, 59, 223–234. [Google Scholar] [CrossRef]
- Likas, A.; Vlassis, N.; Verbeek, J.J. The global K-means clustering algorithm. Pattern Recognit. 2003, 36, 451–461. [Google Scholar] [CrossRef]
- Shang, Y.; Zhou, B.; Wang, Y.; Li, A.; Chen, K.; Song, Y.; Lin, C. Popularity Prediction of Online Contents via Cascade Graph and Temporal Information. Axioms 2021, 10, 159. [Google Scholar] [CrossRef]
- Qiao, M.; Yan, S.; Tang, X.; Xu, C. Deep Convolutional and LSTM Recurrent Neural Networks for Rolling Bearing Fault Diagnosis under Strong Noises and Variable Loads. IEEE Access 2020, 8, 66257–66269. [Google Scholar] [CrossRef]
- Park, D.; Kim, S.; An, Y.; Jung, J. LiReD: A Light-Weight Real-Time Fault Detection Neural Networks. Sensors 2018, 18, 2110. [Google Scholar] [CrossRef]
- Elsheikh, A.; Yacout, S.; Ouali, M. Bidirectional Handshaking LSTM for Remaining Useful Life Prediction. Neurocomputing 2018, 323, 148–156. [Google Scholar] [CrossRef]
- Stoean, C.; Zivkovic, M.; Bozovic, A.; Bacanin, N. Metaheuristic-Based Hyperparameter Tuning for Recurrent Deep Learning: Application to the Prediction of Solar Energy Generation. Axioms 2023, 12, 266. [Google Scholar] [CrossRef]
- Shi, Z.; Chehade, A. A Dual-LSTM Framework Combining Change Point Detection and Remaining Useful Life Prediction. Reliab. Eng. Syst. Saf. 2020, 205, 107257. [Google Scholar] [CrossRef]
- Jeong, K.; Choi, S.B.; Choi, H. Sensor Fault Detection and Isolation Using a Support Vector Machine for Vehicle Suspension Systems. IEEE Trans. Veh. Technol. 2020, 69, 3852–3863. [Google Scholar] [CrossRef]
- Lee, C.; Alena, R.L.; Robinson, P. Migrating fault trees to decision trees for real time fault detection on international space station. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2005. [Google Scholar]
- Yang, X.; Wei, Q. Adaptive Critic Designs for Optimal Event-Driven Control of a CSTR System. IEEE Trans. Ind. Inform. 2021, 17, 484–493. [Google Scholar] [CrossRef]
- Pilario, K.E.S.; Cao, Y. Canonical variate dissimilarity analysis for process incipient fault detection. IEEE Trans. Ind. Inform. 2018, 14, 5308–5315. [Google Scholar] [CrossRef]
- Zhuang, L.; Xu, A.; Wang, W.L. A prognostic driven predictive maintenance framework based on Bayesian deep learning. Reliab. Eng. Syst. Saf. 2023, 234, 109181. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).