Resolvent-Free Method for Solving Monotone Inclusions

Abstract

In this work, we consider the monotone inclusion problem in real Hilbert spaces and propose a simple inertial method that does not include any evaluations of the associated resolvent and projection. Under suitable assumptions, we establish the strong convergence of the method to a minimal norm solution. Saddle points of minimax problems and critical points problems are considered as the applications. Numerical examples in finite- and infinite-dimensional spaces illustrate the performances of our scheme.

1. Introduction

Since Minty [1], and the many others to follow, such as [2,3,4], introduced the theory of the monotone operator, a large number of theoretical and practical developments have been presented. Pascali and Sburian [5] pointed out that the class of monotone operators is important, and due to the simple structure of the monotonicity condition, it can be handled easily. The monotone inclusion problem is one of the highlights due to its important significance in convex analysis and convex optimization problems, which includes convex minimization, monotone variational inequality, convex and concave minimax problems, linear programming problems and many others. For further information and applications, see, e.g., Bot and Csetnek [6], Korpelevich [7], Khanc et al. [8], Sicre et al. [9], Xu [10], Yin et al. [11] and the many references therein [12,13,14,15].

Let H be a real Hilbert space and $A:H\to H$ be a given operator with domain $Dom\left(A\right)=\{x\in H:Ax\ne \varnothing \}$. The monotone inclusion problem is formulated as finding a point $x^{*}$ such that

$$\begin{array}{c}\hfill 0\in A{x}^{*}.\end{array}$$

(1)

The monotonicity term of (1) refers to the monotonicity of A which means that for all $x,y\in H$,

$$⟨u-v,x-y⟩\ge 0,u\in Ax,v\in Ay.$$

We denote the solution set of (1) by $\mathsf{\Omega }=A^{-1}\left(0\right)$.

One of the simplest classical algorithms for solving the monotone inclusion problem (1) is the proximal point method of Martinet [16]. Given a maximal monotone mapping $A:H\to H$ and its associated resolvent $J_r^A={(I+rA)}^{-1}$, the proximal point algorithm generates a sequence according to the update rule:

$$x_{n+1}=J_r^A{x}_n.$$

(2)

The proximal point algorithm, also known as the regularization algorithm, is a first-order optimization method that requires the function and gradient (subgradient) evaluations, and thus attracts much interest. For more relevant improvements and achievements on the regularization methods in Hilbert spaces, one can refer to [17,18,19,20,21,22,23].

One important application of monotone inclusions is the convex minimization problem. Given $C\subseteq R^n$ is a nonempty, closed and convex set and a continuously differentiable function f, the constrained minimization aims to find a point $x^{*}\in C$ such that

$$f\left(x^{*}\right)=\underset{x\in C}{min}f\left(x\right).$$

(3)

Using some operator theory properties, it is known that $x^{*}$ solves (3) if and only if $x^{*}=P_C(I-\lambda \nabla f)x^{*}$ for some $\lambda >0$. This relationship translates to the projected gradient method:

$$x_{n+1}=P_C(x_n-\lambda \nabla f\left(x_n\right)),$$

where $P_C$ is the metric projection onto C and $\nabla f$ is the gradient of f.

The projected gradient method calls for the evaluation of the projection onto the feasible set C as well as the gradient evaluation of f. This guarantees a reduction in the objective function while keeping the iterates feasible. With the set C as above and an operator $A:H\to H$, an important problem worth mentioning is the monotonic variational inequality problem, consisting of finding a point $x^{*}\in C$ such that

$$⟨A{x}^{*},x-x^{*}⟩\ge 0\mathrm{for}\mathrm{all}x\in C.$$

(4)

Using the relationship between the projection $P_C$, the resolvent and the normal cone $N_C$ of the set C, that is,

$$\begin{array}{ccc}\hfill y=J_{\lambda }^{N_C}\left(x\right)& \iff & x\in y+\lambda N_C\left(y\right)\iff x-y\in \lambda N_C\left(y\right)\hfill \\ & \iff & ⟨x-y,d-y⟩\le 0\iff y=P_{C}x,\forall d\in C,\hfill \end{array}$$

we obtain the iterative step rule for solving (4)

$$x_{n+1}=P_C(x_n-\lambda A{x}_n).$$

(5)

Indeed, the mentioned optimization methods above now “dominate” in modern optimization algorithms based on first-order information (such as function values and radial/subgradient), and it can be predicted that they will become increasingly important as the scale of practical application problems increases. For excellent works, one can refer to Teboulle [24], Drusvyatskiy and Lewis [25], etc. However, it is undeniable that they are highly dependent on the structure of the given problem, and computationally, these methods rely on the ability to compute resolvents/projections per iteration; taking algorithm (5), for instance, the complexity of each step depends on the computation of the projection to the convex set C.

Hence, in this work, we wish to combine the popular inertial technology (see, e.g., Nesterov [26], Alvarez [27] and Alvarez–Attouch [28]) and establish a strong convergence iterative method that does not use resolvents or projections, and has good convergence properties due to the inertial technique.

The outline of this paper is as follows. In Section 2, we collect the definitions and results needed for our analysis. In Section 3, the resolvent/projection-free algorithm and its convergence analysis are presented. Later, in Section 4, we present two applications of the monotone inclusion problem, saddle points of the minimax problem and the critical points problem. Finally, in Section 5, numerical experiments illustrate the performances of our scheme in finite- and infinite-dimensional spaces.

2. Preliminaries

Let C be a nonempty, closed and convex subset of a real Hilbert space H equipped with the inner product $⟨·,·⟩$. Denote the strong convergence to x of $\left\{x_n\right\}$ by $x_n\to x$, the $\omega$-weak limit set of $\left\{x_n\right\}$ by

$$w_{\omega }\left(x_n\right)=\{x\in H:x_{n_j}\rightharpoonup x\mathrm{for}\mathrm{some}\mathrm{subsequence}\left\{x_{n_j}\right\}\mathrm{of}\left\{x_n\right\}\}.$$

We recall two useful properties of the norm:

$$\begin{array}{ccc}& & {\parallel x+y\parallel }^2\le {\parallel x\parallel }^2+2⟨y,x+y⟩;\hfill \\ \hfill & & {\parallel \alpha x+\beta y+\gamma z\parallel }^2={\alpha \parallel x\parallel }^2+{\beta \parallel y\parallel }^2+{\gamma \parallel z\parallel }^2-\alpha \beta {\parallel x-y\parallel }^2\hfill \end{array}$$

(6)

$$\begin{array}{c}{-\beta \gamma \parallel y-z\parallel }^2-\alpha \gamma {\parallel x-z\parallel }^2,\hfill \end{array}$$

(7)

for all $x,y,z\in H$ and $\alpha ,\beta ,\gamma \in \mathbb{R}$ such that $\alpha +\beta +\gamma =1$.

Definition 1.

Let H be a real Hilbert space. An operator $A:H\to H$ is called $\mu —$inverse strongly monotone (μ-ism) (or μ-cocoercive) if there exists a number $\mu >0$ such that

$$\begin{array}{c}\hfill ⟨x-y,Ax-Ay⟩\ge {\mu \parallel Ax-Ay\parallel }^2.\end{array}$$

Definition 2.

Let C be a nonempty, closed convex subset of H. The operator $P_C$ is called the metric projection of H onto C: for every element $x\in H$, there is a unique nearest point $P_{C}x$ in C, such that

$$\begin{array}{c}\hfill \parallel x-P_{C}x\parallel =min\{\parallel x-y\parallel :y\in C\}.\end{array}$$

The characterization of the metric projection is

$$\begin{array}{c}\hfill ⟨x-P_{C}x,y-P_{C}x⟩\le 0,\forall x\in H,\forall y\in C.\end{array}$$

(8)

Lemma 1

(Xu [29], Maingé [30]). Assume that $\left\{a_n\right\}$ and $\left\{c_n\right\}$ are nonnegative real sequences such that

$$\begin{array}{c}\hfill a_{n+1}\le (1-{\gamma }_n)a_n+b_n+c_n,\forall n\ge 0,\end{array}$$

where $\left\{{\gamma }_n\right\}$ is a sequence in $(0,1)$ and $\left\{b_n\right\}$ is a real sequence. Provided that

(a) ${lim}_{n\to \infty }{\gamma }_n=0$,  ${\Sigma }_{n=1}^{\infty }{\gamma }_n=\infty$;  ${\Sigma }_{n=1}^{\infty }{c}_n<\infty$;

(b)  $lim{sup}_{n\to \infty }\frac{b_n}{{\gamma }_n}\le 0$.

Then, the limit of the sequence $\left\{a_n\right\}$ exists and ${lim}_{n\to \infty }{a}_n=0$.

Lemma 2

(see, e.g., Opial [31]). Let H be a real Hilbert space and ${\left\{x_n\right\}}_{n=0}^{\infty }\subset H$ such that there exists a nonempty, closed and convex set $S\subset H$ satisfying the following:

(1) For every $z\in S$, ${lim}_{n\to \infty }\parallel x_n-z\parallel$ exists;

(2) Any weak cluster point of ${\left\{x_n\right\}}_{n=0}^{\infty }$ belongs to S.

Then, there exists $\overline{x}\in S$ such that ${\left\{x_n\right\}}_{n=0}^{\infty }$ converges weakly to $\overline{x}$.

Lemma 3

(see, e.g., Maingé [30]). Let $\left\{{\mathsf{\Gamma }}_n\right\}$ be a sequence of real numbers that does not decrease at infinity, in the sense that there exists a subsequence $\left\{{\mathsf{\Gamma }}_{n_j}\right\}$ of $\left\{{\mathsf{\Gamma }}_n\right\}$ such that ${\mathsf{\Gamma }}_{n_j}<{\mathsf{\Gamma }}_{n_j+1}$ for all $j\ge 0$. Also consider the sequence of integers ${\left\{\sigma \left(n\right)\right\}}_{n\ge n_0}$ defined by

$$\begin{array}{c}\hfill \sigma \left(n\right)=max\{k\le n:{\mathsf{\Gamma }}_k\le {\mathsf{\Gamma }}_{k+1}\}.\end{array}$$

Then, ${\left\{\sigma \left(n\right)\right\}}_{n\ge n_0}$ is a nondecreasing sequence verifying ${lim}_{n\to \infty }\sigma \left(n\right)=\infty$ and, for all $n\ge n_0$,

$$\begin{array}{c}\hfill max\{{\mathsf{\Gamma }}_{\sigma \left(n\right)},{\mathsf{\Gamma }}_n\}\le {\mathsf{\Gamma }}_{\sigma \left(n\right)+1}.\end{array}$$

3. Main Result

We are concerned with the following monotone inclusion problem: finding $x^{*}\in H$ such that

$$\begin{array}{c}\hfill 0\in A{x}^{*},\end{array}$$

(9)

where A is a monotone-type operator on H.

Remark 1.

Clearly, if $y_n=z_n=x_n$ for some $n\ge 1$, then $x_n$ is a solution of (9) and the iteration process is terminated in finite iterations. In general, the algorithm does not stop in finite iterations, and thus we assume that the algorithm generates an infinite sequence.

Convergence Analysis

For the convergence analysis of our algorithm, we assume the following assumptions:

(A1)  A is a continuous maximal monotone operator with cocoercive coefficient $\mu$ from H to H;

(A2)  The solution set $\mathsf{\Omega }$ of (9) is nonempty.

Theorem 1.

Suppose that the assumptions (A1)–(A2) hold. If the sequences $\left\{{\alpha }_n\right\}$, $\left\{{\gamma }_n\right\}$ are in $(0,1)$ and satisfy the following conditions:

(B1)  ${lim}_{n\to \infty }{\gamma }_n=0$, $liminf(1-{\alpha }_n-{\gamma }_n){\alpha }_n>0$ and ${\Sigma }_{n=1}^{\infty }{\gamma }_n=\infty$;

(B2)  ${ϵ}_n=o\left({\gamma }_n\right).$

Then, the recursion $\left\{x_n\right\}$ generated by Algorithm 1 converges strongly to an element p which is closest to $0$ in Ω, that is, $p=P_{\mathsf{\Omega }}\left(0\right)$.

Algorithm 1 Convergence Analysis

Initialization: Choose ${\lambda }_n\in (0,2\mu )$, $\theta \in (0,1)$ and ${ϵ}_n\in (0,\infty )$ such that ${\sum }_{n=1}^{\infty }{ϵ}_n<\infty$, select arbitrary starting points $x_0,x_1\in C$, and set $n=1$. Iterative Step: Given the iterates $x_n$ and $x_{n-1}$ for each $n\ge 1$, choose ${\theta }_n$ such that $0<{\theta }_n<{\overline{\theta }}_n$, compute $$\begin{array}{c}\hfill \left\{\begin{array}{c}{y}_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ z_n=y_n-{\lambda }_{n}A{y}_n,\hfill \\ x_{n+1}=(1-{\alpha }_n-{\gamma }_n)y_n+{\alpha }_n{z}_n,\hfill \end{array}\right.\end{array}$$ (10) where $$\begin{array}{c}\hfill {\overline{\theta }}_n=\left\{\begin{array}{c}min\{\theta ,{ϵ}_n[max(\parallel x_n-x_{n-1}{\parallel }^2,\parallel x_n-x_{n-1}{\parallel \left)\right]}^{-1}\},x_n\ne x_{n-1};\hfill \\ \theta .else\hfill \end{array}\right.\end{array}$$ Stopping Criterion: If $y_n=z_n$, then stop. Otherwise, set $n:=n+1$ and return to Iterative Step.

Proof. 

First, we prove that $\left\{x_n\right\}$ is bounded. Without the loss of the generality, let p be the closest element to 0 in $\mathsf{\Omega }$ because $\mathsf{\Omega }\ne \varnothing$. It follows from the cocoercivity of A with coefficient $\mu$ that

$$\begin{array}{c}\hfill ⟨A{x}_n,x_n-p⟩=⟨A{x}_n-Ap,x_n-p⟩\ge \mu {\parallel A{x}_n\parallel }^2.\end{array}$$

Taking into account the definition of $y_n$ in the recursion (10), we have

$$\begin{array}{ccc}\hfill \parallel y_n-p\parallel & =& \parallel x_n+{\theta }_n(x_n-x_{n-1})pz\parallel \hfill \\ & \le & \parallel x_n-p\parallel +{\theta }_n\parallel x_n-x_{n-1}\parallel ,\hfill \end{array}$$

and

$$\begin{array}{ccc}\hfill \parallel z_n{-p\parallel }^2& =& \parallel y_n-{\lambda }_{n}A{y}_n{-p\parallel }^2\hfill \\ \hfill & =& \parallel y_n{-p\parallel }^2+{\lambda }_n^2{\parallel A{y}_n\parallel }^2-2{\lambda }_n⟨A{y}_n,y_n-p⟩\hfill \\ \hfill & \le & \parallel y_n{-p\parallel }^2+{\lambda }_n^2\parallel A{y}_n{\parallel }^2-2\mu {\lambda }_n{\parallel A{y}_n\parallel }^2\hfill \\ & \le & \parallel y_n{-p\parallel }^2+({\lambda }_n-2\mu ){\lambda }_n{\parallel A{y}_n\parallel }^2,\hfill \end{array}$$

(11)

which implies that $\parallel z_n-p\parallel \le \parallel y_n-p\parallel .$ Furthermore, we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-p\parallel & =& \parallel (1-{\alpha }_n-{\gamma }_n)y_n+{\alpha }_n{z}_n-p\parallel \hfill \\ & \le & (1-{\alpha }_n-{\gamma }_n)\parallel y_n-p\parallel +{\lambda }_n^2\parallel z_n-p\parallel +{\gamma }_n\parallel p\parallel \hfill \\ & \le & (1-{\gamma }_n)\parallel y_n-p\parallel +{\gamma }_n\parallel p\parallel \hfill \\ & \le & (1-{\gamma }_n)[\parallel x_n-p\parallel +{\theta }_n\parallel x_n-x_{n-1}\parallel ]+{\gamma }_n\parallel p\parallel \hfill \\ & \le & (1-{\gamma }_n)\parallel x_n-p\parallel +{\gamma }_n[\parallel p\parallel +\frac{{\theta }_n}{{\gamma }_n}\parallel x_n-x_{n-1}\parallel ].\hfill \end{array}$$

In view of the assumption on ${\theta }_n$, we obtain ${\theta }_n\parallel x_n-x_{n-1}\parallel \le {ϵ}_n=o\left({\gamma }_n\right)$, which entails that there exists some positive constant $\sigma$ such that $\sigma =sup\frac{{\theta }_n}{{\gamma }_n}\parallel x_n-x_{n-1}\parallel$; therefore,

$$\begin{array}{ccc}\hfill \parallel x_{n+1}-p\parallel & \le & (1-{\gamma }_n)\parallel x_n-p\parallel +{\gamma }_n(\parallel p\parallel +\sigma )\hfill \\ & \le & max\{\parallel x_0-p\parallel ,\parallel p\parallel +\sigma \},\hfill \end{array}$$

namely, the sequence $\left\{x_n\right\}$ is bounded, and so are $\left\{y_n\right\}$ and $\left\{z_n\right\}$.

It follows from (10) and (11) that

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-p\parallel }^2& =& \parallel (1-{\alpha }_n-{\gamma }_n)y_n+{\alpha }_n{z}_n{-p\parallel }^2\hfill \\ \hfill & =& \parallel (1-{\alpha }_n-{\gamma }_n)(y_n-p)+{\alpha }_n(z_n-p)-{\gamma }_n{p\parallel }^2\hfill \\ \hfill & \le & (1-{\alpha }_n-{\gamma }_n)\parallel y_n{-p\parallel }^2+{\alpha }_n\parallel z_n{-p\parallel }^2+{\gamma }_n{\parallel p\parallel }^2\hfill \\ \hfill & & -(1-{\alpha }_n-{\gamma }_n){\alpha }_n{\parallel y_n-z_n\parallel }^2\hfill \\ \hfill & \le & (1-{\alpha }_n-{\gamma }_n)\parallel y_n{-p\parallel }^2+{\alpha }_n[\parallel y_n{-p\parallel }^2+({\lambda }_n-2\mu ){\lambda }_n\parallel A{y}_n{\parallel }^2]\hfill \\ \hfill & & +{\gamma }_n{\parallel p\parallel }^2-(1-{\alpha }_n-{\gamma }_n){\alpha }_n{\parallel y_n-z_n\parallel }^2\hfill \\ \hfill & =& (1-{\gamma }_n)\parallel y_n{-p\parallel }^2+{\alpha }_n({\lambda }_n-2\mu ){\lambda }_n{\parallel A{y}_n\parallel }^2\hfill \\ & & +{\gamma }_n{\parallel p\parallel }^2-(1-{\alpha }_n-{\gamma }_n){\alpha }_n{\parallel y_n-z_n\parallel }^2.\hfill \end{array}$$

(12)

By using again the formation of $y_n$, we obtain

$$\begin{array}{ccc}\hfill \parallel y_n{-p\parallel }^2& =& \parallel x_n+{\theta }_n(x_n-x_{n-1}){-p\parallel }^2\hfill \\ \hfill & =& \parallel (1+{\theta }_n)(x_n-p)-{\theta }_n(x_{n-1}-p){\parallel }^2\hfill \\ \hfill & \le & (1+{\theta }_n)\parallel x_n{-p\parallel }^2-{\theta }_n\parallel x_{n-1}{-p\parallel }^2+{\theta }_n(1+{\theta }_n){\parallel x_n-x_{n-1}\parallel }^2\hfill \\ & \le & (1+{\theta }_n)\parallel x_n{-p\parallel }^2-{\theta }_n\parallel x_{n-1}{-p\parallel }^2+2{\theta }_n{\parallel x_n-x_{n-1}\parallel }^2.\hfill \end{array}$$

(13)

Substituting (13) into (12), we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-p\parallel }^2& \le & (1-{\gamma }_n)[(1+{\theta }_n)\parallel x_n{-p\parallel }^2-{\theta }_n\parallel x_{n-1}{-p\parallel }^2+2{\theta }_n\parallel x_n-x_{n-1}{\parallel }^2]\hfill \\ & & +{\alpha }_n({\lambda }_n-2\mu ){\lambda }_n\parallel A{y}_n{\parallel }^2+{\gamma }_n{\parallel p\parallel }^2-(1-{\alpha }_n-{\gamma }_n){\alpha }_n{\parallel y_n-z_n\parallel }^2\hfill \\ & =& (1-{\gamma }_n)[\parallel x_n{-p\parallel }^2+{\theta }_n(\parallel x_n{-p\parallel }^2-\parallel x_{n-1}-{p)\parallel }^2)\hfill \\ & & +2{\theta }_n\parallel x_n-x_{n-1}{\parallel }^2]+{\alpha }_n({\lambda }_n-2\mu ){\lambda }_n\parallel A{y}_n{\parallel }^2+{\gamma }_n{\parallel p\parallel }^2\hfill \\ & & -(1-{\alpha }_n-{\gamma }_n){\alpha }_n{\parallel y_n-z_n\parallel }^2\hfill \\ & =& \parallel x_n{-p\parallel }^2+{\gamma }_n{(\parallel p\parallel }^2-\parallel x_n{-p\parallel }^2)+2(1-{\gamma }_n){\theta }_n{\parallel x_n-x_{n-1}\parallel }^2\hfill \\ & & +(1-{\gamma }_n){\theta }_n(\parallel x_n{-p\parallel }^2-\parallel x_{n-1}-{p)\parallel }^2)+{\alpha }_n({\lambda }_n-2\mu ){\lambda }_n{\parallel A{y}_n\parallel }^2\hfill \\ & & -(1-{\alpha }_n-{\gamma }_n){\alpha }_n{\parallel y_n-z_n\parallel }^2,\hfill \end{array}$$

and transposing, we have

$$\begin{array}{ccc}\hfill & & (1-{\alpha }_n-{\gamma }_n){\alpha }_n\parallel y_n-z_n{\parallel }^2+{\alpha }_n(2\mu -{\lambda }_n){\lambda }_n{\parallel A{y}_n\parallel }^2\hfill \\ \hfill & \le & (\parallel x_n{-p\parallel }^2-\parallel x_{n+1}{-p\parallel }^2)+(1-{\gamma }_n){\theta }_n(\parallel x_n{-p\parallel }^2-\parallel x_{n-1}-{p)\parallel }^2)\hfill \\ & & +{\gamma }_n{(\parallel p\parallel }^2-\parallel x_n{-p\parallel }^2)+2(1-{\gamma }_n){\theta }_n{\parallel x_n-x_{n-1}\parallel }^2,\hfill \end{array}$$

(14)

Here, two cases should be considered.

Case I. Assume that the sequence $\parallel x_n-p\parallel$ is decreasing, namely, there exists $N_0>0$ such that $\parallel x_{n+1}-p\parallel \le \parallel x_n-p\parallel$ for each $n>N_0$, and then there is the limit of $\parallel x_n-p\parallel$ and ${lim}_{n\to \infty }(\parallel x_{n+1}-p\parallel -\parallel x_n-p\parallel )=0.$ It turns out from (14) and the condition $\left(B1\right)$ that

$$\begin{array}{c}\hfill (1-{\alpha }_n-{\gamma }_n){\alpha }_n\parallel y_n-z_n{\parallel }^2\to 0;{\alpha }_n(2\mu -{\lambda }_n){\lambda }_n{\parallel A{y}_n\parallel }^2\to 0,\end{array}$$

which implies that $\parallel y_n-z_n{\parallel }^2\to 0$ and $\parallel A{y}_n{\parallel }^2\to 0$.

Furthermore, by the setting of $u_n$, we have $\parallel u_n-y_n\parallel ={\alpha }_n\parallel z_n-y_n\parallel \to 0$ and $\parallel x_{n+1}-u_n\parallel ={\gamma }_n\parallel y_n\parallel \to 0$, which together with $\parallel x_n-y_n\parallel ={\theta }_n\parallel x_n-x_{n-1}\parallel \to 0$ yields that

$$\parallel x_{n+1}-x_n\parallel \le \parallel x_{n+1}-u_n\parallel + \parallel u_n-y_n\parallel + \parallel y_n-x_n\parallel \to 0.$$

Because $\left\{x_n\right\}$ is bounded, it follows from Eberlein–Shmulyan’s theorem, for arbitrary point $q\in w_{\omega }\left(x_n\right)$, that there exits a subsequence $\left\{x_{n_j}\right\}$ of $\left\{x_n\right\}$ such that $x_{n_j}$ converges weakly to q. By $\parallel x_n-y_n\parallel \to 0$, $\parallel A{y}_n{\parallel }^2\to 0$ and A is continuous, we have

$$0=\underset{n\to \infty }{lim}\parallel A{y}_n\parallel =\underset{j\to \infty }{lim}\parallel A{y}_{n_j}\parallel =Aq,$$

which entails that $q\in A^{-1}\left(0\right)$. In view of the fact that the choice of q in $w_{\omega }\left(x_n\right)$ was arbitrary, we conclude that $w_{\omega }\left(x_n\right)\subset \mathsf{\Omega }$, which makes Lemma 2 workable, that is, ${\left\{x_n\right\}}_{n=0}^{\infty }$ converges weakly to some point in $\mathsf{\Omega }$.

Now, we claim that $x_n\to p$, where $p=P_{\mathsf{\Omega }}\left(0\right)$.

For this purpose, let $u_n=(1-{\alpha }_n)y_n+{\alpha }_n{z}_n$, and then we have

$$\begin{array}{ccc}\hfill x_{n+1}& =& (1-{\alpha }_n-{\gamma }_n)y_n+{\alpha }_n{z}_n=(1-{\gamma }_n)u_n+{\gamma }_n(u_n-y_n)\hfill \\ & =& (1-{\gamma }_n)u_n+{\gamma }_n{\alpha }_n(z_n-y_n),\hfill \end{array}$$

which yields that

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-p\parallel }^2& =& \parallel (1-{\gamma }_n)u_n+{\gamma }_n{\alpha }_n(z_n-y_n){-p\parallel }^2\hfill \\ \hfill & =& \parallel (1-{\gamma }_n)(u_n-p)+{\gamma }_n{\alpha }_n(z_n-y_n)-{\gamma }_n{p\parallel }^2\hfill \\ \hfill & \le & {(1-{\gamma }_n)}^2{\parallel u_n-p\parallel }^2-2⟨{\gamma }_{n}p-{\gamma }_n{\alpha }_n(z_n-y_n),x_{n+1}-z⟩\hfill \\ \hfill & =& {(1-{\gamma }_n)}^2{\parallel u_n-p\parallel }^2-2{\gamma }_n{\alpha }_n⟨y_n-z_n,x_{n+1}-p⟩\hfill \\ & & +2{\gamma }_n⟨-p,x_{n+1}-p⟩.\hfill \end{array}$$

(15)

In addition, by using again the formation of $\left\{y_n\right\}$, we obtain

$$\begin{array}{ccc}\hfill \parallel y_n{-p\parallel }^2& =& \parallel x_n+{\theta }_n(x_n-x_{n-1}){-p\parallel }^2\hfill \\ & =& \parallel (1+{\theta }_n)(x_n-p)-{\theta }_n(x_{n-1}-p){\parallel }^2\hfill \\ & \le & (1+{\theta }_n)\parallel x_n{-p\parallel }^2-{\theta }_n\parallel x_{n-1}{-p\parallel }^2+{\theta }_n(1+{\theta }_n){\parallel x_n-x_{n-1}\parallel }^2\hfill \\ & \le & (1+{\theta }_n)\parallel x_n{-p\parallel }^2-{\theta }_n\parallel x_{n-1}{-p\parallel }^2+2{\theta }_n{\parallel x_n-x_{n-1}\parallel }^2,\hfill \end{array}$$

and substituting the above inequality in (15), we have

$$\begin{array}{ccc}\hfill \parallel x_{n+1}{-p\parallel }^2& \le & {(1-{\gamma }_n)}^2{\parallel y_n-p\parallel }^2-2{\gamma }_n{\alpha }_n⟨y_n-z_n,x_{n+1}-p⟩+2{\gamma }_n⟨-p,x_{n+1}-p⟩\hfill \\ \hfill & \le & {(1-{\gamma }_n)}^2[(1+{\theta }_n)\parallel x_n{-p\parallel }^2-{\theta }_n\parallel x_{n-1}{-p\parallel }^2+2{\theta }_n\parallel x_n-x_{n-1}{\parallel }^2]\hfill \\ \hfill & & -2{\gamma }_n{\alpha }_n⟨y_n-z_n,x_{n+1}-p⟩+2{\gamma }_n⟨-p,x_{n+1}-p⟩\hfill \\ \hfill & \le & (1-{\gamma }_n)[\parallel x_n{-p\parallel }^2+{\theta }_n(\parallel x_n{-p\parallel }^2-\parallel x_{n-1}{-p\parallel }^2)+2{\theta }_n\parallel x_n-x_{n-1}{\parallel }^2]\hfill \\ \hfill & & -2{\gamma }_n{\alpha }_n⟨y_n-z_n,x_{n+1}-p⟩+2{\gamma }_n⟨-p,x_{n+1}-p⟩\hfill \\ \hfill & \le & (1-{\gamma }_n)[\parallel x_n{-p\parallel }^2+{\theta }_n\parallel x_n-x_{n-1}\parallel ·(\parallel x_n-p\parallel +\parallel x_{n-1}-p\parallel )\hfill \\ \hfill & & +2{\theta }_n\parallel x_n-x_{n-1}{\parallel }^2]-2{\gamma }_n{\alpha }_n⟨y_n-z_n,x_{n+1}-p⟩+2{\gamma }_n⟨-p,x_{n+1}-p⟩\hfill \\ \hfill & \le & (1-{\gamma }_n)\parallel x_n{-p\parallel }^2+{\theta }_n(1-{\gamma }_n)M\parallel x_n-x_{n-1}\parallel \hfill \\ & & +2{\gamma }_n⟨-p,x_{n+1}-p⟩-2{\gamma }_n{\alpha }_n⟨y_n-z_n,x_{n+1}-p⟩,\hfill \end{array}$$

(16)

where $M=sup(\parallel x_n-p\parallel +\parallel x_{n-1}-p\parallel +2{\theta }_n\parallel x_n-x_{n-1}\parallel )$.

Owing to $p=P_{\mathsf{\Omega }}\left(0\right)$, we can infer that $⟨0-P_{\mathsf{\Omega }}\left(0\right),y-P_{\mathsf{\Omega }}\left(0\right)⟩\le 0$ for each $y\in \mathsf{\Omega }$, so we have

$$limsup⟨-p,x_{n+1}-p⟩=\underset{q\in w_{\omega \left(x_n\right)}}{max}⟨-p,q-p⟩\le 0.$$

In addition, from the assumption on $\left\{{\theta }_n\right\}$, we have

$$\sum _{n=1}^{\infty }{\theta }_n(1-{\gamma }_n)M\parallel x_n-x_{n-1}\parallel <\infty ,$$

and from $y_n-z_n\to 0$, we have

$$\underset{n\to \infty }{lim}sup\{-2{\gamma }_n{\alpha }_n⟨y_n-z_n,x_{n+1}-p⟩+2{\gamma }_n⟨-p,x_{n+1}-p⟩\}/{\gamma }_n\le 0,$$

and therefore (16) enables Lemma 1 to be applicable to, namely, $\parallel x_n-p\parallel \to 0$.

Case II. If the sequence $\parallel x_n-p\parallel$ is not decreasing at infinity, in the sense that there exists a subsequence $\{\parallel x_{n_j}-p\parallel \}$ of $\{\parallel x_n-p\parallel \}$ such that $\parallel x_{n_j}-p\parallel \le \parallel x_{n_{j+1}}-p\parallel$. Owing to Lemma 3, we can induce that $\parallel x_{\sigma \left(n\right)}-p\parallel \le \parallel x_{\sigma \left(n\right)+1}-p\parallel$ and $\parallel x_n-p\parallel \le \parallel x_{\sigma \left(n\right)+1}-p\parallel$, where $\sigma \left(n\right)$ is an indicator defined by $\sigma \left(n\right)=max\{k\le n: \parallel x_k-p\parallel \le \parallel x_{k+1}-p\parallel \}$ and $\sigma \left(n\right)\to \infty$ as $n\to \infty$.

Taking into account the fact that the formula (14) still holds for each $\sigma \left(n\right)$, that is,

$$\begin{array}{ccc}\hfill & & (1-{\alpha }_{\sigma \left(n\right)}-{\gamma }_{\sigma \left(n\right)}){\alpha }_{\sigma \left(n\right)}\parallel y_{\sigma }\left(n\right)-z_{\sigma \left(n\right)}{\parallel }^2+{\alpha }_{\sigma \left(n\right)}(2\mu -{\lambda }_{\sigma \left(n\right)}){\lambda }_{\sigma \left(n\right)}{\parallel A{y}_{\sigma \left(n\right)}\parallel }^2\hfill \\ \hfill & \le & (\parallel x_{\sigma \left(n\right)}{-p\parallel }^2-\parallel x_{\sigma \left(n\right)+1}{-p\parallel }^2)+{\gamma }_{\sigma \left(n\right)}{(\parallel p\parallel }^2-\parallel x_{\sigma }\left(n\right)-p{\parallel }^2)\hfill \\ \hfill & & +(1-{\gamma }_{\sigma \left(n\right)}){\theta }_{\sigma \left(n\right)}(\parallel x_{\sigma \left(n\right)}{-p\parallel }^2-\parallel x_{\sigma \left(n\right)-1}-{p)\parallel }^2)\hfill \\ \hfill & & +2(1-{\gamma }_{\sigma \left(n\right)}){\theta }_{\sigma \left(n\right)}{\parallel x_{\sigma \left(n\right)}-x_{\sigma \left(n\right)-1}\parallel }^2\hfill \\ \hfill & \le & {\gamma }_{\sigma \left(n\right)}{(\parallel p\parallel }^2-\parallel x_{\sigma \left(n\right)}{-p\parallel }^2)+(1-{\gamma }_{\sigma \left(n\right)}){\theta }_{\sigma \left(n\right)}(\parallel x_{\sigma \left(n\right)}{-p\parallel }^2-\parallel x_{\sigma \left(n\right)-1}-{p)\parallel }^2)\hfill \\ \hfill & & +2(1-{\gamma }_{\sigma \left(n\right)}){\theta }_{\sigma \left(n\right)}{\parallel x_{\sigma \left(n\right)}-x_{\sigma \left(n\right)-1}\parallel }^2.\hfill \end{array}$$

In addition, from the theorem’s assumptions $\left(B_1\right)$ and $\left(B_2\right)$ that

$$\begin{array}{c}\hfill \parallel y_{\sigma \left(n\right)}-z_{\sigma \left(n\right)}{\parallel }^2\to 0;{\parallel A{y}_{\sigma \left(n\right)}\parallel }^2\to 0,\end{array}$$

(17)

Similarly to the proofs of (16) in Case I, we have $w_{\omega }\left(x_n\right)\subset \mathsf{\Omega }$ and

$$\begin{array}{c}\hfill limsup⟨-p,x_{\sigma \left(n\right)+1}-p⟩\le 0,\end{array}$$

(18)

and

$$\begin{array}{ccc}\hfill \parallel x_{\sigma \left(n\right)+1}{-p\parallel }^2& \le & (1-{\gamma }_{\sigma \left(n\right)})\parallel x_{\sigma \left(n\right)}{-p\parallel }^2+{\theta }_{\sigma \left(n\right)}(1-{\gamma }_{\sigma \left(n\right)})M\parallel x_{\sigma \left(n\right)}-x_{\sigma \left(n\right)-1}\parallel \hfill \\ \hfill & & -2{\gamma }_{\sigma \left(n\right)}{\alpha }_{\sigma \left(n\right)}⟨y_{\sigma \left(n\right)}-z_{\sigma \left(n\right)},x_{\sigma \left(n\right)+1}-p⟩\hfill \\ & & +2{\gamma }_{\sigma \left(n\right)}⟨-p,x_{\sigma \left(n\right)+1}-p⟩.\hfill \end{array}$$

(19)

Transposing again, we have

$$\begin{array}{ccc}\hfill {\gamma }_{\sigma \left(n\right)}{\parallel x_{\sigma \left(n\right)}-p\parallel }^2& \le & (\parallel x_{\sigma \left(n\right)}{-p\parallel }^2-\parallel x_{\sigma \left(n\right)+1}-p{\parallel }^2)+{\theta }_{\sigma \left(n\right)}(1-{\gamma }_{\sigma \left(n\right)})M\hfill \\ & & \times \parallel x_{\sigma \left(n\right)}-x_{\sigma \left(n\right)-1}\parallel +2{\gamma }_{\sigma \left(n\right)}⟨-p,x_{\sigma \left(n\right)+1}-p⟩\hfill \\ \hfill & & -2{\gamma }_{\sigma \left(n\right)}{\alpha }_{\sigma \left(n\right)}⟨y_{\sigma \left(n\right)}-z_{\sigma \left(n\right)},x_{\sigma \left(n\right)+1}-p⟩\hfill \\ & \le & {\theta }_{\sigma \left(n\right)}(1-{\gamma }_{\sigma \left(n\right)})M\parallel x_{\sigma \left(n\right)}-x_{\sigma \left(n\right)-1}\parallel +2{\gamma }_{\sigma \left(n\right)}⟨-p,x_{\sigma \left(n\right)+1}-p⟩\hfill \\ & & -2{\gamma }_{\sigma \left(n\right)}{\alpha }_{\sigma \left(n\right)}⟨y_{\sigma \left(n\right)}-z_{\sigma \left(n\right)},x_{\sigma \left(n\right)+1}-p⟩,\hfill \end{array}$$

which amounts to

$$\begin{array}{ccc}\hfill \parallel x_{\sigma \left(n\right)}{-p\parallel }^2& \le & \frac{{\theta }_{\sigma \left(n\right)}}{{\gamma }_{\sigma \left(n\right)}}(1-{\gamma }_{\sigma \left(n\right)})M\parallel x_{\sigma \left(n\right)}-x_{\sigma \left(n\right)-1}\parallel +2⟨-p,x_{\sigma \left(n\right)+1}-p⟩\hfill \\ & & -2{\alpha }_{\sigma \left(n\right)}⟨y_{\sigma \left(n\right)}-z_{\sigma \left(n\right)},x_{\sigma \left(n\right)+1}-p⟩.\hfill \end{array}$$

(20)

Noting the grant of ${ϵ}_{\sigma \left(n\right)}=o\left({\gamma }_{\sigma \left(n\right)}\right)$, we have $\frac{{\theta }_{\sigma \left(n\right)}}{{\gamma }_{\sigma \left(n\right)}}(1-{\gamma }_{\sigma \left(n\right)})M\parallel x_{\sigma \left(n\right)}-x_{\sigma \left(n\right)-1}\parallel \to 0$. Putting (18) and (17) into (20), it yields that $\parallel x_{\sigma \left(n\right)}-p\parallel \to 0.$

It follows from (19) that

$$\begin{array}{c}\hfill \underset{n\to \infty }{lim}\parallel x_{\sigma \left(n\right)+1}-p\parallel =\underset{n\to \infty }{lim}{\parallel x_{\sigma \left(n\right)}-p\parallel }^2=0,\end{array}$$

which makes Lemma 3 practicable, and hence

$$\begin{array}{c}\hfill 0\le \parallel x_n-p\parallel \le max\{\parallel x_n-p\parallel ,\parallel x_{\sigma \left(n\right)}-p\parallel \}\le \parallel x_{\sigma \left(n\right)+1}-p\parallel \to 0.\end{array}$$

Consequently, the sequence $\left\{x_n\right\}$ converges strongly to p, which is the closest point to 0 in $\mathsf{\Omega }$. This completes the proof. □

Remark 2.

If the operator A is accretive with $\mu -$ cocoercivity or maximal monotone, then all the above results hold.

4. Applications

4.1. Minimax Problem

Suppose $H_1$ and $H_2$ are two real Hilbert spaces, the general convex–concave minimax problem in a Hilbert space setting is illustrated as follows:

$$\begin{array}{c}\hfill \underset{x\in Q}{min}\underset{\lambda \in S}{max}L(x,\lambda ),\end{array}$$

(21)

where Q and S are nonempty, closed and convex subsets of Hilbert spaces $H_1$ and $H_2$, respectively, and $L(x,\lambda )$ is convex in x (for each fixed $\lambda \in S)$ and concave in $\lambda$ (for each fixed $x\in Q$).

A solution $(x^{*},{\lambda }^{*})\in Q\times S$ of the minimax problem (21) is interpreted as a saddle point, satisfying the following inequality

$$L(x^{*},\lambda )\le L(x^{*},{\lambda }^{*})\le L(x,{\lambda }^{*}),x\in Q,\lambda \in S,$$

which amounts to the fact that $x^{*}\in Q$ is a minimizer in Q of the function $L(·,{\lambda }^{*})$, and ${\lambda }^{*}\in S$ is a maximizer in S of the function $L(x^{*},·)$.

Minimax problems are an important modeling tool due to their ability to handle many important applications in machine learning, in particular, in generative adversarial nets (GANs), statistical learning, certification of robustness in deep learning and distributed computing. Some recent works can be seen in, e.g., Ataş [32], Ji-Zhao [33] and Hassanpour et al. [34].

For example, if we consider the standard convex programming problem,

$$\begin{array}{ccc}\hfill & & minf\left(x\right),\hfill \\ & & s.t.h_i\left(x\right)\le 0,i=1,2,\dots ,l,\hfill \end{array}$$

(22)

where f and $h_i,(i=1,2,\dots ,l)$ are convex functions. Using the Lagrange function L, the problem (22) can be reformulated as the following minimax problem (see, e.g., Qi and Sun [35]):

$$\begin{array}{c}\hfill L(x,\lambda )=f\left(x\right)+\sum _i{\lambda }_i{h}_i\left(x\right).\end{array}$$

(23)

It can be seen that $L(x,\lambda )$ in (23) is a convex–concave function on $Q\times S$, where

$$\begin{array}{c}\hfill Q=\{x:h_i\left(x\right)\le 0,i=1,2,\cdots ,l\},S=\{\lambda :{\lambda }_i\ge 0,i=1,2,\cdots ,l\},\end{array}$$

and the Kuhn–Tucker vector $(x^{*},{\lambda }^{*})$ of (22) is exactly the saddle point of Lagrangian function $L(x,\lambda )$ in (23).

Another nice example is the Tchebychev approximating problem that consists of finding $(x,\lambda )$ such that

$$\underset{\lambda \in Q}{min}\underset{x\in S}{max}{(g\left(x\right)-\lambda \left(x\right))}^2,$$

that is, for given $g:S\subset {\mathbb{R}}^n\to \mathbb{R}$, finding $\lambda \left(x\right)\in Q$ approaching $g\left(x\right)$, where $\lambda :{\mathbb{R}}^n\to \mathbb{R}$ and Q is the space composed of the functions $\lambda$.

It is known that L has a saddle point if and only if

$$\begin{array}{c}\hfill \underset{x\in Q}{min}\underset{\lambda \in S}{max}L(x,\lambda )=\underset{\lambda \in S}{max}\underset{x\in Q}{min}L(x,\lambda ).\end{array}$$

If L is convex–concave and differentiable, let ${\nabla }_{x}L(x,\lambda )$ and $-{\nabla }_{\lambda }L(x,\lambda )$ present the derivatives of L on x and $\lambda$, respectively, and then we have $\partial L\left(z\right)={[{\nabla }_{x}L(x,\lambda ),-{\nabla }_{\lambda }L(x,\lambda )]}^T$, where $z=(x,\lambda )$.

Note that $\partial L$ is maximal monotone for the unconstrained case (i.e., $Q=H_1,S=H_2$), and finding a saddle point $z^{*}=(x^{*},{\lambda }^{*})\in Q\times S$ of L equals to solving the equation $\partial L\left(z^{*}\right)=0$. For more details on the minimax problem and its solutions, one can refer to the von Neumann works from the 1920s and 1930s [36,37] and Ky Fan’s minimax theorem [38].

Now, we consider minimax problems (21) under the unconstrained case, and let the solution set $\mathsf{\Omega }$ of the minimax problem be nonempty. So, by taking $A=\partial L$, we can obtain the saddle point of the minimax problem in $H_1\times H_2$ from the following results.

Theorem 2.

Let $H_1$ and $H_2$ be two real Hilbert spaces. Suppose that the function L is convex–concave and differentiable such that $\mathsf{\Omega }\ne \varnothing$. Under the setting of the parameters in Algorithm 1, if the sequences $\left\{{\alpha }_n\right\}$, $\left\{{\gamma }_n\right\}$, $\left\{{ϵ}_n\right\}$ are in $(0,1)$ and satisfying the conditions as in Theorem 1, then the sequence $\left\{z_n\right\}$ generated by the following scheme

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{y}_n=z_n+{\theta }_n(z_n-z_{n-1}),\hfill \\ {\overline{z}}_n=y_n-{\lambda }_n\partial L\left(y_n\right),\hfill \\ z_{n+1}=(1-{\alpha }_n-{\gamma }_n)y_n+{\alpha }_n{\overline{z}}_n,\hfill \end{array}\right.\end{array}$$

(24)

converges strongly to the least norm element $z^{*}\in \mathsf{\Omega }$, where $z_0\in H_1\times H_2$ and $z_1\in H_1\times H_2$ are two arbitrary initial points.

Proof. 

Noting that $\partial L$ is maximal monotone, so letting A be $\partial L$ in Algorithm 1, and following Theorem 1, we have the result. □

Indeed, if we denote $z_n=(x_n,{\lambda }_n)\in H_1\times H_2$, then the recursions (24) specifically can be rewritten as follows for arbitrary initial points $x_0$, $x_1$, ${\lambda }_0$, ${\lambda }_1$,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_n^{\prime }=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ {\lambda }_n^{\prime }={\lambda }_n+{\theta }_n({\lambda }_n-{\lambda }_{n-1}),\hfill \\ {\overline{x}}_n=x_n^{\prime }-{\nabla }_{x}L(x_n^{\prime },{\lambda }_n^{\prime }),\hfill \\ {\overline{\lambda }}_n={\lambda }_n^{\prime }+{\nabla }_{\lambda }L(x_n^{\prime },{\lambda }_n^{\prime }),\hfill \\ x_{n+1}=(1-{\alpha }_n-{\gamma }_n)x_n^{\prime }+{\alpha }_n{\overline{x}}_n,\hfill \\ {\lambda }_{n+1}=(1-{\alpha }_n-{\gamma }_n){\lambda }_n^{\prime }+{\alpha }_n{\overline{\lambda }}_n,\hfill \end{array}\right.\end{array}$$

(25)

and the sequence pair $(x_n,{\lambda }_n)$ converges strongly to an element $(x^{*},{\lambda }^{*})\in \mathsf{\Omega }$ which is closest to $(0,0)$.

4.2. Critical Points Problem

In this part, we focus on finding the critical points of the functional $F:H\to R\cup \{+\infty \}$ defined by

$$F:=\mathsf{\Psi }+\mathsf{\Phi },$$

(26)

where H is a real Hilbert space, the function $\mathsf{\Psi }:H\to \mathbb{R}\cup \{+\infty \}$ is a proper, convex and lower semi-continuous function and $\mathsf{\Phi }:H\to \mathbb{R}$ is a convex locally Lipschitz mapping.

A point $x^{*}$ is said to be a critical point of $F=\mathsf{\Psi }+\mathsf{\Phi }$ if $x^{*}\in dom\left(\mathsf{\Psi }\right)$ and if it satisfies

$$\mathsf{\Psi }\left(x^{*}\right)-\mathsf{\Psi }\left(v\right)\le {\mathsf{\Phi }}^{\circ }(x^{*},v-x^{*}),$$

where ${\mathsf{\Phi }}^{\circ }$ is the generalized directional derivative of $\mathsf{\Phi }$ at $x^{*}\in C$ in the direction $v\in H$ which is defined by

$${\mathsf{\Phi }}^{\circ }(x^{*},v)=\underset{t\downarrow 0}{lim}\underset{w\to x^{*}}{sup}\frac{\mathsf{\Phi }(w+tv)-\mathsf{\Phi }\left(w\right)}{t}.$$

Critical point theory is a powerful theoretical tool, which has been greatly developed in recent years and has been widely used in many fields, such as differential equations, operations research optimization and so on. For some recent works on the applications of critical point theory, we can refer to Trushnikov et al. [39], Turgut et al. [40] and therein.

A typical instance is finding the solution of the impulsive differential equation model existing in the fields of medicine, biology, rocket and aerospace motion and optimization theory which can be transformed into finding the critical point of some functional.

Specifically, we consider the following impulsive differential equation:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}-\ddot{q}\left(t\right)=\lambda q\left(t\right)+f(t,q\left(t\right)),t\in (s_{k-1},s_k),\hfill \\ \Delta \dot{q}\left(s_k\right)=g_k\left(q\left(s_k^{-}\right)\right),k=1,2,\cdots ,\hfill \end{array}\right.\end{array}$$

(27)

where $k\in \mathbb{Z}, \lambda \ge 0,$$q\left(t\right)\in {\mathbb{R}}^n$, $\Delta \dot{q}\left(s_k\right)=\dot{q}\left(s_k^{+}\right)-\dot{q}\left(s_k^{-}\right)$, $\dot{q}\left(s_k^{\pm }\right)={lim}_{t\to s_k^{\pm }}\dot{q}\left(t\right)$, $f(t,q)=gra{d}_{q}I(t,q)$, $I(t,q)\in C^1(\mathbb{R}\times {\mathbb{R}}^n,\mathbb{R}),g_k\left(q\right)=gra{d}_q{G}_k\left(q\right),G_k\in C^1({\mathbb{R}}^n,\mathbb{R})$. In addition, there exist $m\in \mathbb{N}$ and $T\in {\mathbb{R}}^{+}$ such that $0=s_0<s_1<s_2<\dots \dots <s_m=T,s_{k+m}=s_k+T,g_{k+m}=g_k$ holds for all $k\in \mathbb{Z}$.

Let $H=\{q\in \mathbb{R}\to {\mathbb{R}}^n|qbeabsolutecontinuous,\dot{q}\in L^2((0,T),{\mathbb{R}}^n),q\left(t\right)=q(t+T),t\in \mathbb{R}\}$ and the norm $\parallel ·\parallel$ is induced by the inner product $⟨q,p⟩={\int }_0^T\dot{q}\left(t\right)\dot{p}\left(t\right)+q\left(t\right)p\left(t\right)dt$, $\forall p,q\in H$.

Denote $K=\{1,2,\cdots ,m\}$, and the functional on H is defined as

$$\begin{array}{c}\hfill F\left(q\right)={\int }_0^T\frac{1}{2}{\left|\dot{q}\right|}^2-\frac{1}{2}\lambda q^2-I(t,q)dt+\sum _{k\in K}{G}_k\left(q\left(s_k\right)\right),\end{array}$$

and then the periodic solution of the system (27) corresponds to the critical point of the functional F one to one.

If the functional F in (26) satisfies the Palais–Smale compact conditions and F is bounded from below, then there exists a critical point $x^{*}$ such that $F\left(x^{*}\right)={inf}_{u\in H}F\left(u\right)$ (see, e.g., Motreanu and Panagiotopoulos [41]). From Fermat’s theorem, one can refer that the critical point $x^{*}$ is a solution of the inclusion (see, e.g., Moameni [42]),

$$0\in \partial \mathsf{\Psi }\left(x^{*}\right)+{\partial }_c\mathsf{\Phi }\left(x^{*}\right),$$

where ${\partial }_c\mathsf{\Phi }(·)$ is the generalized derivative of $\mathsf{\Phi }$ defined as

$${\partial }_c\mathsf{\Phi }\left(u\right)=\{u^{*}\in H^{*};{\mathsf{\Phi }}^{\circ }(u,v)\ge ⟨u^{*},v⟩,\forall v\in H\}.$$

From Clarke [43], ${\partial }_c\mathsf{\Phi }$ carries bounded sets of H into bounded sets of $H^{*}$ and is hemicontinuous. Moreover, we can infer that ${\partial }_c\mathsf{\Phi }$ is a monotone mapping because $\mathsf{\Phi }$ is convex, which makes Browder ([17], Theorem 2) applicable, namely, $\partial \mathsf{\Psi }+{\partial }_c\mathsf{\Phi }$ is a maximal monotone mapping. Denoted by $\mathsf{\Omega }$ is the critical points set of the problem (26). By taking $A=\partial \mathsf{\Psi }+{\partial }_c\mathsf{\Phi }$, we have the following result.

Theorem 3.

Let H be a real Hilbert space. Suppose that $F:H\to (-\infty ,\infty ]$ is of the form (26), bounded from below and satisfying the Palais–Smale compact conditions such that $\mathsf{\Omega }\ne \varnothing$. Under the setting of the parameters in Algorithm 1, if $\left\{{\alpha }_n\right\}$, $\left\{{\gamma }_n\right\}$, $\left\{{ϵ}_n\right\}$ are the sequences in $(0,1)$ satisfying the conditions as in Theorem 1, then the sequence $\left\{z_n\right\}$ generated by the following schemes

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{y}_n=z_n+{\theta }_n(z_n-z_{n-1}),\hfill \\ {\overline{z}}_n=y_n-{\lambda }_n(\partial \mathsf{\Psi }+{\partial }_c\mathsf{\Phi })\left(y_n\right),\hfill \\ z_{n+1}=(1-{\alpha }_n-{\gamma }_n)y_n+{\alpha }_n{\overline{z}}_n,\hfill \end{array}\right.\end{array}$$

(28)

converges strongly to an element $\overline{x}\in \mathsf{\Omega }$ which is closest to $0$.

5. Numerical Examples

In this section, we present numerical examples in finite- and infinite-dimensional spaces to illustrate the applicability, efficiency and stability of Algorithm 1. All the codes for the results are written in Matlab R2016b and are performed on an LG dual-core personal computer.

Example 1.

Here, we test the effectiveness of our algorithm in finite-dimensional space which does not need super high dimensions. For the purpose, let $H=R^6$, and define the monotone operators A as follows:

$$A=\left(\begin{array}{cccccc}6& 0& 0& 0& 0& 0\\ 0& 7& 0& 0& 0& 0\\ 0& 0& 8& 0& 0& 0\\ 0& 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 4& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right)$$

(29)

it is easy to verify that the cocoercivity coefficient $\mu =\frac{1}{8}$, so we set ${\lambda }_n=\frac{1}{8}-\frac{1}{10n}$.

Next, let us compare our Algorithm 1 with the regularization method. Specifically, the regularization algorithm (RM) is considered as

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{y}_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ z_n=J_r^A{y}_n,\hfill \\ x_{n+1}=(1-{\alpha }_n-{\gamma }_n)y_n+{\alpha }_n{z}_n.\hfill \end{array}\right.\end{array}$$

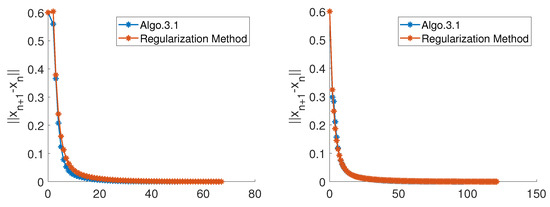
As for the components, both our Algorithm 1 and the regularization method (RM), initial points $x_0$, $x_1$ are generated randomly by Matlab, inertial coefficient ${\theta }_n$ is chosen to satisfy that if $\theta >{ϵ}_n\times (max(\parallel x_{n-1}-x_n\parallel ,\parallel x_{n-1}-x_n{\parallel }^2\left)\right)$, then ${\theta }_n{=1/((n+2)}^2\times (max(\parallel x_{n-1}-x_n\parallel ,\parallel x_{n-1}-x_n{\parallel }^2\left)\right))$; otherwise, ${\theta }_n=\frac{\theta }{2}$, where $\theta =0.6$, ${ϵ}_n=1/{(n+1)}^2$, ${\gamma }_n=1/\left(10n\right)$. The experimental results are listed in Figure 1. Moreover, the iterations and convergence rate of Algorithm 1 for different values of $\left\{{\alpha }_n\right\}$ are presented in Table 1.

Figure 1. Algorithm 1 and the Regularization Method.

Table 1. Example 1 Numerical Results for Algorithm 1 and Regularization Method.

Algorithm 1				Regularization Method
$\left\{{\mathsf{\alpha }}_{\mathit{n}}\right\}$	CPU Time	Iter.	$\frac{\parallel {\mathit{x}}_{\mathit{n}+\mathbf{1}}-{\mathit{x}}^{*}\parallel }{\parallel {\mathit{x}}_{\mathit{n}+\mathbf{1}}-{\mathit{x}}_{\mathbf{0}}\parallel }$	$\mathit{r}$	CPU Time	Iter.	$\frac{\parallel {\mathit{x}}_{\mathit{n}+\mathbf{1}}-{\mathit{x}}^{*}\parallel }{\parallel {\mathit{x}}_{\mathit{n}+\mathbf{1}}-{\mathit{x}}_{\mathbf{0}}\parallel }$
$1-\frac{1}{100n}$	0.0201	42	6.1691 $\times {10}^{-04}$	$0.1$	0.0324	63	5.3741 $\times {10}^{-04}$
$\frac{1}{2}-\frac{1}{100n}$	0.0594	88	9.159 $\times {10}^{-04}$	$0.05$	0.0530	115	0.0013
$\frac{1}{8}-\frac{1}{100n}$	0.0422	276	0.0039	$0.01$	0.2205	367	0.0078

Example 2.

Now, we measure our Algorithm 1 in $H=L_2[0,1]$ with $\parallel ·\parallel ={\left({\int }_0^1{x}^2\left(t\right)dt\right)}^{\frac{1}{2}}$. Define the mappings A by $A\left(x\right)\left(t\right):=2x\left(t\right)/3$ for all $x\left(t\right)\in L_2[0,1]$, and then it can be shown that A is $\frac{3}{2}$-cocoercive monotone mapping. All the parameters ${\theta }_n$, θ, ${\lambda }_n$, ${ϵ}_n$ and ${\gamma }_n$ are chosen as in Example 1. The stop criterion is $\parallel x_{n+1}-x_n\parallel \le {10}^{-6}$. We test Algorithm 1 for the following three different initial points:

Case I: $x_0=2t^3{e}^{5t},x_1=sin\left(3t\right)e^t/100$;

Case II: $x_0=sin(-3t)+cos(-5t)/2,x_1=2tsin\left(3t\right)e^{-5t}/200;$

Case III: $x_0=2tsin\left(3t\right)e^{-5t}/200,x_1=e^t-e^{-2t}.$

In addition, we also test the regularization method as illustrated in Example 1, and the tendency of the sequence is proposed in Figure 2 and Figure 3 and Table 2.

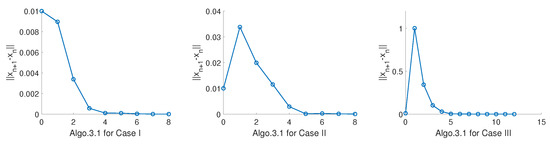
Figure 2. Algorithm 1 for Case I, Case II, Case III in Example 2.

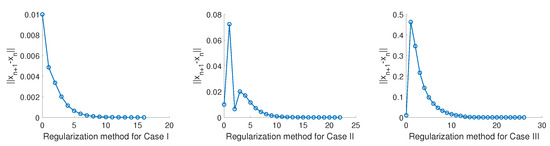
Figure 3. Regularization Method for Case I, Case II, Case III in Example 2.

Table 2. Example 2 Numerical Results for Algorithm 1 and Regularization Method.

	Case I		Case II		Case III
	Algorithm 1	RM	Algorithm 1	RM	Algorithm 1	RM
CPU time	2.64	5.28	4.29	8.6	3.62	7.59
Iteration Number	9	17	9	23	13	27

6. Conclusions

The proximal point method (regularization method) and projection-based method are two classical and significant methods for solving monotone inclusions, variational inequalities and related problems.

However, the evaluations of resolvents/projections in these methods heavily rely on the structure of the given problem, and in the general case, this might seriously affect the computational effort of the given method. Thus, motivated by the ideas of Chidume et al. [44], Alvarez [28], Alvarez–Attouch [27] and Zegeye [45], we present a simple strong convergence method that avoids the need to compute resolvents/projections.

We present several theoretical applications such as minimax problems and critical point problems, as well as some numerical experiments illustrating the performances of our scheme.