Abstract
A 3-restricted edge cut is an edge cut of a connected graph that separates this graph into components, each having an order of at least 3. The minimum size of all 3-restricted edge cuts of a graph is called its 3-restricted edge connectivity. This work determines the upper and lower bounds on the 3-restricted edge connectivity of replacement product graphs and presents sufficient conditions for replacement product graphs to be maximally 3-restricted edge connected. As a result, the 3-restricted edge connectivity of replacement product graphs of some special graphs are determined.
MSC:
05C90; 68R10
1. Introduction
When modeling the reliability of a telecommunication network, it is reasonable to assume that its nodes (vertices) never fail, but links (edges) fail independently with an equally small probability. Such network models are now known as Moore–Shannon ones [1,2,3]. Let M be a Moore–Shannon network model that has size (the number of links or edges) and edge failure probability p, where . If denotes the number of edge cuts of size h, then the reliability of M, namely the probability it remains connected, can be expressed as
The right hand side is called the reliability polynomial of network M. To determine the reliability , one needs only to calculate all the coefficients ’s. However, Provan proves in [4] that it is NP-hard to calculate all these coefficients. Bauer presents a general expression of those coefficients ’s with in [5], where denotes the edge connectivity of M. In order to estimate the reliability more accurately, Esfahanian introduces the concepts of restricted edge cut and restricted edge connectivity in [6], which can be defined as follows.
Definition 1.
A restricted edge cut is an edge cut of a connected graph which disconnects this graph without isolated vertices. The size of a minimum restricted edge cut of graph G is called its restricted edge connectivity.
In this work, we denote by , or simply , the restricted edge connectivity of graph G. With the properties of restricted edge cuts and restricted edge connectivity, Li determines in [7] the first coefficients of the reliability polynomial of networks with topologies being circulant graphs. His results show that for Moore–Shannon models with the same number of nodes and links, those that have a larger restricted edge connectivity and fewer minimum restricted edge cuts are locally more reliable, where a network M is locally more reliable than another network N if there is an integer such that holds for any positive real number . For accurate estimation and comparison of the reliability, the concepts of m-restricted edge cut and m-restricted edge connectivity are introduced in [8,9] as follows.
Definition 2.
An m-restricted edge cut is an edge cut of a connected graph which disconnects this graph with each component having order at least m. The size of a minimum m-restricted edge cut of graph G is called its m-restricted edge connectivity.
We denote by , or simply , the m-restricted edge connectivity of graph G. Let F be a subgraph of graph G or a subset of the vertex set of G. Denote by the graph obtained by removing all the vertices of F from G, that is, the subgraph of G induced by the vertex set . Let be the set of edges with one end in F and the other in (the coboundary of F). Write and or simply min is a connected vertex-induced subgraph of order m of graph . It is proven in [6,8] that when , holds with a few trivial exceptions. So, a graph G is called maximally m-restricted edge connected if the equality holds in the previous inequality.
Let M and N be two Moore–Shannon network models that have the same number of nodes and links, respectively. From the results obtained in [5,7,10], one can easily concludes that if M and N are both maximally m-restricted edge connected and have least equal minimum m-restricted edge cuts for , then N is locally more reliable than M when . So, maximizing 3-restricted edge connectivity of graphs plays an important role in the design of the locally most reliable networks. We prove in [11] that undirected binary Kautz networks are maximally 3-restricted edge connected. Some sufficient conditions for graphs to be maximally 3-restricted edge connected are obtained in [10,12,13] and elsewhere. Fruitful results on maximizing m-restricted edge connectivity are obtained; the readers are suggested to refer to [5,6,7,8,9,14,15,16,17] and their references.
Before proceeding, let us introduce some more symbols and terminologies. Graphs indicated in this work are all simple and connected. They are k-regular if every vertex has degree k. The length of a shortest cycle of a graph G that contains cycles, denoted by , is called its girth. The connectivity and edge connectivity of graph G are denoted by and , respectively. The minimum degree of G is denoted by . Suppose , let denote the subgraph of G induced by X.
Definition 3
([18]). Let be a -regular graph with vertex set and edge-set , be a -regular graph with vertex set and edge-set . For every vertex , label the edges of incident with x with . The replacement product graph has vertex set , two of its different vertices and , where and , are adjacent if and only if either and , or and .
Note that the replacement product graph replaces every vertex of by a copy of and if and only if there is exactly one edge between and in . For an earlier version of the definition of please refer to [19]. An illustration of the replacement product graph of and is provided in Figure 1.
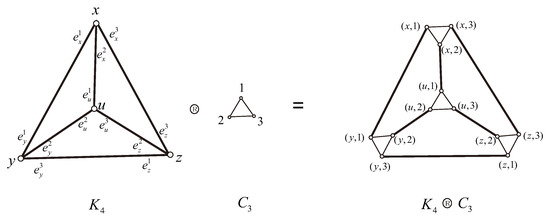
Figure 1.
An illustration of .
For other symbols and terminologies not specified we follow those of [20].
2. Bounds on 3-Restricted Edge Connectivity
In what follows, we assume that is a -regular connected graph on n vertices and is a -regular connected graph with vertex set , where , and . Under this assumption, is -regular and has vertices. Moreover, the vertex set of can be partitioned into such that for each , where . It is clear that has 3-restricted edge cuts when . In this section, we investigate the bounds of the 3-restricted edge connectivity of these replacement product graphs.
Lemma 1
([21]). Let G be a connected k-regular graph of order at least that contains an m-restricted edge cut. If , them .
Note that if a connected regular graph contains 3-restricted edge cuts, then it has cycles, so the following lemma follows directly from Lemma 1.
Lemma 2.
Let G be a k-regular connected graph of order at least 6. If G contains a 3-restricted edge cut, then .
Lemma 3
([18]). for any n-regular connected graph G.
Lemma 4.
If is a 2-regular connected graph (a cycle), then .
Proof.
Since is a cycle, by the definition of replacement product graph, it follows that is also a cycle. Thus, the lemma follows. □
For and , denote the set of edges of G with one end in X and the other end in by .
Lemma 5.
If is a -regular connected graph with , where , then .
Proof.
Write . Let such that is a minimum edge-cut of . Then both and are connected. Therefore, and are both connected, where , . Since and , it follows that is a 3-restricted edge cut of G. By the definition of replacement product graph, there is an edge in if and only if there is exactly one edge between and in G, where is the subgraph of G induced by the vertex set , and is defined similarly. So, if , there exists such that . Hence, and
□
Lemma 6.
If is a -regular connected graph with and , , then .
Proof.
Write . Since is a connected subgraph of G with , it follows that . Recalling that G is -regular, by Lemma 2 we have,
Together with Lemma 5, we have . □
Lemma 7.
If graph is -regular connected, , and , , then .
Proof.
Write . By Lemma 5, we have . From the construction properties of replacement product , we deduce that for every vertex , exactly one edge incident with it is not in . So, if a cycle C of G is not contained in some subgraph of G with then C has a length of at least six. Since has a girth of at least four, it follows that G has a girth of at least four. Hence, G contains 3-restricted edge cuts. By Lemma 2, we have . Thus, the lemma follows. □
Corollary 1.
Let be a -regular connected graph. If , then .
Proof.
If , by Lemma 4 the result follows. If , by Lemma 3, . Since and . By Lemma 6, . Therefore,
The corollary follows. □
Theorem 1.
Let be connected -regular graphs, . If and , then
Proof.
If , since is regular it follows that is the complete graph . If then since . Similarly, if then we can deduce that . Hence, by Corollary 1 we have . □
Theorem 2.
Let be connected -regular graphs, . If and , then
So, if then .
Proof.
The second part of the theorem follows directly from the first one, and the second inequality of the first statement follows directly from Lemma 7. So, it suffices to prove .
If , since is a regular connected graph on vertices with girth , then is the 4-cycle and . Similarly, if then is the 5-cycle . In any case, is a cycle. Write . Let be a minimum 3-restricted edge cut (simply, a -cut) of G, where and X are the vertex sets of two connected vertex-induced subgraphs of G with at least three vertices each and . Let , and be the vertex set of . Then, be a partition of with being isomorphic to .
If every is connected in of all , then either or for any . Note that if and only if G has exactly one edge between and . Since F is a minimal 3-restricted edge cut of G, each edge in F connects a vertex of some to a vertex of some with . Set and there is an edge in F between and , then H is an edge cut of , which disconnects vertex sets and and . It follows that . In what follows we continue to consider the case when at least one is disconnected in .
Firstly, we consider the case when there exists exactly one integer such that is disconnected in .
Case 1. . In this case, . Thus,
The last equality holds since every vertex of is incident with exactly one edge not in . Since F is a 3-restricted edge cut, it follows that . Noting that is an edge-cut of , we have .
Case 2. . Since , it follows that . Thus, , and there are at least two sets of and other than such that and . Since , there exists at least internally vertex-disjoint paths between any two vertices u and v, where . By the definition of G, there exists at least internally vertex-disjoint paths between and in . Each of these paths has at least one edge of F. Hence
Therefore, in this case.
Secondly, we consider the case when there exists exactly two integers such that and are disconnected in .
Case 3. or , say . In this case, and
Without loss of generality, we assume . If , then since otherwise X would be an isolated edge in G by the property that every vertex of is incident with exactly one edge not contained in . Thus, contains at least one vertex which is incident with one edge between and some such that . Therefore,
If , we also have . Thus, the the above formula is also true.
Case 4. and . In this case, there are at least two sets of and other than and such that and . Since , has at least internally vertex-disjoint paths between vertices and . These paths corresponds to the same number of internally vertex-disjoint paths between and in , each of which contains at least one edge of F. Therefore,
Finally, we consider the case when there exists at least three integers such that and are disconnected in . In this case, we have
Thus, the theorem follows. □
Lemma 8.
Let be connected -regular graphs, . If , then
Proof.
Write . Let be a -cut of G, where with . Let be the partition of defined in the proof of Lemma 2. If is connected in for any , then either or . Thus, is an edge-cut of , where . From the construction properties of replacement product we deduce that . So, the lemma follows in this case. In what follows we assume that there is some such that is disconnected in .
Firstly, similarly to the proof of Theorem 2, we consider the case when there exists exactly one integer such that is disconnected in .
Case 1. . In this case, we have . Since every vertex of X is incident with exactly one edge not contained in , it follows that
Note that and in this case. If , then . Therefore,
If , since F is a minimum 3-restricted edge cut it follows that is a restricted edge cut of . Therefore,
If and is connected, then is a 3-restricted edge cut of . Hence,
If and has exactly two connected components, then contains a restricted edge cut and an edge cut of . So,
If and has at least three connected components, then contains at least three edge cuts of . Thus,
Therefore, the lemma follows in this case.
Case 2. . Since , it follows that . So, , and there are at least two sets of and other than such that and . Since , there exists at least internally vertex-disjoint paths between any two vertices and . Correspondingly, G has at least internally vertex-disjoint paths between and in , and each of these paths contains at least one edge of F. Hence,
Therefore, the lemma is also true in this case.
Secondly, we consider the case when there are exactly two integers such that and are disconnected in .
Case 3. or , say . In this case, . For simplicity, we assume without loss of generality that . Then,
When , as shown in the proof of Theorem 2 (case 3), we have . If , then is an edge-cut of , and is a restricted edge-cut of . Noticing , we conclude that
If and , noticing that the vertices of are incident with edges of F and the vertices of are incident with edges of F, thus, we deduce that .
When , is an restricted edge cut of , and is a -cut of . Note that is incident with at least one edge of F which is not contained in , and so does . It follows that
When , by the assumption that , we have . So,
The inequality holds since . So, the lemma follows in this case.
Case 4. and . So, there are two sets of and other than and such that and . Since , has at least internally vertex-disjoint paths between vertices and . Correspondingly, G has at least internally vertex-disjoint paths between and in , and each of these paths contains at least one edge of F. Hence,
Finally, we consider the case when there exist at least three integers such that and are disconnected in . In this case,
Therefore, the lemma follows in all cases. □
Theorem 3.
Let be -regular connected graphs, . If and , then
Proof.
The theorem follows directly from Lemmas 6 and 8. □
Theorem 4.
Let be -regular connected graphs, . If and , then
Proof.
The theorem follows directly from Lemmas 7 and 8. □
Note that a connected regular graph with and does not exist. The results of Theorems 1–4 can be summarized in Table 1.

Table 1.
A summary of the results of Theorems 1–4.
3. Optimization of 3-Restricted Edge Connectivity
This section will present some sufficient conditions for replacement product graphs to be maximally 3-restricted edge connected, namely, sufficient conditions for 3-restricted edge connectivity to arrive to its upper bound.
Theorem 5.
Let be -regular connected graphs, , with and . If , , and is maximally 3-restricted edge connected, then
Proof.
Since is maximally 3-restricted edge connected with and , it follows that
Therefore,
Since , it follows that or . Therefore, . By Theorem 3, , and the theorem follows. □
Corollary 2.
Let be -regular connected graphs, , with , and . If and is maximally 3-restricted edge connected, then
Proof.
This corollary follows directly from Theorem 5. □
Theorem 6.
Let be -regular connected graphs, , with . If , and is maximally 3-restricted edge connected, then
Proof.
Since is maximally 3-restricted edge connected and , it follows that
Therefore,
Since , it follows that either or . So, . By Theorem 4, we have . Hence the theorem follows. □
The following corollary follows directly from Theorem 6.
Corollary 3.
Let be -regular connected graphs, , with and . If and is maximally 3-restricted edge connected, then
Corollary 4.
If G is an n-regular connected graph with and , then .
Proof.
If , then the corollary follows from Corollary 1. If , by Theorem2, we have . Since and , it follows that . So, . If , then is maximally 3-restricted edge connected. Since and , by Theorem 6, we have that . Hence, The corollary follows. □
Theorem 7.
Let be -regular connected graphs, , with , , and . If is maximally 3-restricted edge connected, then is maximally 3-restricted edge connected if and only if .
Proof.
Since , it follows that also has a girth of three. So, . By Theorem 5, we have . Therefore, is maximally 3-restricted edge connected if and only if . □
Theorem 8.
Let be -regular connected graphs, , with , and . If is maximally 3-restricted edge connected, then is maximally 3-restricted edge connected if and only if .
Proof.
Since , it follows that also has a girth of at least four. Then . By Theorem 6, we have . Therefore, is maximally 3-restricted edge connected if and only if . □
4. Conclusions
Two small networks can generate an extensive network by the replacing product operation. In this research, the upper and lower bounds on 3-restricted edge connectivity of a replacement product graphs on two small networks and are determined by the connectivities and degrees of and . Furthermore, some sufficient conditions depicted with and are characterized for to achieve the upper bound and for to be maximally 3-restricted edge connected. However, the method in this research seems to not be effective for the case of (). This is because there would be more cases when considering a connected subgraph with at least four vertices in , and more parameters shall be used to characterize the bounds of (). We will explore new ways to investigate the bounds for () in our future research. Additionally, we will try to improve the bounds of in our future research.
Author Contributions
All the authors have contributed in this article, i.e., Writing—original draft preparation, Y.C.; Supervision, J.O. and S.L., Writing—review and editing, S.L. and Y.C.; Funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China (No. 12201471, 10271105), Guangdong Basic and Applied Basic Research foundation (No. 2020A1515010555) and the Special Foundation in Key Fields for Universities of Guangdong Province (2022ZDZX1034).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
No data have been used in this article.
Acknowledgments
The authors gratefully thank to the Referees for the constructive comments to improve the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Moore, E.F.; Shannon, C. Reliable circuits using less reliable relays (I). J. Frankl. Inst. 1956, 262, 191–208. [Google Scholar] [CrossRef]
- Moore, E.F.; Shannon, C. Reliable circuits using less reliable relays (II). J. Frankl. Inst. 1956, 262, 281–297. [Google Scholar] [CrossRef]
- Ore, O. Note on hamiltonian circuits. Am. Math. Mon. 1960, 67, 55–63. [Google Scholar] [CrossRef]
- Provan, J.S.; Ball, M.O. The complexity of counting cuts and of computing the probability that a graph is connected. SIAM J. Comput. 1983, 12, 77–788. [Google Scholar] [CrossRef]
- Bauer, D.; Boesch, F.; Suffel, C.; Tindell, R. Combinatorial optimization problems in the analysis and design of probabilistic networks. Networks 1985, 15, 257–271. [Google Scholar] [CrossRef]
- Esfahanian, A.H.; Hakimi, S.L. On computing a conditional edge connectivity of a graph. Inf. Process Lett. 1988, 27, 195–199. [Google Scholar] [CrossRef]
- Li, Q.L.; Li, Q. Reliability analysis of circulant graphs. Networks 1998, 28, 61–65. [Google Scholar] [CrossRef]
- Bonsma, P.; Ueffing, N.; Volkmann, L. Edge cuts leaving component of order at least three. Discret. Math. 2002, 256, 431–439. [Google Scholar] [CrossRef]
- Ou, J. Edge Cuts leaving components of order at least m. Discret. Math. 2005, 305, 365–371. [Google Scholar] [CrossRef][Green Version]
- Wang, M.; Li, Q. Conditional edge connectivity properties, reliability comparison and transitivity of graphs. Discret. Math. 2002, 258, 205–214. [Google Scholar] [CrossRef]
- Ou, J.; Cheng, X.H.; Wu, J.C. On 3-restricted edge connectivity of undirected binary Kautz graphs. Discret. Math. 2009, 309, 629–638. [Google Scholar] [CrossRef][Green Version]
- Ou, J.; Zhang, F.J. 3-restrcited edge connectivity of vertex transitive graphs. Ars Combin. 2005, 74, 291–302. [Google Scholar]
- Wang, Y.Q. On optimization problem of 3-restricted edge connectivity of graphs. Sci. China (Ser. A) 2006, 36, 369–377. [Google Scholar]
- Balbuena, C.; García-Vázquez, P.; Marcote, X. Sufficient conditions for λ′-optimality in graphs with girth g. Graph Theory 2006, 52, 73–86. [Google Scholar] [CrossRef]
- Hellwig, A.; Volkmann, L. Sufficient conditions for λ′-optimality in graph of diameter 2. Discret. Math. 2004, 283, 113–120. [Google Scholar] [CrossRef]
- Hellwig, A.; Volkmann, L. Maximally edge-connected and vertex-connected graphs and digraphs, a survey. Discret. Math. 2008, 308, 3265–3296. [Google Scholar] [CrossRef]
- Meng, J.X.; Ji, Y. On a kind of restricted edge connectivity of graphs. Discret. Appl. Math. 2002, 117, 183–193. [Google Scholar] [CrossRef]
- Hong, Z.M.; Xu, J.M. On restricted edge connecitivity of replacement product graphs. Sci. China (Ser. A) 2017, 60, 745–758. [Google Scholar] [CrossRef][Green Version]
- Reingold, O.; Vadhan, S.; Wigderson, A. Entropy waves, the zig-zag graph product, and new constant-degree expanders. Ann. Math. 2002, 155, 157–187. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Macmillan Press: London, UK, 1976. [Google Scholar]
- Ou, J.P.; Zhang, F.J. Bound on m-restriced edge connectivity. Acta Math. Appl. Sin. (Engl. Ser.) 2003, 19, 505–510. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).