An Analysis of the One-Phase Stefan Problem with Variable Thermal Coefficients of Order p
Abstract
1. Introduction
2. Approximate Solutions
2.1. The First Approximation
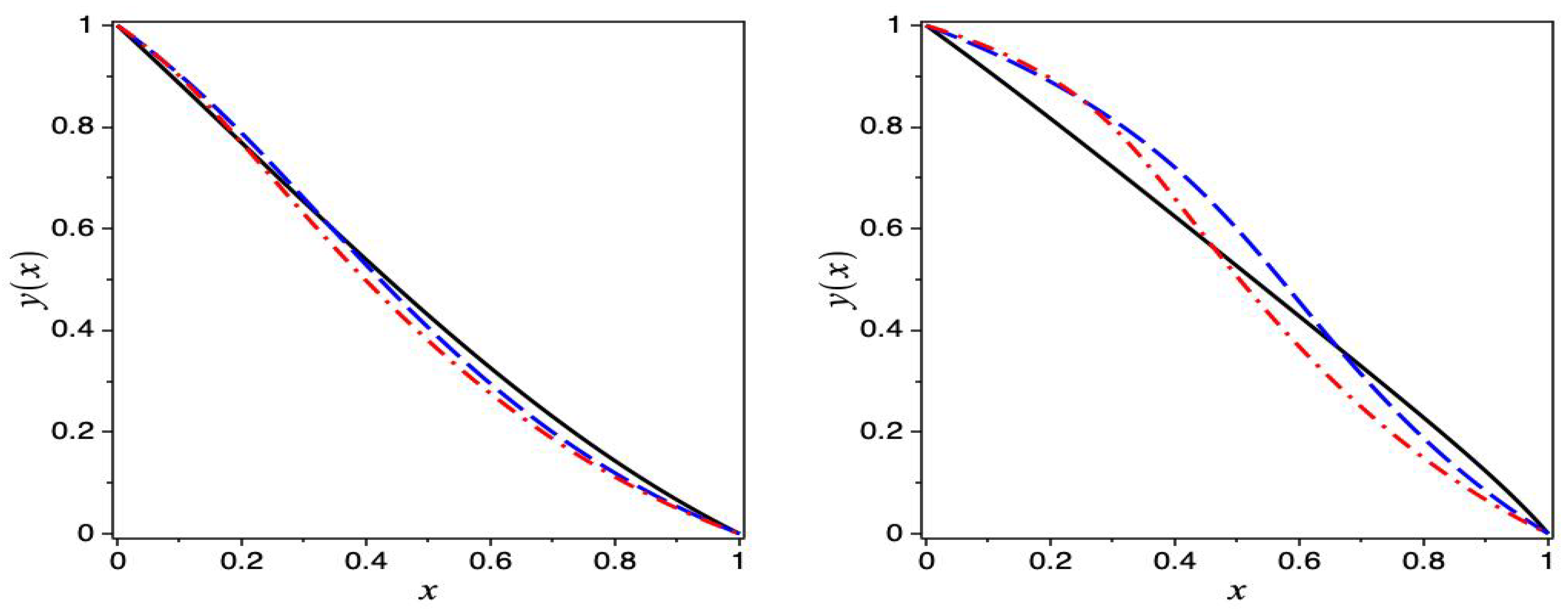
2.2. The Second Approximation
2.3. A Special Case
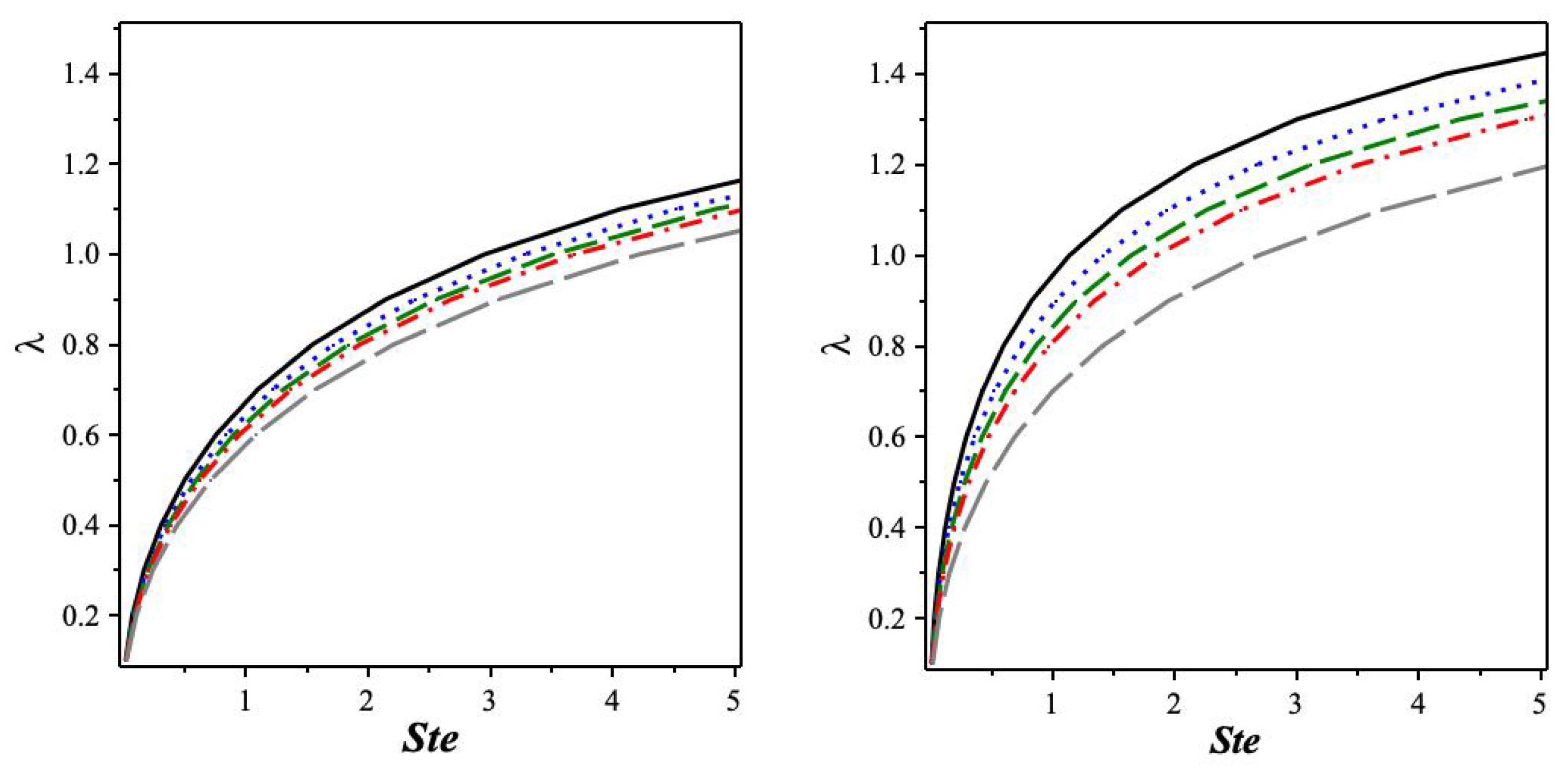
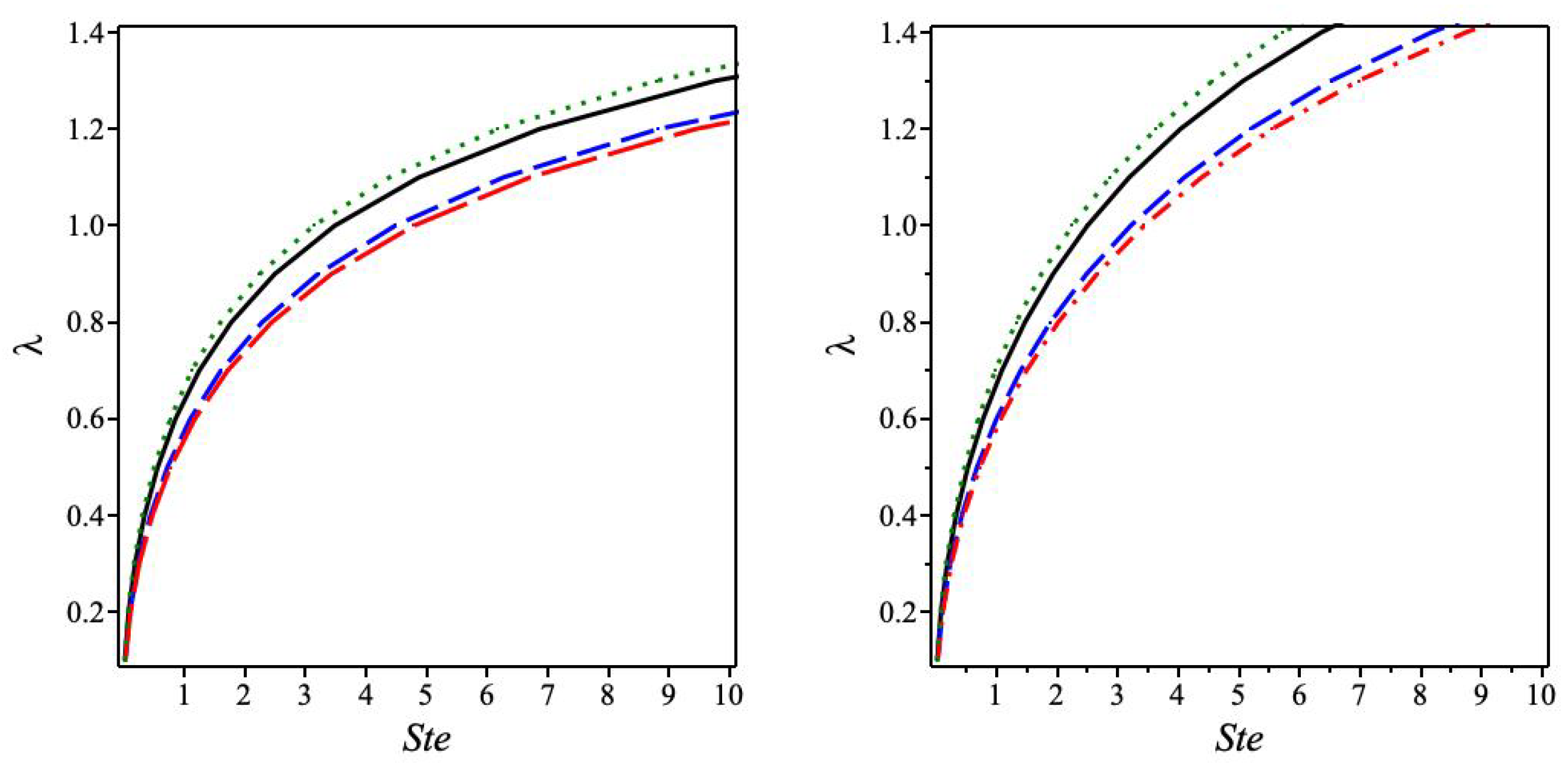
3. The Values of in Terms of the Stefan Number
3.1. Case 1:
3.2. Case 2:
4. Remarks on the General Case: and
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cho, S.H.; Sunderland, J.E. Phase change problems with temperature-dependent thermal Conductivity. J. Heat Transfer 1974, 96, 214–217. [Google Scholar] [CrossRef]
- Oliver, D.L.R.; Sunderland, J.E. A phase-change problem with temperature-dependent thermal conductivity and specific heat. Int. J. Heat Mass Transfer 1987, 30, 2657–2661. [Google Scholar] [CrossRef]
- Ceretani, A.N.; Salva, N.N.; Tarzia, D.A. Existence and uniqueness of the modified error function. Appl. Math. Lett. 1987, 70, 14–17. [Google Scholar] [CrossRef]
- Bougouffa, S.; Khanfer, A.; Bougoffa, L. On the approximation of the modified error function. Math. Meth. Appl. Sci. 2022, 1–9. [Google Scholar] [CrossRef]
- Khanfer, A.; Bougoffa, L. A Stefan problem with nonlinear thermal conductivity. Math. Meth. Appl. Sci. 2022, 1–10. [Google Scholar] [CrossRef]
- Bollati, J.; Natale, M.F.; Semitiel, J.A.; Tarzia, D.A. Exact solution for non-classical one-phase Stefan problem with variable thermal coefficients and two different heat source terms. Comp. Appl. Math. 2022, 41, 375. [Google Scholar] [CrossRef]
- Briozzo, A.C.; Tarzia, D.A. Existence, Uniqueness and an Explicit Solution for a One-Phase Stefan Problem for a Non-Classical Heat Equation, Free Boundary Problems; International Series of Numerical Mathematics; Birkhäuser: Basel, Switzerland, 2006; Volume 15, pp. 117–124. [Google Scholar]
- Bougoffa, L. A note on the existence and uniqueness solutions of the modified error function. Math. Methods Appl. Sci. 2018, 41, 5526–5534. [Google Scholar] [CrossRef]
- Bougoffa, L.; Rach, R.; Mennouni, A. On the existence, uniqueness and new analytic approximate solution of the modified error function in two-phase Stefan problems. Math. Methods Appl. Sci. 2021, 44, 10948–10956. [Google Scholar] [CrossRef]
- Zhou, Y.; Xia, L. Exact solution for Stefan problem with general power-type latent heat using Kummer function. Int. J. Heat Mass Transf. 2015, 84, 114–118. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, A.K. A moving boundary problem with variable specific heat and thermal conductivity. J. King Saud Univ.-Sci. 2020, 32, 384–389. [Google Scholar] [CrossRef]
- Ribera, H.; Myers, T. A mathematical model for nanoparticle melting with size-dependent latent heat and melt temperature. Microfluid. Nanofluidics 2016, 20, 147. [Google Scholar] [CrossRef]
- Font, F.; Myers, T.; Mitchell, S. A mathematical model for nanoparticle melting with density change. Microfluid. Nanofluidics 2015, 18, 233–243. [Google Scholar] [CrossRef]
- Briozzo, A.C.; Natale, M.F. One-phase Stefan problem with temperature-dependent thermal conductivity and a boundary condition of Robin type. J. Appl. Anal. 2015, 21, 89–97. [Google Scholar] [CrossRef]
- Bougoffa, L.; Khanfer, A. On the solutions of a phase change problem with temperature-dependent thermal conductivity and specific heat. Results Phys. 2020, 19, 103646. [Google Scholar] [CrossRef]
- Voller, V.R.; Swenson, J.B.; Paola, C. An analytical solution for a Stefan problem with variable latent heat. Int. J. Heat Mass Transf. 2004, 47, 5387–5390. [Google Scholar] [CrossRef]
- Beasley, J.D. Thermal conductivities of some novel nonlinear optical materials. Appl. Opt. 1994, 33, 1000–1003. [Google Scholar] [CrossRef]
- Aggarwal, R.L.; Fan, T.V. Thermal diffusivity, specific heat, thermal conductivity, coefficient of thermal expansion, and refractive-index change with temperature in AgGaSe_2. Appl. Opt. 2005, 44, 2673. [Google Scholar] [CrossRef]
- Henager, C.H.; Pawlewicz, W.T. Thermal conductivities of thin, sputtered optical films. Appl. Opt. 1993, 32, 91. [Google Scholar] [CrossRef]
- de Azevedo, A.M.; dos Santos Magalhães, E.; da Silva, R.G.D. A comparison between nonlinear and constant thermal properties approaches to estimate the temperature in LASER welding simulation. Case Stud. Therm. Eng. 2022, 35, 102135. [Google Scholar] [CrossRef]
- Xiao, Y.; Wu, H. An explicit coupled method of FEM and meshless particle method for simulating transient heat transfer process of friction stir welding. Math. Probl. Eng. 2020, 2020, 2574127. [Google Scholar] [CrossRef]
- Brizes, E.; Jaskowiak, J.; Abke, T.; Ghassemi-Armaki, H.; Ramirez, A.J. Evaluation of heat transfer within numerical models of resistance spot welding using high-speed thermography. J. Mater. Process. Technol. 2021, 297, 117276. [Google Scholar] [CrossRef]
- Gladkov, S.O.; Bogdanova, S.B. On the Theory of Nonlinear Thermal Conductivity. Tech. Phys. 2016, 61, 157–164. [Google Scholar] [CrossRef]
- Tomeczek, J.; Palugniok, H. Specific heat capacity and enthalpy of coal pyrolysis at elevated temperatures. Fuel 1996, 75, 1089–1093. [Google Scholar] [CrossRef]
- Saxena, S.K. Earth mineralogical model: Gibbs free energy minimization computation in the system MgO–FeO–SiO2. Geochim. Cosmochim. Acta 1996, 60, 2379–2395. [Google Scholar] [CrossRef]
- Hanrot, F.; Ablitzer, D.; Houzelot, J.L.; Dir, M. Experimental measurement of the true specific heat capacity of coal and semicoke during carbonization. Fuel 1994, 73, 305–309. [Google Scholar] [CrossRef]
- Haemmerich, D.; Dos Santos, I.; Schutt, D.J.; Webster, J.G.; Mahvi, D.M. In vitro measurements of temperature-dependent specific heat of liver tissue. Med. Eng. Phys. 2006, 28, 194–197. [Google Scholar] [CrossRef]
- Alam, M.N.; Tunç, C. New solitary wave structures to the (2+1)-dimensional KD and KP equations with spatiotemporal dispersion. J. King Saud Univ.-Sci. 2020, 32, 3400–3409. [Google Scholar] [CrossRef]
- Akinshilo, A.T.; Davodi, A.G.; Rezazadeh, H.; Sobamowoand, G.; Tunç, C. Heat transfer and flow of MHD micropolar nanofluid through the porous walls, magnetic fields, and thermal radiation. Palest. J. Math. 2022, 11, 604–616. [Google Scholar]
- Ascher, U.; Petzold, L. Computer Methods for Ordinary Differential Equations and Differential-Algebraic Equations; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]


| p | 0.1 | 0.5 | 1 | 1.5 | 2 | 5 | 10 |
|---|---|---|---|---|---|---|---|
| −0.7758 | −0.6773 | −0.6096 | −0.5689 | −0.5418 | −0.4741 | −0.4433 | |
| −0.4972 | −0.6441 | −0.6102 | −0.5698 | −0.5427 | −0.4760 | −0.4433 |
| x | ||||||
| 0 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| 0.1 | 0.909960 | 0.909904 | 0.949665 | 0.949618 | 0.957271 | 0.957223 |
| 0.2 | 0.816690 | 0.816590 | 0.889224 | 0.889194 | 0.896205 | 0.896159 |
| 0.3 | 0.721090 | 0.720860 | 0.814792 | 0.814763 | 0.800557 | 0.800429 |
| 0.4 | 0.623984 | 0.623694 | 0.720319 | 0.720219 | 0.659203 | 0.659085 |
| 0.5 | 0.526044 | 0.525706 | 0.599310 | 0.599076 | 0.505868 | 0.505774 |
| 0.6 | 0.427654 | 0.427191 | 0.456012 | 0.455911 | 0.367732 | 0.367636 |
| 0.7 | 0.328695 | 0.328249 | 0.312872 | 0.312859 | 0.248849 | 0.248768 |
| 0.8 | 0.228078 | 0.227540 | 0.187551 | 0.187508 | 0.148830 | 0.148778 |
| 0.9 | 0.122416 | 0.122437 | 0.0837442 | 0.0837148 | 0.0664419 | 0.0664179 |
| 1.0 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
| p | 0.1 | 0.5 | 1 | 1.5 | 2 | 5 | 10 |
|---|---|---|---|---|---|---|---|
| −0.7310 | −0.6382 | −0.5740 | −0.5360 | −0.5102 | −0.4468 | −0.4178 | |
| −0.6851 | −0.8026 | −0.7092 | −0.6315 | −0.5855 | −0.4897 | −0.4539 |
| x | ||||||
| 0 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| 0.1 | 0.88353 | 0.894305 | 0.901384 | 0.905988 | 0.898449 | 0.902000 |
| 0.2 | 0.76533 | 0.785659 | 0.784270 | 0.793780 | 0.764844 | 0.772572 |
| 0.3 | 0.64752 | 0.676322 | 0.653688 | 0.667504 | 0.622902 | 0.633430 |
| 0.4 | 0.53229 | 0.567523 | 0.520863 | 0.536825 | 0.490117 | 0.501984 |
| 0.5 | 0.42178 | 0.460092 | 0.396590 | 0.412553 | 0.371442 | 0.383526 |
| 0.6 | 0.31802 | 0.355452 | 0.286588 | 0.300962 | 0.268065 | 0.279297 |
| 0.7 | 0.22277 | 0.255541 | 0.192562 | 0.204256 | 0.180066 | 0.189469 |
| 0.8 | 0.13746 | 0.161506 | 0.114270 | 0.122498 | 0.106851 | 0.113620 |
| 0.9 | 0.06306 | 0.0753524 | 0.050600 | 0.054836 | 0.0473141 | 0.0508684 |
| 1.0 | 0.00000 | 0.000013 | 0.00000 | 0.00000 | 0.00000 |
| x | ||||||
| 0 | 1.0000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 | 1.00000 |
| 0.1 | 0.859128 | 0.844884 | 0.860807 | 0.855819 | 0.859406 | 0.855716 |
| 0.2 | 0.723092 | 0.696854 | 0.723068 | 0.714310 | 0.719800 | 0.713261 |
| 0.3 | 0.594257 | 0.559926 | 0.591772 | 0.580742 | 0.588046 | 0.579486 |
| 0.4 | 0.474624 | 0.436756 | 0.470282 | 0.458281 | 0.466955 | 0.457202 |
| 0.5 | 0.365737 | 0.328685 | 0.360565 | 0.348677 | 0.357914 | 0.347866 |
| 0.6 | 0.268611 | 0.235952 | 0.263571 | 0.252739 | 0.261613 | 0.252179 |
| 0.7 | 0.183726 | 0.157980 | 0.179527 | 0.170570 | 0.178190 | 0.170217 |
| 0.8 | 0.111045 | 0.093645 | 0.108117 | 0.101710 | 0.107311 | 0.101518 |
| 0.9 | 0.050085 | 0.041510 | 0.0486159 | 0.0452548 | 0.0482536 | 0.0451840 |
| 1.0 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bougoffa, L.; Bougouffa, S.; Khanfer, A. An Analysis of the One-Phase Stefan Problem with Variable Thermal Coefficients of Order p. Axioms 2023, 12, 497. https://doi.org/10.3390/axioms12050497
Bougoffa L, Bougouffa S, Khanfer A. An Analysis of the One-Phase Stefan Problem with Variable Thermal Coefficients of Order p. Axioms. 2023; 12(5):497. https://doi.org/10.3390/axioms12050497
Chicago/Turabian StyleBougoffa, Lazhar, Smail Bougouffa, and Ammar Khanfer. 2023. "An Analysis of the One-Phase Stefan Problem with Variable Thermal Coefficients of Order p" Axioms 12, no. 5: 497. https://doi.org/10.3390/axioms12050497
APA StyleBougoffa, L., Bougouffa, S., & Khanfer, A. (2023). An Analysis of the One-Phase Stefan Problem with Variable Thermal Coefficients of Order p. Axioms, 12(5), 497. https://doi.org/10.3390/axioms12050497








