Review of Quaternion Differential Equations: Historical Development, Applications, and Future Direction
Abstract
1. Introduction
2. Materials and Methods
2.1. Basic Concepts of Quaternion
2.1.1. Quaternion
2.1.2. Derivative of Quaternion Function
- (a)
- , for
- (b)
- (c)
- (d)
- .
2.1.3. Quaternionic Regular Function
2.1.4. Quaternion Differential Equation
- Quaternion frenet frame on differential geometry.
- b.
- Quaternion differential equations in kinematic modeling and attitude dynamics.
- c.
- Quaternion differential equations in fluid mechanics.
- d.
- Quaternion differential equations in quantum mechanics.
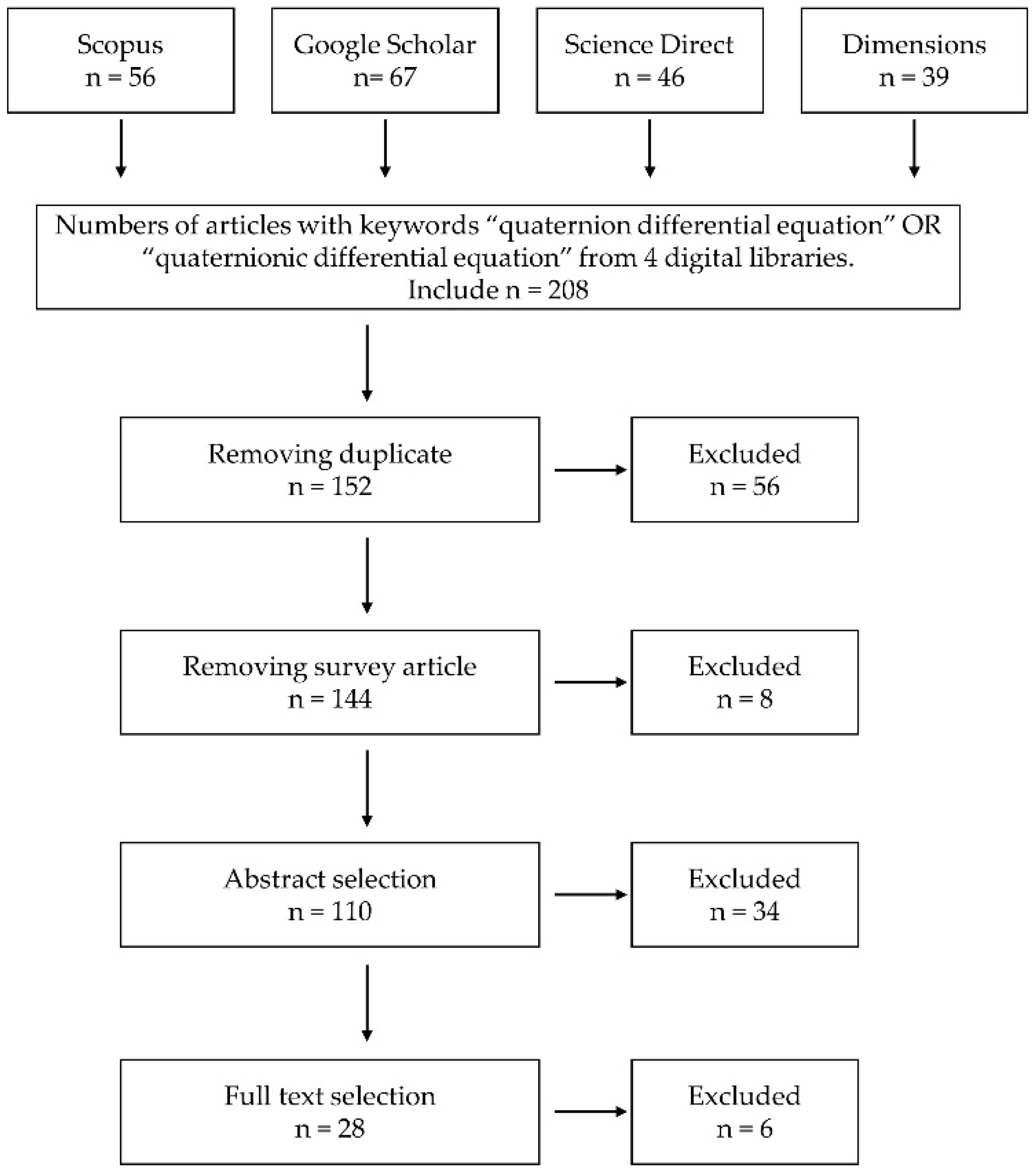
2.2. Database and Search Strategy
2.3. Data Analysis and Visualization
3. Results
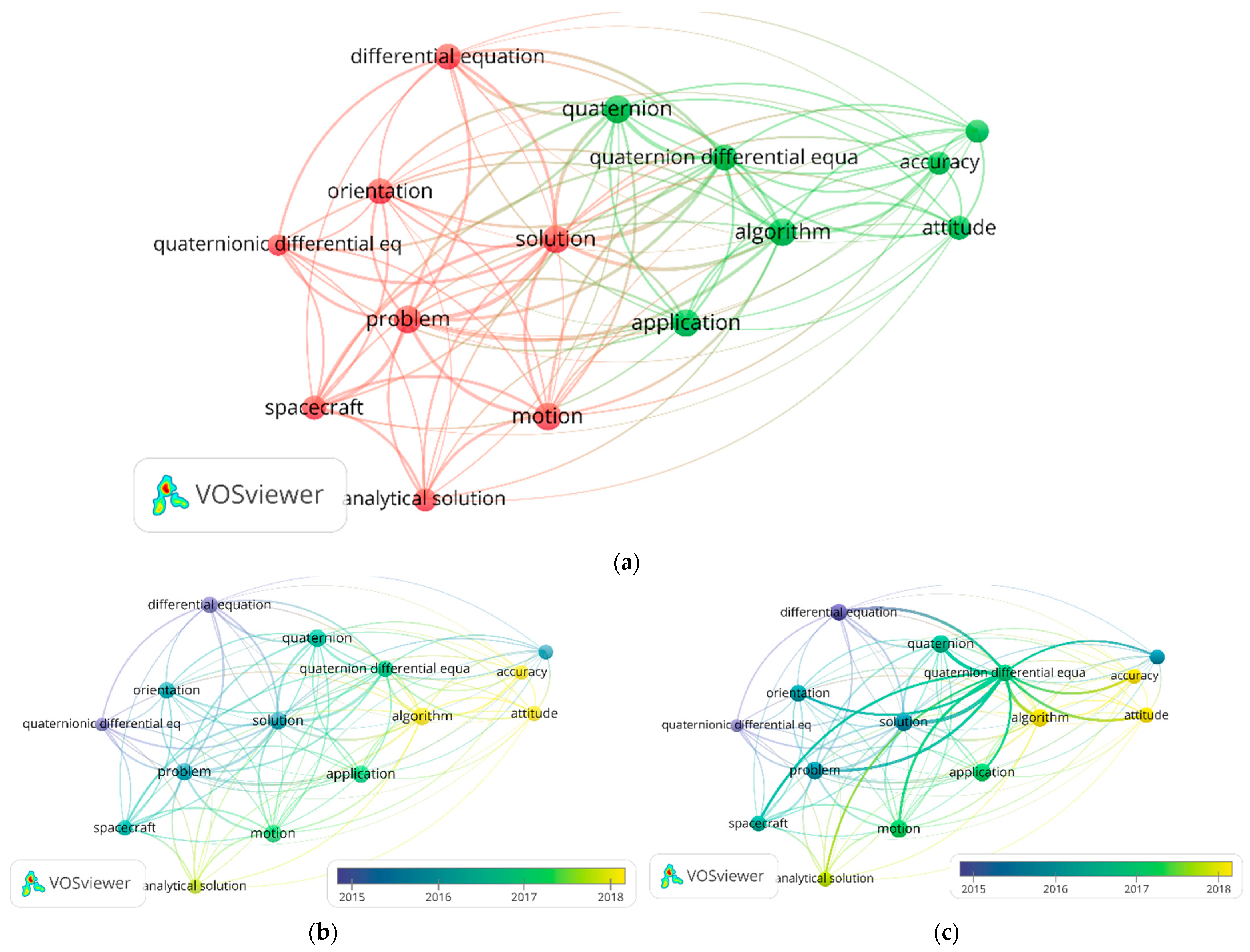
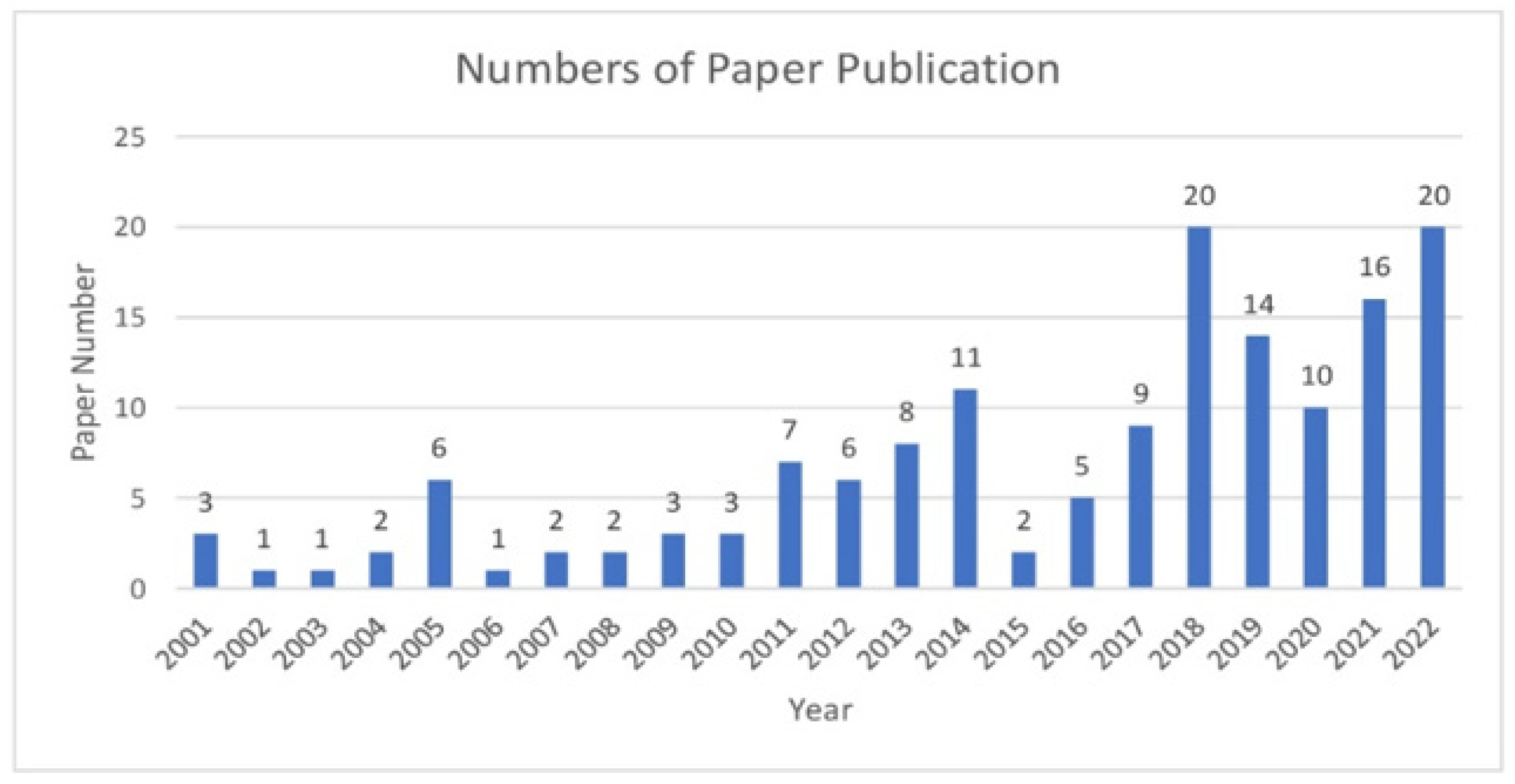
3.1. Result from Bibliometric Analysis
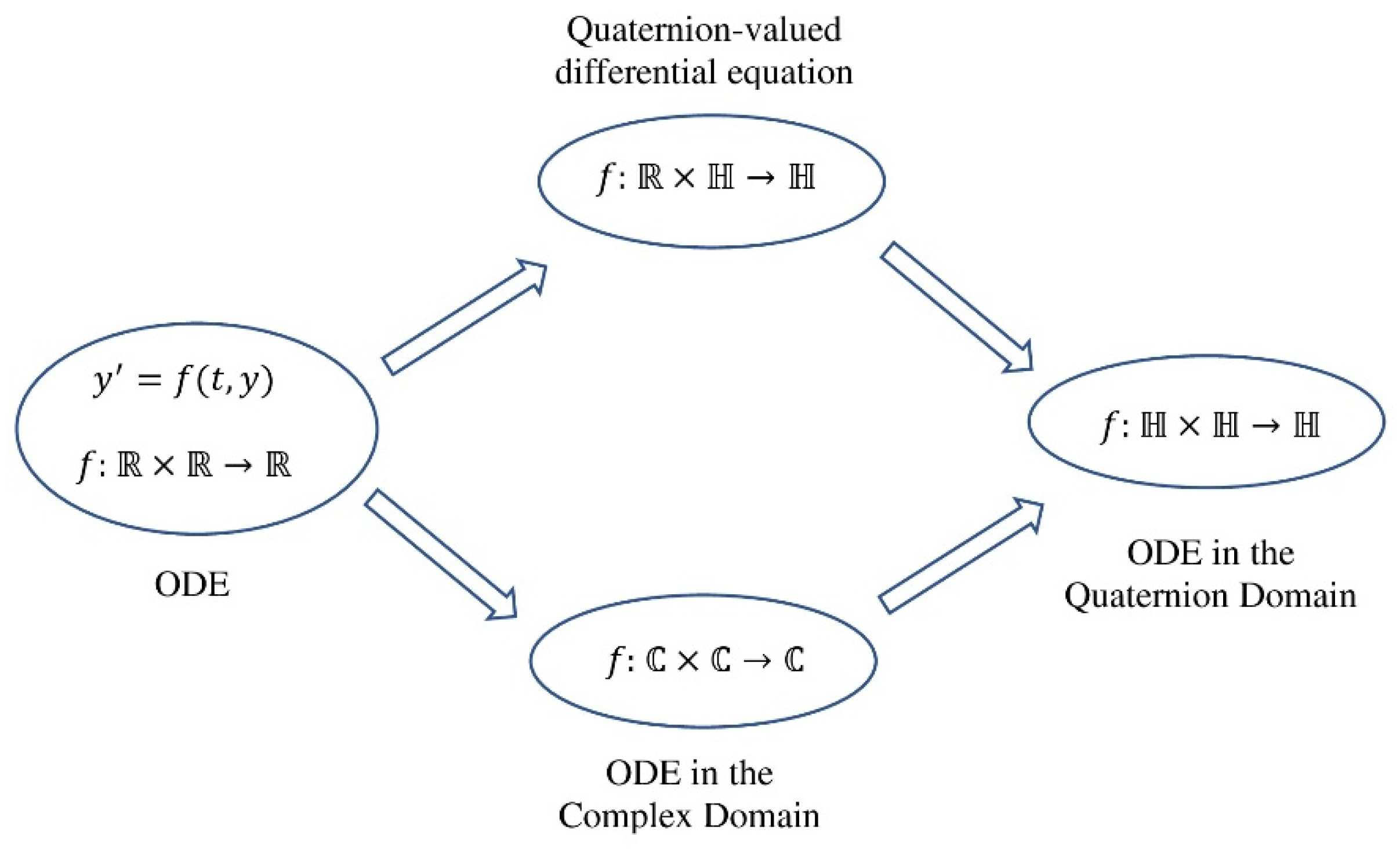
3.2. Development of Quaternion Differential Equation
3.3. Result from Systematic Literature Review
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Familton, J.C. Quaternions: A History of Complex Noncommutative Rotation Groups in Theoretical Physics. Ph.D. Thesis, Columbia University, New York, NY, USA, 2015. [Google Scholar]
- Tait, P.G. An Elementary Treatise Quaternions, 2nd ed.; Nabu Press: Charleston, SC, USA, 1878; ISBN 3663537137. [Google Scholar]
- Voight, J. Quaternion Algebras; Springer Nature: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Kaya, O.; Onder, M. On Fibonacci and Lucas Vectors and Quaternions. Univers. J. Appl. Math. 2018, 13, 156–163. [Google Scholar] [CrossRef]
- Catarino, P. A Note on h(x)—Fibonacci Quaternion Polynomials. Chaos Solitons Fractals 2015, 77, 1–5. [Google Scholar] [CrossRef]
- Halici, S. On Fibonacci Quaternions. Adv. Appl. Clifford Algebr. 2012, 22, 321–327. [Google Scholar] [CrossRef]
- Halici, S.; Karataş, A. On a Generalization for Fibonacci Quaternions. Chaos Solitons Fractals 2017, 98, 178–182. [Google Scholar] [CrossRef]
- Horadam, A.F. Complex Fibonacci Numbers and Fibonacci Quaternions. Am. Math. Mon. 2012, 70, 289–291. [Google Scholar] [CrossRef]
- Tan, E.; Yilmaz, S.; Sahin, M. On a New Generalization of Fibonacci Quaternions. Chaos Solitons Fractals 2016, 82, 1–4. [Google Scholar] [CrossRef]
- Kamano, K. Analytic Continuation of the Lucas Zeta and L-Functions. Indag. Math. 2013, 24, 637–646. [Google Scholar] [CrossRef]
- De Bie, H.; De Schepper, N.; Ell, T.A.; Rubrecht, K.; Sangwine, S.J. Connecting Spatial and Frequency Domains for the Quaternion Fourier Transform. Appl. Math. Comput. 2015, 271, 581–593. [Google Scholar] [CrossRef]
- Bahri, M.; Hitzer, E.S.M.; Hayashi, A.; Ashino, R. An Uncertainty Principle for Quaternion Fourier Transform. Comput. Math. Appl. 2008, 56, 2398–2410. [Google Scholar] [CrossRef]
- Hitzer, E.M.S. Quaternion Fourier Transform on Quaternion Fields and Generalizations. Adv. Appl. Clifford Algebr. 2007, 17, 497–517. [Google Scholar] [CrossRef]
- Lian, P. The Octonionic Fourier Transform: Uncertainty Relations and Convolution. Signal Process. 2019, 164, 295–300. [Google Scholar] [CrossRef]
- Ell, T.A.; Le Bihan, N.; Sangwine, S.J. Quaternion Fourier Transforms for Signal; Castanié, F., Ed.; ISTE Ltd.: London, UK, 2014; ISBN 9781848214781. [Google Scholar]
- Bahri, M.; Toaha, S.; Rahim, A.; Ivan, M. On One-Dimensional Quaternion Fourier Transform On One-Dimensional Quaternion Fourier Transform. J. Phys. Conf. Ser. 2019, 1341, 062004. [Google Scholar] [CrossRef]
- Sudbery, A. Quaternionic Analysis; Cambridge University Press: Cambridge, UK, 1979. [Google Scholar] [CrossRef]
- Dzagnidze, O. On the Differentiability of Quaternion Functions. arXiv 2012, arXiv:1203.5619. [Google Scholar] [CrossRef]
- Chudá, H. Universal Approach to Derivation of Quaternion Rotation Formulas. MATEC Web Conf. 2019, 292, 01060. [Google Scholar] [CrossRef]
- Van Leunen, H. Quaternions and Hilbert Spaces. 2015. Available online: https://www.researchgate.net/publication/282655670_Quaternions_and_Hilbert_spaces (accessed on 19 December 2021).
- Ha, V.T.N. Helmholtz Operator in Quaternionic Analysis. Ph.D Dissertation, Freien Universitat, Berlin, Germany, 10 February 2005. [Google Scholar]
- Hashim, H.A. Special Orthogonal Group SO(3), Euler Angles, Angle-axis, Rodriguez Vector and Unit-Quaternion: Overview, Mapping and Challenges. arXiv. 2019. Available online: https://arxiv.org/abs/1909.06669 (accessed on 19 December 2021).
- Sveier, A.; Sjøberg, A.M.; Egeland, O. Applied Runge-Kutta-Munthe-Kaas Integration for the Quaternion Kinematics. J. Guid. Control. Dyn. 2019, 42, 2747–2754. [Google Scholar] [CrossRef]
- Klitzner, H. The Culture of Quaternions The Phoenix Bird of Mathematics; New York Academy of Sciences, Lyceum Society: New York, NY, USA, 1 June 2015. [Google Scholar] [CrossRef]
- Shoemake, K. Animating Rotation with Quaternion Curves. ACM SIGGRAPH Comput. Graph. 1985, 19, 245–254. [Google Scholar] [CrossRef]
- Dam, E.B.; Koch, M.; Lillholm, M. Quaternions, Interpolation and Animation; Institute of Computer Science University of Copenhagen: Denmark, Copenhagen, 1998. [Google Scholar]
- Waldvogel, J. Quaternions for Regularizing Celestial Mechanics—The Right Way. Celest. Mech. Dyn. Astron. 2008, 102, 149–162. [Google Scholar] [CrossRef]
- Kwasniewski, A.K. Glimpses of the Octonions and Quaternions History and Today’ s Applications in Quantum Physics. Adv. Appl. Clifford Algebr. 2012, 22, 87–105. [Google Scholar] [CrossRef]
- Haetinger, C.; Malheiros, M.; Dullius, E.; Kronbauer, M. A Quaternion Application to Control Rotation Movements in The Three Dimensional Space of an Articulate Mechanical Arm Type Robot Built from Low Cost Materials as a Supporting Tool for Teaching at The Undergraduate Level. In Proceedings of the Global Congress on Engineering and Technology Education, São Paulo, Brazil, 13–16 March 2005. [Google Scholar]
- Solà, J. Quaternion Kinematics for The Error-State Kalman Filter. arXiv 2017, arXiv:1711.02508. [Google Scholar]
- Xie, C.; Kumar, B.V.K.V. Quaternion Correlation Filters for Color Face Recognition. In Proceedings of the Security, Steganography, and Watermarking of Multimedia Contents VII, San Jose, CA, USA, 17–20 January 2005; Volume 5681, pp. 486–494. [Google Scholar]
- Giirlebeck, K.; SproBig, W. Quatemionic Analysis and Elliptic Boundary Value Problems; Birkhäuser Basel: Basel, Switzerland, 1990; ISBN 2013206534. [Google Scholar]
- Georgiev, S. New Aspects on Elementary Functions in the Context of Quaternionic Analysis. Cubo 2012, 14, 93–110. [Google Scholar] [CrossRef]
- Stover, C. A Survey of Quaternionic Analysis; Florida State University: Tallahassee, FL, USA, 2014. [Google Scholar] [CrossRef]
- Dzagnidze, O. On Some New Properties of Quaternion Functions. J. Math. Sci. 2018, 235, 557–603. [Google Scholar] [CrossRef]
- De Leo, S.; Ducati, G.C. Solving Simple Quaternionic Differential Equations. J. Math. Phys. 2003, 44, 2224–2233. [Google Scholar] [CrossRef]
- Campos, J.; Mawhin, J. Periodic Solutions of Quaternionic-Valued Ordinary. Ann. Di Mat. 2006, 185, 109–127. [Google Scholar] [CrossRef]
- Wilczynski, P. Quaternionic-Valued Ordinary Differential Equations. Riccati Equ. 2009, 247, 2163–2187. [Google Scholar] [CrossRef]
- Papillon, C.; Tremblay, S. On a Three-Dimensional Riccati Differential Equation and its Symmetries. J. Math. Anal. Appl. 2018, 458, 611–627. [Google Scholar] [CrossRef]
- Grigorian, G.A. Global Solvability Criteria for Quaternionic Riccati Equations. Arch. Math. 2019, 57, 83–99. [Google Scholar] [CrossRef]
- Zhi, W.; Chu, J.; Li, J.; Wang, Y. A Novel Attitude Determination System Aided by Polarization Sensor. Sensors 2018, 10, 158. [Google Scholar] [CrossRef]
- Kou, K.I.; Xia, Y.; Xia, Y.-H. Linear Quaternion Differential Equations: Basic Theory and Fundamental Results. Stud. Appl. Math. 2018, 141, 1–43. [Google Scholar] [CrossRef]
- Kou, K.I.; Liu, W.-K.; Xia, Y.-H. Solve the Linear Quaternion-Valued Differential Equations Having Multiple Eigenvalues. J. Math. Phys. 2019, 60, 023510. [Google Scholar]
- Cai, Z.; Kou, K.L. Laplace Transform: A New Approach in Solving Linear Quaternion Differential Equations. Math. Methods Appl. Sci. 2017, 41, 4033–4048. [Google Scholar] [CrossRef]
- Donachali, A.K.; Jafari, H. A Decomposition Method for Solving Quaternion Differential Equations. Int. J. Appl. Comput. Math. 2020, 123, 1–7. [Google Scholar] [CrossRef]
- Jia, Y.-B. Quaternions. Com S 2019, 477, 577. [Google Scholar]
- Morris, D. Elementary Calculus from an Advanced Standpoint; Abane and Right: Port Mulgrave, UK, 2016. [Google Scholar]
- Morris, D. Quaternions; Abane and Right: Port Mulgrave, UK, 2015. [Google Scholar]
- Gürlebeck, K.; Sprössig, W. Quaternionic and Clifford Calculus for Physicists and Engineers; Willey: Hoboken, NJ, USA, 1998. [Google Scholar]
- Gentili, G.; Stoppato, C.; Struppa, D.C. Regular Functions of a Quaternionic Variable; Springer: Cham, Switzerland, 2022; ISBN 9783031075308. [Google Scholar] [CrossRef]
- Ellegaard, O.; Wallin, J.A. The bibliometric analysis of scholarly production: How great is the impact? Scientometrics 2015, 105, 1809–1831. [Google Scholar] [CrossRef]
- Simmons, G.F. Differential Equations with Applications and Historical Notes, 3rd ed.; Boggess, A., Rosen, K., Eds.; CRC Press: New York, NY, USA, 2017; Volume 4, ISBN 2013206534. [Google Scholar]
- Nagy, G. Ordinary Differential Equations; Michigan State University: East Lansing, MI, USA, 2020. [Google Scholar]
- Deimling, K. Lecture Notes in Mathematics: Ordinary Differential Equations in Banach Spaces; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2084, ISBN 9783319008240. [Google Scholar]
- Yang, B.; Bao, W. Complex-Valued Ordinary Differential Equation Modeling for Time Series Identification. IEEE Access 2019, 7, 41033–41042. [Google Scholar] [CrossRef]
- Feng, Z.; Kit, C.; Kou, I. Solving Quaternion Ordinary Differential Equations with Two-Sided Coefficients. Qual. Theory Dyn. Syst. 2017, 17, 441–462. [Google Scholar] [CrossRef]
- Hille, E. Ordinary Differential Equations in the Complex Domain by Einar Hille (z-lib.org).pdf; John Willey and Sons: San Diego, CA, USA, 1976. [Google Scholar]
- Laine, I. Complex differential equations. In Handbook of Differential Equations: Ordinary Differential Equations; Chapman and Hall/CRC: Boca Raton, FL, USA, 2008; Volume 4, pp. 269–363. ISBN 9780444530318. [Google Scholar] [CrossRef]
- Haraoka, Y. Linear Differential Equations in the Complex Domain: From Classical Theory to Forefront; Springer: Berlin/Heidelberg, Germany, 2020; Volume 2271, ISBN 9783030546625. [Google Scholar] [CrossRef]


| Keyword | Google Scholar | Scopus | Science Direct | Dimensions |
|---|---|---|---|---|
| “quaternion differential equation” | 55 | 45 | 38 | 27 |
| “quaternionic differential equation” | 13 | 12 | 9 | 11 |
| Total | 68 | 57 | 47 | 38 |
| No | Authors | Title | Year | Topic | Object |
|---|---|---|---|---|---|
| 1 | Anthony Sudbery [17] | Quaternionic Analysis | 1978 | function derivative | |
| 2 | S. Georgiev [33] | New Aspects of Elementary Functions in the Context of Quaternionic Analysis | 2012 | quaternion elementary function derivative | |
| 3 | Christopher Stover [34] | A Survey of Quaternionic Analysis | 2014 | derivative/the analytic function | |
| 4 | Omar Dzagnidze [18] | On the Differentiability of Quaternion Functions | 2012 | function derivative | |
| 5 | Omar Dzagnidze [35] | On Some New Properties of Quaternion Function | 2018 | function derivative | |
| 6 | Stefano De Leo and Gisele C. Ducati [36] | Solving simple Quaternionic differential equations | 2003 | quaternion differential equations | |
| 7 | Juan Campos and Jean Mawhin [37] | Periodic solutions of Quaternionic-valued ordinary differential equations | 2005 | quaternion differential equations | |
| 8 | Paweł Wilczynski [38] | Quaternionic-valued ordinary differential equations. The Riccati equation | 2009 | Riccati quaternion differential equation | |
| 9 | Charles Papillon, Sébastien Tremblay [39] | On a three-dimensional Riccati differential equation and its symmetries | 2018 | three-dimensional Riccati differential equation | |
| 10 | G. A. Grigorian [40] | Global solvability criteria for Quaternionic Riccati equations | 2019 | Riccati quaternion differential equation | |
| 11 | Kit Ian Kou and Yong-Hui Xia [42] | Linear Quaternion Differential Equations: Basic Theory and Fundamental Results | 2018 | linear quaternion differential equations | |
| 12 | Kit Ian Kou, Wan-Kai Liu, and Yong-Hui Xia [43] | Solve the linear Quaternion-valued differential equations having multiple eigenvalues | 2019 | linear quaternion differential equations | |
| 13 | Zhen-Feng Cai dan Kit Ian Kou [44] | Laplace transform, which is a new approach for solving linear Quaternion differential equations | 2017 | linear quaternion differential equations | |
| 14 | A. Kameli Donachali dan H. Jafari [45] | A Decomposition Method for Solving Quaternion Differential Equations | 2020 | quaternion differential equations |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kartiwa, A.; Supriatna, A.K.; Rusyaman, E.; Sulaiman, J. Review of Quaternion Differential Equations: Historical Development, Applications, and Future Direction. Axioms 2023, 12, 483. https://doi.org/10.3390/axioms12050483
Kartiwa A, Supriatna AK, Rusyaman E, Sulaiman J. Review of Quaternion Differential Equations: Historical Development, Applications, and Future Direction. Axioms. 2023; 12(5):483. https://doi.org/10.3390/axioms12050483
Chicago/Turabian StyleKartiwa, Alit, Asep K. Supriatna, Endang Rusyaman, and Jumat Sulaiman. 2023. "Review of Quaternion Differential Equations: Historical Development, Applications, and Future Direction" Axioms 12, no. 5: 483. https://doi.org/10.3390/axioms12050483
APA StyleKartiwa, A., Supriatna, A. K., Rusyaman, E., & Sulaiman, J. (2023). Review of Quaternion Differential Equations: Historical Development, Applications, and Future Direction. Axioms, 12(5), 483. https://doi.org/10.3390/axioms12050483







