Abstract
The work considers formal structure and features of the readability indices widely employed in various information and education fields, including theory of communication, cognitive psychology, linguistics, and multiple applications. In spite of the importance and popularity of readability indices in practical research, their intrinsic properties have not yet been sufficiently investigated. This paper aims to fill this gap between the theory and application of these indices by presenting them in a uniform expression which permits analyzing their features and deriving new properties that are useful in practice. Three theorems are proved for relations between the units of a text structure. The general characteristics are illustrated by numerical examples which can be helpful for researchers and practitioners.
Keywords:
readability indices; generalized index; Flesch reading ease; Flesch–Kincaid readability; Automated Readability Index; generalized index; index structure; optimal features MSC:
91F20; 03B65; 68T50
1. Introduction
Measurements of readability present a wide area of research and applications related to cognitive psychology, theory of communication, phonics and linguistics, and other information and education fields. Various readability indices associated with short-term memory capacity and the difficulty of a text reading have been developed in empirical and heuristic studies during the last 70 years in works by Flesch [1,2], Kincaid et al. [3], Dale and Chall [4,5], Gunning [6], and Spache [7]. An extensive review of earlier studies and other indices was performed by DuBay [8,9]. These indices have been implemented toward multiple practical purposes by educators to assess the reading level of students, by librarians and publishers to rank the difficulty of texts, by medical and other specialists for efficient communication with lay people, and in word-processing programs. Many states use such indices for estimating the comprehensibility of legal documents, including business policies, financial forms, and automobile insurance policies. In military education these indices are used as the standard tests for the evaluation of documents and forms and for assessing the difficulty of technical manuals. Multiple studies have been conducted to find more adequate measures of readability [10,11,12,13], and linguistic assumptions and factors affecting readability have been considered [14,15]. Development of new index forms and their statistical evaluation have been performed as well [16,17,18,19,20]. Many other related problems are described, for example, in [21,22,23].
In spite of the importance and popularity of readability indices in practical applications, their essential properties have not yet been sufficiently studied. This paper considers the theoretical properties of the main indices and presents them in a uniform expression convenient for analyzing their features and deriving new properties useful in practice. Particularly, it proves in a theorem that the same index value can be reached with the two different numbers of words in a text, and it is shown how to find the second number by the first one. Two other theorems can be useful in building and elaborating new texts. The second theorem proves that the average of characters per word for all text is bigger for a constant number of words per sentence than for a constant number of characters per sentence. The third theorem shows that in a text of several paragraphs, or chapters, the average of words per sentence for all text is bigger for the same number of sentences per each chapter than for the same number of words per each chapter. These general characteristics are illustrated and explained in numerical examples. The obtained results could be helpful for researchers and practitioners who can implement readability indices in various applications, including modern studies on artificial intelligence.
2. Classical Readability Indices
Let us briefly describe several of the most popular classical readability indices, starting with the Flesch reading ease (RE) score, which is calculated by the formula:
where the first quotient is the average sentence length (ASL) defined by the number of words divided by the number of sentences, and the second quotient is the average number of syllables per word (ASW) defined as their number divided by the number of words in the given text. RE values cover a 0–100 range, and a higher number corresponds to an easier text. RE scores in the range of 80–100 indicate very easy texts which can be understood even with 5 years of education, while scores in the range of 0–20 are for difficult texts, the understanding of which can require 12–13 years of education.
Flesch–Kincaid readability (FKRA), also known as the Flesch grade-level score, is given by the formula:
which is similar by the predictors to the RE index, although it is oriented in the opposite direction, so a smaller score indicates that students of a lower grade can understand it, and vice versa. For example, FKRA = 8 shows that the text can be understandable for students of the 8th grade, while FKRA = 12 means that the text can be comprehensible for students of the 12th grade or the 1st year of college.
The Automated Readability Index (ARI) is defined as follows:
It differs from the previous indices by the second predictor, which is defined as the number of letters, or average characters per word (ACW), defined by the number of characters divided by the number of words. However, taking an average of about 3 letters per syllable, Formula (3) can be easily transformed to an expression very close to that of FKRA (2), so the features of these two indices are similar.
Formulas (1)–(3) may be the most popular indices of readability, but there are many more indices, so let us describe some of them as well.
The Power–Sumner–Kearl (PSK) readability formula can be presented as:
with the same ASL first variable as in (1), and with the number of syllables (NS) defined as the ASW (1) multiplied by 100. It is usually applied for children aged 7–10 years and is not recommended for older children.
The New Dale–Chall (NDC) readability tool has the following form:
with the same first variable ASL as in (1)–(4) but with the percentage of difficult words (PDW) as the second variable, and the constant 3.6365 is added for score adjustment. The ‘hard’ words were defined as those not appearing in a specially designed list of common words familiar to most fourth-grade students. Originally [4] this list contained 763 non-hard words; it was later [5] revised and expanded to 3000 words.
The Spache readability (SR) index has a similar form:
with the same ASL and percentage of difficult words (PDW) as in (5).
The Gunning’s index (FOG) formula is:
with the same first variable ASL and with the second variable of the percentage of hard words (PHW) estimated as words with three or more syllables with some special features divided by the total number of words.
The SMOG grade index is defined rather differently, as follows:
It uses the number of polysyllables of the words with 3 or more syllables in 30 sentences. It is widely used for checking consumer-oriented healthcare materials, and it is applicable from fourth-grade to college-level students.
There are many simplified versions of these formulae and various other enhanced and improved formulae as well, including multiple linear, polynomial, and nonlinear forms. However, this work focuses on the indices of a similar structure presented in Formulas (1)–(7), and the additional index in (8) serves for comparison with a special feature of the generalized index (given below, in Formula (15)).
3. Indices Structure and Features
The main readability indices (1)–(7) have the same structure and can be represented in the following unified form as a generalized readability index (GRI):
where a, b, and c are the constants used in each of the formulae, words denotes the number of words, sentences denotes the number of sentences, and elements is a generic name denoting a segment of the word structure under consideration—that is, the number of syllables in (1), (2), and (4), the number of characters in (3), or the number of difficult and hard words in (5)–(7). The first quotient in (9) is the same average sentence length (ASL), and the second quotient is the average number of elements per word (AEW), defined similarly to the average number of syllables per word in (1).
For the given numbers of sentences and elements in Formula (9), let us introduce the related parameters A and B, defined as follows:
Then, index (9) can be represented via these parameters (10) as a function of the number of words, denoted as w:
The first and the second items in Function (11) are given as the linear dependence and the hyperbola by w. For positive parameters A and B, as in (2)–(7), the relation in (11) presents a convex function by w, while for both a negative A and B (1), the curve of (11) has a concave form. The last item in (11) shifts the curve vertically up or down for positive or negative c values, respectively—see the illustrations in Figure 1, Figure 2 and Figure 3.
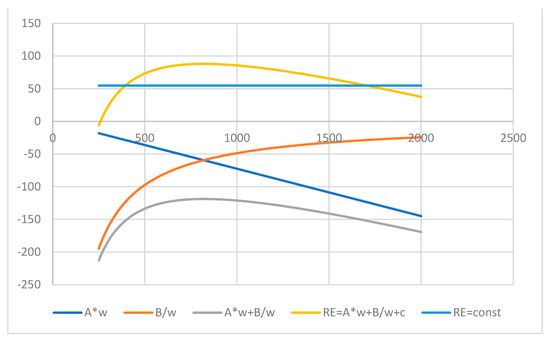
Figure 1.
GRI (11) for RE index (1) and its components profiled by the number of words.
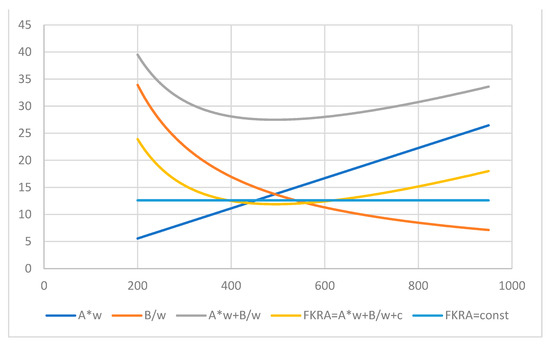
Figure 2.
GRI (11) for FKRA index (2) and its components profiled by the number of words.
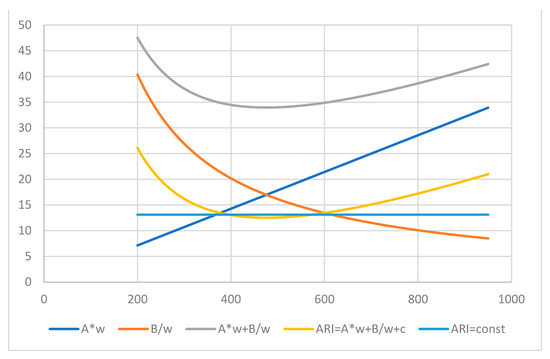
Figure 3.
GRI (11) for ARI index (3) and its components profiled by the number of words.
Although w is measured by natural numbers, it is possible for approximate estimation to consider it as a continuous variable used for finding a location and a value of its extremum. The derivative of (11) by w, put to zero, yields the equation:
Solving (12) gives the optimum location w*:
where notations from (10) are used. The same location corresponds to the point of intersection of the linear and hyperbolic dependences from the total relation in (11):
from which the same solution as in (13) can be obtained.
The value of Function (11) at the point of extremum from (13) equals:
This is a general result for the optimum number of words for any given values of sentences and elements of the words. It is interesting to note that up to the constants, this expression reduces to the structure of the SMOG grade index, with the elements in the expression in (15) in place of the polysyllables in the index defined in (8).
For any given numbers of sentences and elements, the value of (15) corresponds to the maximum point for the concave Function (1), so there cannot be values above it, and the index RE is constrained from above, from the side of the most easily readable texts. Similarly, the value of (15) defines the minimum value for the convex Functions (2)–(7), and there are no points below it, so these indices are limited from the side of the lowest grade level, or younger age.
As is clear from (14), for any number of words w that is less than the optimal value w*, the linear part of the GRI is closer to zero than the hyperbolic part, so for any signs of the parameters a and b (10), the inequality for absolute values holds:
Similarly, according to (14), for any number of words w bigger than the optimal value w*, the hyperbola part of the GRI is closer to zero than the linear part, so for any signs of the parameters a and b, the opposite inequality for absolute values holds:
The relations in (16) and (17) have the following meaning. For an observed number of words lesser than the extremum value (13), the hyperbola part (16) gives the main input into the GRI (9)–(11), so the complexity of a word on average plays the most important role in the text understanding. Therefore, for easier reading it is advisable to increase the number of words up to the optimum w*. In addition, vice versa: for an observed number of words bigger than the extremum value (13), the linear part (17) contributes more to the GRI (9)–(11), so the complexity of a sentence on average plays the main role in the text understanding. Thus, for better readability it can be recommended to modify the number of words to be closer to the optimum w* value. These properties can also be seen in the figures.
An important property of the readability index can be formulated as the following theorem.
Theorem 1.
For a calculated GRI value (11) at the point w1, there exists another point w2 with the same GRI value.
Proof of Theorem 1.
For a calculated GRI value, a horizontal line through this point in the graph of the concave or convex Function (11) intersects another branch of this graph defining the second point of the same GRI value. Formally, for a calculated GRI value, the relation in (11) can be rewritten as:
Multiplying by w and dividing by the parameter A reduces the relation in (18) to the quadratic equation:
Assuming a positive determinant of Equation (19), it has the following roots:
These roots lie on different sides of the point of extremum of (13), and the same GRI value is reached at both points (20). Only at the point of extremum w* do both roots coincide, and the horizontal line of two intersections of a given GRI with the index curve touches it as the tangent at this point. □
Corollary 1.
Two intersection points (20) yielding the same GRI value have the following interpretation: for given numbers of sentences and elements (9) and (10), the same readability can be obtained with a smaller number of words (defining less words per sentence but more elements per word, meaning easier sentences but more complicated words) and with a bigger number of words (defining more words per sentence but less elements per word, meaning more difficult sentences but less complicated words). Due to the well-known Vieta’s rule, the roots in (20) are connected so that their sum equals the first coefficient with the opposite sign and their product equals the last coefficient in Equation (19):
Corollary 2.
Comparison with Equation (13) shows that the product of the roots of (20) equals the optimum value w* squared, so w* equals the geometric mean of the values of (20), and there exists a useful proportion:
Using the relations in (22), from one number of words it is possible to indicate another number of the words which produces the same index value. All features of the generalized index GRI are true for the particular readability indices (1)–(7) as well.
Let us consider some additional features of a text structure. Suppose there are n sentences in a text, and each i-th sentence (i = 1, 2, …, n) contains some number of words wordsi and number of elements elementsi (e.g., syllables, characters, or other measures of words’ structure used in (1)–(9)). The average number of elements per word (AEW) defined as the total number of elements divided by the total number of words in the given text of n sentences is:
The number of elements per word in each i-th phrase, or EWi , is defined as:
Then, the following theorem can be formulated.
Theorem 2.
For a given set of elements per word EWi (24) in the sentences, the average AEW of elements per word (23) by all text will be bigger for a constant number of words per sentence than for a constant number of elements per sentence.
Proof of Theorem 2.
Let us rewrite Equation (23) as the arithmetic mean of EWi weighted by the number of words:
On the other hand, solving (24) for words, we obtain:
Substituting (26) into (23) yields the expression of the mean harmonic elements by words (HEW) value of EWi weighted by the number of elements:
If the numbers of words are the same for all i-th sentences, then (25) reduces to the simple arithmetic mean of the values of (24):
If the numbers of elements are the same for all i-th phrases, then (27) reduces to the simple harmonic mean of the values of (24):
For any set of values of EWi (24), the arithmetic mean AEW (28) is always bigger than the harmonic mean HEW (29):
Therefore, the average of elements per word for the whole text is bigger (30) for a constant number of words per sentence (28) than for a constant number of elements per sentence (29). □
A similar analysis can be performed by studying a longer or more complicated text with many chapters. Consider the average sentence length (ASL) for the whole text defined by the number of words divided by the number of sentences given by the first quotient in the indices (1)–(7) and (9). Suppose there are m chapters in the text (or another kind of text division, e.g., paragraphs or interpunctions), and each j-th chapter (j = 1, 2, …, m) consists of the number of words (wordsj) and number of sentences (sentencesj) per chapter. The average sentence length (ASL) is defined as the total number of words divided by the total number of sentences for all m chapters:
Let us introduce the number of words per sentence for each j-th chapter, or the sentence length SLj, defined as
Then, the following theorem can be stated.
Theorem 3.
For a given set of the sentence length defined by the number of words per sentence SLj (32) in all j-th chapters, the average ASL (31) for all text is bigger for the same number of sentences per chapter than for the same number of words per chapter.
Proof of Theorem 3.
The proof is similar to that of Theorem 2, so we can briefly adjust it to the new meaning. The expression of (31) with definition of (32) can be presented as the weighted arithmetic mean of the SLj values per chapter:
On the other hand, solving (32) for and substituting it into (31) yields the weighted harmonic mean value of the sentence length (HSL) of the partial SLj values:
With the same number of sentences for all j-th chapters, the value of (33) reduces to the simple arithmetic mean of the values of (32):
Additionally, with the same number of words in all j-th chapters, the value of (34) reduces to the simple harmonic mean:
Then, for any set of values of SLj (32), their arithmetic mean ASL (35) is bigger than their harmonic mean HSL (36):
Thus, the average of words per sentence for all text is bigger (37) for the same number of sentences in each chapter (35) than for the same number of words per each chapter (36). □
Theorems 2 and 3 show that to increase the impacts of the AEW (23) or ASL (31) parts on indices (1)–(9), due to the relations in (30) and (37), it makes sense to implement the following rules: on one hand, to build the sentences so that the number of words is similar across all sentences, and on the other hand, to have a similar sentence length in all chapters or paragraphs of the text. For decreasing the influence of the AEW (23) or ASL (31) parts on the indices, it can be recommended to use sentences with a similar number of elements (characters, syllables) across all sentences, and to have a similar number of words in all chapters or paragraphs of the text. Thus, varying the number of words can produce an index change in both directions, as was described in the relations of (16) and (17). However, a similar sentence length in all chapters or paragraphs would lead to an increase in indices, while a similar number of elements (characters, syllables) across the sentences would decrease the indices’ values. The results of these theorems can be used for building and adjusting new texts with higher readability in artificial intelligence (AI) systems.
4. Examples of Readability Tests
For a sample text [24] (chapter 1, part 3) given in Appendix A, the main measures needed for the readability testing are presented in Table 1.

Table 1.
Example of the main text statistics.
Finding the described indices for a given text can be accomplished using Formulas (1)–(8), but it is even easier to apply the calculators available online [25,26,27,28,29,30,31,32]. For the considered sample text, the scores of the tests are as follows. The Flesch reading ease score (1) equals RE = 58.5, denoting a fairly difficult text to read. The Flesch–Kincaid readability, also known as the Flesch grade level (2), is FKRA = 12.1, corresponding to 12th grade students’ reading ability. The Automated Readability Index (3) is ARI = 13.1, which is related to 18–19-year-old students of the college-entry level. The Power–Sumner–Kearl (4) readability is PSK = 6.43, which indicates that this text is readable for those above the sixth grade. The New Dale–Chall (5) readability yields a score of about NDC = 8, which corresponds to 11–12th grade. The Spache readability index (6) equals SR = 10.1, which indicates the 10th-grade level. The Gunning’s index (7) is FOG = 15.9, which means a difficult-to-read text. The index (8) equals SMOG = 10.5, corresponding to 11th-grade students. The scores differ, but they show in general that reading level is fairly difficult, and a reader’s age should be about 17–18 years, corresponding to 12th graders.
Several illustrations for the function for GRI (11) profiled by the word number and its optimal features are presented in Figure 1, Figure 2 and Figure 3.
Function (11) and its components with the parameters for the RE scores (1) for the same example from Appendix A with a number of sentences 14, number of syllables 575, and number of words varying from 100 to 2000, is shown in Figure 1.
The negative parameters of (1) for the linear slope and for the hyperbolic curve in the 4th quadrant of the plane yield in total the concave function shifted up to the 1st quadrant by the positive intercept in (1). The point (13) of interception (14) is w* = 819.12 where the index (1) reaches its maximum, which equals RE(w*) = 88.06. The actual number of words in this example is about twice as small, w = 394, and the index at that point equals RE(w) = 54.81, so the readability reaches about 62% of its maximum value possible with the given number of sentences and syllables. Due to the relations in (22), with w1 = 394 the second point of the same readability score is located at the number of words around w2 = 1703. These two points are defined in Figure 1 by intersections of the index RE concave function with the horizontal line of the constant value RE(w) = 54.81.
By the same example with the number of sentences being 14 and the number of syllables being 575, the function GRI (11) for the index FKRA (2) profiled by the word number is shown in Figure 2.
The positive parameters of (2) for the linear slope and hyperbola produce a convex curve moved down by the negative intercept. The point of interception (14) is at w* = 493.52 where the index (2) reaches its minimum, FKRA(w*) = 11.91. With the lesser actual number of words w = 394, the index at that point equals FKRA(w) = 12.61, so the readability is close to the optimum for the given number of sentences and syllables. Using the relations in (22) with w1 = 394, the second point of the same FKRA value is located at the number of words of about w2 = 618. These two points are also shown in Figure 2 by intersections of the FKRA index’s convex function with the horizontal line of the constant value FKRA(w) = 12.61.
For the same text with 14 sentences and 1714 letters, or characters, the function GRI (11) for the index ARI (3) profiled by the word number is shown in Figure 3.
With the positive parameters of (3) for the linear line and hyperbola, their sum produces a convex curve shifted down by the negative intercept. The point of interception (14) is about w* = 475.44 where the index (3) reaches its minimum, ARI(w*) = 12.53. For the actual number of words w = 394, the index at that point equals ARI(w) = 13.13, so the readability is close to the optimum for the given number of sentences and characters. By the relations in (22) with w1 = 394, the second point of the same ARI value is located at a word number of about w2 = 574, also identified by the points shown in Figure 3 as intersections of the ARI index convex function with the horizontal line of the constant value ARI(w) = 13.13.
The FKRA and ARI indices employ the syllable and character gauges, respectively, but their results are very close. The main input to each of the indices in Figure 1, Figure 2 and Figure 3 is given by the hyperbola B/w or by the linear line Aw at the left- and right-hand sides of their intersection points, respectively. Thus, the easiness of reading in this case of 394 words in each index can be explained by the simple structure of the words, with 1–2 syllables on average, rather than the structure of long sentences with more than 2 dozen words (see Table 1).
5. Summary
The work is devoted to studying the classical readability indices which are widely used in applications but not yet sufficiently understood in their formal structure and basic features. The paper presents several popular indices in a uniform expression convenient for considering their theoretical properties, analyzing their features, and deriving new relations that are useful in practice. Conditions for the extremum value of indices are obtained, and a methodology of fitting a text for better readability by varying the number of words to be closer to the optimum value is described.
Three theorems are proved on the indices’ properties which could be useful for building a new text or adjusting an existing text to have better readability in expert systems and AI research and development. One theorem states that the same index value can be reached with two different numbers of words in a text, and it is shown how to find the second number using the first one. The same value of the readability index can be reached with a smaller number of words defining fewer words per sentence but more characters per word (easier sentences but more complicated words) and with a bigger number of words defining more words per sentence but fewer characters per word (more difficult sentences but less complicated words). Another theorem proves that the average of characters per word for all text is bigger for a constant number of words per sentence than for a constant number of characters per sentence. The third theorem shows that in a text of several paragraphs, or chapters, the average number of words per sentence for all text is bigger for the same number of sentences in each chapter than for the same number of words per each chapter. Making texts with the needed clarity and desirable effects can be especially important in cognitive, conversational, and other open AI systems.
The general characteristics for the most widely used readability indices and their components are illustrated by the graphs of their behavior profiled by the number of words and explained in numerical examples. The obtained results can be helpful for researchers and practitioners in education, communication, insurance, and many other businesses where a clear exposition of the topic of interest is very important and real apprehension of the message is required for the readers.
Further research on readability indices’ renewal and implementations can be performed using regression modeling, item response theory (IRT), and other modern techniques of psychometrics and natural language processing described, for example, in [33,34,35,36,37,38]. The methodology developed in the current work can be extended to investigation of other indices of more complicated forms in future studies.
Funding
This research received no external funding.
Data Availability Statement
The data sources are given in the corresponding references.
Acknowledgments
I am grateful to five reviewers for their comments and suggestions which helped to improve the paper.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
A sample text for the readability tests is taken from [24].
“The rule of rhythm in prose is not so intricate. Here, too, we write in groups, or phrases, as I prefer to call them, for the prose phrase is greatly longer and is much more nonchalantly uttered than the group in verse; so that not only is there a greater interval of continuous sound between the pauses, but, for that very reason, word is linked more readily to word by a more summary enunciation. Still, the phrase is the strict analogue of the group, and successive phrases, like successive groups, must differ openly in length and rhythm. The rule of scansion in verse is to suggest no measure but the one in hand; in prose, to suggest no measure at all. Prose must be rhythmical, and it may be as much so as you will; but it must not be metrical. It may be anything, but it must not be verse. A single heroic line may very well pass and not disturb the somewhat larger stride of the prose style; but one following another will produce an instant impression of poverty, flatness, and disenchantment. The same lines delivered with the measured utterance of verse would perhaps seem rich in variety. By the more summary enunciation proper to prose, as to a more distant vision, these niceties of difference are lost. A whole verse is uttered as one phrase; and the ear is soon wearied by a succession of groups identical in length. The prose writer, in fact, since he is allowed to be so much less harmonious, is condemned to a perpetually fresh variety of movement on a larger scale, and must never disappoint the ear by the trot of an accepted meter. And this obligation is the third orange with which he has to juggle, the third quality which the prose writer must work into his pattern of words. It may be thought perhaps that this is a quality of ease rather than a fresh difficulty; but such is the inherently rhythmical strain of the English language, that the bad writer—and must I take for example that admired friend of my boyhood, Captain Reid?—the inexperienced writer, as Dickens in his earlier attempts to be impressive, and the jaded writer, as any one may see for himself, all tend to fall at once into the production of bad blank verse.”
References
- Flesch, R.F. A new readability yardstick. J. Appl. Psychol. 1948, 32, 221–223. [Google Scholar] [CrossRef] [PubMed]
- Flesch, R.F. How to Write, Speak and Think More Effectively; Harper & Row: New York, NY, USA, 1960. [Google Scholar]
- Kincaid, J.P.; Fishburne, R.P., Jr.; Rogers, R.L.; Chissom, B.S. Derivation of New Readability Formulas (Automated Readability Index, Fog Count and Flesch Reading Ease Formula) for Navy Enlisted Personnel; Institute for Simulation and Training, University of Central Florida: Orlando, FL, USA, 1975; Available online: https://stars.library.ucf.edu/istlibrary/56 (accessed on 22 April 2023).
- Dale, E.; Chall, J. Formula for predicting readability. Educ. Res. Bull. 1948, 27, 37–54. [Google Scholar]
- Chall, J.S.; Dale, E. Readability Revisited: The New Dale-Chall Readability Formula; Brookline Books: New York, NY, USA, 1995. [Google Scholar]
- Gunning, R. The Technique of Clear Writing; McGraw-Hill: New York, NY, USA, 1952. [Google Scholar]
- Spache, G.D. A new readability formula for primary grade reading material. Elem. Sch. J. 1953, 53, 410–413. [Google Scholar] [CrossRef]
- DuBay, W.H. The Principles of Readability; Impact Information: Costa Mesa, CA, USA, 2004. [Google Scholar]
- DuBay, W.H. Unlocking Language: The Classic Readability Studies; Impact Information: Costa Mesa, CA, USA, 2007. [Google Scholar]
- Klare, G.R. Readability. In Handbook of Reading Research; Pearson, P.D., Barr, R., Kamil, M., Mosenthal, P., Eds.; Longman: New York, NY, USA, 1984; pp. 681–744. [Google Scholar]
- Anderson, R.C.; Davison, A. Concepts and empirical bases of readability formulas. In Linguistic Complexity and Text Comprehension: Readability Issues Reconsidered; Davison, A., Green, G.M., Eds.; Lawrence Erlbaum Assoc.: Hillsdale, NJ, USA, 1988; pp. 23–53. [Google Scholar]
- Benjamin, R.G. Reconstructing readability: Recent developments and recommendations in the analysis of text difficulty. Educ. Psychol. Rev. 2012, 24, 63–88. [Google Scholar] [CrossRef]
- Janan, D.; Wray, D. Reassessing the accuracy and use of readability formulae. Malays. J. Learn. Instr. 2014, 11, 127–145. [Google Scholar] [CrossRef]
- Bailin, A.; Grafstein, A. Readability: Text and Context; Palgrave Macmillan: New York, NY, USA, 2016. [Google Scholar]
- Bailin, A.; Grafstein, A. The linguistic assumptions underlying readability formulae: A critique. Lang. Commun. 2001, 21, 285–301. [Google Scholar] [CrossRef]
- Kyle, K.; Crossley, S.; Jarvis, S. Assessing the validity of lexical diversity indices using direct judgements. Lang. Assess. Q. 2021, 18, 154–170. [Google Scholar] [CrossRef]
- Crossley, S.; Skalicky, S.; Dascalu, M. Moving beyond classic readability formulas: New methods and new models. J. Res. Read. 2019, 42, 541–561. [Google Scholar] [CrossRef]
- Crossley, S.; Heintz, A.; Choi, J.S.; Batchelor, J.; Karimi, M.; Malatinszky, A. A large-scaled corpus for assessing text readability. Behav. Res. Methods 2022, 55, 491–507. [Google Scholar] [CrossRef] [PubMed]
- Matricciani, E. A statistical theory of language translation based on communication theory. Open J. Stat. 2020, 10, 936–997. [Google Scholar] [CrossRef]
- Matricciani, E. Readability indices do not say it all on a text readability. Analytics 2023, 2, 296–314. [Google Scholar] [CrossRef]
- Cantos-Gomez, P.; Almela-Sanchez, M. (Eds.) Lexical Collocation Analysis: Advances and Applications; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Lipovetsky, S. The Review on the Book: “Lexical Collocation Analysis: Advances and Applications; Cantos-Gomez, P., Almela-Sanchez, M., Eds.”. Technometrics 2020, 62, 137. [Google Scholar]
- Foster, I.; Ghani, R.; Jarmin, R.S.; Kreuter, F.; Lane, J. (Eds.) Big Data and Social Science: Data Science Methods and Tools for Research and Practice, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2021. [Google Scholar]
- Stevenson, R.L. Essays in the Art of Writing; Chatto & Windus: London, UK, 1905; Available online: https://www.gutenberg.org/files/492/492-h/492-h.htm (accessed on 22 April 2023).
- The Flesch Reading Ease Readability Formula (readabilityformulas.com). Available online: https://readabilityformulas.com/flesch-reading-ease-readability-formula.php (accessed on 22 April 2023).
- The Flesch Grade Level Readability Formula (readabilityformulas.com). Available online: https://readabilityformulas.com/flesch-grade-level-readability-formula.php (accessed on 22 April 2023).
- The Automated Readability Index (Ari)—Learn How to Calculate the Automated Readability Index (readabilityformulas.com). Available online: https://readabilityformulas.com/automated-readability-index.php (accessed on 22 April 2023).
- The Powers-Sumner-Kearl Readability Formula (readabilityformulas.com). Available online: https://readabilityformulas.com/powers-sumner-kear-readability-formula.php (accessed on 22 April 2023).
- The New Dale-Chall Readability Formula: A Vocabulary-Based Readability Formula (readabilityformulas.com). Available online: https://readabilityformulas.com/new-dale-chall-readability-formula.php (accessed on 22 April 2023).
- Spache Readability Formula for Young Readers (readabilityformulas.com). Available online: https://readabilityformulas.com/spache-readability-formula.php (accessed on 22 April 2023).
- The Gunning Fog Readability Formula (readabilityformulas.com). Available online: https://readabilityformulas.com/gunning-fog-readability-formula.php (accessed on 22 April 2023).
- The Smog Readability Formula, a Simple Measure of Gobbledygook (readabilityformulas.com). Available online: https://readabilityformulas.com/smog-readability-formula.php (accessed on 22 April 2023).
- Mair, P. Modern Psychometrics with R; Springer: Cham, Switzerland, 2018. [Google Scholar]
- van der Linden, W.J. (Ed.) Handbook of Item Response Theory, in 3 Volumes; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019. [Google Scholar]
- Lipovetsky, S. The review on the book: “Handbook of Item Response Theory, in 3 volumes, by van der Linden, W.J., Ed.”. Technometrics 2021, 63, 428–437. [Google Scholar] [CrossRef]
- Sijtsma, K.; van der Ark, A.L. Measurement Models for Psychological Attributes; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Lipovetsky, S. The review on the book: “Measurement Models for Psychological Attributes, by Sijtsma, K.; van der Ark, A.L.”. Technometrics 2022, 64, 426–429. [Google Scholar] [CrossRef]
- Sarkar, D. Text Analytics with Python: A Practitioner’s Guide to Natural Language Processing; Apress: Berkeley, CA, USA, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).