Statistical Fuzzy Reliability Assessment of a Blended System
Abstract
1. Introduction
2. Literature Review
2.1. Reliability Evaluation Using Fuzzy Set Theory
2.2. Reliability Evaluation Using IFS
2.3. Reliability Evaluation Using the UGF Method
3. Essential Definitions
3.1. Fuzzy Sets
3.2. Intuitionistic Fuzzy Sets
3.2.1. Operations on IFS
- The subtraction operator for two IFS was defined by Lei and Xu [2]. The subtraction operator for two IFNs is defined as follows:
3.2.2. Score Function and Accuracy Function
- if .
- If then,
- If , then .
- If , then .
3.3. Interval-Valued Intuitionistic Fuzzy Sets
3.3.1. Interval-Valued Intuitionistic Fuzzy Numbers
3.3.2. Operations on IVIFN
- , where .
- , where .
- Zhao et al. [41] gave another important operation of subtraction in IVIFN defined below:
3.3.3. Score and Accuracy Function of IVIFNs
- if .
- If , then,
- if .
- if .
3.4. Universal Generating Function
3.4.1. Algorithm for Evaluation of Reliability of a k-out-of-n System
- Attain .
- If has an expression containing , then it should be removed from and added to R.
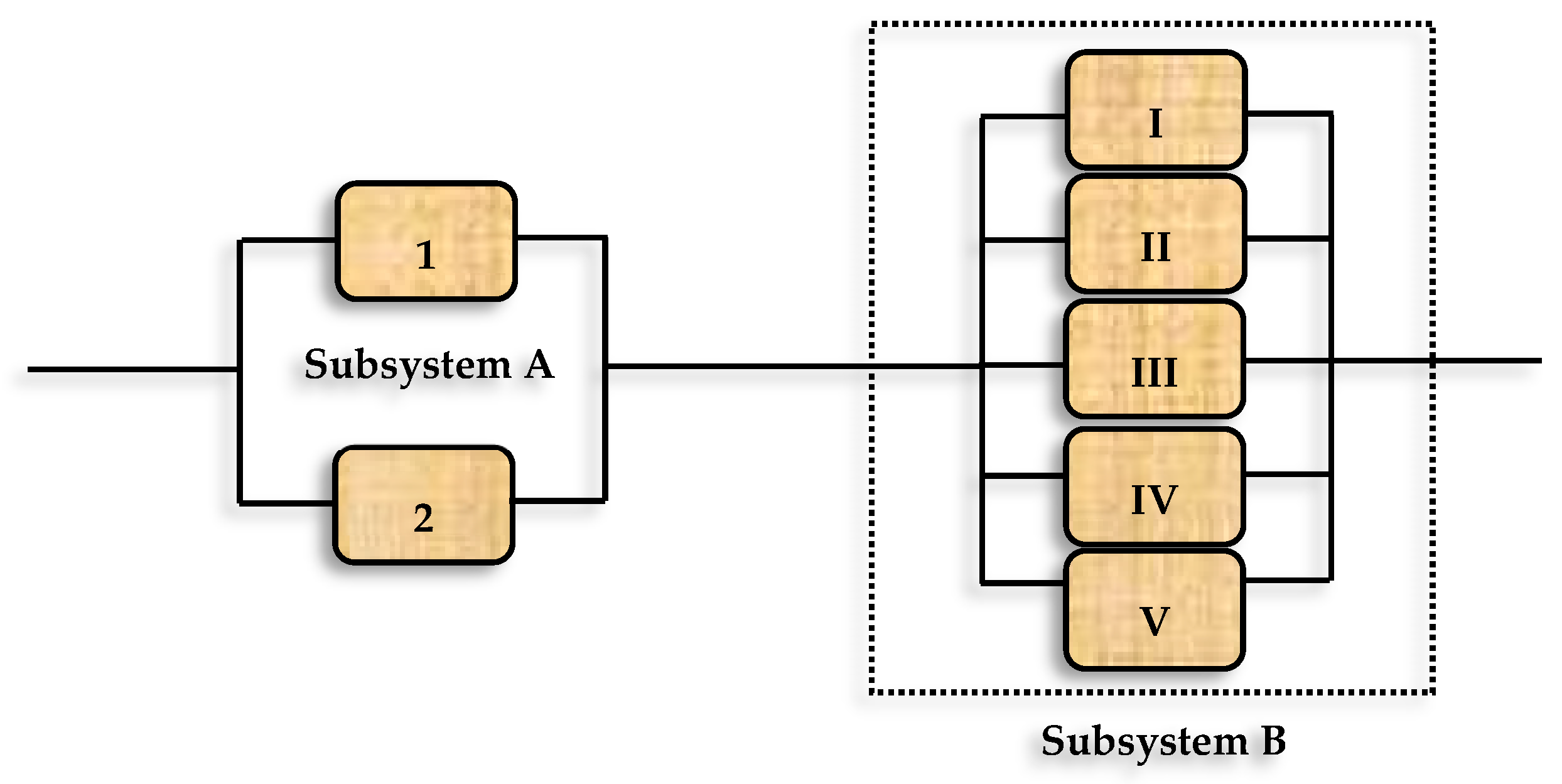
4. Model Description
5. Computation of Reliability Function
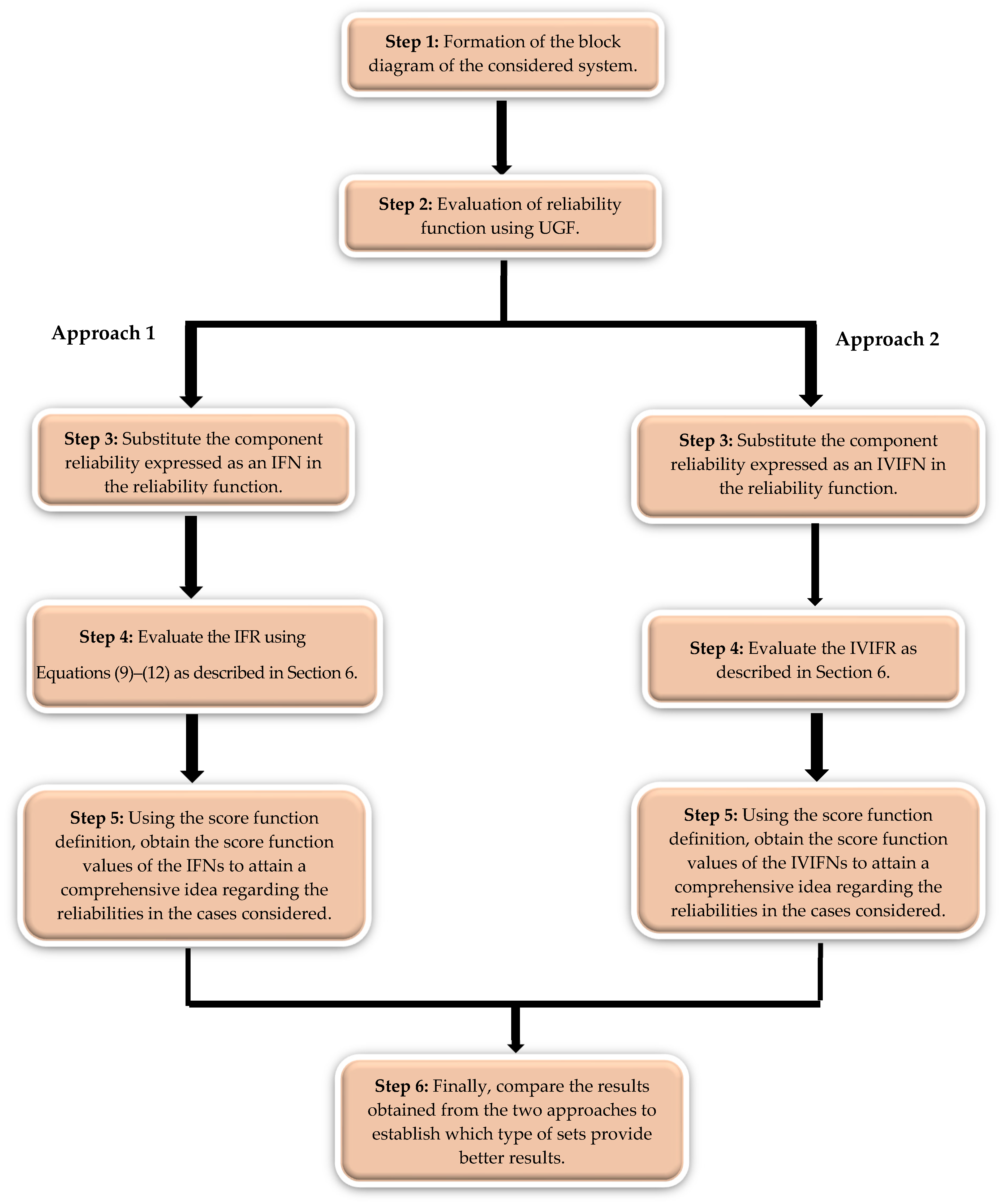
6. Proposed Methodologies
IFN-Based Approach for Fuzzy Reliability Evaluation
7. Evaluation of IFR and IVIFR
7.1. IFR Computation
7.2. IVIFR Computation
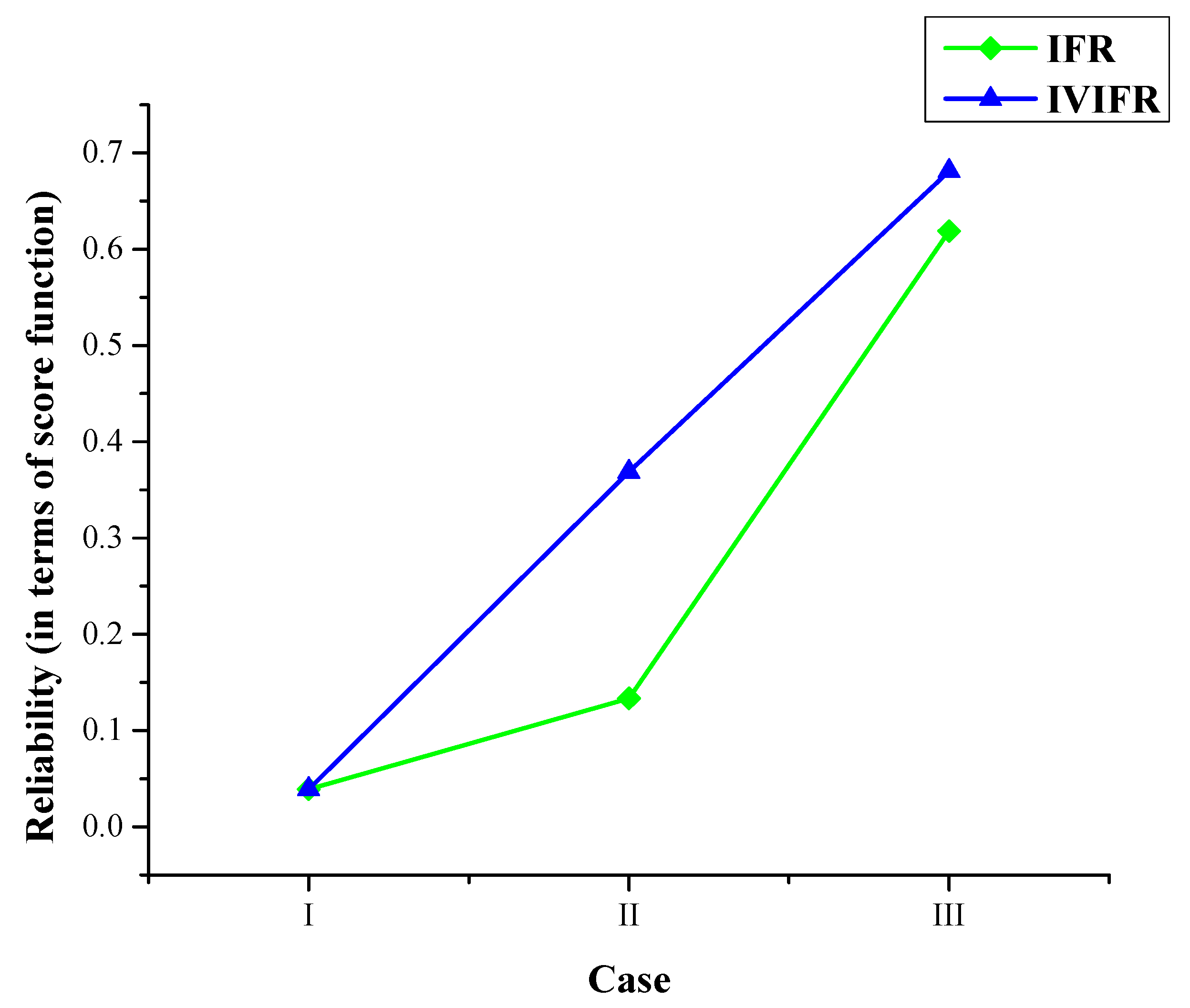
8. Results and Discussion
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Lei, Q.; Xu, Z. Derivative and differential operations of intuitionistic fuzzy numbers. Int. J. Intell. Syst. 2015, 30, 468–498. [Google Scholar] [CrossRef]
- Traneva, V.; Tranev, S. Intuitionistic Fuzzy Analysis of Variance of Movie Ticket Sales. In Intelligent and Fuzzy Techniques: Smart and Innovative Solutions. INFUS 2020. Advances in Intelligent Systems and Computing; Kahraman, C., Cevik Onar, S., Oztaysi, B., Sari, I., Cebi, S., Tolga, A., Eds.; Springer: Cham, Switzerland, 2021; Volume 1197, pp. 340–363. [Google Scholar]
- Lian, K.; Wang, T.; Wang, B.; Wang, M.; Huang, W.; Yang, J. The Research on Relative Knowledge Distances and Their Cognitive Features. Int. J. Cogn. Comput. Eng. 2023, 4, 135–148. [Google Scholar] [CrossRef]
- Bai, W.; Zhang, C.; Zhai, Y.; Sangaiah, A.K. Incomplete intuitionistic fuzzy behavioral group decision-making based on multigranulation probabilistic rough sets and MULTIMOORA for water quality inspection. J. Intell. Fuzzy Syst. 2023, 44, 4537–4556. [Google Scholar] [CrossRef]
- Utkin, L.V.; Gurov, S.V. A general formal approach for fuzzy reliability analysis in the possibility context. Fuzzy Sets Syst. 1996, 83, 203–213. [Google Scholar] [CrossRef]
- Bing, L.; Meilin, Z.; Kai, X. A practical engineering method for fuzzy reliability analysis of mechanical structures. Reliab. Eng. Syst. Saf. 2000, 67, 311–315. [Google Scholar] [CrossRef]
- Dong, Y.G.; Chen, X.Z.; Cho, H.D.; Kwon, J.W. Simulation of fuzzy reliability indexes. KSME Int. J. 2003, 17, 492–500. [Google Scholar] [CrossRef]
- Kumar, A.; Yadav, S.P.; Kumar, S. Fuzzy reliability of a marine power plant using interval valued vague sets. Int. J. Appl. Sci. Eng. 2006, 4, 71–82. [Google Scholar]
- Abdelgawad, M.; Fayek, A.R. Fuzzy reliability analyzer: Quantitative assessment of risk events in the construction industry using fuzzy fault-tree analysis. J. Constr. Eng. Manag. 2011, 137, 294–302. [Google Scholar] [CrossRef]
- Chandna, R.; Ram, M. Fuzzy reliability modeling in the system failure rates merit context. Int. J. Syst. Assur. Eng. Manag. 2014, 5, 245–251. [Google Scholar] [CrossRef]
- Chaube, S.; Singh, S.B. Fuzzy Reliability Theory Based on Membership Function. Int. J. Math. Eng. Manag. Sci. 2016, 1, 34–40. [Google Scholar] [CrossRef]
- Wang, L.; Xiong, C.; Wang, X.; Liu, G.; Shi, Q. Sequential optimization and fuzzy reliability analysis for multidisciplinary systems. Struct. Multidiscip. Optim. 2019, 60, 1079–1095. [Google Scholar] [CrossRef]
- Yang, J.; Xing, L.; Wang, Y.; He, L. Combinatorial Reliability Evaluation of Multi-State System with Epistemic Uncertainty. Int. J. Math. Eng. Manag. Sci. 2022, 7, 312–324. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets, VII ITKR’s Session, Sofia deposed in Central Sci. Tech. Libr. Bulg. Acad. Sci. 1983, 1697, 84. [Google Scholar]
- Mahapatra, G.S.; Roy, T.K. Reliability evaluation using triangular intuitionistic fuzzy numbers arithmetic operations. World Acad. Sci. Eng. Technol. 2009, 50, 574–581. [Google Scholar]
- Kumar, M.; Yadav, S.P.; Kumar, S. A new approach for analysing the fuzzy system reliability using intuitionistic fuzzy number. Int. J. Ind. Syst. Eng. 2011, 8, 135–156. [Google Scholar] [CrossRef]
- Garg, H.; Rani, M.; Sharma, S.P.; Vishwakarma, Y. Intuitionistic fuzzy optimization technique for solving multi-objective reliability optimization problems in interval environment. Expert Syst. Appl. 2014, 41, 3157–3167. [Google Scholar] [CrossRef]
- Song, Y.; Wang, X.; Zhu, J.; Lei, L. Sensor dynamic reliability evaluation based on evidence theory and intuitionistic fuzzy sets. Appl. Intell. 2018, 48, 3950–3962. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, S.B.; Ram, M. Reliability appraisal for consecutive-k-out-of-n: F system of non-identical components with intuitionistic fuzzy set. Int. J. Oper. Res. 2019, 36, 362–374. [Google Scholar] [CrossRef]
- Akbari, M.G.; Hesamian, G. Time-dependent intuitionistic fuzzy system reliability analysis. Soft Comput. 2020, 24, 14441–14448. [Google Scholar] [CrossRef]
- Kumar, A.; Ram, M.; Goyal, N.; Bisht, S.; Kumar, S.; Pant, R.P. Analysis of Fuzzy Reliability of the System Using Intuitionistic Fuzzy Set. In Intelligent Communication, Control and Devices. Advances in Intelligent Systems and Computing; Choudhury, S., Gowri, R., Sena Paul, B., Do, D.T., Eds.; Springer: Singapore, 2021; Volume 1341, pp. 371–378. [Google Scholar]
- Ushakov, I.A. A universal generating function. Sov. J. Comput. Syst. Sci. 1986, 24, 118–129. [Google Scholar]
- Levitin, G.; Lisnianski, A. Importance and sensitivity analysis of multi-state systems using the universal generating function method. Reliab. Eng. Syst. Saf. 1999, 65, 271–282. [Google Scholar] [CrossRef]
- Ding, Y.; Lisnianski, A. Fuzzy universal generating functions for multi-state system reliability assessment. Fuzzy Sets Syst. 2008, 159, 307–324. [Google Scholar] [CrossRef]
- An, Z.W.; Huang, H.Z.; Liu, Y. A discrete stress–strength interference model based on universal generating function. Reliab. Eng. Syst. Saf. 2008, 93, 1485–1490. [Google Scholar] [CrossRef]
- Li, Y.F.; Zio, E. A multi-state model for the reliability assessment of a distributed generation system via universal generating function. Reliab. Eng. Syst. Saf. 2012, 106, 28–36. [Google Scholar] [CrossRef]
- Mi, J.; Li, Y.F.; Liu, Y.; Yang, Y.J.; Huang, H.Z. Belief universal generating function analysis of multi-state systems under epistemic uncertainty and common cause failures. IEEE Trans. Reliab. 2015, 64, 1300–1309. [Google Scholar] [CrossRef]
- Meena, K.S.; Vasanthi, T. Reliability analysis of mobile ad hoc networks using universal generating function. Qual. Reliab. Eng. Int. 2016, 32, 111–122. [Google Scholar] [CrossRef]
- Jaiswal, N.; Negi, S.; Singh, S.B. Reliability analysis of non-repairable weighted k-out-of-n system using belief universal generating function. Int. J. Ind. Syst. Eng. 2018, 28, 300–318. [Google Scholar] [CrossRef]
- Kumar, A.; Ram, M. Computation Interval-Valued Reliability of Sliding Window System. Int. J. Math. Eng. Manag. Sci. 2019, 4, 108–115. [Google Scholar] [CrossRef]
- Liu, X.; Yao, W.; Zheng, X.; Xu, Y. Reliability Analysis of Complex Multi-State System Based on Universal Generating Function and Bayesian Network. arXiv 2022, arXiv:2208.04130. [Google Scholar]
- Li, J.; Lu, Y.; Liu, X.; Jiang, X. Reliability analysis of cold-standby phased-mission system based on GO-FLOW methodology and the universal generating function. Reliab. Eng. Syst. Saf. 2023, 233, 109125. [Google Scholar] [CrossRef]
- Xu, Z.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Xu, Z. Intuitionistic fuzzy aggregation operators. IEEE Trans. Fuzzy Syst. 2007, 15, 1179–1187. [Google Scholar]
- Gou, X.; Xu, Z. Exponential operations for intuitionistic fuzzy numbers and interval numbers in multi-attribute decision making. Fuzzy Optim. Decis. Mak. 2017, 16, 183–204. [Google Scholar] [CrossRef]
- Chen, S.M.; Tan, J.M. Handling multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 1994, 67, 163–172. [Google Scholar] [CrossRef]
- Hong, D.H.; Choi, C.H. Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 2000, 114, 103–113. [Google Scholar] [CrossRef]
- Atanassov, K.T. Interval Valued Intuitionistic Fuzzy Sets. In Intuitionistic Fuzzy Sets. Studies in Fuzziness and Soft Computing; Physica: Heidelberg, Germany, 1990; Volume 35, pp. 139–177. [Google Scholar]
- Xu, Z.; Chen, J. On Geometric Aggregation Over Interval-Valued intuitionistic Fuzzy Information. In Proceedings of the Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007), Haikou, China, 24–27 August 2007; Volume 2, pp. 466–471. [Google Scholar]
- Zhao, H.; Xu, Z.; Yao, Z. Interval-valued intuitionistic fuzzy derivative and differential operations. Int. J. Comput. Intell. Syst. 2016, 9, 36–56. [Google Scholar] [CrossRef]
- Levitin, G. The Universal Generating Function in Reliability Analysis and Optimization; Springer: London, UK, 2005; Volume 6. [Google Scholar]
- Romeu, J.L. Understanding series and parallel systems reliability. Sel. Top. Assur. Relat. Technol. (START) Dep. Def. Reliab. Anal. Cent. (DoD RAC) 2004, 11, 1–8. Available online: https://web.cortland.edu/matresearch/SerieslParallelSTART.pdf (accessed on 4 April 2023).
| Case | Score Function | Ω | Score Function | |
|---|---|---|---|---|
| I | (0.70, 0.30) | 0.40 | (0.60, 0.30) | 0.30 |
| II | (0.82, 0.10) | 0.72 | (0.75, 0.25) | 0.50 |
| III | (0.90, 0.05) | 0.85 | (0.83, 0.10) | 0.73 |
| Case | Intuitionistic Fuzzy Reliability (IFR) | Score Function |
|---|---|---|
| I | (0.46698, 0.42795) | 0.03903 |
| II | (0.55251, 0.41912) | 0.13338 |
| III | (0.79573, 0.17693) | 0.61880 |
| Case | Score Function | Ω | Score Function | |
|---|---|---|---|---|
| I | ([0.60, 0.70], [0.20, 0.30]) | 0.40 | ([0.50, 0.60], [0.20, 0.30]) | 0.30 |
| II | ([0.77, 0.82], [0.05, 0.10]) | 0.72 | ([0.55, 0.60], [0.05, 0.10]) | 0.50 |
| III | ([0.88, 0.90], [0.01, 0.07]) | 0.85 | ([0.79, 0.86], [0.08, 0.11]) | 0.73 |
| Case | Interval-Valued Intuitionistic Fuzzy Reliability (IVIFR) | Score Function |
|---|---|---|
| I | ([0.32062, 0.46698], [0.28145, 0.42795]) | 0.03910 |
| II | ([0.43368, 0.51097], [0.06861, 0.13840]) | 0.36882 |
| III | ([0.74669, 0.82461], [0.07631, 0.13277]) | 0.68111 |
| Case | IFR | IVIFR |
|---|---|---|
| I | 0.03903 | 0.03910 |
| II | 0.13338 | 0.36882 |
| III | 0.61880 | 0.68111 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chachra, A.; Kumar, A.; Ram, M.; Triantafyllou, I.S. Statistical Fuzzy Reliability Assessment of a Blended System. Axioms 2023, 12, 419. https://doi.org/10.3390/axioms12050419
Chachra A, Kumar A, Ram M, Triantafyllou IS. Statistical Fuzzy Reliability Assessment of a Blended System. Axioms. 2023; 12(5):419. https://doi.org/10.3390/axioms12050419
Chicago/Turabian StyleChachra, Aayushi, Akshay Kumar, Mangey Ram, and Ioannis S. Triantafyllou. 2023. "Statistical Fuzzy Reliability Assessment of a Blended System" Axioms 12, no. 5: 419. https://doi.org/10.3390/axioms12050419
APA StyleChachra, A., Kumar, A., Ram, M., & Triantafyllou, I. S. (2023). Statistical Fuzzy Reliability Assessment of a Blended System. Axioms, 12(5), 419. https://doi.org/10.3390/axioms12050419











