Reinsurance Policy under Interest Force and Bankruptcy Prohibition
Abstract
1. Introduction
2. The Model
3. Changing of Variable
4. Solving the HJB Equation
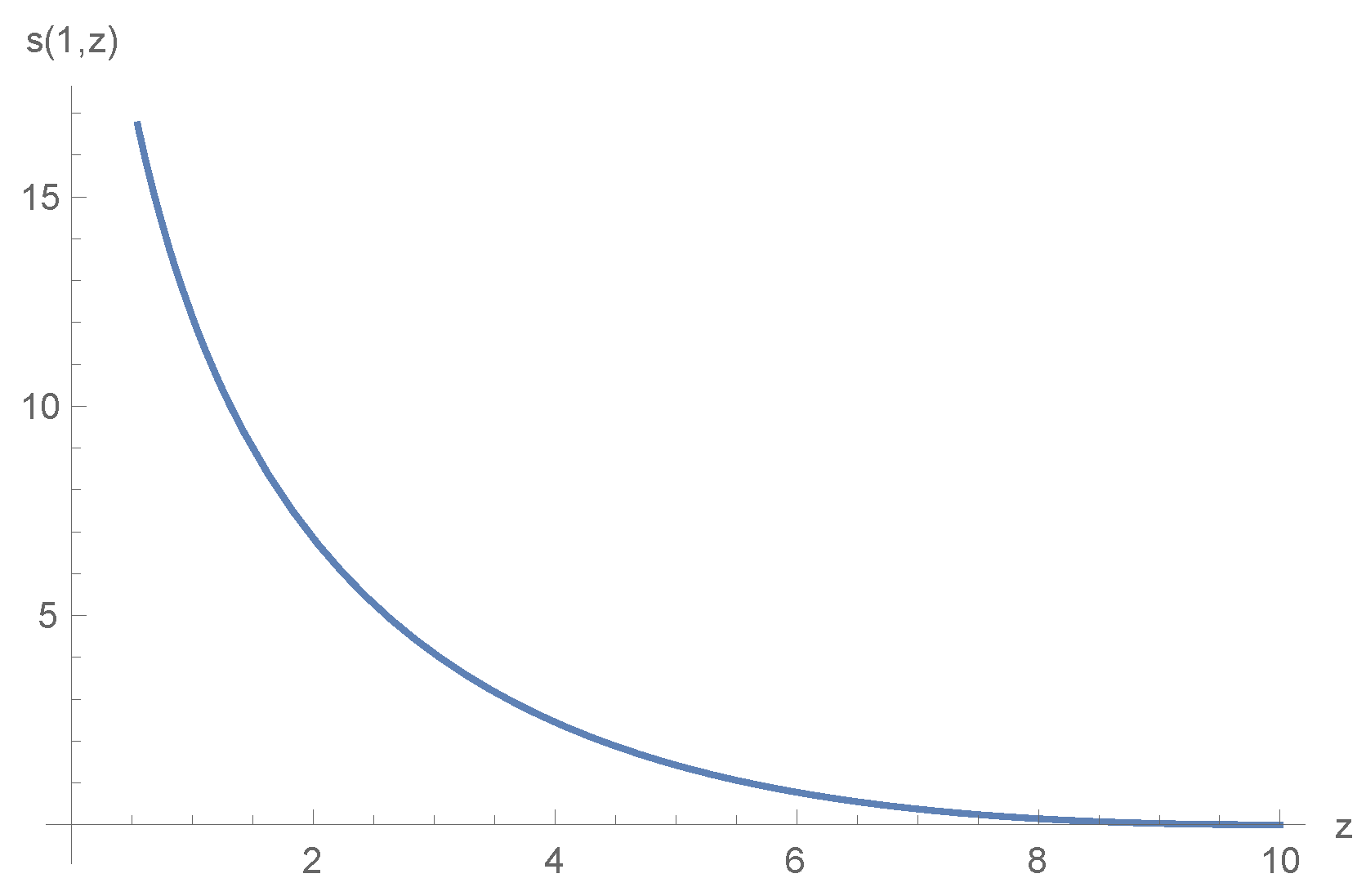
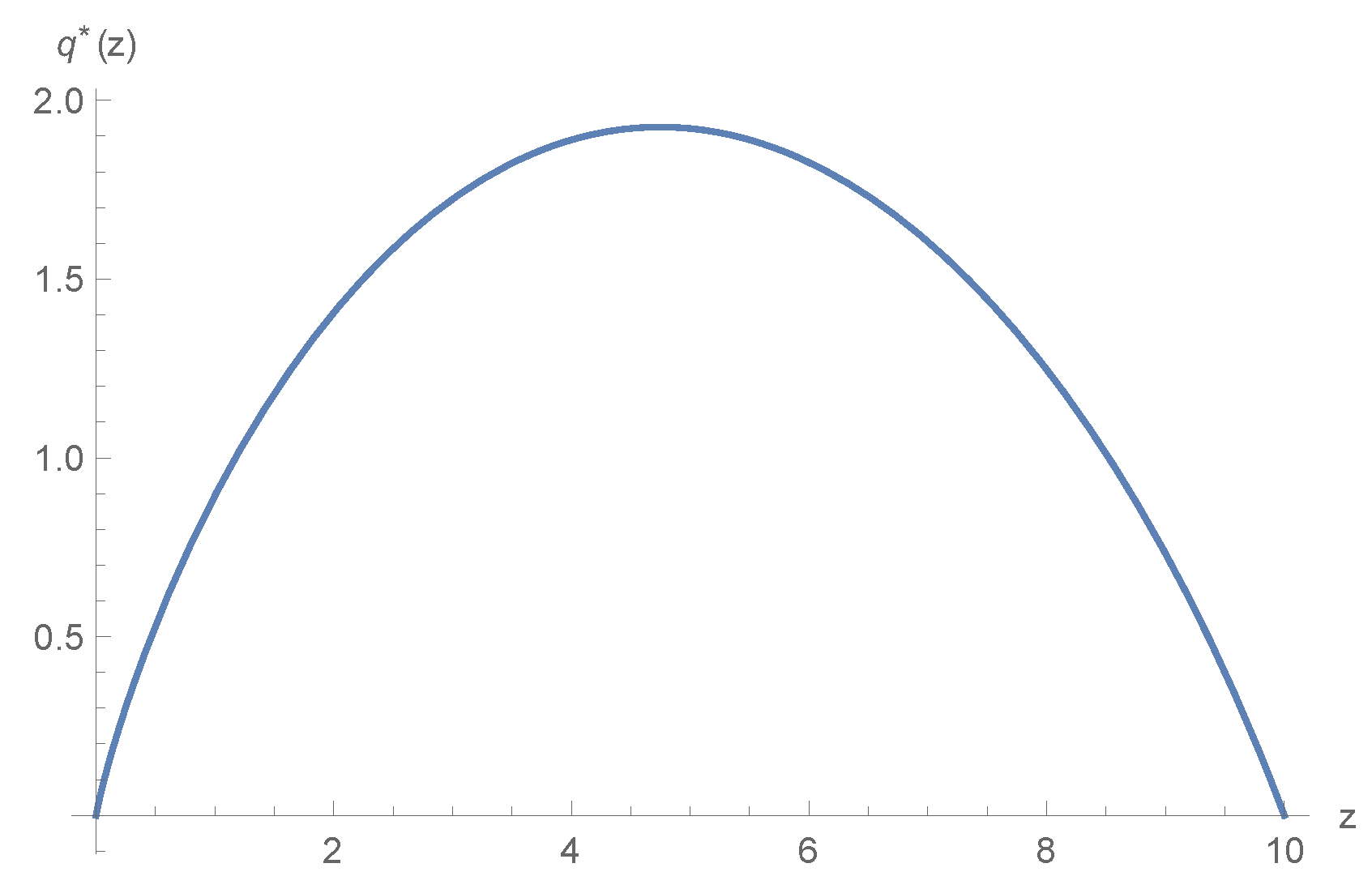
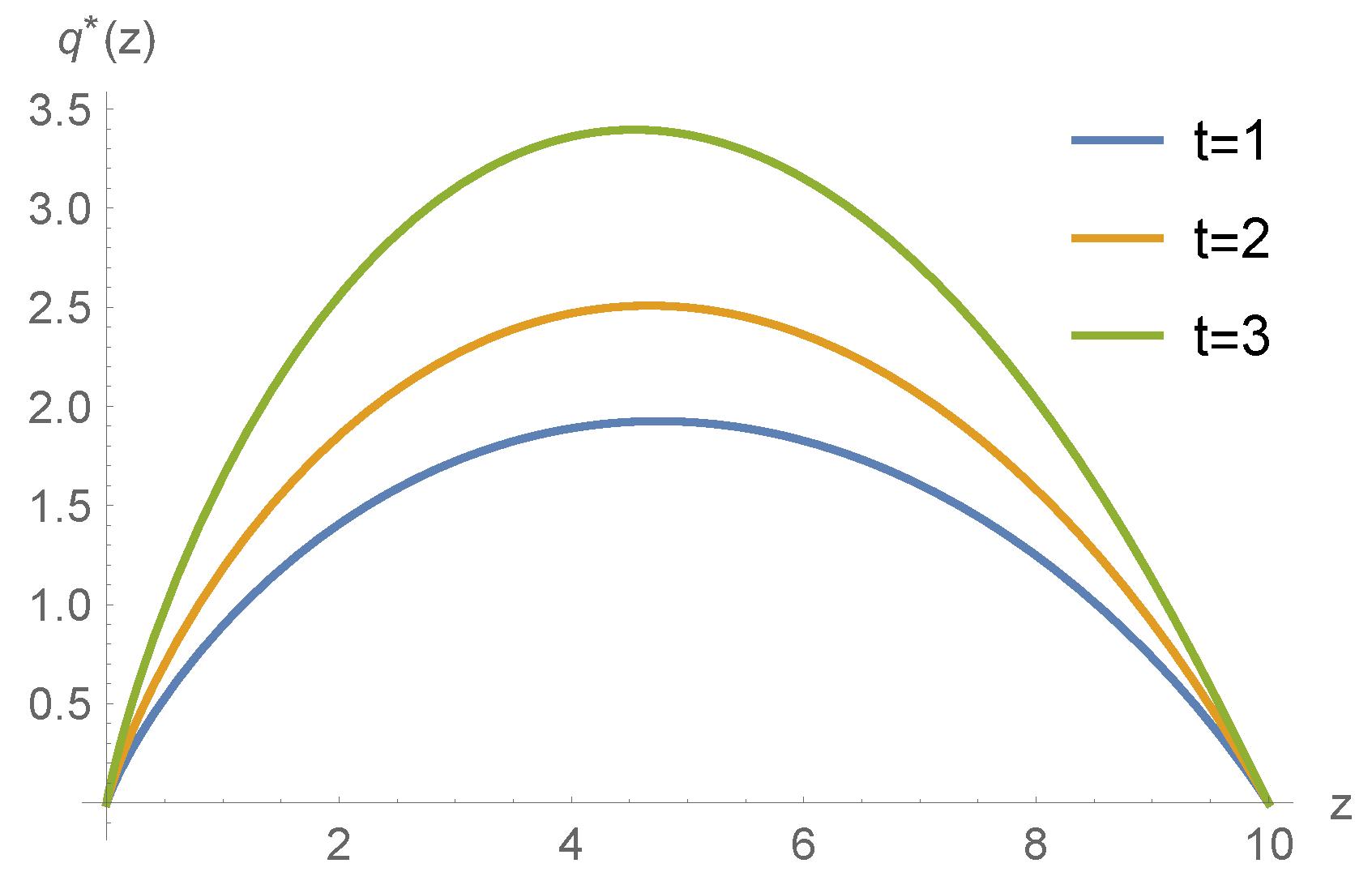
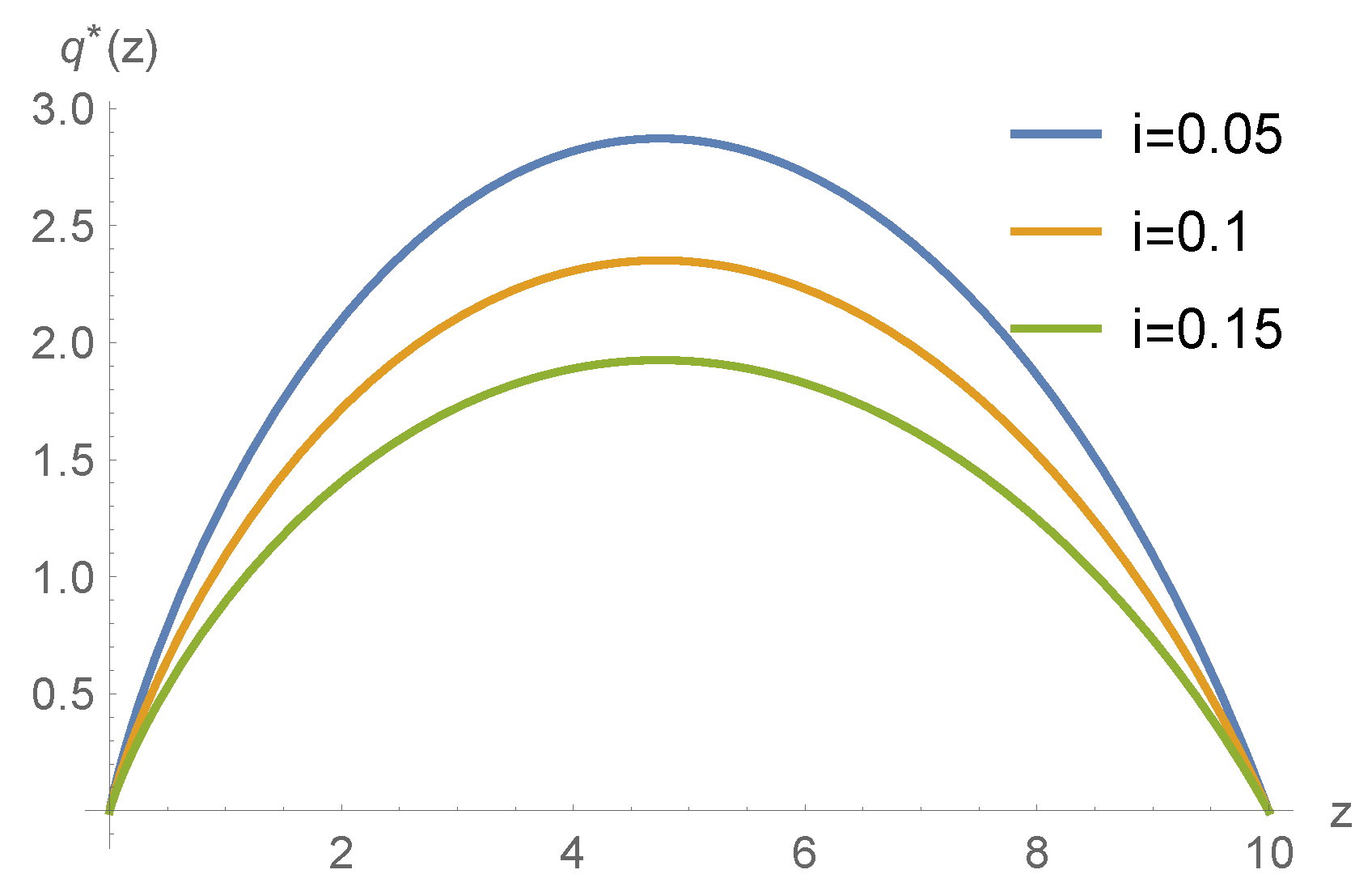
5. Numerical Example
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jøjgaard, B.H.; Taksar, M. Controlling risk exposure and dividends payout schemes: Insurance company example. Math. Financ. 1999, 9, 153–182. [Google Scholar] [CrossRef]
- Irgens, C.; Paulsen, J. Optimal control of risk exposure, reinsurance and investments for insurance portfolios. Insur. Math. Econ. 2004, 35, 21–51. [Google Scholar] [CrossRef]
- Hipp, C.; Taksar, M. Optimal non-proportional reinsurance control. Insur. Math. Econ. 2010, 47, 246–254. [Google Scholar] [CrossRef]
- Azcue, P.; Muler, N. Stochastic Optimization in Insurance: A Dynamic Programming Approach; Springer: New York, NY, USA, 2014. [Google Scholar]
- Schmidli, H. Stochastic Control in Insurance; Springer: London, UK, 2008. [Google Scholar]
- Bäuerle, N. Benchmark and mean-variance problems for insurers. Math. Meth. Oper. Res. 2005, 62, 159–165. [Google Scholar] [CrossRef]
- Bielecki, T.R.; Jin, H.; Pliska, S.R.; Zhou, X.Y. Continuous-time mean-variance portfolio selection with bankruptcy prohibition. Math. Financ. 2005, 15, 213–244. [Google Scholar] [CrossRef]
- Bi, J.; Meng, Q.; Zhang, Y. Dynamic mean-variance and optimal reinsurance problems under the no-bankruptcy constraint for an insurer. Ann. Oper. Res. 2014, 212, 43–59. [Google Scholar] [CrossRef]
- Wong, K.C.; Yam, S.C.P.; Zeng, J. Mean-risk portfolio management with bankruptcy prohibition. Insur. Math. Econ. 2019, 85, 153–172. [Google Scholar] [CrossRef]
- Tang, Q. The finite-time ruin probability of the compound Poisson model with constant interest force. J. Appl. Probab. 2005, 42, 608–619. [Google Scholar] [CrossRef]
- Albrecher, H.; Thonhauser, S. Optimal dividend strategies for a risk process under force of interest. Insur. Math. Econ. 2008, 43, 134–149. [Google Scholar] [CrossRef]
- Gao, Q.; Zhuang, J.; Huang, Z. Asymptotics for a delay–claim risk model with diffusion, dependence structures and constant force of interest. J. Comput. Appl. Math. 2019, 353, 219–231. [Google Scholar] [CrossRef]
- Chen, C.; Wang, S. Asymptotic ruin probability for a by–claim risk model with pTQAI claims and constant interest force. Commun. Stat. Theory Methods 2020, 49, 4367–4377. [Google Scholar] [CrossRef]
- Geng, B.; Liu, Z.; Wang, S. On asymptotic finite–time ruin probabilities of a new bidimensional risk model with constant interest force and dependent claims. Stoch. Models 2021, 37, 608–626. [Google Scholar] [CrossRef]
- Liu, X.; Gao, Q. Uniform asymptotics for the compound risk model with dependence structures and constant force of interest. Stochastics 2022, 94, 191–211. [Google Scholar] [CrossRef]
- Liang, X.; Palmowski, Z. A note on optimal expected utility of dividend payments with proportional reinsurance. Scand. Actuar. J. 2018, 4, 275–293. [Google Scholar] [CrossRef]
- Pham, H. Continuous-Time Stochastic Control and Optimization with Financial Applications; Springer: Berlin, Germany, 2009. [Google Scholar]
- Dadashi, H. Optimal investment strategy post retirement without ruin possibility: A numerical algorithm. J. Comput. Appl. Math. 2020, 363, 325–336. [Google Scholar] [CrossRef]
- Di Giacinto, M.; Federico, S.; Gozzi, F.; Vigna, E. Constrained Portfolio Choices in the Decumulation Phase of a Pension Plan. Carlo Alberto Notebooks, No. 155. 2010. Available online: http://ssrn.com/abstract=1600130 (accessed on 21 March 2023).
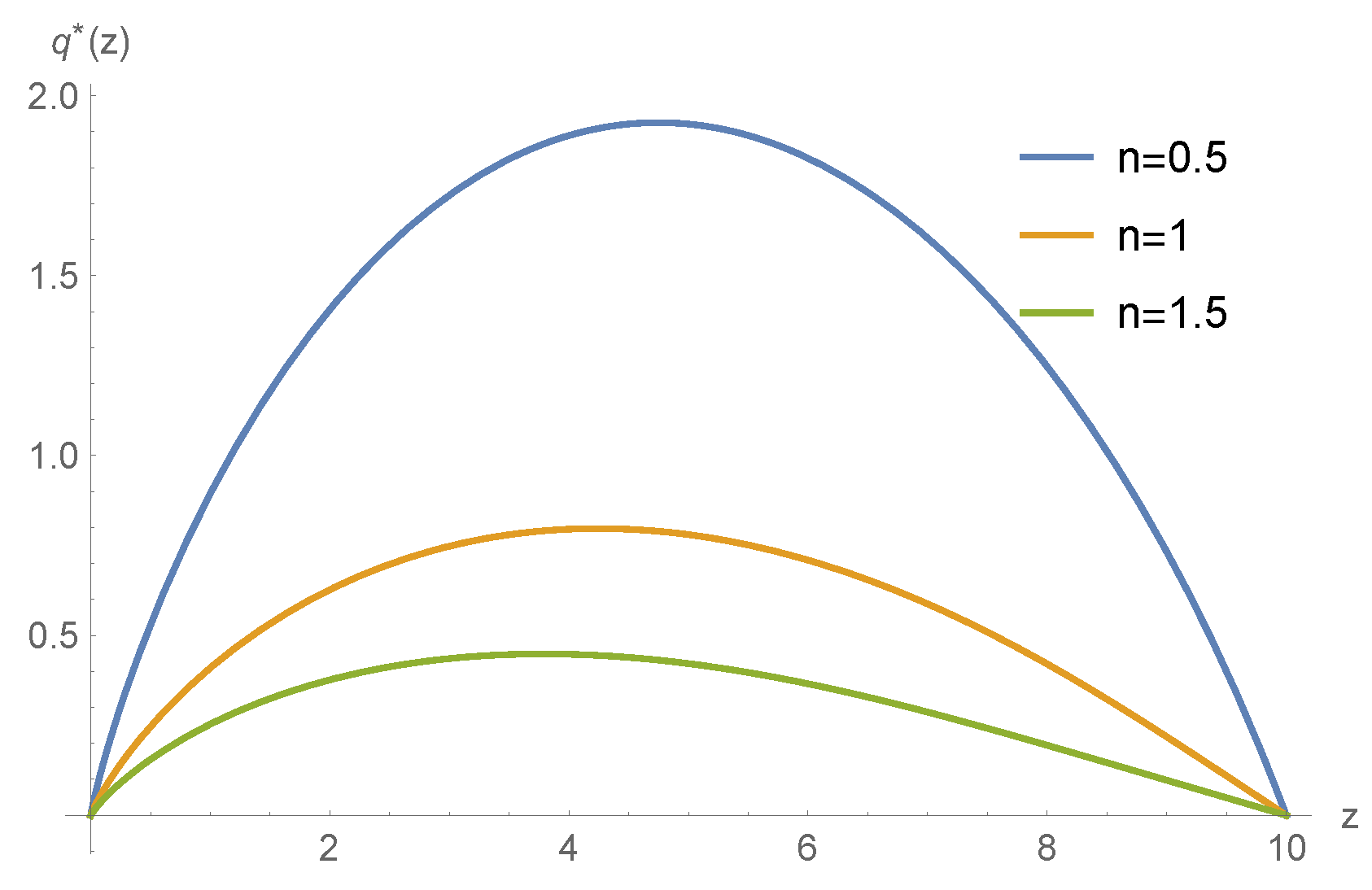
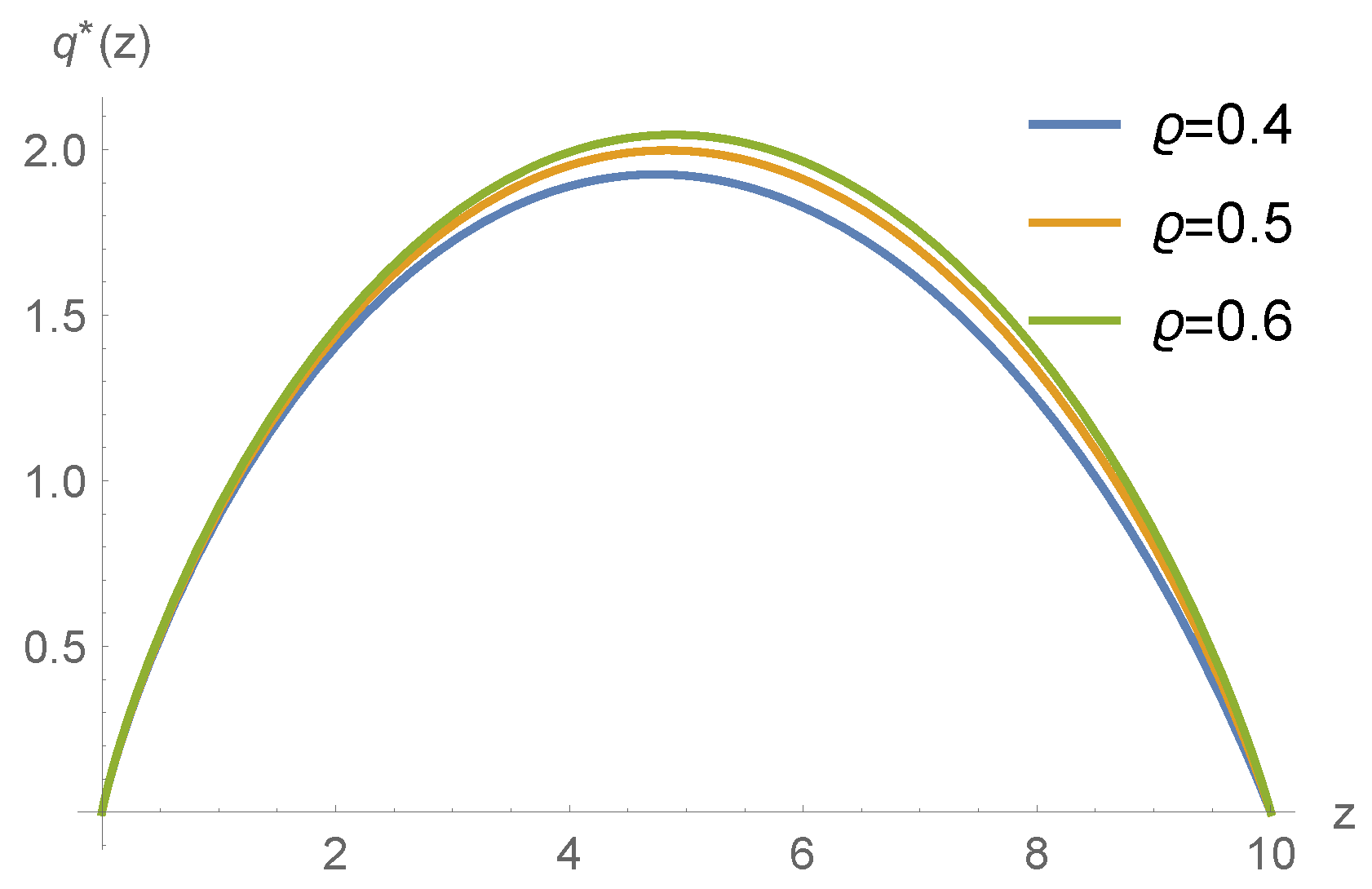

| The Influence Factor | Insurance Retention Level |
|---|---|
| Time | ↑ |
| Interest rate | ↓ |
| Diffusion volatility rate | ↓ |
| Reinsurance safety loading ↑ | ↑ |
| Expected loss in unit time m↑ | ↑ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, Y.; Huang, H. Reinsurance Policy under Interest Force and Bankruptcy Prohibition. Axioms 2023, 12, 378. https://doi.org/10.3390/axioms12040378
Zhong Y, Huang H. Reinsurance Policy under Interest Force and Bankruptcy Prohibition. Axioms. 2023; 12(4):378. https://doi.org/10.3390/axioms12040378
Chicago/Turabian StyleZhong, Yangmin, and Huaping Huang. 2023. "Reinsurance Policy under Interest Force and Bankruptcy Prohibition" Axioms 12, no. 4: 378. https://doi.org/10.3390/axioms12040378
APA StyleZhong, Y., & Huang, H. (2023). Reinsurance Policy under Interest Force and Bankruptcy Prohibition. Axioms, 12(4), 378. https://doi.org/10.3390/axioms12040378






