Abstract
We have proposed a development of the variational iteration method (VIM), or extended Kantorovich method, by studying physically nonlinear (FN) or geometrically nonlinear (GN) Kirchhoff nanoplates as an example. The modified couple stress theory was used for modeling size-dependent factors of the Kirchhoff nanoplates. Nested one into the other iteration procedures of the Birger method of variable elasticity parameters, of the variational iteration method (VIM), and of the Newton–Raphson method for physically nonlinear (FN) Kirchhoff nanoplates were constructed. The solution of problems for geometrically nonlinear (GN) Kirchhoff nanoplates was carried out on the basis of the variational iteration method and the Newton–Raphson method. The validity of the results was ensured by the coincidence of the results obtained via several methods of reducing partial differential equations to ordinary differential equations and via the finite difference method. The computational effectiveness of the proposed iterative procedure was demonstrated in terms of both accuracy and performance. A comparison of the results obtained showed that the variational iteration method (VIM) is the most efficient and fastest of all the methods considered both for problems with physical nonlinearity and for geometrically nonlinear problems.
1. Introduction
The study of elastic–plastic deformations of rectangular macro-sized plates is the subject of a large number of publications. This is due to the extensive use of such structures in aerospace research, in shipbuilding, in bridge construction, and in other engineering structures. Several theories of plastic deformation have been developed in scientific literature. The most common are the deformation theory of plasticity by Kassir [1], Molotnikov, and Molotnikova [2] and the flow theory by Wang et al. [3]. The development of the nanosystems industry has led to the creation of new higher-order theories for predicting size effects in nanostructures, including the coupled stress theory (Tupin [4]), the Mindlin first strain gradient theory [5], non-local elasticity theories (Eringen [6], Eringen [7], Eringen [8], and Shishesaz et al. [9]), the strain gradient theory (Aifantis [10]), the modified couple stress theory (Yang et al. [11]), and the Gurtin–Murdoch model of surface elasticity [12]. In their study, Qiang Liu et al. [13] presented experimental data that highlight the subtlety and importance of accounting for first-order and second-order effects when modeling crystalline materials at small length scales. The elastic–plastic response of a 4H-SiC single crystal using a Berkovich tip in nanoindentation experiments was investigated by Nawaz et al. [14]. They found that the yield strength observed increased as the thickness of the nanofilm decreased. These experimental results show that in order to better approximate the behavior of the real structure, elastic–plastic deformations must be taken into account in the mathematical modelling of nanomechanical objects.
The limited number of publications is indicative of the initial stage of research into nanoplates. Using Reddy’s third-order plate theory in non-local elasticity, Ruocco et al. [15] investigated the elastic–plastic buckling behavior of thick rectangular nanoplates embedded in a Winkler–Pasternak foundation. To explain the elastic–plastic response, two alternative plasticity theories were considered. The authors emphasize that there is a lack of data on the elastic–plastic buckling of nanoplates in the existing literature. Since Ruocco and Reddy published their work, there have been no new publications on the subject.
The stress–strain state of nanostructures is widely studied using finite element methods in software packages such as ANSYS, Comsol, Ls-Dyna, as well as variational and finite difference methods. Recently, in the study of the stress–strain state of nanostructures, the variational iteration method [VIM] [16,17,18,19] and the extended Kantorovich method [20] have been widely used. Krysko V.A. et al. [17] formulated a mathematical proof of the convergence of the variational iteration method for macro-size plates.
Studies analyzing the stress–strain state of geometrically nonlinear nanoplates typically use a single calculation method. This raises concerns about the reliability of the results. Ansari et al. [21] have made a comprehensive study on the effect of surface stresses and surface inertia on large amplitude periodic forced vibration of rectangular nanoplates with first order shear deformation considering Gurtin–Murdoch theory, first-order shear deformation theory (FSDT). To numerically solve geometrically nonlinear forced vibration of nanoplates with different boundary conditions, the generalized differential quadrature (GDQ) method and Galerkin numerical scheme are used, as are periodic time-differential operators and the pseudo-dual continuation method. In another study, Ansari et al. [22] investigated the nonlinear buckling and free vibration of a third-order shear deformable, rectangular, geometrically nonlinear nanoplate with different edge supports in the pre- and post-buckling modes while considering surface effects. Gurtin–Murdoch’s surface stress elasticity theory, combined with third-order shear deformation plate theory, was used to mathematically simulate nanoplates as a function of size. In [23] the problem of axisymmetric post-buckling behavior of annular shear deformable geometrically nonlinear nanoplates as a function of size has been solved in the framework of the Gurtin–Murdoch theory. The resulting set of nonlinear equations has been solved using the generalized differential quadrature method and the pseudo-dual continuation method. Esmaeilzadeh et al. [24] carried out a study of the vibrations of Timoshenko nanoplates on an elastic Winkler–Pasternak base, taking into account the theory of nonlocal elasticity. To solve the Cauchy problem, they used a finite element method to discretization over the spatial domain and a modified Newmark method. Gholami et al. [25] considered the bending and stability loss of Timoshenko nanoplates using gradient Midlin elasticity theory. The method of variational differential quadrature (VDQ) was used to discretize the differential equations in the weak form. Based on the Kirchhoff hypothesis and incorporating the Gurtin–Murdoch surface elasticity, Bochkarev [26] developed a nonlinear von Karman-type bending model for nanoplates. The surface tension was accounted for by quadratic terms equal to the von Karman-type strains, unlike previous related theories. Numerical results were obtained using the built-in bvp6 Matlab@ solver for a simplified one-dimensional problem involving an infinitely long strip. Based on simplified strain gradient elasticity theory and surface elasticity theory, Yue et al. [27] proposed a size-dependent Kirchhoff microplate model with surface effects. A linear formulation was used. A solution was obtained using the extended Kantorovich method (the variational iteration method (VIM)). However, the convergence of the method of solution was not investigated in the paper. In [28,29] conducted an analysis of geometrically nonlinear plates based on the Donnell–Carman theory. Awrejcewicz et al. [28] developed and tested several modifications of the Bubnov–Galerkin method for analyzing flexible rectangular plates. They formulated and proved the convergence theorem for the proposed iterative methods and used these methods to solve problems involving rectangular plates subjected to distributed and local loads under different boundary conditions. The results obtained using the different iteration methods were compared. Krysko Jr. et al. [29] studied nanoplates using the split variable method, and the convergence of the developed iterative procedures was justified using a series of theorems about the static analysis of nanoplates on a rectangular plane.
The finite difference method and its modifications, such as the implicit finite difference scheme, are popular techniques for solving problems described by partial differential equations and ordinary differential equations. The implicit finite difference scheme provides stability theorems for solutions of the considered systems of differential equations, as described in references [30,31].
The variational iteration method (VIM) is a powerful tool for solving nonlinear problems in physics and engineering. It has the advantage of being able to solve a wide range of problems, including both linear and nonlinear differential equations, with high accuracy and efficiency. Many works in the literature emphasize the advantages of the variational iteration method and its applications in various fields, such as fluid dynamics, heat transfer, and structural mechanics. In [32,33,34,35] the static stability of the plates is investigated and the variational iteration method (VIM), an extended Kantorovich method (EKM), is applied to the solutions. It is noted that this method has several advantages over other methods, particularly the finite element method. In this paper, we focus on the analysis of the stress–strain state of elastic–plastic nanoplates and geometrically nonlinear elastic Kirchhoff nanoplates as well as the influence of size-dependent parameters on their behavior.
A review of the scientific literature shows that efficient and fast methods for the analysis of elastic–plastic deformation of nanoplates have not yet been developed. The aim of this paper is to fill this gap by proposing methods for solving both linear and nonlinear differential equations of elliptic type.
The paper is structured as follows: Section 2 provides a self-contained description of the governing relations of the proposed size-dependent CTP. Section 3 discusses the strategy and methods used to solve the problem. Numerical results from the implementation are presented and discussed in Section 4. Finally, the paper concludes with a few remarks in Section 5.
2. Problem Formulation
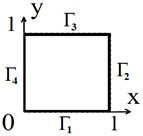
The Materials and Methods section considers a rectangular nanoplate with dimensions a, b, h along the x, y, z axes, respectively (as shown in Figure 1). In the given the Cartesian rectangular coordinate system, the plate is treated as a 3D region Ω defined by: . The origin of the coordinate system is located at the center of the middle surface of the plate, with the x- and the y-axes being parallel to the sides of the plate and the z-axis pointing downwards. For simplicity, it will be assumed that the parameters a and b are equal to 1. The boundaries are denoted as:
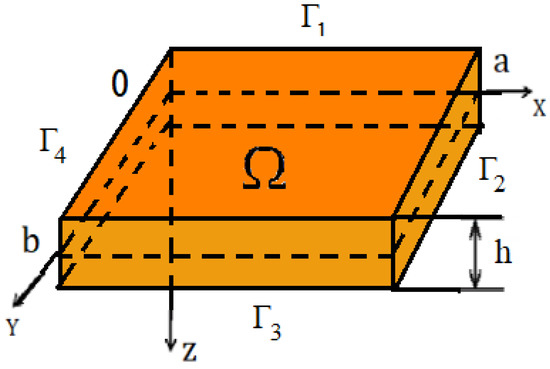
Figure 1.
The investigated plate.
The hypotheses and assumptions were used to construct a mathematical model for the system under study:
- The accepted classical plate theory (CTP), or Kirchhoff plate theory [16], is widely used in mechanical engineering to analyze the behavior of plates under load. Here, —represents the deflection of the plate’s median plane, which is a function of both x and y, —deformations.
- Physical nonlinearity (FN) is introduced using the deformation theory of plasticity. The material from which the nanoplate is fabricated is considered isotropic but not homogeneous: and —Young’s modulus and the Poisson’s ratio, respectively; —the shear modulus and the bulk modulus depend on coordinates and the strain intensity (8).
- The modified couple stress theory [11] is used to model size-dependent factors. The deformation energy U, taking into account small deformations, is expressed according to the modified couple stress theory [11] as follows:where , , and , , denote the components of the strain tensor and stress tensor, respectively. , , —symmetric part of the curvature tensor; ,,—deviatoric part of the couple stress tensor.
After carrying out the variation with respect to w and carrying out the integration by parts, we obtain the equation for the elastic–plastic nanoplate [16] as follows:
where and , where l is the length scale parameter.
Boundary Conditions (4)–(6), corresponding to Equation (3), are given in Table 1.

Table 1.
Visualisation of type of boundary conditions and type of load.
The pictogram colures correspond to blue (Boundary Condition (4)), green (Boundary Condition (5)), and red (Boundary Condition (6)). This color scheme is also used in the numerical results presented in Section 4.1. Local angular loading is indicated by the dark color superimposed on the boundary condition color. On the other hand, the uniformly distributed load corresponds to the colors of the boundary conditions.
For the numerical analysis of Equation (3) with the corresponding Boundary Conditions (4) through (6), the following dimensionless parameters are introduced in the standard manner [16]:
where is the size dependent parameter, is the shear modulus of the elastic body, is the strain rate, is the stress intensity, is the yield stress, and is the yield strength.
Using Relation (7), let us reduce Equation (3) to a dimensionless form:
In the above equations, the dash above the dimensionless parameters is omitted for simplicity.
3. Solution Methods
The analysis of the elastic–plastic behavior of Kirchhoff’s nanoplates is carried out using the approach proposed by the authors. This approach is based on a nested set of three iterative procedures. The ordinary differential equations are solved by the finite difference method with a second order accuracy at each step of the iteration procedure.
Iterative procedure I. This iterative procedure uses Birger’s variable elasticity parameter method (MVPE) [36]. At a fixed load , the plate material was assumed to be elastic. However, according to the accepted hypotheses, the material is inhomogeneous , and depends on the stress–strain state at each point. Therefore, a new problem must be solved to compute the stress–strain state at each point of the plate using the method MVPE. For a given plate material from the experiment, we need to know the dependence . The plate area is covered by a grid . The strain rate is computed at each node of the area grid:
The value is considered equivalent to and , and it is determined from the condition of plane stress , where .
Then, Relation (8) takes the form:
According to Birger’s method of variable elasticity parameters (MVPE), we compute the Young’s modulus—, the Poisson’s ratio—, the shear modulus—, and the bulk modulus——at each point of the grid :
The Simpson formulae are used to compute certain integrals over the plane and through the thickness.
The iterative process of the variable elasticity method continues until the condition is met for a given :
where is the value of deflection in the i step of the iterative procedure of Birger’s method of variable elasticity parameters (MVPE).
This is an internal iterative process. Next, for the same load q, we move on to the external iteration process of the variational iteration method (VIM).
Remark 1.
A proof of the convergence of the elastic solution method is given in the articles [37,38,39].
Iterative procedure II. One of the following methods is used in this iterative procedure: Bubnov–Galerkin method (BGM) [40,41]; Kantorovich–Vlasov method (KVM) [42]; variational iteration method (VIM) [16,17,18,19,20];
Iterative procedure III. This iterative procedure refines the solutions using the Agranovsky–Baglai–Smirnov (ABSM) method [43].
To justify the application of iterative procedures II and III, we will provide a connection between the Fourier method and the Bubnov–Galerkin method. Essentially, the Fourier method is a technique for solving mixed problems and the Cauchy problem based on the spectral properties of the elliptic operator in the equation. In the classical works of Fourier and his followers, the Fourier method was associated with the method of separation of variables in differential equations.
Later, this method found its application to elliptic equations combined with one of the variables using the Bubnov–Galerkin method (BGM). The works of Kantorovich [42] and Vlasov [44] were among the first explorations of this approach. This procedure combined these two eminent names, and the method they developed became known as the Kantorovich–Vlasov method (KVM). The KVM method is very similar to the Bubnov–Galerkin method in terms of its ideology and has given rise to a number of modifications. We will briefly discuss the KVM method and some of its modifications below.
Differential Equation (3) is a fourth-order linear partial differential equation, according to the method of variable elasticity parameters, which includes nanoeffects based on the modified couple stress theory [11]. Key concepts and ideas of these methods will be discussed with the help of the operator type equation of the form:
where A is an operator of a boundary problem including both Differential Operator (3) and Boundary Conditions (5) and (6). is a known function.
The Fourier method is frequently used in applied computational mathematics to obtain approximate solutions of differential equations using the Bubnov–Galerkin method (with various modifications).
3.1. Application of the Bubnov–Galerkin Method (BGM)
Consider the application of the BGM on the example of differential Equation (12). Assume a trial solution corresponding to the BGM:
This solution is based on trial functions that are energy-orthonormal [45,46], meaning that they satisfy the condition:
Next we apply the BGM procedure:
or, using the Equation (12), , so that Solution (12) takes the form:
However, if an energy-orthonormal system of functions is full of energy, then for (i.e., for any solution of Equation (15)), we take the Fourier series as follows:
which converges with energy to . Here, energy convergence means that:
where is an arbitrarily chosen small positive constant. It is clear from Condition (14) that Bubnov–Galerkin Solution (17) can be represented as a truncated Fourier series with some finite number of terms. Therefore, the Bubnov–Galerkin solution also converges in energy due to the equivalence of the truncated Fourier series.
Remark 2.
This approach, based on a decomposition into energy-orthonormalized functions, is theoretically sound, but constructing such a series of functions can be extremely difficult in practice.
3.2. Application of the Kantorovich–Vlasov Method (KVM)
Consider the application of the KVM on the example of Differential Equation (12). Assume a trial solution corresponding to the KVM:
Weight function is given in the form:
Function is the desired value, so the Bubnov–Galerkin method is applied to coordinate :
we obtain a system of ordinary differential equations (ODE) on the coordinate . In Equation (21) and after, is the inner product defined as . By solving the ODE system with the appropriate boundary conditions, we obtain a set of functions . Substituting them into (19), we obtain the desired solution. The proof of convergence of this method for a biharmonic equation with constant coefficients is given by Kantorovich [42].
The relation between the Kantorovich–Vlasov method and the Fourier representation for the solution of the elastic–plastic equation of the nanoplate follow. Let us write down the methodology for coupling Fourier ideas when solving linear partial differential equations with variable coefficients for nanoplates (3) using the Kantorovich–Vlasov method. Let us express in the form of (13). In this approach, the solution for the trial functions is based on the energy-orthonormal property (14). The function is unknown and is determined by applying the BGM to the coordinate (15). This results in a system of ordinary differential equations with respect to the function . Therefore, at the stage of presenting the solution and using the BGM procedure, the variables are separated, similar to the Fourier method. Once the function is found, the BGM procedure can be applied to refine function and obtain a more accurate solution. This approach, which is essentially a combination of a split variable method and an iterative procedure, is called the variational iteration method (VIM) and will be discussed further below.
3.3. Application of the Variational Iteration Method (VIM)
Next, let us consider the application of the VIM [16,17,18,19,20] to an example of the solution of the operator Equation (12). The VIM is a generalization of the KVM method. In this method, the coordinate test solution is selected in the same way as in the KVM method:
In this case, on the first iteration:
Moreover, may not satisfy the given boundary conditions. Apply to BGM using coordinate :
We obtain a system of ordinary differential equations for the coordinate . Solving with appropriate boundary conditions, we obtain the set of and substitute them in (22):
Let’s substitute the solution in the KVM. This is the first iteration in the VIM. Next, we select the set of functions obtained by solving the KVM problem as a trial set of functions:
The functions are unknown and BGM is applied by coordinate :
In this case, we also obtain a system of ordinary differential equations on , from which we obtain a set of functions , allowing us to represent the solution of (22) as:
Then, repeat the procedure again, stopping at step:
The solution to (28) is obtained with the given accuracy if the conditions are met:
The proof of convergence of the variational iteration method (VIM) for a class of equations described by positively determined operators can be found in [16]. The proof is based on the Sophie–Germain–Lagrange equation for full-dimensional plates. When considering nanoplates, the proof given in [16] is still valid and has been reaffirmed in [29].
Let us provide a justification for the application of the VIM to physically nonlinear Kirchhoff nanoplates. While the proof of convergence for full-dimensional problems is given in [47], we can improve the accuracy of the solution for any class of partial differential equations by applying the Agranovsky–Baglai–Smirnov (ABSM) method [16,29].
Consider applying ABSM by solving Equation (12) using one of the methods described above.
Construct a new equation of the following form:
That is, in Equation (7), we have changed the right-hand side to play the role of the inhomogeneity in the original equation. Equation (31) is then solved again using one of the methods described above, and we obtain:
Once again, we construct a new equation of the form:
etc.
The following series is finally taken as the initial solution:
A proof of the convergence of the ABSM is given in [43].
Here is a flowchart of iteration procedures of the VIM, MVPE, and ABSM methods (Figure 2). (For a detailed description of these iterative procedures, see above).
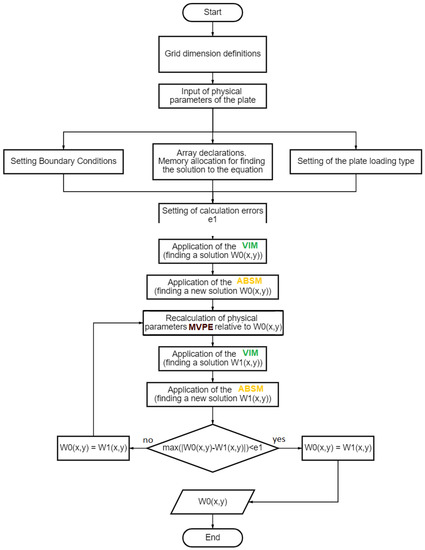
Figure 2.
A flowchart of iterative procedures for methods VIM, MVPE, ABSM.
4. Numerical Results
Section 4 presents the results of two different nonlinear problems: a physically nonlinear problem—Section 4.1 and a geometrically nonlinear problem—Section 4.2. The methods used for both problems were VIM, KVM, and BGM, as well as variational iteration method (VIM) combined with the Agranovsky–Baglay–Smirnov method (ABSM).
4.1. Methods for Solving the Equation in a Physically Nonlinear Kirchhoff Nanoplate
For the first time, methods for reducing partial differential equations to ordinary differential equations were applied to analyze the stress–strain state of physically nonlinear Kirchhoff nanoplates. Specifically, the following methods were used: the variational iteration method (VIM), or the extended Kantorovich method; the Agranovsky–Baglay–Smirnov method (ABSM); the Kantorovich–Vlasov method (KVM); the Bubnov–Galerkin method (BGM); and the variational iteration method (VIM) in combination with the Agranovsky–Baglay–Smirnov method (ABSM).
The basic material of the plate was aluminum with physical and geometrical constants:
The dependency diagram is as follows [48]:
The absolute error in obtaining a solution at each MVPE step: and for procedures VIM and ABSM: .
The convergence of the solution to the VIM has been investigated, resulting in ordinary differential equations at each iteration of the method. These equations are then solved using the second-order finite difference method. Note that the study of solution convergence is important because it allows us to evaluate the accuracy and reliability of the VIM method as well as to identify any potential errors or instabilities that may arise in the solution process.
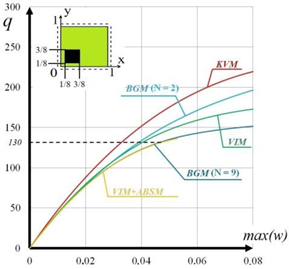
The study is carried out for the size-dependent parameter . The interval was divided into n intervals. Figure 2 shows the dependence of , which represents the behavior of the system at the point .
Using Birger’s MVPE, the strain rate had to be computed at each point in the volume to determine the Young’s modulus and Poisson’s ratio.
The results shown in Figure 3 are obtained by partitioning the plate thickness into of discrete points. This thickness partitioning achieves convergence with a plane partition of . Integration over the plane and over the thickness was performed using Simpson’s formula.
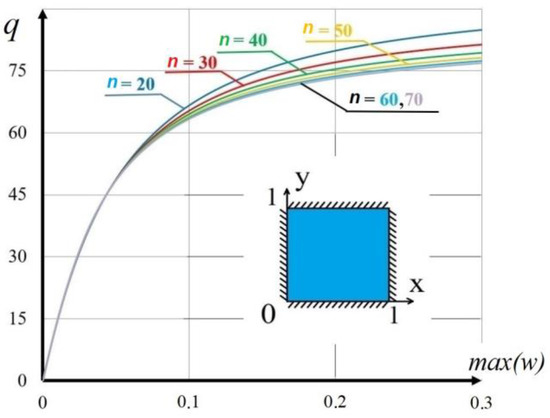
Figure 3.
Convergence of the VIM solution. The value of the load—deflection ), depending versus the parameters: l = 0.3, , .
We also investigated the reliability of the solution results for the elastic–plastic problem using different techniques, including the Bubnov–Galerkin (BGM) [40,41] in higher approximations (n = 2, 9), the Kantorovich–Vlasov (KVM) [42], the VIM, and the combination of the VIM with the Agranovsky–Baglay–Smirnov (ABSM) (i.e., VIM + ABSM).
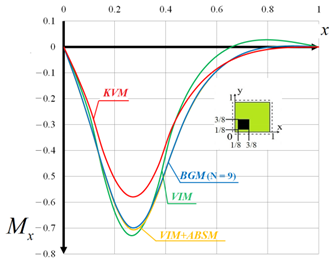
We investigated three types of loading and three boundary conditions. The results for Boundary Condition (4) and local angular loading are shown in Table 2. Our analysis of the results shows that the solutions obtained with the BGM method (n = 9), i.e., 81 consecutive terms, and for VIM and VIM + ABSM methods are almost identical for all three types of loading. Moreover, our analysis shows that the results obtained with the VIM + ABSM method are consistent with those obtained with the BGM method (n = 9) for both plastic zones and load-deflection and moment diagrams. These results are important because they demonstrate the effectiveness of the VIM + ABSM method in providing accurate solutions for a wide range of load and boundary conditions and at the same time highlight the consistency of the results with those obtained by the BGM method (n = 9).

Table 2.
Load-deflection relationships and moment diagrams.
The maximum value of the moments on the plot diagram obtained by the VIM + ABSM and BGM (n = 9) methods differs significantly from those obtained by VIM, BGM (n = 2) and KVM for a uniformly distributed load by 137% and for a localized load in the center by 192%, almost twice the difference. In addition, the comparison of computation times showed that VIM + ABSM was the preferred method between the two. These results are significant because they highlight the limitations of the VIM, BGM (n = 2) and KVM methods in accurately capturing the behavior of the system under study. At the same time, they demonstrate the superiority of the VIM + ABSM and BGM (n = 9) methods. The computational efficiency of VIM + ABSM also makes it attractive for practical applications where time and computational resources are limited.
A time–cost analysis was carried out on a computer with an Intel Core i7 9750H 2.6 GHz processor, 8192 MB of RAM, DDR4, 2666 MHz, and an nVidia GeForce RTX 2060 graphics processor with 6144 MB of memory. The results presented in Table 3 show that the VIM method is more efficient than the other methods analyzed in the study. For systems with an infinite number of degrees of freedom and for any combination of boundary conditions and loads, this method can produce practically exact solutions. This information is crucial for selecting the appropriate method for a given problem, as it allows us to balance the trade-off between accuracy and computational time. In addition, the method has been theoretically proven to converge. This is evidenced by convergence theorems established by the authors. The combination of the VIM with the Birger’s MVPE method is an extremely effective iterative procedure, as confirmed by the numerical experiments. The MVPE is shown to converge, which further increases the reliability and accuracy of this combined approach. This approach involves the nesting of two methods, the variational iteration method and the elasticity variable method, to obtain highly accurate and reliable results.

Table 3.
Calculation time (sec.) by BGM (9), BGM (2), KVM, VIM, and VIM + ABSM for one load step.
The effect of the dimensional coefficient of material length l, boundary conditions, and type of loading on the stress–strain state of the plate was investigated.
The results of this study are shown in Figure 4, which shows the effect of the material length dimensional coefficient for three types of boundary conditions under the action of local angular loading. The yellow dots in the plots show the occurrence of plastic strains, and the red dots show the occurrence of plastic hinges, which occur when the values of strain intensity over the entire thickness exceed the value of the yield stress in at least one point (x, y) in the plane of the plate. These results are significant because they provide an insight into how different parameters influence the behavior of the material and can be used to optimize the design and performance of structures and equipment that rely on the mechanical properties of the plate.
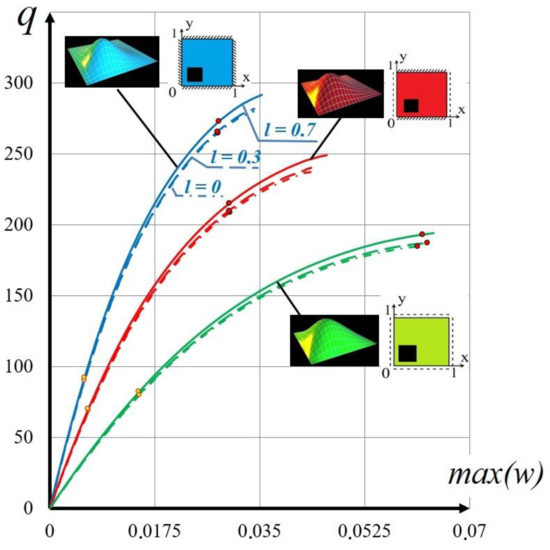
Figure 4.
Convergence of VIM + ABSM solution depending on: size-dependent parameter l, boundary conditions with localized angular loading.
It should be noted that the results for Boundary Condition (5) at l = 0.7 and l = 0.3 are almost identical. The distribution of the plastic strain and the points of the plastic joint are similar to the previous case. However, the difference in deflection at the plastic joint for Boundary Conditions (5) and (6) is almost three times.
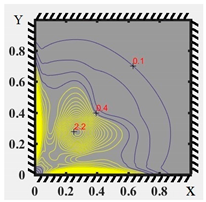
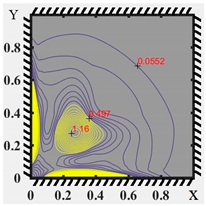
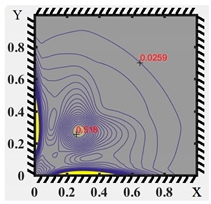
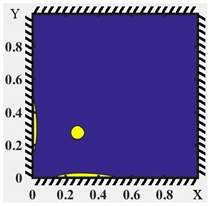
The stress–strain state was examined in the form of lines of equal strain intensity. In addition, charts of the elastic–plastic zones at the points of plastic joint occurrence have been plotted for three boundary conditions, three types of loading (distributed, local in the center, and local in the corner) and three values of the size-dependent parameter l. Results are obtained for three symmetrical pairs of points along the plate thickness: . The results for local angular loading, l = 0.3, and Boundary Condition (3) are shown in Table 4. The first column shows the type of boundary condition, the coordinate z. The second column shows the lines of equal strain intensities, and the third column shows the elastic–plastic zones.

Table 4.
Equal strain intensity lines and elastic–plastic zone diagrams at the beginning of the plastic joint for Boundary Condition (4).
The type of boundary conditions has a significant influence on the distribution of both strain rates and plasticity zones. The largest plasticity zone is observed for Boundary Condition (4), while the smallest is observed for Boundary Condition (5). Moreover, for Boundary Condition (5), the plasticity zones and equal strain intensity lines exhibit pronounced antisymmetry.
Table 5 shows the percentage difference between the highest strain intensity values in the plastic zone for the layers and .

Table 5.
Influence of the types of Boundary Conditions (4) and (5) on the layers for maximum strain intensity .
For the layer z = 0.142, values of strain intensity are available only for Boundary Condition (4), where the type of plastic deformation zones differs significantly from the plastic deformation zones of Boundary Conditions (3) and (5).
The results of Table 5 show that changing the boundary conditions has a significant effect on the stress–strain state of the plate.
Figure 5 presents the relationship between the load- and size-dependent parameters for three types of boundary conditions under a uniformly distributed load with a fixed deflection value of 0.25. The analysis of the results indicates that as the size-dependent parameter is increased, the differences between the results obtained for various boundary conditions become negligible. Specifically, at l = 0, the difference between Boundary Conditions (3) and (4) is 49.3%, while for l = 0.7, the difference is 49.4%.
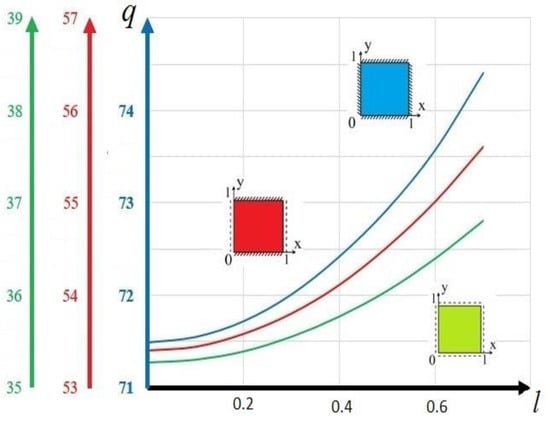
Figure 5.
The value of the load—size-dependent parameter q(l) for the three types of Boundary Conditions (3)–(5) at uniformly distributed load and at a given deflection w(0.5;0.5) = 0.25.
4.2. Methods for Solving the Equation in a Geometrically Nonlinear Kirchhoff Nanoplate
Let us consider the application of the variation iteration method, or the extended Kantorovich method, in the first (VIM 1) and second (VIM 2) approximations, the Kantorovich–Vlasov Method in the second approximation (KVM 2), the Bubnov–Galerkin Method (BGM) in higher approximations, and the finite difference method (FDM) to investigate the stress–strain state of geometrically nonlinear Karman–Donnell’s nanoplates.
In Section 2 of this study, the basic hypotheses have been formulated, and they are sufficient in the case of geometrically nonlinear plates according to the von Karman model. The equations below are derived from a functional that uses the modified couple stress theory to describe the nanoeffects:
Equation (36) are reduced to a dimensionless form by (7) and . To simplify, the dashes above the dimensionless parameters in Equation (36) are omitted, as before.
Furthermore, the stress–strain state of geometrically nonlinear nanoplates (36) was investigated using VIM1, VIM2, BGM, KVM2, and FDM for the boundary conditions of a hinged contour resting on flexible incompressible (inextensible) ribs of the tangent plane [49]:
The algorithms of the VIM, BGM, and KVM methods for physically nonlinear plates are described in detail in the third section of this study. For geometrically nonlinear plates, the algorithms are similar but differ in that when VIM or KVM is applied after the Bubnov–Galerkin procedure for one of the coordinates, we obtain a system of nonlinear ordinary differential equations. We then reduce this system to a system of nonlinear algebraic equations using the finite difference method of second order accuracy, which is solved using the Newton–Raphson method. We also investigated the convergence of the solution as a function of the partition interval of the solution domain. In the results below, the domain was partitioned into intervals.
When solving System (36) with the Bubnov–Galerkin method to satisfy Boundary Condition (37), represent the functions w(x,y) and F(x,y) as
After applying the Bubnov–Galerkin procedure to the x, y coordinates, we obtain the following system:
By integrating each term, we obtain a system of (where is the number of terms) nonlinear algebraic equations with respect to the unknown coefficients . This system is solved using the Newton–Raphson method.

Table 6.
Comparison of solution methods for uniformly distributed loading of the square plate. , , .
The results presented in Table 6 indicate that the largest difference from BGM5 is found in the FDM solution (0.411 and 0.3795%) and VIM2 solution (0.09%). It is important to note that the time required to obtain the true FDM solution is almost 500 times longer than the time needed for the VIM2 solution and 11 times longer than the time required for the BGM5 solution. This demonstrates that the VIM method is the most efficient for solving the given class of problems.
The order of the system of algebraic equations depends on the number of terms N in Expression (38). The convergence was investigated, i.e., a coincidence for solutions of functions and their second derivatives for N and N + 1 was required. Convergence was achieved for n = 7 in (38).
Let us compare the solutions of Systems (36) and (37) obtained via the variational iteration method, or extended Kantorovich method, of the first (VIM 1) and second (VIM 2) approximation, the Bubnov–Galerkin method (BGM) in higher approximations (n = 7), the finite difference method (FDM) of second order accuracy, and the Kantorovich–Vlasov method in the second approximation (VIM 2) for macro-sized, full-dimensional (l = 0), and dimensionally dependent nanoplates (l = 0.5).
Figure 6 illustrates the dependencies , epiures for the second derivative of the deflection function (for y = 0.5; ) and surface for , obtained using VIM 1, VIM 2, BGM, FDM, KVM 2, and Shen [50].

Figure 6.
The value of the load—deflection q(w(0.5;0.5)), for a macro-sized plate (l = 0) obtained via the following methods: VIM 1, VIM 2, BGM, FDM, and KVM 2 and using the perturbation technique (Shen).
The color spectrum of the methods corresponds to the color spectrum of the curves. For the reliability of the results obtained, the solutions obtained by the perturbation technique in [50] are also considered.
The load–deflection relationships are shown in Figure 6 and Figure 7. The load–deflection relationships shown in Figure 6 show that the numerical values obtained using VIM 1, VIM 2, BGM, FDM, KVM 2, and the perturbation technique applied by Shen et al. [50] are almost exactly the same, which indicates the validity of the results obtained by these methods. Taking into account the size-dependent parameter l = 0.5 improves the convergence of the developed methods and the calculation results are almost the same, as shown in Figure 7.
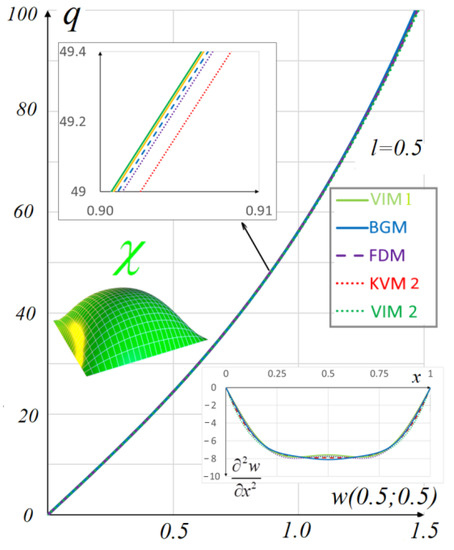
Figure 7.
The value of the load—deflection q(w(0.5;0.5)), at the size-dependent parameter l = 0.5, obtained using the following methods: VIM 1, VIM 2, BGM, FDM, and KVM 2.
5. Conclusions
1. For the first time, mathematical models of physically nonlinear Kirchhoff nanoplates using deformation theory of plasticity, as well as geometrically nonlinear elastic nanoplates in which nanoeffects are taken into account by the modified couple stress theory of Yang, have been constructed.
2. Theoretical and mathematical justification is given for the application of the Kantorovich–Vlasov method (KVM) and variation iteration method (VIM) to the analysis of physically nonlinear (FN) and geometrically nonlinear (GN) Kirchhoff nanoplates.
3. Our analysis has demonstrated that the of variational iterations methodis the most efficient method in terms of both accuracy and speed on a personal computer compared to other methods, such as Bubnov–Galerkin, in higher approximations and Kantorovich–Vlasov for studying the stress–strain state of elastic–plastic nanoplates and geometrically nonlinear elastic nanoplates. These results indicate that the method of variational iterations is a promising and can provide accurate and reliable solutions for a wide range of loading and boundary conditions.
4. The stress–strain analysis of elastic–plastic nanoplates and geometrically nonlinear elastic Kirchhoff nanoplates must take into account the size-dependent parameter since it has a significant influence on the dependence.
5. For geometrically nonlinear elastic nanoplates, accounting for the size-dependent parameter l significantly improves the convergence of VIM.
6. The variational iteration method (VIM) has been shown to be a successful approach for analyzing the statics of nanoplates with high nonlinearity, arbitrary plane geometry, variable thickness, multilayers, and multimodules. VIM can be used to solve problems described by both first approximation and higher-order kinematic models. Additionally, VIM can be applied to the study of functionally graded porous nanoplates, weight optimization problems, and dynamics problems.
Overall, the versatility of VIM makes it a valuable tool for the analysis of various types of nanoplates and their associated problems. Its ability to handle high nonlinearity and various geometries and material properties make it particularly useful for modeling the behavior of complex systems.
Author Contributions
Conceptualization, A.V.K.; methodology, T.V.Y. and A.V.K.; software, A.D.T.; validation, A.V.K. and L.A.K.; formal analysis, A.V.K. and T.V.Y.; investigation, A.D.T.; writing—original draft preparation, T.V.Y. and A.V.K.; writing—review and editing, A.V.K., visualization, L.A.K.; supervision, A.V.K.; project administration, A.V.K.; funding acquisition, T.V.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Russian Science Foundation (RSF), Project No 22-71-10083 (https://rscf.ru/en/project/22-71-10083 (accessed on 30 March 2023)).
Data Availability Statement
No data was used for the research described in the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kassir, M. Applied Elasticity and Plasticity, 1st ed.; CRC Press: Boca Raton, FL, USA, 2017; p. 563. [Google Scholar] [CrossRef]
- Molotnikov, V.; Molotnikova, A. Theory of Elasticity and Plasticity: A Textbook of Solid Body Mechanics, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2021; p. 444. [Google Scholar]
- Wang, Z.R.; Hu, W.L.; Yuan, S.J.; Wang, X.S. Engineering Plasticity: Theory and Applications in Metal Forming, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2018; p. 520. [Google Scholar]
- Toupin, R.A. Elastic materials with couple-stresses. Arch. Rational Mech. Anal. 1962, 11, 385–414. [Google Scholar] [CrossRef]
- Mindlin, R.D.; Eshel, N.N. On first strain-gradient theories in linear elasticity. Int. J. Solids Struct. 1968, 4, 109–124. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal polar elastic continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A. Nonlocal Continuum Field Theories; Springer Science & Business Media: New York, NY, USA, 2002; p. 376. [Google Scholar]
- Shishesaz, M.; Shariati, M.; Yaghootian, A.; Alizadeh, A. Nonlinear Vibration Analysis of Nano-Disks Based on Nonlocal Elasticity Theory Using Homotopy Perturbation Method. Int. J. Appl. Mech. 2019, 11, 1950011. [Google Scholar] [CrossRef]
- Aifantis, E.C. Strain gradient interpretation of size effects. Int. J. Fract. 1999, 95, 299–314. [Google Scholar] [CrossRef]
- Yang, F.; Chong, A.; Lam, D.C.C.; Tong, P. Couple stress based strain gradient theory for elasticity. Int. J. Solids Struct. 2002, 39, 2731–2743. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Murdoch, A.I. Surface stress in solids. Int. J. Solids Struct. 1978, 14, 431–440. [Google Scholar] [CrossRef]
- Liu, Q.; Roy, A.; Silberschmidt, V.V. Size-dependent crystal plasticity: From micro-pillar compression to bending. Mech. Mater. 2016, 100, 31–40. [Google Scholar] [CrossRef]
- Nawaz, A.; Mao, W.G.; Lu, C.; Shen, Y.G. Nano-scale elastic-plastic properties and indentation-induced deformation of single crystal 4H-SiC. J. Mech. Behav. Biomed. Mater. 2017, 66, 172–180. [Google Scholar] [CrossRef]
- Ruocco, E.; Reddy, J.N. Buckling analysis of elastic–plastic nanoplates resting on a Winkler–Pasternak foundation based on nonlocal third-order plate theory. Int. J. Non. Linear Mech. 2020, 121, 103453. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko-jr., V.A.; Kalutsky, L.A.; Zhigalov, M.V.; Krysko, V.A. Review of the methods of transition from partial to ordinary differential equations: From macro- to nano-structural dynamics. Arch. Comput. Methods Eng. 2021, 28, 4781–4813. [Google Scholar] [CrossRef]
- Kirichenko, V.F.; Krys’ko, V.A. Substantiation of the variational iteration method in the theory of plates. Prikl. Mekhanika 1981, 17, 71–76. (In Russian) [Google Scholar] [CrossRef]
- Krysko, A.V.; Awrejcewicz, J.; Zhigalov, M.V.; Krysko, V.A. On the contact interaction between two rectangular plates. Nonlinear Dyn. 2016, 84, 2729–2748. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A.; Zhigalov, M.V.; Krysko, A.V. Contact interaction of two rectangular plates made from different materials with an account of physical non-linearity. Nonlinear Dyn. 2018, 91, 1191–1211. [Google Scholar] [CrossRef]
- Kerr, A.D. An extended Kantorovich method for solution of eigenvalue problem. Int. J. Solid Struct. 1969, 15, 559–572. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R. Surface effect on the large amplitude periodic forced vibration of first-order shear deformable rectangular nanoplates with various edge supports. Acta Astronaut. 2016, 118, 72–89. [Google Scholar] [CrossRef]
- Ansari, R.; Gholami, R. Size-dependent modeling of the free vibration characteristics of postbuckled third-order shear deformable rectangular nanoplates based on the surface stress elasticity theory. Compos. Part B Eng. 2016, 95, 301–316. [Google Scholar] [CrossRef]
- Ansari, R.; Mohammadi, V.; Shojaei, M.F.; Gholami, R. Size-dependent postbuckling of annular nanoplates with different boundary conditions subjected to the axisymmetric radial loading incorporating surface stress effects. Int. J. Multiscale Comput. Eng. 2016, 14, 65–80. [Google Scholar] [CrossRef]
- Esmaeilzadeh, M.; Golmakani, M.E.; Kadkhodayan, M.; Amoozgar, M.; Bodaghi, M. Geometrically nonlinear thermo-mechanical analysis of graphene-reinforced moving polymer nanoplates. Adv. Nano Res. 2021, 10, 151–163. [Google Scholar] [CrossRef]
- Gholami, Y.; Gholami, R.; Ansari, R.; Rouhi, H. Size-dependent geometrically nonlinear bending and postbuckling of nanocrystalline silicon rectangular plates based on mindlin’s strain gradient theory. Int. J. Multiscale Comput. Eng. 2019, 17, 583–606. [Google Scholar] [CrossRef]
- Bochkarev, A. On the account of surface tension nonlinearity under of nano-plate bending. Mech. Res. Commun. 2020, 106, 103521. [Google Scholar] [CrossRef]
- Yue, Y.M.; Xu, K.Y.; Tan, Z.Q.; Wang, W.J.; Wang, D. The influence of surface stress and surface-induced internal residual stresses on the size-dependent behaviors of Kirchhoff microplate. Arch. Appl. Mech. 2019, 89, 1301–1315. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, V.A., Jr.; Kalutsky, L.A.; Krysko, V.A. Computing static behavior of flexible rectangular von Karman plates in fast and reliable way. Int. J. Non-Linear Mech. 2022, 146, 104162. [Google Scholar] [CrossRef]
- Krysko, V.A., Jr.; Awrejcewicz, J.; Kalutsky, L.A.; Krysko, V.A. Quantification of various reduced order modelling computational methods to study deflection of size-dependent plates. Comput. Math. Appl. 2023, 133, 61–84. [Google Scholar] [CrossRef]
- Alqarni, M.M.; Nasir, A.; Alyami, M.A.; Raza, A.; Awrejcewicz, J.; Rafiq, M.; Ahmed, N.; Shaikh, T.S.; Mahmoud, E.E. A SEIR Epidemic Model of Whooping Cough-Like Infections and Its Dynamically Consistent Approximation. Complexity 2022, 2022, 3642444. [Google Scholar] [CrossRef]
- Ahmed, N.; Macías-Díaz, J.E.; Shahid, N.; Raza, A.; Rafiq, M. A dynamically consistent computational method to solve numerically a mathematical model of polio propagation with spatial diffusion. Comput. Methods Programs Biomed. 2022, 218, 106709. [Google Scholar] [CrossRef]
- Liu, B.; Xing, Y.F.; Eisenberger, M.; Ferreira, A.J.M. Thickness-shear vibration analysis of rectangular quartz plates by a numerical extended Kantorovich method. Compos. Struct. 2014, 107, 429–435. [Google Scholar] [CrossRef]
- Khan, Y.; Tiwari, P.; Ali, R. Application of variational methods to a rectangular clamped plate problem. Comput. Math. Appl. 2012, 63, 862–869. [Google Scholar] [CrossRef]
- Kar, S.; Kumari, P. Three-dimensional analytical solution of arbitrarily supported cylindrical panels with weak interfaces using the extended Kantorovich method. Compos. Struct. 2020, 236, 111802. [Google Scholar] [CrossRef]
- Behera, S.; Kumari, P. Free Vibration Analysis of Levy-Type Smart Hybrid Plates Using Three-Dimensional Extended Kantorovich Method. In Structural Integrity Assessment; Prakash, R., Suresh Kumar, R., Nagesha, A., Sasikala, G., Bhaduri, A., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Birger, I.A. Some general methods of solution for problems in the theory of plasticity. Prikl. Mat. I Mekhanika 1951, 15, 765–770. (In Russian) [Google Scholar]
- Vorovich, I.I.; Krasovsky, Y.P. On the method of elastic solutions. DAN USSR 1959, 126, 740–743. (In Russian) [Google Scholar]
- Krysko, A.V.; Awrejcewicz, J.; Bodyagina, K.S.; Krysko, V.A. Mathematical modeling of planar physically nonlinear inhomogeneous plates with rectangular cuts in the three-dimensional formulation. Acta Mech. 2021, 232, 4933–4950. [Google Scholar] [CrossRef]
- Krysko, A.V.; Awrejcewicz, J.; Bodyagina, K.S.; Zhigalov, M.V.; Krysko, V.A. Mathematical modelling of physically nonlinear 3D beams and plates made of multimodulus materials. Acta Mech. 2021, 232, 3441–3469. [Google Scholar] [CrossRef]
- Bubnov, I.G. Review of the Work of Prof. S. P. Timoshenko “On the Stability of Elastic Systems”; Selected Works; Sudpromgiz Publishers: Leningrad, Russia, 1956; pp. 136–139. (In Russian) [Google Scholar]
- Galerkin, B.G. Rods and plates. Series in some questions of elastic equilibrium of rods and plates. Bull. Eng. 1915, 1, 897–908. (In Russian) [Google Scholar]
- Kantorovich, L.V.; Krylov, V.I. Approximate Methods of Higher Analysis, 3rd ed.; Benster, C.D., Translator; Interscience: New York, NY, USA, 1959. [Google Scholar]
- Agranovskii, M.L.; Baglai, R.D.; Smirnov, K.K. Identification of a class of nonlinear operators. Zh Vychisl. Mat Mat Fiz 1978, 18, 284–293. (In Russian) [Google Scholar]
- Vlasov, V.Z. General Theory for Shells and Its Application in Engineering; NASA-TT-F-99; National Aeronautics and Space Administration: Washington, DC, USA, 1964; p. 913.
- Mikhlin, S.G. Variational Methods in Mathematical Physics. In International Series of Monographs in Pure and Applied Mathematics, V. 50; Pergamon Press: New York, NY, USA, 1964; p. 583. [Google Scholar]
- Krasnosel’skii, M.A.; Vainikko, G.M.; Zabreiko, P.P.; Rutitskii, Y.B.; Stetsenko, V.Y. Approximate Solution of Operator Equations; Springer: Dordrecht, The Netherlands, 2011; p. 496. [Google Scholar] [CrossRef]
- Kirichenko, V.F.; Krysko, V.A. On the solution of physically nonlinear problems of the theory of plates and shells, rectangular in plan, by the method of variational iterations. Sov. Math. 1982, 26, 104–107. (In Russian) [Google Scholar]
- Ohashi, Y.; Murakami, S. The elasto-plastic bending of a clamped thin circular plate. In Applied Mechanics; Ortler, H.G., Ed.; Springer: Berlin, Heidelberg, 1966; pp. 212–223. [Google Scholar] [CrossRef]
- Kornishin, M.S.; Isanbaeva, F.S. Flexible Plates and Panels; USSR Academy of Sciences: Moscow, Russia, 1968; p. 260. (In Russian) [Google Scholar]
- Shen, H.S. Nonlinear bending of shear deformable laminated plates under transverse and in-plane loads and resting on elastic foundations. Compos. Struct. 2000, 50, 131–142. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).