Rough-Fuzzy Based Synthetic Data Generation Exploring Boundary Region of Rough Sets to Handle Class Imbalance Problem
Abstract
1. Introduction
1.1. Literature Survey
1.2. Objective
1.3. Contribution
- The dataset is collected and preprocessed to remove the irregularities from the data. The processed dataset is discretized by an efficient discretization algorithm [44]. The discretized dataset is fed on the RST-based feature selection algorithm to retain only the relevant features of the dataset.
- The negative, positive, and boundary regions of the target sets are identified, and the negative region is discarded as an outlier. The positive region is categorized into different groups based on the class labels of the objects. The fuzzy-membership values of each object in the boundary region are computed.
- The rough-fuzzy based oversampling and undersampling method is proposed to generate the minority class objects and remove the majority class objects with the help of positive and boundary regions. During this method, the membership values computed using fuzzy theory take important roles to remove and generate new objects.
- Finally, the method is validated by evaluating different performance measure metrics. Also, the method is compared with some related state-of-the-art methods with the help of the same metrics.
1.4. Summary
2. Preprocessing and Feature Selection
2.1. Rough Set Theory
2.2. Feature Selection
| Algorithm 1: Rough Set Theory based Feature Selection(RSTFS). |
 |
3. Rough-Fuzzy Based Oversampling Technique
| Algorithm 2: Rough-Fuzzy based Class Balancing Method (). |
 |
- is major class: Here, object is of majority class. If its fuzzy membership value for its own class is less than a threshold (say, ), i.e., if , then we remove the object from the dataset, i.e., we perform undersampling. We are not losing valuable information because the object was in a region of uncertainty. On the other hand, if its fuzzy membership value for another class, say class (for and ) is greater than a threshold (say, ), i.e., if then we are allowing to generate a synthetic object of class provided is of minor class. In this case, we create a new object of class from and the representative object of cluster . Thus we create one object from for each class where and are of minor class.
- is minor class: Here, object is of minor class. Let for number of clusters. Then for each of these number of clusters, say, , a new object , for of class is created. So, if there is u number of objects in of minor classes, then the total number of new objects created is .
| Algorithm 3: Oversampling(). |
| Input: , and /* is a dimensional object, and is the representative of the set of objects of class */ Output: , the generated object Let ; Let ; ; ; ; ; return ; |
4. Result and Discussion
Comparison with Other Methods
- SMOTE (Chawla et al. [11]): A well-known oversampling method for uneven data files produced novel minority instances by linear interpolation in the middle of the adjoining points to make the classes even. Random Forest classifier was used on the balanced data file.
- OSM (Lee and Kim [59]): The support vector machine was modified with fuzzy and KNN algorithm as an Overlap-sensitive margin (OSM) to deal with the uneven and overlying datasets.
- OC-SVM (Schölkopf et al. [60]): With the single-class learning method, only minority samples were trained without considering the majority samples. Suitable for severely imbalanced datasets.
- NB-Tomek (Vuttipittayamongkol and Elyan [61]): Here, the majority-class elements were removed from the overlapping area and prevented the excess data removal, which could lead to greater information loss.
- Hybrid(AE+ANN) (Zhenchuan Li [20]): They had found out the overlapping subset. Since this subset had a low imbalanced ratio, a non-linear classifier was used to distinguish datasets.
- Kokkotis et al. [62] developed reliable machine learning (ML) prediction models for stroke disease and coped with a typical severe class imbalance problem. The effectiveness of the proposed ML approach was investigated with well-known classifiers Random Forest(RF), Logistic Regression(LR), Multilayer Perceptron(MLP), XGBoost, Support Vector Machine(SVM), and K-nearest Neighbours(KNN). We have taken the LR model performance for comparison, as it provides the best results.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Priscilla, C.V.; Prabha, D.P. Influence of optimizing xgboost to handle class imbalance in credit card fraud detection. In Proceedings of the 2020 Third International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 20–22 August 2020; pp. 1309–1315. [Google Scholar]
- Rousso, R.; Katz, N.; Sharon, G.; Glizerin, Y.; Kosman, E.; Shuster, A. Automatic recognition of oil spills using neural networks and classic image processing. Water 2022, 14, 1127. [Google Scholar] [CrossRef]
- Rodda, S.; Erothi, U.S.R. Class imbalance problem in the network intrusion detection systems. In Proceedings of the 2016 International Conference on Electrical, Electronics, and Optimization Techniques (ICEEOT), Chennai, India, 3–5 March 2016; pp. 2685–2688. [Google Scholar]
- Song, Y.; Peng, Y. A MCDM-based evaluation approach for imbalanced classification methods in financial risk prediction. IEEE Access 2019, 7, 84897–84906. [Google Scholar] [CrossRef]
- Liu, Y.; Loh, H.T.; Sun, A. Imbalanced text classification: A term weighting approach. Expert Syst. Appl. 2009, 36, 690–701. [Google Scholar] [CrossRef]
- Tao, X.; Li, Q.; Guo, W.; Ren, C.; He, Q.; Liu, R.; Zou, J. Adaptive weighted over-sampling for imbalanced datasets based on density peaks clustering with heuristic filtering. Inf. Sci. 2020, 519, 43–73. [Google Scholar] [CrossRef]
- Tasci, E.; Zhuge, Y.; Camphausen, K.; Krauze, A.V. Bias and Class Imbalance in Oncologic Data—Towards Inclusive and Transferrable AI in Large Scale Oncology Data Sets. Cancers 2022, 14, 2897. [Google Scholar] [CrossRef]
- Vo, M.T.; Vo, A.H.; Nguyen, T.; Sharma, R.; Le, T. Dealing with the class imbalance problem in the detection of fake job descriptions. Comput. Mater. Contin. 2021, 68, 521–535. [Google Scholar] [CrossRef]
- Jang, J.; Kim, Y.; Choi, K.; Suh, S. Sequential targeting: A continual learning approach for data imbalance in text classification. Expert Syst. Appl. 2021, 179, 115067. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, D.; Cai, Y.; Wang, R.; Chen, F. A hybrid method based on ensemble WELM for handling multi class imbalance in cancer microarray data. Neurocomputing 2017, 266, 641–650. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Ramentol, E.; Caballero, Y.; Bello, R.; Herrera, F. Smote-rs b*: A hybrid preprocessing approach based on oversampling and undersampling for high imbalanced data-sets using smote and rough sets theory. Knowl. Inf. Syst. 2012, 33, 245–265. [Google Scholar] [CrossRef]
- Xu, Z.; Shen, D.; Nie, T.; Kou, Y.; Yin, N.; Han, X. A cluster-based oversampling algorithm combining SMOTE and k-means for imbalanced medical data. Inf. Sci. 2021, 572, 574–589. [Google Scholar] [CrossRef]
- Srinilta, C.; Kanharattanachai, S. Application of natural neighbor-based algorithm on oversampling smote algorithms. In Proceedings of the 2021 7th International Conference on Engineering, Applied Sciences and Technology (ICEAST), Bangkok, Thailand, 1–3 April 2021; pp. 217–220. [Google Scholar]
- Mishra, P.; Biancolillo, A.; Roger, J.M.; Marini, F.; Rutledge, D.N. New data preprocessing trends based on ensemble of multiple preprocessing techniques. TrAC Trends Anal. Chem. 2020, 132, 116045. [Google Scholar] [CrossRef]
- Hasib, K.M.; Iqbal, M.; Shah, F.M.; Mahmud, J.A.; Popel, M.H.; Showrov, M.; Hossain, I.; Ahmed, S.; Rahman, O. A survey of methods for managing the classification and solution of data imbalance problem. arXiv 2020, arXiv:2012.11870. [Google Scholar]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef]
- Sharma, A.; Singh, P.K.; Chandra, R. SMOTified-GAN for class imbalanced pattern classification problems. IEEE Access 2022, 10, 30655–30665. [Google Scholar] [CrossRef]
- Srinivasan, R. Sentimental analysis from imbalanced code-mixed data using machine learning approaches. Distrib. Parallel Databases 2021, 41, 1573–7578. [Google Scholar] [CrossRef]
- Li, Z.; Huang, M.; Liu, G.; Jiang, C. A hybrid method with dynamic weighted entropy for handling the problem of class imbalance with overlap in credit card fraud detection. Expert Syst. Appl. 2021, 175, 114750. [Google Scholar] [CrossRef]
- Lee, J.; Park, K. GAN-based imbalanced data intrusion detection system. Pers. Ubiquitous Comput. 2021, 25, 121–128. [Google Scholar] [CrossRef]
- Banerjee, A.; Bhattacharjee, M.; Ghosh, K.; Chatterjee, S. Synthetic minority oversampling in addressing imbalanced sarcasm detection in social media. Multimed. Tools Appl. 2020, 79, 35995–36031. [Google Scholar] [CrossRef]
- Shafqat, W.; Byun, Y.C. A Hybrid GAN-Based Approach to Solve Imbalanced Data Problem in Recommendation Systems. IEEE Access 2022, 10, 11036–11047. [Google Scholar] [CrossRef]
- Yafooz, W.M.; Alsaeedi, A. Sentimental Analysis on Health-Related Information with Improving Model Performance using Machine Learning. J. Comput. Sci. 2021, 17, 112–122. [Google Scholar] [CrossRef]
- Suh, S.; Lee, H.; Lukowicz, P.; Lee, Y.O. CEGAN: Classification Enhancement Generative Adversarial Networks for unraveling data imbalance problems. Neural Netw. 2021, 133, 69–86. [Google Scholar] [CrossRef]
- Imran, A.S.; Yang, R.; Kastrati, Z.; Daudpota, S.M.; Shaikh, S. The impact of synthetic text generation for sentiment analysis using GAN based models. Egypt. Inform. J. 2022, 23, 547–557. [Google Scholar] [CrossRef]
- Mollas, I.; Chrysopoulou, Z.; Karlos, S.; Tsoumakas, G. ETHOS: A multi-label hate speech detection dataset. Complex Intell. Syst. 2022, 8, 4663–4678. [Google Scholar] [CrossRef]
- Chen, H.; Li, T.; Fan, X.; Luo, C. Feature selection for imbalanced data based on neighborhood rough sets. Inf. Sci. 2019, 483, 1–20. [Google Scholar] [CrossRef]
- Zhang, C.; Bi, J.; Xu, S.; Ramentol, E.; Fan, G.; Qiao, B.; Fujita, H. Multi-imbalance: An open-source software for multi-class imbalance learning. Knowl.-Based Syst. 2019, 174, 137–143. [Google Scholar] [CrossRef]
- Behmanesh, M.; Adibi, P.; Karshenas, H. Weighted least squares twin support vector machine with fuzzy rough set theory for imbalanced data classification. arXiv 2021, arXiv:2105.01198. [Google Scholar]
- Saha, A.; Reddy, J.; Kumar, R. A fuzzy similarity based classification with Archimedean-Dombi aggregation operator. J. Intell Manag. Decis. 2022, 1, 118–127. [Google Scholar] [CrossRef]
- Elreedy, D.; Atiya, A.F. A comprehensive analysis of synthetic minority oversampling technique (SMOTE) for handling class imbalance. Inf. Sci. 2019, 505, 32–64. [Google Scholar] [CrossRef]
- Wei, J.; Huang, H.; Yao, L.; Hu, Y.; Fan, Q.; Huang, D. NI-MWMOTE: An improving noise-immunity majority weighted minority oversampling technique for imbalanced classification problems. Expert Syst. Appl. 2020, 158, 113504. [Google Scholar] [CrossRef]
- Das, B.; Krishnan, N.C.; Cook, D.J. RACOG and wRACOG: Two probabilistic oversampling techniques. IEEE Trans. Knowl. Data Eng. 2014, 27, 222–234. [Google Scholar] [CrossRef] [PubMed]
- Shelke, M.S.; Deshmukh, P.R.; Shandilya, V.K. A review on imbalanced data handling using undersampling and oversampling technique. Int. J. Recent Trends Eng. Res. 2017, 3, 444–449. [Google Scholar]
- Muntasir Nishat, M.; Faisal, F.; Jahan Ratul, I.; Al-Monsur, A.; Ar-Rafi, A.M.; Nasrullah, S.M.; Reza, M.T.; Khan, M.R.H. A comprehensive investigation of the performances of different machine learning classifiers with SMOTE-ENN oversampling technique and hyperparameter optimization for imbalanced heart failure dataset. Sci. Program. 2022, 2022, 3649406. [Google Scholar] [CrossRef]
- Swana, E.F.; Doorsamy, W.; Bokoro, P. Tomek link and SMOTE approaches for machine fault classification with an imbalanced dataset. Sensors 2022, 22, 3246. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Yang, Y.; Li, B. Fuzzy rule-based oversampling technique for imbalanced and incomplete data learning. Knowl.-Based Syst. 2018, 158, 154–174. [Google Scholar] [CrossRef]
- Ren, R.; Yang, Y.; Sun, L. Oversampling technique based on fuzzy representativeness difference for classifying imbalanced data. Appl. Intell. 2020, 50, 2465–2487. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar]
- Yu, H.; Yang, X.; Zheng, S.; Sun, C. Active learning from imbalanced data: A solution of online weighted extreme learning machine. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 1088–1103. [Google Scholar] [CrossRef]
- Seiffert, C.; Khoshgoftaar, T.M.; Van Hulse, J.; Napolitano, A. RUSBoost: Improving classification performance when training data is skewed. In Proceedings of the 2008 19th International Conference on Pattern Recognition, Tampa, FL, USA, 8–11 December 2008; pp. 1–4. [Google Scholar]
- Kazerouni, A.; Zhao, Q.; Xie, J.; Tata, S.; Najork, M. Active learning for skewed data sets. arXiv 2020, arXiv:2005.11442. [Google Scholar]
- Qu, W.; Yan, D.; Sang, Y.; Liang, H.; Kitsuregawa, M.; Li, K. A novel Chi2 algorithm for discretization of continuous attributes. In Proceedings of the Progress in WWW Research and Development: 10th Asia-Pacific Web Conference, APWeb 2008, Shenyang, China, 26–28 April 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 560–571. [Google Scholar]
- Lavangnananda, K.; Chattanachot, S. Study of discretization methods in classification. In Proceedings of the 2017 9th International Conference on Knowledge and Smart Technology (KST), Chonburi, Thailan, 1–4 February 2017; pp. 50–55. [Google Scholar]
- Das, A.K.; Chakrabarty, S.; Pati, S.K.; Sahaji, A.H. Applying restrained genetic algorithm for attribute reduction using attribute dependency and discernibility matrix. In Proceedings of the Wireless Networks and Computational Intelligence: 6th International Conference on Information Processing, ICIP, Bangalore, India, 10–12 August 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 299–308. [Google Scholar]
- Kumar, V.; Minz, S. Feature selection: A literature review. SmartCR 2014, 4, 211–229. [Google Scholar] [CrossRef]
- Basu, S.; Das, S.; Ghatak, S.; Das, A.K. Strength pareto evolutionary algorithm based gene subset selection. In Proceedings of the 2017 International Conference on Big Data Analytics and Computational Intelligence (ICBDAC), Andhra Pradesh, India, 23–25 March 2017; pp. 79–85. [Google Scholar]
- Renigier-Biłozor, M.; Janowski, A.; d’Amato, M. Automated valuation model based on fuzzy and rough set theory for real estate market with insufficient source data. Land Use Policy 2019, 87, 104021. [Google Scholar] [CrossRef]
- Yang, X.; Chen, H.; Li, T.; Luo, C. A noise-aware fuzzy rough set approach for feature selection. Knowl.-Based Syst. 2022, 250, 109092. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhao, H. A fuzzy rough set approach to hierarchical feature selection based on Hausdorff distance. Appl. Intell. 2022, 52, 11089–11102. [Google Scholar] [CrossRef]
- Sengupta, S.; Das, A.K. A study on rough set theory based dynamic reduct for classification system optimization. Int. J. Artif. Intell. Appl. 2014, 5, 35. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, Y.; Yang, J. Feature reduction with inconsistency. Int. J. Cogn. Informatics Nat. Intell. IJCINI 2010, 4, 77–87. [Google Scholar] [CrossRef]
- Ruspini, E.H.; Bezdek, J.C.; Keller, J.M. Fuzzy clustering: A historical perspective. IEEE Comput. Intell. Mag. 2019, 14, 45–55. [Google Scholar] [CrossRef]
- Ding, W.; Chakraborty, S.; Mali, K.; Chatterjee, S.; Nayak, J.; Das, A.K.; Banerjee, S. An unsupervised fuzzy clustering approach for early screening of COVID-19 from radiological images. IEEE Trans. Fuzzy Syst. 2021, 30, 2902–2914. [Google Scholar] [CrossRef]
- Marcot, B.G.; Hanea, A.M. What is an optimal value of k in k-fold cross-validation in discrete Bayesian network analysis? Comput. Stat. 2021, 36, 2009–2031. [Google Scholar] [CrossRef]
- Yadav, S.; Shukla, S. Analysis of k-fold cross-validation over hold-out validation on colossal datasets for quality classification. In Proceedings of the 2016 IEEE 6th International Conference on Advanced Computing (IACC), Bhimavaram, India, 27–28 February 2016; pp. 78–83. [Google Scholar]
- Caelen, O. A Bayesian interpretation of the confusion matrix. Ann. Math. Artif. Intell. 2017, 81, 429–450. [Google Scholar] [CrossRef]
- Lee, H.K.; Kim, S.B. An overlap-sensitive margin classifier for imbalanced and overlapping data. Expert Syst. Appl. 2018, 98, 72–83. [Google Scholar] [CrossRef]
- Schölkopf, B.; Platt, J.C.; Shawe-Taylor, J.; Smola, A.J.; Williamson, R.C. Estimating the support of a high-dimensional distribution. Neural Comput. 2001, 13, 1443–1471. [Google Scholar] [CrossRef] [PubMed]
- Vuttipittayamongkol, P.; Elyan, E. Neighbourhood-based undersampling approach for handling imbalanced and overlapped data. Inf. Sci. 2020, 509, 47–70. [Google Scholar] [CrossRef]
- Kokkotis, C.; Giarmatzis, G.; Giannakou, E.; Moustakidis, S.; Tsatalas, T.; Tsiptsios, D.; Vadikolias, K.; Aggelousis, N. An Explainable Machine Learning Pipeline for Stroke Prediction on Imbalanced Data. Diagnostics 2022, 12, 2392. [Google Scholar] [CrossRef] [PubMed]
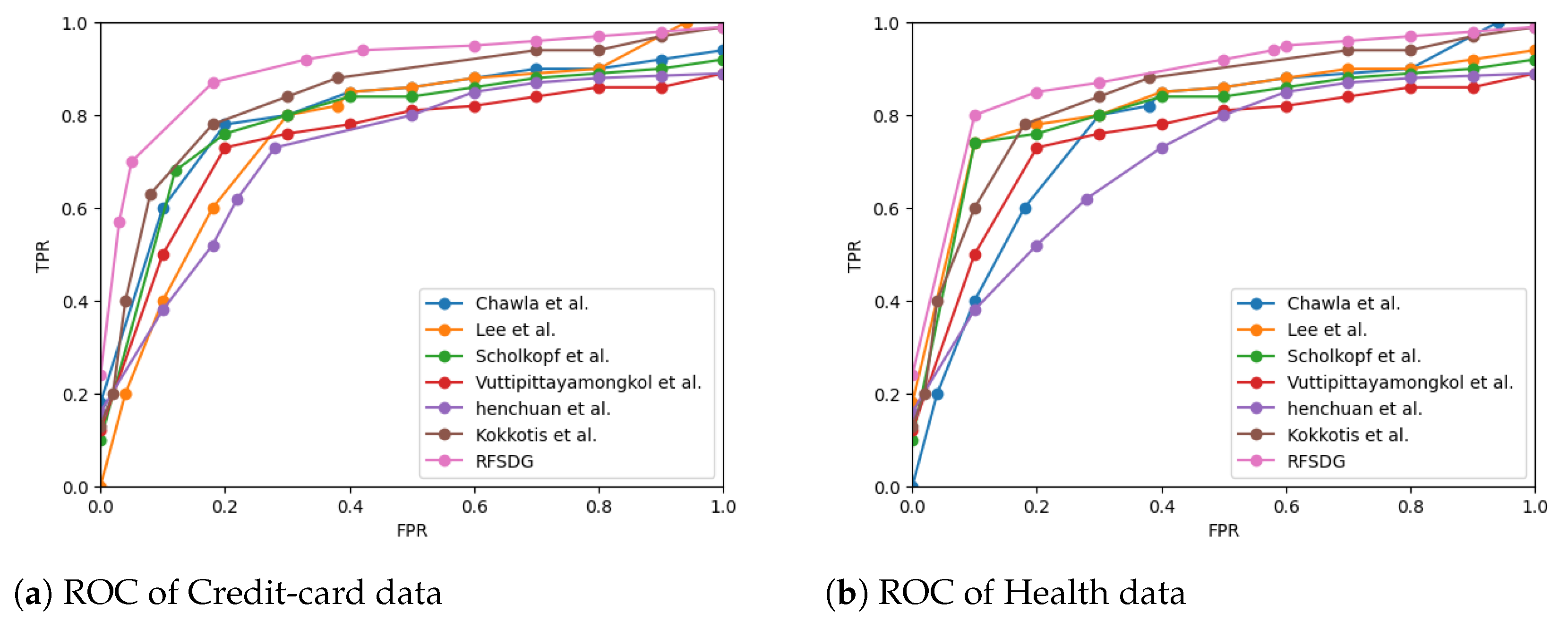
- Hoo, Z.H.; Candlish, J.; Teare, D. What is an ROC curve? Emerg. Med. J. 2017, 34, 357–359. [Google Scholar] [CrossRef]
- Al-shami, T.M. An improvement of rough sets’ accuracy measure using containment neighborhoods with a medical application. Inf. Sci. 2021, 569, 110–124. [Google Scholar] [CrossRef]
- Al-Shami, T.M.; Alshammari, I. Rough sets models inspired by supra-topology structures. Artif. Intell. Rev. 2022, 1–29. [Google Scholar] [CrossRef] [PubMed]
- Szlobodnyik, G.; Farkas, L. Data augmentation by guided deep interpolation. Appl. Soft Comput. 2021, 111, 107680. [Google Scholar] [CrossRef]
- Bayer, M.; Kaufhold, M.A.; Reuter, C. A survey on data augmentation for text classification. ACM Comput. Surv. 2022, 55, 1–39. [Google Scholar] [CrossRef]

| Actual | Predicted | |
|---|---|---|
| Positive | Negative | |
| Positive | True Positive | False Negative |
| Negative | False Positive | True Negative |
| ID (in %) | BO (in %) | BS (in %) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Classifier | A | P | R | F | A | P | R | F | A | P | R | F |
| Naive Bayes | 94 | 21 | 19 | 20 | 82 | 99 | 63 | 77 | 81 | 99 | 59 | 74 |
| Logistic | 95 | - | 0 | - | 82 | 83 | 79 | 81 | 93 | 91 | 95 | 93 |
| MLP | 94 | 16 | 04 | 07 | 87 | 92 | 80 | 86 | 98 | 99 | 95 | 97 |
| SGD | 95 | - | 0 | - | 82 | 81 | 80 | 81 | 96 | 96 | 95 | 95 |
| SimpleLogistic | 95 | - | 0 | - | 82 | 83 | 79 | 81 | 94 | 91 | 95 | 93 |
| SMO | 95 | - | 0 | - | 81 | 81 | 79 | 80 | 95 | 94 | 95 | 95 |
| Voted Perceptron | 95 | - | 0 | - | 79 | 76 | 80 | 78 | 95 | 97 | 93 | 95 |
| IBk | 92 | 14 | 13 | 14 | 92 | 88 | 97 | 92 | 96 | 97 | 95 | 96 |
| KStar | 95 | 15 | 01 | 03 | 90 | 89 | 91 | 90 | 97 | 99 | 95 | 97 |
| AdaBoost | 95 | - | 0 | - | 84 | 84 | 83 | 83 | 95 | 94 | 96 | 95 |
| ASC | 95 | - | 0 | - | 83 | 98 | 64 | 78 | 93 | 90 | 95 | 92 |
| Bagging | 95 | - | 0 | - | 92 | 92 | 91 | 92 | 98 | 99 | 95 | 97 |
| CVR | 95 | - | 0 | - | 90 | 90 | 88 | 89 | 98 | 99 | 95 | 97 |
| FilteredClassifier | 95 | - | 0 | - | 89 | 91 | 86 | 88 | 98 | 99 | 95 | 97 |
| ICO | 95 | - | 0 | - | 87 | 89 | 82 | 85 | 97 | 98 | 95 | 97 |
| LogitBoost | 95 | - | 0 | - | 87 | 89 | 82 | 85 | 97 | 98 | 95 | 97 |
| MCC | 95 | - | 0 | - | 82 | 83 | 79 | 81 | 93 | 91 | 95 | 93 |
| MCC Updateable | 95 | - | 0 | - | 82 | 81 | 80 | 81 | 96 | 96 | 95 | 95 |
| Random Committee | 93 | 11 | 07 | 09 | 93 | 89 | 96 | 92 | 97 | 97 | 95 | 96 |
| RFC | 93 | 07 | 05 | 06 | 92 | 88 | 96 | 92 | 96 | 96 | 96 | 96 |
| RandomSubSpace | 95 | - | 0 | - | 88 | 96 | 77 | 85 | 98 | 99 | 95 | 97 |
| Decision Table | 95 | - | 0 | - | 88 | 91 | 81 | 86 | 97 | 99 | 95 | 97 |
| JRip | 93 | 23 | 02 | 03 | 91 | 91 | 90 | 90 | 98 | 99 | 95 | 97 |
| PART | 95 | 18 | 03 | 06 | 91 | 88 | 93 | 91 | 97 | 99 | 95 | 97 |
| Decision Stump | 95 | - | 0 | - | 80 | 80 | 80 | 80 | 77 | 79 | 78 | 77 |
| HoeffdingTree | 95 | - | 0 | - | 80 | 80 | 80 | 80 | 96 | 97 | 95 | 96 |
| J48 | 95 | - | 0 | - | 92 | 91 | 93 | 92 | 98 | 99 | 95 | 97 |
| LMT | 95 | - | 0 | - | 92 | 90 | 93 | 91 | 98 | 99 | 95 | 97 |
| Random Forest | 94 | 10 | 03 | 05 | 92 | 89 | 95 | 92 | 97 | 99 | 95 | 97 |
| Random Tree | 93 | 15 | 13 | 14 | 92 | 88 | 96 | 92 | 96 | 96 | 96 | 96 |
| REPTree | 95 | 14 | 01 | 01 | 91 | 90 | 91 | 90 | 98 | 99 | 95 | 97 |
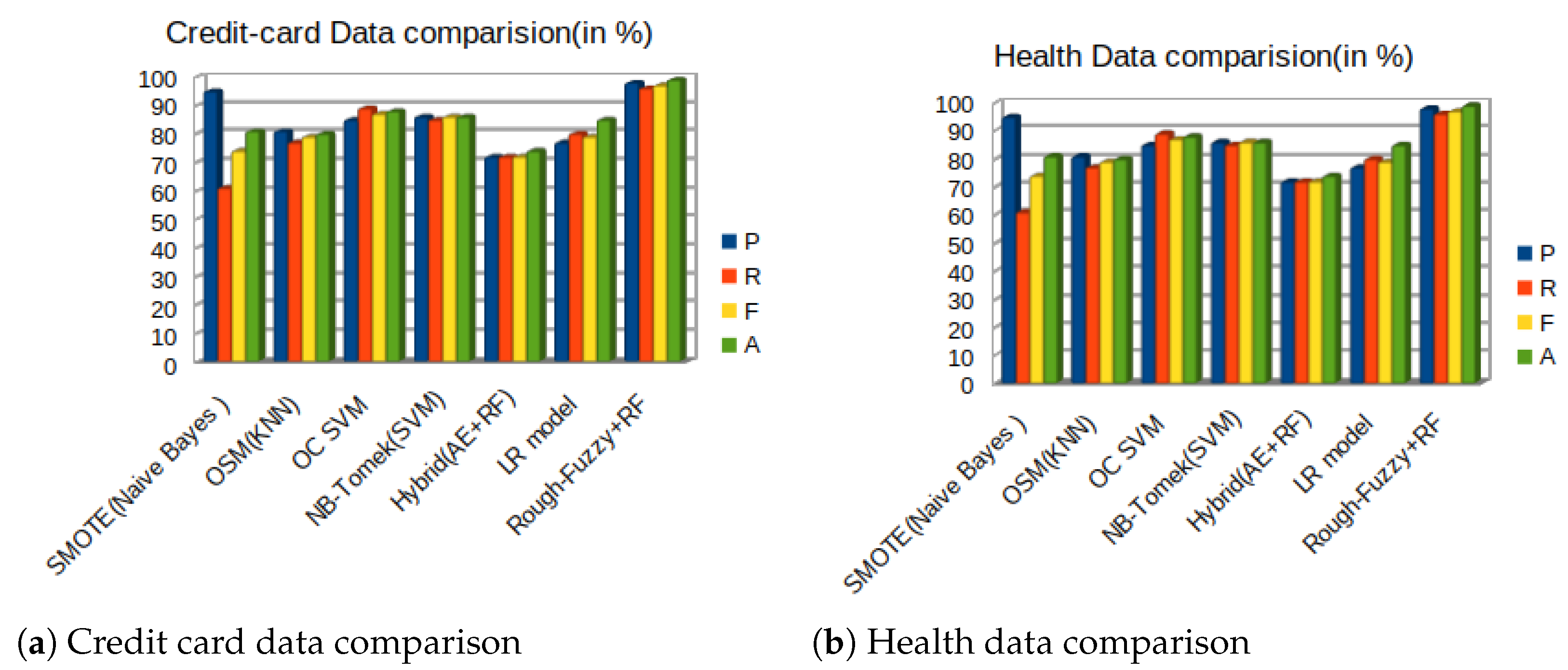
| Model | Method Used | P | R | F | A |
|---|---|---|---|---|---|
| Chawla et al. [11] | SMOTE(Naive Bayes ) | 95 | 61 | 74 | 81 |
| Lee and Kim [59] | OSM(KNN) | 81 | 77 | 79 | 80 |
| Schölkopf et al. [60] | OC SVM | 85 | 89 | 87 | 88 |
| Vuttipittayamongkol and Elyan [61] | NB-Tomek(SVM) | 86 | 85 | 86 | 86 |
| Zhenchuan Li [20] | Hybrid(AE+RF) | 72 | 72 | 72 | 74 |
| Kokkotis et al. [62] | LR model | 77 | 80 | 79 | 85 |
| RFSDG | Rough-Fuzzy+RF | 98 | 96 | 97 | 99 |
| Model | Method Used | P | R | F | A |
|---|---|---|---|---|---|
| Chawla et al. [11] | SMOTE(Naive Bayes ) | 71 | 68 | 69 | 71 |
| Lee and Kim [59] | OSM(KNN) | 79 | 77 | 78 | 78 |
| Schölkopf et al. [60] | OC SVM | 75 | 78 | 77 | 78 |
| Vuttipittayamongkol and Elyan [61] | NB-Tomek(SVM) | 79 | 75 | 77 | 78 |
| Zhenchuan Li [20] | Hybrid(AE+RF) | 60 | 64 | 62 | 64 |
| Kokkotis et al. [62] | LR model | 77 | 78 | 78 | 74 |
| RFSDG | Rough-Fuzzy+RF | 99 | 95 | 97 | 98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naushin, M.; Das, A.K.; Nayak, J.; Pelusi, D. Rough-Fuzzy Based Synthetic Data Generation Exploring Boundary Region of Rough Sets to Handle Class Imbalance Problem. Axioms 2023, 12, 345. https://doi.org/10.3390/axioms12040345
Naushin M, Das AK, Nayak J, Pelusi D. Rough-Fuzzy Based Synthetic Data Generation Exploring Boundary Region of Rough Sets to Handle Class Imbalance Problem. Axioms. 2023; 12(4):345. https://doi.org/10.3390/axioms12040345
Chicago/Turabian StyleNaushin, Mehwish, Asit Kumar Das, Janmenjoy Nayak, and Danilo Pelusi. 2023. "Rough-Fuzzy Based Synthetic Data Generation Exploring Boundary Region of Rough Sets to Handle Class Imbalance Problem" Axioms 12, no. 4: 345. https://doi.org/10.3390/axioms12040345
APA StyleNaushin, M., Das, A. K., Nayak, J., & Pelusi, D. (2023). Rough-Fuzzy Based Synthetic Data Generation Exploring Boundary Region of Rough Sets to Handle Class Imbalance Problem. Axioms, 12(4), 345. https://doi.org/10.3390/axioms12040345








