Abstract
Over the past few decades, a new area of reliability known as classes of life distributions has developed as a result of the creation of metrics for evaluating the success or failure of reliability. This paper proposes a new reliability class-test statistic for life distributions. In some reliability processes, such as convolution, mixture, and homogeneous shock models, the closure characteristics of the proposed class-test statistic are investigated. To compare the proposed class-test against some competitive tests, the Weibull, linear failure rate (LFR), and Makeham distributions are evaluated. In addition, the relationship between sample size, level of confidence, and critical values is considered to assess the efficacy of the proposed class-test. Furthermore, a Monte Carlo null distribution critical points simulation and some applications of the censored and uncensored data are performed to demonstrate the validity of the proposed class-test in reliability analysis.
Keywords:
aging; convolution; Poisson shock model; simulation; goodness-of-fit approach; COVID-19; statistics; numerical data MSC:
62N01; 62N03; 62N05; 62F05; 62F40
1. Introduction
Several reliability analysts and statisticians have shown a strong interest in presenting survival data using rankings of life distributions based on different aging concepts that explain how the number of units or systems improves or deteriorates with age. There are several important types of life distributions used in applications that can be seen in reliability, including bio-metrics, engineering, medical and biological research. It was discovered that the basic distribution of the statistical reliability theory is the exponential distribution; see Mahmoud et al. [1]. Various types of life distributions have been put forward over the past few decades to model different aspects of aging. The most famous of these categories are: increasing failure rate (IFA), increasing failure rate average (IFRA), new better than used (NBU), new better than used in expectation (NBUE), harmonic new better than used in expectation (HNBUE), decreasing mean residual life (DMRL), and new better than renewal used (NBRU). Bryson and Siddiqui [2] and Barlow and Proschan [3] proposed some properties for these aging concepts and their duals, including decreasing failure rate (DFR), decreasing failure rate average (DFRA), new worse than used (NWU), new worse than used in expectation (NWUE). El-Arishy et al. [4] investigated the characterizations and testing hypotheses for decreasing the Laplace transform of the time to failure (DLTTF) class. Abouammoh et al. [5] studied some properties for the NBRU class. Klefsjo [6] introduced some properties for HNBUE and harmonic new worse than used in expectation (HNWUE) classes, and EL-Sagheer et al. [7] introduced characterizations and testing hypotheses for the NBRUL-t class.
Many authors provided tests for the exponentiality of specific types of life distributions based on the Laplace transform approach technique. As an example, Gadallah et al. [8] tested new better than used in the increasing concave order(NBU(2)), Mansour [9] tested the NBU class, and Bakr et al. [10] tested better than aged in the moment generating function order (UBA). For testing exponentiality versus the new better than renewal used in Laplace transform order (NBRUL) class, see Mahmoud et al. [11,12], EL-Sagheer et al. [13], and Kumazawa [14]) for the NBU class. The random variable NBRU, if
whereas the random variable NBRUL, if
or
where and represent the survival function. It is obvious that NBRU NBRUL NBRUE. Based on the goodness-of-fit approach, many authors offered tests for exponentiality against some classes of life distributions. For instance, Kayid et al. [15] tested the new better than used in the increasing concave order “NBU(2)” class, Abu-Youssef and El-Toony [16] tested used better than aged in increasing concave (UBAC(2)L), Mahmoud and Abdul Alim [17] tested new better than used renewal failure rate “NBURFR” and new better than used average renewal failure rate “NBARFR” classes, Bakr et al. [18] tested used better than aged in Laplace “UBAL” transform order, Abu-Youssef and Gerges [19] tested new better than used convex order at the moment generating function “NBUC”, Mahmoud et al. [20] tested renewal new better than used in Laplace transform order “RNBUL”, and Abu-Youssef et al. [21] tested used better than aged in moment generating function “UBA”.
The goal of creating a systematic method for the study of any event and process occurring in the world was forcefully pushed forward by the essential requirements of modern science and technology. It follows that the need for such an approach in the investigation of the issue of the technological product and system reliability is quite natural. There are instances in real life where the system’s components gradually degrade over time t, the amount of time covered by the manufacturer’s warranty, and then there is a need for it to be renewed through the replacement of spare parts. In this case, renewal is intended to enhance the system’s functionality but cannot return it to a superior state than it had at age t. For instance, after several hours of flight, the aviation administration wished to replace a portion of an airplane engine. The airlines contend that this replacement is, at best, unneeded and may potentially be detrimental to the aircraft. Airlines examine if an aviation engine after hours of renewal is as good as a new engine using operational data to support their claim.
We found that there is a lack of test efficiency and a weak test power in the nonparametric tests of life distributions. As a result, in this paper, we have established a brand-new class of life distribution that takes into account the effectiveness and power of the test. This paper can be organized as follows: some definitions for the NBRU and NBRUL classes of life distributions are listed in Section 2. In Section 3, we discuss preservation for the NBRUL class of life distribution under convolution, mixture and homogeneous Poisson shock models. A goodness-of-fit based on a test of exponentiality is discussed against the NBRUL class in Section 4. Section 5 provides the Pitman asymptotic for some life distributions. The power estimates and critical points of the Monte Carlo null distribution are simulated in Section 6. Section 7 deals with data that have been right-censored and tabulates a few critical values. Further, several real data applications are discussed based on the statistical test suggested. Finally, concluding remarks are listed in Section 8.
2. Closure Properties
In this section, the closure characteristics of the NBRUL class under some reliability operations are given as follows.
- 1.
- Property of convolution: The NBRUL class is preserved under convolution, whereThe following example is presented to show that the NWRUL class is not preserved under convolution.Example 1.The convolution of the exponential distribution with itself yields the gamma distribution of order 2: , with strictly increasing failure rate. Thus, is not NWRUL.
- 2.
- Property of mixture: The NWRUL class is preserved under mixture, whereThe following example shows that the NBRUL class is not preserved under mixtures.Example 2.Let “scale parameter” and . Then the failure rate function is which is strictly decreasing; thus, is not NBRUL.
- 3.
- The shock model under a homogeneous Poisson process: Suppose the device is subjected to a series of shocks that occur at random time intervals using the Poisson process with intensity . Further suppose that the device has a probability . From surviving the first shock k, where and . Then, the survival function of the device is given byIf is discrete NBRUL, then is given by (4) is NBRUL, whereFor more details about the proofs of closure properties, see EL-Sagheer et al. [13]).
3. NBRUL Comparative Testing Alternatives
In this section, a test statistic based on the goodness-of-fit approach is presented for testing the null hypothesis the distribution function F is exponential (does not belong to the NBRUL class), against the alternative hypothesis the distribution function is not exponential (belongs to the NBRUL class).
Lemma 1.
Let X be an NBRUL random variable with distribution function F. Then,
where
Proof.
Let be a random sample from a population with distribution F. Based on Lemma 1, “a measure of departure from exponentiality” can be reported as
Under whereas under . The empirical estimate of can be obtained as
To make the test invariant, let which is estimated by , where is the sample mean. Then,
One can note that is an unbiased estimator of . Now, set
and define the symmetric kernel
where in (13) is equivalent to the statistic supplied by the summation over all configurations of .
The following theorem provides a concise statement of the asymptotic normality of .
Theorem 1.
(i) As n, is asymptotically normal with zero mean and variance where
(ii) Under the variance can be expressed as
Proof.
Using standard U-statistics theory (see Lee, [22]) yields
Utilizing (14), and can be formulated as
and
as long as,
Under , , it can be proposed as
□
4. The Pitman Asymptotic Efficiency (PAE) of
In this section, the PAE technique’s effectiveness for the Weibull, near-failure rate (LFR), and Makeham distributions is evaluated using the following probability distributions: (Weibull); (LFR), and (Makeham). The exponential distribution is produced from these distributions by setting for and for and . The PAE of is defined by
where
Hence,
where
Making use of the definition of (20), we have
evaluating (22) at and ,gives
and
Table 1 indicates a comparison of the proposed PAE test with various other tests based on some probability models.

Table 1.
Comparison between PAE test and some competitive tests.
is superior to the alternative tests based on the PAEs. However, EL-Sagheer et al. [12] used the Laplace transform technique with the s and parameters, whereas in our paper, we used the goodness of fit technique with the s parameter only, and the results were as follows: the PAE used by EL-Sagheer et al. [12] is better in the case of Weibull and Makeham distributions, whereas our paper is better in the case of LFR distribution.
5. Critical Points for Monte Carlo Distribution
Using 10,000 size-generated samples with this section simulates the critical points of the Monte Carlo null distribution. We used the Mathematica 12 program for the common exponential distribution.
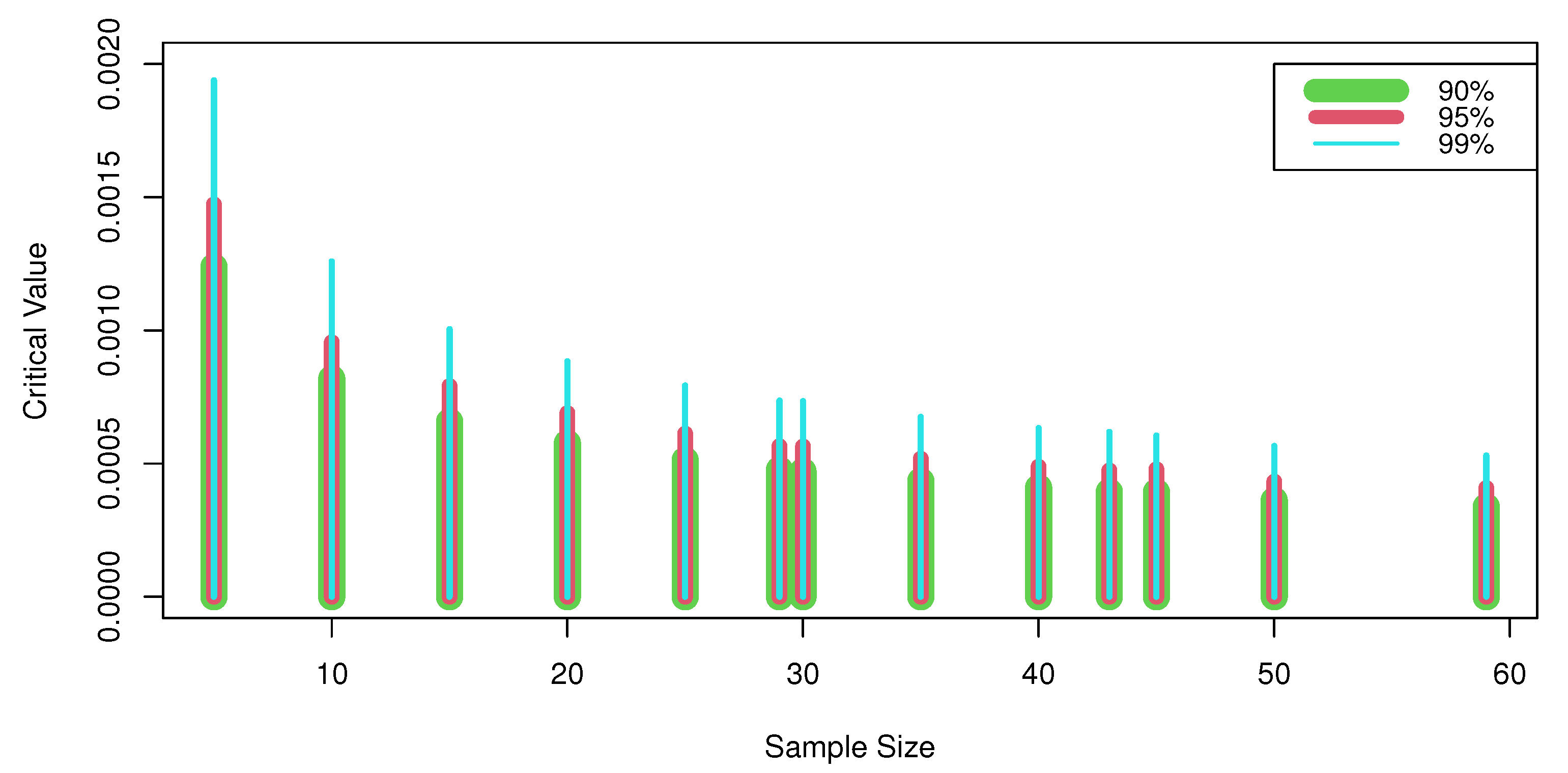
For various levels of confidence, and , Table 2 provides the upper percentile values of statistic . Figure 1 shows our empirical results where the critical values increase with increasing confidence levels and approximately decrease with increasing sample size.

Table 2.
Critical values of the statistic .
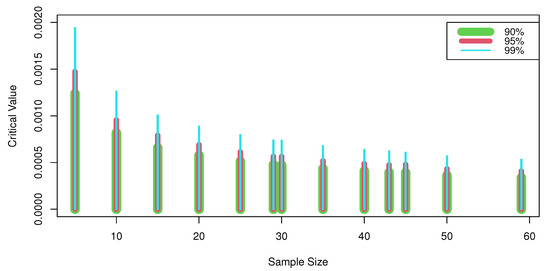
Figure 1.
Relationship between the sample size, the level of confidence, and the critical values.
Estimations of Test Power
For some commonly-used distributions, such as the Weibull and gamma distributions, based on 10,000 samples, the power of the proposed test will be estimated in this section at a confidence level, and appropriate parameter values of at and 30. The results are summarized in Table 3. It is noted that the test’s power estimates are good for all substitutions and rise when increasing the parameter value and sample size.

Table 3.
The power estimates of .
6. Censoring Data Testing
In this section, a test statistic for testing H versus H with randomly right-controlled data is proposed. Such censored data are usually the only information available in a life-test form or in a clinical study where patients may be missed (censored) before the completion of the study. This demo/experimental situation can be formally modeled as follows: suppose n objects are tested, where denote their true lifetime. The lifetimes are independent and identically distributed (i.i.d.) according to a continuous life distribution F. Let be i.i.d. according to a continuous life distribution G. Further, assume X’s and Y’s are independent. In the randomly right-censored model, we observe the pairs where , and
Let denote the ordered Z’s, and is corresponding to Using the censored data Kaplan and Meier [27] proposed the product limit estimator, where
Now, for testing against we propose the following test statistic
where . For computational purposes, may be rewritten as
where
and
To make the test invariant, let
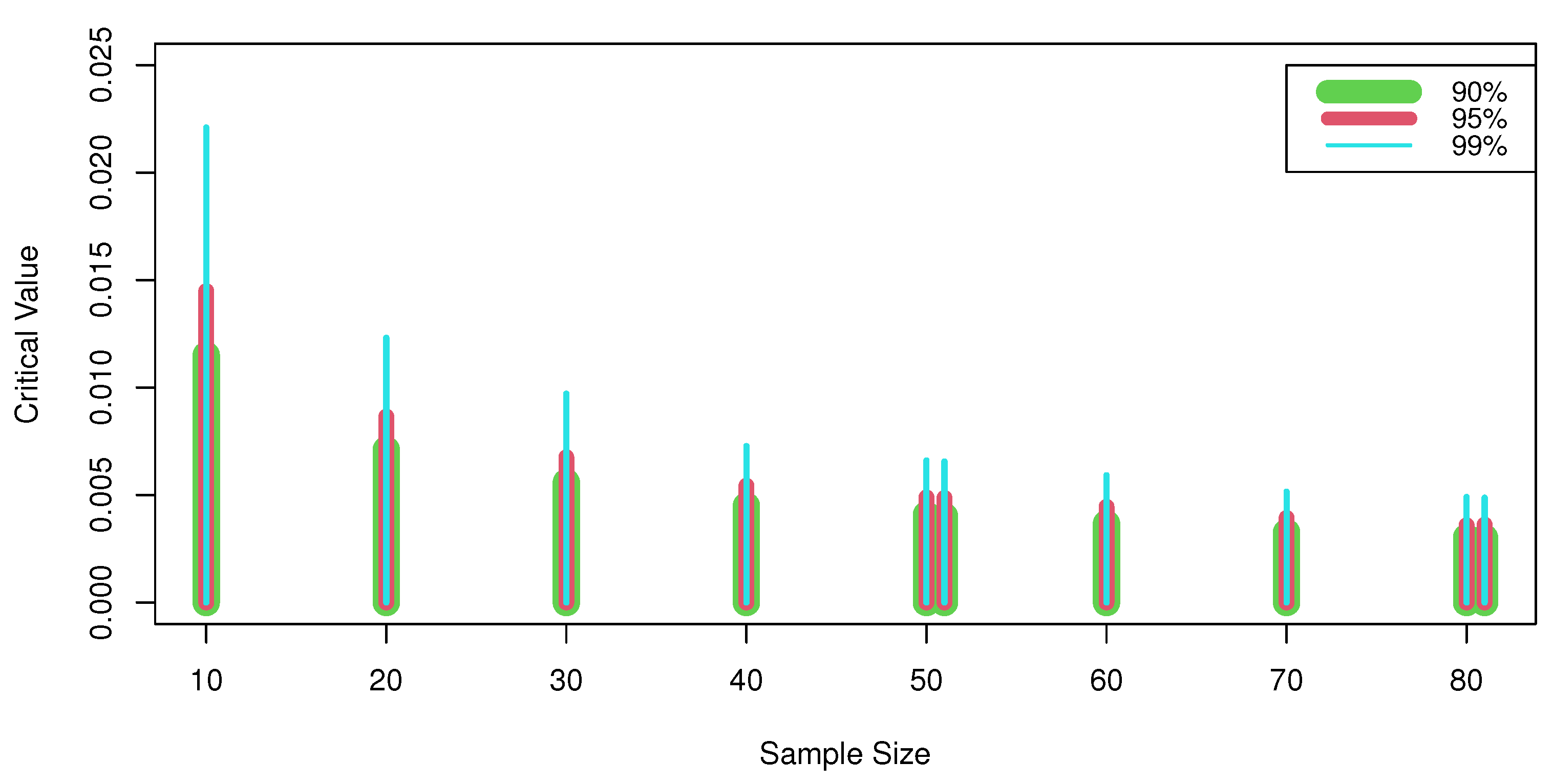
By utilizing the Mathematica 8 software, the common exponential distribution is used to simulate the Monte Carlo null distribution critical values of at for sample sizes of 51, and 81 with 10,000 replications. Table 4 displays the critical value percentile points for the statistic . The critical values rise as the confidence level rises, and they fall as the sample size rises, respectively, as shown in Table 4 and Figure 2.

Table 4.
The upper percentile of at .
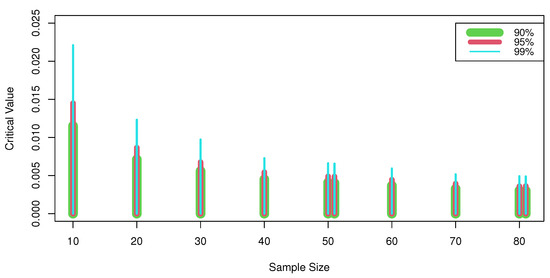
Figure 2.
Relationship between the sample size, the level of confidence, and the critical values.
Test Power Estimates
This section will assess the test’s power at confidence level, , with appropriate parameter values of at and 30, concerning three alternative distributions based on 10,000 samples: Weibull, LFR, and gamma distributions. The results are listed in Table 5. It is clear that the test’s power estimates are good for all substitutions and rise when increasing the parameter value.

Table 5.
Power estimates of .
7. Applications: Uncensored and Censored Observations
In this section, utilizing both censored and uncensored data at a confidence level, the proposed test is applied to a number of applications in the engineering and medical sciences.
7.1. Uncensored Data
7.1.1. Data Set I: COVID-19-Italy
The COVID-19 death rate in Italy from 27 February 2020, to 27 April 2020 is represented in this data set (see Almongy et al. [28]). The data set size is 622.
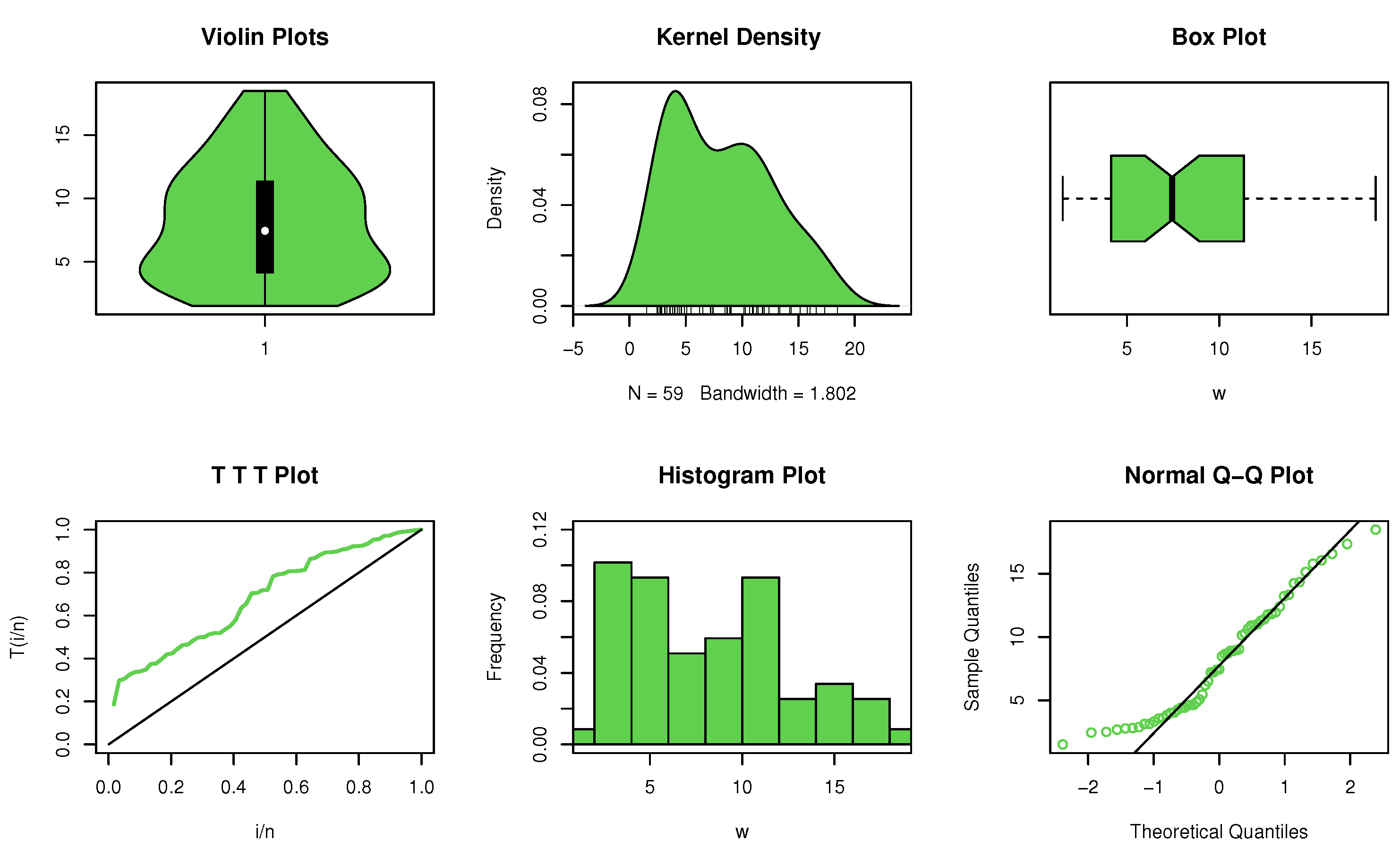
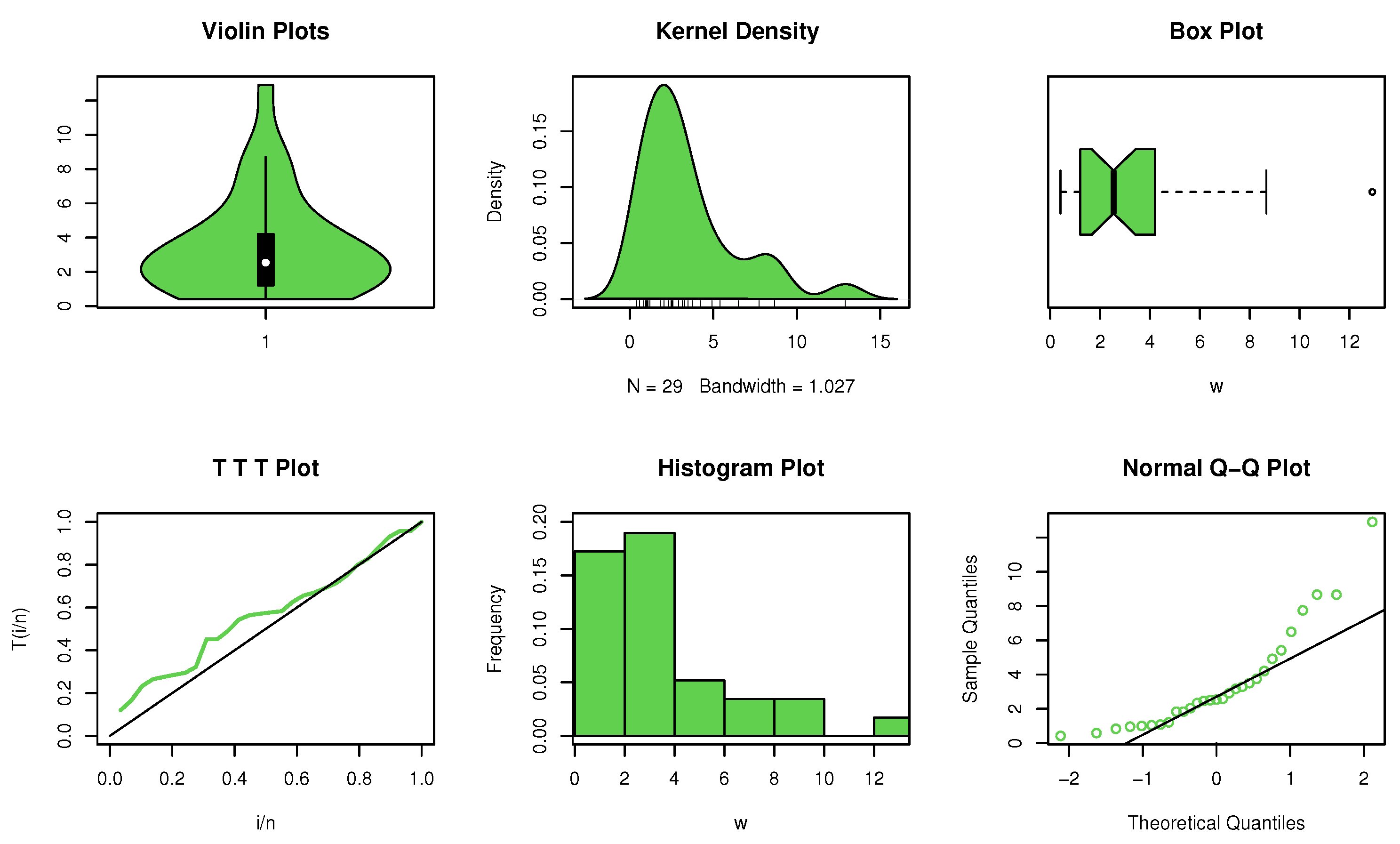
Non-parametric plots are required to discuss the shape of the data set (see Figure 3). The data display an asymmetric dimorphic shape with no extreme observations. In this example, the value shown in Table 2 is less than , indicating that the data set has the property NBRUL.
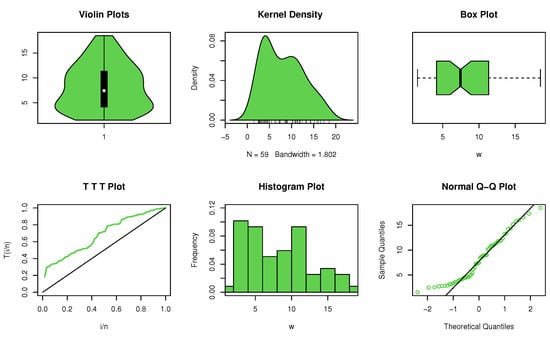
Figure 3.
Non-parametric plots for data set I.
7.1.2. Data Set II: COVID-19-Netherlands
This data set represents a COVID-19 mortality rate in the Netherlands from 31 March to 30 April 2020 (see, EL-Sagheer et al. [29]). The data set is as follows
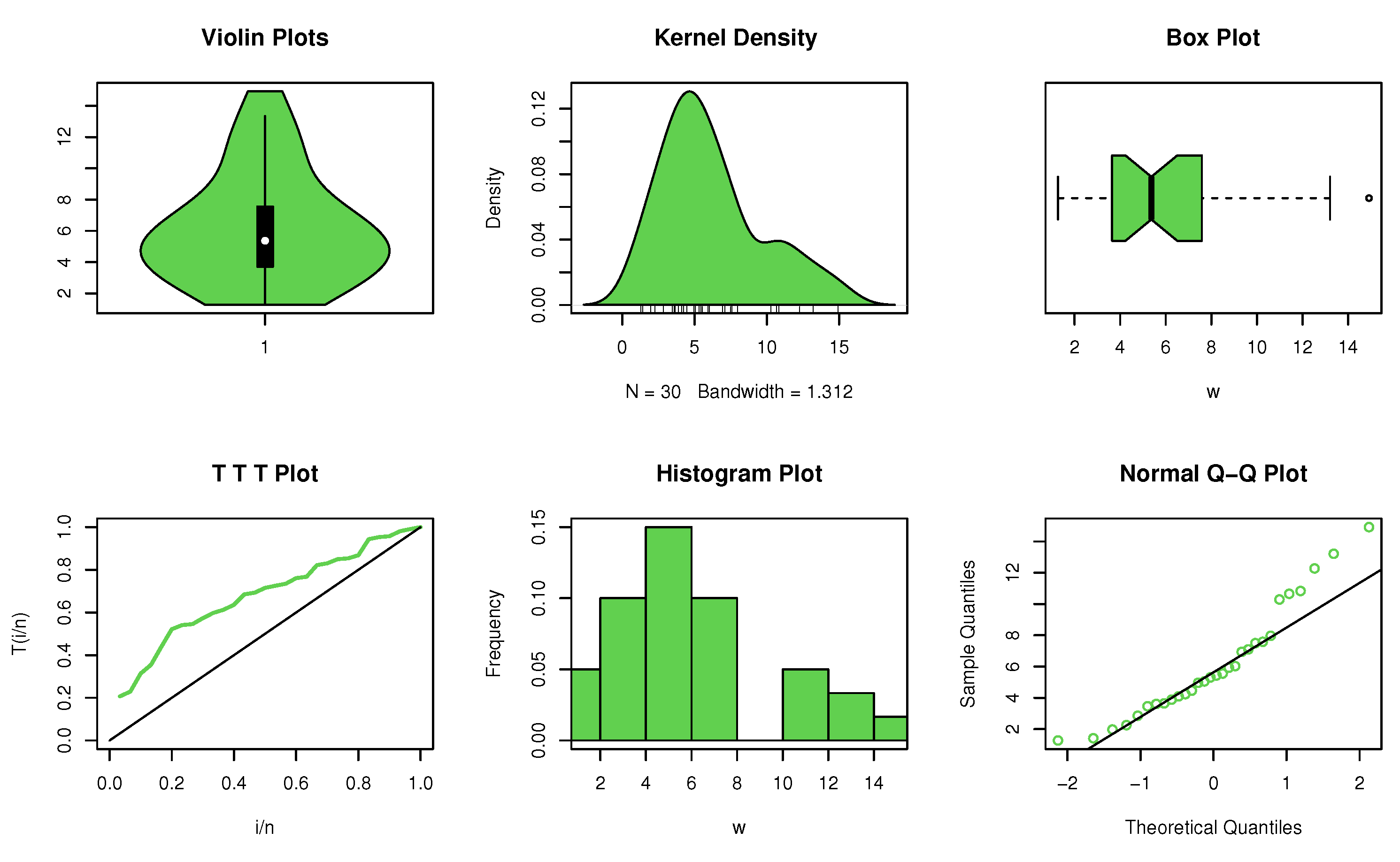
It is clear from the non-parametric plots in Figure 4 that the data has an asymmetric dimorphic with an extreme observation. In addition, the data set has the property NBRUL since is higher than the critical value displayed in Table 2 at a 95% confidence level.
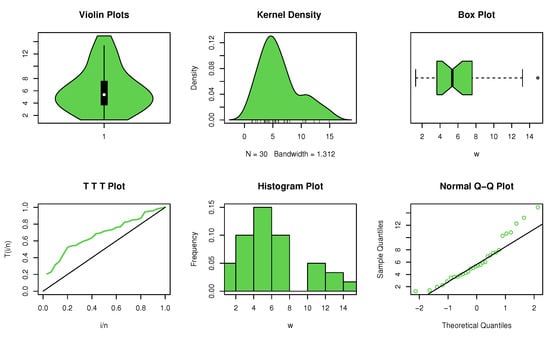
Figure 4.
Non-parametric plots for data set II.
7.1.3. Data Set III: Aircraft Air Conditioning
Consider the classical real data in the study by Keating et al. [30], which were specified at times on operating days between successive malfunctions of the aircraft’s air conditioning equipment. This data set is recorded as
According to the non-parametric plots (see Figure 5), it is noted that the data have an asymmetric multimodal with an extreme observation. In this case, is more than the critical value indicated in Table 2 at a 95% confidence level. Then, we disregard H, which asserts that the dataset exhibits an exponential property.
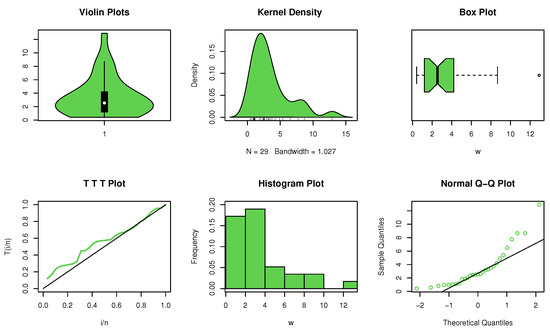
Figure 5.
Non-parametric plots for data set III.
7.1.4. Data Set IV: Leukemia
We take into account the data set in the study by Kotz and Johnson [31], which shows the post-diagnosis survival times (in years) of 43 individuals with a particular type of leukemia.
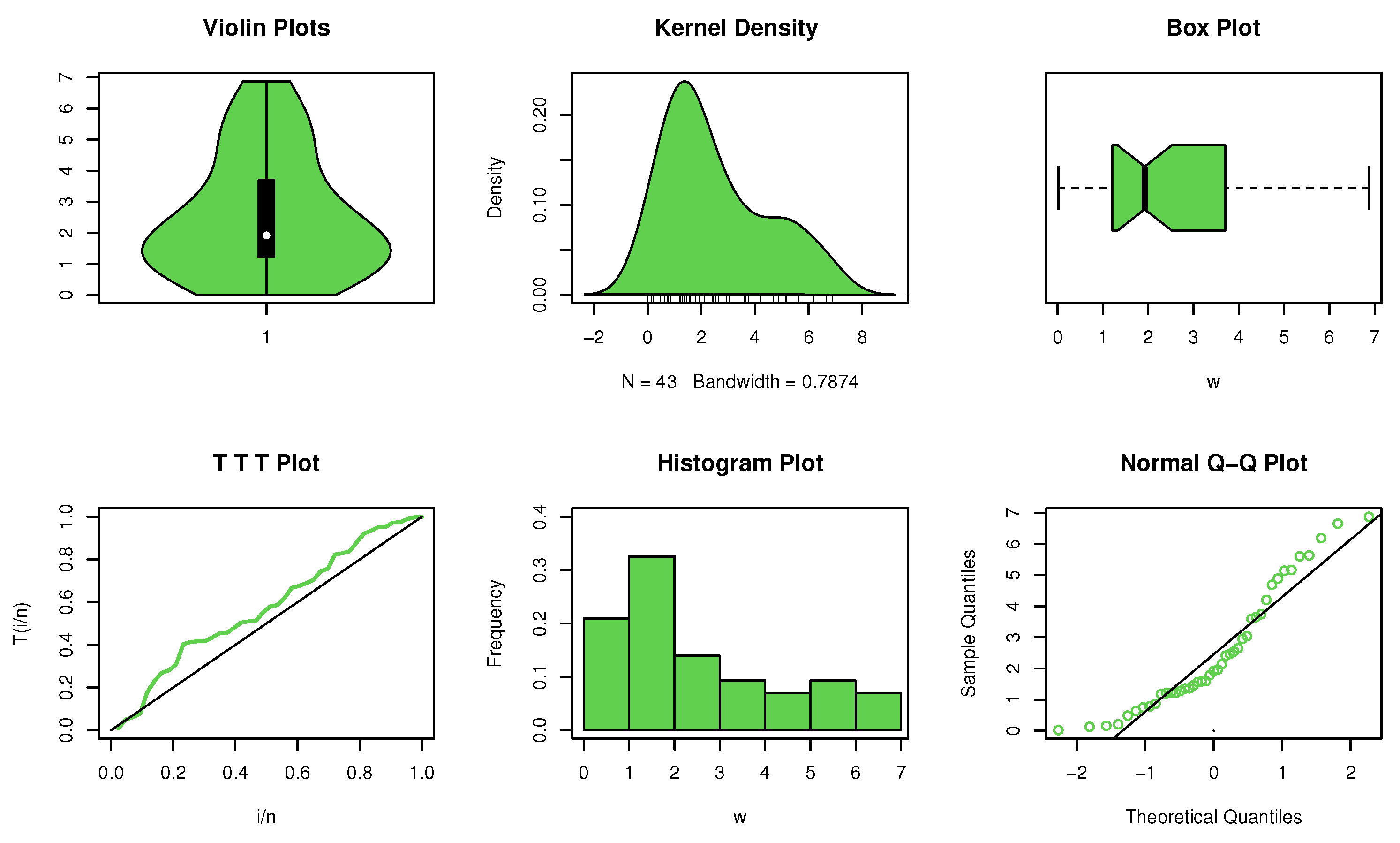
The data set contains a binary form in an asymmetric shape with no extreme values, as shown by the non-parametric plots (see Figure 6). At a 95% level of confidence, it is evident that is higher than the equivalent critical value in Table 2. Therefore, the NBRUL property applies to this data set.
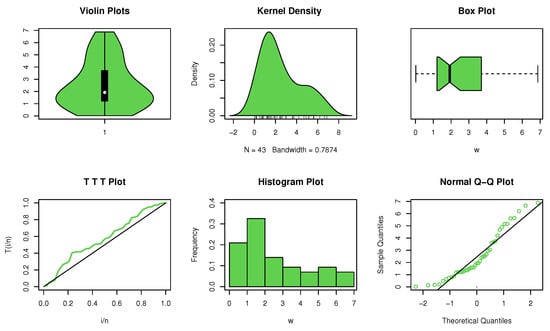
Figure 6.
Non-parametric plots for data set IV.
7.2. Censored Data
7.2.1. Data Set V: Melanoma Patients
Consider the data set in the study by Susarla and Van Ryzin [32], which displays the survival rates of 46 melanoma patients, 35 of which correspond to entire lifetimes (non-censored data). The order of the non-censored observations is given by
whereas the censored observations are ordered as follows
| 13 | 14 | 19 | 19 | 20 | 21 | 23 | 23 | 25 | 26 | 26 | 27 |
| 27 | 31 | 32 | 34 | 34 | 37 | 38 | 38 | 40 | 46 | 50 | 53 |
| 54 | 57 | 58 | 59 | 60 | 65 | 65 | 66 | 70 | 85 | 90 | 98 |
| 102 | 103 | 110 | 118 | 124 | 130 | 136 | 138 | 141 | 234 |
| 16 | 21 | 44 | 50 | 55 | 67 | 73 | 76 | 80 | 81 | 86 | 93 |
| 100 | 108 | 114 | 120 | 124 | 125 | 129 | 130 | 132 | 134 | 140 | 147 |
| 148 | 151 | 152 | 152 | 158 | 181 | 190 | 193 | 194 | 213 | 215 |
In this example, is obtained by considering the entire set of survival data, both censored and uncensored. As shown in Table 4, this result is below the critical value, indicating that the data has exponential properties.
7.2.2. Data Set VI: Blood Cancer
The International Bone Marrow Transplant Registry received 101 reports from patients with advanced acute myelogenous blood malignancy (see Ghitany and Al-Awadhi [33] for further information). In order to restore their immune systems, 50 of these patients experienced an allogeneic bone marrow transplant using the marrow of histocompatibility leukocyte antigen (HLA) matched sibling. After receiving high doses of chemotherapy, 51 individuals experienced a tautologous bone marrow transplant in which their marrow was re-infused to restore their immune systems. The 50 allogeneic transplant patients’ leukemia-free survival times (in months) that represent censored observations are as follows
In the case of the complete set of survival data, which includes both censored and uncensored data, is smaller than the critical value mentioned in Table 4 at the confidence level of Therefore, is accepted, which claims that the data set has exponential properties. For the 51 autologous transplant recipients, the leukemia-free survival periods were (in months)
Taking into account the complete set of survival data (both censored and uncensored) yielded The data set meets the NBRUL property requirements since the value is higher than the critical value in Table 4.
8. Conclusions
This paper introduces a new reliability class-test statistic. The closure characteristics of the new class-test statistic have been discussed using some reliability processes, such as convolution, mixture, and homogeneous shock models. The Weibull, near-failure rate (LFR), and Makeham distributions were evaluated to compare the new class-test to some competitive tests, and a new hypothesis test based on the goodness-of-fit approach was suggested. In order to assess the effectiveness of the new class-test, a Monte Carlo null distribution critical points simulation was performed, and the relationship between sample size, level of confidence, and critical values was considered. For different levels of confidence, and , the upper percentile values of the statistic increase with increasing levels of confidence and nearly drop with growing levels of sample size.
In order to demonstrate the validity of the proposed class-test, some applications in medical and engineering fields are discussed. In both censored and uncensored scenarios, if the value is lower than the critical value at a level of confidence, the data have exponential properties; however, if the value is greater than the critical value at a level of confidence, the data have NBRUL properties. For all substitutions, it is clear that test power estimates are significant and increase when increasing the parameter value.
In future work, we aim to study the problem of testing exponentiality against the NBRUL class based on the Kernel method, defining another class of life distributions, such as NBRUL-t (new better than renewal used in Laplace transform order after a specific time t). We also aim to study the problem of testing exponentiality against these classes from different points of view.
Author Contributions
Conceptualization, W.B.E.; Methodology, W.B.E., R.M.E.-S. and M.S.E.; Software, W.B.E., M.E.-M. and M.S.E.; Validation, M.E.-M.; Formal analysis, M.S.E., R.M.E.-S. and A.A.; Investigation, R.M.E.-S.; Resources, M.E.-M. and A.A.; Data curation, M.S.E. and M.E.-M.; Writing—original draft, W.B.E. and R.M.E.-S.; Writing—review & editing, M.S.E. and A.A.; Supervision, R.M.E.-S. and M.E.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This study is supported via funding from Prince Sattam bin Abdulaziz University, project number (PSAU/2023/R/1444).
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mahmoud, M.A.W.; Abdul Alim, N.A.; Mansour, M.M.M. Testing exponentiality against exponential better than used in Laplace transform order based on goodness of fit approach. Al Azhar Bull. Sci. 2014, 25, 1–6. [Google Scholar]
- Bryson, M.C.; Siddiqui, M.M. Some criteria for aging. J. Am. Stat. Assoc. 1969, 64, 1472–1483. [Google Scholar] [CrossRef]
- Barlow, R.E.; Proschan, F. Statistical Theory of Reliability and Life Testing; Hold, Reinhart and Wiston, Inc.: Silver Spring, MD, USA, 1981. [Google Scholar]
- El-Arishy, S.M.; Diab, L.S.; El-Atfy, E.S. Characterizations on decreasing Laplace transform of time to failure class and hypotheses testing. J. Comput. Sci. Comput. 2020, 10, 49–54. [Google Scholar] [CrossRef]
- Abouammoh, A.M.; Qamber, I.S. New better than renewal-used classes of life distributions. IEEE Trans. Reliab. 2003, 52, 150–153. [Google Scholar] [CrossRef]
- Klefsjo, B. The HNBUE and HNWUE classes of life distributions. Nav. Res. Logist. 1982, 29, 331–344. [Google Scholar] [CrossRef]
- EL-Sagheer, R.M.; Mahmoud, M.A.W.; Etman, W.B.H. Characterizations and testing hypotheses for NBRUL-t∘ class of life distributions. J. Stat. Theory Pract. 2022, 16, 31. [Google Scholar] [CrossRef]
- Gadallah, A.M.; Mohammed, B.I.; Al-Babtain, A.A.; Khosa, S.K.; Kilai, M.; Yusuf, M.; Bakr, M.E. Modeling various survival distributions using a nonparametric hypothesis testing based on Laplace transform approach with some real applications. Comput. Math. Methods Med. 2022, 2022, 5075716. [Google Scholar] [CrossRef] [PubMed]
- Mansour, M.M.M. Assessing treatment methods via testing exponential property for clinical data. J. Stat. Probab. 2022, 11, 109–113. [Google Scholar]
- Bakr, M.E.; Nagy, M.; Al-Babtain, A.A.; Khosa, S.K. Statistical modeling of some cancerous diseases using the Laplace transform approach of basic life testing issues. Comput. Math. Med. 2022, 2022, 8964869. [Google Scholar] [CrossRef]
- Mahmoud, M.A.W.; EL-Sagheer, R.M.; Etman, W.B.H. Testing exponentiality against new better than renewal used in Laplace transform order. J. Stat. Appl. Probab. 2016, 5, 279–285. [Google Scholar] [CrossRef]
- Mahmoud, M.A.W.; EL-Sagheer, R.M.; Etman, W.B.H. Moments inequalities for NBRUL distributions with hypotheses testing applications. Austrian J. Stat. 2018, 47, 95–104. [Google Scholar]
- EL-Sagheer, R.M.; Abu-Youssef, S.E.; Sadek, A.; Omar, K.M.; Etman, W.B.H. Characterrization and testing NBRUL class of life distributions based on Laplace transform technique. J. Stat. Appl. Probab. 2022, 11, 1–14. [Google Scholar]
- Kumazawa, Y. A class of tests statistics for testing whether new is better than used. Commun.-Stat.-Theory Methods 1983, 12, 311–321. [Google Scholar] [CrossRef]
- Kayid, M.; Diab, L.S.; Alzughaibi, A. Testing NBU (2) class of life distribution based on goodness of fit approach. J. King Saud-Univ.-Sci. 2010, 22, 241–245. [Google Scholar] [CrossRef]
- Abu-Youssef, S.E.; El-Toony, A.A. A new class of life distribution based on Laplace transform and It’s applications. Inf. Sci. Lett. 2022, 11, 355–362. [Google Scholar]
- Mahmoud, M.A.W.; Abdul Alim, N.A. A goodness of fit approach to NBURFR and NBARFR classes. Econ. Qual. Control 2006, 21, 59–75. [Google Scholar] [CrossRef]
- Bakr, M.E.; Nagy, M.; Al-Babtain, A.A. Non-parametric hypothesis testing to model some cancers based on goodness of fit. AIMS Math. 2022, 7, 13733–13745. [Google Scholar] [CrossRef]
- Abu-Youssef, S.E.; Gerges, S.T. Based on the goodness of fit approach, a new test statistics for testing NBUCmgf class of life distributions. Pak. J. Stat. 2022, 38, 129–144. [Google Scholar]
- Mahmoud, M.A.W.; Diab, L.S.; Radi, D.M. Testing exponentiality against RNBUL class of life distribution based on goodness of fit. J. Stat. Appl. Probab. 2019, 8, 57–66. [Google Scholar] [CrossRef]
- Abu-Youssef, S.E.; Ali, N.S.A.; Bakr, M.E. Used better than aged in mgf ordering class of life distribution with application of hypothesis testing. J. Stat. Appl. Probab. 2020, 7, 23–32. [Google Scholar]
- Lee, A.J. U-Statistics; Marcel-Dekker: New York, NY, USA, 1989. [Google Scholar]
- Mugdadi, A.R.; Ahmad, I.A. Moment inequalities derived from comparing life with its equilibrium form. J. Stat. Inference 2005, 134, 303–317. [Google Scholar] [CrossRef]
- Kango, A.I. Testing for new is better than used. Commun.-Stat.-Theory Methods 1993, 12, 311–321. [Google Scholar]
- Abdel Aziz, A.A. On testing exponentiality against RNBRUE alternatives. Appl. Math. Sci. 2007, 1, 1725–1736. [Google Scholar]
- Etman, W.B.H.; EL-Sagheer, R.M.; Abu-Youssef, S.E.; Sadek, A. On some characterizations to NBRULC class with hypotheses testing application. Appl. Math. Inf. Sci. 2022, 16, 139–148. [Google Scholar]
- Kaplan, E.L.; Meier, P. Nonparametric estimation from incomplete observations. J. Am. Stat. 1958, 53, 457–481. [Google Scholar] [CrossRef]
- Almongy, H.M.; Almetwally, E.M.; Aljohani, H.M.; Alghamdi, A.S.; Hafez, E.H. A new extended rayleigh distribution with applications of COVID-19 data. Results Phys. 2021, 23, 104012. [Google Scholar] [CrossRef] [PubMed]
- EL-Sagheer, R.M.; Eliwa, M.S.; Alqahtani, K.M.; EL-Morshedy, M. Asymmetric randomly censored mortality distribution: Bayesian framework and parametric bootstrap with application to COVID-19 data. J. Math. 2022, 2022, 8300753. [Google Scholar] [CrossRef]
- Keating, J.P.; Glaser, R.E.; Ketchum, N.S. Testing hypotheses about the shape parameter of a gamma distribution. Technometrics 1990, 32, 67–82. [Google Scholar] [CrossRef]
- Kotz, S.; Johnson, N.L. Encyclopedia of Statistical Sciences; John Wiley and Sons: New York, NY, USA, 1983; 613p. [Google Scholar]
- Susarla, V.; Van Ryzin, J. Empirical bayes estimation of a distribution (survival) function from right censored observations. Ann. Stat. 1978, 6, 740–754. [Google Scholar] [CrossRef]
- Ghitany, M.E.; Al-Awadhi, S. Maximum likelihood estimation of Burr XII distribution parameters under random censoring. J. Appl. Stat. 2002, 29, 955–965. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).