1. Introduction
In December 2019, the World Health Organization wrote about the existence of a new virus: SARS-CoV-2, which causes the COVID-19 disease. Some of its common symptoms are fever, dry cough, and tiredness. Measures to prevent the spread of COVID-19 include physical distancing from other people, face masks, washing one’s hands periodically, and covering one’s mouth with a flexed elbow or a handkerchief when coughing. As of 11 September 2022, 605 million confirmed cases and 6.4 million deaths have been reported worldwide.
However, the vaccine against this virus is already available. Vaccination of inhabitants seems to be the safest and most effective way to control the COVID-19 pandemic. In the Ref. [
1], the authors state that a single dose of vaccine can be a drop in the ocean, but several doses together can save a population.
During the worst of the pandemic and up to this day, there has been high acceptance of the COVID-19 vaccine, and strong demand for it. This is the main reason for designing appropriate vaccination programs is of upmost importance. Having appropriate vaccination programs according to the needs of the population to be vaccinated is an essential element to prevent the re-emergence of this pandemic.
Our research is oriented to humanitarian logistics, looking at cases where the government needs to locate different vaccination points for the inhabitants of a certain region, in such a way that there is the most equitable access to vaccines. Vaccination of inhabitants seems to be the safest and most effective way to control the COVID-19 pandemic. In the Ref. [
1], the authors state that a single dose of vaccine can be a drop in the ocean, but several doses together can save a population.
In this paper, a problem concerns the vaccination strategic decisions is studied. the government needs to locate different vaccination points (VPs). In trying to maintain the healthy distance and avoid agglomerations, two objectives are pursued: (i) that the located VPs are as far as possible from each other, and (ii) that inhabitants are equally distributed (as much as possible) within the VPs.
The vaccination strategy imposes some mobility constraints, such as, only the current inhabitants of the municipality will receive the vaccine in the VPs of that specific municipality. However, the government cannot impose this restriction on an inhabitant, each inhabitant is free to attend the VP he/she prefers. This assumption lead us to take into account the inhabitants preferences towards the VPs. Therefore, the allocation of inhabitants to VPs is chosen by each inhabitant and not by the government.
In summary, the government decides the location of VPs within the municipality and the inhabitants attend the VP they prefer. It is evident that the inhabitants’ decisions directly affect the crowding in the VPs, which is of interest to the government. Hence, due to the existing hierarchy in this situation and the relationship between the decisions, a bi-level programming approach is suitable to study this problem. Two objectives are considered at the upper level, simultaneously, and this prevents application of the well-known single-level reformulation in an efficient manner. That is, despite the fact that the bi-level model may be reformulated as an equivalent single-level one by using the optimality conditions of the lower level, the analysis must not lose sight of the fact that two objective functions are being optimized at the lower level. Thus, a bi-objective single-level complex model must be solved.
In order to handle the inherent complexity of this bi-objective bi-level problem, a cross-entropy algorithm is proposed to approximate the Pareto front of this VPs location problem. Several adaptations are needed to design the proposed algorithm. Firstly, an adaptation is made to guide the search while considering the two objective functions. Secondly, a strategy to deal with the parameterized lower-level problem at each stage of the algorithm is designed.
We can highlight five main contributions of this research to the literature. First, the combination of a p-dispersion problem with a facility location problem that balances the allocation of the users in the located facilities is performed for the first time. This can be considered as an extension of the p-dispersion problem. Second, a bi-objective bi-level program is proposed to model the problem under study. Third, the proposed model is applied to a vaccination system that aims to maintain the healthy distance among inhabitants without imposing restrictions regarding the VPs that they need to attend. In the literature, there are no papers with those characteristics, that is, neither the proposed variant of the p-dispersion problem nor the application to the location of VPs. Fourth, the proposal of a cross-entropy metaheuristic that simultaneously deals with two objectives, and handles the bi-level structure of the problem. That is, it solves the lower-level problem while considering the upper-level decisions. This is the first time that cross-entropy is applied towards solving a bi-objective bi-level problem, so the specific components for dealing with both objectives and the lower-level are carefully designed. Fifth, extensive computational experimentation is conducted to validate the proposed metaheuristic and to obtain important managerial insights regarding the location of VPs and social distancing.
The rest of this paper is organized as follows.
Section 2 reviews the literature of facility location problems, users’ preferences and applications related to COVID-19 pandemic.
Section 3 presents the bi-level formulation of the problem.
Section 4 describes the proposed metaheuristic and its components.
Section 5 presents the computational results on adapted test instances and the respective analyses. Finally,
Section 6 outlines the conclusions of our research and lists some interesting further research directions.
3. Problem Statement and Its Mathematical Model
Consider the situation described in
Section 1, in which the government needs to locate a predefined number of VPs for vaccination inhabitants against COVID-19. The inhabitants are free to attend the VP they prefer. The latter decision directly affects the crowding in the VPs, which is undesirable. This situation can be modeled under a bi-objective bi-level programming approach. The upper level is associated with the government, and the lower level to the inhabitants.
First, the sets, parameters, decision and auxiliary variables involved in the model are defined. Let I be the set of VPs that must be located, and let J be the set of all inhabitants who need to receive the vaccine. The predefined number of VPs that must be located is denoted by p. The distance between a VP and the inhabitant is represented by . Additionally, represents the preference that an inhabitant has for a VP .
The binary decision variables associated with the upper level are , which is 1 when VP is located in location , and 0 if not. On the other hand, binary decision variables of the lower level are denoted by , where 1 is when the inhabitant receives the vaccine from VP , and 0 in other case.
Auxiliary continuous variables U and L compute the maximum and minimum number of inhabitants assigned to any VP, respectively.
As mentioned previously, the government aims to maintain the
healthy distance, and prevent crowds. Therefore, two objectives are considered in this problem. The first one is to balance the number of inhabitants assigned to each VP, that is, that population is equally distributed (as possible) into the VPs. This objective function is formulated as follows:
The second objective function aims to have the VPs as far as possible from each other, that is, to maximize the minimum distance between the located VPs. This objective function is represented as follows:
The latter equation can be linearized by introducing an auxiliary continuous variable
r, which indicates the minimum distance between each pair of located vaccination points. Hence, the linearized second objective function is:
An additional set of constraints must be included to achieve linearization of Equation (
2). Let
M be a sufficiently large positive constant, usually referred to as the big-
M. The distance from each pair of located VPs is computed, and
r will take the minimum value between all of them. This is as follows:
The manner in which the linearization works is explained next. Equation (
4) establishes upper bounds for the value of
r. Since
M is a large constant, note that this constraint is relaxed when neither the
i-th nor
k-th VPs are located. When two specific VPs are located, then the first term of the right-hand side is zero. In this case,
r is bounded by the distance between these two VPs. Due to the sign of the inequality given in Equation (
4) and by the orientation of objective function defined in Equation (
3), the smaller value of the distances involved in the bounding constraints is assigned to
r (which is the maximum possible one).
Consider that there is a predefined number of VPs to be located. This is ensured by the following constraint:
As indicated above, the upper-level decision variables are binary:
Once the government has chosen the VPs to be located (
x), the inhabitants need to be allocated to the VPs to get vaccinated (
y). Since we are assuming that the allocation of inhabitants to VPs is performed by each inhabitant and not imposed by the government, their preferences
towards the VPs are considered. Preferences are given as a ranking of VPs, in which 1 indicates the least preferred VP and
the most preferred one. Therefore, the maximization of these preferences is aimed at. The objective function associated with the lower level is as follows:
There are some constraints associated with the lower level. The first one indicates that inhabitants can be allocated only to located VPs.
Another imposed constraint must guarantee that inhabitants each receive only one vaccine. That is, a unique allocation from inhabitants to VPs is allowed.
Let
n be the total number of inhabitants that will receive a vaccine, that is,
. Therefore, the maximum and minimum numbers of inhabitants allocated to the located VPs are computed by the following constraints, respectively:
Note that Equation (
10) counts the number of inhabitants allocated to the VPs. By considering the inequality of the type greater or equal than, the value of
U that satisfies Equation (
10) is bounded by the maximum number of allocations to a specific VP. On the other hand, Equation (
11) differentiates between opened and closed VPs and helps to compute the minimum number of inhabitants allocated to a specific VP. In detail, if a VP is located at a specific potential site, then the second term of the right-hand side is zero. Due to the sign of the inequality, the value of
L that satisfies Equation (
11) is the minimum number of inhabitants allocated. If a VP is not located, inhabitants cannot be allocated by Equation (
8). Thus, constraint (
11) is relaxed since it is bounded by
n.
Finally, lower-level decision variables are binary.
The resulting bi-objective bi-level programming model is defined by:
where for a fixed
y,
x optimally solves:
It is worthwhile to note that if each of the inhabitants have a different order of preferences for the located VPs, then a unique optimal solution of the lower level exists (see the Ref. [
12]). However, this may be unrealistic in our problem due to the large number of inhabitants in comparison with the located VPs. Thus, it is expected that more than one inhabitant will have the same ranking of preferences, which leads to the existence of multiple optimal solutions for the lower level. In that case, different optimal lower-level solutions, for a fixed upper-level decision, could lead to different values of the upper-level objective function. The optimistic or pessimistic approaches can be assumed to handle that issue [
42,
43]. In the former, the lower-level decision-maker selects the optimal solution that is more convenient to the upper-level decision-maker (cooperative approach), while in the latter, the solution that most negatively affects the upper-level decision-maker is selected by the lower-level decision-maker. In this study, the optimistic approach is followed.
The latter assumption is necessary to have a well-defined bi-level programming problem. Nevertheless, in the problem under study, it is not straightforward to identify the optimistic approach since we are simultaneously optimizing two objective functions. Note that both objective functions can be seen as separable, that is, Equation (
1) is determined by the lower-level variables, and Equation (
3) is only defined by upper-level variables. Therefore, the optimistic approach relies on choosing the optimal solution of the lower level that is more convenient for balancing the inhabitants that attend the vaccination points.
To obtain all the possible multiple optimal solutions of the lower level, the corresponding separation problem is identified [
44]. That is, all the allocations of inhabitants to located VPs are identified and the appropriate constraint is added. This means it is prohibited that all the identified allocations are repeated in the augmented problem. Additionally, a constraint that guarantees that the lower-level objective function value is maintained is included. Then, the augmented lower-level problem is solved. If it is infeasible, it implies that no more optimal lower-level solutions exist. In the other case, the optimal solutions are recorded and at the end, the one that offers greater balance for the crowding in the VPs is selected.
4. A Bi-Objective Nested Cross-Entropy Algorithm (BONXEA)
Cross-entropy (XE) is an iterative method with two main phases. First, it creates a random sample of solutions by a specific mechanism. Then, it updates the parameters involved in the solutions generator. The latter is achieved by considering the characteristics of the previous random sample in order to create improved solutions in the next iteration.
XE has a relatively short history in optimization problems. Rubinstein developed XE as a method for estimating the probability of rare events in complex stochastic networks [
45]. A few years later, XE was applied for the first time in the context of combinatorial optimization, which inspired its application in diverse applications in operational research: capacitated facility location [
46,
47,
48], closed-loop supply chain in the Ref. [
49], sustainable supply chain in the Ref. [
50], job-shop scheduling [
51], facility layout [
52], and water distribution systems [
53], among others.
Described in detail, XE consists of the repeated execution of the following steps [
54]:
- 1.
Generate a random sample of solutions based on a prespecified probability distribution function.
- 2.
Use the random sample to select an elite set that is used to modify the parameters of the probability distribution function seeking to produce a sample with better objective function values in the next iteration.
The general idea is to obtain a sequence of parameter values that are being updated in an appropriate manner from one iteration to the next one. If successful, the search converges to the global optimum, or at least, to a local optimum.
XE has been successfully applied in discrete problems related to the papers studied herein. For example, in the Ref. [
46] a location-allocation problem was studied. Therein, capacity and fixed costs of the facilities are considered, and the minimization of the total cost is aimed. A non-linear mixed-integer formulation is proposed and the XE method is implemented to solve the problem. Three different stages occur, each with different density functions. In the first stage, a location problem with coverage is solved by using a multivariate normal function. In the second stage, the allocation is made by following a multinomial density function. Then, in the third stage, a continuous single-facility location problem is solved. The proposed approach obtains good results in comparison to solutions obtained by GAMS. Additionally, in the Ref. [
47], a hybrid algorithm for the capacitated multiperiod multicommodity lot-sizing problem was presented. In that problem, many commodities competed for the space and limited resources at each period. The proposed solution approach considers a Lagrangian relaxation and applies a metaheuristic based on XE for the uncapacitated version of the problem.
Additionally, XE has been applied to solve facility location problems modeled as bi-level programs. For example, in the Ref. [
48] a bi-level problem was studied. Therein, the upper level is associated with a company that locates capacitated facilities aiming to minimize location and distribution costs. In the lower level, customers seek to maximize their preferences of being allocated to their most preferred facilities. A XE algorithm is designed to obtain upper-level solutions, while the lower level is solved through three different approaches via an adaptive random procedure, via a procedure based on a regret cost, and by an exact method. The XE algorithm builds a set of upper-level solutions and for each of them, the resulting lower-level problem is solved. In other words, the classical nested approach is used, of algorithms designed to solve bi-level problems.
There exist other applications of XE in the context of multi-objective programming. In the Ref. [
55] it was used to find efficient frontiers for problems with multiple multimodal objective functions of continuous variables. To obtain the Pareto fronts, the set of non-dominated solutions is divided in groups and a XE procedure is applied to each of them. That method is very similar to that proposed by the Ref. [
56]. In the Ref. [
57], an adapted XE method for estimating the Pareto front was proposed. To achieve the latter, a uniform grid in the space of the objectives is formed. Each cell in the grid contains its own elite population (with non-dominated solutions). As a consequence, the associated probability vectors are updated, respectively. At the end of the process, the approximation of the Pareto front consists of the union of the set of non-dominated solutions in each cell. Recently, in the Ref. [
50] a multi-objective XE method was designed to solve a sustainable food supply chain. When the solutions’ set is generated, a dominant matrix is considered to identify the best solution.
As mentioned before, the problem studied in this research is to be approached by a bi-objective nested cross-entropy algorithm (BONXEA). To design the BONXEA, the XE methods proposed in the Refs. [
48,
57] are considered. In the former, a discrete bi-level facility location problem with capacities is studied; meanwhile, in the latter, different multi-objective problems are analyzed. To initialize our proposed BONXEA, a grid in the objectives space must be defined. Since we are considering two objective functions, a
grid is created. The number of cells in the grid corresponds to the number of objectives being considered plus one. The rationale is to find the best solutions for each objective and for the central region of the Pareto frontier. To construct the grid, the minimum and maximum values for each objective function are needed. Let
,
and
be the objective functions considered in the BONXEA, where
corresponds to the objective function associated to the distance between the vaccination points,
is associated to the balance of inhabitants in each vaccination point, and
is the weighted sum of the standardization of
and
.
After that, a population of N upper-level solutions (y) is created. For each of these solutions, the lower-level problem is optimally solved (nested attribute of the BONXEA). Now, the upper-level objective functions can be evaluated. Solutions in the initial population are grouped into three subpopulations, each of them associated with , and , respectively. Three samples of size d that contain the best solutions, in terms of the quality of the corresponding objective function, are formed. For each sample, the frequencies of locating a vaccination point are updated in the construction phase. Therefore, new subpopulations of solutions are created based on the updated frequency vectors for each of the three samples. The procedure is repeated until a maximum number of iterations is reached. Non-dominated solutions and their respective objective function values are stored, and given as the output of our algorithm.
A pseudocode of the BONXEA is presented in Algorithm 1.
| Algorithm 1 BONXEA |
| Input: |
| Output: P |
- 1:
- 2:
- 3:
- 4:
- 5:
while
do - 6:
for i: 1..N do - 7:
- 8:
- 9:
- 10:
Evaluate - 11:
end for - 12:
for each non-empty cell c of the grid do - 13:
Identify the d elite solutions - 14:
Update frequency vector - 15:
- 16:
- 17:
end for - 18:
Update P with the non-dominated points - 19:
- 20:
end while
|
4.1. BONXEA Description
Solution encoding
The proposed algorithm explores upper-level solutions, and for each of them, the optimal reaction of the lower level is obtained. In this case, an upper-level solution at iteration k is represented by the binary vector , in which a 1 indicates that a VP is located at site , and 0 otherwise.
Creation of solutions
At iteration k, N random solutions are created but based on a frequency vector , that indicates the probability of locating a facility at each site. At the beginning of the BONXEA, when , probabilities are set as 0.5, that is, . As the algorithm continues, frequency vectors are going to be updated from one iteration to the next. That will lead us to favoring the facilities more convenient to locating VPs.
Repair of solutions
In the case when an upper-level solution at iteration k has not located the p required VPs, a specific routine is performed to repair the solution, that is, to achieve feasibility. Specifically, the non-located VP associated with the higher frequency in vector is located. If more than one VP needs to be located to achieve the p required, the repair procedure continues in an analogous manner. The repairing procedure stops when p VPs are located.
Optimal solution of the lower-level problem
Recall that once the located vaccination points are known, inhabitants are optimally allocated to these facilities. Allocation must take into account inhabitants’ preferences in regard to the VPs. Since capacity at the VPs is not being taken into consideration, all the inhabitants may be allocated to their most preferred located facilities.
Therefore, the lower-level problem may be optimally solved by using an auxiliary matrix of ordered preferences, in which the indices of the facilities are ordered in a decreasing manner based on the preferences of each inhabitant. That is, each column of the auxiliary matrix contains the ordered indices of the VPs. Once the auxiliary matrix is constructed, the lower-level problem can be optimally solved by using an easy procedure. For each inhabitant, their most preferred located VP is identified, and the allocation is made. By following the procedure described, the optimal allocation of inhabitants to VPs is achieved (see the Refs. [
13,
16]). Hence, an optimal solution of the lower level is obtained for a given upper-level fixed solution, that is,
. For sake of simplicity, it is denoted by
.
Evaluation of the objective functions
Once an upper-level solution
and its corresponding lower-level optimal response
are obtained, the objective functions considered in the BONXEA can be evaluated, that is,
,
and
. Recall that
is given by Equation (
1),
is given by Equation (
3), and
is given by
, where
and
are the standardization of
and
, respectively.
Creation of the subpopulations based on dominance
Firstly, we take the elite populations for each of the three cells considered in the grid. Each elite population is associated to each one of the three objective functions considered, that is, , and . Therefore, the best d solutions regarding objective are selected, and the objective is evaluated for such solutions. The non-dominated solutions in that cell are stored, which are denoted by , , ⋯, . After that, the same procedure is repeated to identify the non-dominated solutions in the remaining two cells, that is, regarding and , respectively. The authors emphasize that to identify the non-dominated solutions, only objectives and are used because they are the real objectives in the problem under study. Recall that objective is an auxiliary objective function to identify the central part of the Pareto front.
Under this approach, three Pareto fronts are obtained, one for each of the three cells considered in the grid. Likewise, each subpopulation evolves independently from the other two subpopulations.
Updating the probabilities vector
At iteration
k, vectors
, with
, are vectors that contain the frequency in which a specific VP is located in the solutions of the corresponding elite subpopulation performed, n. The reason for the use of vectors
is to store information of the components of the elite solutions, that is, to identify the repetition of VPs in the good-quality solutions. This is performed so as to favor locating these VPs in the next random-biased solutions. For each subpopulation
l, the probabilities are obtained as follows:
Creation of new solutions
To generate new solutions of each subpopulation l at iteration k, vectors are used to determine whether a VP is located or not. As mentioned before, the procedure seeks to favor the more convenient VPs regarding the information provided by the elite solutions of each subpopulation. For the new created solutions, a random vector of size is generated, and if the random number associated to the i-th position is less than its corresponding probability , then that VP is located.
If a 0 appears in one position within vectors , then it means that in the new created solutions, a VP must not be located in that specific site. Otherwise, when a positive probability appears, the possibility exists to locate a VP at that potential site. In the case where the probability is 1, a VP must be located in that specific site for all the new created solutions. By following this criterion, the algorithm iteratively converges to good-quality solutions.
Stopping criterion
The stopping criteria are established as a fixed maximum number of iterations, and a predetermined number of iterations without updating the non-dominated set of solutions at each subpopulation.
Final Pareto front
At each iteration of the BONXEA, a Pareto front for each one of the three subpopulations is obtained. Furthermore, the obtained frontiers for each cell of the grid are updated at each iteration taking the previous fronts.
At the end of the BONXEA, the non-dominated sets of points obtained for each elite subpopulation are merged to form the final Pareto front. Some non-dominated solutions in a cell are dominated by some solutions of the Pareto front of another cell. Hence, at the end, only the non-dominated solutions of all the three cells are reported.
4.2. Computational Complexity of BONXEA
BONXEA starts by generating an initial population of N solutions of size . Additionally, a repairing phase may be needed if less than p VPs are located. In the worst case, p insertions from all the possibilities are performed. Then, the lower level is optimally solved via an allocation algorithm in ) time.
After that, a sample of d elite solutions is selected for each of the c cells in the grid, which incurs in time. The evaluation of the first objective function requires time. The update of the probability vector requires the same time as the selection of the sample, that is, .
The algorithm repeats its main cycle for a predefined number of iterations. Hence, the computational complexity is times the sum of all the computational complexities identified above. In summary, the computational complexity of BONXEA is , which is of polynomial time.
5. Experimental Results
To measure the performance of the proposed algorithm and its ability to approximate the Pareto front, an intensive computational experimentation was carried out on a set of instances adapted from the literature. All computational experiments were performed on a computer with a 3.60 GHz Intel Core i7-4790 processor with 32.00 GB of RAM running Windows 8.1. The BONXEA code was coded with FICO Xpress 8.11 software.
The set of instances was adapted from the instances used for a discrete facility location problem with balanced customer allocation, which was proposed in the Ref. [
7]. In that problem, the parameters regarding the instance size were included, that is, number of possible facilities and number of clients (VPs and inhabitants in our case, respectively). In addition, the distances between VPs and inhabitants were included. The missing parameters that are needed for our problem have been filled in as is described next. In particular, data related to the preferences of the inhabitants towards VPs were missing. These preferences were generated through the process described in the Ref. [
58]. Basically, this process takes into account the existing costs, and generates modified fictitious costs to rank them in ascending order. Based on this, preferences are generated, ensuring that the closest VP is not always the most preferred by an inhabitant. It is worthwhile mentioning that under these instances’ construction processes, all the generated instances are feasible for our problem.
For the problem studied in this research, the instances must contain the data on the number of VPs, the number of inhabitants, the predefined number of VPs that must be located, the preferences and the distances of the inhabitants towards the VPs, respectively.
We denote an instance as follows:
, as in the Ref. [
7]. For example, 30-50-3-10 means that there are 30 potential VPs, 50 inhabitants, 3 VPs to be opened, and only 10 distance pairs that have been exchanged. The latter refers to a parameter that adds complexity to the instance.
In total, 45 different instances were generated by combining different numbers of the following parameters: (i) VPs to be opened (), which were set from the set ; (ii) the number of inhabitants, which vary between ; (iii) the number of VPs to open p, which were among ; and (iv) the perturbation level v, which was used to modify the values of an instance without losing the structure, those values were chosen from .
Due to the stochasticity inherent in the BONXEA, 100 runs were performed for each instance. A summary of the results obtained from the experimentation is shown in
Table 2. The first column indicates the label of the instance to which we refer. The remaining columns are associated with the non-dominated solutions. The second and fourth columns show the minimum and maximum number of non-dominated solutions obtained by BONXEA, respectively. The third column shows the average of the obtained non-dominated solutions among the 100 runs of the algorithm. The fifth and sixth columns show the minimum and maximum values for the objective function
, respectively. Recall that the said objective function refers to the balance of the inhabitants in the open VPs. Finally, the minimum and maximum values obtained for the second objective function
are shown in the seventh and eighth columns. It should be noted that the second objective function seeks to maximize the minimum distance between two open VPs. With these last four columns, we can identify the extremes of the obtained approximated Pareto front.
From
Table 2 it can be seen that the BONXEA always obtained non-dominated solutions. The largest number of non-dominated solutions that was obtained is eight solutions (see instance 50-100-6-50). On average, there are at least two non-dominated solutions for each instance. We note that
refers to the balancing of inhabitants. In a case of perfect balancing of inhabitants among the VPs,
. If this is not possible, the range in which
varies is very limited. That is, there are not many non-dominated solutions with large
values. For example, for the instances 30-30-3-1 and 30-30-3-100, a perfect balance is found, that is, there are exactly 10 inhabitants that go to each open VP. However, instance 100-100-3-10 shows a surprising result. A total of 100 clients were considered and the worst reported balance was 49. This implies that there is a lot of disparity between the crowding in the open VPs. However, after reviewing this solution, we realized that the balance of 49 corresponds to the best value for
. That is, very distant VPs cause the inhabitants to be mostly concentrated in a central VP. That occurs only in that particular instance, and due to the spatial distribution of the inhabitants and potential VPs. It is also important to clarify that the obtained values of
are integers because that is the manner in which they are defined in the data, and Euclidean distances between inhabitants and VPs are not being calculated.
From the results obtained, we also identify that the proposed algorithm finds solutions that allow us to correctly approximate the Pareto fronts of this hierarchized problem. To illustrate the above, some of the obtained Pareto fronts were randomly selected and have been plotted in
Figure 1.
It can be seen in
Figure 1 that there is an adequate number of solutions plotted. In the graphics presented, the maximum number of solutions obtained in the Pareto front is 9 and the minimum is 6. However, as already mentioned above, it is very important to take into account that the first leader’s objective function (
) seeks to minimize balance among inhabitants that attend to a specific open VP, which is a small integer value, so excessive possible values for that target do not exist.
In addition, these graphs show the grid that is carried out in each iteration to consider the best solutions for the creation of the nine sub-populations of solutions. Within the grid, it is observed that in the specific grid that corresponds to the best values for and , the number of solutions contained is from one to three. This validates the idea of considering the grid to always find the best solution for each objective function. At least in the 45 instances considered in this computational experimentation, this behavior is maintained. Likewise, it can be observed that there is diversity within the solutions, that is, some are better for , others better for , and some others that are in the center, according to the weighted sum considering the objective function.
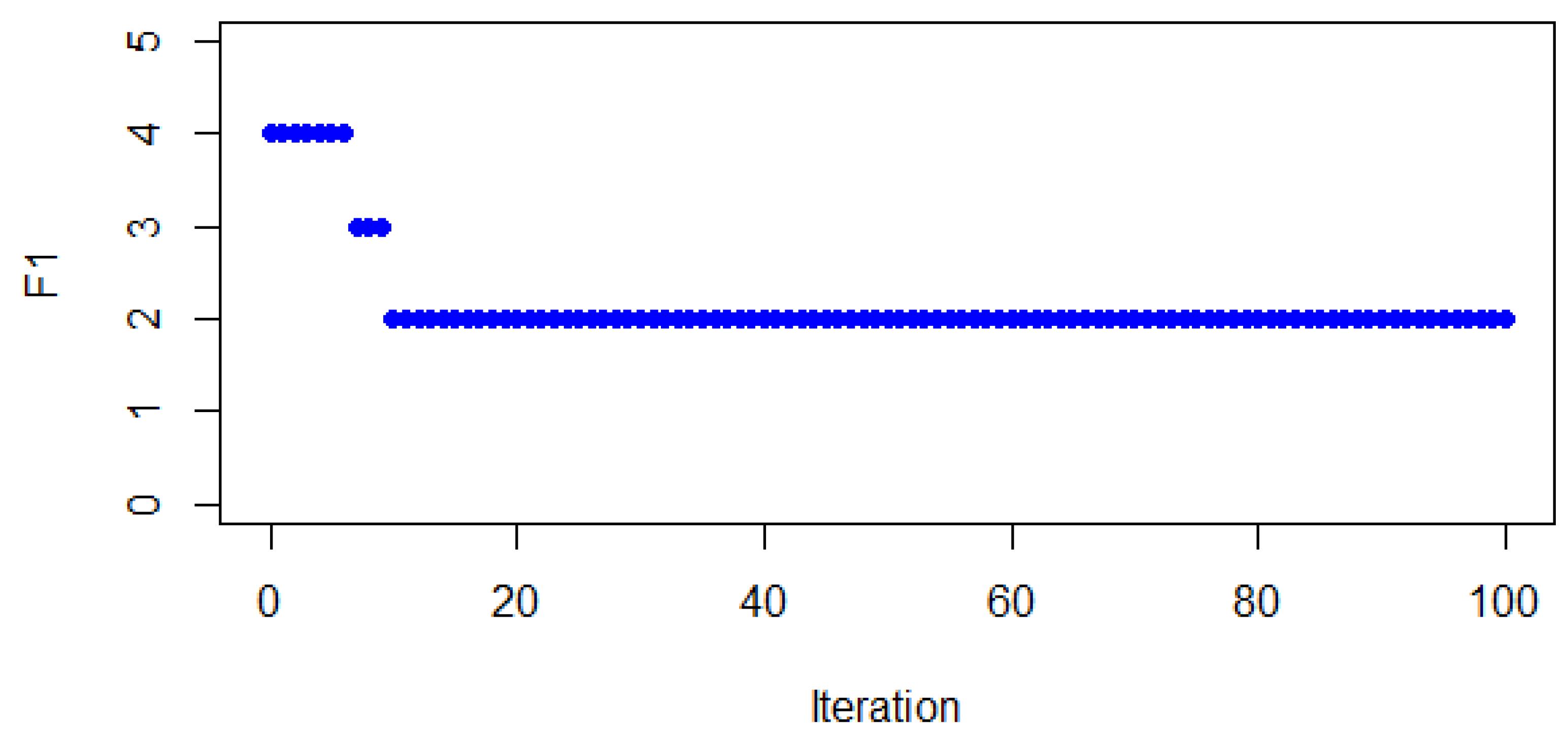
In order to illustrate the limited space in which the leader’s objective function is embedded (regarding the balance), one independent run of the BONXEA was performed and 100 runs were set as the stopping criterion. Therefore, we registered the best value obtained for
at each iteration. This may give us an idea of the convergence capability of the BONXEA. It can be seen in
Figure 2 that from a balance value of 4 it improves to 2, and no further improvement is reported in the remaining 90 iterations. Additionally, at each iteration of the BONXEA, other non-dominated solutions may arise, but this particular analysis is performed to demonstrate the convergence of the BONXEA regarding a particular leader’s objective function. In
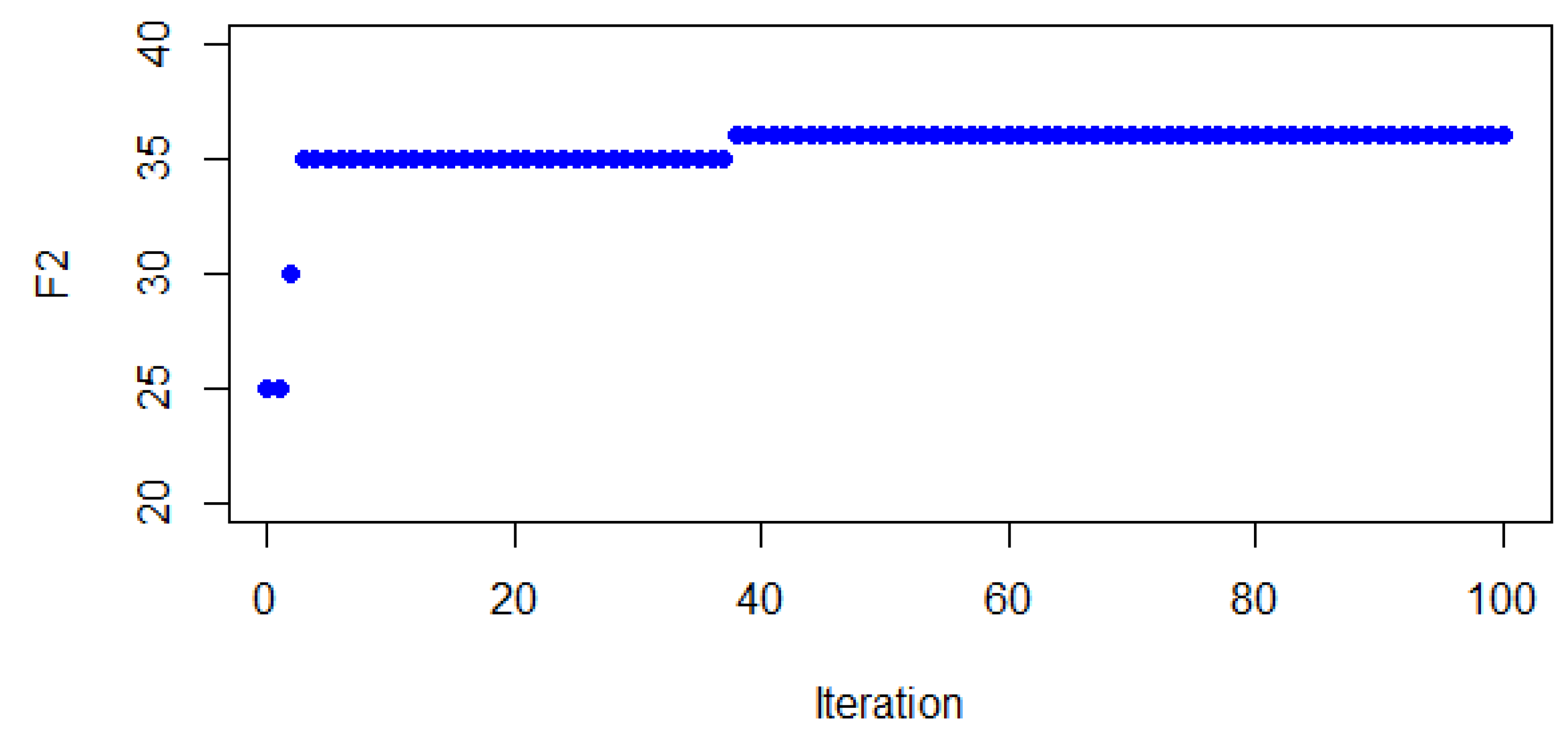
Figure 3, the same analysis is performed, but with respect to
. It can also be noticed that the BONXEA obtains the best value of
in the first 40 iterations. This is a good indicator that the BONXEA contains a well-designed intensification component.
We may summarize that the proposed algorithm generates a reasonably-sized set of efficient solutions for our problem. Therefore, the decision-maker will have to choose the solution that is more convenient to him/her at the moment when the real problem is being solved. In other words, among all the non-dominated solutions obtained by the BONXEA, only one can be implemented in practice. However, this is common for bi-objective practical decision-making problems.
6. Conclusions and Further Research Directions
As mentioned throughout this manuscript, implementing measures to fight the COVID-19 pandemic is crucial. For example, social distancing (healthy distance) and avoiding crowds are globally accepted as good steps to prevent infections and to try to control the pandemic. It is in this context that a vaccination-point location problem that considers inhabitants’ preferences arises. Its purpose is to contribute to maintaining the healthy distance between inhabitants who come to receive their vaccine against the COVID-19 virus. In this paper, the government sought to open vaccinations points as far from each other as possible, but at the same time, sought to have a balanced demand for vaccines at each open vaccination point. This is not straightforward because the government does not impose restrictions on the inhabitants regarding which vaccination point they can go to. On the contrary, inhabitants decide where to go based on their own preferences, which may be decided by distance, personal interests, and type of vaccine, among others. If the government assigns the inhabitants to the VPs in a mandatory manner, the closest assignment rule can be selected and the problem reduces its complexity.
The situation is modeled under a bi-objective bi-level programming approach. the government is associated with the leader, and the inhabitants, with the follower. As mentioned, the inhabitants’ preferences are taken into account when they are allocated to the open vaccination points. Different constraints are considered, which complicate the problem.
To solve this problem, we proposed a metaheuristic approach that is capable of approximating the Pareto front in an effective manner. A bi-objective nested cross-entropy algorithm is designed. Both considered objective functions are taken into account in the algorithm. The pertinent mechanisms are proposed to identify the approximation of the Pareto front. Additionally, for each leader’s solution, the parameterized follower’s problem is optimally solved. This is the nested approach of the proposed algorithm. Therefore, initial solutions are randomly generated followed by a procedure that creates a grid to classify solutions. Then, the more convenient components of a solution are identified, with respect to the cell of the grid that the solution belongs to. Based on the latter, new solutions are generated following a components-biased manner. The algorithms continue until a stopping criterion is reached.
It can be seen from the computational experimentation that the proposed algorithm obtained a Pareto front in good shape. Insights can be gained from the obtained results. However, it is important to point out that the structure of the first leader’s objective function does not have many values. Thus, few values may be obtained, which significantly reduces the number of solutions that may conform to the Pareto front. In the literature, to the best knowledge of the authors, there are no papers with all the characteristics considered in this study. As a consequence, this is the first bi-objective bi-level programming model for a problem with these assumptions. For this reason, there are no benchmark algorithms or instances that can be considered to compare our proposed algorithm.
A future research direction may be the application of this problem to a real case study. However, it is well-known that government agencies are not often open to sharing data or to allowing academic collaborations. A comparison against real implemented decisions would give us interesting managerial insights. As a second research direction, we may apply this model to a different context. Maybe in the private sector, a situation could arise in which a company has similar interests as the ones stated by the leader in our problem. Customers could be considered the inhabitants of our problem. Usually, it is important to allow customers to be free to choose the service of their preference.