Newton-like Normal S-iteration under Weak Conditions
Abstract
1. Introduction
- (i)
- It is only a second-order method;
- (ii)
- The initial approximation should be near the root;
- (iii)
- The denominator term of Newton’s method must not be zero at the root or near the root.
- (i)
- Newton’s method (2) can not be used;
- (ii)
2. Preliminary
3. New Newton-like Method and Its Theoretical Convergence Analysis
- (i)
- is a simple zero of f;
- (ii)
- f is two times differentiable on I;
- (iii)
- , for all , where is neighborhood of and .
4. Numerical Analysis
- (i)
- ;
- (ii)
- ;
- (iii)
- ( is taken as in Wang and Liu [13]).
- (i)
- Functions with third-order differentials:
- (ii)
- Functions that are differentiable only two times
5. Sensitivity Analysis
5.1. The Behavior of Normal S-Iteration Method for Different Values of and
5.2. Normal-S Iteration Method with Variable Value of
5.3. Average Number of Iterations in Normal-S Iteration Method
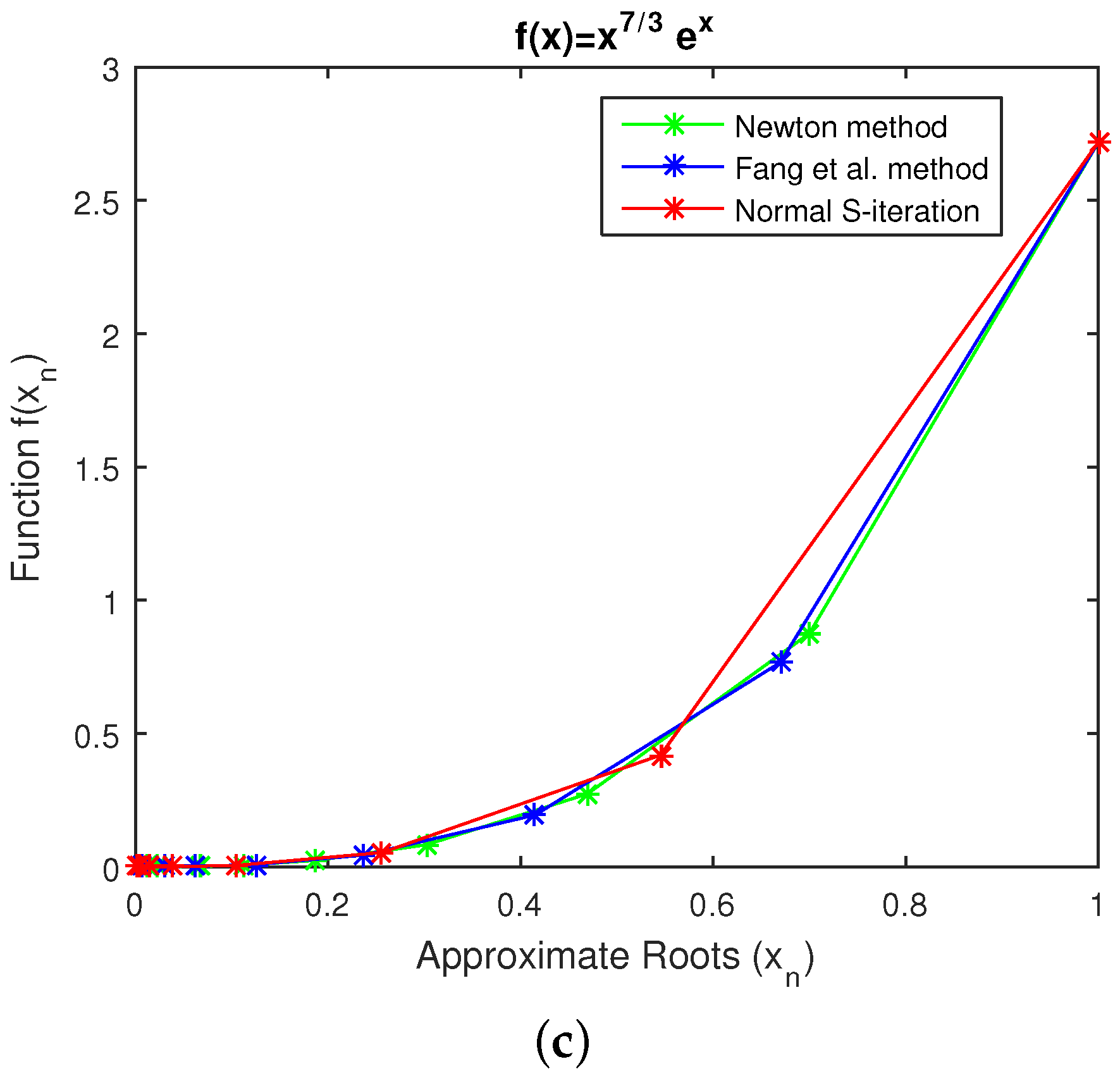
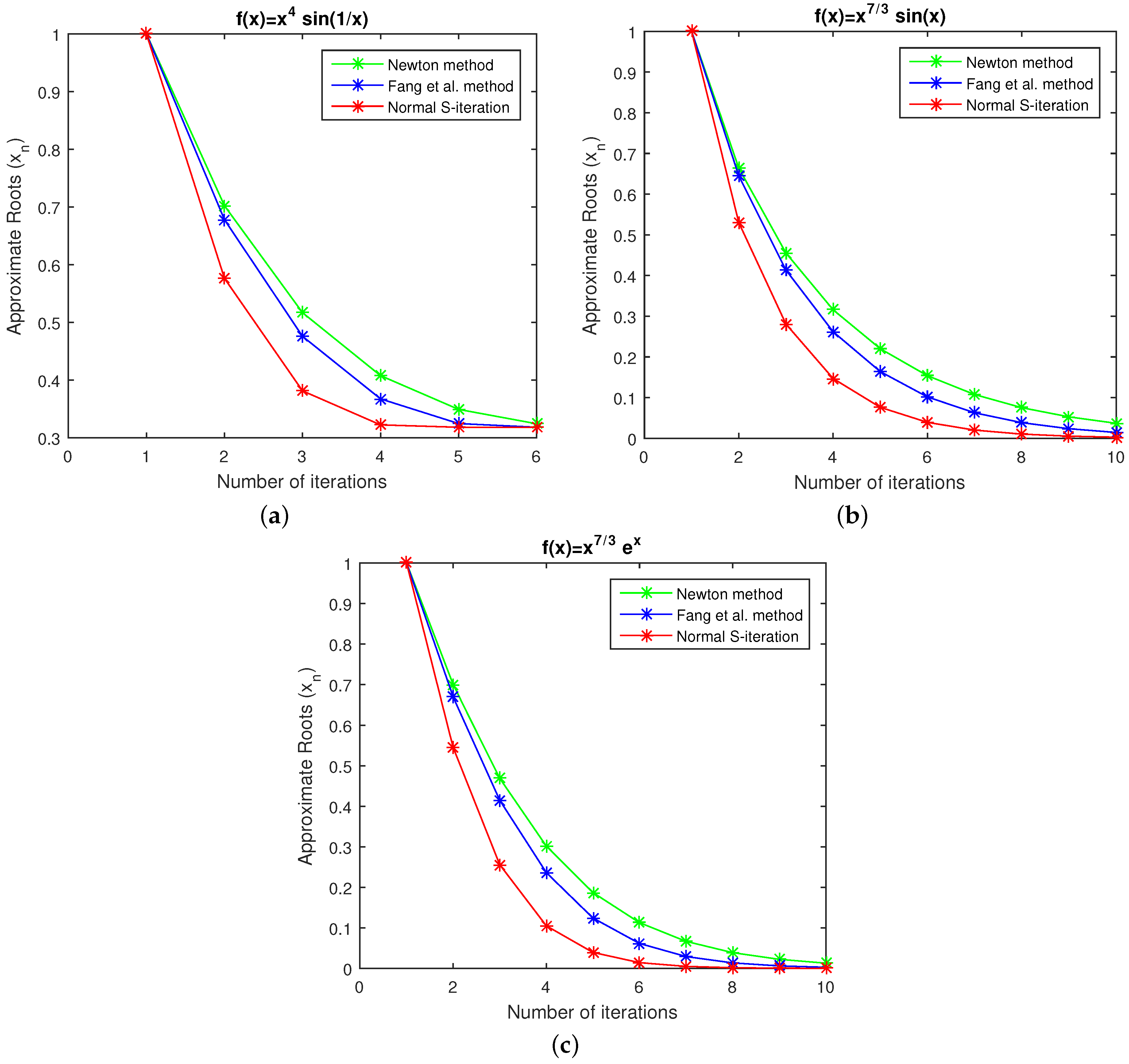
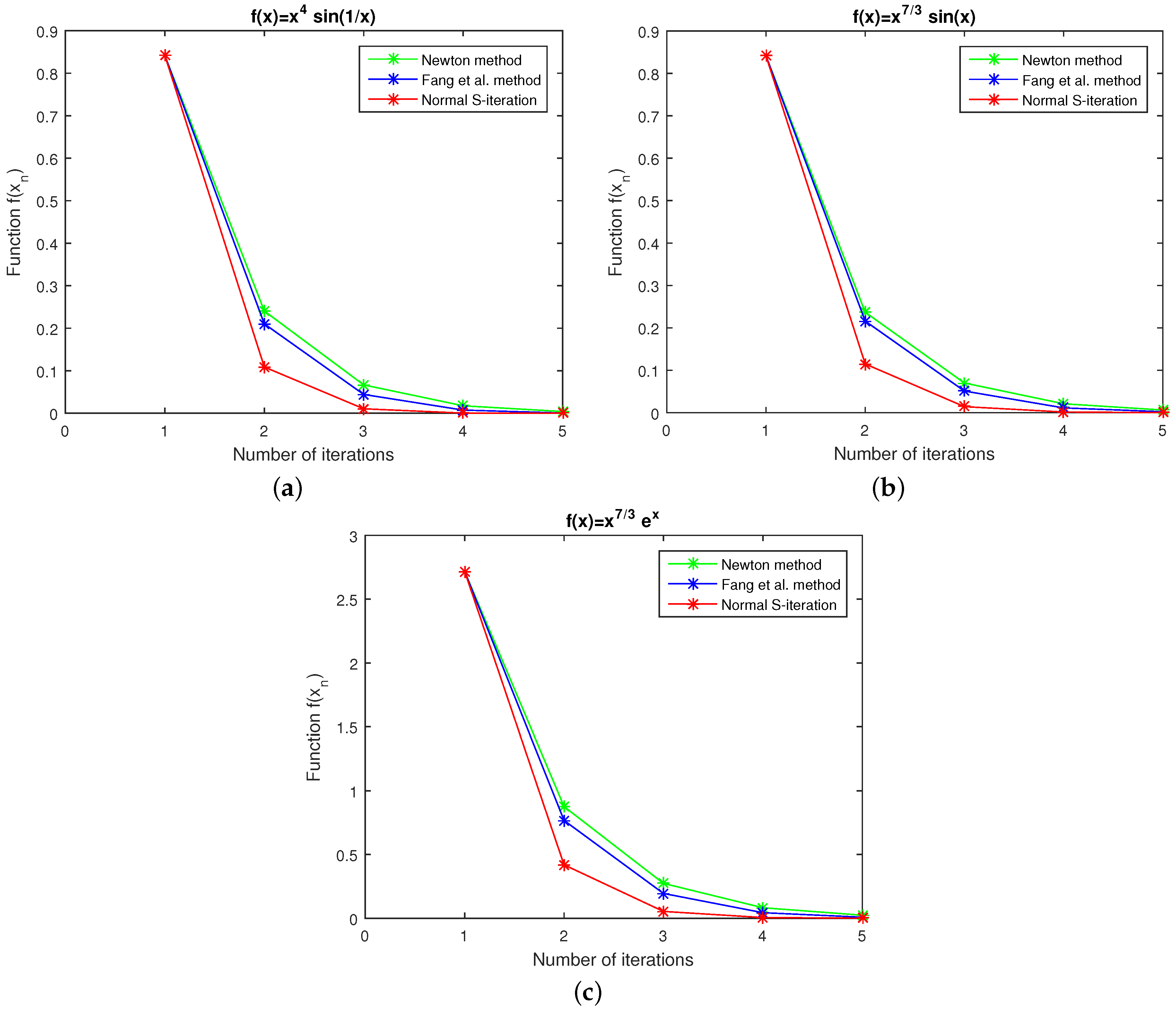
5.4. Convergence Behavior of the Methods of Newton and Fang et al. and the Present Method
- Case 1: The graph between function and root for , , and
- Case 2: Graph of the number of iterations and roots for , , and
- Case 3: Graph of number of iterations and functions for , , and
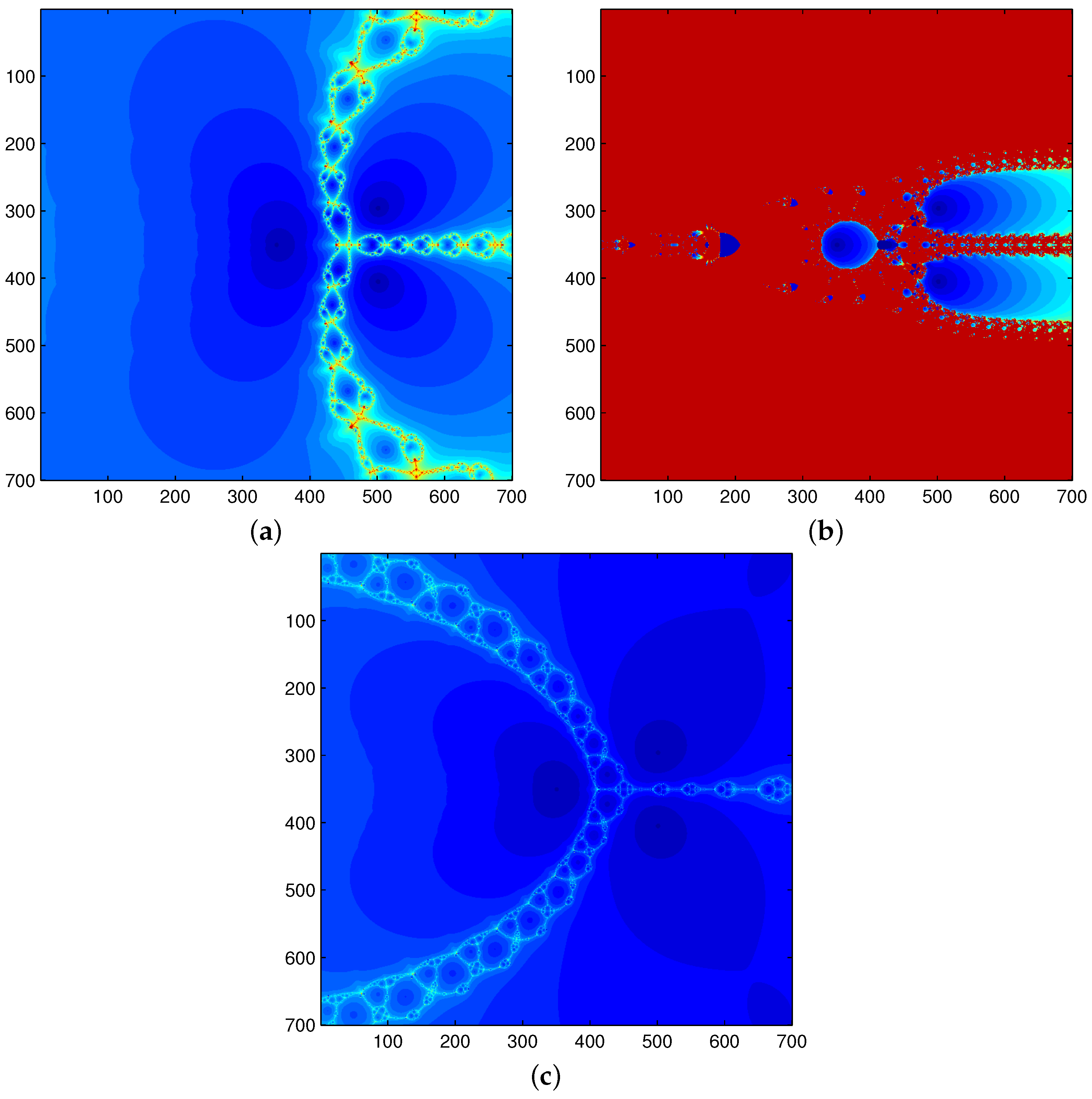
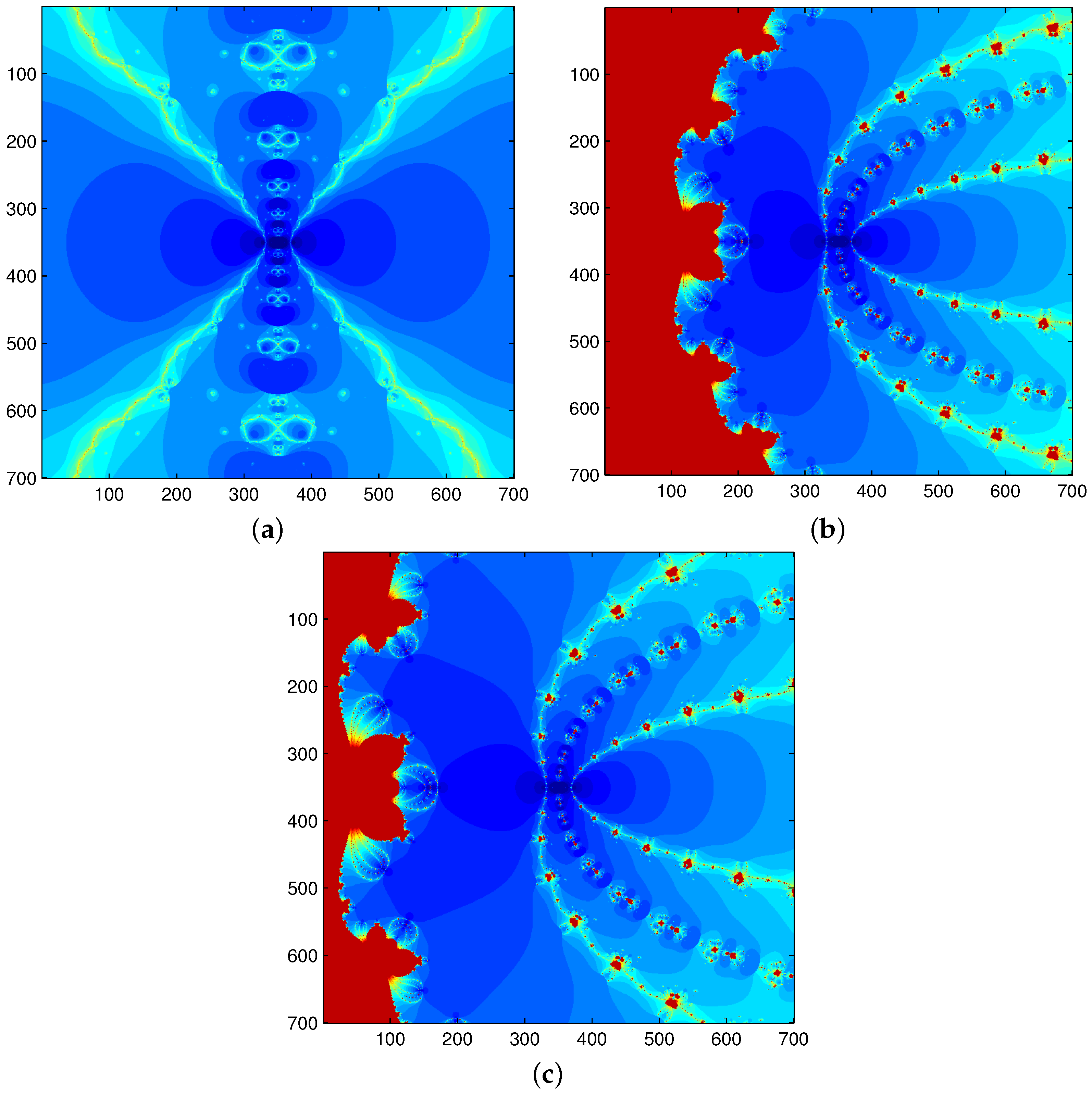
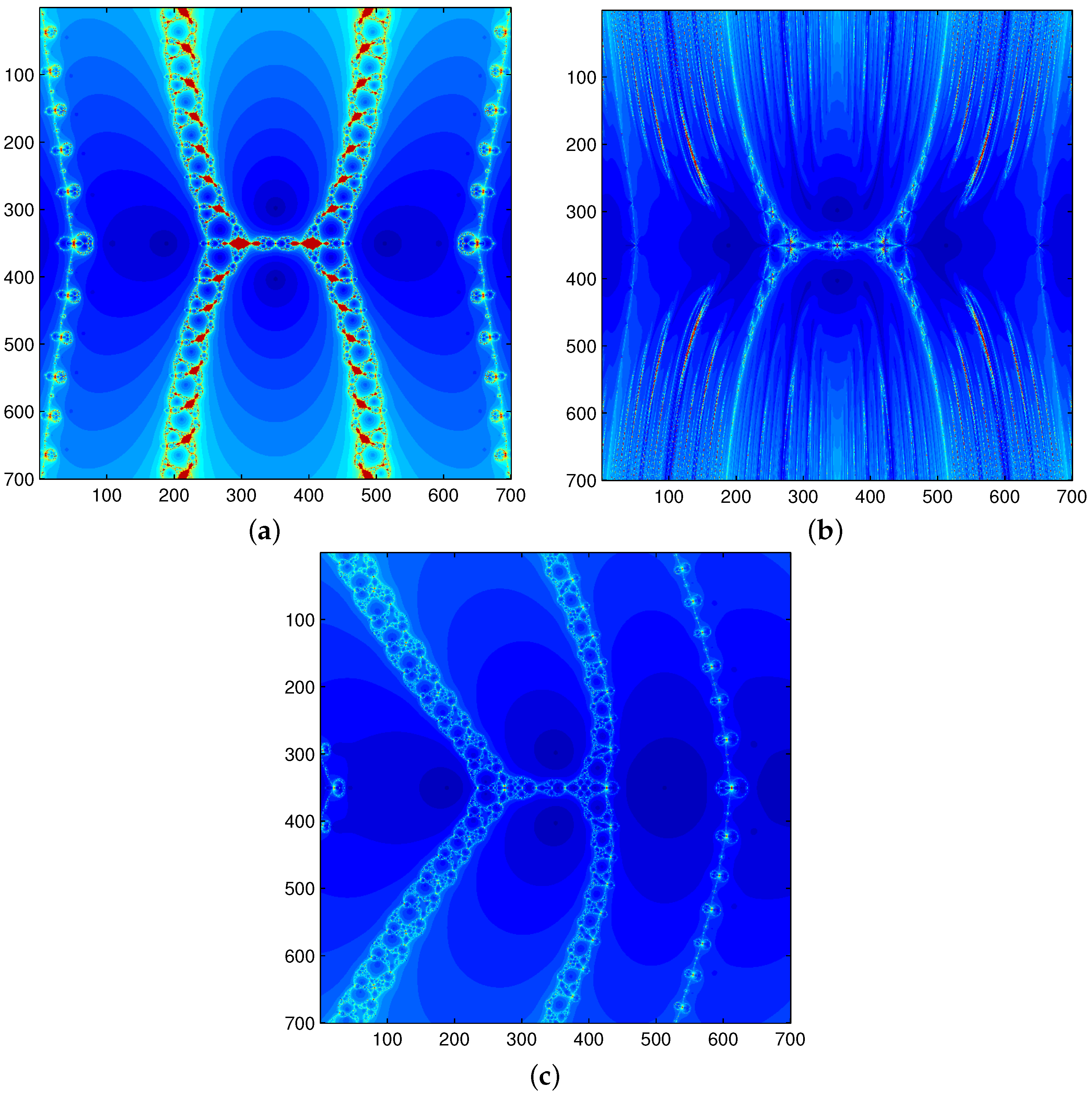
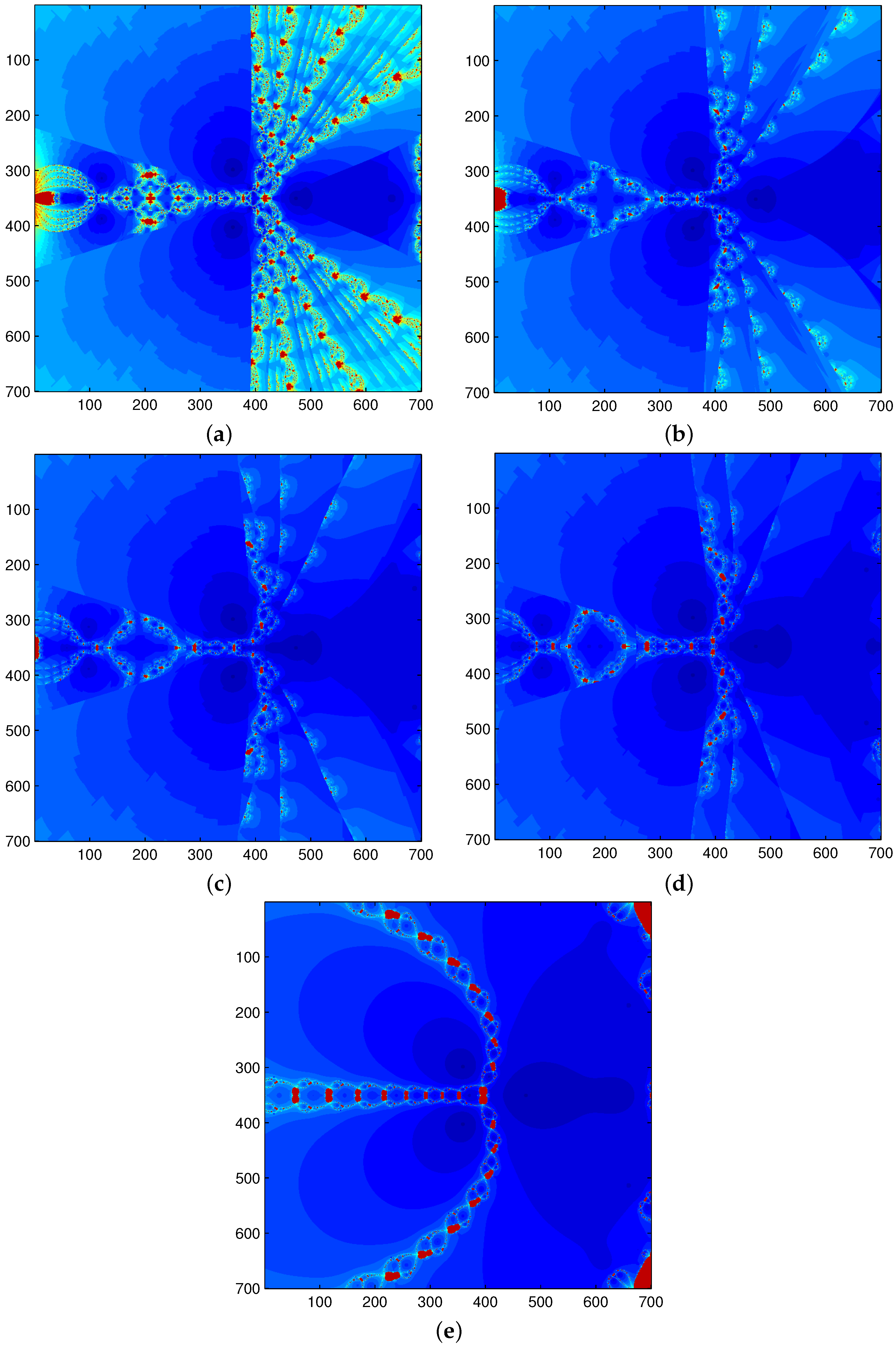
6. Dynamic Analysis of Methods for Functions , , , and
- (i)
- The Julia set of a nonlinear map may also be defined as the common boundary shared by the basins of roots, and the Fatou set may also be defined as the set that contains the basin of attraction.
- (ii)
- Sometimes, the Fatou set of a nonlinear map may also be defined as the solution space and the Julia set of a nonlinear map may also be defined as the error space;
- (iii)
- Fractals are very complicated phenomena that may be defined as self-similar unexpected geometric objects that are repeated at every small scale ([19]).
6.1. Functions for Which the Third-Order Derivative Does Not Exist
6.2. Functions for Which the Third-Order Derivative Exist
6.3. Dynamics of Proposed Method with Variable Value of for Example
7. Future Work
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Baccouch, M. A Family of High Order Numerical Methods for Solving Nonlinear Algebraic Equations with Simple and Multiple Roots. Int. J. Appl. Comput. Math. 2017, 3, 1119–1133. [Google Scholar] [CrossRef]
- Singh, M.K.; Singh, A.K. The Optimal Order Newton’s Like Methods with Dynamics. Mathematics 2021, 9, 527. [Google Scholar] [CrossRef]
- Singh, M.K.; Argyros, I.K. The Dynamics of a Continuous Newton-like Method. Mathematics 2022, 10, 3602. [Google Scholar] [CrossRef]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice Hall: Clifford, NJ, USA, 1964. [Google Scholar]
- Argyros, I.K.; Hilout, S. On Newton’s Method for Solving Nonlinear Equations and Function Splitting. Numer. Math. Theor. Meth. Appl. 2011, 4, 53–67. [Google Scholar]
- Ardelean, G.; Balog, L. A qualitative study of Agarwal et al. iteration procedure for fixed points approximation. Creat. Math. Inform. 2016, 25, 135–139. [Google Scholar] [CrossRef]
- Ardelean, G. A comparison between iterative methods by using the basins of attraction. Appl. Math. Comput. 2011, 218, 88–95. [Google Scholar] [CrossRef]
- Deng, J.J.; Chiang, H.D. Convergence region of Newton iterative power flow method: Numerical studies. J. Appl. Math. 2013, 4, 53–67. [Google Scholar] [CrossRef]
- Kotarski, W.; Gdawiec, K.; Lisowska, A. Polynomiography via Ishikawa and Mann iterations. In International Symposium on Visual Computing; Springer: Berlin/Heidelberg, Germany, 2012; pp. 305–313. [Google Scholar]
- Amat, S.; Busquier, S.; Plaza, S. Review of some iterative root-finding methods from a dynamical point of view. Scientia 2004, 10, 3–35. [Google Scholar]
- Fang, L.; He, G.; Hub, Z. A cubically convergent Newton-type method under weak conditions. J. Comput. Appl. Math. 2008, 220, 409–412. [Google Scholar] [CrossRef]
- Wu, X.Y. A new continuation Newton-like method and its deformation. Appl. Math. Comput. 2000, 112, 75–78. [Google Scholar] [CrossRef]
- Wang, H.; Liu, H. Note on a Cubically Convergent Newton–Type Method Under Weak Conditions. Acta Appl. Math. 2010, 110, 725–735. [Google Scholar] [CrossRef]
- Sahu, D.R. Applications of the S-iteration process to constrained minimization problems and split feasibility problems. Fixed Point Theory 2011, 12, 187–204. [Google Scholar]
- Sahu, D.R. Strong convergence of a fixed point iteration process with applications. In Proceedings of the International Conference on Recent Advances in Mathematical Sciences and Applications; 2009; pp. 100–116. Available online: https://scholar.google.ca/scholar?hl=en&as_sdt=0%2C5&q=Strong+convergence+of+a+fixed+point+iteration+process+with+applications&btnG= (accessed on 18 October 2022).
- Scott, M.; Neta, B.; Chun, C. Basin attractors for various methods. Appl. Math. Comput. 2011, 218, 2584–2599. [Google Scholar] [CrossRef]
- Argyros, I.K.; Magrenan, A.A. Iterative Methods and Their Dynamics with Applications: A Contemporary Study; CRC Press, Taylor and Francis: Boca Raton, FL, USA, 2017. [Google Scholar]
- Julia, G. Memoire sure l’iteration des fonction rationelles. J. Math. Pures et Appl. 1918, 81, 47–235. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1983; ISBN 978-0-7167-1186-5. [Google Scholar]
- Susanto, H.; Karjanto, N. Newton’s method’s basins of attraction revisited. Appl. Math. Comput. 2009, 215, 1084–1090. [Google Scholar] [CrossRef]


| Newton’s Method | Wang and Liu’s Method | Normal S-Iteration Method | |||||
|---|---|---|---|---|---|---|---|
| as Wang and Liu | |||||||
| 0 | F | 5 | 7 | 5 | 5 | 4 | |
| −4 | 6 | 5 | 5 | 4 | 6 | 5 | |
| 1 | F | 7 | 5 | 5 | 5 | 4 | |
| 3 | 7 | 6 | 6 | 6 | 6 | 5 | |
| 5 | D | 5 | 5 | 4 | 7 | 6 | |
| 2 | 6 | 4 | 3 | 3 | 5 | 4 | |
| 3 | D | 4 | 5 | 4 | 5 | 4 | |
| −1 | 5 | 3 | 4 | 3 | 4 | 3 | |
| 4 | NC | 6 | 6 | 5 | 7 | 6 | |
| 2 | 5 | 4 | 4 | 4 | 4 | 4 | |
| 0.73 | D | 8 | 6 | 4 | 8 | 4 | |
| −3 | 23 | 15 | 11 | 9 | 11 | 9 | |
| 0.7 | D | 5 | 4 | 4 | 4 | 4 | |
| 2 | 6 | 4 | 4 | 3 | 4 | 3 | |
| Newton Method | Fang et al. Method | Normal S-Iteration Method | |||||||
|---|---|---|---|---|---|---|---|---|---|
| as Wang and Liu | |||||||||
| F | 7 | 3 | 4 | 3 | 4 | 4 | 5 | ||
| 9 | 9 | 6 | 7 | 6 | 7 | 6 | 8 | ||
| 5 | 5 | 3 | 4 | 3 | 4 | 3 | 4 | ||
| 85 | 58 | 47 | 60 | 47 | 60 | 47 | 60 | ||
| 88 | 61 | 49 | 62 | 49 | 62 | 49 | 62 | ||
| F | 9 | 4 | 5 | 5 | 4 | 4 | 4 | ||
| 89 | 43 | 33 | 42 | 33 | 42 | 33 | 43 | ||
| 10 | F | 3 | 4 | 5 | 4 | 3 | 4 | ||
| Normal S-Iteration Method | |||||
|---|---|---|---|---|---|
| as Wang and Liu | |||||
| 0.1 | 13 | 9 | 9 | ||
| 0.3 | 7 | 8 | 8 | ||
| 0.73 | 0.5 | 6 | 8 | 8 | |
| 0.7 | 5 | 5 | 5 | ||
| 0.9 | 4 | 4 | 4 | ||
| 0.1 | 14 | 15 | 14 | ||
| 0.3 | 12 | 13 | 13 | ||
| −3.0 | 0.5 | 11 | 11 | 11 | |
| 0.7 | 10 | 10 | 10 | ||
| 0.9 | 8 | 9 | 9 | ||
| Normal S-Iteration for Sequence | Normal S-Iteration for Sequence | |||
|---|---|---|---|---|
| as Wang and Liu | as Wang and Liu | |||
| −4.00000000000000 | −4.00000000000000 | −4.00000000000000 | −4.00000000000000 | |
| −3.019890471239318 | −3.269614812666443 | −2.787748595141695 | −3.031336002398129 | |
| −2.647689829523139 | −2.830596759888509 | −2.550732240466982 | −2.602227130430227 | |
| −2.552574309373607 | −2.597269129310047 | −2.546231963106547 | −2.546267106449917 | |
| −2.546259317314531 | −2.547305870288047 | −2.546231731428419 | −2.546231731433164 | |
| −2.546231731968219 | −2.546232155885697 | −2.546231731428418 | ||
| −2.546231731428418 | −2.546231731428486 | |||
| −2.546231731428418 | ||||
| 1.000000000000000 | 1.000000000000000 | 1.000000000000000 | 1.000000000000000 | |
| 0.690862097114279 | 0.713251419170333 | 0.588489366623379 | 0.613537499145787 | |
| 0.500158984920628 | 0.506202917231944 | 0.388129276855868 | 0.391429495638206 | |
| 0.391718592801076 | 0.390681052832476 | 0.323527870651833 | 0.323501217147855 | |
| 0.338547374719877 | 0.337061756299449 | 0.318314259700137 | 0.318313848040219 | |
| 0.320626856711258 | 0.320222652750527 | 0.318309886184780 | 0.318309886184561 | |
| 0.318346374736978 | 0.318333591884421 | 0.318309886183791 | 0.318309886183791 | |
| 0.318309895590689 | 0.318309889954683 | |||
| 0.318309886183791 | 0.318309886183791 | |||
| The average Number of Iterations (ANI) in Normal-S Iteration Method | |||
|---|---|---|---|
| as Wang and Liu | |||
| 0.1 | 5.340000 | 5.080000 | 5.100000 |
| 0.2 | 5.040000 | 4.920000 | 4.920000 |
| 0.3 | 4.800000 | 4.720000 | 4.600000 |
| 0.4 | 4.360000 | 4.480000 | 4.420000 |
| 0.5 | 4.240000 | 4.300000 | 4.280000 |
| 0.6 | 4.100000 | 4.080000 | 4.140000 |
| 0.7 | 3.800000 | 3.760000 | 3.640000 |
| 0.8 | 3.700000 | 3.600000 | 3.540000 |
| 0.9 | 3.620000 | 3.300000 | 3.340000 |
| Average Number of Iterations in Normal-S Iteration Method | |||
|---|---|---|---|
| as Wang and Liu | |||
| 0.1 | 5.725490 | 5.411765 | 5.333333 |
| 0.2 | 5.411765 | 5.196078 | 5.137255 |
| 0.3 | 5.176471 | 4.941176 | 4.882353 |
| 0.4 | 4.980392 | 4.823529 | 4.764706 |
| 0.5 | 4.705882 | 4.666667 | 4.607843 |
| 0.6 | 4.431373 | 4.549020 | 4.450980 |
| 0.7 | 4.254902 | 4.352941 | 4.294118 |
| 0.8 | 3.764706 | 4.137255 | 4.058824 |
| 0.9 | 3.803922 | 3.764706 | 3.666667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, M.K.; Argyros, I.K.; Singh, A.K. Newton-like Normal S-iteration under Weak Conditions. Axioms 2023, 12, 283. https://doi.org/10.3390/axioms12030283
Singh MK, Argyros IK, Singh AK. Newton-like Normal S-iteration under Weak Conditions. Axioms. 2023; 12(3):283. https://doi.org/10.3390/axioms12030283
Chicago/Turabian StyleSingh, Manoj K., Ioannis K. Argyros, and Arvind K. Singh. 2023. "Newton-like Normal S-iteration under Weak Conditions" Axioms 12, no. 3: 283. https://doi.org/10.3390/axioms12030283
APA StyleSingh, M. K., Argyros, I. K., & Singh, A. K. (2023). Newton-like Normal S-iteration under Weak Conditions. Axioms, 12(3), 283. https://doi.org/10.3390/axioms12030283








