Abstract
With the help of advanced digital technologies, product managers can use monitored mission cycles to sustain product reliability. In this study, a random warranty model and a random replacement next (RRN) model are designed to sustain the through-life reliability of the product with monitored mission cycles. The designed random warranty, called a two-stage two-dimensional free repair warranty (2DFRW), can be carried out to sustain the reliability of the product during the warranty stage. In this warranty, ‘whichever occurs first and last’ is used to distinguish the coverage ranges of the latter stage warranties, which is to maintain the warranty fairness by removing the inequity of the former stage warranty. The RRN can be performed to sustain post-warranty reliability, which defines that if the limited number of mission cycles is completed before a working time, then the product will be replaced at next mission cycle completion to extend remaining service life; otherwise, the product will be replaced at a working time. Under the case of the two-stage 2DFRW, the cost rate of the RRN is constructed based on the renewable reward theorem. By simplifying the parameters, some derivative models of the cost rate are presented. Numerical analysis is performed to explore characteristics.
Keywords:
reliability; mission cycle; random warranty; random replacement next; remaining service life; cost rate MSC:
93E20
1. Introduction
Warranty models and policies have always frequently been applied to sustain product reliability during the warranty stage. The growing number of warranties has been researched widely from manufacturers’ perspectives for meeting the needs of practice. Some scholars and researchers have used classic maintenance models to design numerous warranty models, which belong to classic warranties. This category of warranty includes but not limited to the renewable free/pro-rate replacement warranty (RF/PRW) policy (see Liu et al. [1]; Qiao et al. [2]), free repair warranty (FRW) policy (see Chen et al. [3]; Wang et al. [4]; Wang and Ye. [5]; Wang [6]; Ye et al. [7]; Gavish. et al. [8]), nonrenewable replacement warranty (NRW) policy (see Wu and Longhurst [9]) and preventive maintenance warranty (PMW) policy (see Su and Wang [10]; Wang [11]; Peng et al. [12]). Recently, a novel warranty policy is being received with increasing concern, which is called a condition-based warranty policy wherein condition-based maintenance methods in Liu et al. [13]; Li et al. [14]; Wang et al. [15]; Zhu et al. [16]; Qiu et al. [17]; Wang et al. [18]; Zhao et al. [19]; Zhang et al. [20,21]; Chen et al. [22] are integrated into warranty theory. For example, Shang et al. [23] modeled a condition-based RFRW model by integrating condition-based maintenance into a classic RFRW. For the last two years, some scholars and researchers have presented a new kind of warranty, called a random warranty, wherein monitored job/working/mission cycles are modeled as random variables. For example, by modeling working cycles as random variables, Shang et al. [24] proposed a two-dimensional free repair warranty first (2DFRWF) and a two-dimensional free repair warranty last (2DFRWL).
The product reliability can be divided into the product reliability during the warranty stage and the product reliability during the post-warranty stage, wherein the second type of reliability is called the post-warranty reliability of the product (hereinafter similarly). Any of the above warranty models is a core method to sustain the product reliability during the warranty stage. How to sustain post-warranty reliability is a problem that consumers/users must solve. Aiming at sustaining post-warranty reliability, some scholars and researchers have studied maintenance models/policies for reducing maintenance costs, lengthening remaining service life, or minimizing the expected number of post-warranty failures (see Afsahi et al. [25]). Maintenance models/policies to sustain post-warranty reliability include three categories: classic maintenance models, condition-based maintenance models, and random maintenance models. For example, Park et al. [26] and Park and Pham [27] modeled an age replacement model to sustain post-warranty reliability by means of classic age replacement; Shang et al. [23] proposed a condition-based maintenance model by means of an inverse Gaussian process, which belongs to a type of degradation process (see Zhao et al. [28]; Ye and Xie [29]; Qiu and Cui [30]; Yang et al. [31]; Zhao et al. [32]; Qiu et al. [33,34,35,36]; Shang et al. [37] constructed random maintenance models by modeling working cycles as random variables.
From the viewpoint of the types of product failure, the first category of warranty and maintenance models to sustain post-warranty reliability can be applied to sustain the through–life reliability of self-announcing failure products. The second category of related models is a suitable method to sustain the through–life reliability of degradation failure products. For such a category of models, advanced digital technologies become the technical infrastructure of their application, and some models have been applied to the operation and maintenance of some important equipment, such as aircrafts and luxury cars. The third category of related technologies is the ideal tool to sustain the through–life reliability of self-announcing failure products integrated with advanced digital technologies because such technologies can monitor mission cycles in real time. Driven by the fourth industrial revolution, some civil products have been integrated with advanced digital technologies, such as shared bicycles and shared charging piles. Managers/users can monitor mission cycles of these products from respective terminals. With the rapid advance of the fourth industrial revolution, the last two categories of models will be increasingly applied to sustain the through–life reliability of the product integrated with advanced digital technologies.
By designing new constraints as warranty limits, some multi-constrained warranty models have been proposed. For such models, the warranty service periods produced by all limits are not the same. This reality implies that because of the differences in the warranty service periods, multi-constrained warranty models may trigger warranty unfairness from the perspectives of consumers/users, which can be considered warranty discrimination. From the perspective of brand image, the occurrence of warranty discrimination can negatively damage the brand reputation of manufacturers. The above warranty models have never solved this problem. Recently, Shang et al. [38] used the service to prevent warranty discrimination from occurring, where different limits are used to set the coverage ranges of services. As mentioned in Shang et al. [39], ‘whichever occurs first and last’ can form different coverage ranges when the values of the constraints are given the same values. However, in existing works, ‘whichever occurs first and last’ have rarely been used to maintain fairness to prevent warranty discrimination from occurring. When the product goes through a warranty, it has exhausted part of its service life, which is an increasing function with one of the warranty limits. How to lengthen remaining service life at proper expense is an interesting topic, which has been rarely studied by other scholars and researchers.
In this paper, using ‘whichever occurs first and last’, a random warranty is designed. Such a warranty model is divided into two stages. The first stage warranty, called a two-dimensional free repair warranty first (2DFRWF), includes two limits, where ‘whichever occurs first’ is applied to restrict the order of occurrence of such two limits. The warranty of the second stage includes two limits in which ‘whichever occurs first and last’ are applied to sort the order of the occurrence. Because the warranty coverage ranges formed by ‘whichever occurs first’ and ‘whichever occurs last’ are not the same for given values of two limits, applying both in the latter stage warranty can maintain fairness by distinguishing coverage ranges and intensify the attractiveness of the warranty. In the latter-stage warranty, the warranty models related to ‘whichever occurs first’ and ‘whichever occurs last’ are named two-dimensional free discrete repair warranties (2DFDRWs). In view of these factors, such a warranty model is named the two-stage, two-dimensional free repair warranty (2DFRW). The cost measure of the two-stage 2DFRW is derived from the viewpoint of reliability theory, and the cost measures of the related derivative models are presented by simplifying the cost measure of the two-stage 2DFRW. Under the case of using the two-stage 2DFRW as a general warranty model, a random replacement model is proposed to sustain the post-warranty reliability. In such a model, if the limited number of mission cycles is completed before a working time, then the product will be replaced at the next mission cycle completion to lengthen the remaining service life; otherwise, the product will be replaced at a working time. In view of using ‘next’, this model is called a random replacement next (RNN) model. The studied models are numerically illustrated to explore hidden characteristics.
The key novelties/contributions of this study are listed below: ① using the different ranges formed by ‘whichever occurs first and last’ as two coverage areas aims to prevent the discrimination of multi-constrained warranty models from occurring, which has never appeared in existing literature; ② using ‘next’ as a type of replacement limit is designed to avoid the occurrence of using ‘whichever occurs last’ as replacement limit producing the higher maintenance cost.
The remainder of this study is organized as follows. In Section 2, the two-stage 2DFRW is defined to maintain fairness, and the related cost measure is evaluated. In Section 3, the RNN model is defined and modeled to sustain the post-warranty reliability for lengthening remaining service life. Section 4 performs the numerical analysis to extract hidden characteristics. In Section 5, conclusions and further works are presented.
2. Random Warranty Model to Maintain Fairness
The assumptions of this study are given by: the product that belongs to self-announcing failure product (hereinafter similarly) implements missions at mission cycles, and the mission cycles of the () mission are defined random mission cycles following an identical distribution function , wherein no memory exists; the first failure time obeys the distribution function , where is its failure rate function; and the time to repair/replacement is negligible.
2.1. Warranty Definition
Let () be a warranty period; let , and be nonnegative natural numbers. Under such notations, this paper defines a random warranty as follows.
- The warranty service including the former stage warranty and the latter stage warranty sustains the reliability of the product, under which each failure is minimally repaired;
- The former stage warranty is confined to a coverage range formed by the warranty period or the random mission cycle completion, whichever occurs first;
- If the first stage warranty expires at , then the reliability of the related product will be sustained by the second stage warranty whose coverage range is confined to a region formed by the warranty period or the random mission cycle completion, whichever occurs first;
- If the former stage warranty expires at the random mission cycle completion, then the reliability of the related product will still be sustained by the latter stage warranty, whose coverage range is confined to a region formed by the warranty period or the random mission cycle completion, whichever occurs last.
In the warranty of the first stage, ‘whichever occurs first’ is considered, and the coverage range is confined to , which belongs to the two-dimensional free repair warranty first (2DFRWF) in Shang et al. [24]; The warranty service period produced by the warranty period is greater than the warranty service period produced by the random mission cycle completion. The latter stage warranty consists of two discrete limits, i.e., the failure and the random mission cycle completion, and thus is called the two-dimensional free discrete repair warranty (2DFDRW). For the second stage warranty with fixed values of two limits, the coverage range under ‘whichever occurs last’ is greater than the coverage range under ‘whichever occurs first’, and hence ‘whichever occurs last and first’ are respective methods to maintain the fairness of the warranty of consumers whose former stage warranty expires at the random mission cycle completion or to prevent warranty discrimination from occurring. In light of these factors, such a random warranty is called the two-stage two-dimensional free repair warranty (the two-stage 2DFRW) to maintain fairness.
When the random mission cycle is completed, the working time, i.e., the warranty service period, is , which satisfies . Let be a realization of . According to reliability theory, the distribution and reliability functions of are expressed as
which are the n-fold Stieltjes convolution (see Nakagawa [40]).
Similarly, when the random mission cycle is completed or similar cases occur, each function can be obtained by replacing the related parameter. In light of this, the expressions of each function will be offered wherever used.
2.2. The Cost Measure Modeling for the Two-Stage 2DFRW
This section derives the cost measure of the two-stage 2DFRW, i.e., the warranty cost of the two-stage 2DFRW, and presents some derivative warranty models of the two-stage 2DFRW, as shown below.
2.2.1. The Cost Measure of the Former Stage Warranty
Let be the unit cost of minimally repairing. Then, the total cost of minimally repairing for the product going through the former stage warranty at can be computed as , and the total cost of minimally repairing for the product going through the former stage warranty at the random mission cycle completion is given by . Because the occurrence of the product going through the former stage warranty at or the random mission cycle completion can be derived as and , the warranty cost of the former stage warranty can be represented as
2.2.2. The Cost Measure of the Latter Stage Warranty
When the product goes through the former stage warranty at , the failure rate function of the product is , and the latter stage warranty with ‘whichever occurs first’ is triggered to sustain the reliability of such a product. Let be the probability that failures happen exactly in the interval ; then, satisfies . Let be the arrival time of the failure; then, the distribution function and reliability function of satisfy and . Therefore, the total cost of minimally repairing during the latter stage warranty with ‘whichever occurs first’ is given by
where is a realization of .
When the product goes through the former stage warranty at the random mission cycle completion, the failure rate function of the product is , and the latter stage warranty with ‘whichever occurs last’ is triggered to sustain the reliability of such a product. Let be the probability that failures occur exactly in the interval , then the total cost of minimally repairing during the latter stage warranty with ‘whichever occurs last’ is given by
where in Zhao et al. [41] is used.
Because the probability of the events that the product goes through at or the random mission cycle completion are respectively derived as and , the total cost of minimally repairing during the warranty of the second stage can be computed as
2.2.3. The Cost Measure of the Two-Stage 2DFRW
Obviously, for the two-stage 2DFRW, its costs include the warranty cost of the former stage warranty and the warranty cost of the latter stage warranty. Therefore, by summing (1) and (4), the warranty cost of the two-stage 2DFRW can be evaluated as
2.2.4. Derivative Models of the Two-Stage 2DFRW
When , it is obvious for and to hold. The first case signals that the latter stage warranty with ‘whichever occurs first’ is reduced to a one-dimensional free discrete repair warranty (1DFDRW) whose limit is a discrete positive natural number, i.e., the random mission cycle completion. The second case signals that the latter stage warranty with ‘whichever occurs last’ is reduced to a one-dimensional free repair warranty whose limit is remaining service time, which is called the one-dimensional free repair warranty with remaining service life (1DFRW-RSL). Therefore, reduces the two-stage 2DFRW to the two-stage free hybrid repair warranty (FHRW) consisting of 2DFRWF, 1DFDRW and 1DFRW-RSL, and the related warranty cost is represented as
Obviously, makes and . The first case implies that the latter stage warranty with ‘whichever occurs first’ is removed, and the manufacturer no longer maintains the fairness of the warranty that expires at . The second case implies that the latter stage warranty with ‘whichever occurs last’ is reduced to the one-dimensional free discrete repair warranty (1DFDRW) whose limit is the random mission cycle completion. Therefore, reduces the two-stage 2DFRW to the two-stage free hybrid repair warranty (FHRW) consisting of 2DFRWF and 1DFDRW, and the corresponding warranty cost is given by
Clearly, makes and . The first case indicates that the latter stage warranty with ‘whichever occurs first’ is removed, and thus, the manufacturer no longer maintains the fairness of the warranty that expires at . The second case indicates that the latter stage warranty with ‘whichever occurs last’ is reduced to a one-dimensional free repair warranty with remaining service life (1DFRW-RSL), which is similar to the warranty model in (6). In addition, reduces the two-stage 2DFRW to the two-stage FHRW in (6). Therefore, and reduce the two-stage 2DFRW to the two-stage free hybrid repair warranty (FHRW) consisting of 2DFRWF and 1DFRW-RSL, and its cost is given by
Furthermore, and reduce the cost of the two-stage 2DFRW to
which is the cost of the 2DFRWF (see Shang et al. [24]).
When , . This signal can remove the warranty limit , and thus, the former stage warranty is reduced to the free repair warranty (FRW) model. In addition, makes , which means that the latter warranty with ‘whichever occurs last’ is removed. Therefore, under the case of , the two-stage 2DFRW can be reduced to the two-stage FHRW consisting of the FRW in (6) and the 1DFRW-RSL in (8). The related warranty cost is represented as
3. Random Replacement Next Model Sustaining the Post-Warranty Reliability
In the reliability field, ‘whichever occurs first and last’ are two frequently used constraint methods to replace a used product as a new product. The replacement cost under ‘whichever occurs first’ is less than the replacement cost under ‘whichever occurs last’. However, the replacement time under ‘whichever occurs last’ is greater than the replacement time under ‘whichever occurs first’. By ignoring ‘whichever occurs last’, this section will design a novel policy of the random replacement model to sustain the post-warranty reliability for lengthening the remaining service life, as shown below.
3.1. The Design of the Random Replacement Next Model
When and are the working time and random mission cycle number, respectively, the random replacement model is proposed as follows.
- The product through the two-stage 2DFRW is minimally repaired at each failure before replacement.
- If the random mission cycle is completed before the working time is reached, then the product through the two-stage 2DFRW will be replaced at next random mission cycle completion, i.e., the random mission cycle completion; otherwise, it will be replaced at the working time .
In this model, there are two limits, which are and ; ‘next’ rather than any ‘whichever occurs first and last’ is used to restrict the occurrence order of the above two limits. In view of these, such a model is referred to as a random replacement next (RRN) model. Furthermore, the replacement time produced by the random mission cycle completion is longer than the replacement time produced by the random mission cycle completion. Therefore, compared with the random periodic replacement first model considering the random mission cycle completion (see Shang et al. [24]), the RRN can lengthen the remaining service life of the product through the warranty.
3.2. The Expected Cost Rate
To model RRN, a renewable cycle is defined as a time duration that starts from the activation of a new product sold with the two-stage 2DFRW designed in Section 2 to its replacement in the forms of RRN. By means of this definition, in this section, the expected cost rate of the RRN will be derived on the basis of the renewable reward theorem.
3.2.1. The Length of Renewable Cycle
By the design of RRN, the product sold with the two-stage 2DFRW will be replaced at the random mission cycle completion or at the working time . The occurrence probability of the first case is given by , and the corresponding working time equates to , where . The occurrence probability of the second case is given by , and the corresponding working time is equal to . Therefore, the replacement time produced by the RRN is given by
where is a realization of .
Similarly, the warranty service period produced by the former stage warranty is obtained as
The warranty service period produced by the latter stage warranty with ‘whichever occurs first’ is given by
The warranty service period produced by the latter stage warranty with ‘whichever occurs last’ is given by
Because the occurrence probabilities that the product goes through the former stage warranty at or the random mission cycle completion are derived as and , the warranty service period of the latter stage warranty can be computed as
Therefore, by summing (12) and (15), the warranty service period produced by the two-stage 2DFRW can be obtained as
By summing (16) and (11), in the case of using the two-stage 2DFRW and RRN, the length of the renewable cycle is computed as
3.2.2. The Total Cost during the Renewable Cycle
For the product sold with the two-stage 2DFRW, the case at which it goes through the two-stage 2DFRW includes four cases. They are listed as follows: in the case of the second stage warranty with ‘whichever occurs last’, the product goes through the two-stage 2DFRW at or ; under the case of the latter stage warranty with ‘whichever occurs first’, the product goes through the two-stage 2DFRW at or .
When the first case occurs, the related failure rate function is modeled as . Furthermore, the total cost of minimally repairing for the product undergoing the replacement at or the random mission cycle completion is computed as and . Because , , and are subject to distribution functions , , and , the total cost of minimally repairing under RRN can be obtained as
For the product that undergoes the second case, the total cost of minimally repairing under RRN is calculated as
For the product undergoing the third case, the total cost of minimally repairing under RRN is computed as
For the product undergoing the fourth case, the total cost of minimally repairing under RRN is calculated as
Let be the unit replacement cost. Then, by summing all types of costs, the total cost produced by the RRN is computed as
where is the unit failure cost including the unit cost of minimally repairing and
3.2.3. The Expected Cost Rate
Similar to Qiu et al. [42], using the renewable reward theorem in Barlow and Proschan [43], the expected cost rate function formed by both the two-stage 2DFRW and RRN can be given by
where .
Similar to Sheu et al. [44] and Zhang et al. [45], we can discuss the existence and uniqueness of optimal decision variables by means of the first-order derivative of the objective function. They are no longer presented here, and all optimal results will be illustrated in the next section from a numerical perspective.
3.2.4. Other Expected Cost Rates
By the description of the two-stage FHRW in (7), the case in which the product goes through this warranty model includes two cases. They are listed as follows: the product goes through this warranty at ; the product goes through this warranty at .
When the first case occurs, the related failure rate function is given by . Furthermore, the total costs of minimal repair for the product undergoing the replacement at or the random mission cycle completion are computed as and . Because , , and are subject to distribution functions , , and , the total cost of minimally repairing under RRN can be obtained as
When the second case occurs, the total cost of minimally repairing under RRN is computed as
By summing all types of costs, the total cost under the two-stage FHRW in (7) and RRN is computed as
where .
Under the case of using the two-stage FHRW in (7) and RRN, the length of the renewable cycle is computed as
On the basis of the renewable reward theorem, the expected cost rate function under both the two-stage FHRW in (7) and the RRN can be given by
Under the case of using the two-stage FHRW in (8), the case at which the product goes through the warranty includes the case at which the product goes through the warranty at and the case at which the product goes through the warranty at . When the first case occurs, the total costs of minimally repairing are computed as or . Similar to (24), the total cost of minimally repairing under RRN can be obtained as
When the second case occurs, the total cost of minimally repairing under RRN is computed as
By summing all types of costs, the total cost under the two-stage FHRW in (8) and RRN is calculated as
where .
By summing the results, the length of the renewable cycle is computed as
Furthermore, the expected cost rate function formed by both the two-stage FHRW in (8) and the RRN can be given by
By the design of the 2DFRWF in (9), the case in which the product goes through the 2DFRWF is listed as follows: the product goes through such a 2DFRWF at , and the product goes through such a 2DFRWF at . When the former case occurs, the total costs of minimally repairing are computed as and . Similarly, the total cost of minimally repairing under RRN can be obtained as
For the latter case, the total cost of minimally repairing under RRN is computed as
By summing all costs, the total cost under the 2DFRWF in (9) and RRN is computed as
where .
Moreover, the length of the renewable cycle is computed as
Similarly, the expected cost rate function formed by both the 2DFRWF and RRN can be given by
If the replacement at the next random mission cycle completion is ignored, the RRN can be reduced to a random periodic replacement first model as in Shang et al. [24], whose cost rate is given by
where the two-stage FHRW in (8) is used to sustain the product reliability during the warranty stage.
4. Numerical Examples
At present, an increasing number of intelligence appliances are being put into use in China. Advanced digital technologies have been widely integrated into new types of intelligence appliances. With the help of advanced digital technologies, managers can monitor the usage data of intelligence appliances. That is, the deep integration of advanced digital technologies and intelligence appliances enables managers to monitor through-life product usage data. Facilitated by the joining force of advanced digital technologies, such as cyber-physical infrastructure (CPI) and industry application programs (IAPs), manufacturers and users can obtain time span in real time, i.e., mission cycle, which starts from activating before usage and ends with turning off after each mission completion.
For exploring the characteristics of the models proposed in this paper, the latest boiler of X company is considered as an research object, which performs bath missions according to consumers’ instructions. Assisted by advanced digital technologies, consumers activate the boiler before bathing and shut down the boiler after bathing, during which all usage data can be monitored and delivered to the manufacturer. From the statistical perspective, manufacturers have designed the service time of unit boiler as 100,000 times and a limited time span, whichever occurs first. In this study, assume that the occurrence time of the first failure for this latest type of boilers is subject to a Weibull distribution whose failure rate function satisfies where ; assume that all mission cycles of such a type of products are random mission cycles to obey an identical distribution function with a constant failure rate . To conveniently perform numerical experiments, here any of parameter value for the above distribution functions is no longer estimated because parameter estimating belongs to a statistical problem exceeding this study. Similarly, the values of some of the parameters are defined as , and , and other parameters are set to be values wherever used.
Based on these statements and by means of MATLAB software, the two-stage 2DFRW and RNN are illustrated below.
4.1. Exploration of the Characteristics of the Designed Warranty
In Section 2, five warranty models have been presented, which are the two-stage 2DFRW in Section 2.1 and four models in Section 2.2.4. By taking the two-stage 2DFRW as a typical example, some characteristic explorations are provided below.
Let and ; then, Figure 1 has been plotted to explore the characteristics of the two-stage 2DFRW.
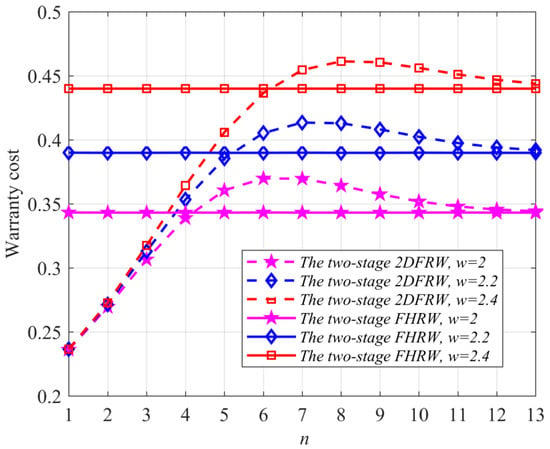
Figure 1.
The impact of the coverage range of the former stage warranty on the two-stage 2DFRW.
Figure 1 shows that the increase in makes the warranty cost of the two-stage 2DFRW enhanced first to a maximum value and then downed to the warranty cost of the two-stage FHRW in (10). The increase in can increase the costs of the former stage warranty and the latter stage warranty with ‘whichever occurs first’ and decrease the cost of the latter stage warranty with ‘whichever occurs last’. This signal that the increase in can produce the following changes: the increment in the costs of the former stage warranty and the latter stage warranty with ‘whichever occurs first’ is first greater than the decrement in the cost of the latter stage warranty with ‘whichever occurs last’ and is second less than the latter decrement. The increase in can reduce the two-stage 2DFRW to the two-stage FHRW in (10). Therefore, the ordered appearance of these changes makes the above laws occur. In addition, the increase in can extend the coverage range of the two-stage 2DFRW, and thus, the warranty cost of the two-stage 2DFRW increases with , as shown in Figure 1.
By setting and , Figure 2 has been used to further explore the characteristics of the two-stage 2DFRW. Figure 2 shows that the increase in can enhance the warranty cost of the two-stage 2DFRW. The core cause of such a law is listed as follows: the increase in can extend the coverage range of the latter stage warranty, which is not affected by any of ‘whichever occurs first and last’. In Figure 2, it is found that when is smaller, the warranty cost of the two-stage 2DFRW increases with ; when is larger, the warranty cost of the two-stage 2DFRW tends to the same value with . The smaller can keep each of the two latter stage warranties, and the increase in can extend the coverage range of the warranty of the last stage. The larger keeps the latter stage warranty with ‘whichever occurs first’ and removes the latter stage warranty with ‘whichever occurs last’, which means that the warranty cost of the latter stage warranty with ‘whichever occurs first’ is a unique cost. Therefore, the above two cases occur.
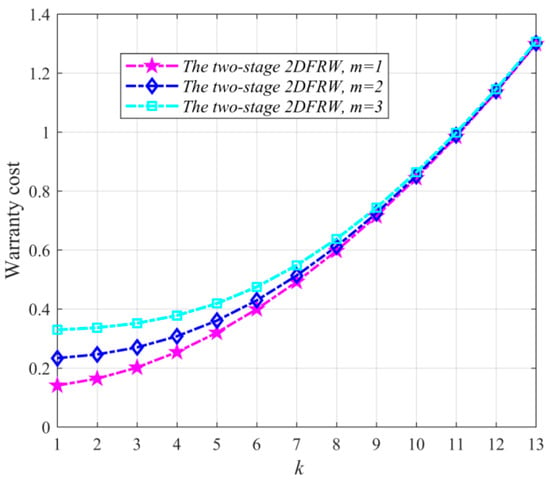
Figure 2.
The impact of the coverage range of the second stage warranty on the two-stage 2DFRW.
4.2. Exploration of the Characteristics of RNNs
Five cost rate models have been presented in Section 3, which are models in (23), (28), (33), (38) and (39). Any of them includes an RNN. In view of this, taking the model in (28) as a typical example, the characteristics of RNN are explored below.
To verify the feasibility of RNN and explore how affects the optimal RNN, Figure 3 has been provided by using , and . Figure 3 shows that the minimum cost rate exists, which signals that the RNN is feasible. In addition, Figure 3 shows that the increase in increases the minimum cost rate , the optimal working time and the optimal mission cycle number .
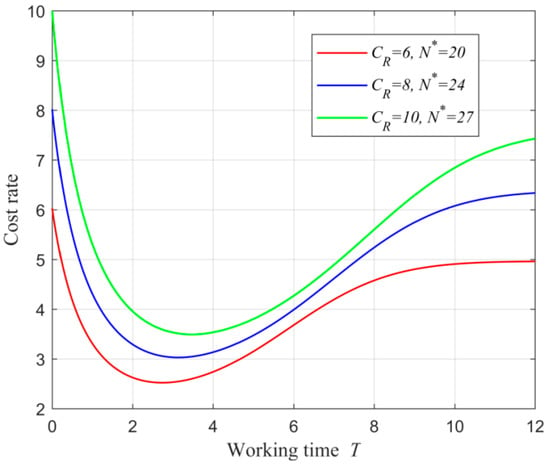
Figure 3.
The impact of on the optimal RNN.
Under the case of , and , Table 1 shows how the former stage warranty affects the optimal RNN. In Table 1, is non-increasing with each of and , is decreasing with and , and is decreasing with as well as increasing with . The former two laws imply that when the coverage range of the first stage warranty increases, the replacement time of the product through the two-stage FHRW in (7) decreases, and vice versa.

Table 1.
The impact of the former stage warranty on the optimal RNN.
Under the case of , , and , Table 2 shows how the latter stage warranty affects the optimal RNN. Table 2 shows that increases with and is non-increasing with , decreases with and increases with , and decreases with and increases with . The former two laws imply that when the coverage range of the latter stage warranty increases, the replacement time of the product through the two-stage FHRW in (7) decreases, which is similar to that of Table 1.

Table 2.
The impact of the latter stage warranty on the optimal RNN.
To illustrate the performance of the RNN, Table 3 has been offered using , , and . The optimal working time of the RNN is greater than the optimal working time of the optimal random periodic replacement whose cost rate has been offered in (39), while the relationship between the optimal cost rates is opposite to that between the optimal working times. These results imply that RNNs can lengthen the remaining service life at a lower cost rate.

Table 3.
The performance illustration of the RNN.
5. Conclusions
Under the case of taking a support background where advanced digital technologies improve the operation and maintenance of products, this paper devises a two-stage two-dimensional free repair warranty (2DFRW) to sustain the product reliability during the warranty stage in order for warranty fairness to be maintained by removing inequality. The cost measure of the two-stage 2DFRW is evaluated from the perspective of reliability theory. By discussing parameter values, some derivative models of the two-stage 2DFRW are presented, and the related cost measures are obtained by solving the problem of the limit. Additionally, a random replacement next (RRN) model that considers two limits is defined to maintain post-warranty reliability for extending the remaining service life of the product through the warranty. By taking the two-stage 2DFRW and some of its derivatives as warranty models, the expected cost rates of the RRN are constructed on the basis of the renewable reward theorem. The characteristics of the two-stage 2DFRW and RRN are mined by means of numerical analysis. Compared with the random periodic replacement first model, the RNN can lengthen the remaining service life of the product through its warranty at a lower cost rate.
The ideas involved in this paper can enrich theories of warranty and post-warranty maintenance and have a certain use for reference in the design of warranty and post-warranty maintenance. In addition, some new models of sustaining the through-life reliability of the product can be constructed, which include but are not limited to the following:
- ◆
- Flexible warranty models under the case of the multi-failure mode;
- ◆
- Customized maintenance models to sustain the different post-warranty reliabilities.
Author Contributions
Conceptualization, L.S. (Lijun Shang) and L.Y.; methodology, L.S. (Lijun Shang); software, L.S. (Lifeng Shang); validation, L.S. (Lifeng Shang)and N.Z.; formal analysis, L.S. (Lifeng Shang); investigation, L.S.(Lijun Shang); resources, L.Y.; writing—original draft preparation, L.S. (Lijun Shang); writing—review and editing, L.S. (Lijun Shang); visualization, L.S. (Lifeng Shang); supervision, N.Z.; project administration, L.Y.; funding acquisition, L.S. (Lijun Shang). All authors have read and agreed to the published version of the manuscript.
Funding
This article is supported by the Base and Basic Applied Study of Guangdong Province (No. 2020A1515011360), the National Natural Science Foundation of China (Nos. 71871181, 72161025, 72271169).
Data Availability Statement
The authors confirm that the data supporting the findings of this study are available within the article.
Acknowledgments
The authors sincerely thank all unknown reviewers for their valuable suggestions and helpful comments that have led to the present form of the original manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, B.; Wu, J.; Xie, M. Cost analysis for multi-component system with failure interaction under renewing free-replacement warranty. Eur. J. Oper. Res. 2015, 243, 874–882. [Google Scholar] [CrossRef]
- Qiao, P.; Shen, J.; Zhang, F.; Ma, Y. Optimal warranty policy for repairable products with a three-dimensional renewable combination warranty. Comput. Ind. Eng. 2022, 168, 108056. [Google Scholar] [CrossRef]
- Chen, C.-K.; Lo, C.-C.; Weng, T.-C. Optimal production run length and warranty period for an imperfect production system under selling price dependent on warranty period. Eur. J. Oper. Res. 2017, 259, 401–412. [Google Scholar] [CrossRef]
- Wang, L.; Pei, Z.; Zhu, H.; Liu, B. Optimising extended warranty policies following the two-dimensional warranty with repair time threshold. Eksploat. Niezawodn. Maint. Reliab. 2018, 20, 523–530. [Google Scholar] [CrossRef]
- Wang, X.; Ye, Z.-S. Design of customized two-dimensional extended warranties considering use rate and heterogeneity. IISE Trans. 2020, 53, 341–351. [Google Scholar] [CrossRef]
- Wang, X.-L. Design and pricing of usage-driven customized two-dimensional extended warranty menus. IISE Trans. 2022, 1–33. [Google Scholar] [CrossRef]
- Ye, Z.; Murthy, D.N.P.; Xie, M.; Tang, L. Optimal burn-in for repairable systems sold with a two-dimensional warranty. IIE Trans. 2013, 45, 164–176. [Google Scholar] [CrossRef]
- Gavish, B.; Sobol, M. Warranty Policy Impact On Net Revenues Due To Optional Purchases. Int. J. Inf. Technol. Decis. Mak. 2010, 9, 507–523. [Google Scholar] [CrossRef]
- Wu, S.; Longhurst, P. Optimising age-replacement and extended non-renewing warranty policies in lifecycle costing. Int. J. Prod. Econ. 2011, 130, 262–267. [Google Scholar] [CrossRef]
- Su, C.; Wang, X. A two-stage preventive maintenance optimization model incorporating two-dimensional extended warranty. Reliab. Eng. Syst. Saf. 2016, 155, 169–178. [Google Scholar] [CrossRef]
- Wang, X.; Li, L.; Xie, M. An unpunctual preventive maintenance policy under two-dimensional warranty. Eur. J. Oper. Res. 2019, 282, 304–318. [Google Scholar] [CrossRef]
- Peng, S.; Jiang, W.; Wei, L.; Wang, X.-L. A new cost-sharing preventive maintenance program under two-dimensional warranty. Int. J. Prod. Econ. 2022, 254, 108580. [Google Scholar] [CrossRef]
- Liu, B.; Pandey, M.D.; Wang, X.; Zhao, X. A finite-horizon condition-based maintenance policy for a two-unit system with dependent degradation processes. Eur. J. Oper. Res. 2021, 295, 705–717. [Google Scholar] [CrossRef]
- Li, H.; Zhu, W.; Dieulle, L.; Deloux, E. Condition-based maintenance strategies for stochastically dependent systems using Nested Lévy copulas. Reliab. Eng. Syst. Saf. 2021, 217, 108038. [Google Scholar] [CrossRef]
- Wang, J.; Qiu, Q.; Wang, H. Joint optimization of condition-based and age-based replacement policy and inventory policy for a two-unit series system. Reliab. Eng. Syst. Saf. 2020, 205, 107251. [Google Scholar] [CrossRef]
- Zhu, W.; Fouladirad, M.; Berenguer, C. Condition-based maintenance policies for a combined wear and shock deterioration model with covariates. Comput. Ind. Eng. 2015, 85, 268–283. [Google Scholar] [CrossRef]
- Qiu, Q.; Maillart, L.M.; Prokopyev, O.A.; Cui, L. Optimal Condition-Based Mission Abort Decisions. IEEE Trans. Reliab. 2022, 1–18. [Google Scholar] [CrossRef]
- Wang, J.; Qiu, Q.; Wang, H.; Lin, C. Optimal condition-based preventive maintenance policy for balanced systems. Reliab. Eng. Syst. Saf. 2021, 211, 107606. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, J.; Qiu, Q.; Chen, K. Optimal inspection and mission abort policies for systems subject to degradation. Eur. J. Oper. Res. 2020, 292, 610–621. [Google Scholar] [CrossRef]
- Zhang, N.; Tian, S.; Cai, K.; Zhang, J. Condition-based maintenance assessment for a deteriorating system considering stochastic failure dependence. IISE Trans. 2022, 1–11. [Google Scholar] [CrossRef]
- Zhang, N.; Fouladirad, M.; Barros, A.; Zhang, J. Condition-based maintenance for a K-out-of-N deteriorating system under periodic inspection with failure dependence. Eur. J. Oper. Res. 2020, 287, 159–167. [Google Scholar] [CrossRef]
- Chen, Y.; Qiu, Q.; Zhao, X. Condition-based opportunistic maintenance policies with two-phase inspections for continuous-state systems. Reliab. Eng. Syst. Saf. 2022, 228, 108767. [Google Scholar] [CrossRef]
- Shang, L.; Si, S.; Sun, S.; Jin, T. Optimal warranty design and post-warranty maintenance for products subject to stochastic degradation. IISE Trans. 2018, 50, 913–927. [Google Scholar] [CrossRef]
- Shang, L.; Qiu, Q.; Wang, X. Random periodic replacement models after the expiry of 2D-warranty. Comput. Ind. Eng. 2021, 164, 107885. [Google Scholar] [CrossRef]
- Afsahi, M.; Kashan, A.H.; Ostadi, B. A Bi-Objective Simulation-Based Optimization Approach for Optimizing Price, Warranty, and Spare Part Production Decisions Under Imperfect Repair. Int. J. Inf. Technol. Decis. Mak. 2021, 20, 903–932. [Google Scholar] [CrossRef]
- Park, M.; Jung, K.M.; Park, D.H. A Generalized Age Replacement Policy for Systems Under Renewing Repair-Replacement Warranty. IEEE Trans. Reliab. 2015, 65, 604–612. [Google Scholar] [CrossRef]
- Park, M.; Pham, H. Cost models for age replacement policies and block replacement policies under warranty. Appl. Math. Model. 2016, 40, 5689–5702. [Google Scholar] [CrossRef]
- Zhao, X.; Fan, Y.; Qiu, Q.; Chen, K. Multi-criteria mission abort policy for systems subject to two-stage degradation process. Eur. J. Oper. Res. 2021, 295, 233–245. [Google Scholar] [CrossRef]
- Ye, S.Z.; Xie, M. Stochastic modelling and analysis of degradation for highly reliable products. Appl. Stoch. Model. Bus. Ind. 2015, 31, 16–32. [Google Scholar] [CrossRef]
- Qiu, Q.; Cui, L. Gamma process based optimal mission abort policy. Reliab. Eng. Syst. Saf. 2019, 190, 106496. [Google Scholar] [CrossRef]
- Yang, L.; Chen, Y.; Qiu, Q.; Wang, J. Risk Control of Mission-Critical Systems: Abort Decision-Makings Integrating Health and Age Conditions. IEEE Trans. Ind. Inform. 2022, 18, 6887–6894. [Google Scholar] [CrossRef]
- Zhao, X.; Chai, X.; Sun, J.; Qiu, Q. Joint optimization of mission abort and protective device selection policies for multistate systems. Risk Anal. 2022, 42, 2823–2834. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Q.; Cui, L.; Wu, B. Dynamic mission abort policy for systems operating in a controllable environment with self-healing mechanism. Reliab. Eng. Syst. Saf. 2020, 203, 107069. [Google Scholar] [CrossRef]
- Qiu, Q.; Kou, M.; Chen, K.; Deng, Q.; Kang, F.; Lin, C. Optimal stopping problems for mission oriented systems considering time redundancy. Reliab. Eng. Syst. Saf. 2020, 205, 107226. [Google Scholar] [CrossRef]
- Qiu, Q.; Cui, L. Optimal mission abort policy for systems subject to random shocks based on virtual age process. Reliab. Eng. Syst. Saf. 2019, 189, 11–20. [Google Scholar] [CrossRef]
- Qiu, Q.; Cui, L.; Dong, Q. Preventive maintenance policy of single-unit systems based on shot-noise process. Qual. Reliab. Eng. Int. 2019, 35, 550–560. [Google Scholar] [CrossRef]
- Shang, L.; Qiu, Q.; Wu, C.; Du, Y. Random replacement policies to sustain the post-warranty reliability. J. Qual. Maint. Eng. 2022; ahead-of-print. [Google Scholar] [CrossRef]
- Shang, L.; Yu, X.; Wang, X.; Qiu, Q. Study of A Two-stage Random Warranty to Maintain Fairness. Procedia Comput. Sci. 2022, 214, 437–440. [Google Scholar] [CrossRef]
- Shang, L.; Liu, B.; Cai, Z.; Wu, C. Random maintenance policies for sustaining the reliability of the product through 2D-warranty. Appl. Math. Model. 2022, 111, 363–383. [Google Scholar] [CrossRef]
- Nakagawa, T. Maintenance Theory of Reliability; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Zhao, X.; Qian, C.; Nakagawa, T. Comparisons of replacement policies with periodic times and repair numbers. Reliab. Eng. Syst. Saf. 2017, 168, 161–170. [Google Scholar] [CrossRef]
- Qiu, Q.; Cui, L.; Gao, H. Availability and maintenance modelling for systems subject to multiple failure modes. Comput. & Ind. Eng. 2017, 108, 192–198. [Google Scholar]
- Barlow, R.E.; Proschan, F. Mathematical Theory of Reliability; John Wiley & Sons: New York, NY, USA, 1965. [Google Scholar]
- Sheu, S.-H.; Liu, T.-H.; Zhang, Z.-G. Extended optimal preventive replacement policies with random working cycle. Reliab. Eng. Syst. Saf. 2019, 188, 398–415. [Google Scholar] [CrossRef]
- Zhang, Q.; Yao, W.; Xu, P.; Fang, Z. Optimal age replacement policies of mission-oriented systems with discounting. Comput. Ind. Eng. 2023, 177, 109027. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).