Impact of Goodwill on Consumer Buying through Advertising in a Segmented Market: An Optimal Control Theoretic Approach
Abstract
1. Introduction
2. Model Formulation
3. Optimal Policy and Local Stability Analysis
3.1. Optimal Dynamic Strategy for Finite Time Horizon
3.2. Optimal Dynamic Strategy for Infinite Time Horizon
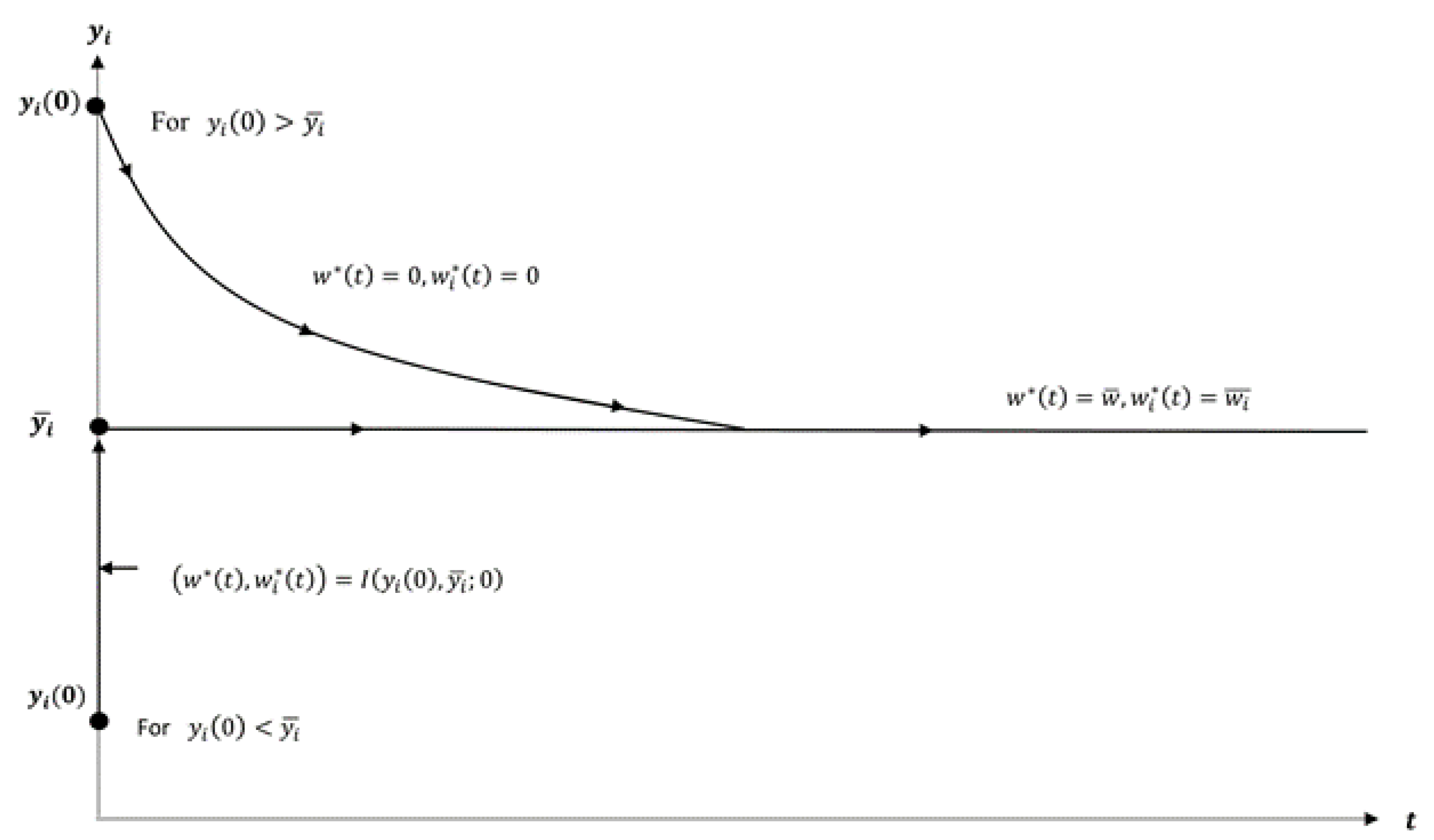
3.3. Local Stability Analysis in the State–Costate-Phase Plane
4. Numerical Illustration and Sensitivity Analysis
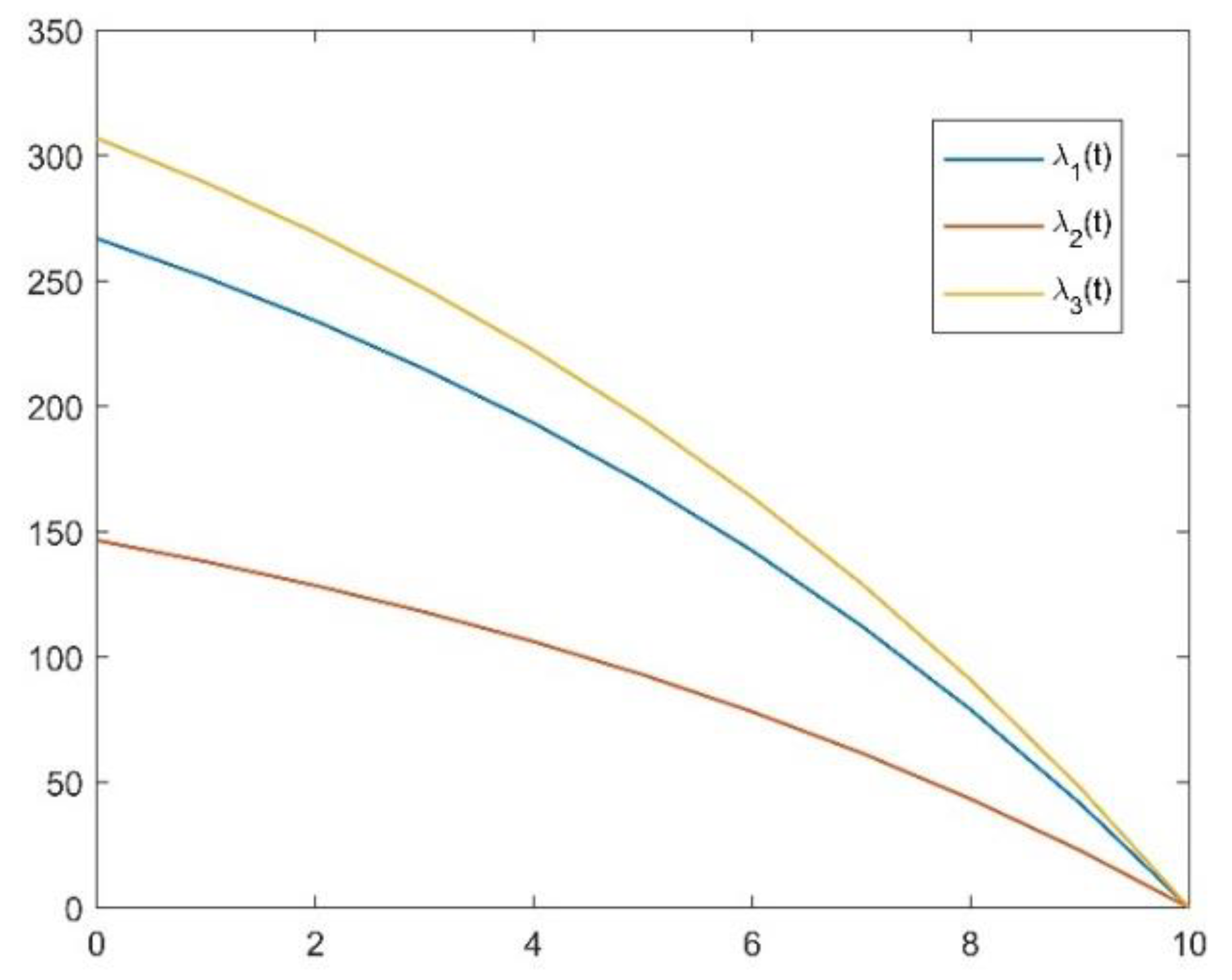
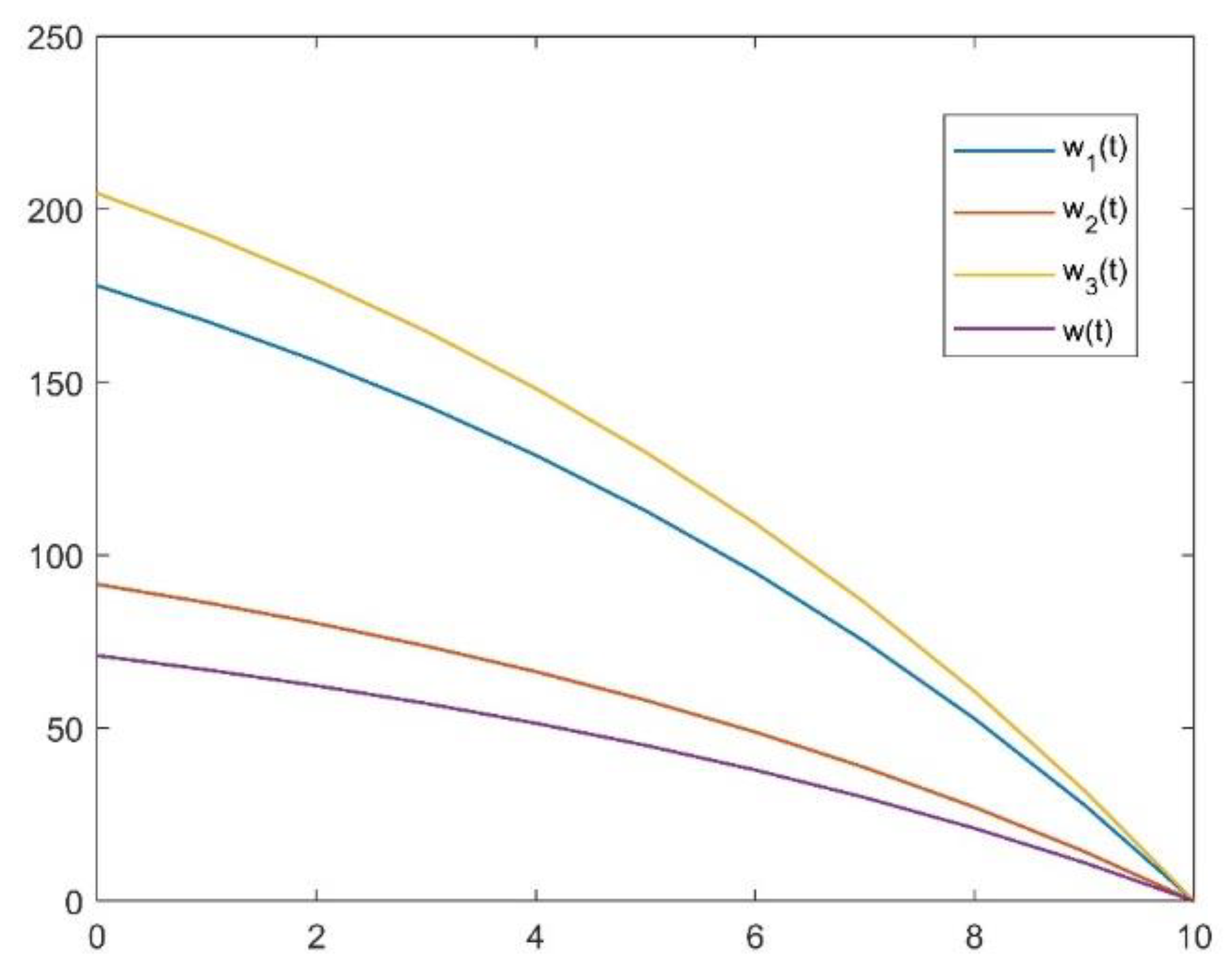
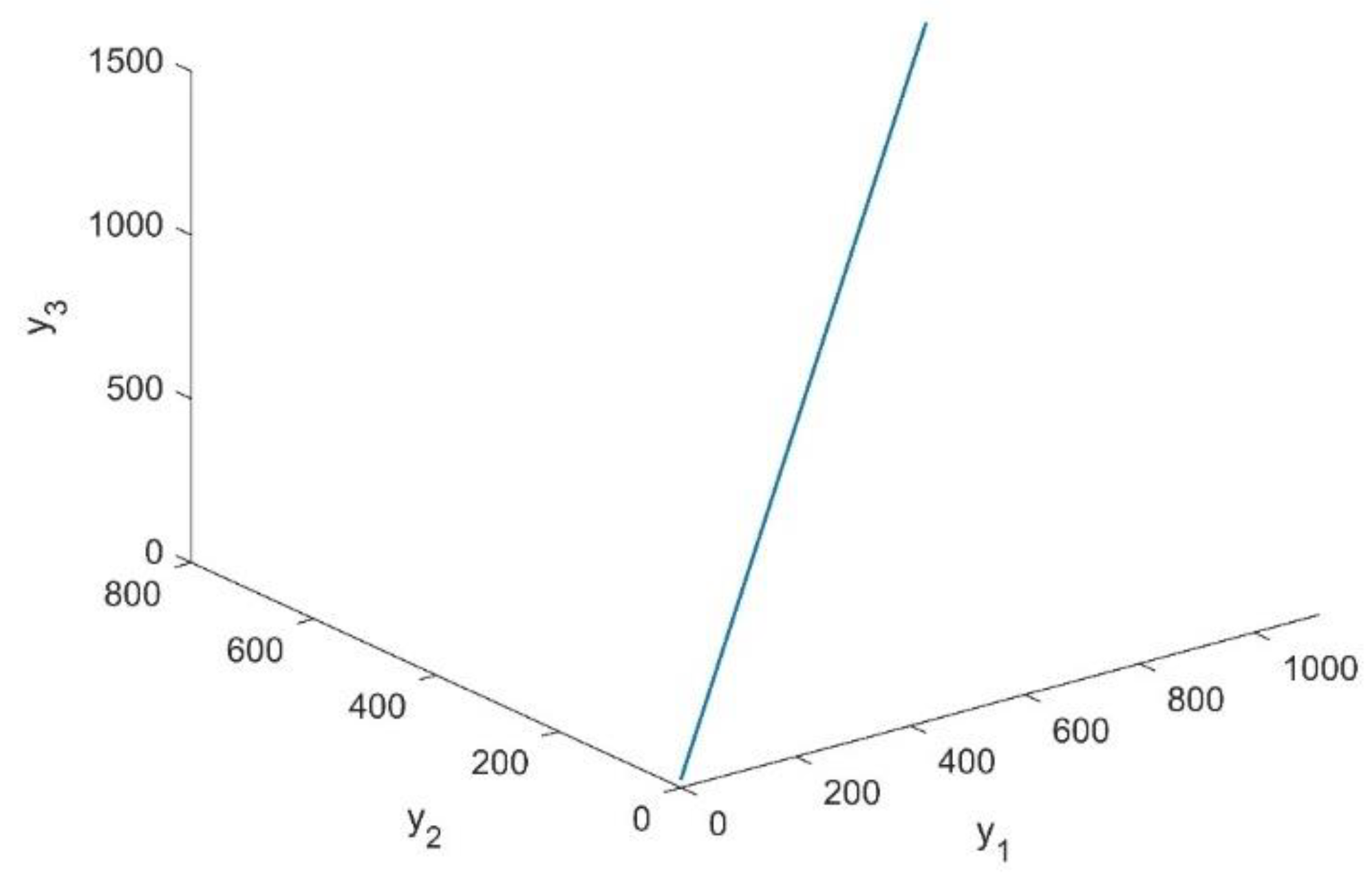
4.1. Numerical Illustrations
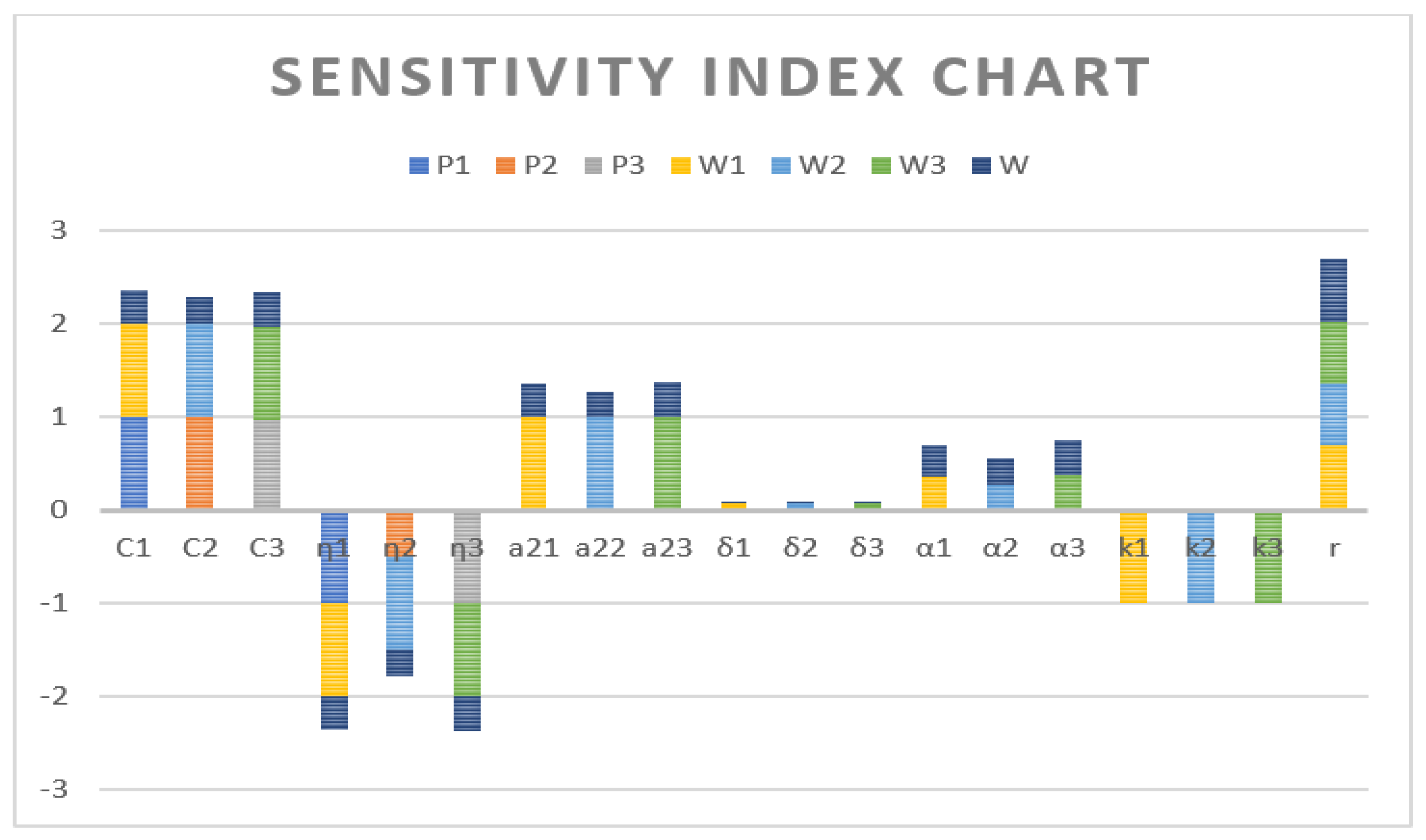
4.2. Local Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Proof of Equations (12)–(15):
References
- Kotler, P. Marketing Management, 11th ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2003. [Google Scholar]
- Kotler, P.; De Bes, F.T. Lateral Marketing: New Techniques for Finding Breakthrough Ideas; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Wedel, M.; Kamakura, W. Market Segmentation: Conceptual and Methodological Foundations, 2nd ed.; Kluwer Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Steenkamp, J.-B.E.; Ter Hofstede, F. International Market Segmentation: Issues and Perspectives. Int. J. Res. Mark. 2002, 19, 185–213. [Google Scholar] [CrossRef]
- Chaturvedi, A.; Carroll, J.D.; Green, P.E.; Rotondo, J.A. A Feature-Based Approach to Market Segmentation Via Overlapping K-Centroids Clustering. J. Mark. Res. 1997, 34, 370–377. [Google Scholar] [CrossRef]
- Lemmens, A.; Croux, C.; Stremersch, S. Dynamics in the International Market Segmentation of New Product Growth. Int. J. Res. Mark. 2012, 29, 81–92. [Google Scholar] [CrossRef]
- Little, J.D.C.; Lodish, L.M. A Media Planning Calculus. Oper. Res. 1969, 17, 1–35. [Google Scholar] [CrossRef]
- Seidmann, T.I.; Sethi, S.P.; Derzko, N.A. Dynamics and Optimization of a Distributed Sales-Advertising Models. J. Optim. Theory Appl. 1987, 52, 443–462. [Google Scholar] [CrossRef]
- Buratto, A.; Grosset, L.; Viscolani, B. Advertising Channel Selection in a Segmented Market. Automatica 2006, 42, 1343–1347. [Google Scholar] [CrossRef]
- Favaretto, D.; Viscolani, B. Advertising and Production of a Seasonal Good for a Heterogeneous Market. 4or-A Q. J. Oper. Res. 2010, 8, 141–153. [Google Scholar] [CrossRef]
- Buratto, A.; Grosset, L.; Viscolani, B. Advertising a New Product in Segmented Market. Eur. J. Oper. Res. 2006, 175, 1262–1267. [Google Scholar] [CrossRef]
- Nerlove, M.; Arrow, K.J. Optimal advertising policy under dynamic conditions. Economica 1962, 29, 129–142. [Google Scholar] [CrossRef]
- Jha, P.C.; Chaudhary, K.; Kapur, P.K. Optimal Advertising Control Policy for A New Product in Segmented Market. OPSEARCH 2009, 46, 225–237. [Google Scholar] [CrossRef]
- Mehta, S.; Chaudhary, K.; Kumar, V. Optimal Promotional Effort Policy in Innovation Diffusion Model Incorporating Dynamic Market Size in Segment Specific Market. Int. J. Math. Eng. Manag. Sci. 2020, 5, 682–696. [Google Scholar] [CrossRef]
- Ma, J.; Jiang, H. Dynamics of a nonlinear differential advertising model with single parameter sales promotion strategy. Electron. Res. Arch. 2022, 30, 1142–1157. [Google Scholar] [CrossRef]
- Chaudhary, K.; Kumar, P.; Chauhan, S.; Kumar, V. Optimal promotional policy of an innovation diffusion model incorporating the brand image in a segment-specific market. J. Manag. Anal. 2022, 9, 120–136. [Google Scholar] [CrossRef]
- Fruchter, G.E.; Jaffe, E.D.; Nebenzahl, I.D. Nebenzahl, Dynamic Brand-Image-based Production Location Decisions. Automatica 2006, 42, 1371–1380. [Google Scholar] [CrossRef]
- Feichtinger, G.; Hartl, R.F.; Sethi, S.P. Dynamic optimal control models in advertising: Recent developments. Manag. Sci. 1994, 40, 195–226. [Google Scholar] [CrossRef]
- Sethi, S.P.; Thompson, G.L. Optimal Control Theory: Applications to Management Science and Economics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2000. [Google Scholar]
- Teng, J.T.; Thompson, G.L. Oligopoly Models for Optimal Advertising When Production Costs Obey a Learning Curve. Manag. Sci. 1983, 29, 1087–1101. [Google Scholar] [CrossRef]
- Mesak, H.I.; Bari, A.; Ellis, T.S. Optimal Dynamic Marketing-Mix Policies for Frequently Purchased Products and Services Versus Consumer Durable Goods: A Generalized Analytic Approach. Eur. J. Oper. Res. 2020, 280, 764–777. [Google Scholar] [CrossRef]
- Kumar, P.; Chaudhary, K.; Kumar, V.; Singh, V.B. Advertising and Pricing Policies for a Diffusion Model Incorporating Price Sensitive Potential Market in Segment Specific Environment. Int. J. Math. Eng. Manag. Sci. 2022, 7, 547–557. [Google Scholar] [CrossRef]
- Huang, J.; Leng, M.; Liang, L. Recent Developments in Dynamic Advertising Research. Eur. J. Oper. Res. 2012, 220, 591–609. [Google Scholar] [CrossRef]
- Dockner, E.J.; Jorgensen, S. Optimal Advertising Policies for Diffusion Models of New Product Innovation in Monopolistic Situations. Manag. Sci. 1988, 34, 119–130. [Google Scholar] [CrossRef]
- Pan, X.; Li, S. Dynamic Optimal Control of Process-Product Innovation with Learning by Doing. Eur. J. Oper. Res. 2016, 248, 136–145. [Google Scholar] [CrossRef]
- Ouardighi, F.E.; Pasin, F. Quality Improvement and Goodwill Accumulation in a Dynamic Duopoly. Eur. J. Oper. Res. 2006, 175, 1021–1032. [Google Scholar] [CrossRef]
- Seierstad, A.; Sydsaeter, K. Optimal Control Theory with Economic Applications; North-Holland: Amesterdam, The Netherlands, 1987. [Google Scholar]
- Kalish, S. Monopolist pricing with dynamic demand and product cost. Mark. Sci. 1983, 2, 135–159. [Google Scholar] [CrossRef]
- Gale, D.; Nikaido, H. The Jacobian matrix and global univalence of mappings. Math. Ann. 1965, 159, 81–93. [Google Scholar] [CrossRef]

| Segment | ||||||||
|---|---|---|---|---|---|---|---|---|
| S1 | 1660 | 0.30 | 2.5 | 2.2 | 20 | 0.01 | 2 | 1.5 |
| S2 | 1670 | 0.32 | 2.3 | 2.3 | 21 | 0.01 | 3 | 1.6 |
| S3 | 1670 | 0.28 | 2.4 | 2.2 | 23 | 0.01 | 2 | 1.5 |
| Parameters | w | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 0 | 0 | 0.3504 | |
| 0 | 1 | 0 | 0 | 1 | 0 | 0.2735 | |
| 0 | 0 | 0.9565 | 0 | 0 | 1 | 0.3761 | |
| −1 | 0 | 0 | −1 | 0 | 0 | −0.3504 | |
| 0 | −0.5 | 0 | 0 | −1 | 0 | −0.2735 | |
| 0 | 0 | −1 | 0 | 0 | −1 | −0.3761 | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0.3504 | |
| 0 | 0 | 0 | 0 | 1 | 0 | 0.2735 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 0.3761 | |
| 0 | 0 | 0 | 0.0645 | 0 | 0 | 0.0236 | |
| 0 | 0 | 0 | 0 | 0.0673 | 0 | 0.0184 | |
| 0 | 0 | 0 | 0 | 0 | 0.0655 | 0.0253 | |
| 0 | 0 | 0 | 0.3504 | 0 | 0 | 0.3504 | |
| 0 | 0 | 0 | 0 | 0.2735 | 0 | 0.2735 | |
| 0 | 0 | 0 | 0 | 0 | 0.3761 | 0.3761 | |
| 0 | 0 | 0 | −1 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 0 | −1 | 0 | 0 | |
| 0 | 0 | 0 | 0 | 0 | −1 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, P.; Chaudhary, K.; Kumar, V.; Chauhan, S. Impact of Goodwill on Consumer Buying through Advertising in a Segmented Market: An Optimal Control Theoretic Approach. Axioms 2023, 12, 223. https://doi.org/10.3390/axioms12020223
Kumar P, Chaudhary K, Kumar V, Chauhan S. Impact of Goodwill on Consumer Buying through Advertising in a Segmented Market: An Optimal Control Theoretic Approach. Axioms. 2023; 12(2):223. https://doi.org/10.3390/axioms12020223
Chicago/Turabian StyleKumar, Pradeep, Kuldeep Chaudhary, Vijay Kumar, and Sudipa Chauhan. 2023. "Impact of Goodwill on Consumer Buying through Advertising in a Segmented Market: An Optimal Control Theoretic Approach" Axioms 12, no. 2: 223. https://doi.org/10.3390/axioms12020223
APA StyleKumar, P., Chaudhary, K., Kumar, V., & Chauhan, S. (2023). Impact of Goodwill on Consumer Buying through Advertising in a Segmented Market: An Optimal Control Theoretic Approach. Axioms, 12(2), 223. https://doi.org/10.3390/axioms12020223







