1. Introduction
Quadratic-phase Fourier transform (QPFT) is a remarkable innovation in the realm of mathematical signal processing that has gained significant attention in recent years. Towards the culmination of the twentieth century, Saitoh et al. [
1] presented a pioneering approach to generalize the classical Fourier transform by incorporating the theory of reproducing kernels in the form of a quadratic function in the exponent of the integral transform. This novel idea paved the way for further studies and applications of the QPFT in various fields, ranging from image processing and quantum mechanics to signal processing and engineering. Inspired by the work of Saitoh and his colleagues, researchers have delved deeper into the potential of the QPFT, exploring its versatility as a tool for solving complex problems. Castro et al. [
2] took the QPFT to new heights by introducing a more general quadratic function in the exponent, allowing for even greater control over the transform and its results. The resulting integral transformation generalizes several well-known signal processing tools, such as Fourier, fractional Fourier, and the much more recent special affine Fourier transforms [
3]. The use of a more general quadratic function in the exponent of the transform allows for greater control over the transform and makes it useful in diverse fields, like image processing, signal processing, quantum mechanics, and so on [
4,
5,
6]. Its ability to handle complex signals with ease and its flexible nature makes it a powerful tool for signal and image processing.
On the flip side, the Hilbert transform is a seminal concept in the field of signal processing that has inspired and revolutionized countless areas of research. This integral transform, named after the renowned mathematician David Hilbert, transforms a real-valued function into a new function of time closely related to the original signal. In other words, the power of the Hilbert transform lies in its ability to extract the analytic signal, which is a complex signal that captures the envelope and instantaneous frequency of a real signal. The analytic signal is particularly useful for analyzing signals that vary in both amplitude and frequency over time, such as audio and biomedical signals [
7,
8]. In addition to its use in signal analysis, the Hilbert transform has also been applied in other areas, such as filtering and demodulation of signals, solving partial differential equations, and even in the analysis of biological signals [
9,
10]. However, a major disadvantage is that its ability to analyze signals is limited to the classical domain and, thus, it cannot represent generalized analytic signals.
The sole aim of this paper was to intertwine the quadratic-phase Fourier transform and the classical Hilbert transform into a new integral transform, coined the quadratic-phase Hilbert transform, making it more robust and able to handle a wider range of signals and functions. This novel integral transform is able to extract more information from signals and provide a more comprehensive representation of the signal in the complex plane. The classical Hilbert transform has limitations when it comes to analyzing non-stationary signals. The quadratic-phase Hilbert transform overcomes this limitation by providing a more general formulation that allows for the analysis of a wider class of signals. The proposed transform can be used to analyze signals with a non-constant frequency, which is not possible with the classical Hilbert transform. The quadratic-phase Hilbert transform can be used in a wider range of applications than traditional transforms, making it a more versatile tool for signal processing. The key points of the article are outlined below:
The introduction of a new integral transform called the quadratic-phase Hilbert transform;
An examination of the fundamental properties of the proposed transform;
The determination of a direct relationship between generalized analytic signals and the quadratic-phase Fourier transform;
An investigation of the Bedrosian theorem related to the quadratic-phase Hilbert transform;
The validation of the results through a representative example.
The rest of the article is organized as follows. In
Section 2, the basic concept of the quadratic-phase Fourier transform and its fundamental properties are reviewed.
Section 3 is completely devoted to formulating the novel Hilbert transform in the context of the quadratic-phase Fourier domain and examining its key features. In
Section 4, we explicitly study the generalized Bedrosian theorem related to the quadratic-phase Hilbert transform. To demonstrate the accuracy of the theoretical findings, simulations are carried out in
Section 5. The article concludes with an epilogue in
Section 6.
2. Quadratic-Phase Fourier Transform
The objective of this section was to familiarize readers with the concept of quadratic-phase Fourier transform. As such, we first present the formal definition of the transform, followed by the Parseval and inversion formulae.
Definition 1
([
6]).
The quadratic-phase Fourier transform, denoted by , of any function with respect to a specific set of parameters , is defined by
where
denotes the kernel of the quadratic-phase Fourier transform and is given by
Definition 1 generalizes several integral transforms ranging from the classical Fourier to the much more recent special affine Fourier transform. Many signal processing operations, such as scaling, shifting, and time reversal, can also be performed via the transformation (
1). Here, we mention the following properties of the quadratic-phase Fourier transform.
- (i).
Introducing the Quadratic-Phase Hilbert Transform with Classical Fourier Transform as a Special Case: For
, the expression (
1) simplifies to the classical Fourier transform
- (ii).
Quadratic-Phase Hilbert Transform Allows Fractional Fourier Transform with Just One Multiplication: If
, then multiplying (
1) by
results in the fractional Fourier transform
- (iii).
Quadratic-Phase Hilbert Transform Unveils a Link to the Linear Canonical Transform: For the specific set of parameters
, multiplying (
1) by
gives the linear canonical transform
- (iv).
Quadratic-Phase Hilbert Transform Reveals the Special Affine Fourier Transform with an Additional Phase Factor: If
, then multiplying (
1) by
yields the special affine Fourier transform
In the following theroem, we assemble some fundamental properties of the quadratic-phase Fourier transform (
1).
Theorem 1.
For any pair of functions and scalars , , the QPFT (1) has the following properties: - (i).
Linearity: ,
- (ii).
Translation: ,
- (iii).
Modulation: ,
- (iv).
Scaling:
- (v).
Parity: ,
- (vi).
Conjugation: .
The inversion formula for the quadratic-phase Fourier transform (
1) is presented in the following theorem.
Theorem 2.
If is the quadratic-phase Fourier transform of any function , then, the following inversion formula holds: Towards the culmination of this section, we recall the orthogonality relation corresponding to the quadratic-phase Fourier transform (
1).
Theorem 3.
For any pair of functions , we have For , the relation (4) yields the energy preserving formula given by It is well established that the convolution and product operations play a crucial role in a variety of areas, including signal and image processing, quantum mechanics, sampling, and filter design [
3]. With this in mind, our next objective was to revisit the novel convolution introduced by Shah et al. [
6] for the quadratic-phase Fourier transform. Our goal was to utilize this novel convolution to establish the convolution theorem for the quadratic-phase Hilbert Fourier transform in a subsequent section.
Definition 2.
For any , the quadratic-phase convolution with respect to the parameter set is defined by 3. Quadratic-Phase Hilbert Transform in
In this section, we delve into the concept of the Hilbert transform within the quadratic-phase Fourier domain. Our main goal was to examine the fundamental properties of this transform, including Parseval’s formula, and then establish important results related to convolution structure in the context of the quadratic-phase Hilbert transform.
Definition 3.
For a given set of real parameters with , the quadratic-phase Hilbert transform of any function is denoted by and is defined as Remark 1.
Definition 3 provides us with additional insight into the concept of quadratic-phase Hilbert transform. More explicitly, we have the following properties of the quadratic-phase Hilbert transform:
(i). For , the quadratic-phase Hilbert transform (7) results in a linear canonical Hilbert transform, expressed as follows: We observe that the linear canonical Hilbert transform (8) is also a generalization of the Hilbert transform, which can handle functions with more complex behavior, such as functions with oscillatory behavior that changes rapidly with time. Additionally, relation (8) is well-suited for the analysis of signals that have undergone linear transformations, such as scaling, rotation, and shearing [
11].
(ii). For the parameter set , the proposed transform (7) reduces to the ordinary fractional Hilbert transform It is evident from (9) that the fractional Hilbert transform is a linear operator that acts on the input function to produce its analytic Hilbert transform . Like the classical Hilbert transform, the fractional Hilbert transform is a singular integral operator, which can be used in a variety of signal processing applications [
12].
(iii). Choosing , Definition 3 yields the classical Hilbert transform given by Next, we study the quadratic-phase Fourier spectrum of the quadratic-phase Hilbert transform.
Theorem 4.
If is the quadratic-phase Hilbert transform of a signal f, then, the quadratic-phase Fourier transform of is given by Proof. Invoking the definition of quadratic-phase Fourier transform, we have
Then, quadratic-phase Hilbert transform can be recast as:
Plugging the estimate (
12) in (
11), we obtain
By virtue of the traditional Hilbert transform, we have
Implementing (
14) in (
13) yields
This completes the proof of Theorem 4. □
Next, we present a theorem that outlines key features of the quadratic-phase Hilbert transform, as described in Equation (
7).
Theorem 5.
For a pair of functions and the scalars , the quadratic-phase Hilbert transform defined in (7) has the following properties: - (i).
;
- (ii).
;
- (iii).
;
- (iv).
.
Proof.
(i) Invoking the definition of quadratic-phase Fourier transform, we have
By virtue of Theorem 4 and (
15), we obtain
(ii) Invoking Theorem 4, we observe that
The application of Definition 1 yields
Plugging (
17) in (
16), we obtain
By virtue of Theorem 4, we obtain
(iv) By straightforward computations, it is easy to show that
This completes the proof of Theorem 5. □
Next, we obtain the Parseval theorem for the quadratic-phase Hilbert transform.
Theorem 6.
For any , the following orthogonality relation holds: Proof. For the sake of brevity, we only provide the proof of relation (
19). The proof of relation (
20) follows in a similar manner.
This completes the proof of Theorem 6. □
The analytic signal is a way of representing a real-valued function by combining the original function and its Hilbert transform. One of the key benefits of this representation is that it retains all the information of the real signal but eliminates negative frequency components in the Fourier domain, making it a useful tool in various fields of science and engineering. The analytic version of a real signal when using the generalized Hilbert transform in the quadratic-phase Fourier domain can be defined as follows:
The theorem below provides a significant expression of the generalized analytic signals defined in Equation (
21). Specifically, it presents a straightforward connection between the generalized analytic signal and the quadratic-phase Fourier transform, which can be used to directly derive the generalized analytic signal from the quadratic-phase Fourier domain.
Theorem 7.
If is the quadratic-phase Fourier transform of a signal and the generalized analytic signal associated with the quadratic-phase Fourier transform, then, has the representation: Proof. By virtue of the Fubini theorem, we have
Plugging (
24) in (
23) yields
This completes the proof of Theorem 7. □
Theorem 8.
Assume that is the generalized analytic function in the quadratic-phase Fourier domain, then we have Proof. Invoking the linearity property of the quadratic-phase Fourier transform (
1), we obtain
Application of Theorem 4 yields
This completes the proof of Theorem 8. □
The convolution theorem associated with the quadratic-phase Hilbert transform is investigated in the following theorem.
Theorem 9.
Let be the quadratic-phase convolution operation operation with respect to a parametric set given by (6) and denote the quadratic-phase Hilbert transform of any square integrable functions f and g, respectively. Then, we have Proof. To prove the desired result, we proceed as:
The proof of relation (
28) follows in the similar manner.
This completes the proof of Theorem 9. □
4. Bedrosian Theorem Associated with the Quadratic-Phase Hilbert Transform
The Bedrosian Theorem has long been considered a crucial tool for analyzing the analytic part of signals in the realm of engineering [
13]. It states that if the Fourier transform of one function vanishes for frequencies greater than a certain value
a, and the Fourier transform of another function vanishes for frequencies lower than
a, then the Hilbert transform of the product of these two functions can be expressed as the original function multiplied by the Hilbert transform of the other. In this section, we aimed to delve into the Bedrosian Theorem as it pertains to the quadratic-phase Fourier transform, first presenting some foundational results to be used in the analysis.
Lemma 1.
If is the quadratic-phase Hilbert transform of any function with respect to the parametric set and is the kernel of the inverse quadratic-phase Fourier transform, then, the following relation holds: Proof. By virtue of the definition of quadratic-phase Hilbert transform given by Definition 3, we have
This completes the proof of Lemma 1. □
Lemma 2.
Assume is the quadratic-phase Hilbert transform of any function with respect to the parametric set and is the kernel of the inverse quadratic-phase Fourier transform. Then, we have Proof. Invoking the definition of quadratic-phase Hilbert transform yields
This completes the proof of Lemma 2. □
We are now in a position to study the Bedrosian theorem associated with the quadratic-phase Hilbert transform.
Theorem 10.
Let and be the quadratic-phase Fourier transform of two complex functions and , respectively. Let vanish for and vanish for . Then, we have where .
Proof.
Invoking the inverse quadratic-phase Fourier transform given by (3), we obtain
This completes the proof of Theorem 10. □
5. Simulations
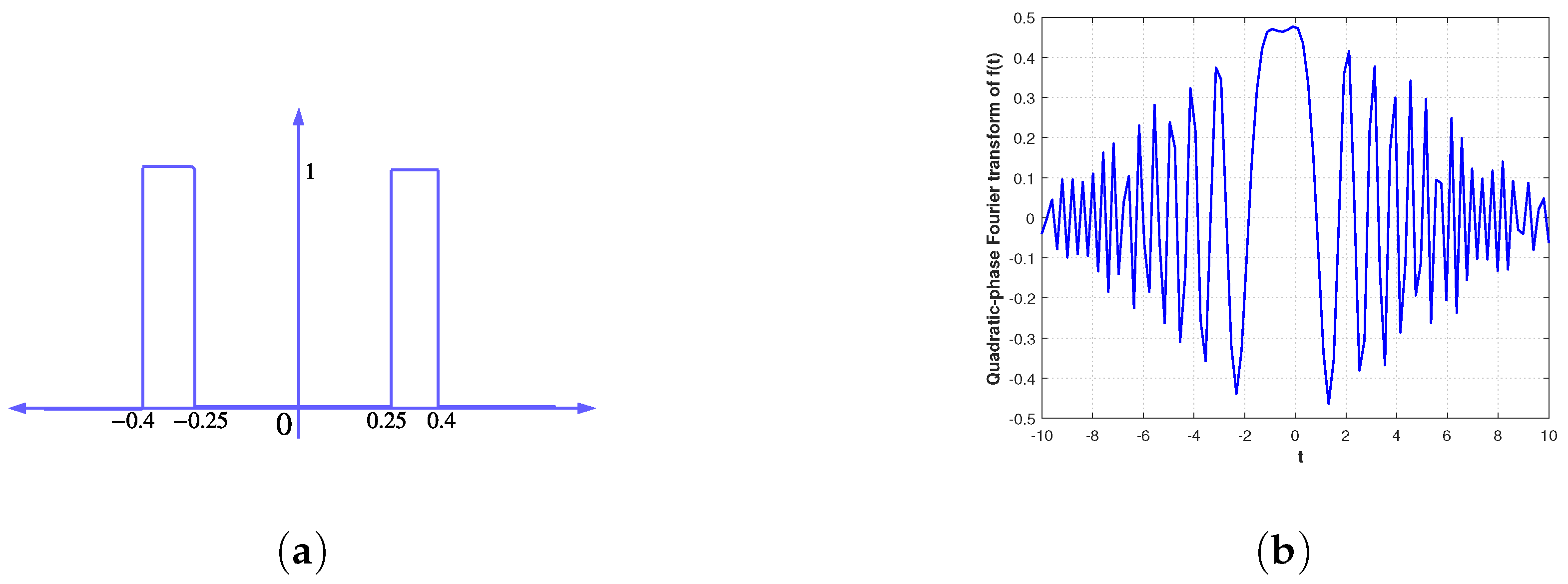
In this section, we illustrate the importance and correctness of the obtained results via a lucid example. To meet our endeavor, we considered the signal
given by
having compact support
, as shown in
Figure 1a. The quadratic-phase Fourier transform of
with respect to the set
could be computed as:
The representation of
in the Quadratic-Phase Fourier Transform (QPFT) domain, as given by Equation (
32), is illustrated in
Figure 1b. The utilization of this type of quadratic-phase with specific parameters is commonly observed in various scientific and engineering fields, such as scalar optical diffraction, digital holography, atomic interferometry, sampling, and filtering, among others [
4,
5]. In
Figure 2a, the QPFT of the Hilbert transform of
is shown, where the quadratic-phase parameters were
. By implementing Theorem 7, the generalized analytic signal of
is depicted in
Figure 2b. It is apparent from the figure that the generalized analytic signal in the QPFT domain contained no negative frequency components, which validated the accuracy of the previously established theoretical results. Furthermore, these results held potential for a range of applications, such as the reconstruction of a signal from its generalized analytic form.
6. Conclusions
In the present article, we introduced the notion of novel integral transformations by intertwining the merits of quadratic-phase Fourier and Hilbert transforms, providing a more comprehensive and efficient tool for signal processing. Firstly, we studied all the necessary properties of the proposed transform and, then, investigated a direct relationship between the generalized analytic signals and the quadratic-phase Fourier transform. Additionally, several results for the kernel function of the inverse quadratic-phase Fourier transform associated with the generalized Hilbert transform were investigated. The generalized Bedrosian theorem associated with the proposed transform was also studied in detail. Finally, to validate the obtained results, simulation results were proposed. The results showed that the methods presented in this paper were correct and effective. The obtained results were of substantial importance and serve as a heuristic entity for the mathematical and signal-processing communities. Future research shall be done in this direction, exploring the real-world applications of the theoretical results.
Author Contributions
Writing original draft preparation, H.M.S. and H.L.Q.; Conceptualization, methodology, F.A.S.; Software and editing, W.Z.L.; Methodology and software, W.Z.L. and M.S.G.; Funding acquisition and research support, H.M.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used to support the findings of this study are included within the article.
Acknowledgments
The authors are deeply indebted to the anonymous referees for meticulously reading the manuscript, pointing out many inaccuracies, and giving several valuable suggestions to improve the initial version of the manuscript to the present stage.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Saitoh, S. Theory of reproducing kernels: Applications to approximate solutions of bounded linear operator functions on Hilbert spaces. Am. Math. Soc. Trans. Ser. 2010, 230, 107–134. [Google Scholar]
- Castro, L.P.; Minh, L.T.; Tuan, N.M. New convolutions for quadratic-phase Fourier integral operators and their applications. Mediterr. J. Math. 2018, 15, 1–17. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Shah, F.A.; Lone, W.Z. Quadratic-phase wave-packet transform in L2(R). Symmetry 2022, 14, 2018. [Google Scholar] [CrossRef]
- Castro, L.P.; Haque, M.R.; Murshed, M.M.; Saitoh, S.; Tuan, N.M. Quadratic Fourier transforms. Ann. Funct. Anal. 2014, 5, 10–23. [Google Scholar] [CrossRef]
- Kumar, M.; Pradhan, T. Quadratic-phase Fourier transform of tempered distributions and pseudo-differential operators. Integral Transform. Spec. Funct. 2022, 33, 449–465. [Google Scholar] [CrossRef]
- Lone, W.Z.; Shah, F.A. Shift-invariant spaces and dynamical sampling in quadratic-phase Fourier domains. Optik 2022, 260, 169063. [Google Scholar] [CrossRef]
- Sun, S.; Jiang, Z.; Wang, H.; Fang, Y. Automatic moment segmentation and peak detection analysis of heart sound pattern via shorttime modified Hilbert transform. Comput. Methods Programs Biomed. 2014, 114, 219–230. [Google Scholar] [CrossRef]
- Scutaru, M.L.; Vlase, S.; Marin, M.; Modrea, A. New analytical method based on dynamic response of planar mechanical elastic systems. Bound. Value Probl. 2022, 2022, 1–16. [Google Scholar] [CrossRef]
- Xu, S.; Feng, L.; Chai, Y.; Hu, Y.; Huang, L. The properties of generalized offset linear canonical Hilbert transform and its applications. Int. Wavelets Multiresolution Inf. 2017, 15, 1750031. [Google Scholar] [CrossRef]
- Deb, S.; Choudhury, N.R.; Ghosh, R.; Chatterjee, B.; Dalai, S. Short time modified Hilbert transform-aided sparse representation for sensing of overhead line insulator contamination. IEEE Sens. J. 2018, 18, 8125–8132. [Google Scholar] [CrossRef]
- Zhang, Y.N.; Li, B.Z. ϕ-linear canonical analytic signals. Signal Process. 2018, 143, 181–190. [Google Scholar] [CrossRef]
- Venkitaraman, A.; Seelamantula, C.S. Fractional Hilbert transform extensions and associated analytic signal construction. Signal Process. 2014, 94, 359–372. [Google Scholar] [CrossRef]
- Abe, S.; Sheridan, J.T. Optical operations on wave functions as the Abelian subgroups of the special affine Fourier transformation. Opt. Lett. 1994, 19, 1801. [Google Scholar] [CrossRef]
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).